Activity motifs reveal principles of timing in transcriptional control of the yeast metabolic network

Abstract

Significant insight about biological networks arises from the study of network motifs—overly abundant network subgraphs^1,2—but such wiring patterns do not specify when and how potential routes within a cellular network are used. To address this limitation, we introduce activity motifs, which capture patterns in the dynamic use of a network. Using this framework to analyze transcription in Saccharomyces cerevisiae metabolism, we find that cells use different timing activity motifs to optimize transcription timing in response to changing conditions: forward activation to produce metabolic compounds efficiently, backward shutoff to rapidly stop production of a detrimental product and synchronized activation for co-production of metabolites required for the same reaction. Measuring protein abundance over a time course reveals that mRNA timing motifs also occur at the protein level. Timing motifs significantly overlap with binding activity motifs, where genes in a linear chain have ordered binding affinity to a transcription factor, suggesting a mechanism for ordered transcription. Finely timed transcriptional regulation is therefore abundant in yeast metabolism, optimizing the organism’s adaptation to new environmental conditions.

Cellular processes are mediated through intricate networks of interacting molecules, whose local^1–3 and global^4,5 topology has been intensively studied. Analysis of network wiring patterns has revealed network motifs—local sets of interaction patterns that occur significantly more often than expected by chance and potentially reflect the functionality of the complex network. However, whereas such network motifs correspond to the static wiring of the network, networks are used dynamically and adapt to external conditions and internal states in functionally distinct ways.

Such dynamic activity is particularly important in metabolic processes, which are tightly controlled based on the cell’s environment. Upon a change in environmental conditions, a cell may have to rapidly reconfigure its metabolism to produce or degrade compounds to ensure its survival in the new environment. Fluxes through metabolic reactions are controlled by enzymes, the activities and abundances of which are further controlled by post-transcriptional mechanisms. Furthermore, protein abundance is partly determined by transcriptional control⁶, which modifies the mRNA level of the gene through binding of transcription factors. This complex hierarchy of regulatory mechanisms raises questions about the individual roles and interplay between the different regulation layers. For instance, is transcription regulation tuned to fit the usage patterns of enzymes in the metabolic network? Recent work argues for the predominance of hierarchical control in the metabolic network^7,8. Yet the metabolic network exhibits significant changes in transcript levels in response to environmental perturbations, suggesting the use of transcriptional control. Moreover, recent work on transcriptional control of metabolism identified cases of finer-grained patterns of co-regulation in S. cerevisiae^9,10. In one specific example in Escherichia coli, the genes in a linear pathway for amino acid biosynthesis were reported to show sequential transcriptional activation (“just-in-time” transcription)¹¹.

We developed an analysis framework based on the notion of an activity motif (Fig. 1a) to systematically study the dynamical behavior of such networks. Given a particular network structure (e.g., a linear cascade of enzymes; Fig. 1b), an activity motif describes a specific pattern of functional data, such as ordered timing of activation of the corresponding genes (Fig. 1c(i)). Unlike network motifs, which reflect the static wiring of the network (analogous to routes in a road map)^1,12, activity motifs reflect dynamic and functional patterns associated with their use (analogous to traffic patterns that emerge before, during and after rush hour). Activity motifs can be identified by assessing the enrichment of activity patterns given the network wiring structure.

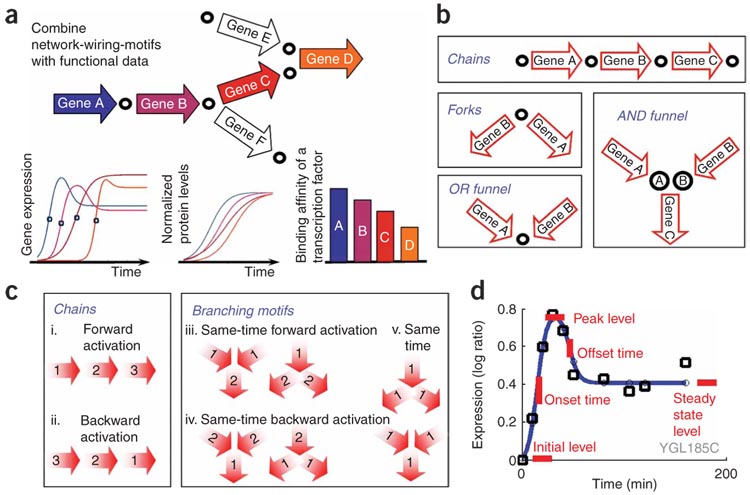
Figure 1. Activity motifs overlay functional data over known network wiring structure.

(a) A fragment of a network (top), whose edges and nodes are annotated with functional data (bottom). In this example, the nodes correspond to metabolites and the edges correspond to genes (A,B,C,D). Each edge (gene) is annotated by the time of expression activation in a particular time course (bottom left), by protein abundance (bottom middle) and by the binding affinity to a specific transcription factor (bottom right). (b) Wiring patterns in a metabolic network— chains, forks and two types of funnels— correspond to the four possible relations between a pair of adjacent reactions in the metabolic network and reflect different dependencies between them: chemical coupling (chains), competition over a common substrate (forks), production of the same compound (OR funnel) and production of cooperating substrates (AND funnel). (c) Examples of activity motifs over enzyme triplets. Order of activity is denoted for each enzyme, yielding forward (i) and backward (ii) orders in chains, as well as combinations of ordered and same-time activation in branched pathways (iii–v). (d) Our impulse response model for an mRNA expression time course interpolates a continuous curve (blue line) to fit a set of measurements (black squares). The model allows for two transitions of expression levels (in this example, first up and then down). The impulse model has six parameters: onset and offset times; initial, peak and steady state level; and slope. The values of these parameters are optimized to fit the measured expression time course of a single gene.

We applied the framework of activity motifs to study the dynamics of regulation of gene expression in the metabolic network in S. cerevisiae. Using our systematic analysis, we identified abundant activity motifs involving timed gene expression regulation, recurring in different forms across many conditions. We demonstrate that the same timing behavior can be conserved in the dynamics of protein abundance, suggesting that timing patterns in mRNA expression can have a direct effect on the timing of metabolic processes. Finally, by studying activity motifs in transcription factor binding affinity, we show that evolution of quantitative transcription factor binding affinities provides a mechanism that can underlie some of this fine-grained control of transcription timing. Overall, the activity motif framework allows us to systematically investigate three levels of regulation in the metabolic network. Our findings suggest that cells have evolved to tune the timing of transcription regulation to better respond to their changing environment.

RESULTS

To identify activity motifs in the transcriptional control of yeast metabolism, we used a four-step approach (Fig. 1), which (i) defines wiring patterns; (ii) specifies, for each wiring pattern, a set of activity patterns involving onsets of transcriptional responses; (iii) extracts transcription timing properties from expression profiles and maps them to the metabolic network’s wiring to identify which activity motifs occur in a particular biological condition; and (iv) compares the transcriptional activity motifs to patterns of transcription factor binding and protein abundance.

We defined a set of wiring motifs using a hand-curated model of the S. cerevisiae metabolic network¹³, comprising 1,181 reactions catalyzed by 598 enzymes. Each motif is a small graph of different topology composed of four basic relationships: chains, forks and two types of funnels (Fig. 1b). The set included 12 patterns, covering all possible local network patterns among enzyme pairs and triplets in the metabolic graph, and extensions to longer chains (Supplementary Table 1 online).

Timing activity motifs in yeast metabolism

We focused on patterns in the transcriptional response of metabolic genes after a sudden change in environmental or nutritional conditions. The response in such experiments often follows a characteristic ‘impulse’ trajectory: an early dramatic ‘onset’ to a transient level, followed by a later ‘offset’ to a new steady state (Fig. 1a,d).We focused here on patterns involving onsets, as these measure a timing property that is relatively invariant to other factors, such as transcription rate or target protein levels.

We specified a set of possible activity motif types for each wiring pattern (Fig. 1c and Supplementary Table 1), each being a specific temporal order of the response onset times of the associated enzymes. For example, for a wiring pattern representing a chain of enzymes (e.g., A→B→C in the network), the forward-activation motif type specifies that the enzymes’ expression is induced in the same order in which they are used in the pathway (A’s onset precedes B’s onset precedes C’s onset; Fig. 1a, bottom left and Fig. 1c(i)). Overall, we enumerated all timing activity motifs (TAMs) that have a consistent ordering (either forward, backward or ‘same time’) for the enzymes in a wiring pattern, resulting in 64 types of activity motifs (Supplementary Table 1).

To identify occurrences of these TAMs, we analyzed experimental data to assign onset activation times for each metabolic gene. We used expression profiles from 76 time-course experiments in yeast (Supplementary Table 2 online). Of these, 63 were previously published and 13 are new time courses intended to broaden the range of environmental perturbations. Each experiment collected data at 5–11 time points measured after a sudden change in environmental or nutritional conditions. Inferring onset times from such time-course experiments is a challenge¹⁴. Based on our observation regarding the typical ‘impulse’ trajectory of the transcriptional response, we devised an impulse response model¹⁵, which captures each gene’s expression profile in terms of six biologically meaningful parameters: onset and offset response times; initial, transient and steady expression levels; and response slope (Fig. 1c and Supplementary Fig. 1 online). The impulse model is fit separately for each gene and provides a very good overall fit (Supplementary Fig. 1). Using the impulse model, we extracted the response onset time for each gene in each condition. Importantly, the timing information that we extract is much more robust to noise than the raw measurements.

We then overlaid these timing data onto the network structure, and identified the occurrences of each TAM in each condition. For example, if, in a particular condition, the enzymes in the chain A→B→C are activated at 5, 10, 20 min, respectively, this chain was labeled as an occurrence of the forward-activation TAM. To further ensure the validity of these motifs, we extract only timing relationships that are robust to the perturbation of the mRNA expression data with noise.

Following previous work on network motifs^1,12, we next aimed to uncover the principles of the organism’s transcriptional response by identifying motif types that occur significantly more often than would be expected by chance. In each condition, we counted the number of occurrences of each type of TAM and compared it to the distribution of such occurrences in activity-randomized networks. This scheme randomly shuffles the assignment of expression profiles to enzymes without changing the network wiring, thus identifying activity profiles that are enriched given the wiring diagram, rather than enriched patterns in the wiring diagram itself.

We found several types of TAMs that are significantly enriched in the yeast metabolic network across multiple conditions (Fig. 1c, Fig 2 and Supplementary Table 3 online). The most frequently enriched TAM was forward-activation, in which enzymes in a metabolic chain are induced in the same order they are used in the pathway (Fig. 1c(i)). This ‘just-in-time transcription’ pattern (also observed in unbranched pathways of amino acid biosynthesis in E. coli¹¹) achieves efficient use of transcriptional resources. Forward activation in three-enzyme chains was significantly enriched (P < 0.01) in ten diverse conditions, including heat shock (268 occurrences found in three-enzyme chains; only 56 expected at random, P = 3.8 × 10⁻⁵, Fig. 2a,d) and short-term anaerobiosis¹⁶ (135 occurrences versus 19 expected at random, P < 10⁻⁴). The complementary forward-shutoff TAM (Fig. 2b), where enzymes in a linear chain are repressed in the same order they are used in the pathway, was enriched upon a temperature shift¹⁷ from 37 °C to 25 °C (144 occurrences in three-enzyme chains, 48 expected at random, P = 0.01) and nitrogen depletion¹⁷ (9 found, 0.2 expected at random, P = 0.0087). This pattern may represent an efficient way of achieving a parsimonious shutoff that gradually concludes the use of metabolic intermediates. More surprising is the backward-activation motif (Fig. 1c(ii)), where the timing of activation of enzymes in the linear chain propagates backwards in the pathway. This pattern was enriched in several conditions (Fig. 2e), including shifts from a fermentable to a non-fermentable carbon source for three-enzyme chains (ethanol: 74 occurrences, 0.5 expected at random, P = 2 × 10⁻⁴ and 139 occurrences, 0.6 expected, P < 10⁻⁵; galactose¹⁶ 58 occurrences, 0.5 expected, P = 0.0044 and 105 occurrences, 23 expected, P = 0.0028). In some cases, this TAM may serve for the fast removal of an end metabolite that is either toxic or otherwise disruptive under the new condition (see below).

Figure 2. Timing activity motifs across conditions.

(a–b) Enrichment of activity motifs relative to a random permutation model. A blue arrow denotes the pattern count in the original network and a red histogram denotes the distribution of pattern counts in networks with randomized expression profiles. Each histogram was obtained from 10,000 randomizations of expression profiles across the network (keeping the network wiring fixed), followed by counting the number of activity motifs observed in the randomized networks. (a) Enrichment of forward activation in heat shock¹⁷: 268 timed motifs observed in the real data compared to 56 expected at random (P = 3.12 × 10⁻⁵). (b) Enrichment of forward shutoff in de-heating: 144 timed motifs observed in the real data compared to 48 expected at random (P < 0.01). (c) Distribution of activity motifs across conditions. Each row in the histogram shows the relative prevalence of four types of activity motif in a single condition (time course). The length of each bar corresponds to the number of occurrences of an activity motif in that condition. Rows are grouped and sorted by the similarity of the experimental conditions. (d) Enrichment of forward activation across all conditions. Abscissa shows an all-condition enrichment score of the motif (arrow) compared to the distribution of scores in activity-shuffled networks. (e) Enrichment of backward activation across all conditions as in d.

Other significantly enriched TAMs are found at branching points. The funnel-same-time triplet (Fig. 1c(v)) is a motif over a wiring pattern with two enzymes that produce complementary metabolites that are both used by a third reaction; this TAM was enriched under exposure to a DNA damaging agent¹⁸ (344 occurrences, 137 expected, P = 0.02) and to 1M KCL (in both wild-type yeasts 276 occurrences, 78 expected at random, P = 0.0151; and an ssk1-ste11 double-deletion strain, 330 occurrences, 65 expected, P = 0.0002). A similar motif is fork-same-time triplet, involving one enzyme producing two metabolites then consumed by two separate reactions that are activated at the same time; this TAM was also enriched under exposure to a DNA damaging agent¹⁸ (412 occurrences, 126 expected at random, P = 0.002). Both TAMs optimize metabolite use by coordinating the production or consumption of metabolites along co-dependent branches. Consistent with previous results^9,10, there is no enrichment for same-time activation in a pair fork motif where the two reactions both consume the same metabolite. A full list of motif enrichment across conditions is given in Supplementary Table 3.

Activity motifs in the pentose phosphate and glycerol pathways

To further study the specific function of TAMs in yeast metabolism, we annotated the complete metabolic graph, in each condition, with the individual occurrences of TAMs from significant types. We note that individual TAM occurrences must be interpreted with caution, as ordered activation could occur by chance, especially because of the large number of wiring network motifs tested (the multiple hypotheses testing problem).

Nevertheless, studying individual motif occurrences provides insight into the role that TAMs can play in fine-tuning the response of the metabolic network. For example, we found a forward-activation motif from glucose to ribulose 5-phosphate production covering the oxidative branch of the pentose phosphate pathway (PPP, Fig. 3a) in multiple conditions, including treatment with diamide, menadione, 1 M sorbitol, amino acid starvation and heat shock (Fig. 3 and Supplementary Fig. 2 online). The time scales of the observed timing motifs varied from a few minutes (heat shock, diamide) to hours (amino acid starvation), consistent with the time scale of the corresponding response. This forward-activation pattern is consistent with the recent observation of redirection of flux from glycolysis to the PPP under oxidative stress—a phenomenon conserved from S. cerevisiae to C. elegans^19,20. Such redirection (and corresponding forward activation) provides reducing power, essential under stress. Consistently, the immediate enzymes of the nonoxidative branch of the PPP (Rpe1, Rki1) are repressed, on the same time scale as the forward-activation TAM. Although previous studies highlighted the role of gluconeogenic flux from lower glycolysis in this response¹⁹, our observed motifs suggest additional flux from glucose, which may indicate the devotion of major energetic resources to increasing reductive power. Notably, in heat shock (Fig. 3b), we observe a second coordinated forward-activation TAM from the gluconeogenic enzyme Fbp1 toward the PPP (accompanied by concomitant repression of the glycolytic counterparts Pfk1 and Pfk2). Thus, upon heat shock, flux through both the upper part of glycolysis and the lower part of gluconeogenesis may contribute to increased PPP flux (Fig. 3b). Finally, we also observe backward activation (in acid and alkali treatments, Supplementary Fig. 2) and forward shutoff (in the de-heating experiment) of the relevant fragment of the pentose phosphate pathway. Backward activation may indicate an immediate need for the change in reducing power, whereas forward shutoff is the result of simple reversal of the heat shock response. Thus, we see that the same region of the metabolic network can exhibit different activity patterns in different conditions that are functionally relevant to the pathways in that region.

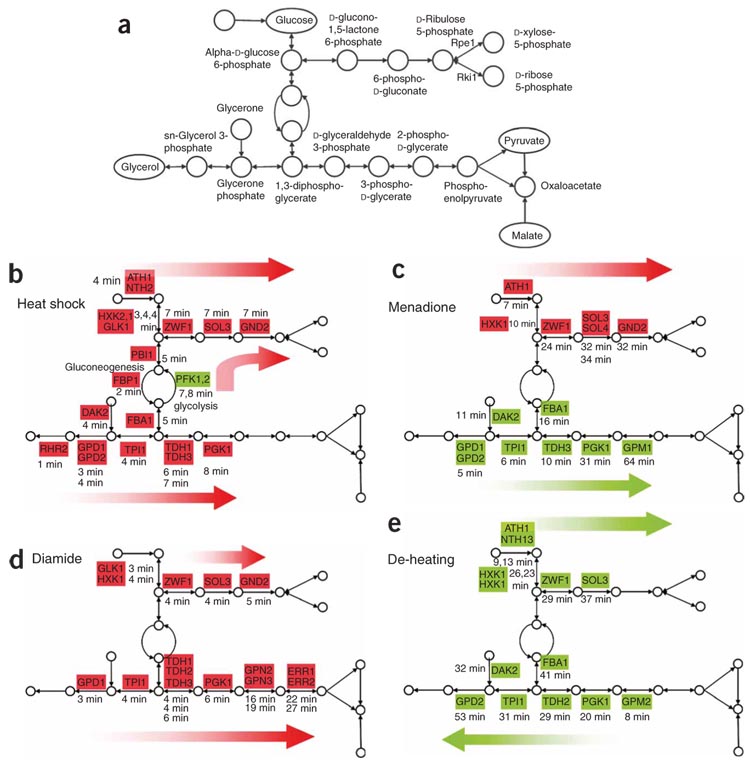
Figure 3. Multiple activity motifs overlay the pentose phosphate pathway and glycerol biosynthesis.

(a–e) Shown are the PPP and glycerol synthesis pathway (GSP) (a), along with activity motifs identified in four different conditions (b–e). Names in rectangles denote catalyzing enzyme; red denotes activation, green denotes repression; values denote the time of activation or repression onset. (b) Forward activation of the PPP and backward activation and funnel-same-time-activation of the GSP in response to a heat shock. (c) Forward-activation of PPP and backward-shutoff of GSP in response to menadione. (d) Forward activation of PPP and backward activation of GSP in response to diamide. (e) Forward shutoff and funnel-same-time forward shutoff in response to de-heating.

Interesting activity patterns can also occur across extended regions composed of multiple connected TAMs. This behavior is illustrated in the glycerol synthesis pathway (Fig. 3a), where we find multiple occurrences of significant motif types across four different conditions (Fig. 3b–d). (i) Upon exposure to diamide, cells increase the production of glycerol to reduce protein denaturation caused by oxidation of sulfhydryl groups. Correspondingly, enzymes directly involved in glycerol production follow a backward-activation motif (Fig. 3d) along six reactions, allowing a rapid build-up of glycerol based on existing reserves of the necessary substrates (2-phospho-d-glycerate and 3-phospho-d-glycerate in this case). (ii) Upon induction of heat shock, the pathway also shows backward activation along four reactions (Fig. 3b, bottom), again permitting for rapid reduction in protein denaturation. Furthermore, the two branches leading to glycerol production are coordinated in a funnel-same-time-activation motif. Interestingly, four upstream reactions that produce necessary compounds for glycerol production are also activated, but this time following a forward-activation pattern (Fig. 3b, top). (iii) Upon a temperature shift from 37 °C to 25 °C, transcription of enzymes is slowly repressed, again in a forward order, to gradually reduce glycerol levels and allow protein renaturation (a forward-shutoff motif, Fig. 3e). (iv) Upon exposure to menadione, glycerol production is also repressed, as both menadione and glycerol increase oxidative stress²¹. In this case, however, glycerol shutoff must occur rapidly—and hence the enzyme that catalyzes the direct production of glycerol is the first to be repressed, and repression then linearly propagates backwards along five reactions (a backward-shutoff motif, Fig. 3c).

Our interpretation of the TAMs in the glycerol pathway suggests a gluconeogenic flux for glycerol production under stress, in contrast to the known glycolytic source during growth on glucose (without stress). This interpretation is supported by the differential expression of glycolytic and gluconeogenic enzymes in the corresponding conditions. For example, in diamide treatment (forward activation of glycerol), glycolytic enzymes (Pfk1, Pfk2, Pgi1) are repressed, whereas gluconeogenesis enzymes (Pyc1, Mdh3) are induced. Similarly, in heat shock (backward activation of glycerol) all gluconeogenic enzymes (Fbp1, Mdh2, Mdh3, Pyc1, Pyc2, Pck1) are induced and upper glycolysis enzymes (Pfk1, Pfk2) are repressed. Furthermore, independent experiments show that upon exposure to high osmotic pressure, when glycerol production is essential for cell survival, glycolytic enzymes are typically repressed and gluconeogenesis enzymes are induced, regardless of the osmolyte accumulated (data not shown). This suggests that gluconeogenic flux may be a source of glycerol production under stress. Interestingly, repression of glycerol production in de-heating (forward shutoff) and menadione treatment (backward shutoff) is consistent with repression of flux through both upper glycolysis and gluconeogenesis.

Functional characterization of activity motifs

The specific instances of enriched TAMs are not randomly distributed across the metabolic network, but rather tend to aggregate within particular regions in a single condition, achieving orchestrated regulation of multiple pathways into a coherent physiological response. Notably, the overwhelming majority of TAMs (1,867 of 1,908 motifs in chains of three enzymes) and the enzymes associated with them (179 of 232 enzymes, P < 10⁻¹³, hypergeomtric test) reside within central carbon metabolism and its immediate periphery (Fig. 4a, Supplementary Fig. 3 and Supplementary Tables 4 and 5 online). This is not a mere effect of network topology as all types of wiring motifs can be found both within and outside central carbon metabolism, with comparable magnitude (e.g., 170 three-enzyme chains all inside central carbon metabolism and periphery, compared to 393 three-enzyme chains that are completely outside). This phenomenon extends across a wide range of conditions, including not only changes in carbon source but also environmental stresses and other nutritional changes. This finding suggests that central carbon metabolism is a key metabolic target for finely tuned temporal regulation of gene expression in S. cerevisiae. In contrast to prior work involving E. coli¹¹, we did not find similar fine-grained timing motifs in the amino-acid metabolism pathways. This may be a consequence of differences between organisms, and is consistent with the lack of ‘just-in-time’ patterns in a recent experiment measuring protein abundance time courses in amino acid metabolic enzymes in S. cerevisiae²².

Figure 4. Functional characterization of activity motifs.

(a) The overwhelming majority of the reactions and enzymes associated with at least one activity motif are within central carbon metabolism (CCM) or one reaction away (CCM+1). The 345 CCM+1 enzymes (57% of 598 total enzymes) intersect with 1,867 of 1,908 three-enzyme chain motifs. Furthermore, 179 (77%) of the 232 enzymes associated with activity motifs are in CCM+1 (hypergeometric, P < 10⁻¹⁵). (b) Metabolic flexibility of timed enzymes²³. Flexibility is defined as the range of flux values that are consistent with optimal growth in a flux-balance analysis for the yeast metabolic network²⁴. Shown is the distribution of number of conditions in which an enzyme is associated with an activity motif for low- (orange, top) and high- (blue, bottom) flexibility enzymes²³ in CCM+1, indicating that enzymes associated with activity motifs are much more flexible than other CCM+1 genes (t-test, n = 75, P < 10⁻¹⁵). Arrows denote the mean of each distribution; short error bars denote the s.e.m. and long bars the s.d. of each distribution. The flexibility of an enzyme was also strongly correlated with the number of conditions in which it participated in activity motifs (Spearman correlation for metabolic genes P < 10⁻⁵⁶, for CCM+1 genes P < 10⁻¹⁴). (c) Distribution of evolutionary volatility²⁵, defined based on the number of duplication and loss events. The volatility of timed genes is compared to other genes in CCM+1. The background distribution of volatility for all CCM+1 transporters and enzymes, as approximated by a Gamma distribution, is shown in gray. Red bars denote volatility values that are significantly different from the background distribution (P < 0.01, tail of the Gamma distribution). These timed enzymes are more evolutionary volatile than expected, suggesting that timed enzymes are more strongly tuned during evolution.

We also found that the extent to which an enzyme participates in TAMs is strongly correlated (Spearman correlation, P < 10⁻¹⁴; Fig. 4b) with the ‘metabolic flexibility’ of the reaction it catalyzes²³, as defined by the range of flux values consistent with optimal growth in a flux-balance analysis model²⁴ (Fig. 4b). This observation suggests a model where reactions that admit a broad range of flux values require finer-grained transcriptional control. In addition, many of the enzymes associated with significant TAMs also exhibited greater evolutionary volatility²⁵, sustaining a significantly (P < 0.01) higher number of duplication and loss events compared to other metabolic enzymes (Fig. 4c). This correlation may reflect a need to tune these key genes to evolutionary niches. Such mechanisms may be particularly critical within central carbon metabolism, which coordinates many of the most essential aspects of yeast metabolism. Nonetheless, timed enzymes are enriched for these properties even more than other enzymes of central carbon metabolism.

Binding activity motifs

Which mechanisms could underlie the extensive ordered timing of transcription control? On the conceptual level, timed control patterns could be the result of an interactive feedback, where levels of individual metabolites are continuously monitored and affect the transcription of each enzyme; or, they can arise from a ‘pre-programmed’ response, where the system executes pre-defined timed control patterns. One mechanism for achieving the latter is by having differences in the affinity of a common transcription factor for the promoters of various genes in the pathway, resulting in different transcription onsets. Such a mechanism has been reported in the flagella pathway²⁶ and the SOS response²⁷ in E. coli. Other recent work also supports the functional relevance of transcription factor binding site affinity^28–31. The continuous values obtained by chromatin immunoprecipitation (ChIP-chip) assays can be interpreted as quantitative transcription factor binding affinities and have biological significance throughout a broad range of binding P-values²⁸.

To systematically test for the presence of an affinity-based mechanism, we applied our activity motif framework in a different manner. Here, we mapped transcription factor binding affinities (rather than onset times) onto the network wiring. We used genome-wide ChIP-chip^32,33 for multiple transcription factors across several conditions, focusing on 48 pairs of experiments where transcription factor binding and gene expression were measured in comparable conditions (12 pairs in heat shock, 34 pairs in adenine starvation, 2 pairs in acid exposure, Supplementary Table 6 online). We restricted attention to the set of genes bound by a transcription factor with a P-value smaller than 0.5, and used the binding P-values to define binding activity motifs (BAMs): linear chains of enzymes whose genes exhibited patterns of ordered affinity for that transcription factor (Fig. 1a). We then used the same permutation test above to measure whether the set of three-enzyme chain forward-activation TAMs (within the bound genes) were enriched for ordered binding. Importantly, the permutation test corrects for any artifacts that may arise from overlap between different motifs. In 20/48 of the binding-expression pairs, we find significant overlap (at a false discovery rate (FDR) of q = 0.05) between forward-activation TAMs and BAMs (overall P < 1.9 × 10⁻¹⁴). The partial correspondence between TAMs and BAMs could be due to several factors: the fact that mRNA levels reflect a balance of transcription and mRNA degradation; possible epistasis between transcription factors; or lack of binding measurements of relevant transcription factors. Overall, our finding suggests that a fine-grained tuning of transcription factor binding affinities may play a significant role in the temporal regulation of metabolic transcription.

Protein timing activity motifs

A key question regarding the biological significance of our results is the extent to which patterns that are observed in mRNA profiles are indicative of activity levels of the corresponding enzymes, which execute the metabolic reactions. The levels of active enzymes are only partially determined by mRNA levels, with multiple levels of subsequent regulatory control, including translational efficiency and protein activation. In general, although there is a high general correlation between mRNA levels and active enzymes³⁴, there is also significant intergene variation, with some genes exhibiting much lower correlations³⁴. Moreover, protein half-life can also affect the relation between changes in mRNA levels and protein levels⁶. Importantly, however, our motifs are based not on mRNA levels, but rather on transition times in the mRNA profiles, a quantity that is more likely to be robust to variation in the downstream efficiency of protein creation and stability.

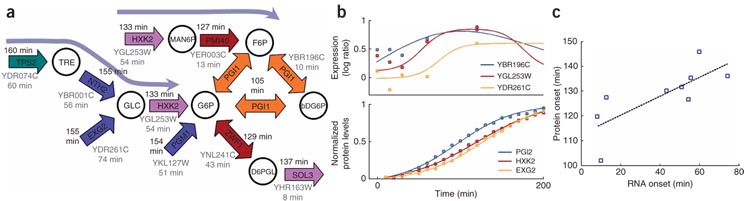
To test whether these transitions induce corresponding changes at the protein level, we measured a time course of protein levels for the nine genes participating in timed motifs after exposure to dithiothreitol (DTT) (Fig. 5 and Supplementary Fig. 4 online). Treatment with DTT was chosen because it does not interfere with measuring the protein profiles and it induces expression activation, which can be reliably measured. We observed that the level of an activated gene’s protein product roughly resembles a scaled, time-delayed integral of its mRNA level (Fig. 5b), with protein levels increasing after the increase in mRNA levels, and then stabilizing. This finding is consistent with well-understood cellular mechanisms: an increase in the level of mRNA allows an increase in protein production; but once protein is produced, its relatively slow degradation rate allows the new protein levels to be maintained with lower mRNA levels. To quantify the relationship between the timings of the mRNA and protein activation, we extracted the onset time of the activation of the proteins in our timed motifs, and found them to be in good correlation with the onset time of the mRNA activation (P < 0.0025 in 1^st replicate; P < 0.015 in 2^nd replicate; Spearman correlation, n = 9; Fig. 5c). By contrast, there was no correlation between the mRNA response level and the protein response level (r = −0.05). When considering our finer-grained timing motifs (Fig. 5a), we found that 9 of the 11 pairs of ordered timing relationships that were observed at the mRNA level were conserved at the protein level (permutation test, P = 0.0043), although the differences in timing were smaller in the protein level. Similarly, six of eight ordered three-enzyme chain motifs found in the mRNA were also conserved at the protein level (permutation test, P = 0.0080). This result demonstrates that timing relationships that are observed in mRNA can also carry through to protein activation timing, and supports the predictive ability of our analysis.

Figure 5. Protein timing motifs in response to DTT.

(a) Part of central carbon metabolism that contained backward activation of RNA TAM’s in response to DTT. Protein onsets are denoted in black and RNA onsets in gray. Arrow colors correspond to time (ranging from orange for early, to green for late). (b) Protein and RNA profiles of three enzymes that participate in a backward-activation three-enzyme-chain TAM. Overall, we saw significant correlation between mRNA onsets and protein onsets; 9 of the 11 pairs (Supplementary Fig. 5) of ordered timing relationships that were observed at the mRNA level were conserved in the protein level (permutation test, P = 0.0043); 6 of 8 ordered three-enzyme-chain motifs found in the mRNA were also conserved at the protein level (permutation test, P = 0.0080). (c) Onset time extracted from nine RNA and protein profiles. Onsets are significantly correlated (n = 9, Spearman r = 0.87, P = 0.0025, Pearson P = 0.01). Correlation remains significant even when removing the bottom left measurement (Spearman, r = 0.83, n = 8, P = 0.01).

DISCUSSION

Our results shed light on the relative contribution of transcriptional and hierarchical control in the metabolic network. Although others have argued compellingly that ‘hierarchical control’—using primarily feedback loops at the protein level—is predominant in metabolic networks^7,8 their conclusions were based on experiments performed in an equilibrium condition. In contrast, the current analysis specifically focuses on transitions induced by changes in environmental conditions. It is well established that drastic changes in transcript levels occur after such transitions¹⁷. It is likely that changes in transcript levels cause corresponding changes in protein levels³⁵, allowing the cell to produce enough active protein to survive in the new condition. These slower changes in protein levels can mimic and reinforce faster changes in protein activity, which allow the cell to adjust rapidly to drastic environmental perturbations. Subsequently, the transcript levels generally return to a new steady state, which is often significantly closer to the original transcript level before the transition. At that point, which corresponds to the previous experiments^7,8, it is plausible that the cell contains sufficient protein product, and enters a regime where hierarchical control dominates. Indeed, our protein experiments suggest that protein abundances persist essentially at their new levels even after transcript levels return to the new steady state. This demonstrates that the short-term mRNA impulse has long-term effects on protein levels and suggests that the metabolic network may undergo two distinct control regimes. First, transcriptional control is necessary in times of sudden environmental change to adjust the overall levels of the required protein product. Hierarchical feedback control is then used more predominantly, to allow a rapid adjustment of active enzyme levels to small fluctuations.

The situation for repression of mRNA levels is probably more complex. Here a transcriptional response may not be sufficient to induce a rapid reduction in protein levels, and may well be accompanied or even entirely driven by regulation at the post-transcriptional³⁶ or post-translational levels. Indeed, only our binding affinity analysis is related specifically to transcription, and it is plausible that some of the observed changes in mRNA levels are caused by regulated degradation³⁶. Understanding the mechanisms by which post-transcriptional regulation can lead to fine-grained temporal effects, of the type we observe, is an exciting direction for future study.

Recent studies have identified important principles of network function by considering functional data in the context of the topology of a metabolic^9,10 or protein-protein interaction network^37,38. Activity motifs can provide a tool for identifying functional patterns in different networks. In their general form, they can represent frequently occurring patterns in labels on the edges and nodes of any network, including cis-regulatory networks, signaling networks, or even social and World-Wide-Web networks. However, they can also encode functional patterns involving rich, quantitative data of many different types, like the timing and binding motifs studied here, as well as phylogenetic or phenotypic profiles, genetic interactions or protein abundances.

When applied to transcription control, the activity-motifs approach reveals two intriguing regulatory mechanisms. First, we find that cells have evolved to carefully coordinate the timing of crucial metabolic processes, to optimize responses to environmental perturbations. Second, we show that some of this fine-grained regulation of timing may be achieved by a corresponding fine-tuning of the affinity of transcription factor binding, suggesting that even small differences in transcription factor binding sites may play a functional role. It would be interesting to study the extent to which similar mechanisms occur in other biological pathways and in other organisms.

Overall, our findings demonstrate that our approach for the definition and discovery of activity motifs provides a useful framework for systematic and refined investigation of network function.

METHODS

Metabolic network and motif finding

As a model of the S. cerevisiae metabolic network, we used the model reconstructed by Forster et al.¹³. The 13 metabolites with highest degree (metabolic currencies) were removed from the network before extracting the network wiring motifs. Bidirectional reactions were represented as pairs of directed reactions. To find the wiring motifs, we then searched the set of reactions for pairs and triplets that follow the relevant constraints (the entire list can be found in Supplementary Table 1). For example, a chain of two enzymes is a pair of reactions where the products of the first reaction were equal to the substrates of the second one. Funnel motifs are triplets of reactions, (R₁, R₂, R₃) where the third reaction, R₃, uses at least one product of R₁ and one product of R₂ as its substrates. Similar constraints were used for finding forks.

Gene expression time courses

We generated a set of 13 time courses by measuring gene expression after a metabolic change. Yeast strain KCN118 (MATalpha ade2) was grown at 28 °C in 400 ml of synthetic complete media with 2% dextrose (SCD) to an OD₆₀₀ of 0.6. Synthetic complete was prepared using the standard recipe, except 75 µM inositol was included. At OD₆₀₀ of 0.6, 100 ml of cells were collected by centrifugation and frozen as a reference sample, and the remaining cells were rapidly collected by filtration, washed with distilled water and resuspended in 300 ml of one of the following media: SCE (SC + 2% ethanol), SCG (SC + 2% galactose), SM1 (SCD lacking amino acids A, R, N, C, Q, G, K, P, S, F and T), SM2 (SCD lacking amino acids L, I, V, W, H and M), S0 (SCD lacking all amino acids), S0G (no amino acids, 2% galactose) or S0E (no amino acids, 2% ethanol).

To measure response profiles, we resuspended 50 ml aliquots of yeast and added them to 500-ml flasks shaking in a 28 °C water bath for 15, 30, 60, 120 or 240 min. At the indicated times, cells were collected by centrifugation for 2 min at 3,700 r.p.m., and were flash frozen in liquid nitrogen. Poly-A RNA extraction, mRNA labeling and cDNA microarray hybridization were performed as previously described³⁹.

We also collected 63 gene expression time courses from multiple published experiments, including responses to changing media^16,17,39,40 and stress^{17,18,41–44}. A detailed list can be found in Supplementary Table 2a.

Impulse model for expression time courses

Each of the conditions above had expression levels measured on multiple time points after a change in environmental conditions (Supplementary Table 2b). To model the profile of a time course, we develop an impulse model to fit each gene separately¹⁵. After environmental perturbation, typical expression profiles follow a two-phase behavior: an early change to a transient level is often followed by a second change to a new steady-state level. We use a model that allows for two changes in expression levels, each modeled as a sigmoid. Formally, the family of impulse functions is specified by six parameters: The initial level (h₀), the transient level (h₁), the steady state level (h₂), the time of the first and second transition (t₁ and t₂) and the transition slope (β). Together these parameterize an impulse function: $\mathrm{f}\left(\mathrm{x}\right)=\frac{1}{h_1}{\mathrm{s}}_1\left(x\right)s_2\left(x\right)$, where s₁(x) = h₁ + (h₁ − h₀)Sigmoid(β, t₁), s₂(x) = h₁ + (h₁ − h₂)Sigmoid(−β, t₂), and Sigmoid(β, t) = 1/ exp(−β(x − t)). In some experiments, the measurement at time zero was used to normalize the data, yielding a zero value for the expression in log space. To push the fit impulse functions to be near zero before the onset of environmental change, three pseudo measurements were added at time (−30, −20, −10), with value zero. This favors functions that have near-zero values and near-zero gradient before time zero, but in a soft way, rather than as a hard constraint. Given a fit of an impulse function to the expression measurements, we identified the onset time of the response of each gene as the time at which the gene first reached half of its peak level. Additional details of the model and algorithms, and empirical evaluations that include comparison to other parametric models for gene expression time courses, can be found in ref. 15.

Defining temporal transcription patterns

The transcriptional response of a pair of genes is ordered when the onset time of one gene precedes the onset time of the other. However, this relationship may be sensitive to small perturbations in the gene expression data. To provide a robust definition of ordered transcriptional response, we repeatedly perturbed the log-ratio expression values for each gene with Gaussian noise with zero mean and a s.d. of 0.1, and performed the impulse model fitting for each perturbed time course. This level of noise was chosen because estimates of individual gene’s variability demonstrate lower average variability⁴⁵ (in terms of the mean absolute deviation, MAD = 0.035). None of the genes participating in our chains motifs had a variability > 0.1 in a previous study⁴⁵. We repeated the perturbation process 30 times for each gene yielding a distribution of onset times. A pair of genes is viewed as ordered if the distributions of their onset times, in the perturbed data, is significantly different (P < 0.01). The P-value is estimated using a Wilcoxson test relative to the 30 perturbed measurements of onsets for each gene in the pair. We further define a chain of enzymes to be ordered if the geometric average of the P-values of all pairs in the chain is significant (P < 0.01). We defined same-time motifs as an onset time within 2 min, with significance measured in the same way.

Statistical analysis of pattern abundance

Overrepresentation of patterns was estimated using a Monte Carlo approach. The assignment of expression profiles to enzymes was randomly shuffled, without changing the wiring pattern of the network. This last point is important, as motifs often overlap, and randomizing the network structure could introduce biases. We repeated this process for 10,000 randomized assignments, and counted the number of patterns in each one. This process was used to obtain an empirical P-value by calculating the fraction of randomizations with higher pattern count than the true network. In addition, for very significant patterns (P < 10⁻⁴), we further refined the P-value in the following way: each random distribution of counts was fit using a gamma distribution (Fig. 2a,b), and a P-value was calculated as the tail of the cumulative distribution. This P-value is calculated in a similar way that a z-score is calculated from the mean and variance of a sample, but instead of using a Gaussian distribution, it uses a Gamma distribution, which fits better a distribution over positive values. A Kolmogorov-Smirnov (KS) test was used to test the adequacy of the fit by measuring the similarity of the empirical and the fit distribution. This KS test usually rejected the hypothesis of different distributions (P = 0.1) (cases where the hypothesis was not rejected did not have a significant P-value in the first place). The P-values based on the gamma distribution were highly correlated with the empirical P-values obtained from shuffling (data not shown).

To quantify overrepresentation of an activity motif over all conditions (Fig. 2d,e), we first calculated an enrichment score for each condition, which was the log base-10 of the individual empirical P-values of the motif in that condition. The total score is a sum of the 76 independent scores for the different conditions, and is well fit by a Gaussian distribution (KS test, probability of null hypothesis > 0.9).

Affinity data and coverage

We used genome-wide ChIP-chip^32,33 for multiple transcription factors across several conditions, and used binding P-value as a measure of binding affinity, as previously done³².

We analyzed the relation between TAMs and BAMs using a Monte Carlo approach that is similar to our general analysis of activity motif, and to our specific TAM analysis. We focused on a set of 48 binding experiments that were measured in conditions that match the RNA expression measurements (Supplementary Table 6), and analyzed each pair of expression and binding data separately, as follows. We consider only enzymes that are more strongly bound by the corresponding transcription factor (with P-value lower than a threshold P_bind < 0.5). We identify the set of three-enzyme-chain TAMs that are strongly bound by the transcription factor, and the set of three-enzyme-chain BAMs for the same transcription factor (those where the binding P-values were ordered). We counted the overlap between these two sets, and evaluated the probability of observing such an overlap at random, by shuffling the binding affinity values across all bound genes 10⁵ times. Importantly, this permutation approach corrects for any potential artifacts arising from the structure of the motifs, including overlaps between different three-enzyme chains, as these same artifacts also hold in the permuted data. Given the set of P-values for all 48 conditions, we used FDR to correct for multiple hypotheses, and found 20 conditions to be significant at q = 0.05 (22 at q = 0.1, 17 at q = 0.005).We also calculated an upper bound on the overall probability of observing 20 conditions that are significant at q = 0.05, using a binomial distribution B(48,0.05), yielding P < 1.9 × 10⁻¹⁴.

Protein time courses

Stress conditions were selected based on the compatibility of strains tested in genomic expression studies¹⁷ and the green fluorescent protein (GFP)-tagged library (Invitrogen)⁴⁶. The genotype of the collection is as follows: MATa his3Δ1 leu2Δ3 met15Δ0 ura3Δ0 XXX-GFP(S65T)-His3MX, where XXX represents the gene fused to GFP(S65T)⁴⁷. We cultured 5 ml cultures overnight with a single colony in rich medium (YEPD) at 25 °C (for DTT exposure) or 30 °C (for diamide treatment) and shaken at 250 r.p.m.¹⁷. Overnight cultures were back diluted to an OD₆₀₀ of 0.1 in 40 ml of YEPD, and grown to an OD₆₀₀ of 0.4 at the same temperature and shaker speed. A 200 µl sample was taken as the zero time point before the addition of stress at a final concentration of 2.5 mM for DTT exposure and 1.5 mM for diamide treatment. We manually delivered 200 µl samples to an analytical cytometer (LSR-II; Becton Dickinson) using an auto sampler device (HTS; Becton Dickinson) every 10 min for 4.5 h. GFP was excited at 488 nm and fluorescence emission was collected at 505 nm⁴⁶. To eliminate systematic errors in uneven sample flow, raw cytometry data was processed as previously described⁴⁶. Each time point collected reflects the median GFP intensity over an isogenic population in arbitrary units. The resulting time courses can be found in Supplementary Figure 5 online.

Extraction of onset times from protein profiles

To extract the onset time from each protein profile, we first linearly rescaled each set of measurements to the range [0,1], then added three zero pseudo measurements at times −10, −20, −30 min, and added three pseudo measurements with level 1 and times +10, +20, +30 after the last measurement. We then fit a sigmoid to each profile, Sigmoid(β, t) = 1/ exp(−β(x − t)), tuning the two free parameters, the onset t and the slope β, to minimize the squared fit error.

P-value for protein activity motifs

The probabilities of observing 9 ordered pairs out of 11 pairs, and 6 triplets out of 8 were calculated using a permutation test, over 10⁵ permutations, yielding P = 0.0043 for pairs and 0.0080 for triplets. This permutation test correctly takes into account that the pairs and triplets are not independent.

Supplementary Material

Supplement

Note: Supplementary information is available on the Nature Biotechnology website.