Skip to main content
PMC home page
The Journal of Neuroscience logoLink to The Journal of Neuroscience
. 2008 Aug 20;28(34):8553–8559. doi: 10.1523/JNEUROSCI.2182-08.2008

The Relationship between Subthreshold and Suprathreshold Ocular Dominance in Cat Primary Visual Cortex

Nicholas J Priebe 1,✉
PMCID: PMC2651840  NIHMSID: NIHMS85986  PMID: 18716214

Abstract

Primary visual cortex (V1) is the site at which right and left eye pathways are first integrated, leading to a representation of the visual world in depth. The ocular dominance (OD) of individual cortical neurons varies and may be changed by altering visual experience during the developmental critical period. Estimates of OD, commonly used to quantify the right and left eye synaptic inputs, have previously been based on spike rate. Membrane potential (V m), however, is more closely related to the synaptic inputs onto neurons and should therefore more closely reflect the degree of input from the two eyes. To determine the relationship between OD based on membrane potential and on spike rate, intracellular recordings were made from visual cortical neurons. OD based on spike rate was systematically more monocular than OD based on membrane potential. The discrepancy between membrane-potential OD and spike-rate OD may be accounted for by a simple model of V m-to-spike-rate transformation.

Keywords: primary visual cortex, spike threshold nonlinearity, intracellular recording, ocular dominance, vision, binocular

Introduction

Synaptic connections in primary visual cortex (V1) create neurons whose receptive field properties lay the foundation for our representation of the visual world. Binocularity, resulting from the integration of segregated pathways from the two eyes, first appears in V1 neurons, where it not only plays a critical role in the generation of a three-dimensional visual representation (Cumming and DeAngelis, 2001), but also serves as a prime example of experience-dependent development and plasticity in the brain. Disrupting visual experience during development by monocular eyelid closure [monocular deprivation (MD)], for example, leads to a weakening of the input from the deprived eye and a strengthening of the input from the experienced eye (Wiesel and Hubel, 1963); strabismus during development leads to cells that are almost exclusively monocular (Hubel and Wiesel, 1965).

The analysis of binocularity in normal V1 and the changes produced by disrupted visual experience has relied almost exclusively on extracellular recordings, which reveal only the suprathreshold spiking responses of these neurons. There is good reason to believe that the binocularity measured from spiking responses does not accurately characterize the ocular dominance (OD) of the synaptic input to the neuron. Because a neuron must depolarize to a critical threshold potential to fire spikes, smaller synaptic inputs may not be represented in the spike rate of the neuron. Thus, although a neuron may be activated by stimulation to both eyes, as evidenced by membrane-potential (V m) depolarization, if the synaptic drive from one of the eyes is not sufficient for the cell to reach spike threshold, the neuron would be classified as monocular based on spike rate. Even if both right and left eye stimulation elicit suprathreshold membrane-potential depolarizations, the nonlinear relationship between membrane potential and spike rate could accentuate the differences between the subthreshold responses (Frégnac et al., 1996; Moore and Nelson, 1998; Azouz and Gray, 2000; Tan et al., 2004; Mariño et al., 2005; Priebe and Ferster, 2005; Finn et al., 2007). Because membrane potential recorded at the soma represents the summed synaptic input onto the neuron, it provides a much more direct physiological means, relative to spike rate, of estimating the amount of synaptic input coming from right and left eye pathways.

Previous work has demonstrated that spike threshold plays a role in shaping orientation tuning, direction selectivity, and spatial tuning in visual cortical neurons. Orientation tuning, when measured from membrane potential, is broader than tuning measured from spike rate for the same neuron (Volgushev et al., 1996, 2000; Azouz and Gray, 2000; Carandini and Ferster, 2000; Cardin et al., 2007; Finn et al., 2007). Threshold acts to narrow orientation tuning because the smaller depolarizations to nonpreferred orientations often do not reach spike threshold. In a similar manner, direction selectivity is enhanced by spike threshold because the depolarization to the nonpreferred direction sometimes does not reach threshold (Jagadeesh et al., 1997; Priebe and Ferster, 2005). Whereas the nonpreferred direction often elicits no spikes, measurements of the membrane potential reveal robust depolarizations (Jagadeesh et al., 1993; Priebe and Ferster, 2005). For the same reason, the spatial extent of receptive fields is also narrower when based on spike rate than when based on membrane potential (Frégnac et al., 1996).

To address whether the spike threshold also alters estimates of OD, subthreshold and suprathreshold responses were measured from V1 neurons using intracellular recordings in vivo. OD based on spike rate was systematically more monocular than OD based on membrane potential in individual neurons. As with orientation and direction selectivity, small biases in OD in membrane potential are enhanced by the spike threshold. By recording the membrane potential, latent inputs elicited by the stimulation of the nonpreferred eye were unmasked.

Materials and Methods

Physiological recordings and visual stimulation.

Whole-cell patch-clamp recordings were made in vivo from V1 neurons in anesthetized, paralyzed cats (2–2.5 kg) as described previously (Priebe and Ferster, 2005). Anesthesia was induced with ketamine (5–15 mg/kg) and acepromazine (0.7 mg/kg) and followed by intravenous administration of sodium thiopental (10–20 mg/kg) during surgery. After surgery, the animal was placed in the stereotaxic frame until the end of the experiment. Recording stability was increased by both suspending the thoracic vertebrae from the stereotaxic frame and performing a pneumothoracotomy. Eye drift was minimized with the intravenous infusion of vecuronium bromide (Norcuron; 0.2 mg/kg/h). Anesthesia was maintained for the duration of the experiment with the continuous infusion of sodium thiopental (2 mg/kg/h). Body temperature, electrocardiogram, EEG, CO2, and autonomic signs were continuously monitored. The nictitating membrane was retracted using phenylephrine hydrochloride, and the pupils were dilated using topical atropine. Contact lenses with 4 mm artificial pupils were inserted to protect the corneas. Supplementary lenses were selected by direct ophthalmoscopy to focus the display screen onto the retina.

Borosilicate glass electrodes (A-M Systems) were filled with a K+-gluconate solution that included Ca2+ buffers, pH buffers, and cyclic nucleotides. Electrodes were advanced into the cortex (area 17; ∼2 mm lateral of the midline) with a motorized microdrive (Sutter Instrument). After the electrode was in place, warm agarose solution (3% in normal saline) was placed over the craniotomy to protect the surface of the cortex and reduce pulsations. All procedures were approved by the Northwestern Institutional Animal Care and Use Committee.

Visual stimuli were generated by a Macintosh computer (Apple) using the Psychophysics Toolbox (Brainard, 1997; Pelli, 1997) for Matlab (MathWorks) and presented on a ViewSonic video monitor placed 48 cm from the cat's eyes. The video monitor had a non-interlaced refresh rate of 100 Hz and a spatial resolution of 1024 × 768 pixels, which subtended 40 cm horizontally and 30 cm vertically. The video monitor had a mean luminance of 20 cd/cm2.

Grating stimuli were presented for 4 s, preceded and followed by 250 ms blank (mean luminance) periods. After initially characterizing the stimulus orientation, spatial frequency, spatial location, and size that elicited the best response for each eye alone, contrast-response functions were measured for each eye by presenting gratings of six different contrasts in a pseudorandom manner. Voltage responses were sampled at 4096 Hz and stored for subsequent analysis.

Analysis.

Spikes were identified from the large characteristic deflections in membrane potential. The membrane potential was passed through a 5 ms median filter to remove the action potentials. The spike rate and average membrane potential were computed by cycle-averaging the responses for each contrast and eye condition. Further analyses are described in the appropriate section of the Results.

Results

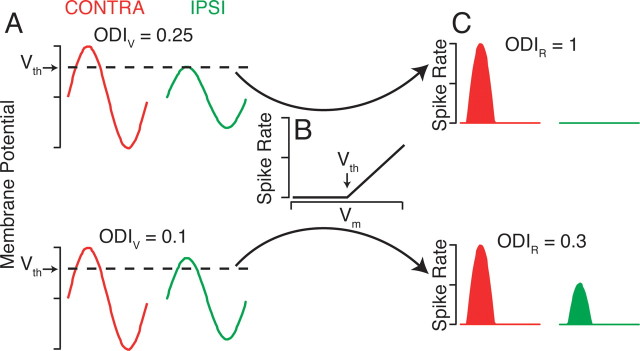
OD was developed to quantify the relative degree of input from the two eyes to a visual cortical neuron (Wiesel and Hubel, 1963). One of the reasons, however, that the traditional OD metric based on spike rate may not reflect the accurate degree of right and left eye innervation to a neuron is that it is based on neuronal output (spike rate) instead of the synaptic input. To understand how spike threshold may alter the OD of a neuron, we start with a model simple cell in V1 that responds with a characteristic membrane-potential modulation to a drifting grating, but the subthreshold responses to stimulation of the right and left eyes are unequal (Fig. 1 A). The membrane-potential responses are then passed through a threshold-linear transformation (Fig. 1 B) to generate a spike rate. The degree of OD can be quantified by the OD index (ODI) (Cang et al., 2005):

graphic file with name zns03408-5203-m01.jpg

where C is the peak response to contralateral eye stimulation, and I is the peak response to ipsilateral eye stimulation, after background subtraction. The ODI ranges from −1 to 1, where −1 and 1 are purely monocular ipsilateral and contralateral eye responses, respectively, and 0 indicates equal responses to both eyes. For our model neuron with unequal subthreshold responses to the two eyes, the ODI for membrane potential (ODIV) is equal to 0.25, reflecting a bias for the contralateral eye but innervation by both eyes nonetheless. Yet because the membrane potential never reaches the threshold potential for spiking in response to the ipsilateral eye stimulation, the ODI for spike rate (ODIR) is equal to 1, indicating that the neuron is completely monocular for the contralateral eye. As such, in this case, the extracellular recording experiment classifies the cell as monocular, in other words, receiving no ipsilateral eye input, although the neuron actually does receive input from both eyes.

Figure 1.

Figure 1.

Open in a new tab

A threshold-linear model increases monocularity. A, Model simple cell membrane-potential responses to stimulation by a drifting grating in the contralateral (CONTRA; red trace) or ipsilateral (IPSI; green trace) eye. V th indicates the threshold membrane potential to elicit spikes. ODIV is the ODI (Eq. 1) for membrane potential. B, The threshold-linear transformation of membrane potential to spike rate. C, Spike rates resulting from the membrane-potential responses in A and the transformation in B.

Even when both contralateral and ipsilateral eye stimulation elicit spikes, the degree of OD is still different for membrane potential and for spike rate (Fig. 1 A,C, bottom). Small differences between the subthreshold responses for each eye are magnified by the threshold nonlinearity, which leads the OD to be systematically more monocular (larger-magnitude ODI) for spike rate than for membrane potential.

To determine the relationship between OD estimated from membrane potential and spike rate, whole-cell recordings from cortical neurons in vivo were made using patch electrodes. After first identifying the preferred orientation, spatial frequency, and receptive field location for each neuron, drifting gratings of varying contrasts were presented separately to the right and left eyes (Fig. 2). The spike rate and membrane potential were cycle-averaged, and the peak response was computed from the sum of the mean and first modulation response components.

Figure 2.

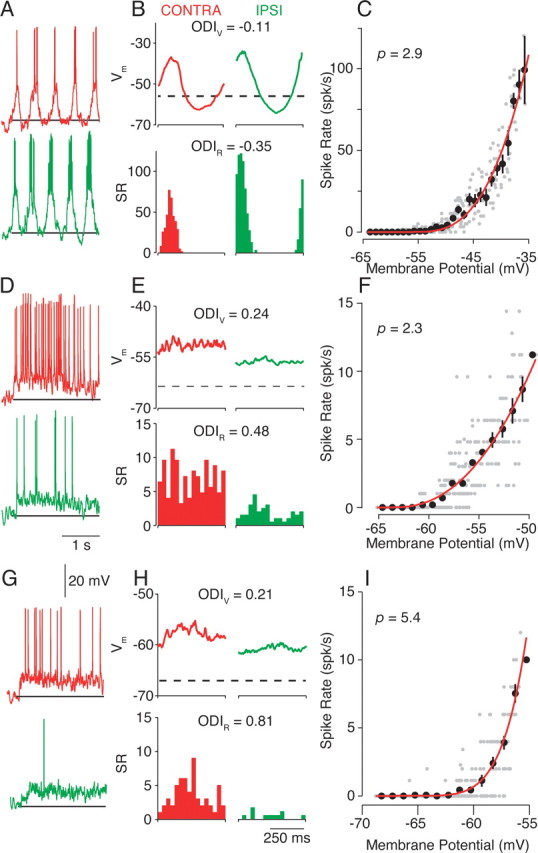
Figure 2.

Open in a new tab

Intracellular measurements of ocular dominance. A, Single-trial responses to high-contrast (64%) drifting gratings in the preferred orientation. Both contralateral (CONTRA; red trace) and ipsilateral (IPSI; green trace) responses are shown. The horizontal line indicates the resting membrane potential and marks the stimulation presentation. B, Cycle-averaged responses for V m (in millivolts; top) and spike rate (SR) [in spikes (spk) per second; bottom]. Resting membrane potential is indicated by the dashed line. C, The V m-to-spike-rate transformation is fit by a power-law function (Eq. 2; red line). Thirty millisecond epochs of mean membrane potential and spike rate are indicated by gray dots. The fit exponent value, p (Eq. 2), is indicated in the top left corner. The average and SE firing rate for membrane potentials in 1 mV bins are indicated by black dots. D–F and G–I follow the conventions of A–C for two additional neurons.

Clear depolarizing responses to contralateral and ipsilateral eye stimulation were evident, although the differences in responses were larger for the spike rate. ODIV and ODIR shared the same ocular bias, but the magnitude of the ODI was larger for the spike rate than for the membrane potential. The increased magnitude of the ODI for spike rate indicates that neurons appear more monocular for spike rate than for membrane potential. The difference in the ODI for membrane potential and spike rate did not depend on whether the neuron was classified by spike-rate response modulation as simple (Fig. 2 A–C), complex (Fig. 2 D–F), or in between (Fig. 2 G–I).

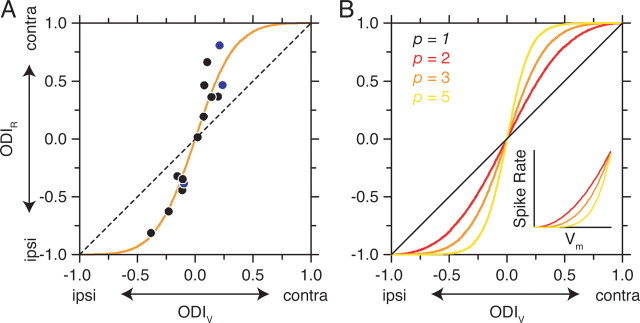
For 14 cortical neurons, the ODIV ranged from −0.38 to 0.24, whereas the ODIR values fell within a larger range (−0.81 to 0.80) for 64% contrast drifting gratings (Fig. 3 A). The magnitude of ODIV (mean |ODIV| = 0.15 ± 0.09, SD) was significantly different from the magnitude of ODIR (mean |ODIR| = 0.45 ± 0.22, SD) (paired t test, p < 0.001). Therefore, measurements of OD based on spike rate are more monocular than those based on membrane potential. The discrepancy between membrane-potential and spike-rate OD was also evident at a 32% contrast (mean |ODIV| = 0.19 ± 0.14; mean |ODIR| = 0.48 ± 0.27; paired t test, p < 0.01).

Figure 3.

Figure 3.

Open in a new tab

The transformation between membrane-potential and spike-rate ocular dominance. A, Measured ODI is plotted for membrane potential and spike rate is plotted for each neuron (filled circles). The three neurons in Figure 2 are indicated by blue circles. The dashed line indicates a relationship with slope = 1 and y-intercept of 0. The solid orange line indicates the prediction based on the power-law function in Equation 2 with the exponent p = 3. B, Predictions of the relationship between ODIV and ODIR for different exponents in the power-law function. Inset, The relationship between membrane potential and spike rate for exponents 2, 3, and 5. contra, Contralateral; ipsi, ipsilateral.

To determine whether the spike threshold nonlinearity could account for this increase in spike-rate monocularity, the shape of the V m-to-spike-rate transformation was characterized for each neuron. Cycle-averaged responses for all stimulus conditions were divided into 30 ms epochs, and the mean spike rate was plotted against the mean membrane potential (Fig. 2 C,F,I). The V m-to-spike-rate transformation is similar to the threshold-linear model (Fig. 1 B) but differs in detail. Instead of a sharp inflection at a threshold membrane potential, the spike rate smoothly increases as the mean depolarization increases. The relationship is well fit using a power-law nonlinearity (Hansel and van Vreeswijk, 2002; Miller and Troyer, 2002):

graphic file with name zns03408-5203-m02.jpg

where R is the spike rate, V̄ m is trial-averaged membrane potential, V rest is resting membrane potential, p is the exponent of the nonlinearity, and the subscript + indicates rectification (R for V m < V rest is 0). The power law accounts for the impact of trial-to-trial variability on the threshold-linear relationship and effectively smoothes the transformation between average membrane potential and average spike rate (Hansel and van Vreeswijk, 2002; Miller and Troyer, 2002), but other expansive nonlinear functions could also be applied (Heeger, 1992; Ringach and Malone, 2007). Exponents of the power law in visual cortex range from 1.5 to 6.5 [n = 102; mean = 3.32; SD = 0.89 (Priebe et al., 2004)]. Predictions of spike rate were generated by applying the V m to spike-rate transformation to the recorded membrane potential. Using the predicted spike-rate responses, ODIR was estimated, and the values accounted for 94.7% of the variance, indicating that the threshold nonlinearity is sufficient to account for the discrepancy between membrane-potential and spike-rate OD.

Because the increase in ODI seems to be caused entirely by the spike threshold nonlinearity, the relationship between the ODIV and ODIR should match the observations. The relationship between ODIV and ODIR, based on the different exponents of the power law (p; Eq. 2), is derived in the Appendix:

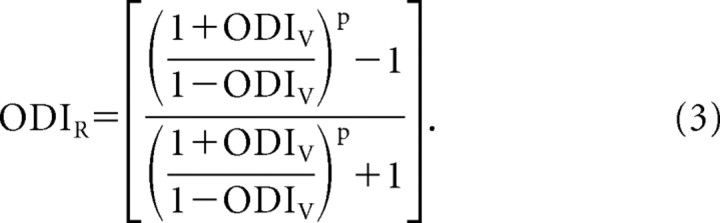graphic file with name zns03408-5203-m03.jpg

Assuming an exponent p = 3 (a typical value for cortical neurons) results in a prediction that closely matches the recorded relationship between these indices (Fig. 3 A, solid line). The critical free parameter of this nonlinear relationship is the exponent p of the transformation. Increasing the exponent causes the function to become increasingly steep at values near zero (Fig. 3 B). Assuming the same exponent for all neurons (p = 3), however, only modestly reduces the variance accounted for by the model to 90.1 from 94.7%.

Discussion

Ocular dominance represents an important feature of visual cortical organization in cats, monkeys, and humans. In addition, OD plasticity serves as a highly used model system for the study of experience-dependent development. I have demonstrated that the OD of individual neurons is different for membrane potential and for spike rate. Spike-rate measures of OD are systematically more monocular than membrane-potential measures of OD. The V m-to-spike-rate transformation, which depends on both the biophysical spike threshold and the variability of neuronal responses, is sufficient to account for the increased degree of monocularity observed in the spike rate. This enhanced monocularity in spike rate over membrane potential is analogous to the increased selectivity for orientation, direction, and spatial location seen in spike rate relative to membrane potential in visual cortical neurons (Jagadeesh et al., 1993; Frégnac et al., 1996; Azouz and Gray, 2000; Carandini and Ferster, 2000).

Although such a discrepancy does exist between subthreshold and suprathreshold OD, we have demonstrated a consistent relationship between ODIR and ODIV. It is possible to predict ODIR or ODIV based on the exponent of the V m-to-spike-rate transformation and the complementary ODI (Eq. 3; see also Appendix). This functional relationship indicates that it should be possible to approximate the subthreshold OD based on spike-rate measurements alone. The relationship requires an assumption about the power-law exponent of individual cortical neurons, which varies between 1.5 and 6.5, but assuming a single exponent for all the neurons only mildly reduces the variance accounted for by the V m-to-spike-rate model. Alternative quantitative definitions for the ODI, such as only including the ipsilateral response in the numerator (Macy et al., 1982) or computing the ratio of the nonpreferred to preferred eye (Leventhal and Hirsch, 1978, 1980), still reveal the discrepancy between subthreshold and suprathreshold OD.

It is important to note that the ODI metric used here differs from the OD metric originally developed by Wiesel and Hubel (1963) and used extensively to date. The original OD metric scored cortical neurons on a scale of 1–7 based on the relative response to alternating stimulation of the two eyes singly. Macy et al. (1982) measured OD using both the 1–7 scale as well as ODI. They demonstrated a direct relationship between these two metrics (Macy et al., 1982). This direct relationship, Equation 13 (Appendix), makes it possible to predict the underlying membrane-potential OD from a reported spike-rate OD and an assumption of the exponent of the power law.

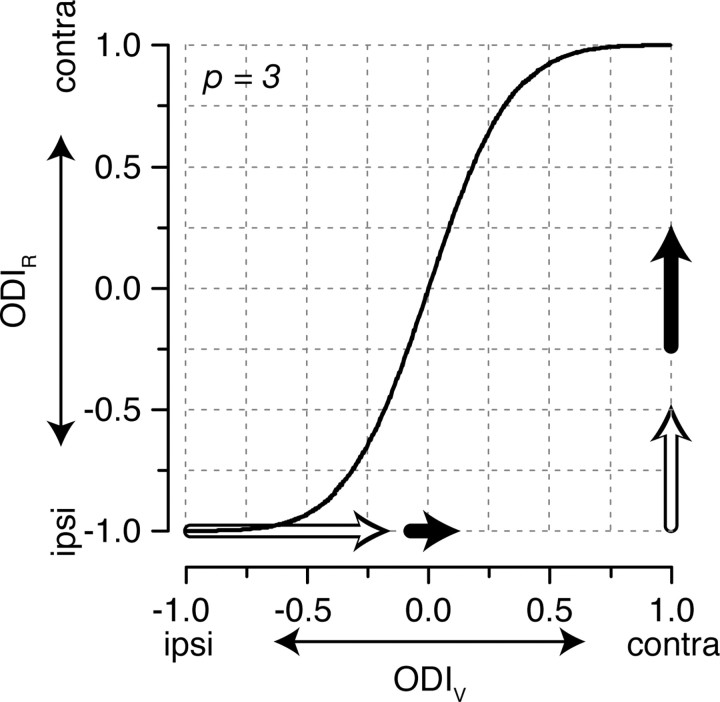
The discrepancy in OD between membrane potential and spike rate is particularly important for our understanding of developmental plasticity. As Wiesel and Hubel (1963) originally described, spike-rate OD distributions shift after MD during the developmental critical period, such that a higher proportion of neurons respond with spikes to stimulation of the open (nonoccluded) eye. Such a shift in the spike-rate OD profile should be matched by a corresponding shift in the membrane-potential OD profile, but the two shifts may be of different magnitudes. For example, for a neuron to shift its ODIR from −0.25 to 0.25 (ΔODIR = 0.5), a small change in the ODIV is required (ΔODIV = 0.17) (Fig. 4, filled arrows). In comparison, for a neuron to shift its ODIR from −1 to −0.5 (ΔODIR = 0.5, the same ODIR shift as in the previous example), a large change in the ODIV is required (ΔODIV = 0.82,) (Fig. 4, open arrows). In cat V1, which is predominantly binocular, critical-period MD requires only small shifts in synaptic input to shift neuronal responses away from the occluded eye. However, for neurons that receive more monocular inputs, as in mouse V1, changes in spike-rate OD that occur with critical-period MD require much larger shifts in synaptic input (Gordon and Stryker, 1996). The shape of the underlying distribution of ODIV may thus account for the different magnitude shifts induced by MD across different animal models (Wiesel and Hubel, 1963; Gordon and Stryker, 1996). It is important to emphasize, however, that although the magnitude of OD shifts after MD are predicted to be distinct, the direction of OD shifts should be the same for membrane potential and spike rate.

Figure 4.

Figure 4.

Open in a new tab

The same magnitude shifts in spike-rate ocular dominance require different magnitude shifts in membrane-potential ocular dominance. To shift the ODIR from −0.25 to 0.25 requires a ΔODIV of 0.17, whereas a shift of ODIR from −1 to −0.5 requires a ΔODIV of 0.82. The magnitudes of these changes are indicated by the filled and open arrows, respectively. contra, Contralateral; ipsi, ipsilateral.

Because the spike threshold masks the synaptic response to the nonpreferred eye, and thus enhances monocularity in visual cortical neurons, there may also be implications for understanding and treating strabismus. Inducing strabismus before the developmental critical period leads to an increase in the monocularity of cortical neurons as measured by spiking responses after the critical period (Hubel and Wiesel, 1965; Blakemore, 1976; Yinon, 1976; Smith et al., 1979). The increased monocularity has been interpreted as evidence for segregation of right and left eye inputs onto different target neurons in V1, instead of the normal integration of the afferents onto V1 target neurons to create stereo vision (McKee et al., 2003). Strabismus clearly changes the degree of monocularity of synaptic input, but spike threshold may also play a role by masking the smaller input from the nonpreferred eye, rather than or in addition to impacting segregation of inputs from the two eyes. In support of this hypothesis, simultaneous binocular stimulation in strabismic animals has revealed that even for neurons that appear monocular based on spike rate, the nonpreferred eye modulates the response of the preferred eye (Smith et al., 1997). If threshold were masking functional/residual input from the nonpreferred eye in strabismus, it would suggest a clinical solution targeting the potentiation of still existing but weakened synaptic connections, rather than necessitating the remodeling or regrowth of synaptic connections.

OD has also been measured using a number of imaging techniques that are related to, or at least influenced by, neuronal spiking activity. OD maps of cortex have been generated based on changes in blood flow either with functional magnetic resonance imaging (Cheng et al., 2001; Goodyear and Menon, 2001) or intrinsic signal imaging (Bonhoeffer and Grinvald, 1991; Crair et al., 1998), both of which measure changes in oxygenated hemoglobin, primarily driven by spiking. Imaging neural activity, by flavoprotein autofluorescence (Husson et al., 2007) or by cytochrome oxidase staining (Horton and Hubel, 1981; Horton, 1984), is also related to spiking activity in that they are both related to mitochondrial activity, which provides ATP for the sodium–potassium pump to maintain resting membrane potential. Imaging with voltage-sensitive dyes is also influenced by the large voltage signals caused by spiking (Slovin et al., 2002). Because these techniques are influenced by spiking activity, measures of OD will overestimate monocularity in the same manner as extracellular recording.

We have demonstrated that relatively small synaptic input changes can dramatically impact the OD of individual cortical neurons. The mechanisms underlying such OD plasticity, however, are not fully understood. A clear anatomical basis for OD (Wiesel et al., 1974; LeVay et al., 1975) and OD plasticity (LeVay et al., 1978; Antonini and Stryker, 1996; Horton and Hocking, 1998; Antonini et al., 1999) exists. Thalamic neurons representing the two eyes make patchy projections to layer 4 of V1 of cats and monkeys, which form the foundations for OD columns (Wiesel et al., 1974; LeVay et al., 1975). MD leads to both a retraction of the thalamic axonal projections of the deprived eye as well as an expansion of the axonal projections of the open eye in V1 (Antonini and Stryker, 1996; Antonini et al., 1999). Although these anatomical changes are observed in concert with the physiological shifts in OD measured for individual neurons, it is not clear how much these anatomical changes contribute to OD plasticity relative to synaptic changes. MD causes rapid physiological changes (Wiesel and Hubel, 1963) that are followed within 1 week by anatomical changes (LeVay et al., 1980; Antonini and Stryker, 1996). The asynchrony of these events indicates that, at least initially, synaptic plasticity is sufficient to account for OD plasticity. It may nonetheless be that the long-term effects of OD plasticity require anatomical changes. It is therefore still an open question as to how much disruptions such as MD and strabismus alter the anatomy and physiology of synaptic inputs onto cortical neurons. A better understanding of the mechanisms underlying ocular dominance plasticity should aid in clinical efforts to recover normal visual function.

Appendix

We would like to be able to make a prediction about the relationship between OD based on membrane potential and OD based on spike rate. Starting with the definition of the ODI for membrane potential,

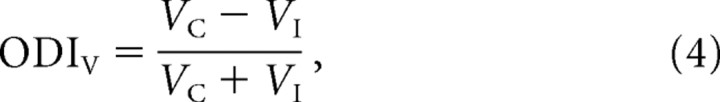graphic file with name zns03408-5203-m04.jpg

where V C and V I are the membrane-potential responses to contralateral and ipsilateral eye stimulation, relative to the resting membrane potential.

Equation 4 can be reorganized into

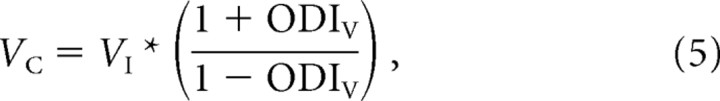graphic file with name zns03408-5203-m05.jpg

or

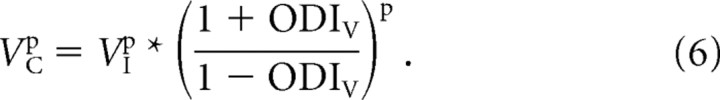graphic file with name zns03408-5203-m06.jpg

We know that the relationship between membrane potential and spike rate may be fit by the power-law nonlinearity, with the resting membrane potential subtracted off and only depolarizing responses considered.

graphic file with name zns03408-5203-m07.jpg

and

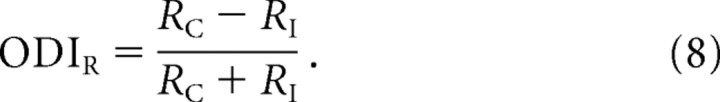graphic file with name zns03408-5203-m08.jpg

ODIR may now be rewritten in terms of the membrane-potential responses:

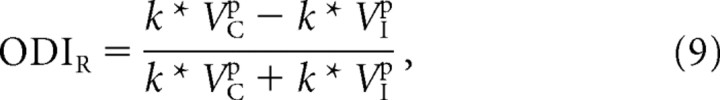graphic file with name zns03408-5203-m09.jpg

which may be rearranged as

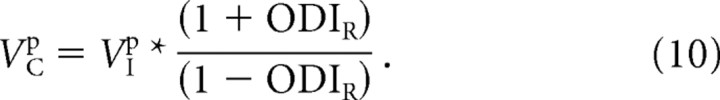graphic file with name zns03408-5203-m10.jpg

Note the similarity of Equation 10 and Equation 6. The two indices are now directly related to one another.

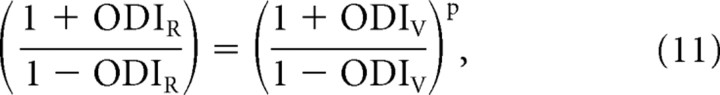graphic file with name zns03408-5203-m11.jpg

which can be rearranged to the following:

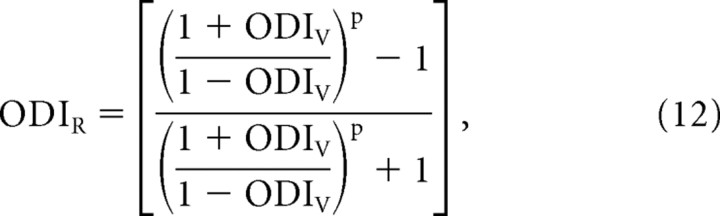graphic file with name zns03408-5203-m12.jpg

and

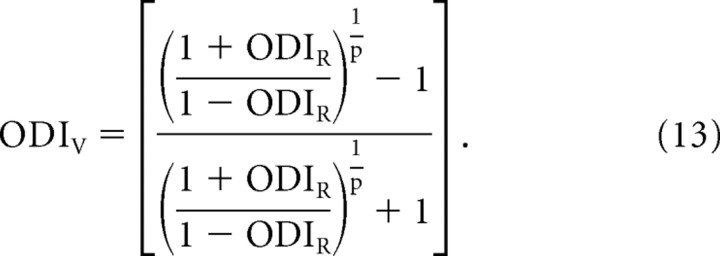graphic file with name zns03408-5203-m13.jpg

Equations 12 and 13 provide a direct relationship between the ODIR and ODIV that only depends on the exponent of the power law.

We would also like to derive the conditions under which ODIR is greater than ODIV.

graphic file with name zns03408-5203-m14.jpg

Equation 14 may be rewritten in terms of the membrane-potential response as in Equation 9.

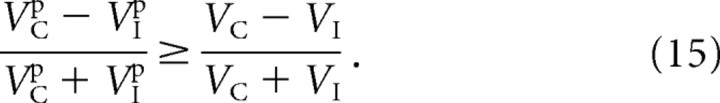graphic file with name zns03408-5203-m15.jpg

Equation 15 may then be rearranged in the following steps:

graphic file with name zns03408-5203-m16.jpg
graphic file with name zns03408-5203-m17.jpg
graphic file with name zns03408-5203-m18.jpg

By Equation 18, the conditions for which ODIR is greater than ODIV are that p > 1, and V C is greater than V I. In addition, ODIR is less than ODIV when p > 1, but V I is greater than V C. Therefore, for p > 1, ocular dominance is always more monocular for spike rate than for membrane potential. The only exceptions occur when ODIV equals 1 or 0 (ODIR and ODIV are equivalent in those cases).

Footnotes

This work was supported by National Institutes of Health Grant EY-04726. I am grateful to K. Miller and J. Hanover for helpful discussions. I also thank David Ferster for the use of his laboratory space and for his support throughout this project.

References

  1. Antonini A, Stryker MP. Plasticity of geniculocortical afferents following brief or prolonged monocular occlusion in the cat. J Comp Neurol. 1996;369:64–82. doi: 10.1002/(SICI)1096-9861(19960520)369:1<64::AID-CNE5>3.0.CO;2-I. [DOI] [PubMed] [Google Scholar]
  2. Antonini A, Fagiolini M, Stryker MP. Anatomical correlates of functional plasticity in mouse visual cortex. J Neurosci. 1999;19:4388–4406. doi: 10.1523/JNEUROSCI.19-11-04388.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Azouz R, Gray CM. Dynamic spike threshold reveals a mechanism for synaptic coincidence detection in cortical neurons in vivo. Proc Natl Acad Sci U S A. 2000;97:8110–8115. doi: 10.1073/pnas.130200797. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Blakemore C. The conditions required for the maintenance of binocularity in the kitten's visual cortex. J Physiol. 1976;261:423–444. doi: 10.1113/jphysiol.1976.sp011566. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Bonhoeffer T, Grinvald A. Iso-orientation domains in cat visual cortex are arranged in pinwheel-like patterns. Nature. 1991;353:429–431. doi: 10.1038/353429a0. [DOI] [PubMed] [Google Scholar]
  6. Brainard DH. The Psychophysics Toolbox. Spat Vis. 1997;10:433–436. [PubMed] [Google Scholar]
  7. Cang J, Kalatsky VA, Löwel S, Stryker MP. Optical imaging of the intrinsic signal as a measure of cortical plasticity in the mouse. Vis Neurosci. 2005;22:685–691. doi: 10.1017/S0952523805225178. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Carandini M, Ferster D. Membrane potential and firing rate in cat primary visual cortex. J Neurosci. 2000;20:470–484. doi: 10.1523/JNEUROSCI.20-01-00470.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Cardin JA, Palmer LA, Contreras D. Stimulus feature selectivity in excitatory and inhibitory neurons in primary visual cortex. J Neurosci. 2007;27:10333–10344. doi: 10.1523/JNEUROSCI.1692-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Cheng K, Waggoner RA, Tanaka K. Human ocular dominance columns as revealed by high-field functional magnetic resonance imaging. Neuron. 2001;32:359–374. doi: 10.1016/s0896-6273(01)00477-9. [DOI] [PubMed] [Google Scholar]
  11. Crair MC, Gillespie DC, Stryker MP. The role of visual experience in the development of columns in cat visual cortex. Science. 1998;279:566–570. doi: 10.1126/science.279.5350.566. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Cumming BG, DeAngelis GC. The physiology of stereopsis. Annu Rev Neurosci. 2001;24:203–238. doi: 10.1146/annurev.neuro.24.1.203. [DOI] [PubMed] [Google Scholar]
  13. Finn IM, Priebe NJ, Ferster D. The emergence of contrast-invariant orientation tuning in simple cells of cat visual cortex. Neuron. 2007;54:137–152. doi: 10.1016/j.neuron.2007.02.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Frégnac Y, Bringuier V, Chavane F, Glaeser L, Lorenceau J. An intracellular study of space and time representation in primary visual cortical receptive fields. J Physiol Paris. 1996;90:189–197. doi: 10.1016/s0928-4257(97)81422-2. [DOI] [PubMed] [Google Scholar]
  15. Goodyear BG, Menon RS. Brief visual stimulation allows mapping of ocular dominance in visual cortex using fMRI. Hum Brain Mapp. 2001;14:210–217. doi: 10.1002/hbm.1053. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Gordon JA, Stryker MP. Experience-dependent plasticity of binocular responses in the primary visual cortex of the mouse. J Neurosci. 1996;16:3274–3286. doi: 10.1523/JNEUROSCI.16-10-03274.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Hansel D, van Vreeswijk C. How noise contributes to contrast invariance of orientation tuning in cat visual cortex. J Neurosci. 2002;22:5118–5128. doi: 10.1523/JNEUROSCI.22-12-05118.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Heeger DJ. Half-squaring in responses of cat striate cells. Vis Neurosci. 1992;9:427–443. doi: 10.1017/s095252380001124x. [DOI] [PubMed] [Google Scholar]
  19. Horton JC. Cytochrome oxidase patches: a new cytoarchitectonic feature of monkey visual cortex. Philos Trans R Soc Lond B Biol Sci. 1984;304:199–253. doi: 10.1098/rstb.1984.0021. [DOI] [PubMed] [Google Scholar]
  20. Horton JC, Hocking DR. Effect of early monocular enucleation upon ocular dominance columns and cytochrome oxidase activity in monkey and human visual cortex. Vis Neurosci. 1998;15:289–303. doi: 10.1017/s0952523898152124. [DOI] [PubMed] [Google Scholar]
  21. Horton JC, Hubel DH. Regular patchy distribution of cytochrome oxidase staining in primary visual cortex of macaque monkey. Nature. 1981;292:762–764. doi: 10.1038/292762a0. [DOI] [PubMed] [Google Scholar]
  22. Hubel DH, Wiesel TN. Binocular interaction in striate cortex of kittens reared with artificial squint. J Neurophysiol. 1965;28:1041–1059. doi: 10.1152/jn.1965.28.6.1041. [DOI] [PubMed] [Google Scholar]
  23. Husson TR, Mallik AK, Zhang JX, Issa NP. Functional imaging of primary visual cortex using flavoprotein autofluorescence. J Neurosci. 2007;27:8665–8675. doi: 10.1523/JNEUROSCI.2156-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Jagadeesh B, Wheat HS, Ferster D. Linearity of summation of synaptic potentials underlying direction selectivity in simple cells of the cat visual cortex. Science. 1993;262:1901–1904. doi: 10.1126/science.8266083. [DOI] [PubMed] [Google Scholar]
  25. Jagadeesh B, Wheat HS, Kontsevich LL, Tyler CW, Ferster D. Direction selectivity of synaptic potentials in simple cells of the cat visual cortex. J Neurophysiol. 1997;78:2772–2789. doi: 10.1152/jn.1997.78.5.2772. [DOI] [PubMed] [Google Scholar]
  26. LeVay S, Hubel DH, Wiesel TN. The pattern of ocular dominance columns in macaque visual cortex revealed by a reduced silver stain. J Comp Neurol. 1975;159:559–576. doi: 10.1002/cne.901590408. [DOI] [PubMed] [Google Scholar]
  27. LeVay S, Stryker MP, Shatz CJ. Ocular dominance columns and their development in layer IV of the cat's visual cortex: a quantitative study. J Comp Neurol. 1978;179:223–244. doi: 10.1002/cne.901790113. [DOI] [PubMed] [Google Scholar]
  28. LeVay S, Wiesel TN, Hubel DH. The development of ocular dominance columns in normal and visually deprived monkeys. J Comp Neurol. 1980;191:1–51. doi: 10.1002/cne.901910102. [DOI] [PubMed] [Google Scholar]
  29. Leventhal AG, Hirsch HV. Receptive-field properties of neurons in different laminae of visual cortex of the cat. J Neurophysiol. 1978;41:948–962. doi: 10.1152/jn.1978.41.4.948. [DOI] [PubMed] [Google Scholar]
  30. Leventhal AG, Hirsch HV. Receptive-field properties of different classes of neurons in visual cortex of normal and dark-reared cats. J Neurophysiol. 1980;43:1111–1132. doi: 10.1152/jn.1980.43.4.1111. [DOI] [PubMed] [Google Scholar]
  31. Macy A, Ohzawa I, Freeman RD. A quantitative study of the classification and stability of ocular dominance in the cat's visual cortex. Exp Brain Res. 1982;48:401–408. doi: 10.1007/BF00238616. [DOI] [PubMed] [Google Scholar]
  32. Mariño J, Schummers J, Lyon DC, Schwabe L, Beck O, Wiesing P, Obermayer K, Sur M. Invariant computations in local cortical networks with balanced excitation and inhibition. Nat Neurosci. 2005;8:194–201. doi: 10.1038/nn1391. [DOI] [PubMed] [Google Scholar]
  33. McKee SP, Levi DM, Movshon JA. The pattern of visual deficits in amblyopia. J Vis. 2003;3:380–405. doi: 10.1167/3.5.5. [DOI] [PubMed] [Google Scholar]
  34. Miller KD, Troyer TW. Neural noise can explain expansive, power-law nonlinearities in neural response functions. J Neurophysiol. 2002;87:653–659. doi: 10.1152/jn.00425.2001. [DOI] [PubMed] [Google Scholar]
  35. Moore CI, Nelson SB. Spatio-temporal subthreshold receptive fields in the vibrissa representation of rat primary somatosensory cortex. J Neurophysiol. 1998;80:2882–2892. doi: 10.1152/jn.1998.80.6.2882. [DOI] [PubMed] [Google Scholar]
  36. Pelli DG. The VideoToolbox software for visual psychophysics: transforming numbers into movies. Spat Vis. 1997;10:437–442. [PubMed] [Google Scholar]
  37. Priebe NJ, Ferster D. Direction selectivity of excitation and inhibition in simple cells of the cat primary visual cortex. Neuron. 2005;45:133–145. doi: 10.1016/j.neuron.2004.12.024. [DOI] [PubMed] [Google Scholar]
  38. Priebe NJ, Mechler F, Carandini M, Ferster D. The contribution of spike threshold to the dichotomy of cortical simple and complex cells. Nat Neurosci. 2004;7:1113–1122. doi: 10.1038/nn1310. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Ringach DL, Malone BJ. The operating point of the cortex: neurons as large deviation detectors. J Neurosci. 2007;27:7673–7683. doi: 10.1523/JNEUROSCI.1048-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Slovin H, Arieli A, Hildesheim R, Grinvald A. Long-term voltage-sensitive dye imaging reveals cortical dynamics in behaving monkeys. J Neurophysiol. 2002;88:3421–3438. doi: 10.1152/jn.00194.2002. [DOI] [PubMed] [Google Scholar]
  41. Smith EL, 3rd, Bennett MJ, Harwerth RS, Crawford ML. Binocularity in kittens reared with optically induced squint. Science. 1979;204:875–877. doi: 10.1126/science.441743. [DOI] [PubMed] [Google Scholar]
  42. Smith EL, 3rd, Chino YM, Ni J, Cheng H, Crawford ML, Harwerth RS. Residual binocular interactions in the striate cortex of monkeys reared with abnormal binocular vision. J Neurophysiol. 1997;78:1353–1362. doi: 10.1152/jn.1997.78.3.1353. [DOI] [PubMed] [Google Scholar]
  43. Tan AY, Zhang LI, Merzenich MM, Schreiner CE. Tone-evoked excitatory and inhibitory synaptic conductances of primary auditory cortex neurons. J Neurophysiol. 2004;92:630–643. doi: 10.1152/jn.01020.2003. [DOI] [PubMed] [Google Scholar]
  44. Volgushev M, Vidyasagar TR, Pei X. A linear model fails to predict orientation selectivity of cells in the cat visual cortex. J Physiol. 1996;496:597–606. doi: 10.1113/jphysiol.1996.sp021711. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Volgushev M, Pernberg J, Eysel UT. Comparison of the selectivity of postsynaptic potentials and spike responses in cat visual cortex. Eur J Neurosci. 2000;12:257–263. doi: 10.1046/j.1460-9568.2000.00909.x. [DOI] [PubMed] [Google Scholar]
  46. Wiesel TN, Hubel DH. Single-cell responses in striate cortex of kittens deprived of vision in one eye. J Neurophysiol. 1963;26:1003–1017. doi: 10.1152/jn.1963.26.6.1003. [DOI] [PubMed] [Google Scholar]
  47. Wiesel TN, Hubel DH, Lam DM. Autoradiographic demonstration of ocular-dominance columns in the monkey striate cortex by means of transneuronal transport. Brain Res. 1974;79:273–279. doi: 10.1016/0006-8993(74)90416-8. [DOI] [PubMed] [Google Scholar]
  48. Yinon U. Age dependence of the effect of squint on cells in kittens' visual cortex. Exp Brain Res. 1976;26:151–157. doi: 10.1007/BF00238279. [DOI] [PubMed] [Google Scholar]

Articles from The Journal of Neuroscience are provided here courtesy of Society for Neuroscience

RESOURCES