An Evolutionary Hybrid Cellular Automaton Model of Solid Tumour Growth

Abstract

We propose a cellular automaton model of solid tumour growth, in which each cell is equipped with a micro-environment response network. This network is modelled using a feed-forward artificial neural network, that takes environmental variables as an input and from these determines the cellular behaviour as the output. The response of the network is determined by connection weights and thresholds in the network, which are subject to mutations when the cells divide. As both available space and nutrients are limited resources for the tumour this gives rise to clonal evolution where only the fittest cells survive. Using this approach we have investigated the impact of the tissue oxygen concentration on the growth and evolutionary dynamics of the tumour. The results show that the oxygen concentration affects the selection pressure, cell population diversity and morphology of the tumour. A low oxygen concentration in the tissue gives rise to a tumour with a fingered morphology that contains aggressive phenotypes with a small apoptotic potential, while a high oxygen concentration in the tissue gives rise to a tumour with a round morphology containing less evolved phenotypes. The tissue oxygen concentration thus affects the tumour at both the morphological level and on the phenotype level.

1 Introduction

It is a well known fact that evolution plays an extensive role in the development of cancer and that tumours consist of a large number of different subclones that compete for space and resources (Alexandrova, 2001; Nowell, 1976). Tumour invasion has successfully been modeled by both continuous and discrete mathematical approaches, but most of these models have failed to capture the evolutionary dynamics of tumour growth, and thus neglected a very important aspect of carcinogenesis. The aim of this work is to introduce a novel cellular automaton model that incorporates the evolution of subclones within the tumour. In order to include evolutionary dynamics into the model the cells need to be equipped with a genotype, that determines their behaviour, and that is inherited by the daughter cells. This poses problems, as the cell is an extremely complex structure and contains a vast amount of genetic material. The solution to this is, as always in mathematical modelling, to simplify the system. This simplified model should be straight-forward enough to be computationally feasible but still complex enough to capture the interesting dynamics of clonal evolution. This will be done by viewing the genotype of the cell as decision mechanisms and to focus on a few traits and behaviours that are often transformed in cancer cells. The decision mechanism of the cells will be modeled using artificial neural networks (Haykin, 1999) that map the environment of the cells to a behaviour or action.

1.1 Biological background

Cancer is a genetic disease, which arises from mutations in single somatic cells. These mutations alter the proliferation control of the cells which leads to uncontrolled cell division (Hanahan and Weinberg, 2000). The transformed cells form a neoplastic lesion that may be invasive, in which case it is labeled a carcinoma, or benign, an adenoma. The decisive factor between these two behaviours is the growth rate and invasiveness of the cells in the neoplasm. These two properties are in turn driven by what mutations the cells have acquired. In the invasive case the tumour grows in an uncontrolled manner up to a size of approximately 10⁶ cells. At this size the diffusion driven nutrient supply of the tumour becomes insufficient and the tumour must initiate angiogenesis. When the tumour has been vascularised the tumour can grow further and at this stage metastases are often observed. The process of angiogenesis has been modeled successfully by Anderson and Chaplain (1998), but our work will focus on the earlier stages of tumour development.

The purpose of this model is to investigate the pre-vascular stage of invasive tumour growth, when the growth is limited by the diffusion of nutrients. The structure of a tumour at this stage is often disordered compared to healthy tissue. The reason for this is that the cancer cells are non-responsive to normal growth inhibiting signals (Hanahan and Weinberg, 2000), and thus compete against each other for space and nutrients in the tumour. Although the cancer cells have escaped normal growth control, most tumours exhibit a layered structure, which is due to the diffusion limited supply of nutrients (Sutherland, 1988). When the tumour reaches a critical size the diffusion of nutrients is not enough to supply the inner parts of the tumour with oxygen, this leads to cell death or necrosis in the core of the tumour. Outside the necrotic core a rim of quiescent cells is found and further out a thin rim of proliferating cells. The mitotic activity therefore only takes place in a small fraction of the tumour, while the majority of the tumour consists of cells that are either quiescent or dead. In this competitive environment any cell with a growth advantage gives that cell and its genotype a higher probability of surviving. For example cells that have a weaker apoptotic response to hypoxia will have a growth advantage in the tumour where the oxygen concentration is low. This competition between the cells is similar to the process of Darwinian evolution of species (Darwin, 1910) with the exception that the evolution inside a tumour takes place on a much faster time-scale (Michor et al., 2001). The reason for this seems to be that most cancer cells are genetically unstable, which means that they have a much higher mutation probability than normal cells (Loeb et al., 2003). One of the main causes of this is that many cancer cells have acquired mutations in the p53-gene, which when unmutated acts as a guardian of the genome and maintains the genetic integrity of the cell (Soussi and Lozano, 2005).

Another feature that is often observed in cancer cells is their tendency to rely on anaerobic metabolism even in the abundance of oxygen, known as the glycolytic phenotype. This is known as the Warburg effect and was discovered in the 30's (Warburg, 1930). This behaviour is surprising because the anaerobic metabolic pathway is much less efficient and the acid that is produced in this pathway is harmful for the cells, as it lowers the intracellular pH. But seen from an evolutionary perspective it must lead to some form of growth advantage for the cells that utilise it. Advantages that have been proposed are the possibility to survive in poorly oxygenated environments and that the acid produced degrades the surrounding tissue and thus increases the invasiveness of the tumour (Gatenby and Gillies, 2004; Smallbone et al., 2005).

The properties that cancer cells acquire at this early stage of tumour development are mainly driven by the micro-envrionment in which the cancer cell population evolves. This early selection pressure may also to some extent, determine the later development and invasiveness of the tumour. Recent experimental data has shown that tumour hypoxia is an important factor in tumour development being directly linked to both tumour morphology (Höckel et al., 1996) and cancer cell aggressiveness (Graeber et al., 1996; Kim et al., 1997). The relationship between tumour morphology and invasive potential is a known pathological fact, however, the evolutionary reasons for this link have still not fully been understood. The main aim of this paper is therefore to introduce a model capable of capturing the dynamics of clonal evolution and to use this to investigate the impact of tissue oxygen concentration on both the morphology and the genetic makeup of cancer during the early avascular stage of development. We therefore hope this paper will give insight into the effects of tumour hypoxia and its impact on clonal evolution in tumour development.

1.2 Previous work

Cellular automaton models have been used extensively in mathematical modelling of biological systems (Deutsch and Dormann, 2005). The first work using cellular automata in cancer modelling was done by Düchting and Vogelsaenger (1984), who used it to investigate the effects of radio-therapy. More recent work includes Ferreira's et al. work on tumour morphology (Ferreira et al., 2002), Patel's et al. work on the glycolytic phenotype (Patel et al., 2001) and Anderson's model of tumour invasion (Anderson, 2005). The two former models use a hybrid cellular automaton model, where the CA-elements interact with continuous fields of chemicals. Ferreira's model, which uses a probabilistic updating rule based on the concentration of nutrients, reproduces various tumour morphologies observed in vivo depending on nutrient consumption. Patel's et al. work highlights the importance of the glycolytic phenotype in cancer invasion and the impact of vessel density. Both these models use static update rules, which means that all cells share the same phenotype. This limits their ability to deal with phenomena that are not related to evolutionary dynamics. Anderson's model is somewhat different from a standard CA-model as it derives the migratory behaviour of the cancer cells from a discretisation of a PDE. What more importantly makes this model different from the previous ones is that the cancer cells have different phenotypes, which allows for the investigation of evolutionary dynamics.

A three-dimensional cellular automaton approach was also used in (Kansal et al., 2000a), where the growth of glioblastoma tumours was investigated. Using a Voronoi tesselation with variable grid size they can simulate the tumour growth over several orders of magnitude with good agreement to experimental data. Further they show that the survival probability of a subclone depends on the growth advantage it has over other subclones, and that the survival probability is non-zero although no growth advantage exists (Kansal et al., 2000b). In a another study the above model was extended by introducing a game-theoretic element (Mansury et al., 2006). Assuming that the tumour consists of two distinct subpopulations (one proliferative and one migratory genotype) the authors show that the growth dynamics depends on pay-offs for different cell interactions and that there exists an optimal pay-off for which the tumour velocity (i.e. growth rate) is maximised. The role of cellular response to the micro-environment was investigated by Mansury et al. (2002) in an agent-based model of brain cancer growth. They show that the morphology of the resulting tumour depends on how the cancer cells process information about the micro-environment, and finds a phase transition that separates two distinct growth regimes of the tumour, where the cancer cells grow in either small or large clusters.

The evolutionary dynamics of carcinogenesis has also been investigated by Gatenby and Vincent (2003), using continuous techniques from game theory and population dynamics. Using this approach they identify conditions necessary for invasive growth and suggest that the ordinary cytotoxic treatment of the tumour is often unsuccessful due to the adaptation of the cancer cells to new growth conditions. Another aspect of evolutionary modelling of cancer is considered in Komarova et al. (2003), a study of a stochastic mutation-selection model of early cancer formation. Considering mutations in one tumour suppressor gene and chromosomal instability they show that if chromosomal instability occurs before a mutation, in the considered tumour suppressor gene, it becomes a driving force in early cancer development.

Artificial neural networks have traditionally been used for classification and prediction tasks, some examples are: detection of heart abnormalities (Leung et al., 1990), finger-print recognition (Baxt, 1991) and breast cancer prediction (Floyd et al., 1994). In these tasks the network is trained with a data set that consists of a number of variables from each sample together with the outcome of each sample (in the case of breast cancer the variables are uniformity of cell size, uniformity of cell shape, marginal adhesion etc. and the outcome is if the breast contains a tumour or not). The goal of this procedure is to construct a network that will be able to predict the outcome of an unknown sample which was not in the training set. There are two approaches to solve this problem, either by using a single network that is optimised with respect to the training set using an error minimising algorithm like back-propagation (Haykin, 1999) or by an evolutionary algorithm where an evolving population of networks adapts by mutation and selection (Yao, 1993), where the fitness of a network is determined by how well it can classify the training set. A more recent application of neural networks is to model cell signalling pathways, which was first suggested by Bray (1990). He argues that the performance of cell signalling networks is similar to that of artificial neural networks and that neural networks therefore can be used to model and simulate real signalling pathways. Further he argues that evolution and adaptation of signalling pathways occur by small changes in the network parameters that alter the network connections, and change the behaviour of the cell. Vohradsky (2001) used a neural network approach to model the λ bacteriophage lysis/lysogeny decision circuit. This model, which incorporates multigenic regulation, is in good agreement with experimental results, gives further insight into the experimental observations and shows that neural networks can successfully be used to model regulatory pathways.

The model presented in this paper is aimed at extending the present hybrid cellular automaton models and creating a model that is better suited for the investigation of the role of evolution in tumour invasion. This will be done by modelling the regulatory pathways of each cancer cell with an artificial neural network. This approach is of course not the only way to model clonal evolution, but can be viewed as an alternative to the traditional CA techniques mentioned above. The increased complexity of this model is a disadvantage as it renders mathematical analysis of the model difficult, but this approach also gives some clear advantages compared to previous CA models. Firstly it allows for a more open-ended model of the evolutionary process where the cells are not confined to a predetermined set of possible genotypes and secondly it gives a natural interpretation of how the micro-environment impacts upon clonal evolution.

2 The Model

The basic structure of the model is a two-dimensional grid on which the cells reside and represents a slice of the tissue under consideration. The step size of the grid is chosen so that each automaton element is approximately the same size as a real cell. Each automaton element can either be occupied by a cancer cell or be empty. This of course neglects the complex interactions between the cancer cells and the host tissue which may contain fibroblasts, macrophages, blood vessels and many other cell types and stimuli. These interactions have been shown to be important factors in tumorigenesis (Rubin, 2003), but in order to keep the model simple and to focus on the role of tissue oxygen concentration on tumour development we have chosen not to include these aspects in the current model. In order to remove any growth bias that might be introduced by explicitly incorporating a vascular oxygen supply to the tumour we have also chosen to exclude any interaction between the tumour and the blood supply. Instead the oxygen is supplied from the boundary of the domain, which corresponds to a situation where a neoplastic lesion develops in a tissue surrounded by blood vessels. In order to keep track of concentration fields of oxygen etc., each grid point also holds the concentration of each field at that point in space. The concentration fields are governed by partial differential equations that describe how the chemicals are produced, consumed, degrade and how they diffuse.

In previous CA models for cancer growth the automaton rules that govern the evolution of the system have been static, which means that all cancer cells in the model posses the same properties. In order to include an evolutionary aspect in our model each cancer cell is modeled as an individual entity or agent. This implies that the state of an automaton element is not just characterised by if it holds a cancer cell or not, but by which cell it holds. This means that the update rule for the automaton element is dependent on the cell that it holds, much like in the model by Anderson (2005).

2.1 The Cell

A cell can be thought of as a computing unit that given a certain input “calculates” an output or response. A classical example of this is when normal epithelial cells perform apoptosis (programmed cell death) when they loose adhesion to other cells (Giancotti and Rouslahti, 1999). Information from the receptors at the cell surface (i.e. the micro-environment is the input) is transmitted through molecular pathways (i.e. determined by the genotype) and a response is produced (i.e. the phenotype is the output). Ultimately, the genotype of a cell determines how it responds to certain stimuli (i.e. the genotype “processes” the input and produces an output), and this response can be thought of as the phenotype (see fig. 1). The abnormal behaviour of cancer cells can be viewed as disruptions in the response or decision mechanism due to genetic mutations.

Fig. 1.

A schematic representation of how a cell takes the micro-environment as an input which is then ultimately processed by the cell genotype which in turn decides on an output response which is the phenotype. The resulting cell phenotype then has the potential to modify the micro-environment thus setting up a possible feedback loop.

In the spirit of this, each cell in the model is equipped with a decision mechanism, that determines the actions of the cell based on the cell genotype, the micro-environment in which it resides and interactions between these. The decision mechanism is subject to mutations during cell division. The decision mechanism is modeled using an artificial feed-forward neural network (Haykin, 1999), which have been used extensively in solving classification and recognition problems and have been proven to have the property of being able to approximate any continuous function (Castro et al., 2000). A typical example of a feed-forward neural network can be found in fig. 2.

Fig. 2.

Typical structure of a feed-forward neural network. Information is given to the input layer and the input is fed through the network via the hidden layer and produces a response at the output layer.

Including a neural network as a decision mechanism in each cell of course introduces a higher degree of complexity to the model, but it also makes it possible to model the interactions between the micro-environment and clonal evolution in a more accurate way. With this approach each cell will have an individual response based on the local environment and how it chooses to process it, compared to conventional cellular automata approaches where the behaviour of the cells is decided by global parameters that do not change or evolve e.g. the critical oxygen concentration below which the cells die. This difference is fundamental to why our approach is suitable for investigating clonal evolution, as the underlying mechanism of clonal evolution and selection is that different sub-clones behave in different ways. Another advantage of this model is that the fitness of a cell is not just defined by its genotype, but is also implicitly defined by the micro-environment of the cell (cf. fig. 1). This means that a cell that is adapted for hypoxic conditions will have a high “fitness” in a poorly oxygenated environment, but may have a low “fitness” in other conditions. The fitness of a cell thus depends on how it responds and interacts with its environment, a relationship that is difficult to capture without including an evolvable response network that determines the behaviour of the cell. Finally the use of a neural network allows for a more open-ended model of the evolutionary process as the cells are not confined to a predetermined set of phenotypes as in Anderson (2005) and mutations can occur that have a range of effects on the resulting phenotype.

2.1.1 The Network

The response network of the cells (fig. 3) consists of a number of nodes that can take real number values. The nodes are organised into three layers: one input layer, that takes information from the environment, one hidden layer, and finally an output layer that determines the action of the cell. The nodes in the different layers are connected with varying weights, determined by two matrices w and W, and the nodes in the hidden and output layer are equipped with internal thresholds θ and ϕ. The value of the input layer is determined by the mirco-environment of the cell, these values are then fed through the network and produce a response in the output layer that determines the behaviour of the cell (further details of this procedure can be found in the Appendix).

Fig. 3.

The layout of the response network in the cells, the connections between the input layer and the hidden layer are determined by the connection matrix w and the connections between the hidden layer and the output layer are determined by W.

This neural network approach only serves as an abstract model of cellular behaviour, but still shares some features of the real signaling and regulatory network of the cell. The input layer of the network can be thought of as receptors on the cell surface that interact with extra-cellular molecules. The connections (weight matrix, w) between the input and hidden layer represents the signaling strength of these receptors. The hidden layer functions as regulatory genes that control the behaviour of the cell through the weights of the connection matrix (W) between the hidden and output layer. Finally the output layer can be thought of as the phenotype, as it determines the behaviour of the cell. The connections between the hidden layer and output layer may therefore be considered as a mapping from the genes to the behaviour of the cell, and thus as a mapping from the genotype to the phenotype of the cell. With this analogy in mind we can think of changing a connection between the input and hidden layer as changing the expression level of a certain type of receptor and changing a connection between the hidden and output layer as altering the expression level of a regulatory gene.

This network structure is very versatile since there is no restriction as to what the input nodes represent, they can represent any environmental factor we choose to put in the model. In the most basic setting of our model the only input to the network is the number of neighbours of the cell and the local oxygen concentration. The reason for this choice is that cancer cells often show weaker response to hypoxia-induced apoptosis (Lowe and Lin, 2000) and that they tend to adhere less to their neighbours (Cavallaro and Christofori, 2004). In order to investigate the role of the glycolytic phenotype and tumour acidity we will also include the glucose and hydrogen ion concentration as inputs to the network. This implies that the input vector ξ will have four components, $\xi =(n(\overrightarrow{x},t),c(\overrightarrow{x},t),g(\overrightarrow{x},t),h(\overrightarrow{x},t))$, where $n(\overrightarrow{x},t)$ is the number of neighbours, $c(\overrightarrow{x},t)$ the oxygen concentration, $g(\overrightarrow{x},t)$ the glucose concentration and $h(\overrightarrow{x},t)$ is the hydrogen ion concentration. The assignment of the input nodes can be found in table 1. The output from the network is deterministic and depends only on the weight matrices w, W, the threshold vectors θ, ϕ and the environmental input vector ξ. The phenotype of the cell is then determined by the values of the nodes in the output layer. In our model the output nodes represent the response for proliferation, quiescence, apoptosis, movement and metabolic pathway. As the first three form a group of mutually exclusive behaviours (a cell can not perform these responses simultaneously) the behaviour with the strongest response is chosen from these three, we call this the life-cycle response. If the proliferation node has the strongest response the cell divides and produces a daughter cell, if the quiescence node has the strongest response the cell remains dormant and if the apoptosis node is strongest then the cell dies via apoptosis. The cell is allowed to move if the movement response is sufficiently large (see Appendix for details). The cell metabolism is determined by the response of the metabolic node, and has either anaerobic or aerobic metabolism depending on the sign of the response (see Appendix for details). The assignment of the output nodes is summarised in table 1 and the layout of the network can be found in fig. 3.

Table 1.

The input and output nodes with corresponding function and variable name.

Node	Function	Variable
ξ1	No. of neighbours	$n(\overrightarrow{x},t)$
ξ2	Oxygen concentration	$c(\overrightarrow{x},t)$
ξ3	Glucose concentration	$g(\overrightarrow{x},t)$
ξ4	Acidity [H+]	$h(\overrightarrow{x},t)$
O1	Proliferation	P
O2	Quiescence	Q
O3	Apoptosis	A
O4	Metabolism	M
O5	Movement	Mov

2.1.2 Cell Metabolism

The metabolism of cancer cells has been shown to differ from that of normal cells (Dang and Semenza, 1999). Their metabolic rate is often higher than normal cells and more importantly they have a high tendency to exploit the anaerobic metabolic pathway even in the presence of high oxygen concentrations. This is a somewhat puzzling result as the anaerobic pathway is much less efficient and therefore requires a higher uptake of glucose to maintain the same energy turnover. The two metabolic pathways can be written in a simplified form as:

• Aerobic: 1 Glucose + 6 O₂ → 36 ATP

• Anaerobic: 1 Glucose → 2 ATP

As can be seen the anaerobic pathway is 18 times less efficient at creating ATP molecules, which are the energy units in the cell. Also, both metabolic pathways produce hydrogen ions (H⁺), but the fact that the anaerobic pathway produces 18 times less ATP implies that the hydrogen ion production is much higher for the same energy turn-over. This high hydrogen ion production exceeds the metabolic buffering and in order to maintain a normal intracellular pH cells relying on anaerobic metabolism must transport the excess hydrogen ions to the extracellular space, which leads to an increased acidity in the surrounding tissue (Robergs et al., 2004).

The metabolism of the cancer cells is a crucial aspect of tumour growth and is therefore important to include in the model. The switch to anaerobic metabolism is already included in the response network of the cell, but we would also like to include variations in glucose and oxygen uptake between different subclones in the tumour. For the metabolic pathway the variation in consumption is modeled by letting the cells utilising the anaerobic pathway consume 18 times more glucose whilst not consuming any oxygen. The difference in metabolism between cells with different response networks is modelled by taking into account the strength of the network output. The magnitude of the network output is assumed to be directly proportional to the cell metabolism i.e. a high output results in a high metabolic rate and vice versa. The logic behind this is that different amounts of “energy” will be required to perform different network responses e.g. more for proliferation and less for quiescence. In order to implement this we must define a response that corresponds to normal metabolism and some function that relates the network response to the metabolism. This is done by introducing a“target response” T_r and a modulation function F = F(R), which depends linearly on the response R of the network. The value F of the modulation function is then multiplied by the base consumption/production rates to give the metabolism of each individual cell (see section 2.2). The response R is set to the highest value among the life-cycle nodes, and thus corresponds to the life-cycle response performed by the cell (either P or Q). This is of course a crude way of modelling cell metabolism, but we believe the metabolism to be an important aspect of clonal evolution and therefore important to include in an evolutionary model although in a somewhat simplified manner. The modulation function is given by,

$$F=\max (k(R-T_r)+1,0.25)$$ (1)

where k determines the strength of the modulation and the use of max(•, 0.25) guarantees that the cell has a minimal metabolism, which is a quarter of the initial one. If the network for example gives an additional response of 0.2, then R = T_r + 0.2 and the metabolism of that cell will be F(T_r + 0.2) = (1 + 0.2k) times higher than that of a cell with normal metabolism, i.e. a target response of R = T_r. The parameter k therefore determines to what degree a change in the network response affects the metabolism. Note that R is a function of the input of the network ξ, but also of the weight matrices w, W and the thresholds θ, ϕ. So R = R(ξ, G), where G = (w, W, θ, ϕ) determines the wiring and thresholds of the response network.

The fact that quiescent cells consume less oxygen than active cells is introduced by dividing their consumption by a factor q. This factor is not experimentally well determined and is assumed to lie somewhere between 2 and 100 (Freyer et al., 1984).

2.1.3 Cell Death

Cell death can occur in two distinct ways in the model. If a cell tries to consume more oxygen or glucose than is available at the grid point where the cell resides it will die from starvation (necrosis). The other mechanism is by apoptosis, which occurs if the apoptosis node of the network gets the strongest response.

2.1.4 Cell Movement

Cell movement is determined by the movement node in the response network. As in Anderson (2005) we will use the notion of an internal adhesion value a_i, which is the number of neighbours a cell prefers to adhere to. If the number of neighbours of a cell is higher than the internal adhesion value $(n(\overrightarrow{x},t)\ge a_i)$ the cell is allowed to move, if not it remains stationary. In our network model of cell response this means that the input node corresponding to the number of neighbours will be connected to the movement node, and therefore if $n(\overrightarrow{x},t)\ge a_i$ the movement node takes on a positive value and the cell is allowed to move.

2.1.5 Proliferation

In order for a cell to divide in the model it has to be in the proliferative state, this can only happen if the P-node gets the strongest response among the three life-cycle output nodes. The cell also has to have reached the proliferation age in order to divide. If this is the case the cell tries to divide and places a daughter cell at random in one of the four neighbouring automaton elements. If none of the four CA elements are empty the cell division fails and the cell becomes quiescent. As cancer cells are fast growing cells it is a reasonable to assume that most of the energy metabolised by the cell is used for cell division. Using this assumption we connect the proliferation age to the metabolism of the cells and model cell proliferation in the following way: Each time a daughter cell is created the proliferation age of that cell is picked randomly from N(A_p, A_p/2) normal distribution (taking into account that the proliferation age varies among identical cells), where A_p is the base proliferation age. Every time step the cell is updated an internal counter X_p is incremented with F (eq. 1), and when X_p > A_p the cell has reached its proliferation age. This means that a cell with a low proliferation age will have a higher metabolism.

2.1.6 Mutations

The network wiring of the parent cell, which is represented by the two matrices w, W and the thresholds θ and ϕ, are copied to the daughter cell under mutations. The number of mutations that occur in the daughter cell wiring is chosen from a Poisson distribution with parameter p. These mutations are then distributed equally over the matrices and threshold vectors. The parameter p is thus the average number of mutations per cell division, as the mean value of a Poisson distribution equals the parameter in the distribution, which in this case is p. It should be noted that the mutation rate in this model does not correspond to the somatic mutation rate in human cells, as the amount of information copied by a real cell is approximately 10⁸ orders higher in magnitude. The incorrect copying is modeled by adding a normal distributed number s ∈ N(0, σ) to the daughter cell matrix or threshold entry, which means that x → x + s, for those entries x that are chosen for mutation. The mutations alter the connection strength between the nodes, which in turn changes how the cells responds to the micro-environment. If for example a mutation occurs in a connection that links the oxygen concentration with the apoptosis node this changes how the cell responds to the local oxygen concentration. A detailed description of how the mutations affect the behaviour of the cells is given in the Appendix.

2.2 Chemical Fields

In the pre-vascular stage of carcinogenesis the tumour has not yet acquired its own vasculature, the nutrients therefore have to diffuse from the surrounding blood vessels to the tumour. The metabolic waste products of the cancer cells also diffuse in to the tissue and are transported away from the tissue when they reach a blood vessel. The metabolism of cancer cells includes a large number of different chemicals that are all needed for maintenance and cell division, but it is known that oxygen and glucose concentrations limit the growth of the tumour (Sutherland, 1988). We will therefore only incorporate these two fields into the model as well as a field for the hydrogen ion concentration. A further simplification of the chemical fields is that we neglect the decay of the nutrients and that we include the production of oxygen and glucose in the boundary conditions by applying Dirichlet boundary conditions with constant functions. These boundary conditions are meant to imitate a situation were the tissue is surrounded by blood vessels, with constant nutrient and hydrogen ion concentrations, that supply the tumour with nutrients and remove hydrogen ions from the tissue. This gives the equations that describe the fields a simple form, similar to those in the models of Patel et al. (2001) and Ferreira et al. (2002). The time evolution of the oxygen (2), glucose (3) and hydrogen ion (4) fields are governed by the following set of partial differential equations,

$$\frac{\partial c(\overrightarrow{x},t)}{\partial t}=D_c\Delta c(\overrightarrow{x},t)-f_c(\overrightarrow{x},t)$$ (2)

$$\frac{\partial g(\overrightarrow{x},t)}{\partial t}=D_g\Delta g(\overrightarrow{x},t)-f_g(\overrightarrow{x},t)$$ (3)

$$\frac{\partial h(\overrightarrow{x},t)}{\partial t}=D_h\Delta h(\overrightarrow{x},t)+f_h(\overrightarrow{x},t)$$ (4)

where D_i are the diffusion constants and the $f_i(\overrightarrow{x},t)$ give the individual cell consumption or production of the chemical i = c, g, h for the cell at position $\overrightarrow{x}$ at time t. The concentrations of the chemicals are solved on a grid of the same step size as the cells, which implies that the consumption and production terms in (2)-(4) are determined by each individual cell. The $f_i(\overrightarrow{x},t)$'s are thus defined in the following way,

$$f_i(\overrightarrow{x},t)=\{\begin{array}{cc}0\hfill & \text{if the automaton element at}\overrightarrow{x}\text{is empty i.e. no tumour cell at that lattice point}\hfill \\ r_{i}F\left(\overrightarrow{x}\right)\hfill & \text{if the automaton element is occupied, i.e. tumour cell exists at that lattice point}\hfill \end{array}\phantom{\}}$$ (5)

where r_i are the base consumption/production rates and $F\left(\overrightarrow{x}\right)$ is the modulated energy consumption (1) of the individual cell occupying the automaton element at $\overrightarrow{x}$.

2.3 Cellular Automaton

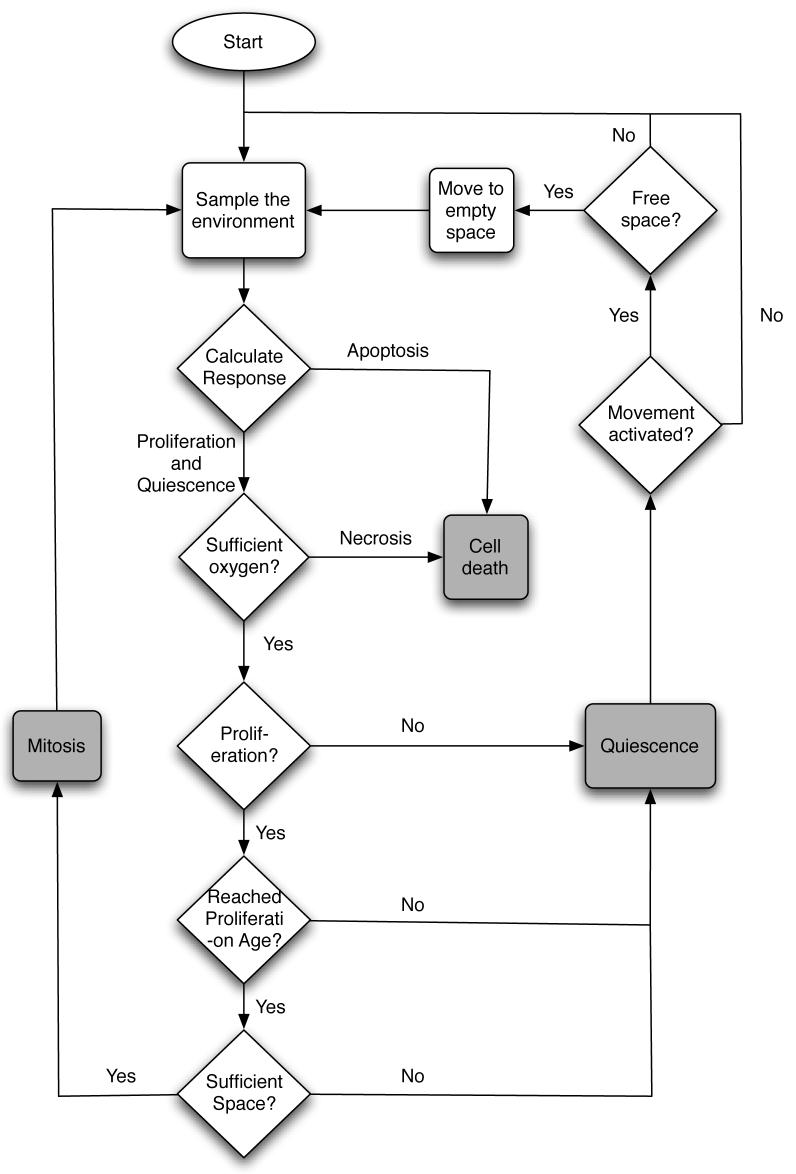
We have so far described the building blocks that constitute the model, and in this section we will describe how all these blocks interact and form the complete model. The two-dimensional tissue under consideration is represented by a N × N grid. The grid is characterised by a grid constant d, which determines the spacing between the cells. The grid points are identified by a coordinate $\overrightarrow{x}=d(i,j)i,j=0,1,\dots .,N-1$. The chemical concentrations interact with the cells according to cellular production or consumption and are given appropriate initial and boundary conditions. The partial differential equations (2), (3) and (4) are discretised using standard five-point finite central difference formulas with space step d and time step Δt. Each time step the chemical concentrations are solved using the discretised equations and everyone of the tumour cells are updated in a random order. Every time step of the simulation each cell is updated according to the schematic life-cycle flowchart in fig. 4 and as follows:

1. The input vector ξ is sampled from the local environment (i.e the grid point where the cell resides).

2. A response R = R(ξ, G) is calculated from the network.

3. The cell consumes nutrients according to the action taken and the metabolic pathway chosen.

4. The life-cycle action determined by the network is carried out:

   • If proliferation (P) is chosen, check if the cell has reached proliferation age and if there is space for a daughter cell. If both are true the cell divides and the daughter cell is placed in a neighbouring grid point, if not the cell does nothing.
   • If quiescence (Q) is chosen the cell becomes quiescent.
   • If apoptosis (A) is chosen the cell dies.

5. If movement is activated and the cells has not divided, it tries to move at random to an empty neighbouring grid point. If none can be found the cell remains stationary.

Fig. 4.

Flowchart describing the life-cycle of a cancer cell.

If a cell dies from either apoptosis or necrosis it is no longer updated. If the cell dies by apoptosis the grid point where it resided is considered empty, but if the cell dies from necrosis (starvation) the cell still occupies the grid point. The reason for this is that the two death processes occur in different ways. When apoptosis occurs the cell membrane collapses and the cell shrinks, while when necrosis occurs the cell keeps it shape and thus still occupies physical space (Alberts et al., 1994).

2.4 Parameters

The parameters in the model can roughly be divided into three categories: cell behaviour, tissue structure and modelling parameters. The first category encompasses all parameters related to the response network and cellular metabolism, the second relates to the chemical fields and the third category contains the parameters related to the discrete nature of the model.

One of the most essential groups of cell parameters are those that define the network wiring and thresholds for the initial cancer cells, as these cells are used as “seeds” in every simulation and determine the initial behaviour of the population. As in Anderson (2005) these cells should be defined in such a way that their behaviour resembles that of an initial cancer cell phenotype. The response of the network therefore has to capture the essential behaviour of real cancer cells. The important features that we want to capture are:

• Cells should perform apoptosis if the oxygen concentration $c(\overrightarrow{x},t)$ falls below a certain threshold c_ap.

• Cells should die if the glucose concentration $g(\overrightarrow{x},t)$ falls below a certain threshold g_ap.

• Cells should not divide if there is no space for the daughter cell (contact inhibition) i.e if $n(\overrightarrow{x},t)>3$

• Cells should perform apoptosis if the acidity $h(\overrightarrow{x},t)$ is a above a certain threshold h_ap.

• Cells should switch to anaerobic metabolism if the oxygen concentration $c(\overrightarrow{x},t)$ falls below c_m.

• A cell is allowed to move if the number of neighbours exceeds the internal adhesion value a_i.

The value of c_ap is difficult to estimate as it depends on the cell type under consideration, but measurement performed in several types of tumours reveal that the oxygen concentration in the necrotic centre of the tumour is 0.5-30%of the concentration in the surrounding tissue (Brown and Wilson, 2004). We therefore estimate c_ap to be 15 % of the initial oxygen concentration. The threshold for glucose induced necrosis is set to 50% of the normal glucose concentration, below which hypoglycemia occurs (Ganong, 1999). The acidity threshold is set to match the critical pH = 7.1 below which cells go into apoptosis (Casciari et al., 1992). The metabolic threshold is set to c_m = 0, as we are interested in the emergence of cells that utilise the anaerobic pathway. Finally we set a_i=3, which means that a cell is allowed to move if it has at least three neighbours. A phenotype with the above specification was written by hand and the details of the response network are given in the Appendix.

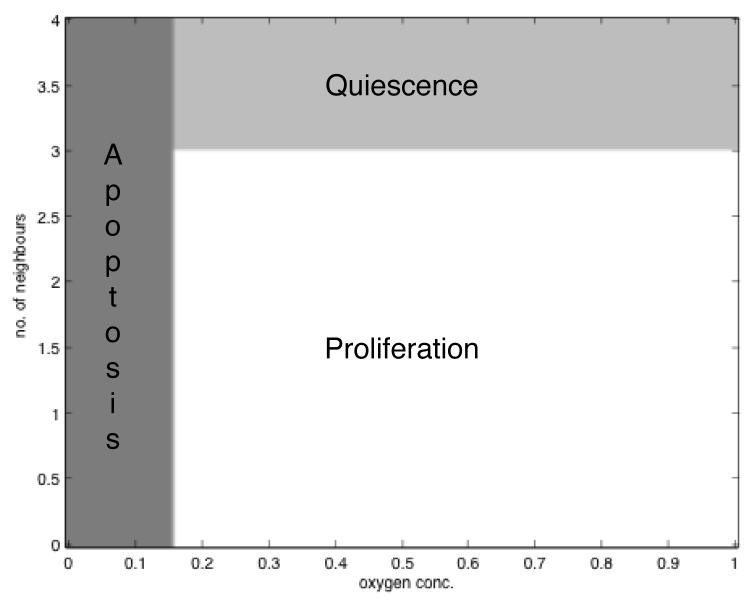
If we only look at the number of neighbours and the oxygen concentration as input to the network the resulting behaviour of the network can be represented in a two dimensional plot, which shows the life-cycle response of the network as a function of the two inputs. A plot for the initial network can be found in fig. 5, which shows that for low oxygen (c < 0.15) concentrations the cell performs apoptosis irrespective of the number of neighbours. For higher oxygen concentrations (c > 0.15) the behaviour of the cell depends on the number of neighbours, if it exceeds 3 the cell becomes quiescent, if not it will proliferate.

Fig. 5.

A plot showing the response of the life-cycle nodes as a function of the oxygen concentration and the number of neighbours. The glucose and acid concentrations are kept constant at g = 1 and h = 0. At low O₂ concentrations c < 0.15 the cells performs apoptosis (A > Q and A > P) and for high concentrations c > 0.15 it proliferates if n < 3 (P > A and P > Q) or becomes quiescent if n > 3 (Q > P and Q > A).

2.5 Parameter Estimation and Non-dimensionalisation

Cancer cells in multi-cell spheroids are known to consume oxygen at a rate of 2.3 × 10⁻¹⁶ mol cells⁻¹ s⁻¹ (Freyer and Sutherland, 1986) and we therefore set the base oxygen consumption rate r_c = 2.3 × 10⁻¹⁶. The glucose consumption rates are estimated using the simplified reaction formulas to $r_g^a=r_c∕6=3.8\times {10}^{-17}$ mol cells⁻¹ s⁻¹ for the aerobic pathway and mol cells⁻¹ s⁻¹ for the anaerobic, assuming that the amount of energy is independent of the metabolic pathway. The hydrogen ion production rate for cells relying on anaerobic metabolism is harder to estimate as it depends on how efficiently the hydrogen ions are transported through the cell membrane and on tissue buffering. We will use r^h = 1.5×10⁻¹⁸ mol cells⁻¹ s⁻¹, the same as in Patel et al. (2001). The quiescent metabolic factor q is set to 5, within the experimentally determined range (Freyer et al., 1984). The target response is set to T_r = 0.675. This value is chosen so that it matches the response of the initial network, giving cells with the initial network consumption/production rates of r_i. We have choosen a modulation strength in (1) of k = 6, because we want to limit the maximum metabolism to be 3 times the base metabolism (similar to the difference in the least and most aggressive phenotypes in Anderson (2005)) i.e. if the network produces the maximal response of R = 1 the metabolism will be approximately 3 times higher than the base metabolism. The proliferation age, the time it takes for a cell to move through the entire cell-cycle once has been experimentally measured to lie between 8 and 24 h depending the type of cells (Calabresi and Schein, 1993), we use the intermediate value A_p = 16 h. The mutation rate in this model should be related to the somatic mutation rate in human cells, but it should not be compared to the per site mutation rate, but rather to the number of mutations that occur per cell division in genes that are related to the cellular responses we consider. This is of course very hard to estimate and we therefore set the mutation rate to p = 0.01, which means that on average 1 % of the matrix and vector entries are copied incorrectly. A summary of these cell specific parameters can be found in table 2 along with appropriate references.

Table 2.

A summary of the cell specific parameters in the model.

Parameter	Meaning	Value	Reference
rc	base oxygen consumption rate	2.3 × 10−16 mol cells−1 s−1	(Freyer and Sutherland, 1986)
$r_g^a$	aerobic glucose consumption rate	3.8 × 10−17 mol cells−1 s−1	Calculated from (Freyer and Sutherland, 1986)
$r_c^{\mathit{an}}$	anaerobic glucose consumption rate	6.9 × 10−16 mol cells−1 s−1	Calculated from (Freyer and Sutherland, 1986)
rh	hydrogen ion production rate	1.5 × 10−18 mol cells−1 s−1	(Patel et al., 2001)
Ap	proliferation age	16 h	(Calabresi and Schein, 1993)
p	mutation probability	0.01	(Anderson, 2005)
q	quiescent metabolism factor	5	(Freyer et al., 1984)
Tr	target response	0.675	Model specific
k	modulation strength	6	Model specific
σ	mutation strength	0.25	Model specific

In order to make the simulation and analysis of the model simpler we non-dimensionalise the equations (2) - (5) in the standard way. Time is rescaled by the typical time of the cell-cycle, τ = 16 h, and the length by the maximal size of a early stage tumour, L = 1 cm. This rescaling of the length gives each square cell an area of 6.25 × 10⁻⁶ cm², which is approximately the same as a cancer cell (Casciari et al., 1992). The chemical concentrations are rescaled using background concentrations: c₀ = 1.7 × 10⁻⁸ mol O₂ cm⁻² (Anderson, 2005), g₀ = 1.3 × 10⁻⁸ mol cm⁻² (Walenta et al., 2001) and h₀ = 1.0 × 10⁻¹³ mol cm⁻² (corresponding to normal tissue pH = 7.4) (Patel et al., 2001) and the tumour cell density n₀ = 0.0025⁻² = 1.6 × 10⁵ cells cm⁻² (as the cells reside on a 2-dim. grid). The diffusion constants for the nutrients and the hydrogen ions have been measured experimentally and are set to D_c = 1.8 × 10⁻⁵cm²/s (Grote et al., 1977), D_g = 9.1 × 10⁻⁵cm²/s (Crone and Levitt, 1984) and D_h = 1.1 × 10⁻⁵cm²/s (Crone and Levitt, 1984). A summary of these micro-environment specific parameters can be found in table 3 along with appropriate references. The new non-dimensional variables are thus given by,

$$\begin{array}{cc}\hfill & \tilde{\overrightarrow{x}}=\frac{\overrightarrow{x}}{L},\tilde{t}=\frac{t}{\tau },\hfill \\ \hfill & \tilde{c}=\frac{c}{c_0},{\tilde{D}}_c=\frac{D_c\tau }{L^2},{\tilde{r}}_c=\frac{\tau n_0{r}_c}{c_0},\hfill \\ \hfill & \tilde{g}=\frac{g}{g_0},{\tilde{D}}_g=\frac{D_g\tau }{L^2},{\tilde{r}}_g=\frac{\tau n_0{r}_g}{g_0},\hfill \\ \hfill & \tilde{h}=\frac{h}{h_0},{\tilde{D}}_h=\frac{D_h\tau }{L^2},{\tilde{r}}_h=\frac{\tau n_0{r}_h}{h_0}.\hfill \end{array}$$ (6)

For notational convenience we will drop the tildes on the non-dimensional variables.

Table 3.

A summary of the micro-environment specific parameters in the model in dimensional units.

Parameter	Meaning	Value	Reference
Dc	oxygen diffusion constant	1.8 × 10−5cm2 s−1	(Grote et al., 1977)
Dg	glucose diffusion constant	9.1 × 10−5cm2 s−1	(Crone and Levitt, 1984)
Dc	hydrogen ion diffusion constant	1.1 × 10−5cm2 s−1	(Crone and Levitt, 1984)
c0	oxygen background conc.	1.7 × 10−8 mol cm−2	(Anderson, 2005)
g0	glucose background conc.	1.3 × 10−8 mol cm−2	(Walenta et al., 2001)
h0	hydrogen ion background conc.	1.0 × 10−13 mol cm−2	(Patel et al., 2001)
n0	cancer cell density	1.6 × 105 cells cm−2	(Casciari et al., 1992)

The grid size was set to N = 400, which means that we can simulate a tumour of radius 200 cells, which if we assume radial symmetry in a 3-dimensional setting would correspond to a tumour consisting of approximately 200³ = 8 × 10⁶ cells. The time step in the simulation was set to Δt = 5 × 10⁻⁴ and the space step to d = 0.0025.

3 Simulations

The model presented here is quite complex and contains many parameters. Due to this complexity we decided to investigate the dynamics of a subsystem of this model initially. Specifically we removed cell movement, the choice of anaerobic metabolism and therefore the chemical fields for glucose and hydrogen ions. The corresponding input and output nodes in the cellular response network were also removed. Using this “minimal” system we will investigate how the oxygen background concentration impacts on the growth and evolutionary dynamics of the system.

Note that due to the non-dimensionalisation varying the oxygen background concentration c_o is equivalent to either varying the dimensional consumption rate r_c or the initial background concentration of oxygen in the tissue c_o see eq. (6). In the following we will refer to changing the oxygen concentration, but this also corresponds directly to changing the consumption rate of the cells and thus changing the cell type of which the tumour consists.

In all simulations the initial condition for oxygen is a homogeneous concentration of $c(\overrightarrow{x},t)=1$ with a constant oxygen concentration of c = 1 on the boundary. This boundary condition is meant to imitate a situation where the tissue is surrounded by blood vessels that supply the tumour with oxygen via perfusion. Every simulation is started with an initial cancer cell population of 4 cells in the centre of the grid, each of which has the same initial network (A.4). In the next section we present results that investigate two important aspects of our model: (i) growth dynamics and (ii) evolutionary dynamics.

The growth dynamics of the system were investigated for three different values of the oxygen background concentration that represent low to standard oxygen concentration: c_o/10, c_o/2.5 and c₀. We have examined the spatial distribution of different cell states in the tumour (proliferating, quiescent and dead cells) after 33, 66 and 100 time steps on a grid of size 400×400. We have also measured the time evolution of the total number of cells (including dead cells) in the tumour and the time evolution of the invasive distance, which is the distance from the centre of the grid (where the tumour starts growing) to the most distant cancer cell in the tumour. As the mutations introduce randomness into the model both of these measurements were averaged over 20 simulations with different random seeds.

The impact of the oxygen concentration on the evolutionary dynamics was investigated by analysing the diversity of the cancer cell populations by looking at the time evolution of the Shannon index, a measure of the diversity in the population, for oxygen consumption rates of c₀ and c₀/10. We also analysed the phenotypes of the tumour cells that emerge in the simulations for the two different values of the oxygen consumption rate.

4 Results

4.1 Growth Dynamics

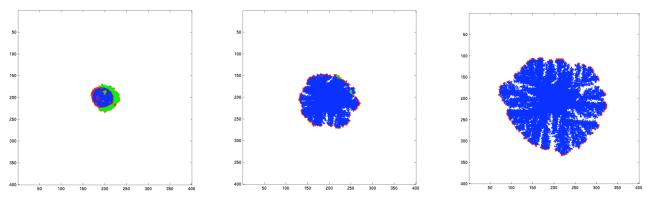
For the lowest oxygen concentration c₀/10 the tumour consists almost exclusively of dead cells and exhibits an obvious fingering morphology (fig. 6), similar to the sort of structures obtained from diffusion limited aggregation (DLA) (Sander, 1986), growth patterns of bacteria (Matsushita and Fujikawa, 1990) and to the tumour morphologies in Ferreira's et al. model (Ferreira et al., 2002). For this oxygen concentration cell death appears early in the simulation at t ≈ 10 (7 days)¹ , as the diffusion limited oxygen supply can't provide the inner parts of the tumour with sufficient oxygen. From this stage the number of cells in the tumour grows approximately linearly in time (fig. 9b), with the number of proliferating and quiescent cells remaining constant throughout the simulation. Only the cells residing on the boundary of the tumour have sufficient oxygen for proliferation, but even here the oxygen concentration is not enough to sustain normal growth as compared with standard oxygen consumption (fig. 8). Instead the cells have to compete with their neighbours for oxygen, which ultimately leads to the fingering morphology, where the proliferating cells reside on the tips of the fingers. When a cell divides and places its daughter cell outside the existing tumour boundary it reduces the chance for neighbouring cells to survive, as the daughter cell “steals” oxygen from cells that surround it. This type of growth can be seen as a race towards regions of higher oxygen concentration.

Fig. 6.

Spatial distribution of the cells at t = 33, 66 and 100 (approx. 22, 44 and 66 days) for c₀/10 on a grid of size 400×400. Proliferating cells are shown as red, quiescent cells as green, dead cells as blue and empty grid points are white. For this setting hypoxia appears early in the simulation and after the onset of hypoxia the tumour continues to grow with a fingered morphology due to the low oxygenconcentration.

Fig. 9.

The time evolution of the a) invasive distance and b) total number of cells, for consumption rates: c₀/10, c₀/2.5 and c₀.

Fig. 8.

Spatial distribution of the cells at t = 33, 66 and 100 (approx. 22, 44 and 66 days) for c₀ on a grid of size 400×400. Proliferating cells are shown as red, quiescent cells as green, dead cells as blue and empty grid points are white. The tumour exhibits an almost smooth proliferating boundary with a homogeneous distribution of dead cells in the interior.

When the oxygen concentration is increased to c₀/2.5 the dynamics of the system changes. The growth of the tumour is now more regular, although a vague fingering pattern is still visible (fig. 7). The lowering of the oxygen consumption also changes the temporal behaviour of the model. The higher oxygen concentration in the tissue makes it possible for the tumour to grow larger before the centre of the tumour becomes hypoxic. This happens at t ≈ 35 (23 days), after which the tumour continues to grow, but now dominated by dead cells and a thin rim of proliferating cells on the boundary, similar to that seen in Anderson (2005). The asymmetric boundary seen at t = 22 in fig. 7, and the absence of a quiescent rim at t =66 and 100 is due to the fact that the cells have lost contact inhibition due to mutations and try to proliferate although there is no space available.

Fig. 7.

Spatial distribution of the cells at t = 33, 66 and 100 (approx. 22, 44 and 66 days) for c₀/2.5 on a grid of size 400×400. Proliferating cells are shown as red, quiescent cells as green, dead cells as blue and empty grid points are white. For this value of the background oxygen concentration the hypoxia appears later than for c₀/10, but the tumour still exhibits a fingering pattern though less prominent.

For the highest oxygen concentration c₀ the hypoxia in the centre of the tumour appears, as expected, at a later stage compared with the other results. After the onset of hypoxia the tumour continues to grow in a circular manner with a necrotic core and a thin rim of proliferating cells (fig. 8). The fingering structure found for c₀/10 and c₀/2.5 is now completely gone and the tumour exhibits an almost homogeneous distribution of dead cancer cells within its interior. Again there is an absence of a quiescent rim due to the loss of contact inhibition.

From figure 9 it is clear that the oxygen concentration affects the growth rate of the tumour. Both the invasive distance and the total number of cells grow at the highest rate for the high oxygen concentration, although the difference is more notable in the time evolution of the total number of cells. In order to further investigate how the oxygen concentration affects the growth dynamics we measured how the tumour size depends on the oxygen concentration in the tissue. This was measured by letting the simulation run for t = 100 time steps and counting the number of cells present on the grid (including dead cells). This was averaged over 20 runs for each value of the oxygen consumption rate and the result can be found in fig. 10a. In order to measure the impact of mutations on the growth the above simulations were also performed without any mutations (p = 0) and the result can be found in fig. 10b.

Fig. 10.

These plots show the total number of cells with standard deviation bars after t = 100 time steps (66 days) as a function of the background oxygen concentration a) with mutations b) without mutations. In both plots the x-axis is scaled with c₀, i.e. c₀ = 1.

4.2 Evolutionary Dynamics

The Shannon index H (Shannon, 1948) is given by,

$$H=-\frac{1}{\ln \left(N\right)}\underset{i=0}{\overset{N}{\Sigma }}\left(p_i\ln p_i\right)$$ (7)

where p_i is the probability of finding subclone i in the population and N is the number of distinct subclones present in the population. We consider cells to be of the same subclone if they have identical response networks. The Shannon index reaches its maximum of 1 when all existing subclones are different $(\mathrm{i}.\mathrm{e}{p}_i=\frac{1}{N}\text{for all}i)$, and its minimum 0 when the population consists of only one subclone. The time evolution of the Shannon index was measured for typical simulations in both settings and the results can be found in fig. 11.

Fig. 11.

The time evolution of the Shannon index H for c₀ and c₀/10. For c₀/10 H increases much faster and reaches a maximum of H ≈ 0.9 at t ≈ 30 and then slowly decreases, while for c₀ it increases at a slower rate and settles at H ≈ 0.8 after t ≈ 80.

In order to measure the behaviour or phenotype of the cells we have devised a measure on the response network that quantifies the behaviuor of the cell. As already shown in fig. 5 the response of the network for a 2-dimensional input vector can be visualised by identifying subsets of the input space with a cellular response. We now measure the fraction of the input space that each of the corresponding responses occupy. This gives us a 3-dimensional vector S, that we term the response vector, which reflects the behaviour of the cell. Formally we define three sets x_i = {ξ ∈ I;R(ξ) = i}, where R(ξ) is the network response to input vector ξ, i = P, Q, A and I = [0,1] × [0, 4] is the set of all possible inputs to the network. The sizes of these subset are now given by,

$$\left|x_i\right|=\frac{1}{B}\underset{I}{\int }{\delta }_{i,R\left(x\right)}\mathit{dx}$$ (8)

where δ_ij is the Kronecker delta (δ_ij = 1 if i = j, 0 otherwise) and B = 4 is the area of the entire input space. The response vector can now be defined as S = (|x_P| , |x_Q| , |x_A|). The initial cell (fig. A.1) has a measure of S = (0.67, 0.18, 0.15), which means that 67 % of the input space corresponds to proliferation, 18 % to quiescence and 15 % to apoptosis. Note that this measure doesn't give any detailed information about the behaviour, but rather serves as a measure of the “average” behaviour of the cell or the potential the cell has for each response. The measure can also be interpreted as the probability of a certain response if a random point in the input space is used as input.

Fig. A.1.

The wiring of the initial cell's network. The weights of the connections are given next to the arrows and the node thresholds are displayed inside the nodes.

For both c₀/10 and c₀ the system was run for 50 time steps (30 days) after which a cell from the dominating subclone (the most abundant clone at the end of the 50 time steps) was extracted from the system. For each cell the response vector S and the mean consumption rate (1) (averaged over the entire input space) was calculated. The results were averaged over 120 different simulations (with different random seeds) for each of the oxygen concentrations and the results can be found in table 4.

Table 4.

This table shows the average response vector and consumption rate for cells that have evolved under c₀ and c₀/10. The standard deviations are given in brackets. The response of the initial network is given for comparison.

Environment	Proliferation	Quiescence	Apoptosis	Consumption
Initial	0.67	0.18	0.15	1.0
c0	0.68 (0.08)	0.17 (0.05)	0.15 (0.03)	1.0 (0.17)
c0/10	0.83 (0.14)	0.11 (0.11)	0.06 (0.06)	1.14 (0.23)

5 Discussion

From the simulations investigating the growth dynamics it is obvious that the background oxygen concentrations of the tissue affect the growth dynamics of the tumour. In all the simulations the tumour starts growing consisting of quiescent cells and a thin rim of proliferating cells. This structure eventually breaks down when cells start dying in the centre of the tumour because of the low oxygen concentration. The time at which this happens depends on the oxygen concentration. As expected this happens earlier for a low concentration compared to a high concentration. When the oxygen concentration is high the cells can sustain a smoothly growing leading edge that leaves a homogeneous distribution of dead cells in its wake. In the case of low concentrations this mechanism breaks down because there is not enough oxygen available to support the growth of all the cells on the boundary. This gives rise to a competition between different subclones in the tumour, where they compete for the limited supply of oxygen. The low oxygen concentration also amplifies the advantage of cells that already have a small growth advantage, as they grow at the expense of their closest neighbours. If a cell divides too slowly it may get trapped inside the tumour by the surrounding cells and therefore die out as the oxygen concentration drops rapidly as the tumour grows. The low concentration case is thus more competitive than the high concentration one, as an inferior phenotype will have a higher probability of being eliminated in the former case.

The similarity between the observed tumour morphologies and patterns generated by diffusion limited aggregation (DLA) arise because the two processes are in fact quite similar. Both structures are the product of a laplacian growth process, where the structure grows proportional to the gradient of a potential field. In the case of DLA the field is the probability distribution of the random walkers, and in our model it is the oxygen concentration field, which in the limit of low oxygen concentration approximates a potential field.

As seen in fig. 9 the oxygen concentration influences the speed at which the tumour grows. The oxygen concentration of the tissue affects both the time evolution of the invasive distance (fig. 9a) and total number of cells (fig. 9b). A higher oxygen concentration gives rise to a tumour that grows faster with respect to both invasive distance and total number of cells. The reason for this is that a low oxygen concentration reduces the amount of oxygen available at the tumour boundary. This naturally leads to a reduced growth of the tumour as the cells rely on oxygen for survival and proliferation. This behaviuor is quite expected, but what is interesting to observe is that the invasive distance doesn't depend as strongly on the oxygen concentration as the total number of cells. The average total number of cells after 100 time steps is approximately 5 × 10⁴ cells for c₀ and 1 × 10⁴ cells for c₀/10, giving a ratio of approximately 5. As the cells grow in a single layer the total number of cells is proportional to the area of the tumour, which for a compact tumour is proportional to R², the radius squared. If the tumours from c₀ and c₀/10 shared the same compact morphology then the ratio between the invasive distance of c₀ and c₀/10 would be $\sqrt{5}\approx 2.24$, as the invasive distance is approximately the radius of the tumour. But the ratio is in fact 160/110 ≈ 1.45 and the reason for this is that the fingered morphology doesn't grow as a compact structure, but rather as a “fractal” object (fig. 6) where the total number of cells scales as the R^α, where 1 < α < 2 (Mandelbrot, 1977). In fact we calculated α ≈ 1.6 for c₀/10, which means that although the growth rate of the total number of cells is much lower than for c₀, the fractal morphology gives the tumour a considerable invasive distance.

If we now turn to fig. 10 we see as expected that the tumour size is smaller as the oxygen concentration decreases, but what is interesting to observe is how the mutations affect the growth dynamics. The simulations performed with mutations give rise to tumours that are approximately twice the size compared to simulations with corresponding concentrations but without mutations. The reason for this is that the cells acquire mutations that increase their capability to proliferate and which reduce their proliferation age, both which clearly increase the growth rate of the tumour. What we also can observe is that the standard deviations depend on the oxygen concentration when mutations are present (fig. 10a). The variability of the simulation results are significantly higher for high oxygen concentrations compared to the low, but obviously when no mutations (fig. 10b) occur this behaviour disappears. This effect occurs because the selection pressure is different in the low and high concentration cases. A tumour growing in a tissue with a high oxygen concentration can grow at different rates because the environment in which it grows is not very harsh. The selection pressure on the population is therefore weak, which implies that the tumour may consist of cells with a low growth rate, which in turn leads to a smaller tumour. In the case of a tumour growing in a hypoxic environment the selection pressure is stronger as the micro-environment is now harsher. This means that only cells with a high growth rate will survive, and thus the tumour will always consist of fast growing cells and exhibit a lower variance in the size.

The oxygen concentration also influences the time evolution of the Shannon index. Figure 11 displays two qualitatively different behaviours in the time evolution of the index. In the low concentration setting H increases fast and reaches a maximal value of H ≈ 0.9 after about 30 time steps (20 days). It then decreases slowly until it reaches a value of H ≈ 0.8 at the end of the simulation (65 days). In the high concentration case H increases at a lower pace, but settles around the same value of H ≈ 0.8 at the end of the simulation. The explanation for the different behaviours can be found in the morphology of the tumours. In the low concentration case the living cells reside on the tips of the fingered tumour. As there is no contact between these tips they are essentially isolated colonies of cells that evolve independently. This structure facilitates a higher diversity in the population and as a result we see a fast increase in the population diversity. In the high concentration case, which has a more regular growth, the morphology of the tumour allows for a higher degree of competition between different subclones. This competition leads to lower diversity, as some subclones are eliminated by superior ones. As a result the Shannon index increases slower than in the high consumption case. These observations are in agreement with experimental studies of diversity in bacterial colonies that grow in structured and unstructured environments (Korona et al., 1994). What is interesting to observe is that the increase in the Shannon index correlates with the appearance of cell death in the tumour. In the low concentration case cell death appears almost instantaneously in the simulation and we consequently see an early increase in the Shannon index. In the high concentration case the tumour consist of a core of quiescent cells with a rim of proliferating cells for t < 40. During this time the Shannon index remains almost constant at H ≈ 0.2 (after an initial increase). When cell death appears at t ≈ 40 the Shannon index starts to increase and eventually settles at approximately the same value as for 10 · r_c. The appearance of cell death changes the selection pressure on the population, and makes it possible for subclones to exploit the new environment and we consequently observe an increase in the population diversity. For both settings H settles approximately around the same value H ≈ 0.8. This value depends on evolutionary settings such as the mutation probability and mutation strength, which are identical for the two compared here.

The two settings also give rise to different phenotypes. The averages shown in table 4 display a significant difference between the cells that have evolved in the high and low oxygen concentrations. The dominant subclones from the high concentration differ little from the initial cells, the only difference is a slight increase in proliferation potential and decrease in quiescence potential. The apoptosis potential is the same as for the initial cells and the consumption rate is also unchanged. For the cells from the low concentration on the other hand we can see an obvious difference. They have on average increased proliferation potential and consequently decreased quiescence and apoptosis potentials. We also see an increase in the consumption rate, which also means a decrease in the proliferation age. The cells from the high consumption settings have thus evolved further away from the initial cell. They can also be said to be more aggressive as they will be proliferative in a larger part of the input space and thus in a wider range of environmental conditions.

The reason for this is that a lower oxygen concentration in the tissue creates an environment which is harsher and therefore more competitive, and as a result the selection pressure on the population is stronger. As mentioned earlier the growth in the low concentration case can be viewed as a race towards regions of higher oxygen concentration and it is this mechanism that makes the selection in the high consumption case so strong. If a cell can't go into mitosis because the oxygen concentration is too low or because it has not yet reached it's proliferation age it might be trapped inside the tumour, and as the oxygen concentration drops rapidly over the tumour boundary the cell will eventually die. It is therefore a selective advantage to have a large proliferation potential and to have a low proliferation age, exactly what we observe in the cells from the high consumption simulations. The high concentration case also exhibits competition between the cells, but as cell death appears later in the simulation and the oxygen concentration doesn't decay as rapidly over the tumour boundary, the selective forces are less evident in this case. What is also interesting to observe is that the cells from the low concentration sacrifice normal consumption for a low proliferating age, as the two are linked through the response modulation (1). This means that the proliferation age is under stronger selective pressure than the consumption rate. Although a high consumption increases the possibility of death by starvation this is over-shadowed by the advantage of a faster cell cycle.

Combining the results from the growth and evolutionary dynamics we can observe that there is a clear connection between the morphology of the tumour and the phenotypes it contains. The high concentration case gives rise to a round tumour morphology and phenotypes with a low proliferation potential, while the low concentration case gives rise to a fingered morphology containing aggressive cells with a higher proliferation potential and faster cell cycle. This implies that the oxygen concentration (or base consumption rate) affects the tumour on both a global morphological level and on the phenotypic level of the individual cells.

If we compare the results from this model with the results from Anderson (2005) and Anderson et al. (2006) we see that although the two models are quite different, both with respect to how cell behaviour and mutations are modelled, they give similar results. Anderson's model uses a simplistic model for mutations, where the mutations are either linear (the phenotypes become progressively more aggressive) or completely random, whereas in this model the mutations are random but the daughter cells are always similar to their parents as they inherit the response network. In Anderson's model the tumour growth is driven by a combination of proliferation and migration via haptotaxis in response to gradients within the extra-cellular matrix (ECM), while in our model growth only occurs by proliferation. Despite these differences both models suggest that an aggressive phenotype is more likely to appear in a tumour exhibiting a fingered morphology. In Anderson's model the morphology is heavily influenced by the structure of the ECM, where a heterogeneous ECM gives rise to a fingered tumour containing aggressive phenotypes. This heterogeneous ECM could be interpreted as a harsh environment. In this model it is the tumour hypoxia that drives the fingering morphology, but we observe the same connection between morphology and cancer cells aggressiveness as in Anderson's model.

Overall the model results make some interesting predictions about links between tumour aggressiveness, morphology, genetic heterogeneity and the micro-environment. Some of these predictions are in agreement with recent experimental results, in particular Graeber et al. (1996); Kim et al. (1997) show that cancer cells from hypoxic tumours have a smaller apoptotic potential. The hypoxic micro-environment provides a selection pressure in the tumour for subclones which can withstand the low oxygen concentration. This is precisely what we observe in our model i.e. a low oxygen concentration (a higher degree of hypoxia) gives rise to phenotypes with a smaller apoptotic potential. In another experimental study on lung carcinoma cells, Koshikawa et al. (2006) show that sub-clones with smaller apoptotic potential have a growth advantage in hypoxic tumours, which also supports our findings. Tumour hypoxia has been linked to tumour morphology in clinical studies (Höckel et al., 1996) and more recently in an experimental study (Pennacchietti et al., 2003). In the clinical study on cervical cancers, it was shown that tumours with a high degree of hypoxia exhibited larger tumour extensions compared to well-oxygenated tumors of similar clinical stage and size. Additionally, they show that patients with these same hypoxic tumours had a significantly worse survival probability compared to patients with non-hypoxic tumours. In the experimental study it was found that tumour spheroids grown in collagen gels under hypoxic conditions produced fingered invasive tumour morphologies, in contrast to the spherical structures that grew under normoxic conditions. Both of these in vivo and in vitro results show a clear correlation with our in silico simulations, in particular we show that a low oxygen concentration (a higher degree of hypoxia) gives rise to a fingered morphology and that these fingered tumours contain a more aggressive population (thus more life threatening).

Whilst the experimental evidence discussed above is in good agreement with the predictions from our model, it is clear that a more explicit experimental approach would be required to fully validate the model predictions. One such experiment would be to seed tumours in vivo in different mouse tissues that are known to have distinct levels of oxygenation. The morphology of the resulting tumours which grow could then be measured. By additionally taking biopsies from the tumour, experimental assays could then be used to measure both the proliferative and apoptotic potential of the tumour. This type of experimental procedure would be able to give results on both the macroscopic level of morphology and on the phenotype level of individual cells simultaneously, which could then easily be compared with the results from our model.

6 Conclusions

In this paper we have presented a novel hybrid cellular automaton model which is aimed at investigating the evolutionary dynamics of early tumour development. Simulations performed with a subsystem of this model show that the the tissue background oxygen concentration (or base oxygen consumption rate) affects both the growth dynamics of the tumour and the evolutionary dynamics of the competition between different subclones within the tumour.

The results reveal that there is a connection between the morphology of the tumour and the phenotypes that it contains. The fingered morphology, which occurs when the tumour grows in a tissue with a low background oxygen concentration (c₀/10), contains phenotypes that have evolved further away from the ancestral cell and that exhibit a more aggressive phenotype compared to tumour grown under normoxic conditions (c₀), that grows with a round morphology. The oxygen concentration also influences the population diversity of the cancer cells. We observe a higher heterogeneity in the population in harsh growth conditions, where the oxygen concentration is low, compared to the high concentration case. Although this is the case it should be noted that a harsh environment gives rise to a lower variance in the tumour size, which suggests that the evolution is more directed towards aggressive phenotypes in the low concentration case.

Tumour morphology under hypoxic conditions has already been investigated by Ferreira et al. (2002) and several previous models have investigated clonal selection (Kansal et al., 2000b; Mansury et al., 2006; Gatenby and Vincent, 2003), but crucially it is the link between morphology and clonal evolution that is the central result of this paper. The model presented here is quite complex, but it is this complexity that makes it possible to obtain the results presented in the paper. As mentioned in the introduction this approach has both advantages and disadvantages, but based on our results we believe that the former out-weighs the latter and that our model can give important insights into the dynamics of tumour growth and evolution.

The results from our model show that the micro-environment in which the tumour grows is very much the driving force of the type of tumour that will evolve both genetically and morphologically (Anderson, 2005). This implies that a tumour which grows in a tissue that is poorly oxygenated or consisting of cells with a high oxygen consumption rate is more likely to exhibit a fingering morphology and to contain aggressive cancer cells. Of course the avascular growth regime only spans a short time in the growth of a tumour, but the results from our model highlight the importance of the conditions under which this initial growth occurs. This could have implications for cancer treatment, where it might be possible to prevent the evolution of aggressive cancer cells by altering the micro-enviroment in which the tumour grows. Intriguingly it also implies that the use of anti-angiogenic treatment might actually increase the invasiveness of the tumour by creating a harsh micro-environment that destabilises the tumour morphology (Cristini et al., 2005) and creates a selection pressure that favours aggressive phenotypes. Instead treatment should aim at normalising the tissue micro-environment which would lead to a non-invasive tumour with a well-defined boundary that is less likely to contain aggressive phenotypes.

Appendix

Here we discuss in detail the structure of the response network, describe the network parametrisation and explain precisely how mutations change the behaviour of the cells.

Mathematical Formulation of the Response Network

The network consists of a number of nodes that can take real number values. The nodes are organised into three layers: the input layer ξ, the hidden layer V, which can be interpreted (for our model) as the processing layer, and the output layer O. The nodes in the different layers are connected via links, of varying connection strengths, which can modify the value of each node via the transfer function (T(x), below). The connections between the input layer and the hidden layer are defined by a connection matrix w, where w_ij determines the connection strength between node j in the input layer (ξ_j) and node i in the hidden layer (V_i). Likewise the connections between the hidden layer and the output layer are defined by a connection matrix W , where W_ij determines the connection strength between node j in the hidden layer (V_j) and node i in the output layer (O_i). The nodes in the hidden and output layer are also equipped with thresholds, where θ_i is the threshold of node i in the hidden layer (V_i) and ϕ_j is the threshold of node j in the output layer O_j. These are real valued parameters used to modulate the impact of the connections to each node.

The response of the network for a given input vector is calculated in the following way: First the values of the input nodes are set to the input vector $\xi =(n(\overrightarrow{x},t),c(\overrightarrow{x},t),g(\overrightarrow{x},t),h(\overrightarrow{x},t))$. The node values of the input layer are then fed to the hidden layer using a standard transfer function, T(x), and the connection matrix w.

$$T\left(x\right)=\frac{1}{1+e^{-2x}}.$$ (A.1)

This is a standard function used in neural networks (Haykin, 1999) and guarantees that the resulting node values of the hidden layer are in the range [0,1]. The value of node j in the hidden layer is given by

$$V_j=T(\underset{k}{\Sigma }{w}_{\mathit{jk}}{\xi }_k-{\theta }_j),$$ (A.2)

which is the sum of the input nodes weighted with the connection matrix w and the threshold θ_j. The same procedure is repeated for the output layer, which means that value of node i in the output layer is given by

$$O_i=T(\underset{j}{\Sigma }{W}_{\mathit{ij}}{V}_j-{\varphi }_i)=T(\underset{j}{\Sigma }{W}_{\mathit{ij}}T(\underset{k}{\Sigma }{w}_{\mathit{jk}}{\xi }_k-{\theta }_j)-{\varphi }_i).$$ (A.3)

The behaviour of the cells is then determined by the values of the nodes in the output layer. From (A.3) we can see that the value of each output node is a function of all input nodes and that the impact of each input node depends on the network parameters w, W, θ and ϕ. Therefore the behaviour of the network is determined by these parameters. When a cell divides, to model mutation, we allow these parameters to be copied to the daughter cells with a small variation (see below for further detail).

Movement and Metabolism

Unlike the life cycle response nodes which are linked (proliferation, quiescence and apoptosis) the movement and metabolism responses are independent and can occur simultaneously. A cell is allowed to move if the movement response is above above 0.5, which corresponds to a positive input to the movement node (as T(0) = 0.5). The switch between aerobic and anaerobic metabolism is determined by the response of the metabolic node, if the input to the metabolism node is negative the cell performs anaerobic metabolism and aerobic if the input is positive.

Network Parametrisation

The response network of the initial cell population in shape of the connection matrices and threshold vector is as follows,

$$\begin{array}{cc}\hfill & w=\left(\begin{array}{cccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0.5\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill -2\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill -2\hfill & \hfill 0.5\hfill \\ \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right),W=\left(\begin{array}{ccccc}\hfill -0.5\hfill & \hfill 1\hfill & \hfill -0.5\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0.55\hfill & \hfill -0.5\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 2\hfill & \hfill 2\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right),\hfill \\ \hfill & \theta =\left(\begin{array}{ccccc}\hfill 0.55\hfill & \hfill 0\hfill & \hfill 0.7\hfill & \hfill -0.25\hfill & \hfill 0\hfill \end{array}\right),\hfill \\ \hfill & \varphi =\left(\begin{array}{ccccc}\hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0.75\hfill \end{array}\right).\hfill \end{array}$$ (A.4)

These matrices are quite sparse and gives rise to a response network that can be seen in fig. A.1. This network satisfies the basic specifications given above (see section 2.4) for a real cancer cell, but is in no way the only network that does so. A network with different wiring and thresholds could give the same response, but what is important to stress here is that we are interested in studying the evolution of the network, which is largely independent of the initial structure. The network weights and thresholds are therefore chosen only to produce the correct response, not to mimic any specific signalling pathways. Another approach could be to evolve the inital network from a population of random networks using the desired response as the training set (Yao, 1993).

Mutations

Mutations in the model occur during cell division when the network parameters of the parent cell are copied to the daughter cell and are modelled by adding a normal randomly distributed number to the parameters chosen for mutation. In order to understand how different mutations affect the phenotype of the cell we now discuss the impact of mutations upon the initial network (A.4). First consider a mutation in w₁₁: an increase in this connection will reduce the response (A.1) of the proliferation node as a function of the number of neighbours (as the secondary connection W₁₁ is negative), see fig A.1. On the other hand if w₁₁ is decreased the proliferation response (A.1) will be stronger, as ${\xi }_1=n(\overrightarrow{x},t)$ (the no. of neighbours) this corresponds to a cell with a weaker response to contact inhibition.

Now consider a mutation in W₃₃, which connects oxygen concentration and apoptosis. An increase in this weight will reduce the response (A.1) to apoptosis as a function of the oxygen concentration, while a decrease in this weight will increase the dependence of oxygen on apoptosis. A cell with a lower dependence of oxygen on apoptosis will clearly have an advantage in hypoxic regions and will consequently have more of an opportunity to proliferate. This highlights the fact that the fitness of the cell depends on both the phenotype of the cell and the environment in which lives (i.e the fitness of the cell is implicit).

From these two examples we can see that mutations in different parts of the network will affect different aspects of the cellular behaviour. Additionally, it is important to realise that mutations can also occur at links that are initially set to zero. For example a sub-clone that acquires a link between the oxygen concentration and the choice of metabolic pathway may emerge. Such a sub-clone would have a growth advantage in poorly oxygenated regions, even though this was not predefined in the model. This highlights the fact that we model clonal evolution in an open-ended manner, which is an important aspect of the true evolutionary process.