Skip to main content
PMC home page
The Journal of Physiology logoLink to The Journal of Physiology
. 2008 Jun 10;586(Pt 17):4193–4208. doi: 10.1113/jphysiol.2008.154732

Phosphate metabolite concentrations and ATP hydrolysis potential in normal and ischaemic hearts

Fan Wu 1, Eric Y Zhang 2, Jianyi Zhang 2, Robert J Bache 2, Daniel A Beard 1
PMCID: PMC2652194  PMID: 18617566

Abstract

To understand how cardiac ATP and CrP remain stable with changes in work rate – a phenomenon that has eluded mechanistic explanation for decades – data from 31phosphate-magnetic resonance spectroscopy (31P-MRS) are analysed to estimate cytoplasmic and mitochondrial phosphate metabolite concentrations in the normal state, during high cardiac workstates, during acute ischaemia and reactive hyperaemic recovery. Analysis is based on simulating distributed heterogeneous oxygen transport in the myocardium integrated with a detailed model of cardiac energy metabolism. The model predicts that baseline myocardial free inorganic phosphate (Pi) concentration in the canine myocyte cytoplasm – a variable not accessible to direct non-invasive measurement – is approximately 0.29 mm and increases to 2.3 mm near maximal cardiac oxygen consumption. During acute ischaemia (from ligation of the left anterior descending artery) Pi increases to approximately 3.1 mm and ATP consumption in the ischaemic tissue is reduced quickly to less than half its baseline value before the creatine phosphate (CrP) pool is 18% depleted. It is determined from these experiments that the maximal rate of oxygen consumption of the heart is an emergent property and is limited not simply by the maximal rate of ATP synthesis, but by the maximal rate at which ATP can be synthesized at a potential at which it can be utilized. The critical free energy of ATP hydrolysis for cardiac contraction that is consistent with these findings is approximately −63.5 kJ mol−1. Based on theoretical findings, we hypothesize that inorganic phosphate is both the primary feedback signal for stimulating oxidative phosphorylation in vivo and also the most significant product of ATP hydrolysis in limiting the capacity of the heart to hydrolyse ATP in vivo. Due to the lack of precise quantification of Piin vivo, these hypotheses and associated model predictions remain to be carefully tested experimentally.

ATP synthesis in the healthy mammalian heart is primarily oxidative, with greater than 90% of total ATP synthesized in the mitochondria via oxidative phosphorylation (Stanley et al. 2005). The mitochondrial oxidative capacity of both skeletal and cardiac muscle cells may be diminished in disease such as in heart failure (Garnier et al. 2003). The results are that chemical energy, in the form of the ATP hydrolysis potential, available for the heart to do work is diminished (Montgomery et al. 1992; Neubauer et al. 1992; Zhang et al. 1993; Liao et al. 1996; Murakami et al. 1999; Jung et al. 2000; Feygin et al. 2007) and consequently the contractile performance of the failing heart may be limited by the free energy at which mitochondria can synthesize ATP (Zhang et al. 1993; Murakami et al. 1999; Ochiai et al. 2001; Gong et al. 2003; Feygin et al. 2007). Thus, an altered metabolic pattern observed in heart failure has a potential impact on the energetic state of the heart: the potential consequences of a diminished energetic state include an impaired ability of the heart to work and respond to acute and chronic stresses (Zhang & McDonald, 1995; Zhang et al. 1996).

Measuring a number of key energy metabolites in vivo is possible using 31P magnetic resonance spectroscopy (MRS), in which signals from creatine phosphate (CrP), ATP and inorganic phosphate (Pi), and intracellular pH are quantifiable from measured spectra (Balaban et al. 1986; Zhang et al. 1993; Kushmerick, 1995; Murakami et al. 1999). Based on these measurements, the myocardial free ADP concentration may be estimated using a model of apparent creatine kinase equilibrium (Veech et al. 1979). In addition, it is possible to simultaneously measure oxy-myoglobin saturation using 1H-MRS in tissue with significant myoglobin content (Kreutzer & Jue, 1991; Zhang et al. 2001). Thus, MRS is a powerful tool for non-invasive assessment of energetic state and for assessing tissue oxygenation. In fact, the measured ratio of CrP/ATP in the heart is a better predictor of cardiovascular mortality than usual clinical indices, such as ejection fraction (Neubauer et al. 1997). 31P-MRS is able to detect significant alterations in phosphate metabolites both in animal models of cardiac hypertrophy (Zhang et al. 1993; Murakami et al. 1999; Spindler et al. 1999; Lee et al. 2006; Feygin et al. 2008) and in patients with heart disease (Neubauer et al. 1992, 1997; Jung et al. 1998; Weiss et al. 2005). In addition, metabolic dysfunction can precede and may play a role in initiating structural remodelling and mechanical malfunction (Taegtmeyer & Overturf, 1988; Friehs et al. 1999; Taegtmeyer et al. 2002; Young et al. 2002). Thus, quantitative diagnosis of metabolic dysfunction would be clinically valuable.

However, 31P-MRS provides only relative measures of certain metabolite concentrations, including ATP and CrP, while others, such as ADP and Pi, are too low to be directly observable under baseline conditions in normal hearts based on human and large-animal model studies. None of these metabolites can be directly quantified in terms of mass per unit volume by current 31P-MRS techniques applicable in the clinic. In addition, interpretation of 31P-MRS from the heart is made ambiguous by the relatively large mitochondrial pool compared to other tissues, such as glycolytic muscle, in which the mitochondrial contribution to the phosphate spectra is assumed to be negligible (Blei et al. 1993). During transient ischaemia in skeletal muscle, the rate of ATP consumption can be estimated from the initial rate of decline of CrP (Blei et al. 1993; Vicini & Kushmerick, 2000). However, due to higher rates of ATP consumption in cardiac tissue, free energy for ATP hydrolysis is dissipated during ischaemia so rapidly that the rate of ATP hydrolysis diminishes before the initial decline in CrP can be resolved, as is demonstrated here.

Here we demonstrate how data from 31P-MRS may be analysed to quantify cytoplasmic and mitochondrial phosphate metabolite concentrations and ATP hydrolysis rate in the normal state, at high cardiac work states, during graded hypoperfusion, and during acute ischaemia and reactive hyperaemic recovery. This analysis is based on an integrated simulation of oxygen transport and energy metabolism in the myocardium that tracks energy metabolite concentrations and their breakdown into multiple cation-bound species in the cytoplasmic and mitochondrial pools.

Methods

Experimental methods

All studies were conducted in accordance with the Guiding Principles in the Care and Use of Animals approved by the council of the American Physiological Society and under the supervision of the Animal Care Committee of the University of Minnesota.

Surgical preparation

Normal adult mongrel dogs (n= 9) weighing 19–24 kg were anaesthetized with sodium pentobarbital (30 mg/kg i.v.) intubated and ventilated with a respirator with supplemental oxygen; arterial blood gases were maintained within the physiological range. A heparin-filled polyvinyl chloride catheter, 3.0 mm O.D., was introduced into the right femoral artery and advanced into the descending aorta. A left thoracotomy was performed in the fourth intercostal space and the heart suspended in a pericardial cradle. A heparin-filled catheter was introduced into the left ventricle through the apical dimple and secured with a purse-string suture. A similar catheter was placed into the left atrium through the atrial appendage for microsphere injections. About 1 cm of proximal left anterior descending coronary artery (LAD) was dissected free and a Doppler flow probe (Instrumentation Development Laboratory; Houston, TX, USA) was placed on it. A 28 mm diameter 31P-MRS surface coil was sutured to the epicardium of the left ventricular (LV) anterior free wall. The leads of the surface coil were soldered to a balanced tuned circuit. The pericardial cradle was then released and the heart allowed to assume its normal position. The animal was placed in a lucite cradle and positioned within the magnet.

31P magnetic resonance spectroscopy

31P-MRS spectroscopy was performed using the single adiabatic excitation pulse which was optimized as previously described (Zhang et al. 1995). This pulse sequence was 1 ms long (see Zhang et al. (1995) for detailed description of optimization). Data acquisition was gated to the cardiac and respiratory cycles using the LV pressure trace as the master clock to drive both the respirator and the spectrometer as previously described (Zhang et al. 1995). This gating also turned off the Doppler signal to avoid MRS signal interference. 31P- and 1H-MRS frequencies were 81 and 200.1 MHz, respectively. Spectra were acquired during late diastole with a repetition time of 6–7 s. The pulse repetition time of 6 s allowed full relaxation for ATP and inorganic phosphate (Pi), and more than 90% relaxation of the creatine phosphate (CrP) resonance (Zhang et al. 1995). CrP resonance intensities were corrected for this minor saturation. The correction factor was determined for each study by acquiring two spectra consecutively: one with 15 s repetition time to generate a fully relaxed spectra and the other with 6–7 s repetition time used in all the other measurements. Each of the two spectra was summed from 16 scans to increase the signal-to-noise ratio. Resonance intensities were quantified using integration routines provided by the SISCO (Fremont, CA, USA) software. For each spectrum the numerical values for CrP and ATP were obtained and the ratio of CrP/ATP was calculated. When Pi was detectable under basal conditions (1 of 9 hearts), the integral value of the basal Pi was subtracted from the following Pi values acquired during subsequent conditions to obtain ΔPi values. The measured change of the Pi signal is expressed here as the ΔPi/CrP ratio.

Myocardial blood flow measurements

Myocardial blood flow was measured using 15 μm diameter radionuclide-labelled microspheres. Microspheres labelled with four different radioisotopes (51Cr, 85Sr, 95Nb and 46Sc), were agitated in an ultrasonic mixer for 10 min prior to injection. A microsphere suspension containing 2 × l06 microspheres was injected through the left atrial catheter and flushed with 10 ml of normal saline. A reference sample of arterial blood was drawn from the aortic catheter at a rate of 15 ml min−1 beginning 5 s before microsphere injection and continuing for 120 s (Zhang et al. 1995). At the end of the study the hearts were removed, weighed and fixed in 10% buffered formalin. The region of myocardium beneath the surface coil was removed and sectioned into three transmural layers from epicardium to endocardium, weighed and placed into vials for counting. Similar myocardial specimens were obtained from the lateral and posterior LV wall to insure that the measurements from the region beneath the surface coil were representative of the entire left ventricle. Radioactivity in the myocardial and blood reference specimens was determined using a gamma spectrometer (model 5912, Packard Instrument Company, Downers Grove, IL, USA) at window settings chosen for the combination of radioisotopes used during the study. Activity in each energy window was corrected for background activity and overlap between isotopes. 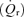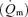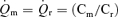Knowing the rate of withdrawal of the reference blood specimen Inline graphic and the radioactivity of the reference specimen (Cr), myocardial radioactivity (Cm) was used to compute myocardial blood flow Inline graphic as Inline graphic. Blood flow was expressed as ml (g of myocardium) min−1.

Study protocol

The experimental group consisted of nine dogs in which 36 s coronary artery occlusion and 120 s reperfusion were produced without drug or pacing intervention. Anaesthesia was maintained by continuous intravenous infusion of sodium pentobarbital at a rate of 4 mg kg−1 h−1. Arterial blood gases and pH were monitored throughout the study and the volume and inspired O2 content of the ventilator were adjusted to maintain physiological values. Aortic, left ventricular pressure and coronary blood flow with Doppler flow velocity were monitored continuously throughout the study. During MRS data acquisition the flow signal was turned off for 200 ms, controlled by the gating program (Zhang et al. 2001), to ensure that MRS signal is not affected by the Doppler signal. Fully relaxed 31P-MRS spectra of the whole wall were first acquired in 24 scans with a repetition time of 16 s. The repetition time was then adjusted to 6 s for the remainder of the study. Under the stable basal conditions, one microsphere injection was performed for later Doppler signal calibration. An MRS pulse train of 28 scans was generated with repetition time of 6 s. The first four spectra were acquired during control conditions. After the 4th spectrum was obtained, a complete LAD occlusion was initiated and maintained for the following 36 s, during which the 6th to 10th spectra were obtained. After the 10th spectrum was obtained, the occluder was released and the 11th to 28th spectra were acquired in the following 108 s. Duplicate sets of data were acquired 20 min later for each heart.

After completion of the experimental protocol, the animals were killed by intravenous administration of a solution (an overdose of 200 mg kg−1 sodium pentobarbital i.v. and 25 mg kg−1 sodium phenytoin i.v.) to induce cardiac arrest.

Computational methods

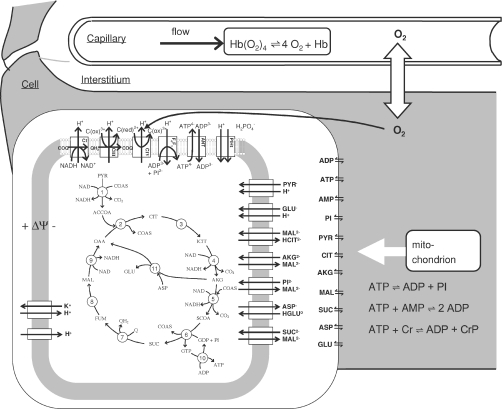
Oxygen transport and energetic metabolism in cardiac tissue are simulated based on previously described and validated computational models (Beard, 2005 2006; Wu et al. 2007a,b). In brief, the model assumes that within the capillary, interstitial space and cellular (myocyte) space, the concentrations of oxygen and other metabolites vary primarily along the length of the capillaries, as illustrated in Fig. 1. Advective transport is modelled in the capillary region; the interstitial and cellular spaces are assumed to be stagnant (non-flowing). The cellular region is further subdivided into cytoplasmic and mitochondrial compartments. The mitochondrial metabolism model incorporates tricarboxylic acid cycle fluxes, mitochondrial oxidative phosphorylation fluxes, and substrate and cation transport fluxes, as illustrated in the figure. The model simulates 53 biochemical reactant concentrations, matrix-free Mg2+ and K+, matrix pH, and inner membrane electrostatic potential. The 53 biochemical concentration variables represent 32 biochemical reactants, some of which are distributed in multiple compartments. Each of the 32 biochemical reactants is made up of several rapidly interconverting species. For example, the reactant ATP is considered to be made up of the four ionic species, ATP4−, HATP3−, MgATP2− and KATP3−. For all reactants, binding of H+, K+ and Mg2+ is explicitly accounted for where such binding is significant. Details of the metabolic model are provided elsewhere (Wu et al. 2007b).

Figure 1. Diagram of model used to simulate cardiac tissue oxygen transport and energy metabolism.

Figure 1

Open in a new tab

Oxygen is transported via advection in capillaries, diffusion into cardiomyocytes from capillaries through interstitium, and reduced into water via the complex IV reaction in mitochondria. Cellular energy metabolism is simulated by a computer model of mitochondrial tricarboxylic acid cycle, oxidative phosphorylation, metabolite transport and electrophysiology (Wu et al. 2007b).

Oxygen extraction and consumption in the model is driven by the rate of ATP hydrolysis in the tissue. ATP hydrolysis is coupled to ATP synthesis by mitochondria, which is coupled to oxidative phosphorylation, which consumes oxygen. Mitochondrial oxygen consumption is in turn coupled to diffusion of oxygen from blood to tissue, and extraction of blood along the length of capillaries.

For the analyses described here the oxygen transport and metabolic components of our model was updated two ways. First, the single-pathway model of Beard (2006) was replaced by a multiple-pathway model, where 10 parallel pathways are used to account for heterogeneity in tissue oxygenation. Second, the metabolic model was updated with an improved mechanistic model for the ANT transporter (Metelkin et al. 2006). Details and independent validation of the multiple-pathway model and the updated ANT model are provided in the online Supplementary material.

Results

Overview

In the following sections we analyse steady-state and transient data on phosphate metabolite concentrations. First, the integrated oxygen transport and mitochondrial energetics model is validated based on comparison to data on phosphate metabolite concentrations in the heart at different cardiac workloads. This analysis allows us to generate model-based predictions of the ATP hydrolysis potential and cytoplasmic free Pi and ADP concentrations as a function of oxygen consumption, variables that are not easily measured in vivo. In addition, the steady-state analysis yields the hypothesis that the rate of ATP consumption (and rate of oxygen consumption) of the heart is limited by the rate at which cardiac mitochondria can deliver ATP to the cytoplasm at a hydrolysis potential at or above a critical level. This hypothesis and our estimate of the critical hydrolysis potential are tested in analysing the transient data on ischaemia and recovery. Finally, the integrated model is compared to an additional independent data set on steady-state phosphate metabolite levels during graded hypoperfusion.

Steady-state cardiac energetics

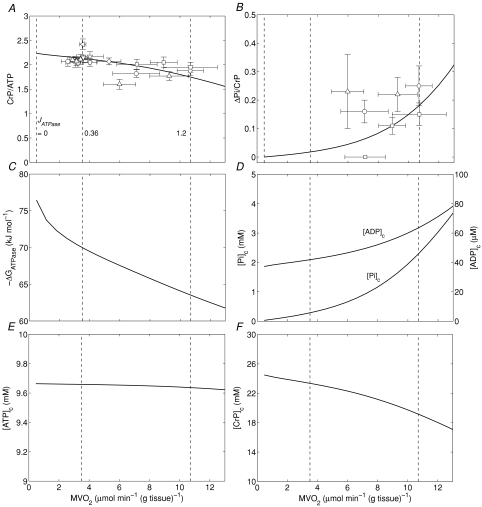
Figure 2A and B illustrate steady-state measures of the CrP/ATP ratio and ΔPi/CrP measured at different levels of myocardial cardiac oxygen consumption, M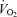Inline graphic, in the canine heart compiled from several studies by Zhang et al. (Bache et al. 1999; Gong et al. 1999, 2003; Ochiai et al. 2001; Zhang et al. 2003, 2005). In these experiments, cardiac work is elevated from baseline based on several different protocols, as indicated in the figure legend. Since the peak due to 2,3-diphosphoglycerate (2,3-DPG) overlaps with the Pi peak in 31P-MRS at 4.7 Tesla, only the change in Pi signal (ΔPi) from baseline is evaluated. Therefore the variable ΔPi/CrP is not defined for the baseline and is only plotted for the stimulated conditions. Non-zero values of ΔPi/CrP = 0 indicated a detectable increase in Pi signal over baseline.

Figure 2. Steady-state energetics phosphate metabolites as functions of myocardial oxygen consumption.

Figure 2

Open in a new tab

A, model-predicted steady-state CrP/ATP level plotted as a function of oxygen consumption rate, 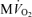Inline graphic, and compared to experimental data from canine heart in vivo. B, model-predicted steady-state ΔPi/CrP plotted as a function of 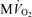Inline graphic. C, model-predicted steady-state free energy of ATP hydrolysis, −ΔGATPase, is plotted as a function of 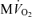Inline graphic. D, model-predicted steady-state cytoplasmic inorganic phosphate concentration, [Pi]c and ADP, [ADP]c, plotted as a functions of 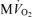Inline graphic. E, model-predicted steady-state cytoplasmic ATP, [ATP]c, plotted as a function of 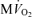Inline graphic. F, model-predicted steady-state cytoplasmic CrP [CrP]c, plotted as a function of 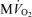Inline graphic. For all simulations, 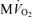Inline graphic is varied by varying the rate of ATP hydrolysis, JATPase, in the cytoplasm. Experimental data are obtained from the following sources: ○, Zhang et al. (2005) (dobutamine + dopamine); ▵, Zhang et al. (2003), ◊, Gong et al. (2003) (dobutamine + dopamine); ▵, Ochiai et al. (2001) (dobutamine + dopamine); ▿, Gong et al. (1999), □, Bache et al. (1999) (dobutamine, dobutamine +dopamine). Here protocols used to elevate work load from baseline are indicated in parentheses. The values of JATPase corresponding to baseline and maximal 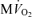Inline graphic, 0.36 and 1.2 mmol s−1 (l cell)−1, respectively, are indicated in A. Error bars indicate standard error.

To compare model predictions to the observed data, the cellular rate of ATP hydrolysis (JATPase) was varied from 0 to 1.6 mmol s−1 (l cell)−1 and the steady-state values of phosphate metabolites were computed. The observed ATP signal is assumed to arise from the total mass of ATP (cytoplasmic plus mitochondrial) while the CrP signal arises from only cytoplasm. At baseline ATP consumption rate (JATPase= 0.36 mmol s−1 (l cell)−1 and 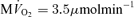Inline graphic (g tissue)−1) the cytoplasmic creatine phosphate and ATP concentrations are 23.4 mm and 9.66 mm, respectively. The ATP concentration in mitochondria, which take up approximately 28% of cellular volume, is computed to be 3.3 mm at baseline. The resulting predicted CrP/ATP ratio at the baseline work rate is 2.1, which closely matches the data. As the rate of ATP hydrolysis is increased, the 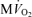Inline graphic increases and the CrP/ATP drops to 1.8 at near the observed maximal ATP consumption rate of JATPase= 1.2 mmol s−1 (l cell)−1 and 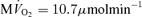Inline graphic (g tissue)−1.

In normal dog (or pig) heart, the myocardial Pi level is too low to be detected at basal workload (Balaban et al. 1986; Robitaille et al. 1989; Zhang et al. 1993; Gong et al. 1999; Murakami et al. 1999). Simulated values of ΔPi/CrP are plotted along with the measured values in Fig. 2B. The data point falling at ΔPi/CrP = 0 corresponds to a measurement under low stimulation level for which Pi remained below the limit of detectability of approximately 1.0 mm (Bache et al. 1999). Inorganic phosphate peaks from 31P-MRS are noisy compared to the CrP and ATP, as indicated by the large error bars in these data. In addition, the data are not as consistent as the CrP/ATP data, with variability in the ΔPi/CrP resulting from both individual variability and the noise of the measurement. Although, given the noise and variability, taken by themselves these data would not provide strong validation of the model, the model predictions are consistent with the observed level of increase in Pi at high work rate compared to baseline conditions. The major outlier (obtained from Ochiai et al. 2001) and plotted as a triangle at 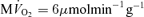Inline graphic) in Fig. 2B corresponds to the major outlier in Fig. 2A. Since the model simulates a single mean individual, it cannot capture the observed individual variability and noise apparent in these data. Yet its predictions are consistent with the observed ΔPi/CrP at the maximal observed oxygen consumption rate obtained from several independent studies.

The data and corresponding model simulations of Fig. 2 allow us to estimate phosphate metabolite concentrations in molar units and to determine the solution thermodynamics of the cytoplasm as a function of oxygen consumption rate. The predicted free energy of ATP hydrolysis in the cytoplasm, ΔGATPase, is plotted in Fig. 2C. The magnitude of ΔGATPase drops with increasing oxygen consumption as the free energy at which ATP can be synthesized drops with increasing flux. The critical value of ΔGATPase, which is defined here as the ATP hydrolysis free energy at the observed maximal work state, can be estimated from Fig. 2C. Here we obtain an approximate value of ΔGcrit of −63.5 kJ mol−1. Our mitochondrial model can synthesize ATP at ATP hydrolysis and 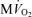Inline graphic levels higher than those associated with the maximal observed oxygen consumption rate. However, the model can only deliver the synthesized ATP at a magnitude of free energy lower than ΔGcrit at higher oxygen consumption rates. Therefore the value of ΔGcrit represents an estimate of the free energy level necessary for the heart to function.

Cytoplasmic Pi concentrations predicted over the oxygen consumption range of Fig. 2A and B are plotted in Fig. 2D. These model predictions provide quantitative estimates of Pi that are not available from the raw data. The model predicts that baseline Pi concentration in the canine myocyte cytoplasm is approximately 0.29 mm and increases to 2.3 mm at highest cardiac workload. Cytoplasmic ATP and ADP are predicted to vary little over the observed range of cardiac workstates, with ATP decreasing from 9.66 mm at baseline to 9.64 mm at maximum cardiac workload and the free ADP increasing from 0.042 mm to 0.064 mm.

Energetics during ischaemia and recovery

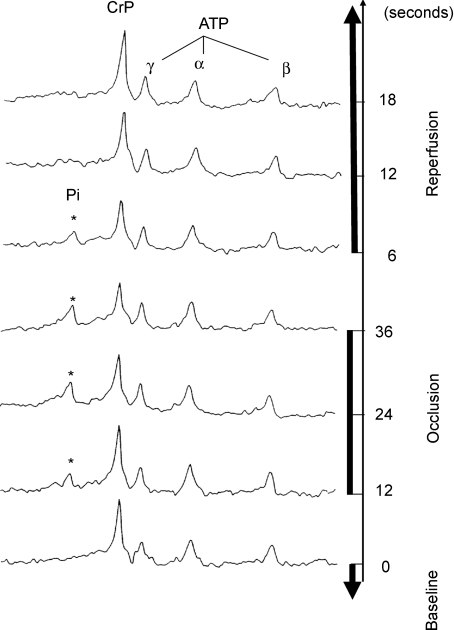
The preceding analysis of steady-state data yields the hypothesis that the consumption of ATP in the myocardium is limited by the free energy at which it is synthesized by oxidative phosphorylation at maximal oxygen consumption. This hypothesis was tested by measuring relative CrP and ΔPi/CrP in ischaemia and recovery. Specifically, these variables were measured at 6 s intervals before occlusion, during ischaemia and during recovery. Haemodynamic measurements obtained during control conditions, at the end of coronary occlusion and during peak reactive hyperaemia are summarized in Table 1 for this study. Heart rate did not change significantly throughout the study. Mean aortic pressure and left ventricular (LV) systolic pressure did not change significantly during coronary occlusion or during reactive hyperaemia. The rate pressure products (heart rate × LV systolic pressure) did not change significantly throughout the study. Figure 3 shows typical spectra from one of these experiments. Myocardial pH, calculated from Pi chemical shift relative to CrP when the Pi level was detectable (Bailey et al. 1981; Brindle et al. 1988), varied by less than 0.2 units throughout the protocol. The baseline spectrum shown in Fig. 3 is similar to baseline spectra reported for the experiments from which the steady-state data for Fig. 2 were obtained. The Pi signal is too low to be detected above the noise in the spectrum at baseline and does not rise above the noise until the ischaemic period.

Table 1.

Haemodynamics during occlusion and reperfusion (n= 9)

Control Occlusion Peak RH
HR (beats min−1) 141 ± 9 145 ± 9 145 ± 9
Mean Ao (mmHg) 98 ± 6 96 ± 6 99 ± 6
LVSP (mmHg) 112 ± 6 108 ± 6 111 ± 6
LVEDP (mmHg) 12 ± 1 13 ± 1 12 ± 1
RPP × 103 (mmHg min−1) 15.40 ± 0.94 15.28 ± 1.16 15.74 ± 1.17
Open in a new tab

Values reported as mean ±s.e.m.; HR, heart rate; mean Ao, mean aortic pressure; LVSP, left ventricular systolic pressure; LVEDP, left ventricular end-diastolic pressure; RPP, rate–pressure product (HR × lVSP); RH, reactive hyperemia.

Figure 3. Sample 31P-MRS spectra during transient occlusion and recovery.

Figure 3

Open in a new tab

Spectra from baseline, occlusion and recovery periods are shown. A 31P-MRS pulse train of 28 scans was generated with repetition time of 6 s. The number of transients is one (NT = 1) for each spectrum. The resonance peaks for CrP, Pi and the 3 resonances from ATP are identified. One of the four spectra acquired during baseline conditions for a single experiment is shown, indicated as time point 0. Following the baseline period, complete LAD occlusion was initiated and maintained for the following 36 s, during which the 6th to 10th spectra were obtained. The 6th, 8th and 10th spectra (at the 12, 24 and 36 s time points during LAD occlusion, respectively) are shown demonstrating the progressive increase of the Pi and decrease of CrP during LAD occlusion. After the 10th spectrum was obtained, the occluder was released and the 11th to 28th spectra were acquired in the following 108 s. The first 3 spectra during reperfusion are shown demonstrating the fast recovery of CrP and Pi levels during the reperfusion.

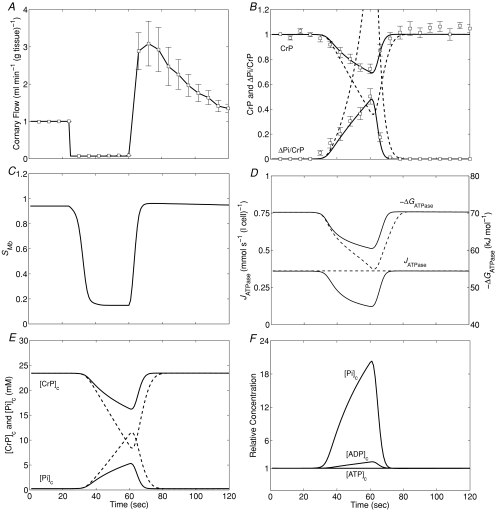
The data and corresponding model predictions are illustrated in Fig. 4. The coronary flow (Fig. 4A, 9 animals) at baseline was 1.00 ± 0.14 ml min−1 (g tissue)−1 and decreased to 0.07 ± 0.2 ml min−1 (g tissue)−1 in the region of interest during ligation. (The flow was non-zero during ligation due to collateral flow.) Reactive hyperaemic flow transiently increased to three times its baseline value within 9.3 ± 1.0 s of the removal of the occlusion. Flow returned to the baseline value within 102 ± 13 s following the release of the occlusion. The mean and standard error of CrP and ΔPi/CrP for this experiment are plotted in Fig. 4B.

Figure 4. Energetic phosphate metabolites and myoglobin saturation during ischaemia and recovery.

Figure 4

Open in a new tab

A, the mean time course of experimentally determined coronary blood flow (with the total occlusion starting at t= 24 s and ending at t= 60 s). Data points correspond to mean of nine experiments; error bars indicate standard error. B, model simulations compared to experimental observations of CrP (normalized to baseline value) and ΔPi/CrP. Model-predicted time courses of myoglobin saturation SMb (C), ATP hydrolysis flux, JATPase, and free energy, ΔGATPase (D), cytoplasmic creatine phosphate and inorganic phosphate concentrations, [CrP]c, and [Pi]c (E), and relative levels of cytoplasmic Pi, ADP and ATP (F) are illustrated for this experiment. Continuous lines in B, D and E represent the model prediction using the ATP hydrolysis flux expression of eqn (1), and dashed lines represent the model prediction assuming constant ATP hydrolysis flux.

To simulate the experiment, the following Michaelis–Menten function was used to simulate ATP consumption in the cytoplasm:

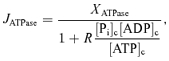graphic file with name tjp0586-4193-m1.jpg (1)

where [Pi]c, [ADP]c and [ATP]c are the cytoplasmic Pi, ADP and ATP concentrations, respectively. This equation provides a hypothetical phenomenological relationship between ATP hydrolysis rate and ATP hydrolysis potential. Based on this equation, the ATP hydrolysis rate is simulated to be approximately constant at the baseline rate at baseline levels of ATP, ADP and Pi. When ATP drops (and ADP and Pi increase), resulting in a diminished hydrolysis potential, the rate of ATP consumption drops. The parameters in this function are obtained from the steady-state analysis described above: XATPase= 0.39 mmol s−1 (l cell)−1 so that the baseline JATPase computed from eqn (1) is equal to 0.36 mmol s−1 (l cell)−1 as determined above, and R is the mass-action ratio associated with the critical value of ATP hydrolysis potential (R= 65 800 m−1).

Model predictions associated with using eqn (1) to simulate ATP hydrolysis are plotted as continous lines in Fig. 4B. Since these model predictions use parameters (baseline XATPase and R) obtained from the independent analysis described above, the continuous lines provide an independent verification of our estimate of ΔGcrit. To demonstrate that these data are indeed sensitive to ΔGcrit (and the corresponding value of R), model predictions assuming constant JATPase= 0.36 mmol s−1 (l cell)−1 are illustrated as dashed lines in Fig. 4B. It is apparent that if the baseline rate of ATP hydrolysis were maintained, then CrP would be depleted much more rapidly than is observed experimentally. Figure 4D plots the time course of the ATP hydrolysis flux predicted by the model. The predictions associated with eqn (1) are shown as continuous lines while the constant ATP hydrolysis rate is shown as a dashed line. The ATP hydrolysis rate, associated with the continuous-line model predictions, is predicted to drop to 50% of its baseline value within 22 s following the onset of ischaemia. At this time point, the CrP and ATP concentrations are 82% and 99.8% of their baseline values, respectively, indicating that ATP consumption is severely restricted long before the CrP pool is depleted. This model prediction is consistent with the observations from a similar full-occlusion protocol in pig hearts in vivo, in which systolic segment shortening in the ischaemic region reduced to 40%–50% of its normal level within 15 s following occlusion, while CrP and ATP concentration are reduced to ∼80% and ∼92% of their baseline values, respectively (Schwartz et al. 1990, 1991).

Note that although the continuous-line model predictions plotted in Fig. 4 use values for baseline XATPase and R obtained from the independent steady-state analysis, the values used represent optimal values with respect to prediction of these time-dependent data. In other words, it is not possible to obtain significantly better matches between the data and the model simulation in Fig. 4 by adjusting parameter values, and significant changes to the parameter values would result in a significantly worse match between experimental data and model simulations.

As for the steady-state analysis above, the model-based analysis of these data provides quantitative estimates of model variables that are not directly measured. Model-predicted myoglobin saturation and CrP and Pi concentrations are plotted in Fig. 4C and E. CrP and Pi concentrations take approximately 14 s to return to baseline values following reperfusion. Myoglobin saturation, predicted to be 0.95 at baseline, drops to 0.15 during ischaemia. Figure 4F illustrates the model predictions for cytoplasmic Pi, ADP and ATP, relative to their baseline values during ischaemia and recovery. Similar to the variations in steady-state work rate, the largest observed variation during this transient experiment is in inorganic phosphate. The cytosolic ADP increases to approximately twice baseline level and ATP decreases to only 99.5% of its baseline level, while [Pi]c is predicted to increase to more than 20 times its baseline value during this experiment.

Energetics during graded hypoperfusion

In a previous study we compared model predictions to data on oxygenation and phosphate metabolite levels during graded hypoperfusion using a single-pathway blood–tissue exchange model (Beard, 2006). Here we compare our current model predictions to the same data analysed in that study as a vehicle to further validate our multi-pathway oxygen transport model, and the estimated values of baseline ATP hydrolysis rate and critical ATP hydrolysis potential estimated from the steady-state analysis described above.

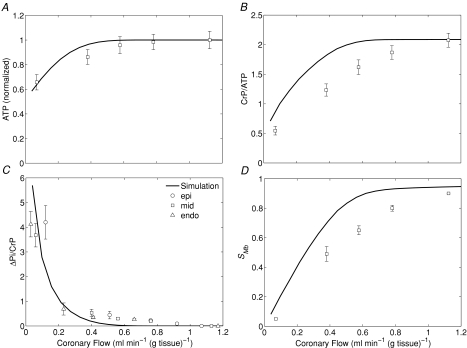
To simulate cardiac response to graded hypoperfusion, JATPase is again set to the baseline value of 0.36 mmol s−1(l cell)−1 and flow is varied between 1.20 and 0.04 ml min−1 (g tissue)−1, corresponding to the range of coronary flow imposed in the study of Zhang et al. (2001). Over this range of flow, Zhang et al. (2001) measured relative ATP, CrP, ΔPi and oxymyoglobin saturation (SMb) using 31P- and 1H-MRS methods. These data are compared to steady-state model predictions in Fig. 5. The model predictions are in good agreement with the data, although at the assumed ATP hydrolysis rate the model tends to overestimate CrP and SMb. A closer match between model and data would be possible by increasing the ATP consumption rate. However, increasing the rate of ATP hydrolysis would lower the predicted ATP and ΔPi levels.

Figure 5. Cardiac energetic phosphate metabolite levels and myoglobin saturation during coronary hypoperfusion.

Figure 5

Open in a new tab

A, model-predicted steady-state ATP levels (normalized to baseline value) as a function of coronary blood flow. B, model-predicted steady-state CrP levels (normalized to ATP) (CrP/ATP). C, model-predicted steady-state ΔPi/CrP, as a function of coronary blood flow. D, model-predicted steady-state myoglobin saturation, SMb, as a function of coronary blood flow. Experimental data obtained from Zhang et al. (2001). In C, data are divided into epicardium (epi), midwall (mid) and endocardium (endo), as indicated in the figure. Error bars indicate standard error.

Note that the simulations shown in Fig. 5 match the data significantly better than those reported in Beard (2006). This is because the previous simulations were based on a single-path model and did not account for the observed ΔGcrit. The improved match between the simulations shown in Fig. 5 compared to Fig. 5 of Beard (2006) is due to the adoption of the multiple-path transport model, which captures the heterogeneity of cardiac tissue oxygenation better than a single-path model.

Discussion

Observations on phosphate metabolites in the heart

It is long established that cytoplasmic Pi increases drastically with work in skeletal muscle (Kushmerick et al. 1983; Meyer, 1988; Westerhoff et al. 1995; Jeneson et al. 2000; Wu et al. 2007a). Based on model predictions, it has been suggested that Pi increases with work rate in heart as well (Saks et al. 2000; Vendelin et al. 2000; Beard, 2006). Yet experimental observations have not been able to determine the range over which cytoplasmic Pi varies in the heart in vivo. In in vivo large animal cardiac 31P-MRS measurements, the Pi level is too low to be detected under the basal conditions. In addition, in non-spatially localized 31P-MRS experiments the resonance peaks of 2,3-DPG from erythrocytes in the LV chamber overlap with the Pi peak, further complicating quantification of myocardial free inorganic phosphate.

Our model predictions of steady-state phosphate metabolite levels (Fig. 2) are consistent with the observations that CrP/ATP decreases slightly while Pi increases when high cardiac work states reached rate–pressure products (RPP) above 40 000 mmHg beats min−1 in the canine heart in vivo. In normal canine hearts in vivo, changes in myocardial high energy phosphate (HEP) levels are not detectible from 31P-MRS during moderate increases of cardiac workload produced by catecholamine infusion to produce RPP up to 35 000 mmHg beats min−1 (Balaban et al. 1986; Robitaille et al. 1990; Zhang et al. 1995). Our model predictions agree with these observations (Katz et al. 1989; Zhang et al. 1995, 1999) that the total Pi (cytosolic plus mitochondrial) remains constant within limits of detection at moderate work rates. However, more intense catecholamine stimulation to very high work states with RPP above 45 000 mmHg beats min−1causes a significant increase of Pi and decrease of the CrP/ATP ratio reflecting an increase of cytosolic free ADP and Pi (Zhang et al. 1995, 1999). The increase in Pi and decrease in CrP/ATP during very high work states implies that mitochondrial oxidative phosphorylation is stimulated by an increased level of free ADP and/or Pi to maintain the driving force for ATP production (Zhang et al. 1995, 1999).

Since our computational model was developed independently and not fitted to the data in Fig. 2, the internal consistency between our theoretical predictions and experimental observations lends support to the position that myocardial phosphate metabolite levels, particularly inorganic phosphate, change with cardiac work. More validation is provided by the consistency between steady-state model predictions of Fig. 2 and independent studies in human (Lamb et al. 1997), pig (Massie et al. 1994) and rat (Headrick et al. 1994), and between the transient data and model predictions of Fig. 4 and the independent studies of Schwartz et al. (1990, 1991).

Control of oxidative phosphorylation in vivo

The prediction that Pi varies over an 8-fold range from baseline to maximal work in the heart supports the hypothesis that Pi is an important controller of oxidative phosphorylation in the heart (Saks et al. 2000; Bose et al. 2003; Beard, 2006). If correct, this hypothesis helps to explain the observed stability in cardiac ATP and CrP with work rate, a phenomenon that has eluded mechanistic explanation for decades (Balaban, 1990,2002,2006). In fact, an important role of Pi in controlling mitochondrial metabolism in the heart has been hypothesized previously (Saks et al. 2000; Bose et al. 2003). Saks et al. (Saks et al. 2000; Vendelin et al. 2000) have developed models that predict that Pi varies over approximately the same range reported here. However, those previous studies relied on measurements in skinned fibres (Saks et al. 2000) and purified mitochondria (Bose et al. 2003) in which substrate concentrations are varied to observe their impacts on oxidative phosphorylation. Here, data from the in vivo system, in which Pi and other metabolites vary based on intracellular biochemical mechanisms, are analysed to demonstrate that this phenomenon occurs in vivo.

Mechanisms underlying the rapid reduction in myocardial contractility during ischaemia are potentially complex (Reiermann et al. 1977; Kentish, 1986; Allen & Orchard, 1987; Schmidt-Ott et al. 1990; Hogan et al. 1998). It has been proposed that increased cytoplasmic Pi concentration ([Pi]c) leads to reduction of calcium-activated tension and myosin ATPase activity in myofibrils (Reiermann et al. 1977; Kentish, 1986; Schmidt-Ott et al. 1990; Hogan et al. 1998). As shown in Fig. 4E, the model predicts that [Pi]c increases from 0.29 mm to 3.1 mm within 22 s after the total occlusion. This 10-fold increase may reduce the developed tension to less than half of the control value (Allen & Orchard, 1987). While our model predictions are consistent with these observations (as well as our own experimental observations), the mechanistic details may be more complex than the model's simple explanation in terms of a drop in ATP hydrolysis potential. Since the model is driven by an ATP hydrolysis flux that combines all cytoplasmic ATP-consuming processes, we are not able to estimate how much of ATP hydrolysis is being used for support contractile function versus other cellular functions.

Yet it is compelling that the simple function of eqn (1)– which explains the drop in capacity of cardiac ATP hydrolysis as a function of the ATP hydrolysis potential (or equivalently the ATP hydrolysis mass-action ratio) – simultaneously explains the maximal observed steady-state oxygen consumption rate and the time course of phosphate metabolites during ischaemia and reperfusion in vivo. The observation that ATP remains near baseline values when ATP hydrolysis potential approaches the critical value explains observations that date back to Pool et al. (1966) that ‘hypoxic depression of myocardial function is not associated with any measurable change in myocardial ATP’. This is because the ATP hydrolysis potential is more important than the absolute ATP concentration in governing the ability of the heart to physiologically function. The rate of ATP consumption in the heart must be matched by the rate at which the mitochondria deliver chemical energy in the form of the ATP hydrolysis potential in vivo. While mitochondria are capable of synthesizing ATP at rates higher than the maximally observed cytoplasmic ATP hydrolysis rate, the free energy at which ATP may be synthesized drops with the rate at which it is consumed. Therefore the maximal oxygen consumption rate of the cardiomyocyte in vivo is limited not simply by the maximal rate of ATP synthesis, but by the maximal rate at which ATP can be synthesized at a potential at which it can be utilized by the heart. The maximal in vivo rate of oxidative phosphorylation is not an intrinsic property of cardiac mitochondria: it is not the maximal possible mitochondrial oxidative phosphorylation flux that would be obtained in saturating concentrations of substrates. Instead, it is a property of the mitochondria and the cellular system they are imbedded in.

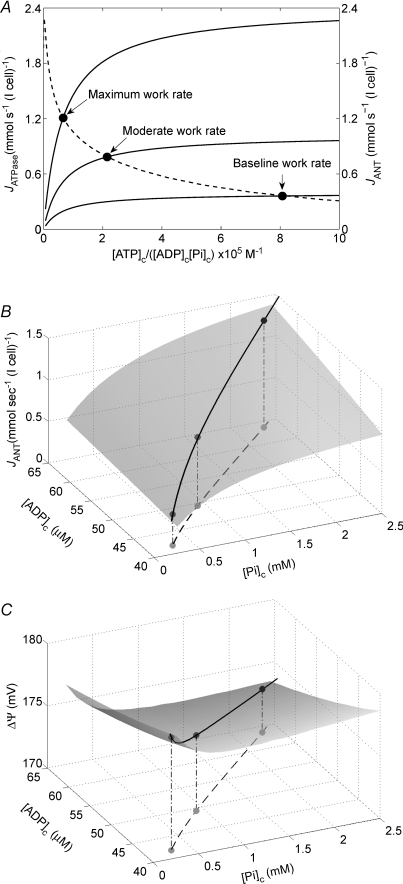
Our computational model of cardiac oxidative ATP synthesis and the phenomenological model for the dependency of ATP hydrolysis on cytoplasmic phosphate metabolite concentrations of eqn (1) provide a theoretical basis to explore the relationship between cardiac ATP synthesis and ATP hydrolysis. In Fig. 6A we plot the predicted relationship between ATP hydrolysis rate and the mass-action ratio [ATP]c/([ADP]c[Pi]c) at different steady-state ATP consumption rates obtained by varying the value of XATPase. The predicted relationship between JANT, the flux through adenine nucleotide translocase, and the mass-action ratio is also plotted in this figure, illustrating that the mass-action ratio decreases as the rate of ATP synthesis and 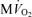Inline graphic increase. The curve for JANTversus[ATP]c/([ADP]c[Pi]c) is obtained by varying the XATPase and computing the steady-state ATP synthesis flux and values of cytoplasmic phosphate metabolites; the JATPase and JANT curves intersect at the steady-solution for a given work state.

Figure 6. Regulation of ATP synthesis and hydrolysis in vivo.

Figure 6

Open in a new tab

A, the phenomenological relationship of eqn (1) between ATP hydrolysis rate and mass-action ratio ATP]c/([ADP]c[Pi]c) is plotted as continuous lines for different steady-state work rates. The different continuous lines correspond to different values of XAtC, corresponding to three different work rates, as indicated on the figure. Also plotted (dashed line) is the relationship between the steady-state ATP synthesis rate (the flux through adenine nucleotide translocase JANT) and ATP]c/([ADP]c[Pi]c) predicted by the integrated model. B, control of ATP synthesis by inorganic phosphate. With [ATP]c fixed at 10 mm, the model-predicted relationship between JANT and cytoplasmic ADP and Pi is plotted. Both [ADP]c and [Pi]c are varied over the predicted in vivo ranges for these variables. The continuous line traces the predicted in vivo values over the range of cardiac work rates studied. The three points correspond to the baseline, moderate and high work rates illustrated in A. C, variation in mitochondrial membrane potential with cardiomyocyte work rate. The model-predicted ΔΨ is plotted for the conditions described for panel B. The values of JANT and ΔΨ plotted in panels B and C correspond to average tissue values.

Our analysis predicts that, of the three variables [ATP]c, [ADP]c and [Pi]c, the one that varies the most during increases in work is [Pi]c. The model-predicted dependency of ATP synthesis on [Pi]c and [ADP]c is illustrated in Fig. 6B, which plots the ATP synthesis flux (JANT, the flux through adenine nucleotide translocase) over the predicted in vivo ranges of [Pi]c and [ADP]c with [ATP]c fixed at 9.66 mm. The model predicts that over the expected in vivo range of [ATP]c, [ADP]c and [Pi]c, the rate of oxidative ATP synthesis is most sensitive to [Pi]c. Therefore we postulate that [Pi]c is both the primary feedback signal for stimulating oxidative phosphorylation in vivo, and is the most significant product of ATP hydrolysis in limiting the capacity of the heart to hydrolyse ATP in vivo. Since cytoplasmic ATP is maintained at effectively constant concentration, the source of increasing inorganic phosphate concentration with increasing work is CrP. From baseline to the maximal observed work rate, [CrP]c drops approximately 3.5 mm, while [Pi]c increases approximately 2.0 mm. The drop in CrP concentration exceeds the increase in Pi because Pi is distributed through the cytoplasm and the mitochondria while CrP is restricted to the cytoplasm.

The model-predicted mitochondrial membrane potential (ΔΨ), which is the driving force for ATP synthesis and ATP transport out of the mitochondrial matrix, is illustrated over the range of [Pi]c and [ADP]c in Fig. 6B is plotted in Fig. 6C, demonstrating that ΔΨ is predicted to remain fairly constant (within a range of 5 mV) over the observed range of ATP and oxygen consumption.

Summary

Phosphate metabolite data obtained non-invasively in canine heart using 31P-MRS methods were analysed using a detailed computer simulation of cardiac energy metabolism and oxygen transport. The computational model provides quantitative estimates of phosphate metabolite concentrations that are not directly available from the MRS data.

Key findings of this study are: (1) We estimate baseline inorganic phosphate (Pi) concentration in the canine myocyte cytoplasm to be approximately 0.29 mm and increases to 2.3 mm near maximal cardiac work states; (2) During acute ischaemia (LAD ligation) Pi increases to approximately 3.1 mm and ATP consumption in the ischaemic tissue is reduced to half of its baseline value before the creatine phosphate (CrP) pool is 18% depleted. After the full 36 s of ligation, Pi increases to 5.3 mm; (3) The drop in ATP hydrolysis in the cytoplasm during ischaemia is associated with the ATP hydrolysis free energy approaching and going above a critical value, approximately −63.5 kJ mol−1, above which the heart cannot effectively work; (4) Inorganic phosphate, although difficult to detect, varies over a dynamic range significantly greater than that of ATP, ADP or CrP during changes in work rate or perfusion in the heart. Over a 3-fold range of ATP hydrolysis rate, cytoplasmic Pi is predicted to vary over an 8-fold range, while ATP, ADP and CrP vary less than 0.3%, 52% and 15%, respectively.

In addition, we introduce the following novel hypotheses based on our model-based analysis of the steady-state and transient data in Figs 2 and 4:

  1. Over the expected in vivo range of [ATP]c, [ADP]c and [Pi]c, the rate of oxidative ATP synthesis is most sensitive to [Pi]c. Therefore we predict that inorganic phosphate is the primary feedback signal for stimulating oxidative phosphorylation in vivo. Since ATP is maintained at an effectively constant concentration and ADP concentrations are low compared to Pi, the major source of increasing [Pi] during increases in work rate is CrP. The less than 15% decrease in [CrP] is associated with the predicted 8-fold increase in [Pi]c during increased work.

  2. The maximal oxygen consumption rate of the heart is an emergent property that is limited not simply by the maximal rate of oxidative ATP synthesis, but by the maximal rate at which ATP can be synthesized at a free energy (ΔGATPase) at which it can be utilized. Since the reductions in the magnitude of ΔGATPase that occur with increasing work and during acute ischaemia are determined largely by increasing inorganic phosphate concentration, inorganic phosphate is the most significant product of ATP hydrolysis in limiting the capacity of the heart to hydrolyse ATP in vivo.

Since myocardial free Pi is one of the metabolites most difficult to measure in vivo in its physiological concentration range, our hypotheses regarding its role as a critical feedback signal may be controversial. Indeed, due to the lack of precise quantification of Piin vivo, these hypotheses and associated model predictions remain to be carefully tested experimentally. We have demonstrated that a model of cardiac energetics in which feedback of substrate concentrations is the sole mechanism of control of oxidative phosphorylation is consistent with the observed relationships between phosphate metabolites and cardiac 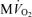Inline graphic. If the hypothesized powerful action of Pi in stimulating ATP synthesis is correct then it provides a sufficient explanation of in vivo data on the control of oxidative phosphorylation using only feedback control. However, the present simulations do not rule out the possibility that other regulatory mechanisms, including feedforward control, are at work in the heart in vivo.

Acknowledgments

The authors thank Ranjan Dash for helpful discussions and assistance with numerical methods. Computational work was supported by NIH grant HL072011 (D.A.B.); experimental studies were supported by HL50470 (J.Z.), HL67828 (JZ), HL21872 (R.B.).

Supplementary material

Online supplemental material for this paper can be accessed at:

tjp0586-4193-SD1.pdf (91.6KB, pdf)

http://jp.physoc.org/cgi/content/full/jphysiol.2008.154732/DC1

Supplemental Data
2008.154732_index.html (665B, html)

References

  1. Allen DG, Orchard CH. Myocardial contractile function during ischemia and hypoxia. Circ Res. 1987;60:153–168. doi: 10.1161/01.res.60.2.153. [DOI] [PubMed] [Google Scholar]
  2. Bache RJ, Zhang J, Murakami Y, Zhang Y, Cho YK, Merkle H, Gong G, From AH, Ugurbil K. Myocardial oxygenation at high workstates in hearts with left ventricular hypertrophy. Cardiovasc Res. 1999;42:616–626. doi: 10.1016/s0008-6363(98)00332-0. [DOI] [PubMed] [Google Scholar]
  3. Bailey IA, Williams SR, Radda GK, Gadian DG. Activity of phosphorylase in total global ischaemia in the rat heart. A phosphorus-31 nuclear-magnetic-resonance study. Biochem J. 1981;196:171–178. doi: 10.1042/bj1960171. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Balaban RS. Regulation of oxidative phosphorylation in the mammalian cell. Am J Physiol Cell Physiol. 1990;258:C377–C389. doi: 10.1152/ajpcell.1990.258.3.C377. [DOI] [PubMed] [Google Scholar]
  5. Balaban RS. Cardiac energy metabolism homeostasis: role of cytosolic calcium. J Mol Cell Cardiol. 2002;34:1259–1271. doi: 10.1006/jmcc.2002.2082. [DOI] [PubMed] [Google Scholar]
  6. Balaban RS. Maintenance of the metabolic homeostasis of the heart: developing a systems analysis approach. Ann N Y Acad Sci. 2006;1080:140–153. doi: 10.1196/annals.1380.013. [DOI] [PubMed] [Google Scholar]
  7. Balaban RS, Kantor HL, Katz LA, Briggs RW. Relation between work and phosphate metabolite in the in vivo paced mammalian heart. Science. 1986;232:1121–1123. doi: 10.1126/science.3704638. [DOI] [PubMed] [Google Scholar]
  8. Beard DA. A biophysical model of the mitochondrial respiratory system and oxidative phosphorylation. PLoS Comput Biol. 2005;1:e36. doi: 10.1371/journal.pcbi.0010036. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Beard DA. Modeling of oxygen transport and cellular energetics explains observations on in vivo cardiac energy metabolism. PLoS Comput Biol. 2006;2:e107. doi: 10.1371/journal.pcbi.0020107. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Blei ML, Conley KE, Kushmerick MJ. Separate measures of ATP utilization and recovery in human skeletal muscle. J Physiol. 1993;465:203–222. doi: 10.1113/jphysiol.1993.sp019673. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Bose S, French S, Evans FJ, Joubert F, Balaban RS. Metabolic network control of oxidative phosphorylation: multiple roles of inorganic phosphate. J Biol Chem. 2003;278:39155–39165. doi: 10.1074/jbc.M306409200. [DOI] [PubMed] [Google Scholar]
  12. Brindle KM, Rajagopalan B, Williams DS, Detre JA, Simplaceanu E, Ho C, Radda GK. 31P NMR measurements of myocardial pH in vivo. Biochem Biophys Res Commun. 1988;151:70–77. doi: 10.1016/0006-291x(88)90560-8. [DOI] [PubMed] [Google Scholar]
  13. Feygin J, Hu Q, Swingen C, Zhang J. Relationships between regional myocardial wall stress and bioenergetics in hearts with left ventricular hypertrophy. Am J Physiol Heart Circ Physiol. 2008;294:H2313–H2321. doi: 10.1152/ajpheart.01288.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Feygin J, Mansoor A, Eckman P, Swingen C, Zhang J. Functional and bioenergetic modulations in the infarct border zone following autologous mesenchymal stem cell transplantation. Am J Physiol Heart Circ Physiol. 2007;293:H1772–H1780. doi: 10.1152/ajpheart.00242.2007. [DOI] [PubMed] [Google Scholar]
  15. Friehs I, Moran AM, Stamm C, Colan SD, Takeuchi K, Cao-Danh H, Rader CM, McGowan FX, del Nido PJ. Impaired glucose transporter activity in pressure-overload hypertrophy is an early indicator of progression to failure. Circulation. 1999;100:II187–II193. doi: 10.1161/01.cir.100.suppl_2.ii-187. [DOI] [PubMed] [Google Scholar]
  16. Garnier A, Fortin D, Delomenie C, Momken I, Veksler V, Ventura-Clapier R. Depressed mitochondrial transcription factors and oxidative capacity in rat failing cardiac and skeletal muscles. J Physiol. 2003;551:491–501. doi: 10.1113/jphysiol.2003.045104. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Gong G, Liu J, Liang P, Guo T, Hu Q, Ochiai K, Hou M, Ye Y, Wu X, Mansoor A, From AH, Ugurbil K, Bache RJ, Zhang J. Oxidative capacity in failing hearts. Am J Physiol Heart Circ Physiol. 2003;285:H541–H548. doi: 10.1152/ajpheart.01142.2002. [DOI] [PubMed] [Google Scholar]
  18. Gong G, Ugurbil K, Zhang J. Transmural metabolic heterogeneity at high cardiac work states. Am J Physiol Heart Circ Physiol. 1999;277:H236–H242. doi: 10.1152/ajpheart.1999.277.1.H236. [DOI] [PubMed] [Google Scholar]
  19. Headrick JP, Dobson GP, Williams JP, McKirdy JC, Jordan L, Willis RJ. Bioenergetics and control of oxygen consumption in the in situ rat heart. Am J Physiol Heart Circ Physiol. 1994;267:H1074–H1084. doi: 10.1152/ajpheart.1994.267.3.H1074. [DOI] [PubMed] [Google Scholar]
  20. Hogan MC, Gladden LB, Grassi B, Stary CM, Samaja M. Bioenergetics of contracting skeletal muscle after partial reduction of blood flow. J Appl Physiol. 1998;84:1882–1888. doi: 10.1152/jappl.1998.84.6.1882. [DOI] [PubMed] [Google Scholar]
  21. Jeneson JA, Westerhoff HV, Kushmerick MJ. A metabolic control analysis of kinetic controls in ATP free energy metabolism in contracting skeletal muscle. Am J Physiol Cell Physiol. 2000;279:C813–C832. doi: 10.1152/ajpcell.2000.279.3.C813. [DOI] [PubMed] [Google Scholar]
  22. Jung WI, Hoess T, Bunse M, Widmaier S, Sieverding L, Breuer J, Apitz J, Schmidt O, van Erckelens F, Dietze GJ, Lutz O. Differences in cardiac energetics between patients with familial and nonfamilial hypertrophic cardiomyopathy. Circulation. 2000;101:E121. doi: 10.1161/01.cir.101.12.e121. [DOI] [PubMed] [Google Scholar]
  23. Jung WI, Sieverding L, Breuer J, Hoess T, Widmaier S, Schmidt O, Bunse M, van Erckelens F, Apitz J, Lutz O, Dietze GJ. 31P NMR spectroscopy detects metabolic abnormalities in asymptomatic patients with hypertrophic cardiomyopathy. Circulation. 1998;97:2536–2542. doi: 10.1161/01.cir.97.25.2536. [DOI] [PubMed] [Google Scholar]
  24. Katz LA, Swain JA, Portman MA, Balaban RS. Relation between phosphate metabolites and oxygen consumption of heart in vivo. Am J Physiol Heart Circ Physiol. 1989;256:H265–H274. doi: 10.1152/ajpheart.1989.256.1.H265. [DOI] [PubMed] [Google Scholar]
  25. Kentish JC. The effects of inorganic phosphate and creatine phosphate on force production in skinned muscles from rat ventricle. J Physiol. 1986;370:585–604. doi: 10.1113/jphysiol.1986.sp015952. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Kreutzer U, Jue T. 1H-nuclear magnetic resonance deoxymyoglobin signal as indicator of intracellular oxygenation in myocardium. Am J Physiol Heart Circ Physiol. 1991;261:H2091–H2097. doi: 10.1152/ajpheart.1991.261.6.H2091. [DOI] [PubMed] [Google Scholar]
  27. Kushmerick MJ. Skeletal muscle: a paradigm for testing principles of bioenergetics. J Bioenerg Biomembr. 1995;27:555–569. doi: 10.1007/BF02111654. [DOI] [PubMed] [Google Scholar]
  28. Kushmerick MJ, Meyer RA, Brown TR. Phosphorus NMR spectroscopy of cat biceps and soleus muscles. Adv Exp Med Biol. 1983;159:303–325. doi: 10.1007/978-1-4684-7790-0_27. [DOI] [PubMed] [Google Scholar]
  29. Lamb HJ, Beyerbacht HP, Ouwerkerk R, Doornbos J, Pluim BM, van der Wall EE, van der Laarse A, de Roos A. Metabolic response of normal human myocardium to high-dose atropine-dobutamine stress studied by 31P-MRS. Circulation. 1997;96:2969–2977. doi: 10.1161/01.cir.96.9.2969. [DOI] [PubMed] [Google Scholar]
  30. Lee J, Hu Q, Nakamura Y, Wang X, Zhang X, Zhu X, Chen W, Yang Q, Zhang J. Open-chest 31P magnetic resonance spectroscopy of mouse heart at 4.7 Tesla. J Magn Reson Imaging. 2006;24:1269–1276. doi: 10.1002/jmri.20766. [DOI] [PubMed] [Google Scholar]
  31. Liao R, Nascimben L, Friedrich J, Gwathmey JK, Ingwall JS. Decreased energy reserve in an animal model of dilated cardiomyopathy. Relationship to contractile performance. Circ Res. 1996;78:893–902. doi: 10.1161/01.res.78.5.893. [DOI] [PubMed] [Google Scholar]
  32. Massie BM, Schwartz GG, Garcia J, Wisneski JA, Weiner MW, Owens T. Myocardial metabolism during increased work states in the porcine left ventricle in vivo. Circ Res. 1994;74:64–73. doi: 10.1161/01.res.74.1.64. [DOI] [PubMed] [Google Scholar]
  33. Metelkin E, Goryanin I, Demin O. Mathematical modeling of mitochondrial adenine nucleotide translocase. Biophys J. 2006;90:423–432. doi: 10.1529/biophysj.105.061986. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Meyer RA. A linear model of muscle respiration explains monoexponential phosphocreatine changes. Am J Physiol Cell Physiol. 1988;254:C548–C553. doi: 10.1152/ajpcell.1988.254.4.C548. [DOI] [PubMed] [Google Scholar]
  35. Montgomery C, Hamilton N, Ianuzzo CD. Energy status of the rapidly paced canine myocardium in congestive heart failure. J Appl Physiol. 1992;73:2363–2367. doi: 10.1152/jappl.1992.73.6.2363. [DOI] [PubMed] [Google Scholar]
  36. Murakami Y, Zhang Y, Cho YK, Mansoor AM, Chung JK, Chu C, Francis G, Ugurbil K, Bache RJ, From AH, Jerosch-Herold M, Wilke N, Zhang J. Myocardial oxygenation during high work states in hearts with postinfarction remodeling. Circulation. 1999;99:942–948. doi: 10.1161/01.cir.99.7.942. [DOI] [PubMed] [Google Scholar]
  37. Neubauer S, Horn M, Cramer M, Harre K, Newell JB, Peters W, Pabst T, Ertl G, Hahn D, Ingwall JS, Kochsiek K. Myocardial phosphocreatine-to-ATP ratio is a predictor of mortality in patients with dilated cardiomyopathy. Circulation. 1997;96:2190–2196. doi: 10.1161/01.cir.96.7.2190. [DOI] [PubMed] [Google Scholar]
  38. Neubauer S, Krahe T, Schindler R, Horn M, Hillenbrand H, Entzeroth C, et al. 31P magnetic resonance spectroscopy in dilated cardiomyopathy and coronary artery disease. Altered cardiac high-energy phosphate metabolism in heart failure. Circulation. 1992;86:1810–1818. doi: 10.1161/01.cir.86.6.1810. [DOI] [PubMed] [Google Scholar]
  39. Ochiai K, Zhang J, Gong G, Zhang Y, Liu J, Ye Y, Wu X, Liu H, Murakami Y, Bache RJ, Ugurbil K, From AH. Effects of augmented delivery of pyruvate on myocardial high-energy phosphate metabolism at high workstate. Am J Physiol Heart Circ Physiol. 2001;281:H1823–H1832. doi: 10.1152/ajpheart.2001.281.4.H1823. [DOI] [PubMed] [Google Scholar]
  40. Pool PE, Covell JW, Chidsey CA, Braunwald E. Myocardial high energy phosphate stores in acutely induced hypoxic heart failure. Circ Res. 1966;19:221–229. doi: 10.1161/01.res.19.2.221. [DOI] [PubMed] [Google Scholar]
  41. Reiermann HJ, Herzig JW, Ruegg JC. Ca++ activation of ATPase activity, ATP-Pi exchange, and tension in briefly glycerinated heart muscle. Basic Res Cardiol. 1977;72:133–139. doi: 10.1007/BF01906351. [DOI] [PubMed] [Google Scholar]
  42. Robitaille PM, Merkle H, Lew B, Path G, Hendrich K, Lindstrom P, From AH, Garwood M, Bache RJ, Ugurbil K. Transmural high energy phosphate distribution and response to alterations in workload in the normal canine myocardium as studied with spatially localized 31P NMR spectroscopy. Magn Reson Med. 1990;16:91–116. doi: 10.1002/mrm.1910160110. [DOI] [PubMed] [Google Scholar]
  43. Robitaille PM, Merkle H, Sublett E, Hendrich K, Lew B, Path G, From AH, Bache RJ, Garwood M, Ugurbil K. Spectroscopic imaging and spatial localization using adiabatic pulses and applications to detect transmural metabolite distribution in the canine heart. Magn Reson Med. 1989;10:14–37. doi: 10.1002/mrm.1910100103. [DOI] [PubMed] [Google Scholar]
  44. Saks VA, Kongas O, Vendelin M, Kay L. Role of the creatine/phosphocreatine system in the regulation of mitochondrial respiration. Acta Physiol Scand. 2000;168:635–641. doi: 10.1046/j.1365-201x.2000.00715.x. [DOI] [PubMed] [Google Scholar]
  45. Schmidt-Ott SC, Bletz C, Vahl C, Saggau W, Hagl S, Ruegg JC. Inorganic phosphate inhibits contractility and ATPase activity in skinned fibers from human myocardium. Basic Res Cardiol. 1990;85:358–366. doi: 10.1007/BF01907128. [DOI] [PubMed] [Google Scholar]
  46. Schwartz GG, Schaefer S, Meyerhoff DJ, Gober J, Fochler P, Massie B, Weiner MW. Dynamic relation between myocardial contractility and energy metabolism during and following brief coronary occlusion in the pig. Circ Res. 1990;67:490–500. doi: 10.1161/01.res.67.2.490. [DOI] [PubMed] [Google Scholar]
  47. Schwartz GG, Schaefer S, Trocha SD, Steinman S, Gober J, Garcia J, Massie B, Weiner MW. Metabolic and functional consequences of blunted myocardial reactive hyperemia. Am J Physiol Heart Circ Physiol. 1991;261:H892–H900. doi: 10.1152/ajpheart.1991.261.3.H892. [DOI] [PubMed] [Google Scholar]
  48. Spindler M, Saupe KW, Tian R, Ahmed S, Matlib MA, Ingwall JS. Altered creatine kinase enzyme kinetics in diabetic cardiomyopathy. A 31P NMR magnetization transfer study of the intact beating rat heart. J Mol Cell Cardiol. 1999;31:2175–2189. doi: 10.1006/jmcc.1999.1044. [DOI] [PubMed] [Google Scholar]
  49. Stanley WC, Recchia FA, Lopaschuk GD. Myocardial substrate metabolism in the normal and failing heart. Physiol Rev. 2005;85:1093–1129. doi: 10.1152/physrev.00006.2004. [DOI] [PubMed] [Google Scholar]
  50. Taegtmeyer H, McNulty P, Young ME. Adaptation and maladaptation of the heart in diabetes: Part I: general concepts. Circulation. 2002;105:1727–1733. doi: 10.1161/01.cir.0000012466.50373.e8. [DOI] [PubMed] [Google Scholar]
  51. Taegtmeyer H, Overturf ML. Effects of moderate hypertension on cardiac function and metabolism in the rabbit. Hypertension. 1988;11:416–426. doi: 10.1161/01.hyp.11.5.416. [DOI] [PubMed] [Google Scholar]
  52. Veech RL, Lawson JW, Cornell NW, Krebs HA. Cytosolic phosphorylation potential. J Biol Chem. 1979;254:6538–6547. [PubMed] [Google Scholar]
  53. Vendelin M, Kongas O, Saks V. Regulation of mitochondrial respiration in heart cells analyzed by reaction-diffusion model of energy transfer. Am J Physiol Cell Physiol. 2000;278:C747–C764. doi: 10.1152/ajpcell.2000.278.4.C747. [DOI] [PubMed] [Google Scholar]
  54. Vicini P, Kushmerick MJ. Cellular energetics analysis by a mathematical model of energy balance: estimation of parameters in human skeletal muscle. Am J Physiol Cell Physiol. 2000;279:C213–C224. doi: 10.1152/ajpcell.2000.279.1.C213. [DOI] [PubMed] [Google Scholar]
  55. Weiss RG, Gerstenblith G, Bottomley PA. ATP flux through creatine kinase in the normal, stressed, and failing human heart. Proc Natl Acad Sci U S A. 2005;102:808–813. doi: 10.1073/pnas.0408962102. [DOI] [PMC free article] [PubMed] [Google Scholar]
  56. Westerhoff HV, van Echteld CJ, Jeneson JA. On the expected relationship between Gibbs energy of ATP hydrolysis and muscle performance. Biophys Chem. 1995;54:137–142. doi: 10.1016/0301-4622(94)00129-8. [DOI] [PubMed] [Google Scholar]
  57. Wu F, Jeneson JA, Beard DA. Oxidative ATP synthesis in skeletal muscle is controlled by substrate feedback. Am J Physiol Cell Physiol. 2007a;292:C115–C124. doi: 10.1152/ajpcell.00237.2006. [DOI] [PubMed] [Google Scholar]
  58. Wu F, Yang F, Vinnakota KC, Beard DA. Computer modeling of mitochondrial tricarboxylic acid cycle, oxidative phosphorylation, metabolite transport, and electrophysiology. J Biol Chem. 2007b;282:24525–24537. doi: 10.1074/jbc.M701024200. [DOI] [PubMed] [Google Scholar]
  59. Young ME, McNulty P, Taegtmeyer H. Adaptation and maladaptation of the heart in diabetes: Part II: potential mechanisms. Circulation. 2002;105:1861–1870. doi: 10.1161/01.cir.0000012467.61045.87. [DOI] [PubMed] [Google Scholar]
  60. Zhang J, Duncker DJ, Xu Y, Zhang Y, Path G, Merkle H, Hendrich K, From AH, Bache RJ, Ugurbil K. Transmural bioenergetic responses of normal myocardium to high workstates. Am J Physiol Heart Circ Physiol. 1995;268:H1891–H1905. doi: 10.1152/ajpheart.1995.268.5.H1891. [DOI] [PubMed] [Google Scholar]
  61. Zhang J, From AH, Ugurbil K, Bache RJ. Myocardial oxygenation and high-energy phosphate levels during KATP channel blockade. Am J Physiol Heart Circ Physiol. 2003;285:H1420–H1427. doi: 10.1152/ajpheart.00167.2003. [DOI] [PubMed] [Google Scholar]
  62. Zhang J, Gong G, Ye Y, Guo T, Mansoor A, Hu Q, Ochiai K, Liu J, Wang X, Cheng Y, Iverson N, Lee J, From AH, Ugurbil K, Bache RJ. Nitric oxide regulation of myocardial O2 consumption and HEP metabolism. Am J Physiol Heart Circ Physiol. 2005;288:H310–H316. doi: 10.1152/ajpheart.00518.2004. [DOI] [PubMed] [Google Scholar]
  63. Zhang J, McDonald KM. Bioenergetic consequences of left ventricular remodeling. Circulation. 1995;92:1011–1019. doi: 10.1161/01.cir.92.4.1011. [DOI] [PubMed] [Google Scholar]
  64. Zhang J, Merkle H, Hendrich K, Garwood M, From AH, Ugurbil K, Bache RJ. Bioenergetic abnormalities associated with severe left ventricular hypertrophy. J Clin Invest. 1993;92:993–1003. doi: 10.1172/JCI116676. [DOI] [PMC free article] [PubMed] [Google Scholar]
  65. Zhang J, Murakami Y, Zhang Y, Cho YK, Ye Y, Gong G, Bache RJ, Ugurbil K, From AH. Oxygen delivery does not limit cardiac performance during high work states. Am J Physiol Heart Circ Physiol. 1999;277:H50–H57. doi: 10.1152/ajpheart.1999.277.1.H50. [DOI] [PubMed] [Google Scholar]
  66. Zhang J, Ugurbil K, From AH, Bache RJ. Myocardial oxygenation and high-energy phosphate levels during graded coronary hypoperfusion. Am J Physiol Heart Circ Physiol. 2001;280:H318–H326. doi: 10.1152/ajpheart.2001.280.1.H318. [DOI] [PubMed] [Google Scholar]
  67. Zhang J, Wilke N, Wang Y, Zhang Y, Wang C, Eijgelshoven MH, Cho YK, Murakami Y, Ugurbil K, Bache RJ, From AH. Functional and bioenergetic consequences of postinfarction left ventricular remodeling in a new porcine model. MRI and 31 P-MRS study. Circulation. 1996;94:1089–1100. doi: 10.1161/01.cir.94.5.1089. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

tjp0586-4193-SD1.pdf (91.6KB, pdf)
Supplemental Data
2008.154732_index.html (665B, html)
2008.154732_1.pdf (91.6KB, pdf)

Articles from The Journal of Physiology are provided here courtesy of The Physiological Society

RESOURCES