Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2010 Feb 1.
Published in final edited form as: Metabolism. 2009 Feb;58(2):220–225. doi: 10.1016/j.metabol.2008.09.017

Validity of the Reduced-Sample-Insulin-Modified-Frequently Sampled Intravenous Glucose Tolerance Test Using the Nonlinear Regression Approach

Anne E Sumner 1, Marcella F Luercio 1, Barbara A Frempong 1, Madia Ricks 1, Sabyasachi Sen 1, Harvey Kushner 2, Marshall K Tulloch-Reid 3
PMCID: PMC2652479  NIHMSID: NIHMS94659  PMID: 19154955

Abstract

The Disposition Index, the product of the insulin sensitivity index (SI) and the acute insulin response to glucose, is linked in African-Americans to chromosome 11q. This link was determined with SI calculated with the nonlinear regression approach to the minimal model and data from the Reduced-Sampled-Insulin-Modified-Frequently-Sampled-Intravenous-Glucose-Tolerance-Test (Reduced-Sample-IM-FSIGT). However, the application of the nonlinear regression approach to calculate SI using data from the Reduced-Sample-IM-FSIGT has been challenged as being not only inaccurate but also having a high failure rate in insulin-resistant subjects. Our goal was to determine the accuracy and failure rate of the Reduced-Sample-IM-FSIGT using the nonlinear regression approach to the minimal model. With SI from the Full-Sample-IM-FISGT considered the standard and using the nonlinear regression approach to the minimal model, we compared the agreement between SI from the Full and Reduced-Sample-IM-FSIGT protocols. One hundred African-Americans, (BMI 31.3±7.6 kg/m2 (mean±SD), range 19.0-56.9 kg/m2) had FSIGTs. Glucose (0.3g/kg) was given at baseline. Insulin was infused from 20 to 25 minutes (total insulin dose 0.02U/kg). For the Full-Sample-IM-FSIGT, SI was calculated based on the glucose and insulin samples taken at -1, 1, 2, 3, 4, 5, 6, 7, 8,10, 12, 14, 16, 19, 22, 23, 24, 25, 27, 30, 40, 50, 60, 70, 80, 90, 100, 120, 150, 180. For the Reduced-Sample-FSIGT, SI was calculated based on the timepoints which appear in bold. Agreement was determined by Spearman correlation, concordance and the Bland-Altman method. In addition, for both protocols, the population was divided into tertiles of SI. Insulin resistance was defined by the lowest tertile of SI from the Full-Sample-IM-FSIGT. The distribution of subjects across tertiles was compared by rank order and kappa statistic. We found that the rate of failure of resolution of SI by the Reduced-Sample-IM-FSIGT was 3%(3/100). For the remaining 97 subjects, SI for the Full and Reduced-Sample-IM-FSIGT were: 3.76±2.41 L.mU-1.min-1, range 0.58-14.50 and 4.29±2.89 L.mU-1.min-1, range 0.52-14.42, relative error 21±18%, Spearman r=0.97, concordance 0.94, (both P<0.001). After log transformation the Bland Altman limits of agreement were: -0.29 and 0.53. The exact agreement for distribution of the population in the insulin-resistant tertile versus the insulin-sensitive tertiles was 92%, kappa 0.82±0.06. Using the nonlinear regression approach and data from the Reduced-Sample-IM-FSIGT in subjects with a wide range of insulin sensitivity, failure to resolve SI occurred in only 3% of subjects. The agreement and maintenance of rank order of SI between protocols supports the use of the nonlinear regression approach to the minimal model and the Reduced-Sample-IM-FSIGT in clinical studies.

Introduction

The combination of insulin resistance and beta-cell failure is the most widely accepted construct of the etiology of type 2 diabetes. This concept was reinforced by the discovery that the Disposition Index (DI) predicts type 2 diabetes1. DI represents the ability of beta-cells to overcome insulin resistance 2. Importantly, a genome scan for glucose homeostasis traits in the Insulin Resistance Atherosclerosis (IRAS) Family Study found in African-Americans that DI is linked to chromosome 11q3.

DI, a hyperbolic function, is calculated as the product of the insulin sensitivity index (SI) and the acute insulin response to glucose (AIRg)2. SI is determined by a mathematical model, the minimal model4. The input for the minimal model is data obtained from the frequently sampled intravenous glucose tolerance test (FSIGT). There are several FSIGT protocols and more than one mathematical approach to the minimal model5-8. The calculated value of SI differs depending on the FSIGT protocol and the mathematical approach. In contrast, the determination of AIRg is the straightforward analysis of an area under a curve.

Consequently the strength of DI is dependent on the validity of SI. The link between DI and chromosome 11q was determined with SI calculated with the nonlinear regression approach to the minimal model and data from the Reduced-Sample-Insulin-Modified-Frequently-Sampled-Intravenous-Glucose-Tolerance-Test (Reduced-Sample-IM-FSIGT). However, the application of the nonlinear regression approach to Reduced-Sample-IM-FSIGT has been challenged as being not only inaccurate but also having a high failure rate in insulin-resistant subjects6, 7. Yet, the IRAS Family Study as well as other important epidemiological studies are using the nonlinear regression approach to the minimal model with data from the Reduced-Sample-IM-FSIGT. Therefore we believe it is important to review the history of the development of Reduced-Sample-IM-FSIGT and systematically test the validity of SI calculated from the minimal model using the nonlinear regression approach with data from the Reduced-Sample-IM-FSIGT.

For background, the minimal model is based on two differential equations4. The final result for SI depends not only on these equations but also on the specific FSIGT protocol used to collect the data that is entered into the minimal model. The first FSIGT protocol used was the glucose-only FSIGT9. In a glucose-only-FSIGT, a glucose bolus (0.3 g/kg) is given at baseline. Glucose and insulin concentrations are measured at 30 timepoints over three hours. However, in the presence of beta-cell failure, a glucose-only-FSIGT cannot be used to calculate insulin resistance. This is because with a standard glucose bolus, the absence of a robust beta-cell response makes it impossible to model the influence of insulin on glucose disappearance. To address this challenge, additional FSIGT protocols were developed: specifically the tolbutamide-boosted-FSIGT, the insulin-modified-FSIGT and the high-glucose-dose-FSIGT6, 8, 10. In the tolbutamide-boosted-FSIGT an intravenous bolus of glucose is administered at baseline and then at 20 minutes intravenous tolbutamide, an insulin secretagogue, is given. In an insulin-modified-FSIGT, an intravenous bolus of glucose is given at time 0 and intravenous insulin is administered at 20 minutes. In the high-glucose-dose-FSIGT the dose of glucose given at baseline is 0.5g/kg. This is higher than the standard glucose dose of 0.3g/kg and thereby provides extra stimulus for endogenous beta-cell secretion of insulin6. No exogenous insulin is given in the high-glucose-dose-FSIGT.

The insulin-modified-FSIGT is now the FSIGT protocol most commonly used. Originally the insulin-modified-FSIGT was performed over 3 hours with glucose and insulin sampled at 30 time points. However the cost and labor of this insulin-modified-FSIGT precluded its widespread application. To address this problem, a less frequently sampled FSIGT was developed using only 12 time points 11. Steil et. al. designed the reduced sample protocol empirically with the first 4 time points selected to capture acute insulin secretion (0, 2, 4, 8 minutes), the next 2 time points selected to be immediately before and after the exogenous insulin injection (10 and 22 minutes) and the remaining 6 time points chosen to minimize parameter variance and reduce error in reconstructing the insulin profile (30, 50, 90 and 180 minutes)11. Since the publication of the reduced sample protocol the reduced sample time points have been widely accepted. Consequently a debate in the literature has risen as to the proper mathematical protocol to apply to the minimal model equations when the reduced sample protocol is used6, 7. In this investigation we refer to the insulin-modified-FSIGT which uses 30 time points as the Full-Sample-IM-FSIGT. The FSIGT protocol which uses only 12 time points is known as the Reduced-Sample-IM-FSIGT.

Initially, data from the Reduced-Sample-IM-FSIGT was entered into the minimal model using individual estimates and nonlinear regression11. Some investigators have suggested that when data from a Reduced-Sampled-FSIGT protocol is entered into the minimal model using a nonlinear regression approach, SI cannot be resolved in many insulin resistant subjects7. Therefore, alternative approaches to the minimal model have been proposed using much more computationally complex population based methods such as Bayesian hierarchal analyses5-7. However, the analyses which linked DI to chromosome 11q in African-Americans calculated SI based on data from a Reduced-Sampled-IM-FSIGT and a nonlinear regression approach to the minimal model3.

Our goal was to determine the rate of resolution and accuracy of the Reduced-Sample-IM-FSIGT, using the nonlinear regression approach to the minimal model. Accuracy was determined by comparing SI calculated from the Full and Reduced-Sample-IM-FSIGT.

Research Design and Methods

One hundred African-Americans (46M, 54W, age 35±7, mean±SD, range 22-50y, BMI 31.3±7.6, range 19.0-56.9kg/m2) participating in Triglyceride and Cardiovascular Risk in African-Americans (TARA), a cross-sectional study at NIH, Bethesda, Maryland were evaluated. Basic demographics for these subjects are provided in Table 1. Results from these subjects have previously been reported12. Forty-eight percent of the subjects were obese and 24% glucose intolerant. Recruitment was by newsletters, flyers and websites. The Institutional Review Board of NIDDK approved the study. Subjects gave informed consent.

Table.

Characteristics of the Participants

Variable (n=101) Mean±SD Range
Age (y) 35±7 22 - 50
Percent Male 46
BMI (kg/m2) 31.4±7.6 19.0-56.9
Waist Circumference (cm) 99±16 67-142
Systolic Blood Pressure (mmHg) 117±14 92-153
Diastolic Blood Pressure (mmHg) 70±9 48-92
Fasting Glucose (mg/dL) 84±9 66-112
Fasting Insulin (mU/mL) 8.3±4.5 1.9-25.0
Percent Glucose Intolerant 31
Open in a new tab

As described 12, subjects had a Full-Sample-IM-FSIGT in the morning after a 12h overnight fast. Glucose (0.3g/kg) was injected at baseline and insulin was infused from 20 to 25 min (4 mU.kg-1.min-1). The total dose of insulin administered over 5 minutes was 0.02U/kg. Glucose and insulin levels were determined at -10, -5, -1, 1, 2, 3, 4, 5, 6, 7, 8,10, 12, 14, 16, 19, 22, 23, 24, 25, 27, 30, 40, 50, 60, 70, 80, 90, 100, 120, 150, 180 minutes. The Reduced-Sample-IM-FSIGT timepoints are in bold. We note that in the original design of the reduced sample protocol, the 90 minute time point was used11. We chose to report our results using the 100 minute time point because the IRAS Family Investigators chose this time point3. However, all analyses were performed with SI calculated using the 90 minute time point and again with SI calculated using the 100 minute point. SI calculated with the 90 minute time point was 4.31±2.89 mU.L-1.min, range 0.58-14.26. When the 100 minute time point was substituted for the 90 minute timepoint, SI was essentially unchanged. Specifically, SI using the 100 minute time point was 4.29±2.89 mU.L-1.min, range 0.52-14.42.

SI was calculated for the Full and Reduced-Sample-IM-FSIGT using MinMOD Millenium v.6.0213. The minimal model equations are:

•G‵(t)=−(X+Sg)G(t)+Sg.Gb Eqn 1
•X‵(t)=−p2.X(t)+p3(I(t)−Ib) Eqn 2
•SI=p3/p2.

Equation 1 is the net rate of change of glucose concentration. Equation 2 is net rate of change of insulin action over time at an insulin concentration above basal. X represents insulin action in the remote compartment. Sg is glucose effectiveness. P2 stands for the loss of insulin from the remote site. P3 describes circulating insulin crossing the capillary endothelium into the remote site to promote glucose disposal.

Failure of resolution of SI was defined as parameter coefficient of variation (PCV)>100%6. SI calculated with nonlinear regression approach and the Full-Sample-IM-FSIGT is the accepted standard used to compare methodologies5. Initially 101 subjects were analyzed. However using the Full-Sample-IM-FSIGT for one of the subjects the PCV for SI was 177%. As SI from this subject could not be calculated with the accepted standard method, this subject was excluded.

Statistical Analyses

With the Full-Sample-IM-FSIGT considered the standard, percent relative error of SI 7 was calculated as: ((absolute value of Full minus Reduced)/Full)*100. Spearman correlation coefficient was used to compare SI obtained from the Full and Reduced-Sample-IM-FSIGT.

The agreement of SI between FSIGT protocols was assessed by the Lin concordance correlation coefficient14. This coefficient determines whether the observed data from each method significantly deviates from the line of perfect concordance (that is, a line at 45 degrees when both measurements are plotted against each other)14, 15.

In addition, the agreement of SI by the two FSIGT protocols was assessed by the Bland Altman method. In this method the mean of the values obtained from each protocol is plotted against their difference16. With good agreement the mean difference in the measurements is close to zero and there is limited and uniform variation around a zero difference line along the full range of the average values. The limits of agreement demonstrate the range of differences that might be expected from both methods. Due to the variability in measurements, limits of agreement are usually based on log transformed data17.

To assess the ability of these methods to maintain rank order, subjects were grouped into tertiles using values obtained from the Full and Reduced-Sample-IM-FSIGT. Then rank order agreement for both methods was assessed using percent agreement and the kappa statistic. In this investigation, insulin resistance was defined a priori by the lowest tertile of SI determined by data from the Full-Sample-IM-FSIGT.

All results are presented as mean±SD unless specified otherwise. Analyses were performed with STATA, version 10.0 (College Station, TX).

Results

Using the nonlinear regression method with the Reduced-Sample-IM-FSIGT, SI was successfully resolved in 97% (97/100) of participants. Therefore the rate of failure of resolution with the Reduced-Sample-IM-FSIGT was 3% (3/100).

The three subjects for whom SI could not be calculated with the Reduced-Sample-IM-FSIGT had SI values from the Full-Sample-IM-FSIGT of: 2.23, 2.76 and 10.1 L.mU-1.min-1. As insulin resistance was defined by the lowest SI tertile (SI of ≤2.37 L.mU-1.min-1), for the three subjects for whom SI could not be resolved by the Reduced-Sample-IM-FSIGT, two were relatively insulin-resistant and one was insulin-sensitive.

All subsequent analyses are based on the 97 subjects who achieved successful resolution of SI by both FSIGT protocols. The frequency distributions of SI for the two protocols are provided in Figure 1. SI for the Full and Reduced-Sample-IM-FSIGT were: 3.76±2.41 and 4.29±2.89; relative error 21±18%, Spearman correlation 0.97, P<0.001 (Figure 2) and concordance 0.92, P<0.001. For log transformed data, the Bland Altman limits of agreement were: -0.29 and 0.53 and the mean difference was 0.12 (Figure 3).

Figure 1.

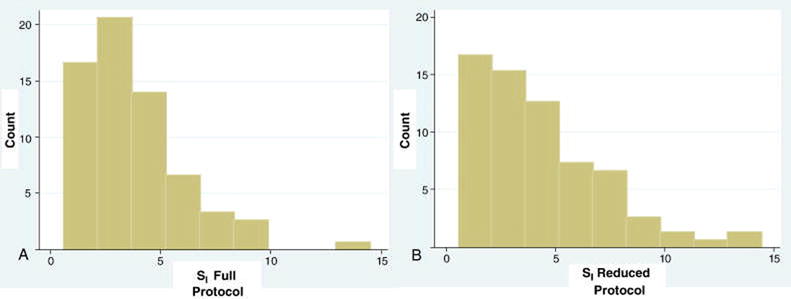
Figure 1

Open in a new tab

Histograms of the Frequency of SI according to FSIGT protocol.

(A) Full-Sample-IM-FSIGT. (B) Reduced-Sample-IM-FSIGT.

Figure 2.

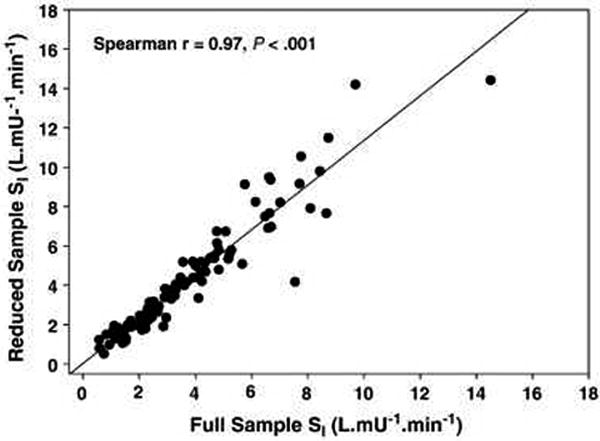
Figure 2

Open in a new tab

SI from the Full-Sample-IM-FSIGT versus SI from the Reduced Sample-IM-FSIGT. Spearman correlation is 0.97, P<0.001.

Figure 3.

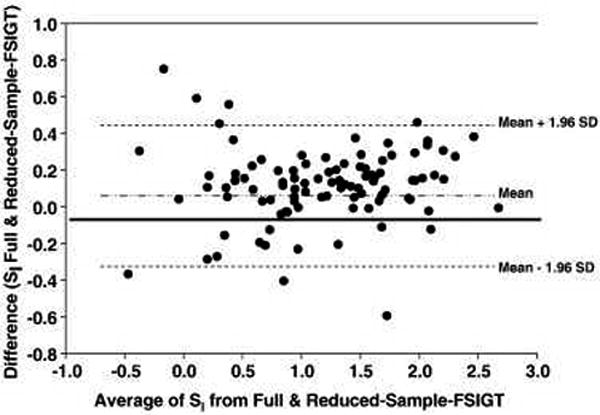
Figure 3

Open in a new tab

Bland Altman Plot for agreement between SI calculated from Full and Reduced-Sample-IM-FSIGT. Data is log transformed. X-axis presents the mean of the two determinations of SI. Y-axis presents the difference. With back transformation, the limits of agreement were 0.75 and 1.69 and the geometric mean difference was 1.12. The mean difference of 1.12 suggests that SI is overestimated when data from the Reduced-Sample-IM-FSIGT protocol is used.

When the tertile distribution of SI for each of the two FSIGT protocols is compared, the exact agreement by tertile category is 86% with kappa 0.78±0.07 (SE). However insulin resistance was defined by SI calculated from the lowest tertile. Those in the middle and upper SI were classified as insulin-sensitive. The exact agreement for the distribution of the population in the lowest tertile versus the combination of the middle and upper tertiles is 92% with kappa 0.82±0.06 (SE). Therefore, predicting insulin-resistant subjects with tertiles led to a misclassification error by the Reduced-Sample-IM-FSIGT of only 8%.

Discussion

There is controversy as to whether SI can be accurately and successfully resolved in insulin-resistant subjects using the nonlinear regression approach to the minimal model6, 7. We enter the debate by presenting results from subjects with a wide range of insulin sensitivity and a prevalence of glucose intolerance of 24%. We found a failure rate in the resolution of SI of only 3% with the Reduced-Sample-IM-FSIGT. Therefore when data from the Reduced-Sample-IM-FSIGT are entered into the minimal model with a nonlinear regression approach a high rate of success in resolving SI can be expected. Furthermore we suggest that insulin resistance does not preclude the use of the nonlinear regression approach to the minimal model. In this investigation of the three subjects for whom SI could not be resolved with the Reduced-Sample-IM-FSIGT, two were relatively insulin-resistant (2.23 and 2.76 L.mU-1.min-1) and one was insulin-sensitive (10.1 L.mU-1.min-1).

Yet, other investigators have reported high failure rates using the nonlinear regression approach to the minimal model. Using only a Reduced-Sample-FSIGT and the nonlinear regression approach, Godsland et. al. reported a failure rate of 7%6. Krudys et. al. found a failure rate in the resolution of SI of 17% 7. With glucose intolerant subjects Krudys et. al. reported a failure rate of 31%7.

The higher failure rate in the resolution of SI reported by both Godsland et. al. and Krudys et. al. may be due, at least in part, to differences in the FSIGT protocol rather than to the mathematical approach used. The FSIGT protocol that we used was insulin-modified. Godsland et. al. used a high-glucose-dose-FSIGT protocol6. Even though Godsland et. al. administered a higher dose of intravenous glucose than we did (0.5g/kg vs. 0.3g/kg), the absence of an intravenous bolus of insulin may account for their higher failure rate. The high failure rate by Krudys et. al. may also be protocol dependent7. First they provided an intravenous glucose bolus based on body surface area (BSA) (11.4g/m2) rather than weight (0.3g/kg). In obese subjects a dose of glucose based on BSA is generally lower than a dose of glucose based on weight. For example, using the DuBois formula for BSA in a person with a BMI of 35.7 kg/m2 and a weight of 106.1 kg, the dose of glucose administered would be 24.9g. However, if the glucose dose is based on weight, the glucose dose at 0.3g/kg would be 31.8g or 28% higher than the dose based on BSA. A smaller glucose dose will provoke a lower endogenous insulin response and consequently poorer resolution of SI. Further, they infused intravenous tolbutamide rather than insulin at 20 minutes. Differences in SI determined from the tolbutamide-boosted versus the insulin-modified FSIGTs are well recognized18.

SI calculated with the nonlinear regression approach to the minimal model has been validated against glucose clamp measures of insulin resistance19. Further the agreement of SI calculated from the Full and Reduced-Sample-IM-FSIGT is highly significant11. Yet, in any modeling endeavor, when the number of samples is decreased, there is a loss of accuracy. Comparing SI from the Full and Reduced-Sample-IM-FSIGT, we found a relative error of 21%. This relative error is consistent with the work of Steil et.al. as they report an error rate of 20% with the Reduced-Sample-tolbutamide-boosted-FSIGT 11. In interpreting this error, we found that the mean difference in SI between protocols was positive. Thus, the error between the two determinations may be accounted for by an overestimation of SI with the Reduced-Sample-IM-FSIGT protocol. Krudys et. al. also found that SI calculated with data from the Reduced-Sample-tolbutamide-FSIGT consistently overestimated SI7. Despite the overestimation of SI when the reduced sample protocol is used, rank order of SI is maintained. In fact, our tertile analyses of SI demonstrated that subjects identified as insulin-resistant with the Full-Sample-IM-FSIGT had a misclassification error by the Reduced-Sample-IM-FSIGT of only 8%. However, due to the persistent and consistent overestimation of SI with the reduced sample protocol, in any single study results from the reduced and the full sample FSIGT cannot be combined.

In this investigation using the nonlinear regression approach to the minimal model, we tested the validity of SI obtained from the Reduced-Sample-IM-FSIGT. Even in the presence of insulin resistance, the Reduced-Sampled-IM-FSIGT was very successful in resolving SI. Further, the agreement and maintenance of rank order of SI between the Full and Reduced-Sample-IM-FSIGT provides support for the value of the Reduced-Sample-IM-FSIGT. Consequently we suggest that it is not necessary to switch from nonlinear regression analyses to more complicated mathematical techniques such as Bayesian hierarchal analyses to calculate SI. Indeed the IRAS Family Study linking DI to Chromosome 11 is an example of how the application of the Reduced-Sample-IM-FSIGT can be utilized to obtain important information about glucose homeostasis3. Therefore, we encourage the use of the Reduced-Sample-IM-FSIGT with the nonlinear regression approach for epidemiological studies to better understand the role of insulin resistance in human disease.

Acknowledgments

This work was supported by the intramural research program at NIDDK.

Footnotes

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

References

  • 1.Bergman RN. Orchestration of glucose homeostasis: from a small acorn to the California Oak. Diabetes. 2007;56:1489–501. doi: 10.2337/db07-9903. [DOI] [PubMed] [Google Scholar]
  • 2.Bergman RN, Marilyn A, Huecking K, Van Critters G. Accurate Assessment of Beta-Cell Function: The Hyperbolic Correction. Diabetes. 2002;51(Supp 1):S212–S20. doi: 10.2337/diabetes.51.2007.s212. [DOI] [PubMed] [Google Scholar]
  • 3.Palmer ND, Langefeld CD, Campbell JK, et al. Genetic Mapping of the Disposition Index and Acute Insulin Response Loci on Chromosome 11q, The Insulin Resistance Atherosclerosis Study (IRAS) Family Study. Diabetes. 2006;55:911–8. doi: 10.2337/diabetes.55.04.06.db05-0813. [DOI] [PubMed] [Google Scholar]
  • 4.Bergman RN. Toward Physiological Understanding of Glucose Tolerance, Minimal-Model Approach. Diabetes. 1989;38:1512–27. doi: 10.2337/diab.38.12.1512. [DOI] [PubMed] [Google Scholar]
  • 5.Erichsen L, Agbaje OF, Luzio SD, Owens DR, Hovorka R. Population and Individual Minimal Modeling of the Frequently Sampled Insulin-Modified Intravenous Glucose Tolerance Test. Metabolism. 2004;53:1349–54. doi: 10.1016/j.metabol.2004.04.011. [DOI] [PubMed] [Google Scholar]
  • 6.Godsland IF, Agbaje OF, Hovorka R. Evaluation of Nonlinear Regression Approaches to Estimation of Insulin Sensitivity by the Minimal Model with Reference to Bayesian Hierarchical Analysis. Am J Physiol Endocrinol Metab. 2006;291:E167–E74. doi: 10.1152/ajpendo.00328.2004. [DOI] [PubMed] [Google Scholar]
  • 7.Krudys KM, Kahn SE, Vicini P. Population Approaches to Estimate Minimal Model Indexes of Insulin Sensitivity and Glucose Effectiveness Using Full and Reduced Sampling Schedules. Am J Physiol Endocrinol Metab. 2006;291:E716–E23. doi: 10.1152/ajpendo.00346.2005. [DOI] [PubMed] [Google Scholar]
  • 8.Saad MF, Steil GM, Riad-Gabriel M, et al. Method of Insulin Administration Has No Effect on Insulin Sensitivity Estimates From the Insulin-Modified Minimal Model Protocol. Diabetes. 1997;46:2044–8. doi: 10.2337/diab.46.12.2044. [DOI] [PubMed] [Google Scholar]
  • 9.Bergman RN, Ider YZ, Bowden DW, Cobelli C. Quantative Estimation of Insulin Sensitivity. Am J Physiol Endocrinol Metab. 1979;5:E667–E77. doi: 10.1152/ajpendo.1979.236.6.E667. [DOI] [PubMed] [Google Scholar]
  • 10.Yang YJ, Youn JH, Bergman RN. Modified Protocols Improve Insulin Sensitivity Estimation Using the Minimal Model. Am J Physiol. 1987;253:E595–E602. doi: 10.1152/ajpendo.1987.253.6.E595. [DOI] [PubMed] [Google Scholar]
  • 11.Steil GM, Volund A, Kahn SE, Bergman RN. Reduced Sample Number for Calculation of Insulin Sensitivity and Glucose Effectiveness From the Minimal Model, Suitability for Use in Population Studies. Diabetes. 1993;42:250–6. doi: 10.2337/diab.42.2.250. [DOI] [PubMed] [Google Scholar]
  • 12.Sumner AE, Finley KB, Genovese DJ, Criqui MH, Boston RC. Fasting Triglyceride and the Triglyceride-HDL Cholesterol Ratio Are Not Markers of Insulin Resistance in African Americans. Arch Intern Med. 2005;165:1395–400. doi: 10.1001/archinte.165.12.1395. [DOI] [PubMed] [Google Scholar]
  • 13.Boston RC, Stefanovski D, Moate PJ, Sumner AE, Watanabe RM, Bergman RN. Minmod Millennium: A computer program to calculate glucose effectiveness and insulin sensitivity from the frequently sampled intravenous glucose tolerance test. Diabetes Technology & Therapeutics. 2003;5:1003–15. doi: 10.1089/152091503322641060. [DOI] [PubMed] [Google Scholar]
  • 14.Lin LI. A Concordance Correlation Coefficient to Evaluate Reproducibility. Biometrics. 1989;45:225–68. [PubMed] [Google Scholar]
  • 15.Barnhart HX, Haber MJ, Lin LI. An Overview on Assessing Agreement with Continuous Measurements. Journal of Biopharmaceutical Statistics. 2007;17:529–69. doi: 10.1080/10543400701376480. [DOI] [PubMed] [Google Scholar]
  • 16.Bland JM, Altman DG. Statistical Methods for Assessing Agreement Between Two Methods of Clinical Measurement. Lancet. 1986;i:307–10. [PubMed] [Google Scholar]
  • 17.Bland JM, Altman DG. Measuring Agreement in Method Comparison Studies. Stat Methods Med Res. 1999;8:135–60. doi: 10.1177/096228029900800204. [DOI] [PubMed] [Google Scholar]
  • 18.Saad MF, Steil GM, Kades WW, et al. Differences Between the Tolbutamide-Boosted and the Insulin-Modified Minimal Model Protocols. Diabetes. 1997;46:1167–71. doi: 10.2337/diab.46.7.1167. [DOI] [PubMed] [Google Scholar]
  • 19.Saad MF, Anderson RL, Laws A, et al. A Comparison Between the Minimal Model and the Glucose Clamp in the Assessment of Insulin Sensitivity Across the Spectrum of Glucose Tolerance. Diabetes. 1994;43:1114–21. doi: 10.2337/diab.43.9.1114. [DOI] [PubMed] [Google Scholar]

RESOURCES