Coronary calcium predicts events better with absolute calcium scores than age-gender-race percentiles – The Multi-Ethnic Study of Atherosclerosis (MESA)

Abstract

Background

The presence and extent of coronary artery calcium (CAC) correlates with the overall magnitude of coronary atherosclerotic plaque burden and with the development of subsequent coronary events. In this study we aim to establish whether age-gender specific percentiles of CAC predict cardiovascular outcomes better than the actual (absolute) CAC score.

Methods

MESA is a prospective cohort study of asymptomatic 6814 participants, followed for coronary heart disease (CHD) events including myocardial infarction, angina, resuscitated cardiac arrest, or CHD death. Time to incident CHD was modeled using Cox regression, and we compared models using percentiles based on age, gender and/or race/ethnicity to categories commonly used(0, 1-100, 101-400, 400+ Agatston units).

Results

There were 163(2.4%) incident CHD events (median follow-up 3.75 years). Expressing CAC in terms of age and gender specific percentiles had significantly lower area under the ROC curve(AUC) than using absolute scores (women: AUC 0.73 versus 0.76,p=0.044; men: AUC 0.73 versus 0.77,p<0.001). Akaike’s information criterion (AIC) indicated better model fit using the overall score. Both methods robustly predicted events(>90^th percentile associated with a hazard ratio(HR) of 16.4(95% c.i. 9.30,28.9), and score >400 associated with HR of 20.6(95% c.i. 11.8, 36.0). Within groups based on age/gender/race/ethnicity specific percentiles there remains a clear trend of increasing risk across levels of the absolute CAC groups. In contrast, once absolute CAC category is fixed, there is no increasing trend across levels of age/gender/race/ethnicity specific categories. Patients with low absolute scores are low risk, regardless of age-gender-ethnicity percentile rank. Persons with an absolute CAC score of >400 are high risk, regardless of percentile rank.

Conclusion

Using absolute CAC in standard groups performed better than age-gender-ethnicity percentiles in terms of model fit and discrimination. We recommend using cut-points based on the absolute CAC amount and the common CAC cutpoints of 100 and 400 appear to perform well.

INTRODUCTION

Computed tomography (CT) is a noninvasive tool for the detection and quantification of coronary artery calcium (CAC), a marker for atherosclerosis. The presence and extent of CAC correlates with the overall magnitude of coronary atherosclerotic plaque burden and with the development of subsequent coronary events.^1-4 CAC occurs only in the setting of atherosclerosis, and is a better index of global atherosclerotic burden than stenosis severity.⁵ CAC has been shown to add independent prognostic information in every study to date. Recently, overall results from the Multi-Ethnic Study of Atherosclerosis (MESA), demonstrated that CAC improved risk prediction after taking into account Framingham risk score (FRS) in a multi-ethnic population based study.⁶

The National Cholesterol Education Program (NCEP Adult Treatment Panel III)⁷, American Heart Association⁵ and American College of Cardiology⁸ have each stated that it may be reasonable to measure CAC in selected patients at intermediate risk, but the precise method to utilize these scores has been of debate in the CT literature. Early data supports that having a CAC above an age-gender specific cutpoint, (CAC >/= 75th percentile), is associated with increased CHD events, and could be used as marker to identify individuals requiring aggressive preventive management.⁹ The hypothesis that a low score in a young person is more abnormal than a low score in an older person, and may carry independent risk, has been incorporated into guidelines including those from the NCEP, which recommends that persons with CAC >75th percentile for their age and sex would be candidates for intensified LDL-lowering therapy.⁷ Others have reported that increasing events are most associated with increasing absolute scores (i.e. >100 or >400), rather than based upon demographic specific percentiles.¹⁰

The large population based observational study, MESA, with 6,814 persons undergoing calcium scoring and longitudinal follow-up, allows evaluation of the robustness of these different scoring approaches. In this study we aim to establish whether absolute CAC scores predict cardiovascular outcomes better than age-gender and/or race/ethnicity specific CAC percentiles of the MESA cohort. In other words, whether it is the actual amount of calcium present, or their relative amount compared to others of the same age, gender and race/ethnicity, that is most strongly associated with risk.

METHODS

Recruitment and Baseline Examination

The MESA cohort¹¹ is a longitudinal, population-based study of 6,814 men and women, free of clinical cardiovascular disease, aged 45-84 at baseline recruited from six Field Centers: Baltimore, MD ; Chicago, IL; Forsyth County, NC ; Los Angeles, CA ; New York, NY ; and St. Paul, MN. Specific ethnicity groups enrolled included white, black, Hispanic and Chinese. Over 50% of the participants enrolled were female. Details of the MESA recruitment strategy are contained elsewhere (19). The baseline visit took place between July 2000 and September 2002. The study was approved by Institutional Review Boards at each site and all participants gave written informed consent.

The purpose of the study is to examine the risk factors and progression of subclinical cardiovascular disease. The design of the study has been described in detail previously,¹² but we describe the collection of pertinent variables here.

Measurement of CAC

Computed Tomographic Scanning

Scanning centers assessed coronary calcium by chest computed tomography using either a cardiac-gated electron-beam computed tomography scanner (Chicago, Los Angeles, and New York Field Centers) or a multi-detector computed tomography system (Baltimore, Forsyth County and St. Paul Field Centers). Certified technologists scanned all participants twice over phantoms of known physical calcium concentration. A radiologist or cardiologist read all CT scans at a central reading center (Los Angeles Biomedical Research Institute at Harbor-UCLA in Torrance, CA). We used the average Agatston score¹³ for the two scans in all analyses. Carr et al have reported the details of the MESA computed tomography scanning and interpretation methods.¹⁴

Events Surveillance

To date, the cohort has been followed for incident cardiovascular events for a median of 46 months.⁶ At intervals of 9-12 months, a telephone interviewer contacted each participant to inquire about interim hospital admissions, cardiovascular outpatient diagnoses, and deaths. In order to verify self-reported diagnoses, we requested copies of all death certificates and medical records for hospitalizations and outpatient cardiovascular diagnoses and conducted next-of-kin interviews for out of hospital cardiovascular deaths. We obtained records on 98% of reported hospitalized cardiovascular events. Some information was available on 95% of reported outpatient diagnostic encounters.

Trained personnel abstracted medical records suggesting possible cardiovascular events. Two physicians independently classified and assigned incidence dates. If, after review and adjudication, disagreements persisted, a full mortality and morbidity review committee made the final classification. For purposes of this study, we used all incident CHD events as the endpoint, including definite or probable MI, resuscitated cardiac arrest, fatal CHD, definite angina, and probable angina if accompanied by revascularization. Definitions for each of these events are as follows. Reviewers classified MI as definite, probable, or absent, based primarily on combinations of symptoms, ECG, and cardiac biomarker levels. In most cases, definite or probable MI required either abnormal cardiac biomarkers (2 times upper limits of normal) regardless of pain or ECG findings; evolving Q waves regardless of pain or biomarker findings; or a combination of chest pain, and ST-T evolution or new LBBB, and biomarker levels 1-2 times upper limits of normal.

Reviewers classified resuscitated cardiac arrest when a patient successfully recovered from a full cardiac arrest through cardiopulmonary resuscitation (including cardioversion). Angina was classified, except in the setting of MI and/or angina required symptoms of typical chest pain or atypical symptoms, as asymptomatic coronary artery disease is not a MESA endpoint. Probable angina required, in addition to symptoms, a physician diagnosis of angina and medical treatment for it. Definite angina required one or more additional criteria, including CABG surgery or other revascularization procedure; 70% or greater obstruction on coronary angiography; or evidence of ischemia by stress tests or by resting ECG. We considered coronary revascularization or a physician diagnosis of angina or CHD, in the absence of symptoms, to not be angina. Fatal CHD required a documented MI within the previous 28 days, chest pain within the 72 hours before death, or a history of CHD, and required the absence of a known non-atherosclerotic or non-cardiac cause of death.

Statistics

(i) Estimating Age, Gender, and/or Race/ethnicity Specific Percentiles

The methodology for estimating the age, gender and/or race/ethnicity specific percentiles is described in detail in McClelland et al.¹⁵ A brief description is provided below. The distribution of baseline CAC in this population is heavily skewed, with approximately 50% of participants having zero calcium. The positive portion of the CAC distribution is fairly symmetric and bell shaped on the log scale. As a first step in obtaining age, gender and race/ethnicity specific quantiles, we model the mean of the log CAC distribution (positive CAC scores only) as a linear function of age, within each gender and race/ethnicity. Within each gender and race/ethnicity the residuals from this model are then ranked, and we calculate the jth percentile for each of j=1,…,100 of the residuals. Adding these to the fitted value for a particular age, gender and race/ethnicity yields an estimated percentile for the log transformed positive CAC variable. Taking the exponential of this percentile yields the jth percentile of the positive portion of the CAC distribution. If a certain proportion p have zero calcium, then the jth percentile calculated above is the $100\times \left(p+\frac{(1-p)j}{100}\right)$ percentile of the overall CAC distribution (i.e. including the zeroes). We model p as a gender and race/ethnicity specific function of age using logistic regression. To estimate age and gender specific percentiles, we follow the strategy outlined above, but the models are only gender specific, not race/ethnicity and gender specific, and residuals are ranked without regard to race/ethnicity. Percentiles by age and race/ethnicity, and age only are obtained similarly. Gender and race/ethnicity specific percentiles as well as overall percentiles are obtained by simply ranking the values within each group of interest. In all cases, participants with zero CAC are assigned a midrank percentile, equal to half the predicted probability of zero CAC from the logistic regression model above.

(ii) Models for Time to Incident CHD

Time to incident CHD was modeled using Cox proportional hazards models. We also considered parametric survival models including exponential, Weibull, log-normal, and log-logistic, but conclusions were unaffected and only the Cox model results are presented. We compared models using continuous versions of the percentiles, and also categorized versions. For models based on the continuous variables, each model contained a percentile ranking of CAC, and an indicator for whether CAC was positive at baseline. The indicator term allows a different intercept for those with and without CAC, and is necessary due to the possible discontinuity between the continuous positive CAC values and zero CAC. In addition we also fit continuous model using log(CAC+1) instead of CAC percentile. Since the percentiles would likely be categorized for use clinically, we also fit models using the following groups: zero CAC, <=75^th percentile, 75^th-90^th percentile, and >90^th percentile. A final model used CAC in four groups based on cutpoints commonly seen in the literature (zero CAC, 1-100, 101-400, >400).

Models were compared on the basis of several metrics, each of which reflects a different characteristic of a desirable prediction model. The hazards ratios represent the multiplicative increase in risk association with a one-percentile point difference in ranking (or a one log Agatston unit for the log CAC model). Assuming the scales are comparable, a stronger predictor should have a higher hazards ratio. These are useful to compare the various percentile rankings, though they are not comparable between the percentile rankings and the model with log CAC or CAC group. For each model we calculated a proportion of variation explained, using a modified version of R-squared for censored data described in Royston.¹⁶ Additionally we estimated the area under the receiver-operator characteristic (ROC) curve, and Akaike’s Information Criterion (AIC). These statistics are comparable across all models within a given gender. The R-squared is a measure of model fit, while the AUC is a measure of discrimination. For both of these, higher values are preferable. AIC is also a measure of model fit, but includes a penalty for models with more parameters (such as with CAC group in four levels). Lower values of AIC indicate better model fit.

RESULTS

Overall the study population consisted of 6809 individuals at baseline (mean age: 62±10 years, 47% males). There were 163 incident CHD events (2.4%) observed over a median of 3.75 years. Table 1 demonstrates that the cardiovascular risk profile was less favorable in those who subsequently developed CHD than in those in who did not. In addition, baseline CACS was significantly higher among those who suffered an incident CHD event compared to those who did not.

Table 1.

Baseline Characteristics According to Absolute and Age-Gender-Race Adjusted CAC Scores

	No CHD Event (n=6646)	CHD Events (n=163)	P value
Age (years)	62±10	68±9	<0.0001
Male Gender (%)	47%	71%	<0.0001
Race (%)
Caucasians	38%	45%
Chinese American	12%	9%	0.22
African American	28%	24%
Hispanic	22%	22%
LDL-C (mg/dl)	117±31	121±36	0.08
HDL-C (mg/dl)	51±15	47±15	0.001
Diabetes Mellitus (%)	14%	27%	<0.0001
Current Cigarette smoker (%)	13%	16%	0.001
Hypertension (%)	44%	66%	<0.0001
Lipid Lowering Medication	15%	28%	<0.0001
10 Year risk (%) of CHD*	8±7	14±7	<0.0001
Mean CAC Scores (%)	136±398	529±700	<0.0001
CAC Score>400 (%)	9%	34%	<0.0001
CAC>75th percentile Age-gender-race adjusted (%)	9%	28%	<0.0001

^*10 year risk of CHD event (%) based on NCEP ATP III criteria

Table 2a and 2b displays the sample size, event rates, hazards ratios and AIC statistics for models using categories based on various adjusted percentile rankings (age-gender & age-gender-race adjusted) as well as based on absolute CAC cutoffs (0, 1-100, 101-400 & >400) in women and men. The best fitting model as measured by the lowest AIC used absolute CAC cutpoints, and these correspond quite closely to the 75^th and 90^th overall percentile. Using the percentiles continuously and comparing to a model containing log(CAC+1) yielded the same conclusions, in that the overall percentile or the model using log(CAC+1) performed best. This was also true in terms of area under the ROC curve, and R-squared. For example, among women the area under the ROC curve was 0.76 for overall percentile (or log(CAC+1)), and was 0.73 for age and gender specific percentiles (p=0.04). For men, the AUC was 0.77 for overall percentile (or log(CAC+1)) and 0.73 for age and gender specific percentiles (p<0.001). The modified R-squared was 0.53 for the log(CAC+1) model for women, 0.50 for men. In contrast the modified R-squared was much lower for age and gender specific percentiles at 0.46 for women, and 0.38 for men. As shown in supplemental table 1, age specific percentile rankings had the worst model fit, regardless of whether gender and race/ethnicity were also considered.

Table 2.

a: Prediction of incident CHD as a function of CAC percentiles & CAC absolute scores in women
	CAC Cutoffs	n	CHD (n=48)	Rate*	HR (95% CI)	AIC
ADJUSTED CAC SCORES
Age and Gender Specific	CAC=0	2167	8	1.0	1 (reference)
	<75th percentile	637	13	5.9	6.10 (2.53, 14.7)
	75th-90th percentile	448	14	8.9	8.99 (3.77, 21.4)	726
	>90th percentile	349	13	10.6	10.7 (4.42, 25.7)
Age –Gender-Race Specific	CAC=0	2167	8	1.0	1 (reference)
	<75th percentile	632	13	5.9	6.09 (2.52, 14.7)
	75th-90th percentile	455	15	9.4	9.58 (4.96, 22.6)	726
	>90th percentile	347	12	9.9	9.94 (4.06, 24.3)
ABSOLUTE CAC SCORES
CAC Group	CAC=0	2167	8	1.0	1 (reference)
	CAC 1-100	859	17	5.5	6.09 (2.52, 14.7)
	CAC 101-400	373	11	8.6	9.58 (4.96, 22.6)	718
	CAC>400	202	12	18.9	9.94 (4.06, 24.3)
b: Prediction of incident CHD as a function of CAC percentiles & CAC absolute scores in men
	CAC Cutoffs	n	CHD (n=115)	Rate*	HR (95% CI)	AIC
ADJUSTED CAC SCORES
Age and Gender Specific	CAC=0	1249	8	1.8	1 (reference)
	<75th percentile	1189	47	11.7	6.51 (3.08, 13.8)
	75th-90th percentile	468	26	16.1	9.07 (4.10, 20.0)	1731
	>90th percentile	307	34	34.0	18.9 (8.73, 40.8)
Age –Gender-Race Specific	CAC=0	1249	8	1.8	1 (reference)
	<75th percentile	1181	47	11.7	6.51 (3.08, 13.8)
	75th-90th percentile	476	26	16.2	8.97 (4.06, 19.8)	1731
	>90th percentile	307	34	33.8	18.9 (8.73, 40.8)
ABSOLUTE CAC SCORES
CAC Group	CAC=0	1249	8	1.8	1 (reference)
	CAC 1-100	935	22	6.7	6.09 (2.52, 14.7)
	CAC 101-400	554	41	22.1	9.58 (4.96, 22.6)	1712
	CAC>400	475	44	29.2	9.94 (4.06, 24.3)

^*event rate is expressed per 1000 person years at risk; HR=hazards ratio from a Cox regression model

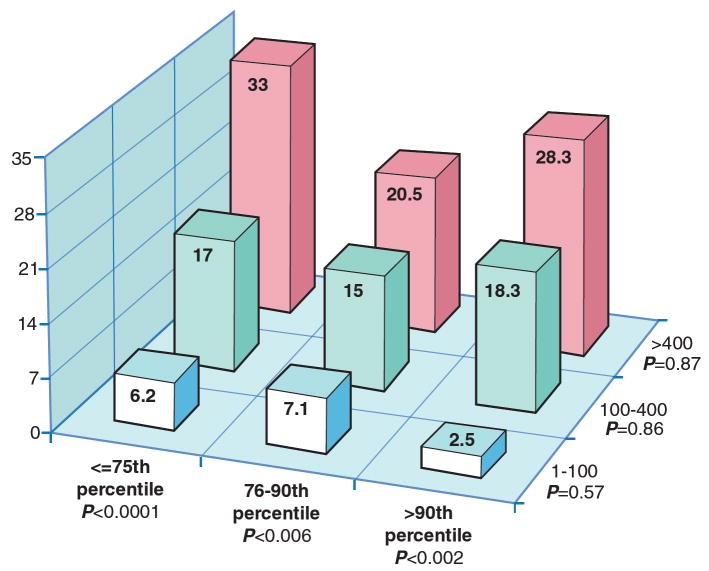
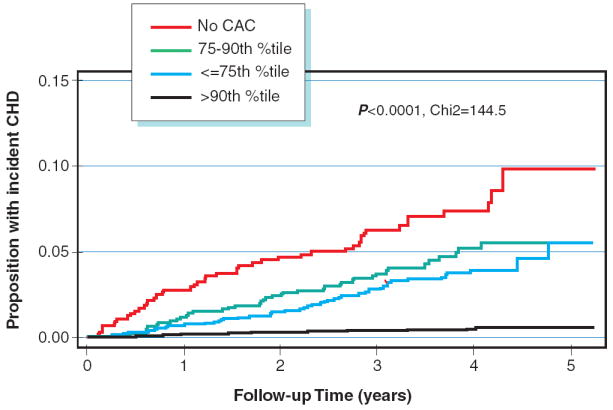
Figure 1 compares the display the incidence of CHD over time by CAC group. The absolute CAC categories yield curves with much better separation, indicating greater risk stratification ability. In figure 2, we display the rates of incident CHD per 1000 person years at risk by joint categories of absolute CAC group and age/gender/race/ethnicity specific percentiles. We note that the overall 75^th and 90^th percentiles for the MESA cohort are 88 and 398 CAC units respectively, and hence the absolute CAC groups are essentially equivalent to dividing based on the overall percentiles. Within a particular level of age/gender/race/ethnicity specific percentile, there remains a clear trend of increasing risk across levels of the absolute CAC groups. In contrast, once absolute CAC category is fixed, there is no increasing trend across levels of age/gender/race/ethnicity specific categories.

Fig. 1.

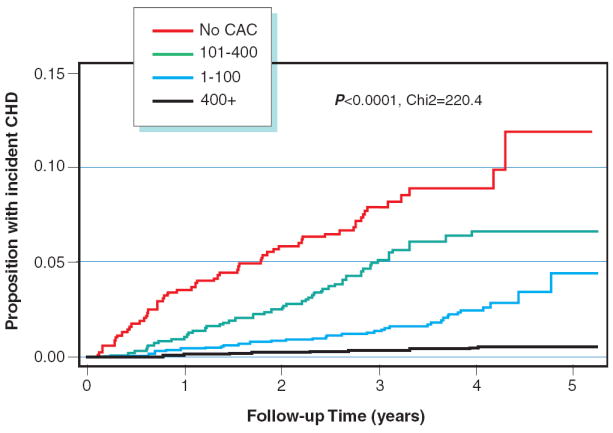
A Kaplan Meyer curve for events according to absolute CAC scores

B Kaplan Meyer curve for events according to Age-Gender-Race Adjusted Percentile CAC scores

Figure 1 compares the display the incidence of CHD over time by CAC group. The absolute CAC categories yield curves with much better separation (A), indicating greater risk stratification ability than Age-Gender-Race Adjusted Percentile CAC scores (B).

Fig. 2. Rates of incident CHD per 1000 person years at risk by joint categories of absolute CAC group and age/gender/race specific percentiles.

Within a particular level of age/gender/race/ethnicity specific percentile, there remains a clear trend of increasing risk across levels of the absolute CAC groups. In contrast, once absolute CAC category is fixed, there is no increasing trend across levels of age/gender/race/ethnicity specific categories.

In addition, we also assessed the risk of incident CHD according to increasing absolute CAC scores across age-gender-race specific percentiles (table 3a). Among individuals with CAC scores<75^th percentile for age-gender-race as compared to those with CAC 1-100 (reference group), the hazard ratio (95% CI) for incident CHD after taking into account Framingham risk score was 2.50 (1.27-4.92) with CAC 101-400 and 5.58 (2.34-13.33), respectively. On the other hand, within absolute CAC score categories (table 3b), a higher adjusted percentile CAC was not associated with increased risk of incident CHD.

Table 3.

a: Risk of CHD Events Associated with Increasing Absolute CAC Scores across Age-Gender-Race CAC Percentiles
	All CHD Events (n=163)
	Un-adjusted HR (95% CI)	FRS* Adjusted HR (95% CI)
Age-Gender-Race CAC <75th Percentile (n=1811)
CAC 1-100 (n=1314)	1 (reference group)	1 (reference group)
CAC 101-400 (n=421)	2.77 (1.60-4.77)	2.50 (1.27-4.92)
CAC>400 (n=76)	5.53 (2.52-12.15)	5.58 (2.34-13.33)
Age-Gender-Race CAC 75-90th percentile (n=931)
CAC 1-100 (n=379)	1 (reference group)	1 (reference group)
CAC 101-400 (n= 322)	2.16 (0.98-4.78)	2.33 (0.78-6.96)
CAC>400 (n=230)	2.99 (1.34-6.68)	2.18 (0.65-7.37)
Age-Gender-Race CAC >90th percentile (n=652)
CAC 1-100 (n=100)	1 (reference group)	1 (reference group)
CAC 101-400 (n=183)	7.31 (0.95-56.29)	5.41 (0.68-42.86)
CAC>400 (n=369)	11.22 (1.53-82.19)	5.97 (0.78-47.23)
b: Risk of CHD Events Associated with Age-Gender-Race CAC Percentiles across Increasing Absolute CAC Scores
	All CHD Events (n=163)
	Un-adjusted HR (95% CI)	FRS Adjusted HR (95% CI)
CAC 1-100 (n=1793)
Age-Gender-Race CAC <75th Percentile (n=1314)	1 (reference group)	1 (reference group)
Age-Gender-Race CAC 75-90th percentile (n=379)	1.09 (0.53-2.25)	1.37 (0.47-3.97)
Age-Gender-Race CAC >90th percentile (100)	0.38 (0.05-2.78)	1.07 (0.13-8.65)
CAC 101-400 (n=926)
Age-Gender-Race CAC <75th Percentile (n=421)	1 (reference group)	1 (reference group)
Age-Gender-Race CAC 75-90th percentile (n=322)	0.88 (0.47-1.65)	1.30 (0.62-2.72)
Age-Gender-Race CAC >90th percentile (n=183)	1.08 (0.54-2.16)	2.04 (0.85-4.80)
CAC>400 (n=675)
Age-Gender-Race CAC <75th Percentile (n=76)	1 (reference group)	1 (reference group)
Age-Gender-Race CAC 75-90th percentile (n=230)	0.68 (0.26-1.46)	0.59 (0.24-1.45)
Age-Gender-Race CAC >90th percentile (n=652)	0.86 (0.40-1.86)	0.94 (0.41-2.14)

^*Framingham Risk Score

DISCUSSION

The results of this study demonstrate that there is no advantage, and in some cases considerable disadvantage, to expressing CAC score relative to age, gender and/or race/ethnicity. Comparing the various percentiles, the overall percentile does just as well as any other percentile ranking, and in fact better than any percentile that is age adjusted. Consider a qualitative example: a 50-year old Hispanic female with a CAC of 25 Agatston units is at the 95^th percentile relative to her age, gender and race/ethnicity, with an annual risk of only 0.25% (10-year estimated risk of only 2.5%) based on this model (table 2). Now consider an 83 year old white male with a CAC of 1572 Agatston units. Relative to his age, gender and race/ethnicity he is at the 72^nd percentile. However, the high absolute score drives the overall risk and the annual risk is 2.8% (10-year estimated 28% risk). So, the age/gender/race/ethnicity specific percentiles would say the Hispanic woman is at much higher risk. Clearly, the estimates from the age/gender/race/ethnicity specific percentile model do not reflect what we know about CHD risk. The overall percentiles provide a more realistic picture.

Although individuals with a higher demographic adjusted CAC percentile will have higher CAC scores, there are still some major differences in classification. In the MESA study, approximately fifty percent of participants with age-gender-race/ethnicity adjusted percentile scores in the 75-90% group had CACS<100. On the other hand, nearly 1/3 (35%) of MESA subjects with CACS 100-399 were considered to have an adjusted percentile <75%. Our study results indicate that within an absolute score group there is no difference in the rate of individuals suffering CHD events associated with worsening CAC percentiles (figure 2 and table 4b). Patients with low absolute scores are low risk, regardless of adjusted CAC percentile rank. Conversely, within the age-gender-race/ethnicity specific percentiles a positive relationship with events is observed across increasing CAC scores. In addition, after taking into account Framingham risk scores, those with CAC>100 were 2-5 times higher risk of suffering an acute CHD event in the near-term follow-up (table 4a) this demonstrates that percentile rank is not as robust a risk stratifier as absolute scores.

Our data differ somewhat from previously published reports on this topic. Whether age-gender based scores or absolute scores are better predictors has only been evaluated in two small studies to date. One such approach was taken by Raggi et al⁹ who reported on the occurrence of hard events in 632 patients followed for 32 ± 7 months from the time of EBT calcium scanning and on the CT findings of 172 patients undergoing CT imaging within a few days of suffering an acute myocardial infarction. In both groups the majority of patients (70%) who suffered a myocardial infarction or a coronary death showed a calcium score above the age-gender adjusted 75th percentile at the time of screening (70% found vs 25% expected, p < 0.001). Of interest, the event rate in patients with large calcium scores (> 401) was high (~ 5%/year) but only a small proportion of the subjects studied (7%) presented this level of calcification. Therefore, though a large calcium score represents a serious risk of developing coronary events, the authors felt its low frequency in the population renders it inadequate for risk stratification purposes. This observation contrasted with the powerful risk stratification ability demonstrated by relative calcium scores. In fact, the risk of suffering a hard event in patients with a calcium score > 75th percentile was 19 times that of patients with a score < 25th percentile, while the risk of events in patients in the upper risk factor quartile was 6.5 times greater than that of patients in the lowest quartile.

Wong et al.¹⁰ published a report on 926 asymptomatic patients followed for an average of 3.3 years from the time of EBT screening. Patients with coronary artery calcium deposits on EBT had more prevalent risk factors and the calcium scores were significantly greater in patients with events than in those without events. The risk ratio for events in patients in the upper quartile of absolute calcium score (score > 271) was twelve times higher than for patients in the lowest quartile (score < 15; annual risk: 8.8 and 0.72, respectively, risk ratio: 12). In multivariable analysis adjusted for other risk factors, there was a modest increase in CVD events seen among those in the 3rd age and gender quartile (relative risk [RR] 4.3, P = .02), with a greater risk seen among those in the 4th quartile (RR 6.0, P < .01) (compared with the 1st quartile). Results of this dataset demonstrated that age-sex stratification by percentile rank of CAC was not as accurate as absolute CAC scores for predicting CVD events in asymptomatic persons.

The NCEP (ATP III) has recommended age-gender cutpoints; “In persons with multiple risk factors, high coronary calcium scores (e.g., >75^th percentile for age and sex) denotes advanced coronary atherosclerosis and provides a rationale for intensified LDL-lowering therapy.”⁷ However, the results of MESA indicate that the relative percentiles do not predict incident CHD as well as simply using the absolute scores, or overall percentiles. If adjusted CAC scores are used as a basis to identify high risk individuals, nearly 1/3 of individuals with adjusted CAC <75^th percentile have absolute CAC scores>100 and may not be considered candidates for lipid lowering medications. It appears that the amount of CAC (as a surrogate for plaque burden) is more important than the relative percentile of an individual based upon age and gender. This is consistent with cardiovascular risk factors (such as cholesterol or blood pressure values) which are not normalized based upon age.

We would like to emphasize that cut points for treatment may still need to be gender or age specific. If the goal is to identify and treat patients that have at a particular level of risk, say at least 2% per year, then the CAC threshold for women will have to be higher than that for men, since women have lower baseline risk. Using gender based percentiles however, actually does the opposite of this. By fixing the percentage of patients to target, rather than the underlying risk, the threshold for women is lower than for men. Targeting the top 25% of each gender for instance, we would be treating women with much lower CAC scores, and consequently at much lower risk, than men.

Conclusion

Using overall percentile or CAC in standard groups performed much better than age/gender/race specific percentiles in terms of model fit and discrimination. Cut-points based on demographic specific percentiles have the additional problem that they are study-specific, and so we recommend using cut-points based on the absolute CAC scores for evaluating risk of CHD events in short-term follow-up. Further study based on a greater number of events may help elucidate which specific cutpoints are best, however at the moment the common choices of 100 and 400 appear to perform well.