An improved spatial tracking algorithm applied to coronary veins into Cardiac Multi-Slice Computed Tomography volume

Abstract

This paper describes an enhanced vessel tracking algorithm. The method specifity relies on the coronary venous tree extraction through Cardiac Multi-Slice Computed Tomography (MSCT). Indeed, contrast inhomogeneities are a major issue in the data sets that necessit a robust tracking procedure. The method is based on an existing moment-based algorithm designed for coronary arteries into MSCT volume. In order to extract the whole path of interest, improvements concerning progression strategy are proposed. Furthermore, the original procedure is combinated with an automatic recentring method based on ray casting. This enhanced method has been tested on three data sets. According to the first results, the method appears robust to curvatures, contrast inhomogeneities and low contrast blood veins.

I. INTRODUCTION

Cardiac resynchronization therapy (CRT) aims at the restoration of contractile coordination in hearts with severe heart failure, sinus rhythm and ventricular conduction delay [5]. The procedure consists in pacing simultaneously or with a small delay, both the right ventricle (RV) and the left ventricle (LV). Daubert and al. proposed a totally transvenous approach [2]. Endocardial leads are positionned in the right atrium and the RV through the vena cava while LV lead is placed through the coronary sinus into the coronary veins on the LV free wall. LV lead is the most challenging one to implant, due to the difficulty in accessing some pacing sites and the risk of dissecting the coronary sinus. In order to improve and secure the implant procedure, the objective of a project supported by the French Research Minister is to provide cardiologists with a CRT planning. Our work takes part in that project and relies on the study of a patient’s coronary venous anatomy to define pre-operatively the target vein, find the best path to reach it and confirm its accessibility. In this paper, the study is carried out using the new Mutli-Slice Computed Tomography (MSCT) capabilities in imaging the heart.

Many works propose vessel extraction techniques. They differ according to the imaging modality, application domain, method being automatic or semi-automatic and other specific factors. The simplest methods are based on intensity thresholding. The threshold definition remains the principal difficulty in case of inhomogeneities in contrast product distributions. Adaptative thresholding based on an intensity distribution model, computed in a given neighbourhood, has been proposed for MRA in [7]. Region growing approaches can be seen as an extension of the previous ones while adding a connectivity restriction [4]. Due to variations in image intensities, region growing can result in holes and over-segmentation. As regards vessel tracking, the key idea consists in applying local operators on the object and following it along its central axis. A structured description of the vascular tree can be obtained [8]. Deformable models have also been used for 3D vessel extraction. They allow arbitrary shape delineation, but raise the computation time. In [3], the 2D active contour technique (snake) detects the abdominal aorta borders from consecutive CT slices.

A spatial tracking algorithm has been designed in order to extract coronary arteries through MSCT [1]. This algorithm makes use of geometrical moments calculation to adjust the tracking on the vessel axis and to define their local features such as local orientation and diameter. We propose to improve the previous algorithm for the coronary venous tree extraction. Coronary veins introduce different features due to cardiac anatomy. Indeed, blood passes first through the coronary arteries and then is gathered by the coronary veins. As a consequence, we observe a non uniform distribution and an attenuation of contrast medium in coronary venous tree, leading to low contrast and contrast inhomogeneities, which are the major issues in our data bases. The application of the initial moment-based method on the coronary venous tree allows to extract only short segments. We studied the limits of the original algorithm due to veins specifities, and we propose some improvements to extract the whole path of interest. First of all, a brief description of the original method and its limits is given in section II, followed by the enhanced algorithm. Results are then presented in section III.

II. Moment-Based Vessel Tracking Algorithm

This section introduces our spatial tracking algorithm designed for the coronary veins extraction from MSCT data sets. In order to support the LV lead implantation, the method has to explore the path going from the entrance of the coronary sinus, through the great vein to a lateral or posterolateral vein. The algorithm yields a tracked point list approximating the path centerline with associated local diameter. The original algorithm designed for coronary arteries is first introduced as well as the difficulties depending on the coronary veins.

A. Initial algorithm and coronary vein constraints

First of all, vessel segments are considered as tube-like structures. The vessel is locally modelled by a cylinder of centre of gravity P, radius r and orientation (α,β) in 3D space [1]. The mean intensity inside (I_v) and outside (I_b) the vessel are estimated from a histogram computed on an extended region (including the vessel and the background) around the point P, using an expectation maximization algorithm. Given an initial rough position of the point P and a priori estimation of the two intensities, (I_v) and (I_b), geometrical moments allow to calculate the four parameters of the model [6]. These 3D moments are computed in a spherical window, which has to be centered on the vessel central axis and fit the vessel. To achieve this goal, we use an iterative multiresolution algorithm [1], which alternatively moves the sphere towards its centre of gravity, estimates the vessel radius and adjust the size of the sphere until convergence of the sphere radius on the vessel size. Any new point is iteratively computed this way. The next point estimation is calculated along the previous local orientation.

Contrast inhomogeneities present in the coronary venous tree, involve some deviations from the ideal cylindrical model and may have a strong impact on the tracking efficiency and the vessel features estimation. Therefore, the previous local orientation and the two intensities, (I_v) and (I_b) used to estimate the next point, are not reliable enough and may lead to a bad estimation. Thus, when applied to coronary venous tree, the tracking cannot be based only on the previous local features. In order to make the moment-based method robust to local artefacts, the algorithm has to consider more information. This improvement is introduced in II-B.1.

Furthermore, the original algorithm meets difficulties when the densities of the enhanced blood and the close surrounding tissues partially overlap, due to the attenuation of contrast medium. The densities of the surrounding tissues can even be higher. In absence of higher-intensity voxels belonging to the vessel, the centring procedure cannot converge towards the vessel axis. Thus, to face this difficulty, we designed an automatic recentring procedure based on ray casting, which starts when a tracked point is considered away from the vessel axis (see II-B.2).

B. Enhanced algorithm

The flow chart of the whole enhanced method is illustrated in Fig. 1. The tracking process consists of the four following stages:

Fig. 1.

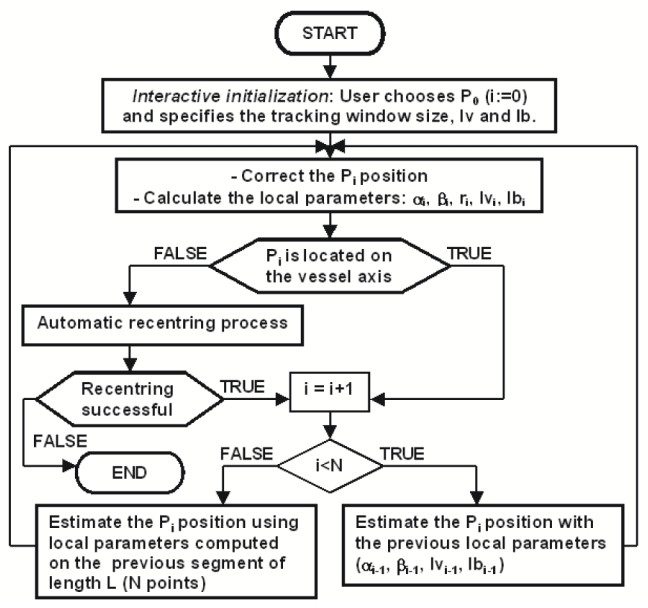
Flowchart of the tracking process.

1. Interactive initialisation: the user chooses a first position by pointing at the entrance of the coronary sinus. Some parameters have also to be specified, such as the tracking window size and the intensities (I_v) and (I_b).

2. “Training” stage: the original algorithm is carried out on a segment of lenght L (N points), i.e. for each point, the local parameters are used to estimate the next point.

3. Tracking process: for any new points, the moment-based tracking algorithm considers the local parameters estimated on tbe previous segment to compute the local parameters at the next point (the first point is estimated on the segment computed at the previous stage). The moment-based method is replaced by an automatic recentring procedure when the tracking fails.

4. Stopping criteria: the tracking stops when several conditions are not fulfilled anymore, due for instance to a vessel no more contrasted.

As introduced previously, the first improvement brought to the initial moment-based algorithm deals with the vessel orientation and the intensities (I_v) and (I_b). Since the previous features are used to estimate the next tracked point, we can speak about progression strategy.

1. Progression strategy

For any new position, the last tracked segment of length L is considered to compute an adaptive direction, a mean vessel intensity and a mean background intensity. These previous values are then used with geometrical moments to calculate the local features.

An improper local direction and the presence of other structures close to the vessel may prevent the centring procedure from adjusting the next position on the vessel axis. In order to keep a coherent orientation to estimate any new position all along the vessel, we calculate an adaptive direction based on the previous segment orientation. The adaptive direction corresponds then to the vector director computed from the two segment extremities.

In similar manner, the intensities (I_v) and (I_b) are made adaptive, to face the contrast inhomogeneities in both vessel and background regions. The procedure considers the intensities (I_v) and (I_b) estimated along the previous tracked segment and apply a truncated mean on (I_v) values and (I_b) values respectively, by removing the lowest values, considered as local artefacts.

The tracking is reiterated while the P_i position is considered as centered on the vessel axis. This decision relies on:

• the mean intensity and standard deviation values estimated into the current tracking window compared to mean values calculated on the previous segment;

• the difference of value between the vessel intensity and the backgroung intensity (Iv > Ib);

• the estimated radius compared the previous one;

• the voxel values considered as belonging to the vessel compared to the vessel intensity range;

• the distance between two tracked points (d_max).

If one of the previous conditions is not satisfied, the following recentring procedure is applied.

2. Automatic recentring procedure

This is our solution to keep progressing into the vessel even in lack of contrast with close surrounding structures. The procedure vocation at this stage is not to detect accurately the vessel centreline but at least to allow the tracking to stay into the vessel. The procedure is based on a ray casting (Fig. 2). Voxels belonging to the lumen are detected along the rays and a center is computed. An additional condition using a Region of Interest (ROI), allows to detect rays which passed beyond the vessel boundary, i.e. where densities of the enhanced blood and the close surrounding structures overlap.

Fig. 2.

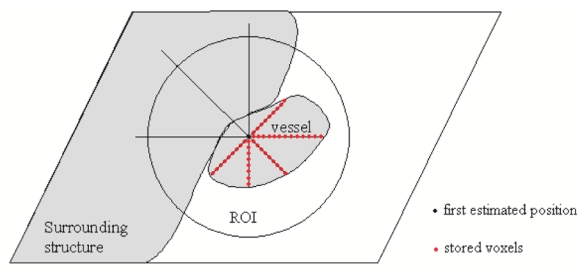
Scheme of ray casting. A spherical ROI is centered on the first estimated position. Equiangular rays are spread out from this position.

The whole procedure is described in Fig. 3 and operates as follows: the P_i position is re-estimated from the P_i−1 position in its local direction given by the angles α_i−1 and β_i−1 with a step of one voxel, so as to be sure to be inside the vessel. Let us consider now the orthogonal plane to the previous local direction. A Region of Interest (ROI) is centered on P_i, of radius 2. r_i−1 + 1. Equiangular rays are spread out on this orthogonal plane from the first estimated position. The number of rays is defined to cover the whole lumen. Voxels belonging to the lumen are detected by thresholding along the ray. The previous local vessel intensity I_vi−1 is used to compute a lower threshold. I_vi is considered as similar to I_vi−1 due to the one voxel displacement. The lower threshold tmin is then defined to I_vi−1 − δ, where δ is set to 80. The upper threshold tmax is fixed to 500 (gray value range into the vessel never exceeds this value). Then, the position along each ray is incremented with a step of one voxel while the threshold condition (tmin<voxel value<tmax) is satisfied and its length does not exceed the ROI radius. All voxels positions traversed by rays which stopped before the ROI radius are assumed to belong to vessel lumen (and are stored in stack), whereas rays which passed beyond the ROI reach the surrounding tissues. Then a geometrical mean is computed from the stored positions which yields an approximative centered P_i position.

Fig. 3.

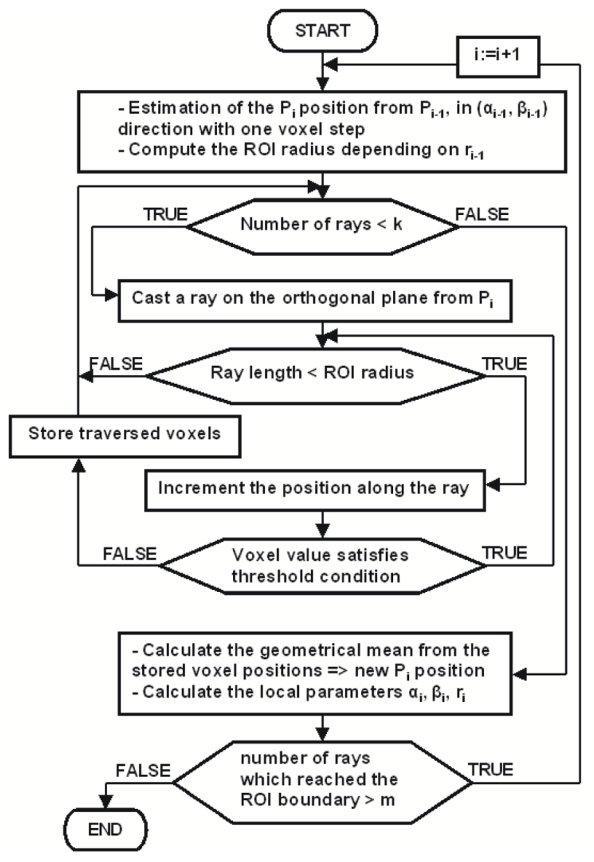
Flowchart of the automatic recentring procedure.

In case of a high number of rays which passed beyond the ROI boundary, the lack of contrast is still obvious. Then, the procedure is reiterated for the next position, otherwise the moment-based method restarts.

3. Stopping Conditions

The stopping conditions check if the automatic recentring procedure managed to reinitialize the tracking. The tracking is considered as lost when:

• a loop is detected;

• the estimated vessel level Iv or its diameter are higher (or lower) than the allowed upper (or lower) limits.

III. Results

Experiments have been carried out on three MSCT data sets acquired on a General Electric LightSpeed VCT 64-slice Scanner. The identical protocol was used for all the acquisitions. Each data set includes 20 volumes reconstructed from slices acquired every 5% of the cardiac cycle. There are approximately 200 slices per volume, with 512 × 512 pixels per slice. The resolution is about 0:4 × 0:4mm² per pixel. A preliminary interpolation was performed to make the datasets isotropic. Coronary venous tree is better contrasted from the 65% volume to the 75% volume corresponding to the end of the diastole phase. The algorithm was tested on these three volumes of each data set, that is to say on nine volumes. The parameters described in section II have been set experimentally. For instance, the number of points N is equal to 20 to minimize the local artefacts effects, (d_max) is set to 14 voxels, above this value the next estimated point is always outside of the vessel, and the upper and lower limits for (I_v) are 480 and 90 respectively. Identic values have been used for the nine volumes. Thus, the previous values give stability to our method. We present three examples of tracking in Fig. 4, 5 and 6 (a different data set is used for each example). On the left-hand side, the whole tracked path is superposed on a Maximum Intensity Projection (MIP) reconstructed from the last slices traversed by the tracking, allowing to visualize the last tracked vessel segment and the encountered problems. On the right-hand size, curvilinear reconstruction are used to visualize the whole tracked path.

Fig. 4.

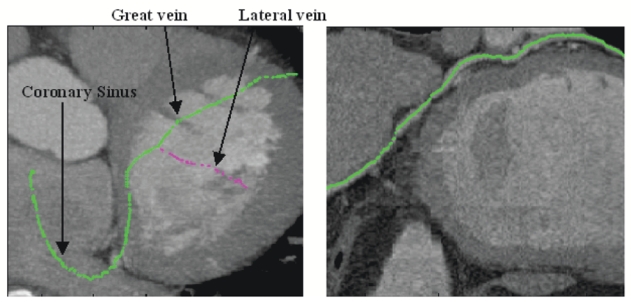
Tracked path on MIP (Left) and Curvilinear reconstruction (Right) (the automatic recentring procedure was not useful on that base).

Fig. 5.

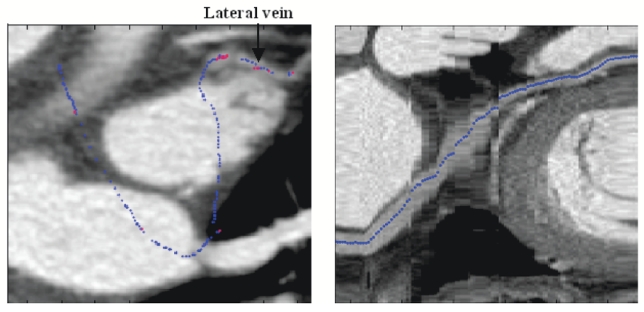
Tracked path on MIP (Left) and Curvilinear reconstruction (Right)(blue points were extracted with the moment-based process and red ones with the automatic recentring process).

Fig. 6.

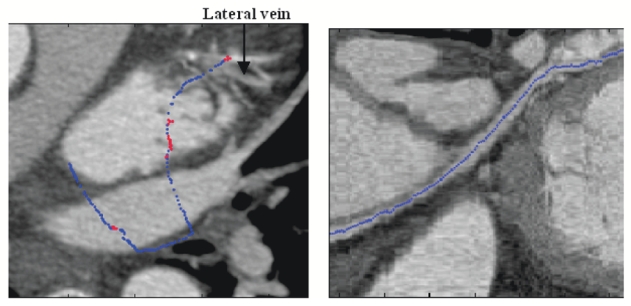
Tracked path on MIP (Left) and Curvilinear reconstruction (Right) (blue points were extracted with the moment-based process and red ones with the automatic recentring process).

On each volume, the path of interest has been extracted properly from the coronary sinus entrance to the great vein (radius from 4mm to 2mm). As regards the lateral vein (radius <2mm), close arteries (sometimes higher contrasted) make its tracking difficult. Indeed, we can notice the short progression in the lateral vein in Fig. 5 whereas in Fig. 6, vessels with similar or higher intensities cross the lateral vein, preventing the tracking from following it. Only one user interaction is necessary to track a branch (interactive initialization to choose the first point). In case of two extracted branches as introduced in Fig. 4, another interactive initialization is needed to extract the lateral vein. The calculation takes about thirty seconds to extract the whole path of interest.

IV. Conclusion and Perspectives

We have proposed a enhanced vessel tracking algorithm to extract coronary veins into MSCT data sets. This paper presents the first results obtained with this method. The main difficulty depending on the coronary veins is the lack of contrast with surrounding tissues contrary to the coronary arteries. The results obtained are much better than those obtained with the initial moment-based algorithm designed for coronary arteries tracking. Indeed, coronary sinus and the great vein are extracted with only one tracking process. Our method is robust to curvatures, contrast inhomogeneities and low contrast blood veins. Nevertheless, the contrast issue still remains for the lateral vein. Thus, improvements have to be made to track thin low contrast veins.