Latent Coinfection and the Maintenance of Strain Diversity

Abstract

Technologies for strain differentiation and typing have made it possible to detect genetic diversity of pathogens, both within individual hosts and within communities. Coinfection of a host by more than one pathogen strain may affect the relative frequency of these strains at the population level through complex within- and between-host interactions; in infectious diseases that have a long latent period, interstrain competition during latency is likely to play an important role in disease dynamics. We show that SEIR models that include a class of latently coinfected individuals can have markedly different long-term dynamics than models without coinfection, and that coinfection can greatly facilitate the stable coexistence of strains. We demonstrate these dynamics using a model relevant to tuberculosis in which people may experience latent coinfection with both drug sensitive and drug resistant strains. Using this model, we show that the existence of a latent coinfected state allows the possibility that disease control interventions that target latency may facilitate the emergence of drug resistance.

1. Introduction

Some infectious diseases of humans are characterized by a long latent period between the time of infection and the onset of infectiousness. Although an individual with a latent infection may acquire some immunity to subsequent infection, for many pathogens, this protection is incomplete. As such, a latently infected individual may be reinfected after a new exposure to the pathogen and may become coinfected with more than one strain. The advent of technologies which allow for the differentiation of strains of pathogens has greatly enhanced our ability to recognize and measure the frequency of coinfection, and coinfection has been reported for a wide range of infectious agents including viruses (Casado et al., 2007), bacteria (van Rie et al., 2005), parasites (Shigidi et al., 2004), and fungi (Almeida et al., 2007). The frequency of coinfection depends on the level of immunity conferred by a first infection, the length of the latent period, and the incidence of infection, with coinfection being most common among those pathogens that do not provoke long lasting immunity, that have long latent periods and for which the force of infection is highest.

Research on the interactions of pathogen strains has shown that factors such as contact heterogeneity (Li et al., 2003), age structure (Martcheva et al., 2007), stochastic effects (Murrell and Law, 2003; Schinazi, 1997) and the contact network structure in the population (Eames and Keeling, 2006) can allow for long-term coexistence of strains, which in the absence of such heterogeneities, would undergo competitive exclusion. Independent of these factors, coinfection can provide a mechanism by which strain diversity is maintained in a population, and can affect the evolution of the pathogens themselves (Claessen and de Roos, 1995; Levin and Pimentel, 1981; Levin, 1983; May and Nowak, 1995; Mosquera and Adler, 1998; Wodarz and Levy, 2007). Furthermore, coinfection alters model predictions of the effects of interventions such as vaccination (Elbasha and Galvani, 2005; Iannelli et al., 2005; Lipsitch, 1997) and antibiotic therapy (Cohen et al., 2006). Rodrigues et al. (2007) argue in the context of multi-strain models for TB that reinfection can modify the conditions for coexistence of competing strains, and include a model in which reinfection can lead to coinfection, though in this work the qualitative outcome of interventions was not altered by the inclusion of coinfection at the latent stage. However, with this exception, the literature on coinfection has generally focused on coinfection occurring during the infectious phase and has not primarily considered the impact of coinfection during latency.

For some infectious diseases, the great majority of infected individuals are asymptomatic and either completely noninfectious (latent infection with M. tuberculosis) or minimally infectious (for example, HIV-positive individuals with low viral load). Both of these pathogens manifest within-host strain diversity (Casado et al., 2007; van Rie et al., 2005) which may affect the natural history of disease. In a study based in Cape Town, South Africa, Warren et al. (2004) used a polymerase chain reaction-based strain classification method to identify M. tuberculosis strains from the very distinct Beijing and non-Beijing lineages. They found that both strains were present in 19% of patients, and the non-Beijing type was found in 57% of patients with Beijing-type M. tb. They argued that their results imply that reinfection may be quite frequent and often results in coinfection with diverse strains. In the case of HIV, Troyer et al. (2005) studied viral isolates from 10 patients at different points in time and found that such isolates had sequentially increasing fitness, which was decreased in isolates taken after antiretroviral therapy was initiated, linking viral genetic diversity to in-host phenotypic diversity. From a public health standpoint, within-host interstrain competition during latency will likely have secondary effects on the population dynamics of infections in which latent stages play a key epidemiological role.

Here, we develop a simple model of an infectious disease which incorporates a latent phase in which coinfection is possible. We contrast the results of this model to one in which a second exposure leads to superinfection, i.e., replacement of the first strain with the second, and determine the effect of coinfection on interstrain competition at the population level. We then modify this simple model to capture the dynamics of drug resistant tuberculosis and examine the effect of latent coinfection on interventions that target individuals in the latent class.

2. Simple models: with and without latent coinfection

For many pathogens in many locations, there is a “most common” or dominant strain, and possibly one or more secondary strains, which may be from different pathogen lineages, or which may have acquired some level of resistance to therapies. Where there is a most common strain, we label this strain 1. Our approach is to find the stability boundary at which the endemic equilibrium with only strain 2, the less common (or where appropriate, the drug-resistant) strain gains local stability. When its endemic equilibrium is locally stable, there is a risk that strain 2 could completely replace the more common strain in the population; this is particularly concerning when strain 2 is a drug-resistant strain. We take this approach because regardless of whether the model supports a coexisting equilibrium, or whether there is acquired resistance; all formulations of the models we develop have a strain 2-only equilibrium. Its stability boundary is therefore a comparable feature across the range of assumptions and models we explore.

2.1. Baseline model

We first present a generalized baseline model for an infectious agent with two strains. We assume that the organism has a latent phase, but that there is no coinfected class. We let susceptible individuals be infected with either strain, at rates β₁ and β₂ which incorporate both a person to person contact rate which is not related to strain type, and a per-contact risk of transmission which may differ between the strains. Upon infection, individuals enter a latent stage, where they may progress to active disease at rate k, be cleared at rate μ, or be exposed and reinfected with the other strain of disease. On reinfection, each strain replaces the other within the host, so that reinfected individuals move to the latent class of the newly-acquired strain. Individuals may have some partial immunity (1 − x) conferred by the first infection. It is assumed that reinfection with the same strain does not change an individual's state. Upon progression, infected individuals become infectious and also experience a higher clearance rate μ_d , which includes death and replacement as well as recovery back to the susceptible class through self-recovery or treatment. In order to capture the acquisition of drug resistance due to imperfect treatment within this multi-strain model, we allow strain 1 to transform into strain 2 at rate a_q, which is small or 0.

The baseline model (model A) is given by

$$\begin{array}{cc}\hfill {\stackrel{.}{L}}_1& ={\beta }_1{I}_{1}S+x{\beta }_1{I}_1{I}_2-(\mu +k)L_1-x{\beta }_2{I}_2{L}_1,\hfill \\ \hfill {\stackrel{.}{I}}_1& =k{L}_1-({\mu }_d+a_q)I_1,\hfill \\ \hfill {\stackrel{.}{L}}_2& ={\beta }_2{I}_{2}S+x{\beta }_2{I}_2{L}_1-(\mu +k)L_2-x{\beta }_1{I}_1{L}_2,\hfill \\ \hfill {\stackrel{.}{I}}_2& =k{L}_2+a_q{I}_1-{\mu }_d{I}_2,\hfill \end{array}$$ (1)

where L_i are the proportions of the population in each latent class, I_i are the proportions infectious, i = 1, 2, and S = 1 − L₁ − L₂ − I₁ − I₂ represents the susceptible proportion. We assume that the population N has reached its limiting value and scale the model such that N = 1. We choose a time scale such that μ_d = 1 (i.e., we replace t with the dimensionless τ = μ_dt and take derivatives with respect to τ , thus nondimensionalizing the rates in the model). For simplicity, we first assume that no protection is conferred by the first infection against the second (i.e., x = 1), although in reality, immune specificity depends on the pathogen and the host immune response.

Each of the strains has a reproduction number, given by

$$R_1=\frac{{\beta }_{1}k}{(k+\mu )(a_q+1)}\text{and}{R}_2=\frac{{\beta }_{2}k}{k+\mu },$$ (2)

representing the average number of new infections of the same strain caused by one individual with strain 1 and 2, respectively, over their infectious period in a susceptible population. Note that these are not thresholds for the existence of an endemic equilibrium, because strain 1 can become strain 2. The threshold is given by R₀ ≡ max{R₁, R₂}. However, because R₁ and R₂ summarize the reproductive ability of each strain, they are useful for describing interstrain competition. The model with a_q ≠ 0 has three equilibria:

• E_f : the disease-free equilibrium with S = 1 and (L₁, I₁, L₂, I₂) = (0, 0, 0, 0)

• E₂: the endemic equilibrium with strain 2 only:

  $$(L_1,I_1,L_2,I_2)=\left(0,0,\frac{1}{1+k}\left(1-\frac{1}{R_2}\right),\frac{k}{1+k}\left(1-\frac{1}{R_2}\right)\right)$$
• E_c: a coexisting equilibrium given by

  $$(L_1^c,I_1^c,L_2^c,I_2^c)=\left(\frac{d}{k+1}\Gamma ,\frac{k}{k+1}\Gamma ,\frac{a_q}{k+1}\left(1-\frac{1}{R_1}\right)\Lambda ,\frac{a_{q}k}{d(k+1)}\left(1-\frac{1}{R_1}\right)\Lambda \right)$$

where $\Gamma =\frac{R_1-R_2}{d{R}_1-R_2}$, $\Lambda =\frac{R_2}{d{R}_1-R_2}$, and d = a_q + 1 is the clearance rate from disease with strain 1.

When a_q = 0, the coexisting equilibrium reduces to the strain-1 only equilibrium

• E₁: endemic equilibrium with strain 1 only (no acquisition)

  $$(L_1,I_1,L_2,I_2)=\left(\frac{1}{1+k}\left(1-\frac{1}{R_1}\right),\frac{k}{1+k}\left(1-\frac{1}{R_1}\right),0,0\right).$$

When R₀ = max{R₁, R₂} < 1 it is easy to show that the disease-free equilibrium E_f is stable.

The Jacobian of model A (1) at E₂ is given by

$$\left(\begin{array}{cccc}\hfill -{\beta }_2{\stackrel{‒}{I}}_2-\mu -k\hfill & \hfill {\beta }_1(1-{\stackrel{‒}{I}}_2)\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill k\hfill & \hfill -(1+a_q)\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill -({\beta }_2+{\beta }_1){\stackrel{‒}{I}}_2\hfill & \hfill -{\beta }_2{\stackrel{‒}{I}}_2-\mu -k\hfill & \hfill {\beta }_2(1-{\stackrel{‒}{L}}_2-2{\stackrel{‒}{I}}_2)\hfill \\ \hfill 0\hfill & \hfill a\hfill & \hfill k\hfill & \hfill -1\hfill \end{array}\right),$$

where the bars indicate the values of I₂ and L₂ at E₂.

The characteristic polynomial factors into the following two quadratic equations:

$$(\lambda +{\beta }_2{\stackrel{‒}{I}}_2+\mu +k)(\lambda +a_q+1)-k{\beta }_1(1-{\stackrel{‒}{I}}_2)=0$$ (3)

and

$$(\lambda +{\beta }_2{\stackrel{‒}{I}}_2+\mu +k)(\lambda +1)-k{\beta }_2(1-{\stackrel{‒}{L}}_2-2{\stackrel{‒}{I}}_2)=0.$$ (4)

Local stability requires that the constant terms in both (3) and (4) be positive. For (4), this requirement reduces to R₂ > 1, while (3) places a requirement on the relationship between R₁ and R₂ as follows:

$$R_1<f_b(k,R_2)=\frac{1+\frac{1}{k+1}{R}_2\left(1-\frac{1}{R_2}\right)}{1-\frac{k}{k+1}\left(1-\frac{1}{R_2}\right)}.$$ (5)

When R₂ = 1, this condition reduces to R₁ < 1. As the reproductive number R₂ of the second strain increases, i.e., in the limit as R₂ → ∞, the condition becomes R₁ < R₂. When a = 0, this is simply competitive exclusion and the strain with higher basic reproductive number dominates.

2.2. Latent coinfection

In contrast to the scenario described above, we now suppose that a reinfection event does not bring about strain replacement within the host, but rather that latently infected individuals will obtain a new infection with the other strain in addition to their original infection, giving rise to a class of coinfected individuals. To model this, we allow individuals infected with both strains to enter a coinfected latent class, from which they experience a total progression rate k_m to active disease. We begin by assuming that the progression rates (k) for both strains are equal, and that latently coinfected individuals have a total progression rate k_m which is divided equally into progression to disease with strain 1 or strain 2. In Section 3, some of these simplifying assumptions are relaxed.

We obtain the following model (model B):

$$\begin{array}{cc}\hfill {\stackrel{.}{L}}_1& ={\beta }_1{I}_{1}S-(\mu +k)L_1-x{\beta }_2{I}_2{L}_1,\hfill \\ \hfill {\stackrel{.}{I}}_1& =k{L}_1+\frac{1}{2}{k}_{m}M-({\mu }_d+a_q)I_1,\hfill \\ \hfill {\stackrel{.}{L}}_2& ={\beta }_2{I}_{2}S-(\mu +k)L_2-x{\beta }_1{I}_1{L}_2,\hfill \\ \hfill {\stackrel{.}{I}}_2& =k{L}_2+\frac{1}{2}{k}_{m}M+a_q{I}_1-{\mu }_d{I}_2,\hfill \\ \hfill \stackrel{.}{M}& =x{\beta }_2{I}_2{L}_1+x{\beta }_1{I}_1{L}_2-(k_m+\mu )M,\hfill \end{array}$$ (6)

where M denotes the latently coinfected (mixed) class. This model has the same equilibrium E₂ and again when a_q = 0 there is a strain 1-only equilibrium, E₁. Because R₁ and R₂ are defined at the disease-free equilibrium, the existence of the latent coinfected class does not affect them and they remain unchanged (Eq. (2)). Again, we proceed with the assumption that x = 1.

We linearize the system about equilibrium E₂, and compare its stability region with that of the same equilibrium in model A. The Jacobian at E₂ is

$$\left(\begin{array}{ccccc}\hfill -{\beta }_2{\stackrel{‒}{I}}_2-\mu -k\hfill & \hfill {\beta }_1(1-{\stackrel{‒}{I}}_2-{\stackrel{‒}{L}}_2)\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill k\hfill & \hfill -(1+a_q)\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill k_m∕2\hfill \\ \hfill -{\beta }_2{\stackrel{‒}{I}}_2\hfill & \hfill -{\beta }_2{\stackrel{‒}{I}}_2-{\beta }_1{\stackrel{‒}{L}}_2\hfill & \hfill -{\beta }_2{\stackrel{‒}{I}}_2-\mu -k\hfill & \hfill {\beta }_2(1-{\stackrel{‒}{L}}_2-2{\stackrel{‒}{I}}_2)\hfill & \hfill -{\beta }_2{\stackrel{‒}{I}}_2\hfill \\ \hfill 0\hfill & \hfill a\hfill & \hfill k\hfill & \hfill -1\hfill & \hfill k_m∕2\hfill \\ \hfill {\beta }_2{\stackrel{‒}{I}}_2\hfill & \hfill {\beta }_1{\stackrel{‒}{L}}_2\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill -k_m-\mu \hfill \end{array}\right).$$ (7)

The characteristic polynomial can be written as the product of a quadratic and a cubic polynomial. The quadratic is the same as that given in (4), and for $\mathfrak{R}\left\{\lambda \right\}<0$ it requires R₂ > 1.

The cubic polynomial can be written in the form (see Appendix)

$${\lambda }^3+a{\lambda }^2+b\lambda +c$$ (8)

for which the Routh–Hurwitz stability criterion implies that for negative real parts of λ, we must have a, b, c > 0 and ab > c. It is clear that a > 0, and the three remaining conditions can be written

$${\beta }_1<f_1,{\beta }_1<f_2\text{and}{\beta }_1<f_3.$$

All conditions are met when β₁ < min{f₁, f₂, f₃}. It turns out that f₂, which is derived from the condition c > 0 in (8), is the minimum of these three functions and so defines the stability boundary for E₂; see the Appendix for details.

The interesting feature of this analysis is the shape of $f_2=\frac{c_1\left(R_2\right)}{c_2\left(R_2\right)}$ as a function of R₂, the reproductive number of the resistant strain (c₁ and c₂ are defined in the Appendix). With α = d(1 + k)(k_m + μ) and $\beta =\frac{1}{2}\frac{k_m}{{(k+1)}^2}$, we can write

$$f_2=\frac{\alpha R_2^2+\alpha k{R}_2}{\beta R_2^2+2k\beta R_2+k-\beta (2k+1)}.$$ (9)

From this form, it is clear that

$$\underset{R_2\to \infty }{\text{lim}}{f}_2=\frac{\alpha }{\beta }.$$

The stability boundary approaches a constant at large R₂, in striking contrast to the analogous stability boundary in the model without latent coinfection, which is asymptotically linear in R₂ as R₂ increases. Figure 2 illustrates the difference.

Fig. 2.

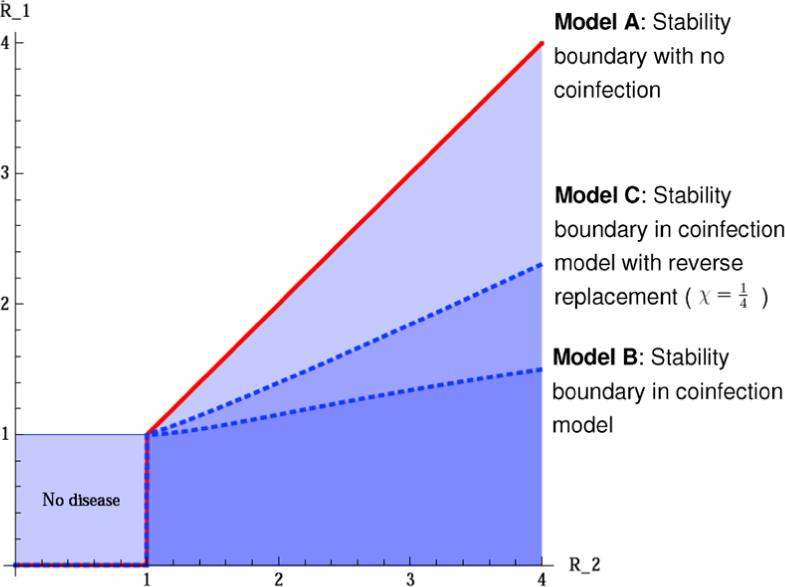
Stability of E₂ in models A, B, and C. Parameters are k = 0.5, μ = 0.06, a_q = 0.15, k_m = 0.4, μ_d = 1, χ = 0, $\frac{1}{4}$ (lower and upper dashed blue lines, respectively) and β₁ and β₂ are independent (and related to R₁ and R₂). The stability region of E₂ is the area below the solid line (red) in the model without coinfection (model A) and below the curved dashed lines (blue) in model B, where the upper of these refers to the coinfection model with strain replacement (see Section 2.3). (Color figure online.)

The central result here is that the presence of latent coinfection creates a large region in parameter space in which the equilibrium with strain 2 only (E₂) is not locally stable, but would have been stable without coinfection. The coinfected class is “protecting” the population against complete strain 2 takeover, thus promoting the diversity of strains within the population.

2.3. Strain replacement after coinfection

The dynamics of in-host strain replacement can offer some intuition as to why the coinfected class in model B has such a strong effect on the stability of E₂. In model B, while one strain can effect partial in-host strain replacement (moving an individual from L₁ into M), strain replacement from the coinfected state is not allowed in the model. The result is that the latent coinfected state is “protected” compared to the latent states of either strain alone; once an individual is dually infected, no number of subsequent infections can result in further in-host strain replacement, whereas partial strain replacement is allowed from either singly-infected latent state upon infection with the other strain. This results in the greatly increased capacity of the two strains to coexist.

To see this, we can generalize model B to allow a proportion χ of individuals in the latent coinfected class who are reinfected to return to the singly-infected class, giving model C (with x = 1):

$$\begin{array}{cc}\hfill {\stackrel{.}{L}}_1& ={\beta }_1{I}_{1}S-(\mu +k)L_1-{\beta }_2{I}_2{L}_1+\chi {\beta }_1{I}_{1}M,\hfill \\ \hfill {\stackrel{.}{I}}_1& =k{L}_1+\frac{1}{2}{k}_{m}M-({\mu }_d+a_q)I_1,\hfill \\ \hfill {\stackrel{.}{L}}_2& ={\beta }_2{I}_{2}S-(\mu +k)L_2-{\beta }_1{I}_1{L}_2+\chi {\beta }_2{I}_{2}M,\hfill \\ \hfill {\stackrel{.}{I}}_2& =k{L}_2+\frac{1}{2}{k}_{m}M+a_q{I}_1-{\mu }_d{I}_2,\hfill \\ \hfill \stackrel{.}{M}& ={\beta }_2{I}_2{L}_1+{\beta }_1{I}_1{L}_2-(k_m+\mu )M-\chi {\beta }_1{I}_{1}M-\chi {\beta }_2{I}_{2}M.\hfill \end{array}$$ (10)

Model C with χ = 0 is the same as model B; with χ > 0, the difference between models B and C is schematically represented by the dashed lines in Fig. 1(b). The Jacobian is similar to that given in the previous section, with modified terms J(5, 5) = −k_m − μ − χβ₂I₂ rather than −k_m = − μ, and a similar modification to J(3, 5), reflecting the new structure. The analysis is much the same, but the coefficients of the cubic polynomial are now given by (A.7).

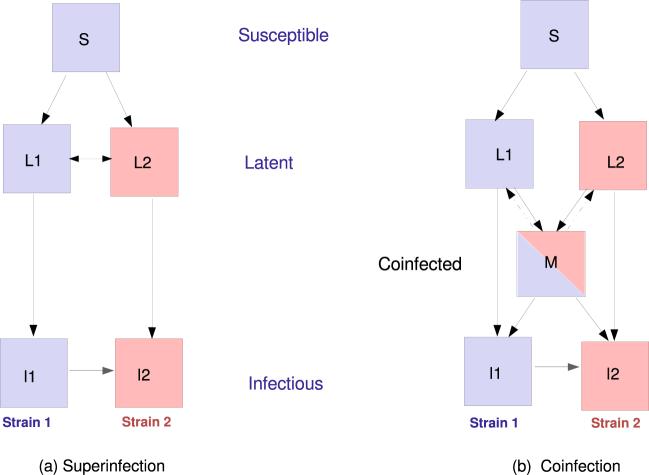
Fig. 1.

Schematic diagram of the baseline model (model A) with superinfection (a) and model B with coinfection (b). Dashed arrows in (b) represent the possibility that coinfected individuals undergo “reverse” strain replacement upon subsequent re-infection (model C).

The argument that ${\beta }_1<f_2=\frac{c_1}{c_2}$ is the stability boundary still applies when χ ≠ 0. However, due to the structural change, the asymptotic shape of f₂ is different: in the limit as R₂ → ∞, the stability boundary of equilibrium E₂ can be written

$$R_1<\frac{2k}{k_m}\chi R_2.$$

This is asymptotically linear in R₂, in contrast to the asymptotically flat function defining the boundary when χ = 0. Under the assumption that reverse strain replacement can occur when coinfected individuals are reinfected, the coinfected latent class does not have as strong a coexistence-promoting effect.

The extent of the coexistence-promoting effect depends on the interplay between k_m, k, and χ. For example, suppose that k_m = k, so that the total progression to disease from the latent coinfected class (M) is the same as the progression from either singly-infected latent class. Then the coexistence-promoting effect of the coinfected class (in the large R₂ limit) is removed when $\chi =\frac{1}{2}$ because at this point stability boundary in the limit R₂ → ∞ is equal to the analogous limit in model A (no coinfection), namely R₁ < R₂. However, if alternatively we were to assume that the two infections behave completely independently, then we could write k_m = 2k, as either infection could be considered equally likely to result in disease as if the other were not there. In this case, then any choice of χ < 1 would still leave an unbounded region of parameter space in which E₂ is unstable, but would be stable in the absence of coinfection.

The choice $\chi =\frac{1}{2}$ can be interpreted, when k_m = k, as the assumption that when a latently coinfected individual is reinfected with (for example) strain 1, strain 1 is just as likely to replace itself as it is to replace strain 2. In the first case, the individual remains in the coinfected class, and in the second, there is a transition to the singly-infected L₁ class. While some choices of k_m and χ may reduce the coexistence-promoting effect of the latent coinfected class, this analysis reveals the importance of within-host strain interactions, and particularly the probability that reinfection results in strain replacement, for the long-term dynamics of multiple strain models.

3. Tuberculosis: can interventions speed resistant takeover?

Tuberculosis (TB) is a disease which can potentially have a very long, asymptomatic latent period during which the infected individual is not infectious to others. It is also a disease with distinct strains, defined lineages and/or different drug resistance profiles, making it a good example of an infection for which latent coinfection may play an important role in epidemic dynamics. The disease is caused by infection with the bacterium Mycobacterium tuberculosis, and is transmitted when a person with active pulmonary disease coughs, sneezes, or otherwise aerosolizes TB bacilli that are then taken into a new host through the respiratory route. Once a new host is infected, he or she rapidly mounts an immune response that contains the infection, which then remains latent, neither causing disease nor resulting in further transmission of the organism. While it is estimated that 1/3 of the world's population is infected with TB, only approximately 10% of those infected are expected ever to progress to clinical disease. Those who do develop active disease may do so soon after an infection event or upon reactivation of a latent infection. Individuals with active disease may recover if they are treated with appropriate antibiotic regimens, although these individuals remain at risk of relapse. Factors playing a role in progression to active disease include strain virulence, host immune status, reinfection, coinfection with other pathogens and variations in host susceptibility. Settings are generally considered “high burden” if the prevalence of active TB is greater than 100 cases in 100,000 (less than 0.1% of the population).

In recent years, multi- and extensively- drug-resistant strains of TB have emerged and have threatened to undermine global TB control efforts, particularly in locations with high HIV prevalence. Furthermore, in high incidence areas there are increasing reports of coinfection among clinically observed patients; since multiple strain infection is rarely assessed, the frequency of this phenomenon is not known. It is essential to identify interventions which could assist in controlling the rise of drug-resistant strains, and to identify potential perverse effects of such interventions.

Interventions can target the latent class by preventing progression to active disease. One such intervention is isoniazid preventative therapy (IPT), a 6 to 12 month course of antibiotic therapy with the drug isoniazid (INH), which can prevent progression when the infection is sensitive to this antibiotic. Isoniazid, as one of the most effective TB drugs available, is part of all standard TB treatment regimens. Although there is no clear evidence that preventative INH monotherapy leads to acquired drug resistance within infected individuals, widespread use of IPT might be expected to alter the distribution of drug sensitive and resistant strains at the population level, if these strain types are competing for hosts.

Here, we extend our latent coinfection models to capture the dynamics of drug resistant tuberculosis by introducing drug sensitive and drug resistant strains, each with its own specific progression rate, by allowing recovery of infectious individuals back to the latent stage, and by simulating the population-wide implementation of IPT.

Strain 1 represents a fully susceptible strain of tuberculosis which can be transformed into strain 2, a strain resistant to at least INH, through inadequate treatment which leads to the emergence of drug resistance at rate a_q. Infections with strains 1 and 2 progress to disease at rates k₁ and k₂, while coinfected individuals progress to active disease with strain 1 or 2 at rates k_m1 and k_m2, respectively. We assume that k_m2/k_m1 = k₂/k₁, so that the coinfected individuals are not comparatively “protected” from progression simply by being coinfected. We denote k_m = k_m1 + k_m2. As there is no evidence that reinfection with one strain can clear a previous infection with another strain of TB we set χ = 0. In this simple framework, coinfected individuals do not have increased risk of progression to active TB compared to individuals latently infected with only a single strain. However, numerical simulations in more complex models including variable progression rates (a risk of immediate “fast progression” upon reinfection, for example) support our results on the effect of coinfection on population-level strain composition. Individuals with active disease due to strains 1 and 2 recover from disease at rates r₁ and r₂. We model the effect of IPT as follows: individuals latently infected with a sensitive strain are returned to the susceptible class upon treatment with IPT at a rate z, while those latently infected with resistant strains remain in that state. The parameter z captures both the proportion of latently infected individuals who receive therapy (coverage) and the efficacy of that therapy. If IPT is administered to an individual with latent coinfection, it clears the sensitive infection but not the resistant one.

The TB models are given by

$$\begin{array}{cc}\hfill {\stackrel{.}{L}}_1& ={\beta }_1{I}_{1}S+x{\beta }_1{I}_1{L}_2-(\mu +k_1)L_1-x{\beta }_2{I}_2{L}_1+r_1{I}_1-z{L}_1,\hfill \\ \hfill {\stackrel{.}{I}}_1& =k_1{L}_1-(1+a_q+r_1)I_1,\hfill \\ \hfill {\stackrel{.}{L}}_2& ={\beta }_2{I}_{2}S+x{\beta }_2{I}_2{L}_1-(\mu +k_2)L_2-x{\beta }_1{I}_1{L}_2+r_2{I}_2,\hfill \\ \hfill {\stackrel{.}{I}}_2& =k_2{L}_2+a_q{I}_1-(1+r_2)I_2\hfill \end{array}$$ (11)

without latent coinfection, and

$$\begin{array}{cc}\hfill {\stackrel{.}{L}}_1& ={\beta }_1{I}_{1}S-(\mu +k_1)L_1-x{\beta }_2{I}_2{L}_1+r_1{I}_1-z{L}_1,\hfill \\ \hfill {\stackrel{.}{I}}_1& =k{L}_1+k_{m1}M-(1+a_q+r_1)I_1,\hfill \\ \hfill {\stackrel{.}{L}}_2& ={\beta }_2{I}_{2}S-(\mu +k_2)L_2-x{\beta }_1{I}_1{L}_2+r_2{I}_2+zM,\hfill \\ \hfill {\stackrel{.}{I}}_2& =k_2{L}_2+k_{m2}M+a_q{I}_1-(1+r_2)I_2,\hfill \\ \hfill \stackrel{.}{M}& =x{\beta }_2{I}_2{L}_1+x{\beta }_1{I}_1{L}_2-(k_m+\mu +z)M\hfill \end{array}$$ (12)

with latent coinfection, where we have again scaled the time variable such that μ_d = 1 and non-dimensionalized all the rates accordingly. The models both have reproductive numbers (again not thresholds, as in Section 2) given by

$$\begin{array}{cc}\hfill R_1& =\frac{{\beta }_1{k}_1}{(\mu +k_1)(1+r_1+a_q)-r_1{k}_1},\hfill \\ \hfill R_2& =\frac{{\beta }_2{k}_2}{(\mu +k_2)(1+r_2)+r_2{k}_2}.\hfill \end{array}$$ (13)

Equilibrium E₂ is now given in both models by

$$\begin{array}{cc}\hfill {\stackrel{‒}{L}}_2& =\frac{\frac{{\beta }_2{k}_2+r_2{k}_2}{(\mu +k_2)(1+r_2)}-1}{\frac{{\beta }_2{k}_2}{(1+r_2)(\mu +k_2)}\left(1+\frac{k}{1+r_2}\right)},\hfill \\ \hfill {\stackrel{‒}{I}}_2& =\frac{k_2}{1+r_2}{\stackrel{‒}{L}}_2\hfill \end{array}$$ (14)

and L̄₁ = Ī₁ = M̄ = 0. While it is thought that some partial immunity to reinfection occurs for TB, the observations of mixed infection described above, together with the lack of empirical determination of the amount of partial protection motivate keeping the assumption x = 1 for simplicity.

The basic structure of the Jacobians are unaltered from the previous section, and without coinfection the stability boundary is again linear. We give the coefficients of the cubic polynomial defining the stability boundary in Eqs. (A.8)–(A.10).

In the TB models, the fact that recovered individuals can relapse means that the steady-state disease levels are not simply functions of R₁ and R₂, and hence the stability boundary does not take the form R₁ < g(R₂). However, R₁ and R₂ are linear functions of the transmission rates β₁ and β₂. Though the explicit forms of f₁, f₂ and f₃ are cumbersome, it remains the case that the stability boundary of E₂ is defined by the condition c > 0 in Eq. (A.10). Figure 3 compares the boundaries in the two models, both with and without IPT. When a_q > 0 numerical evidence indicates that the white regions in Figs. 3(a) and (b) contains a stable coexisting equilibrium; when a_q = 0 symmetry arguments indicate that there will also be a strain-1 only equilibrium with an analogous stability boundary to those shown in the figure. As in the simpler models, the coinfected latent class has the effect of promoting coexistence in an unbounded region in parameter space and preventing the drug-resistant strain from completely replacing the sensitive strain. This is shown graphically in the curved shape of the dashed lines in Fig. 3, which are asymptotically flat as β₂ → ∞.

Fig. 3.

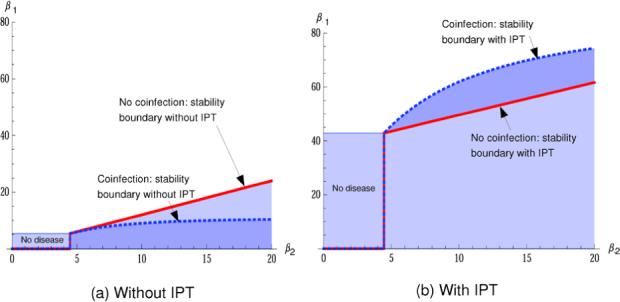
Stability of E₂ in the models for tuberculosis with and without latent coinfection. The stability region of E₂ is the area below the curved dashed lines (blue) in the coinfection model, and below the straight solid lines (red) in the model without coinfection. (Color figure online.)

Because the drug-sensitive strain is affected more by the intervention, β₁ must be considerably higher in order for the sensitive strain to persist, and the disease-free region is substantially larger. For this reason, the boundary with IPT in place is much higher on the plot in Fig. 3 than in the case where z = 0 (no IPT). Such interventions can eradicate disease in this and similar models when R₂ < 1. However, when R₂ > 1, the region in which the resistant strain can take over is much larger.

This change takes place because an intervention that has a differential effect on the two strains alters the balance when the strains compete for hosts, and it occurs with or without latent coinfection. However, the incorporation of latent coinfection alters the boundary so that it lies above the boundary in the absence of latent coinfection: in Fig. 3(b), the dashed line is above the solid one, where in (a) it is below. In other words, the within-host selection of the resistant strain under IPT expands the stability region of the resistance-only equilibrium in the region where 1 < R₂ < ∼6(∼ 5 < β₂ < ∼30). Latent coinfection loses its “protective” effect against single-strain takeover, and instead provides a mechanism that facilitates takeover by the resistant strain. This potential increase in strain 2's dominance depends on z being large enough to have a substantial effect, and on the competition for hosts between the two strains. In low-prevalence areas, or areas in which disease is being eradicated (max{R₁, R₂} < 1), IPT will have beneficial effects on disease levels, while in high-prevalence areas the widespread use of IPT may facilitate takeover by emerging resistant strains.

A tuberculosis isolate is classed as multi-drug resistant (MDR) if it is resistant to at least isoniazid and rifampin, and extensively drug resistant (XDR) if it is MDR and also exhibits resistance to at least one fluorquinolone and one injectable TB antibiotic. Recent epidemiologic data indicate that MDR and XDR TB strains can be transmitted (Gandhi et al., 2006; Li et al., 2007), which indicates that the basic reproductive number of R₂ may be greater than 1, at least in some settings and for some resistant strains. However, drug resistance is thought to be conferred by a series of single-point mutations that allow the bacteria to survive in the presence of chemotherapeutic agents (Rattan et al., 1998); typically, such mutations have a cost to the overall fitness of the pathogen and may result in substantial loss of transmissibility (Davies et al., 2000). So, although R₂ is large enough for transmission, and although it may increase under evolutionary pressure, it is likely that R₂ for MDR and XDR TB strains is currently in the region (just above 1) where the effect of IPT on latent coinfections most effectively enables the resistant strain to spread and take over the population, compared to its potential in the absence of latent coinfection.

4. Discussion

Latent coinfection can dramatically alter the long-term dynamics in SEIR models with two interacting strains. In some scenarios, it serves as a strong coexistence-promoting mechanism, allowing both strains to persist where they would not otherwise. Over long time scales, this is expected to increase the diversity of strains circulating within communities. The presence of variants, some of which may have genetic properties that facilitate the further development of resistance, such as increased growth or mutation rates, or benign mutations that enable further resistance-conferring mutations, may be increased.

The extent to which latent coinfection promotes strain diversity depends on the in-host response to reinfection. Latent coinfection promotes coexistence of the two strains most strongly when reinfection does not result in strain replacement within an individual host. Conversely, if subsequent reinfection can clear one of the strains in the coinfection, coinfection need not promote the coexistence of two strains. We note that in-host mechanisms of strain interaction are not generally well understood for human pathogens; our results identify this as an important area for future study. Pathogens for which infection does not confer complete immunity, which result in potentially long periods of infection (with or without symptoms), and for which there is an opportunity for multiple exposure events are the most appealing subjects of such inquiry. Examples include TB and HIV, as mentioned here, as well as chronic virus infections (e.g., Herpesviruses, Human Papilloma Virus) or chronic bacterial infections (e.g., Helicobacter pylori).

In our models, the pathogen virulence and transmissibility have remained constant. However, coinfection at the infectious stage is also expected to alter the optimal evolutionary strategies of pathogens (see, for example Adler and Losada, 2002; Carrillo et al., 2007; Claessen and de Roos, 1995; May and Nowak, 1995; Mosquera and Adler, 1998). The effects of latent coinfection on pathogen evolution are likely to be complicated because in-host competition occurs at an uninfectious stage and the trade-offs between transmissibility and virulence, as well as effects on the duration of latency would affect fitness. It is also possible that coinfection occurs both at the latent and infectious stages, which would give pathogens access to an even more diverse set of strategies. Particularly in the case where strain 2 is a drug-resistant strain and is relatively new, the assumption of constant virulence, transmissibility and latent periods is a conservative one because strains would be selected on the basis of reproductive ability; this selection is expected to further enable takeover by the resistant strain.

Our simple models of TB epidemics assume that latent TB does not revert from mixed to single latent infection upon reinfection, and allow for strain-specific progression rates as well as recovery with the risk of relapse. The stability analysis indicates that under these model assumptions, the existence of a coinfected latent class results in drug-resistant strains of TB being disadvantaged in their ability to take over disease in the population. Even under this constraint, however, interventions such as IPT, that target the latent class and differentially affect drug-resistant and drug-sensitive strains, can have the perverse effect of substantially increasing the ability of the resistant strain to take over.

Appendix

Starting from the Jacobian at E₂:

$$\left(\begin{array}{ccccc}\hfill -{\beta }_2{\stackrel{‒}{I}}_2-\mu -k\hfill & \hfill {\beta }_1(1-{\stackrel{‒}{I}}_2-{\stackrel{‒}{L}}_2)\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill k\hfill & \hfill -(1+a_q)\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill k_m∕2\hfill \\ \hfill -{\beta }_2{\stackrel{‒}{I}}_2\hfill & \hfill -{\beta }_2{\stackrel{‒}{I}}_2-{\beta }_1{\stackrel{‒}{L}}_2\hfill & \hfill -{\beta }_2{\stackrel{‒}{I}}_2-\mu -k\hfill & \hfill {\beta }_2(1-{\stackrel{‒}{L}}_2-2{\stackrel{‒}{I}}_2)\hfill & \hfill -{\beta }_2{\stackrel{‒}{I}}_2\hfill \\ \hfill 0\hfill & \hfill a\hfill & \hfill k\hfill & \hfill -1\hfill & \hfill k_m∕2\hfill \\ \hfill {\beta }_2{\stackrel{‒}{I}}_2\hfill & \hfill {\beta }_1{\stackrel{‒}{L}}_2\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill -k_m-\mu \hfill \end{array}\right)$$ (A.1)

the characteristic polynomial can be written as the product of a quadratic and a cubic polynomial; the quadratic part gives the necessary criterion R₂ > 1 for stability of E₂.

Writing d = μ_d+a_q, A = β₂Ī₂+μ+k, B = β₁(1−Ī₂−L̄₂), C = β₂Ī₂ and F = β₁L̄₂, the cubic polynomial is then

$$(A+\lambda )(d+\lambda )(k_m+\mu +\lambda )-\frac{1}{2}{k}_m(A+\lambda )F-kB(k_m+\mu +\lambda )-\frac{1}{2}{k}_{m}BC,$$ (A.2)

where

$$\begin{array}{cc}\hfill A& =(\mu +k)\left(1+\frac{R_2-1}{k+1}\right),C={\beta }_2\frac{k}{k+1}\left(1-\frac{1}{R_2}\right),\hfill \\ \hfill F& ={\beta }_1\frac{1}{k+1}\left(1-\frac{1}{R_2}\right),B={\beta }_1∕R_2\hfill \end{array}$$ (A.3)

are shorthand for several elements of the Jacobian.

In the form λ³ + aλ² + bλ + c, the coefficients of the cubic polynomial (A.2) are given by

$$a=A+d+k_m+\mu ,b=Ad+(k+\mu )(A+d)-\frac{1}{2}{k}_{m}F-kB$$

and

$$c=Ad(k_m+\mu )-\frac{1}{2}{k}_{m}AF-Bk(k_m+\mu )-\frac{1}{2}{k}_{m}BC.$$

so that R₂ > 1 implies a > 0. We seek the relationships between R₁ and R₂ that determine the stability of equilibrium E₂, analogous to the condition in Eq. (5).

The coefficients b and c have the structure b = b₁ + b₂β₁ and c = c₁ + c₂β₁, with positive b₁, b₂, c₁, and c₂, so that the relations between R₁ and R₂ that determine stability can be found from:

$${\beta }_1<\frac{b_1}{b_2}\equiv f_1,{\beta }_1<\frac{c_1}{c_2}\equiv f_2\text{and}{\beta }_1<\frac{a{b}_1-c_1}{a{b}_2-c_2}\equiv f_3.$$

If β₁ < min{f₁, f₂, f₃}, then the equilibrium E₂ is locally stable.

We now show that f₂ is the smallest of these, and hence determines the stability. We have

$$\begin{array}{cc}\hfill a& =A+d+k+\mu ,\hfill \\ \hfill b_1& =(A+d)(k_m+\mu )+Ad,\hfill \\ \hfill b_2& =\frac{1}{2}\frac{k_m}{k+1}\left(1-\frac{1}{R_2}\right)+\frac{k}{R_2},\hfill \\ \hfill c_1& =Ad(k_m+\mu ),\hfill \\ \hfill c_2& =\frac{1}{2}\frac{k_m}{k+1}\left(1-\frac{1}{R_2}\right)(A+k+\mu )+\frac{k(k_m+\mu )}{R_2}\hfill \end{array}$$ (A.4)

so that since b₁, b₂, c₁, and c₂ are all positive,

$$\frac{b_1}{b_2}>\frac{c_1}{c_2}\iff b_1{c}_2-b_2{c}_1>0.$$

With $\Gamma =\frac{1}{}\frac{k_m}{k+1}(1-\frac{1}{R_2})$, this term can be written

$$\begin{array}{cc}\hfill b_1{c}_2-b_2{c}_1\ge & \Gamma \frac{A+\mu +k}{\mu +k_m}(Ad+(A+d)(k+\mu ))+\frac{k}{R_2}Ad\hfill \\ \hfill & +\frac{k}{R_2}(A+d)(k+\mu )-\left(Ad\Gamma +\frac{k}{R_2}Ad\right)\hfill \\ \hfill =& \Gamma Ad\frac{A+\mu +k}{\mu +k_m}+\Gamma A(A+\mu +k)+\Gamma d(\mu +k)\hfill \\ \hfill & +\frac{k}{R_2}(A+d)(k_m+\mu ),\hfill \end{array}$$ (A.5)

which is positive, so that f₁ > f₂.

In comparing f₂ and f₃, note that when ab₂ − c₂ > 0, $\frac{c_1}{c_2}<\frac{a{b}_1-c_1}{a{b}_2-c_2}\iff \frac{c_1}{c_2}<\frac{b_1}{b_2}$, which means that if ab₂ − c₂ > 0, then f₂ = min{f₁, f₂, f₃} and so defines the stability of equilibrium E₂. After some algebraic manipulation, ab₂ − c₂ > 0 can be written

$$\begin{array}{cc}\hfill & (\mu +k)\left(1+\frac{R_2-1}{k+1}\right)\frac{k}{R_2}+\frac{1}{2}\frac{k_m}{k+1}\left(1-\frac{1}{R_2}\right)(d+k_m)+\frac{kd}{R_2}\hfill \\ \hfill & >\frac{1}{2}\frac{k_m}{k+1}\left(1-\frac{1}{R_2}\right)k.\hfill \end{array}$$ (A.6)

Now, comparing the first term on the left with the term on the right, it is clear that μ + k > k_m/2 is sufficient. Alternatively, when we compare the middle term on the left with the term on the right, it is clear that if d + k_m > k this is also sufficient. If k ≥ k_m, the first holds, and if k < k_m, the second holds. Therefore, ab₂ − c₂ > 0 and the stability boundary is given by ${\beta }_1<\frac{c_1}{c_2}=f_2$, or equivalently,

$$R_1<\frac{c_1\left(R_2\right)}{c_2\left(R_2\right)}\frac{k}{(k+\mu )d}.$$

In model C, where χ > 0, we perform a similar analysis except that the polynomial coefficients are given by

$$\begin{array}{cc}\hfill a& =A+d+\chi C+k+\mu ,\hfill \\ \hfill b_1& =(A+d)(\chi C+k_m+\mu )+Ad,\hfill \\ \hfill b_2& =\frac{1}{2}\frac{k_m}{k+1}\left(1-\frac{1}{R_2}\right)+\frac{k}{R_2},\hfill \\ \hfill c_1& =Ad(\chi C+k_m+\mu ),\hfill \\ \hfill c_2& =\frac{1}{2}\frac{k_m}{k+1}\left(1-\frac{1}{R_2}\right)(A+k+\mu )+\frac{k(\chi C+k_m+\mu )}{R_2},\hfill \end{array}$$ (A.7)

where $C=\frac{\mu +k}{k+1}(R_2-1)$, instead of those given in Eq. (A.4). In the TB model of Section 3, Eq. (A.2) takes the form

$$(A+\lambda )(d+\lambda )(k_m+\mu +z+\lambda )-k_{m1}(A+\lambda )F-k_{1}B(k_m+\mu +z+\lambda )-k_{m1}BC$$ (A.8)

with

$$\begin{array}{cc}\hfill d& =1+a_q,\hfill \\ \hfill A& =\mu +k_1+z+{\beta }_2{\stackrel{‒}{I}}_2,\hfill \\ \hfill B& =r_1+{\beta }_1(1-{\stackrel{‒}{L}}_2-{\stackrel{‒}{I}}_2),\hfill \\ \hfill C& ={\beta }_2{\stackrel{‒}{I}}_2,\hfill \\ \hfill F& ={\beta }_1{\stackrel{‒}{L}}_2.\hfill \end{array}$$ (A.9)

With this notation, the stability of E₂ is defined by the condition R₂ > 1 and the cubic part of the characteristic polynomial, λ³ + aλ² + bλ + c with

$$\begin{array}{cc}\hfill a& =A+d+k_m+\mu ,\hfill \\ \hfill b& =Ad+(k_m+\mu +z)(A+d)-k_{m1}F-k_{1}B,\hfill \\ \hfill c& =Ad(k_m+\mu +z)-k_{m1}AF-B{k}_1(k_m+\mu +z)-k_{m1}BC.\hfill \end{array}$$ (A.10)