Statistical Inference for Semiparametric Varying-coefficient Partially Linear Models with Generated Regressors (F06-463)

Abstract

We study semiparametric varying-coefficient partially linear models when some linear covariates are not observed, but ancillary variables are available. Semiparametric profile least-square-based estimation procedures are developed for parametric and nonparametric components after we calibrate the error-prone covariates. Asymptotic properties of the proposed estimators are established. We also propose the profile least-square-based ratio test and Wald test to identify significant parametric and nonparametric components. To improve accuracy of the proposed tests for small or moderate sample sizes, Wild bootstrap version is also proposed to calculate the critical values. Intensive simulation experiments are conducted to illustrate the proposed approaches.

1 Introduction

Various efforts have been made to balance the interpretation of linear models and flexibility of nonparametric models. Important results from these efforts include semiparametric varying-coefficient partially linear models (SVCPLM), in which the response variable Y depends on variables Z, X and U in the form of

$$Y={\mathbf{\Theta }}^{\text{T}}\mathbf{Z}+{\mathit{\alpha }}^{\text{T}}(U)\mathbf{X}+\epsilon ,$$ (1.1)

where Θ is a p-dimensional vector of unknown parameters, α(·) is a q-variate vector of unknown functions, U is a vector of nonparametric components, which may be multivariate, and the model error ε has mean zero and finite variance. For notational simplicity, we assume that U is scalar. α^T(U)X is referred to as a nonparametric component since α(U) is nonparametric.

Model (1.1) permits the interaction between the covariates U and X in such a way that a different level of covariate U is associated with a different linear model about Θ^TZ, and allows one to examine the extent to which covariates X interact. This model presents a novel and general structure, which indeed covers many well-studied important semiparametric regression models. For example, when Z = 0, (1.1) reduces to varying-coefficient models, which were originally proposed by Hastie and Tibshirani (1993), and studied by Fan and Zhang (1999), Xia and Li (1999), and Cai, Fan and Li (2000). When q = 1 and X = 1, model (1.1) reduces to well-known partially linear models, in which Y depends on Z in a linear way but is related to another independent variable U in an unspecified form. There is a great deal of literature on the study of partially linear models (e.g., Engle et al., 1986;, Robinson, 1988; and Speckman, 1988). A survey of partially linear models was given by Härdle, Liang and Gao (2000). The study of SVCPLM has been investigated by Zhang, Lee and Song (2002), and Fan and Huang (2005) among others. Zhang, Lee and Song (2002) developed the procedures for estimation of the linear and nonparametric parts of the SVCPLM. Fan and Huang (2005) proposed a profile likelihood technique for estimating parametric components and established the asymptotic normality of their proposed estimator.

All studies of the SVCPLM are limited to considerations of exactly observed data. However, in biomedical research observations are measured with error. Simply ignoring measurement errors, known as the naive method, will result in biased estimators. Various attempts have been made to correct for such bias, see Fuller (1987) and Carroll et al. (2006) for extensive discussions and examples of linear and nonlinear models with measurement errors. In this paper, we are concerned with the situation where some components (ξ) of Z are unobserved directly, but auxiliary information is available to remit ξ. Let Z = (ξ^T, W^T)^T, where ξ is a p₁ × 1 vector and W is a vector of the remaining observed components. We assume that ξ is related to observed η and V through the relationship ξ = E(η|V). Thus, we study the following model

$$\{\begin{array}{l}Y={\mathit{\beta }}^{\text{T}}\mathit{\xi }+{\mathit{\theta }}^{\text{T}}\mathbf{W}+{\mathit{\alpha }}^{\text{T}}(U)\mathbf{X}+\epsilon ,\hfill \\ \mathit{\eta }=\mathit{\xi }(\mathbf{V})+\mathbf{e},\hfill \end{array}$$ (1.2)

where E(ε|Z, X, U) = 0, E(ε²|Z, X, U) = σ²(Z, X, U), and e is an error with mean zero and positive finite covariance matrix Σ_e = E(ee^T). The four covariates V, W, X and U are different. In our structure, we allow that V and (X, W, U) may overlap. Model (1.2) is flexible enough to include a variety of models of interest. We give three examples to illustrate its flexibility.

Example 1.1

(Errors-in-variable models with validation data) Z is a p-variate variable vector and is not observed. Z̃ is an another p-variate vector and is observed associated with vector Z. Assume that we have primary observations {Y_j, Z̃_j, U_j, j = 1, ···, n}, and n₀ independent validation observations {Z_j, Z̃_j, U_i, i = n + 1, ···, n + n₀}, which are independent of the primary observations. Let V = (Z̃^T, U)^T. The partial errors-in-variable model with validation data is written as

$$\{\begin{array}{l}Y={\mathit{\beta }}^{\text{T}}E(\mathbf{Z}\mid \mathbf{V})+\alpha (U)+\varepsilon ,\hfill \\ \epsilon =e+{\mathit{\beta }}^{\text{T}}\{\mathbf{Z}-E(\mathbf{Z}\mid \mathbf{V})\}.\hfill \end{array}$$ (1.3)

This model has been studied by Sepanski and Lee (1995), Sepanski and Carroll (1993), and Sepanski, Knickerbocker and Carroll (1994). Taking X = 1, θ = 0, η = Z, and ξ = E(Z|V) in model (1.2), we know that model (1.3) is a sub-model of (1.2).

Example 1.2

(De-noise linear model) The relation between the response variable Y and covariates (ξ, W) is described by Y = β^Tξ + θ^TW + ε, where β and θ are parametric vectors respectively. The covariate ξ is measured with error since instead of observing ξ directly we observe its surrogate η. This forms a de-noise linear model:

$$\{\begin{array}{l}Y={\mathit{\beta }}^{\text{T}}\mathit{\xi }+{\mathit{\theta }}^{\text{T}}\mathbf{W}+\epsilon ,\hfill \\ \mathit{\eta }=\mathit{\xi }+e,\hfill \end{array}$$ (1.4)

where ξ = ξ(t) is subject to measurement error at time t and the measurement errors ε and e are independent of each other at each time t.

Cai, Naik and Tsai (2000) used this model to estimate the relationship between awareness and television rating points of TV commercials for certain products. Cui, He and Zhu (2002) proposed an estimator of the coefficients and established asymptotic results of the proposed estimator. It is easy to see that model (1.2) embeds (1.4).

Example 1.3

(Rational expectation model) Consider the following rational expectation model:

$$Y_t={\gamma }^{\text{T}}{\mathbf{S}}_t+{\mathit{\zeta }}^{\text{T}}\{{\mathit{\eta }}_t-E({\mathit{\eta }}_t\mid {\mathbf{V}}_t)\}+{\epsilon }_t,$$ (1.5)

where η_t − E(η_t|V_t) is the expectation payoff for price variable η_t given historical information V_t. In this model, (Y_t, S_t, η_t, V_t) except E(η_t|V_t) can be observed directly.

Beside estimation and inference of γ and ζ, within the econometric community, the following model is of interest.

$$Y_t={\gamma }^{\text{T}}{\mathbf{S}}_t+{\mathit{\zeta }}^{\text{T}}{\mathit{\eta }}_t-{\mathit{\beta }}^{\text{T}}E({\mathit{\eta }}_t\mid {\mathbf{V}}_t)+{\epsilon }_t.$$ (1.6)

It is worthy to note that model (1.6) is a sub-model of (1.2). An interesting question is to test whether the model (1.6) satisfies the rational expectation model (1.5), that is to test following hypothesis:

$$H_0:\mathit{\beta }=\mathit{\zeta }\text{VS}{H}_1:\mathit{\beta }\ne \mathit{\zeta },$$ (1.7)

In the econometric literature, regressing unobserved covariates is also called generated regression. This topic has been widely studied. Pagan (1984) gave a comprehensive review on the estimation of parametric models with generated regression. Ai and Mcfadden (1997) presented a procedure for analyzing a partially specified nonlinear regression model in which the nuisance parameter is an unrestricted function of a subset of regressors. Ahn and Powell (1993) and Powell (1987) considered the case with the generated regressors in the nonparametric part of the model. Li (2002) considered the problems of estimating a semiparametric partially linear model for dependent data with generated regressors. Their models are special cases of the rational expectation model.

Various procedures similar to generated regression have been proposed to reduce the bias due to mis-measurement. Regression calibration and simulation extrapolation have been developed for measurement errors models (Carroll et al., 2006). Liang, Härdle and Carroll (1999) studied a special case of (1.2), partially linear errors-in-variables models, and proposed an attenuated estimator of the parameter based on the semiparametric likelihood estimate. Wang and Pepe (2000) used a pseudo-expected estimating equation method to estimate the parameter in order to correct the estimation bias.

In an attempt to develop a unified estimation procedure for model (1.2), we propose a profile-based procedure, which is similar to regression calibration method in spirit. The procedure consists of two steps. In the first step, we calibrate the error-prone covariate ξ by using ancillary information and applying nonpara-metric regression techniques. In the second step, we use profile least-square-based principle for estimating the parametric and nonparametric components. Under the mild assumptions, we derive the asymptotic representives of the proposed estimators, and use the representives to establish asymptotic normality. We also propose the profile least-square-based ratio test and Wald test for the parametric part of model (1.2), and a goodness-of-fit test for the varying coefficients in the nonparametric part. The asymptotic distribution of the proposed test statistics is derived. Wild bootstrap versions are introduced to calculate the critical values for those tests.

The paper is organized as follows. In Section 2, we focus on the estimation of the parameters and nonparametric functions, and on the development of asymptotic properties of the resulting estimators. The error-prone covariates are first calibrated. Bandwidth selection strategy is also discussed. In Section 3, we develop profile least-square-based ratio tests for parametric and nonparametric components. Wild bootstrap methods are proposed to calculate the critical values. The results of applications to simulated and real data are reported in Section 4. Section 5 gives a conclusion. Regularity assumptions and technical proofs are relegated to the Appendix.

2 Estimation of the parametric and nonparametric components

When ξ is observed, estimators of β and α(u), and associated tests have been developed to study model (1.2). These estimators and tests cannot be used directly when ξ is unobservable. We first need to calibrate ξ by using ancillary variables and V because a direct replacement of ξ by η will result in bias.

2.1 Covariate calibration

For notational simplicity, we assume V is univariate in the remainder of this paper. Let η_i,k be the kth entry of vector η, and L_b(·) = L(·/b)/b, b = b_k (k = 1, 2, ···, p₁) is a bandwidth for the kth component of η. Assume throughout the paper that ξ_k(υ) has r + 1 derivatives and we approximate ξ_k(υ) by a r-order polynomial within the neighborhood of υ₀ via Taylor expansion

$${\xi }_k(v)\approx {\xi }_k(v_0)+{\xi }_k^{\prime }(v_0)(v-v_0)+\dots +\frac{{\xi }_k^{(r)}(v_0)}{r!}{(v-v_0)}^r=\sum _{j=0}^r{a}_{j,k}{(v-v_0)}^j.$$

Denote

$${\mathbf{V}}_v=\left[\begin{array}{cccc}1& (V_1-v)& \cdots & {(V_1-v)}^r\\ ⋮& ⋮& \cdots & \cdots \\ 1& (V_n-v)& \cdots & {(V_n-v)}^r\end{array}\right],{\mathit{\eta }}^{(k)}=\left(\begin{array}{c}{\eta }_{1k}\\ ⋮\\ {\eta }_{nk}\end{array}\right),$$

W_υ = diag{L_b(V₁ − υ), ···, L_b(V_n − υ)}. The local polynomial estimator (Fan and Gijble, 1996) of (a_0,k, …, a_r,k)^T can be expressed as ${\widehat{\mathbf{a}}}_k^{\text{T}}={({\mathbf{V}}_v^{\text{T}}{W}_v{\mathbf{V}}_v)}^{-1}{\mathbf{V}}_v^{\text{T}}{W}_v{\mathit{\eta }}^{(k)}$. As a consequence, ξ_k(v) is estimated by ${\widehat{\xi }}_k(v)={\zeta }_1^{\text{T}}{({\mathbf{V}}_v^{\text{T}}{W}_v{\mathbf{V}}_v)}^{-1}{\mathbf{V}}_v^{-1}{W}_v{\mathit{\eta }}^{(k)}$, for k = 1, …, p₁, where ζ₁ is a (r + 1) × 1 vector with 1 in the first position and 0 in other positions.

In what follows, we denote A^⊗2 = AA^T, μ_j = ∫ u^jL(u)du, ν_j = ∫ u^jL²(u)du, S_u = (μ_j+l)_0≤j,l≤r, and c_p = (μ_r+1, ···, μ_2r+1)^T. f_υ(υ) is the density function of V.

Under the assumptions given in the Appendix, we can prove (Fan and Gijbels, 1996, pp 101–103 or Carroll et al., 1997, pp 486) that

$$\begin{array}{c}\widehat{\mathit{\xi }}(v)-\mathit{\xi }(v)=\frac{{\zeta }_1{S}_u^{-1}{c}_p{b}^{r+1}}{(r+1)!}{\mathit{\xi }}^{(r+1)}(v)+\frac{1}{n{f}_v(v)}\sum _{i=1}^n{L}_b(V_i-v){\mathbf{e}}_i\\ +o(b^{r+1}+log{b}^{-1}/\sqrt{nb}),\end{array}$$ (2.1)

uniformly on υ ∈ . This fact will be used for proving the main results in the Appendix.

2.2 Estimation of the parametric component

Let (Y_i, η_i, V_i, W_i, X_i, U_i), i = 1, 2 ···, n, be the observations from model (1.2). The unknown covariates ξ_i are substituted by their estimators given in the above section. We therefore have following “new” model:

$$\{\begin{array}{l}{Y}_i={\mathit{\beta }}^{\text{T}}{\widehat{\mathit{\xi }}}_i+{\mathit{\theta }}^{\text{T}}{\mathbf{W}}_i+{\mathit{\alpha }}^{\text{T}}(U_i){\mathbf{X}}_i+{\widehat{\epsilon }}_i,\hfill \\ {\widehat{\epsilon }}_i={\epsilon }_i+{\mathit{\beta }}^{\text{T}}\{{\mathit{\xi }}_i-\widehat{\mathit{\xi }}({\mathbf{V}}_i)\},\hfill \end{array}i=1,\dots ,n,$$ (2.2)

where ${\left\{{\widehat{\epsilon }}_i\right\}}_{i=1}^n$ are still treated as errors. If ξ̂_i would be an unbiased estimator of ξ_i, then Eε̂_i = 0.

Approximate α_j(U) within the neighbors of u by a_j(u) + b_j(u)(U − u) for j = 1, …, q. Write ${\widehat{\mathbf{Z}}}_i={({\widehat{\mathit{\xi }}}_i^{\text{T}},{\mathbf{W}}_i^{\text{T}})}^{\text{T}}$ and Θ = (β^T, θ^T)^T. Following the profile likelihood based procedure proposed by Fan and Huang (2005), our profile least-square-based estimator of Θ is defined as

$${\widehat{\mathbf{\Theta }}}_n={\{{\stackrel{\sim }{\mathbf{Z}}}^{\text{T}}\stackrel{\sim }{\mathbf{Z}}\}}^{-1}{\stackrel{\sim }{\mathbf{Z}}}^{\text{T}}(\mathbf{I}-\mathbf{S})\mathbf{Y},$$ (2.3)

where Z̃ = (I − S)Ẑ, I is the n × n identity matrix,

$$\mathbf{S}={\left(\begin{array}{cc}({\mathbf{X}}_1^{\text{T}}& {\mathbf{0}}_q^{\text{T}}){({\mathbf{D}}_{u_1}^{\text{T}}{\mathbf{W}}_{u_1}{\mathbf{D}}_{u_1})}^{-1}{\mathbf{D}}_{u_1}^{\text{T}}{\mathbf{W}}_{u_1}\\ & ⋮\\ ({\mathbf{X}}_n^{\text{T}}& {\mathbf{0}}_q^{\text{T}}){({\mathbf{D}}_{u_n}^{\text{T}}{\mathbf{W}}_{u_n}{\mathbf{D}}_{u_n})}^{-1}{\mathbf{D}}_{u_n}^{\text{T}}{\mathbf{W}}_{u_n}\end{array}\right)}_{n\times 2q},{\mathbf{D}}_u={\left(\begin{array}{cc}{\mathbf{X}}_1^{\text{T}}& h^{-1}(U_1-u){\mathbf{X}}_1^{\text{T}}\\ ⋮& ⋮\\ {\mathbf{X}}_n^{\text{T}}& h^{-1}(U_n-u){\mathbf{X}}_n^{\text{T}}\end{array}\right)}_{n\times 2q},$$

and Y = (Y₁, …, Y_n)^T, W_u = diag{K_h(U₁ − u), …, K_h(U_n − u)}_n×n, Ẑ = (Ẑ₁, ···, Ẑ_n)^T, 0_q is the q×1 vector with all the entries being zero, K(·) is a kernel function, h is a bandwidth and K_h(·) = K(·/h)/h.

We now give a representation of Θ̂_n. This representation can be used to obtain the asymptotic distribution of $\sqrt{n}({\widehat{\mathbf{\Theta }}}_n-\mathbf{\Theta })$, which we give in Theorem 2. This result extends the method of Fan and Huang (2005) to a SVCPLM with generated regressors.

Write Φ(U) = E(XZ^T|U), Γ(U) = E(XX^T|U), B(V) = E[{Z − Φ^T(U)Γ⁻¹(U)X}|V], ψ(Z, X, U) = Z − Φ^T(U)Γ⁻¹(U)X, and Σ = E(ZZ^T) − E{Φ^T(U) Γ⁻¹(U)Φ(U)}.

Theorem 1

Under Assumptions 1–5 in Appendix, we have

$$\begin{array}{l}{\widehat{\mathbf{\Theta }}}_n-\mathbf{\Theta }={\mathbf{\sum }}^{-1}[\frac{1}{n}\frac{b^{r+1}}{(r+1)!}{\zeta }_1^{\text{T}}{S}_u^{-1}{c}_p\sum _{i=1}^n\psi ({\mathbf{Z}}_i,{\mathbf{X}}_i,U_i){\{{\mathit{\xi }}^{(r+1)}({\mathbf{V}}_i)\}}^{\text{T}}{\mathit{\beta }}_0\\ +\frac{1}{n}\sum _{j=1}^n\mathrm{\Delta }({\mathbf{V}}_j){\mathbf{e}}_j^{\text{T}}{\mathit{\beta }}_0+\frac{1}{n}\sum _{i=1}^n\psi ({\mathbf{Z}}_i,{\mathbf{X}}_i,U_i){\epsilon }_i]\{1+o_p(1)\}\end{array}$$

where $\mathrm{\Delta }({\mathbf{V}}_j)=\frac{1}{n}{\sum }_{i=1}^n\psi ({\mathbf{Z}}_i,{\mathbf{X}}_i,U_i)L_b({\mathbf{V}}_j-{\mathbf{V}}_i)/f_v({\mathbf{V}}_i)$.

Theorem 2

Let nb^2(r+1) → 0. Under Assumptions 1–5 in Appendix, $\sqrt{n}({\widehat{\mathbf{\Theta }}}_n-\mathbf{\Theta })$ converges to a normal distribution with mean zero and covariance matrix Σ₁, where Σ₁= Σ⁻¹DΣ⁻¹,

$$\mathbf{D}=E[{\sigma }^2(\mathbf{X},\mathbf{Z},U){\{\psi (\mathbf{X},\mathbf{Z},U)\}}^{\otimes 2}]+E[{({\mathbf{e}}^{\text{T}}\mathit{\beta })}^2{\{B(\mathbf{V})\}}^{\otimes 2}]+{\mathit{\beta }}^{\text{T}}E\{E[\mathbf{e}\epsilon \mid \mathbf{Z},\mathbf{X},U,\mathbf{V}]{\{B(\mathbf{V})\}}^{\otimes 2}\}.$$

Furthermore, if e is independent of ε given (Z, X, U, V), and ε is independent of (Z, X, U), the asymptotic covariance can be simplified as Σ⁻¹(σ²Σ + E[(e^Tβ)²{B(V)}^⊗2])Σ⁻¹. If e is also independent of V, the asymptotic covariance can further be simplified as σ²Σ⁻¹ + β^TΣ_eβΣ⁻¹E{B(V)^⊗2Σ⁻¹.

The proof of Theorem 2 can be completed by using Theorem 1. We omit the details.

The asymptotic variance has a similar structure to that of Das (2005). The first term of asymptotic variance can be viewed as the variance from the first stage estimation without measurement error/missing data, the second one is the variance of the second stage for estimating unobserved variable and the third one is the covariance of two stage estimators. If e = 0 in model (1.2), i.e., the covariate can be exactly observed, the variance of Θ̂_n is the same as that of Fan and Huang (2005). To achieve the root-n estimator of Θ, Theorem 2 indicates that undersmoothing is required in estimating ξ(υ), and the optimal bandwidth does not satisfy the condition of Theorem 2.

Example 1.1 (con.) Let β̂_n be the estimator of β in model (1.3). Assume n₀/n → λ. Checking the conditions of Theorem 2, we can conclude that $\sqrt{n}({\widehat{\mathit{\beta }}}_n-{\mathit{\beta }}_0)\stackrel{\mathcal{L}}{\to }N(0,{\mathbf{\sum }}_{\ast })$ where Σ_⋆ = Σ⁻¹{σ² + λβ^TE[E{Z − E(Z|U)|V}]^⊗2β} and Σ = E[{ξ − E(ξ|U)}^⊗2].

Example 1.2 (con.) For the de-noised models introduced in Section 1, we apply Theorem 2 to derive the asymptotic distribution of the estimator, Θ̂ = (β̂^T, θ̂^T)^T, given by Cui, He, and Zhu (2002), and obtain that $\sqrt{n}(\widehat{\mathbf{\Theta }}-\mathbf{\Theta })\stackrel{\mathcal{L}}{\to }N\{0,{\mathbf{\sum }}^{-1}({\sigma }^2+{\mathit{\beta }}^{\text{T}}{\mathbf{\sum }}_e\mathit{\beta })\}$.

The asymptotic covariance of Θ̂_n can be consistently estimated by Σ̂_n = nΣ̂^{− 1}σ̂² + Σ̂^{− 1}Q̂Σ̂⁻¹, where Σ̂⁻¹ = (Z̃^TZ̃)⁻¹Z̃^T(I−S)^T(I−S)Z̃(Z̃^TZ̃)⁻¹, $\widehat{\mathbf{Q}}=\frac{1}{n}{\sum }_{i=1}^n{({\mathit{\eta }}_i-{\widehat{\mathbf{Z}}}_i)}^{\text{T}}{\widehat{\mathbf{\Theta }}}_n{\{\widehat{\mathbf{B}}({\mathbf{V}}_i)\}}^{\otimes 2}$, and ${\widehat{\sigma }}^2=\frac{1}{n}{\sum }_{i=1}^n{\{Y_i-\widehat{\alpha }(U_i){\mathbf{X}}_i-{\widehat{\mathbf{\Theta }}}^{\text{T}}\widehat{\mathbf{Z}}\}}^2$, and B̂(v) = Ẑ − Ê{Φ^T(U)Γ⁻¹(U)X|V = v} and Ê{Φ^T(U)Γ⁻¹(U)X|V = v} is a nonparametric regression estimator of Φ^T(U)Γ⁻¹(U)X on V. α̂(·) will be given in the next section.

Generally Σ̂_n is difficult to calculate. However, implementation will become simpler in some cases. For example, in the errors-in-variables model with validation data, a direct simplification yields B(V) = Z − Φ^T(U)Γ⁻¹(U)X, D = {β^TE(ee^T|V)β}Σ, and the asymptotic covariance matrix equals Σ⁻¹{σ² + λβ^TE(ee^T|V)β}. This matrix can be estimated by a standard sandwich procedure. The similar situation also applies for the asymptotic covariance matrix, Σ⁻¹{σ² + β^TE(ee^T|V)β}, of the de-noise model.

2.3 Estimation of the nonparametric components

After obtaining estimates Θ̂_n, we can estimate a_j(u) and b_j(u) for j = 1, …, q, and then α_j(u). Write Ψ(u) = {a₁(u), …, a_q(u), b₁(u), …, b_q(u)}^T. An estimator of the nonparametric components Ψ(u) is defined as

$$\widehat{\mathbf{\Psi }}(u)={\mathbf{H}}^{-1}{({\mathbf{D}}_u^{\text{T}}{\mathbf{W}}_u{\mathbf{D}}_u)}^{-1}{\mathbf{D}}_u^{\text{T}}{\mathbf{W}}_u(\mathbf{Y}-\widehat{\mathbf{Z}}{\widehat{\mathbf{\Theta }}}_n).$$ (2.4)

Correspondingly, a(u) is estimated by $\widehat{\mathbf{a}}(u)=({\mathbf{I}}_q,{\mathbf{0}}_q){({\mathbf{D}}_u^{\text{T}}{\mathbf{W}}_u{\mathbf{D}}_u)}^{-1}{\mathbf{D}}_u^{\text{T}}{\mathbf{W}}_u(\mathbf{Y}-\widehat{\mathbf{Z}}{\widehat{\mathbf{\Theta }}}_n)$, where I_q is the q×q identity matrix, H = diag(1, h)⊗I_q. We have the following asymptotic representation for the resulting estimator.

Theorem 3

Under Assumptions 1–5 given in Appendix, we have

$$\begin{array}{l}\sqrt{nh}\mathbf{H}\{\widehat{\mathbf{\Psi }}(u_0)-\mathbf{\Psi }(u_0)\}=\sqrt{nh}\{\frac{h^2}{2({\mu }_2-{\mu }_1^2)}\left(\begin{array}{c}{\mu }_2^2-{\mu }_1{\mu }_3\\ {\mu }_3-{\mu }_1{\mu }_2\end{array}\right){\mathit{\alpha }}^{″}(u_0)\\ -\frac{b^{r+1}}{(r+1)!}{\zeta }_1^{\text{T}}{S}_u^{-1}{c}_p\left(\begin{array}{c}{\mathrm{\Gamma }}^{-1}(u_0)E[\mathbf{X}{\{{\mathit{\xi }}^{(r+1)}(\mathbf{V})\}}^{\text{T}}{\mathit{\beta }}_0\mid U=u_0]\\ 0\end{array}\right)+o(h^2+b^{r+1})\}\\ +\frac{\sqrt{nh}{\mathrm{\Gamma }}^{-1}(u)}{n{f}_u(u)({\mu }_2-{\mu }_1^2)}\sum _{i=1}^n{K}_h(U_i-u)\{{\mathbf{X}}_i{\epsilon }_i+E({\mathbf{X}}_i\mid {\mathbf{V}}_i){\mathbf{e}}_i^{\text{T}}\mathit{\beta }\}\\ \otimes \left(\begin{array}{c}{\mu }_2-{\mu }_1(U_i-u)/h\\ (U_i-u)/h-{\mu }_1\end{array}\right)\{1+o_p(1)\}.\end{array}$$

Based on this representation, we can derive the asymptotic normality of the proposed nonparametric estimators of the varying coefficient functions. The proof is straightforward but tedious. We omit the details.

For notational simplicity, we assume that ε is independent of (Z, X, U) and e is independent of (V, U) in the remaining part of this paper.

Theorem 4

Under Assumptions 1–5, we have

$$\begin{array}{l}\sqrt{nh}[\mathbf{H}\{\widehat{\mathbf{\Psi }}(u_0)-\mathbf{\Psi }(u_0)\}-\frac{h^2}{2({\mu }_2-{\mu }_1^2)}\left(\begin{array}{c}({\mu }_2^2-{\mu }_1{\mu }_3){\mathit{\alpha }}^{″}(u_0)\\ ({\mu }_3-{\mu }_1{\mu }_2){\mathit{\alpha }}^{″}(u_0)\end{array}\right)\\ -\frac{b^{r+1}}{(r+1)!}{\zeta }_1^{\text{T}}{S}_u^{-1}{c}_p\left(\begin{array}{c}{\mathrm{\Gamma }}^{-1}(u_0)E[\mathbf{X}{\{{\mathit{\xi }}^{(r+1)}(\mathbf{V})\}}^{\text{T}}{\mathit{\beta }}_0\mid U=u_0]\\ \text{0}\end{array}\right)+o(h^2+b^{r+1})]\stackrel{\mathcal{L}}{\to }N(\text{0},{\mathbf{\sum }}_2),\end{array}$$

as n → ∞, where

$${\mathbf{\sum }}_2=\frac{1}{f_u(u_0)}\{{\sigma }^2{\mathrm{\Gamma }}^{-1}(u_0)+{\mathrm{\Gamma }}^{-1}(u_0){\mathbf{\sum }}_1^{\ast }{\mathrm{\Gamma }}^{-1}(u_0)\}\otimes \mathcal{G},$$

and

$$\mathcal{G}=\frac{1}{{({\mu }_2-{\mu }_1^2)}^2}\left(\begin{array}{cc}{\mu }_2^2{\nu }_0-2{\mu }_1{\mu }_2{\nu }_1+{\mu }_1^2{\nu }_2& ({\mu }_1^2+{\mu }_2){\nu }_1-{\mu }_1{\mu }_2{\nu }_0-{\mu }_1{\nu }_2\\ ({\mu }_1^2+{\mu }_2){\nu }_1-{\mu }_1{\mu }_2{\nu }_0-{\mu }_1{\nu }_2& {\nu }_1-{\mu }_1(2{\nu }_1+{\mu }_1{\nu }_0)\end{array}\right)$$

in which ${\mathbf{\sum }}_1^{\ast }={\mathit{\beta }}^{\text{T}}{\mathrm{\sum }}_e\mathit{\beta }\mathrm{\Lambda }(u_0)$, Λ(u₀) = {E[{E(X|V)}|U = u₀]}^⊗2 q₀ = μ₂/(μ₂ − μ₁), $q_1=-{\mu }_1/({\mu }_2-{\mu }_1^2)$.

Furthermore, if nhb^2r+2 → 0, then

$$\sqrt{nh}\left\{\widehat{\mathit{\alpha }}(u)-\mathit{\alpha }(u)-\frac{h^2}{2}\frac{{\mu }_2^2-{\mu }_1{\mu }_3}{{\mu }_2-{\mu }_1^2}{\mathit{\alpha }}^{″}(u)+o(h^2+b^{r+1})\right\}\stackrel{L}{\to }N(0,{\mathbf{\sum }}_{\mathbf{2}}^{\ast }),$$

where ${\mathbf{\sum }}_2^{\ast }={\sigma }^2(q_0^2{\nu }_0+2q_0{q}_1{\nu }_1+q_1^2{\nu }_2)\{{\mathrm{\Gamma }}^{-1}(u_0)+{\mathrm{\Gamma }}^{-1}(u_0){\mathbf{\sum }}_1^{\ast }{\mathrm{\Gamma }}^{-1}(u_0)\}/f_u(u)$,

The first term of Σ₂ is the asymptotic covariance of the usual profile likelihood estimator (Cai, Fan, and Li 2000) when ξ_j is observed. The second term is attributed to calibrating the error-prone covariates. In the error-in-variable model with validation data, if X is independent of V and E(X) = 0, the measurement errors have no impact on the effect of the covariance Σ₂. Theorem 4 also indicates that if n^1/2 max(h^5/2, b^r+1) → 0, the bias of α̂(u) tends to zero and α̂(u) is asymptotically normally distributed with rate (nh)^1/2.

After obtaining Θ̂_n and α̂(u), one can easily give an estimator of the variance σ² of the error ε:

$${\widehat{\sigma }}_n^2=\frac{1}{n}\sum _{i=1}^n{\{Y_i-{\widehat{\mathit{\beta }}}^{\text{T}}{\widehat{\mathit{\xi }}}_n^{\text{T}}(V_i)-{\widehat{\mathit{\theta }}}_n^{\mathbf{T}}{\mathbf{W}}_i-{\widehat{\alpha }}^{\text{T}}(U_i){\mathbf{X}}_i\}}^2.$$

In our simulation, a simple version of ${\widehat{\sigma }}_n^2$ is used. Note that S depends only on the observations ${\{(U_i,{\mathbf{X}}_i)\}}_{i=1}^n$, and we can derive a “synthetic linear model”, that is, Y − ZΘ = M + ε, where M = α^T(U)X. A straight-forward derivation yields (I − S)Y = (I − S)ZΘ + (I − S)ε. Standard regression gives the least square estimates Θ̂ and then M̂ = S(Y − ZΘ̂). Note that Z is not always observed. Replacing Z by its estimates, we obtain a consistent estimator M̂ of M; that is, M̂ = S(Y − ẐΘ̂). A consistent estimator σ² may be defined as ${\widehat{\sigma }}_n^2=\frac{1}{n}{\sum }_{i=1}^n{(Y_i-{\widehat{\mathbf{\Theta }}}^{\text{T}}{\widehat{\mathbf{Z}}}_i-{\widehat{M}}_i)}^2$, where M̂_i is the ith element of M̂.

2.4 Bandwidth selection

The proposed procedure involves two bandwidths, h and b, to be selected. To derive asymptotic distributions of the proposed estimators, we theoretically impose the rates of convergence for the bandwidths. It is worthy to point out that undersmoothing is necessary when we estimate ξ and the optimal bandwidth for b is then violated.

As mentioned before, the optimal bandwidth for b cannot be obtained because undersmoothing the nonparametric estimators of the covariates is needed. The consequence of undersmoothing ξ is that the bias is kept small and precludes the optimal bandwidth for b. The asymptotic variances of the proposed estimators for constant coefficients depend on neither the bandwidth nor the kernel function. Hence, we can use the similar method of mixture of higher-order theoretical expansions, proposed by Sepanski, Knicherbocker and Carroll (1994) or the typical curves approach by Brookmeyer and Liao (1992) to select the bandwidth b. As done by Sepanski, et al. (1994), the suitable bandwidth is b = Cn^−1/3, where C is a constant depending on unknown function ξ(υ) and its twice derivatives. In practice, one can use a plug-in rule to estimate the constant C. A useful and simple candidate C is σ̂_V, the sample deviation of V. This method is fairly effective and easy to implement. In our simulation example, the bandwidth is b = σ̂_υn^−1/3. Based on the asymptotic analysis and empirical experience for fixed time case (i.e. de-noise models), we suggest a simple rule of thumb as follows: the smoothing parameter b is so chosen that intervals of size 2b would contain around 5 points for n up to 100 and between 8⁻¹n^1/3 and 4⁻¹n^1/3 points for larger n.

We use “leave-one-sample-out” method to select the bandwidth h. This method has been widely applied in practice, for example Cai, et al. (2000) and Fan and Huang (2005). We define the cross-validation score for h as $CV(h)=n^{-1}{\sum }_{i=1}^n{\{Y_i-{\widehat{\alpha }}_{h,-i}^{\text{T}}(U_i){\mathbf{X}}_i-{\widehat{\mathbf{\Theta }}}_{n,-i}^{\text{T}}{\widehat{\mathbf{Z}}}_i\}}^2$, where Θ̂_n,−i is the estimated profile least-square-based estimator defined by (2.3), and computed from the data with measurements of the i-th observation deleted and α̂_h,−i(·) is the estimator defined in (2.4) with Θ̂_n replaced by Θ̂_n,−i. The likelihood cross-validation smoothing parameter h_cυ is the minimizer of CV(h). That is, h_cυ = arg min_h CV(h).

3 Tests for parametric and nonparametric components

3.1 Test for parametric components

An interesting question is to consider the following hypothesis

$$H_0:\mathbf{A}\mathbf{\Theta }=0\text{VS}\mathbf{A}\mathbf{\Theta }\ne 0$$ (3.1)

where A is a given l × p full rank matrix.

Let ${\widehat{\mathbf{\Theta }}}_0={({\widehat{\mathit{\beta }}}_0^{\text{T}},{\widehat{\mathit{\theta }}}_0^{\text{T}})}^{\text{T}}$ be the estimators of Θand α̂₀(·) be the estimator of α(u) under the null hypothesis. Denote $RS{S}_0={\sum }_{i=1}^n{\{Y_i-{\widehat{\mathit{\beta }}}_0^{\text{T}}{\widehat{\mathit{\xi }}}_i^{\text{T}}-{\widehat{\mathit{\theta }}}_0^{\text{T}}{\mathbf{W}}_i-{\widehat{\mathit{\alpha }}}_0^{\text{T}}(U_i){\mathbf{X}}_i\}}^2$. RSS₀ can be further expressed as ${\sum }_{i=1}^n{\{Y_i-{\widehat{\mathit{\beta }}}_0^{\text{T}}{\widehat{\mathit{\xi }}}_i^{\text{T}}-{\theta }_0^{\text{T}}{\mathbf{W}}_i-\mathbf{S}(Y-\widehat{\mathbf{Z}}{\widehat{\mathbf{\Theta }}}_0)\}}^2$, where Θ̂₀ = Θ̂ − (Z̃^TZ̃)⁻¹A^T{A(Z̃^TZ̃)⁻¹A^T}^{− 1}AΘ̂, and Θ̂ = (Z̃^TZ̃)⁻¹Z̃^TỸ, an estimator of Θ without the restriction, with Z̃ = (I − S)Ẑ and Ỹ = (I − S)Ŷ.

Similarly, let ${\widehat{\mathbf{\Theta }}}_1={({\widehat{\mathit{\beta }}}_1^{\text{T}},{\widehat{\mathit{\theta }}}_1^{\text{T}})}^{\text{T}}$ and α̂₁(·) be the estimators of Θ and α(·) under the alternative hypothesis, respectively. Denote $RS{S}_1={\sum }_{i=1}^n{\{Y_i-{\widehat{\mathit{\beta }}}_1^{\text{T}}{\widehat{\mathit{\xi }}}_i-{\widehat{\mathit{\theta }}}_1^{\text{T}}{\mathbf{W}}_i-{\widehat{\mathit{\alpha }}}_1^{\text{T}}(U_i){\mathbf{X}}_i\}}^2$, which can be expressed as ${\sum }_{i=1}^n{\{Y_i-{\widehat{\mathit{\beta }}}_1^{\text{T}}{\widehat{\mathit{\xi }}}_i-{\widehat{\mathit{\theta }}}_1^{\text{T}}{\mathbf{W}}_i-S(Y-\widehat{\mathbf{Z}}{\widehat{\mathbf{\Theta }}}_1)\}}^2$. Following Fan and Huang (2005), we define a profile least-square-based ratio test by

$$T_n=\frac{n}{2}(RS{S}_0-RS{S}_1)/RS{S}_1.$$

Under their set-up, Fan and Huang (2005) showed that statistic T_n is the profile likelihood ratio when the error distribution is normally distributed. In the present situation, because of effect of measurement error on variables, no central χ²-distribution as that of Fan and Huang (2005) is available. However, we can still prove that 2T_n has the asymptotic noncentral χ² distribution under the alternative hypothesis of (3.1), which we summarize in the following theorem.

Theorem 5

Suppose that Assumptions 1-5 in Appendix are satisfied and nb^2r+2 → 0, as n → ∞. Under the alternative hypothesis of (3.1),

$$2T_n-n{\sigma }^{-2}{\mathbf{\Theta }}^{\text{T}}{\mathbf{A}}^{\mathbf{T}}{(\mathbf{A}{\mathbf{\sum }}^{-1}{\mathbf{A}}^{\text{T}})}^{-1}\mathbf{A}\mathbf{\Theta }\stackrel{L}{\to }\sum _{i=1}^l{\omega }_i{\chi }_{i1}^2$$

where ω_i for 1 ≤ i ≤ l are the eigenvalues of ${({\sigma }^2\mathbf{A}{\mathbf{\sum }}^{-1}{\mathbf{A}}^{\text{T}})}^{-1}(\mathbf{A}{\mathbf{\sum }}_1^{-1}{\mathbf{A}}^{\text{T}})$ and ${\chi }_{i1}^2$ is the central χ² distribution with degree of freedom 1. Furthermore, let Σ̂₁ and Σ̂ be the consistent estimators of Σ₁ and Σ, respectively. Then $2_{\varrho n}{T}_n\stackrel{L}{\to }{\chi }_{(l)}^2(\lambda )$, where ${\varrho }_n=l/tr\{{({\sigma }^2\mathbf{A}{\widehat{\mathbf{\sum }}}^{-1}{\mathbf{A}}^{\text{T}})}^{-1}(\mathbf{A}{\widehat{\mathbf{\sum }}}_1^{-1}{\mathbf{A}}^{\mathrm{T}})\},{\chi }_{(l)}^2(\lambda )$ is noncentral χ² distribution with degrees of freedom l, and the noncentral parameter λ = σ⁻²ϱ lim_n→∞ nΘ^TA^T(AΣ⁻¹A^T)⁻¹AΘ with $\varrho =l/tr\{{({\sigma }^2\mathbf{A}{\mathbf{\sum }}^{-1}{\mathbf{A}}^{\text{T}})}^{-1}(\mathbf{A}{\mathbf{\sum }}_1^{-1}{\mathbf{A}}^{\mathrm{T}})\}$.

In a similar way, we may construct the Wald test for hypothesis (3.1) as W_n =Θ̂^TA^T(AΣ̂₁A^T)⁻¹AΘ̂ and demonstrate that W_n and 2ϱ_nT_n have the same asymptotic distribution under the alternative hypothesis. These properties can therefore be used to calculate power of the proposed tests.

Example 1.3 (con.) Generalize (1.6) to a more flexible model:

$$Y_t={\mathit{\beta }}^{\text{T}}E(\mathit{\eta }\mid {\mathbf{V}}_t)+{\mathit{\zeta }}^{\text{T}}\mathit{\eta }+{\gamma }^{\text{T}}{\mathbf{S}}_t+\alpha (U_t){\mathbf{X}}_t+{\epsilon }_t.$$

Write Θ = (β^T, ζ^T, γ^T)^T and $\mathbf{Z}={\{E({\mathit{\eta }}^{\text{T}}\mid \mathbf{V}),{\mathit{\eta }}^{\text{T}},{\mathbf{S}}_t^{\text{T}}\}}^{\text{T}}$. The hypothesis (1.7) is equivalent to

$$\mathbf{A}\mathbf{\Theta }=0\text{VS}\mathbf{A}\mathbf{\Theta }\ne 0,$$ (3.2)

where A = (1_p1, −1_p1, 0), 1_p1 is p₁-variate vector with all entries 1. This is an expression of (3.1). As a consequence, the proposed profile least-square-based ratio test and Wald test can be applied to test this hypothesis.

For hypothesis (3.2), one may also propose a Wald-type statistic: W_n(h) = Θ̂^TA^T(AΣ̂_hA^T)⁻¹AΘ̂, where Σ̂_h = Σ̂⁻¹(σ̂² + β̂^TΣ̂_eβ̂). It can be proved that 2ϱ_nT_n and W_n have the same asymptotic χ² distribution.

3.2 Tests for the nonparametric part and Wild bootstrap version

It is also of interest to check whether the varying-coefficient functions α(u) in model (1.2) are parametric functions. Specifically speaking, we consider the following hypothesis:

$$H_0:{\alpha }_i(U)={\alpha }_i(U,\gamma )\text{VS}{H}_1;{\alpha }_i(U)\ne {\alpha }_i(U,\gamma ),i=1,2\cdots ,q,$$

where γ is an unknown vector, α_i(·, ·) is a known function, i = 1, 2, ···, q.

For simplicity of presentation, we test the homogeneity:

$$H_0:{\alpha }_1(U)={\alpha }_1,\cdots ,{\alpha }_q(U)={\alpha }_q.$$ (3.3)

Let α̃₁, ···, α̃_q and Θ̃ be the profile estimator under H₀. The weighted residual sum of squares under H₀ is $\mathit{RSS}(H_0)={\sum }_{i=1}^n{w}_i{\left(Y_i-{\sum }_{j=1}^q{\stackrel{\sim }{\alpha }}_j{X}_{ij}-{\stackrel{\sim }{\mathbf{\Theta }}}^{\text{T}}{\widehat{\mathbf{Z}}}_i\right)}^2$, where w_i(·) are weighted functions such that ${\sum }_{i=1}^n{w}_i=1$, and w_i ≥ 0. In general, the weight function w has a compact support, designed to reduce the boundary effects on the test statistics. When σ²(Z, X, U) = υ(Z, X, U)σ² for some known function υ(Z, X, U), we may choose w_i = υ⁻¹(Z_i, X_i, U_i). See Fan, Zhang, and Zhang (2001) for a similar argument.

Under the general alternative that all the varying-coefficient functions are allowed to be varying of random variable U, we use the local likelihood method to obtain estimator β̂ and α̂(U). Therefore, the corresponding weighted residual sum of squares is

$$\mathit{RSS}(H_1)=\sum _{i=1}^n{w}_i{\left\{Y_i-\sum _{j=1}^q{\widehat{\alpha }}_j(U_i)X_{ij}-{\widehat{\mathbf{\Theta }}}^{\text{T}}{\widehat{\mathbf{Z}}}_i\right\}}^2.$$

In a similar way as in Section 3.1, we propose a generalized likelihood ratio (GLR) statistic:

$$T_{\text{GLR}}=\{\mathit{RSS}(H_0)-\mathit{RSS}(H_1)\}/\mathit{RSS}(H_1).$$ (3.4)

Under mild assumptions, one can derive the asymptotic distribution of T_GLR. This distribution can be used to gain the empirical level. See Fan, Zhang and Zhang (2001) for a related discussion.

These arguments can be applied to the following partially parametric null hypothesis:

$$H_0:{\alpha }_1(U)={\alpha }_1,\cdots ,{\alpha }_l(U)={\alpha }_r,r<q.$$

The difference is only the definition of RSS(H₀), for which we use the profile likelihood procedure to estimate constant coefficient α_i, i = 1, 2, ···, r and Θ, and use the profile linear procedure to estimate the nonparametric component α_i(·), i = r + 1, ···, q under the null hypothesis.

Although the asymptotic level of T_GLR is available, T_GLR may not perform well when sample sizes are small. For this reason and for practical purposes, we suggest using a bootstrap procedure. To be specific, let

$${\widehat{\epsilon }}_i=Y_i-{\widehat{\mathbf{\Theta }}}^{\text{T}}{\widehat{\mathbf{Z}}}_i-{\widehat{\mathit{\alpha }}}^{\text{T}}(U_i){\mathbf{X}}_i$$

be the residuals based on estimators (2.3) and (2.4) for parametric and nonparametric parts, respectively. We use the Wild bootstrap (Wu, 1986; Härdle and Mammen, 1993) method to calculate the critical values for test T_GLR. Let τ be a random variable with a distribution function F(·) such that Eτ = 0, Eτ² = 1 and E|τ|³ < ∞. We generate the bootstrap residual ${\epsilon }_i^{\ast }={\widehat{\epsilon }}_i{\tau }_i$, where τ_i is independent of ε̂_i. Define bootstrap version $T_{\text{GLR}}^{\ast }$ like T_GLR based on the bootstrap sample ( $Y_i^{\ast },{\mathbf{X}}_i,{\widehat{\mathbf{Z}}}_i,U_i$), where $Y_i^{\ast }=\widehat{\mathbf{\Theta }}{\widehat{\mathbf{Z}}}_i+\widehat{\mathit{\alpha }}(U_i){\mathbf{X}}_i+{\epsilon }_i^{\ast }$ for i = 1, 2 ···, n. On a basis of the distribution of $T_{\text{GLR}}^{\ast }$, we have the (1 − α) quantile $t_{1-\alpha }^{\ast }$ and reject the parametric hypothesis if $T_{\text{GLR}}>t_{1-\alpha }^{\ast }$.

4 Numerical Examples

4.1 Performance of the proposed estimators

In this section, we conducted simulation experiments to illustrate the finite sample performances of the proposed estimators and tests. Our simulated data were generated from the following model:

$$\{\begin{array}{l}Y={\beta }_1\xi +{\beta }_2{W}_1+{\beta }_3{W}_2+{\alpha }_1(U)X_1+{\alpha }_2(U)X_2+\epsilon ,\hfill \\ \xi =\xi (V),\eta =\xi (V)+e.\hfill \end{array}$$ (4.1)

W₁ and W₂ are bivariate normal with marginal mean zero, marginal variance 1 and correlation $1/\sqrt{5}$, while X₁ and X₂ are independent and normal with mean zero and variance 0.8. The unobserved covariate ξ is related to auxiliary variable (η, V) through ξ(V) = 3V − 2 cos(4πV) and η = ξ(V) + e. V is a uniform random variable on [0, 1] and U is a uniform random variable on [0, 3]. The errors ε and e are independent each other, and normal variables with mean 0 and variances ${\sigma }_{\epsilon }^2$ and ${\sigma }_e^2$, respectively. The varying-coefficient functions are

$${\alpha }_1(U)=exp(-U^2)+sin(\pi U),$$ (4.2)

$$\text{or}{\stackrel{\sim }{\alpha }}_1(U,\varrho )=m+\varrho \{{\alpha }_1(U)-m\},$$ (4.3)

$${\alpha }_2(U)=\frac{1}{2}{U}^2-cos(2\pi U),$$ (4.4)

where $m={\int }_0^3{\alpha }_1(t)dt/3$, and ϱ is chosen one from the set {0.0, 0.2, 0.5, 0.7, 1.0}.

The sample size was 100. We generated 500 data sets in each case, applying to each simulated sample the bootstrap test proposed for the parametric part based on 500 bootstrap repetitions. The Gaussian kernel has been used in this example. The optimal bandwidth h were chosen by the leave-one-out cross-validation method described in Section 2.4 and the bandwidth b was selected as b = σ_υn^−1/3, where σ_υ is the sample deviation of V.

We consider four scenarios. In the first three scenarios ${\sigma }_{\epsilon }^2=1$ and ${\sigma }_e^2=2$.

1. β = (0, c − 1, 1)^T for c ∈ {0, 0.1, 0.2, 0.25, 0.5, 0.7, 1.0} and α₁(u) and α₂(u) are given in (4.2) and (4.4);

2. β = (0, −0.8, 1)^T and α₁(u) and α₂(u) are given in (4.3) and (4.4) with ϱ ∈ {0.0, 0.2, 0.5, 0.7, 1.0};

3. β = (0.2, −1, 1)^T and α₁(u) and α₂(u) are the same as in (ii).

4. The setting is the same as that of (iii). But the signal-noise ratio ( $r={\sigma }_{\xi }^2/({\sigma }_{\xi }^2+{\sigma }_e^2)$) varies from 0.3 to 0.8 by 0.1.

The corresponding results are presented in Tables 1–4, in which we display the estimated values and associated standard errors, standard derivations, and coverage probabilities based on the benchmark estimator (i.e., all covariate measured exactly), the proposed estimator and the naive estimator (η_i directly used as the covariates). We summarize our findings as follows.

When β₁ = 0 (scenario (i) and (ii)), all estimates are close to the true values regardless of the non-parametric functions α₁(u) and α₂(u). The differences among the estimated values based on three methods are slight and can be ignored. However, when β₁ = 0.2, the estimates of β₁ based on the naive method have severe biases and the associated coverage probabilities are also substantially smaller than 0.95. These biases were not improved when the sample size was increased (not listed here). But the proposed estimation procedure performs well. On the other hand, the estimates of β₂ and β₃ are similar based on the three methods. From Table 4, we can see that the naive estimator of β₁ has zero coverage probabilities when r = 0.3, while the proposed estimator has fairly reasonable coverage probabilities. With increase of r, it is readily seen that coverage probabilities of the proposed estimator are closer to the nominal level, which indicates the proposed method is promising.

Table 4.

Results of simulation study for scenario (iv).

		β1				β2				β3
r		Est.	SE	SD	COV	Est.	SE	SD	COV	Est.	SE	SD	COV
0.30	B	0.194	0.038	0.046	0.970	−0.987	0.145	0.159	0.980	1.005	0.149	0.156	0.980
	P	0.173	0.040	0.042	0.850	−0.986	0.150	0.152	0.970	1.005	0.150	0.149	0.970
	N	0.073	0.025	0.025	0.000	−0.976	0.159	0.137	0.920	0.996	0.153	0.135	0.920
0.40	B	0.199	0.043	0.044	0.950	−1.002	0.123	0.147	0.970	1.002	0.131	0.147	0.980
	P	0.185	0.045	0.041	0.890	−1.003	0.124	0.144	0.970	0.999	0.130	0.144	0.980
	N	0.096	0.029	0.028	0.060	−1.002	0.127	0.134	0.970	1.002	0.135	0.134	0.960
0.50	B	0.199	0.043	0.042	0.960	−0.981	0.134	0.142	0.960	1.020	0.122	0.143	0.970
	P	0.190	0.044	0.040	0.920	−0.981	0.133	0.139	0.950	1.019	0.127	0.141	0.950
	N	0.116	0.033	0.030	0.200	−0.988	0.137	0.133	0.930	1.020	0.132	0.135	0.930
0.60	B	0.194	0.035	0.040	0.970	−0.993	0.136	0.141	0.950	1.025	0.137	0.138	0.930
	P	0.192	0.038	0.040	0.950	−0.994	0.140	0.140	0.950	1.025	0.138	0.137	0.910
	N	0.131	0.028	0.032	0.450	−0.998	0.152	0.137	0.910	1.020	0.138	0.134	0.940
0.70	B	0.198	0.038	0.039	0.960	−1.018	0.137	0.133	0.970	1.004	0.140	0.131	0.930
	P	0.194	0.040	0.038	0.950	−1.017	0.138	0.132	0.960	1.004	0.142	0.131	0.930
	N	0.152	0.038	0.033	0.660	−1.021	0.142	0.130	0.920	1.004	0.144	0.128	0.920
0.80	B	0.203	0.036	0.038	0.950	−1.001	0.142	0.132	0.930	1.005	0.136	0.132	0.960
	P	0.203	0.038	0.038	0.950	−1.002	0.143	0.131	0.940	1.005	0.135	0.132	0.960
	N	0.172	0.035	0.035	0.870	−1.002	0.147	0.131	0.920	1.000	0.136	0.131	0.930

4.2 Performance of the proposed tests

We now explore the numerical performance of the proposed tests. Firstly, we want to test hypothesis of the parametric component of form:

$$H_0:A\mathit{\beta }=0\text{VS}{H}_1:A\mathit{\beta }=c$$ (4.5)

where A = (1, 1, 1)^T, c is a value from the set {0, 0.1, 0.2, …, 0.7, 1}, β = (0.2, c − 1.2, 1)^T, α₁(·) and α₁(·) are the same those as scenarios (i). The same models and error distribution as in section 4.1 are used.

The power to detect H₁ were calculated by using the critical values from chi-squared approximation and Wild bootstrap approximation. To compare test performances, the powers of the tests based on the benchmark estimator, the proposed estimator and the naive estimator are presented. In implementing the Wild bootstrap method, we generated 500 bootstrap samples from the model

$$\{\begin{array}{l}{Y}_i^{\ast }={\widehat{\beta }}_1{\widehat{\xi }}_i+{\widehat{\beta }}_2{W}_{1i}+{\widehat{\beta }}_3{W}_{2i}+{\widehat{\alpha }}_1(U_i)Z_{1i}+{\widehat{\alpha }}_2(U_i)Z_{2i}+{\epsilon }_i^{\ast },\hfill \\ {\widehat{\xi }}_i=\widehat{\xi }(V_i),\hfill \end{array}$$

here, ${\epsilon }_i^{\ast }$ is a wild bootstrap residual; i.e., ${\epsilon }_i^{\ast }={\tau }_i{\widehat{\epsilon }}_i$, with ε̂_i = Y_i − {β̂₁ξ̂_i + β̂₂W_1i + β̂₃W_2i + α̂₁(U_i)Z_1i + α̂₂(U_i)Z_2i}, and ${\tau }_i=-(\sqrt{5}-1)/2$ with probability $(\sqrt{5}+1)/(2\sqrt{5})$ and ${\tau }_i=(\sqrt{5}+1)/2$ with $1-(\sqrt{5}+1)/(2\sqrt{5})$. Using this bootstrap sample ( $Y_i^{\ast },{\widehat{\xi }}_i,{\mathbf{W}}_i,{\mathbf{Z}}_i,U_i$), we can calculate the $T_n^{\ast }$ and $W_n^{\ast }$, and get the 95% percentiles as the critical values for the proposed tests at the significance level 0.05.

The power of T_n associated to scenario (iii) is presented in Table 5 for β₁ = 0.2. Note that the power is actually the empirical level when c = 0. All empirical levels close nominal level 0.05 and the empirical level based on the Wild bootstrap procedure are consistently smaller than those based on the χ² approximation and are closer to the nominal level. These facts apply for β₁ = 0 (not listed here). As c increases to 0.7, the powers of two tests based on χ² approximation is greater than 0.92. Similar conclusions can be drawn for the Wald test, whose simulation results are also given in Table 5.

Table 5.

Empirical power of profile least square ratio test T_n and the Wald test W_n at level 0.05 for hypothesis (4.5). Data were generated from models (4.1) with β = (0.2, c − 1.2, 1)^T and c ∈ {0, 0.1, 0.2, 0.25, 0.5, 0.7, 1} and α₁(u) and α₂(u) given by (4.2) and (4.4), respectively. The methods used are “Asm” for the asymptotic version, and “Boot” for the bootstrap version.

		Tn			Wald
c		B	P	N	B	P	N
0	Aym	0.060	0.070	0.080	0.050	0.050	0.080
	Boot	0.050	0.060	0.060	0.060	0.060	0.060
0.10	Aym	0.150	0.140	0.150	0.130	0.130	0.150
	Boot	0.130	0.100	0.080	0.130	0.120	0.080
0.20	Aym	0.190	0.220	0.120	0.150	0.150	0.120
	Boot	0.170	0.160	0.080	0.190	0.180	0.080
0.25	Aym	0.350	0.340	0.240	0.320	0.310	0.240
	Boot	0.290	0.280	0.180	0.310	0.300	0.180
0.50	Aym	0.740	0.710	0.530	0.670	0.660	0.530
	Boot	0.700	0.630	0.500	0.720	0.630	0.500
0.70	Aym	0.940	0.940	0.870	0.930	0.920	0.870
	Boot	0.920	0.890	0.800	0.930	0.890	0.800
1.00	Aym	1.000	1.000	1.000	0.990	0.990	1.000
	Boot	0.990	0.990	0.960	0.990	0.990	0.960

We further study the numerical performance of the test by checking the nonparametric component. We consider the following hypothesis:

$$H_0:{\alpha }_1(u)=m\text{VS}{\alpha }_1(u)={\alpha }_1(u,\varrho )\text{given}\text{by}(4.3)$$ (4.6)

The simulation results obtained by using the Wild bootstrap approximation method to choose critical value are shown in Table 6. When ϱ = 0, the results are the empirical levels, which are close to the nominal level. The power is greater than 0.99 when ϱ = 0.5. Table 6 also indicates that the power is a monotone increasing function of ϱ.

Table 6.

Empirical power of level 0.05 for hypothesis (4.6) using the Wild bootstrap procedure. Data were generated from (4.1) and (4.3) with β = (0.2, −1, 1)^T and ϱ ∈ {0, 0.5, 0.10, 0.15, 0.5, 0.7}.

ϱ	B	P	N
0	0.060	0.050	0.080
0.05	0.110	0.140	0.160
0.10	0.240	0.260	0.250
0.15	0.410	0.360	0.360
0.20	0.520	0.510	0.500
0.50	0.990	0.990	1.000
0.70	1.000	1.000	1.000

4.3 Real data example

To illustrate the proposed estimation method, we consider a dataset from Duchenne Muscular Dystrophy (DMD) study. See Andrews and Herzberg (1985) for a detailed discussion on the dataset. The dataset contains 209 observations corresponding to blood samples on 192 patients (17 patients have two samples) collected from a project to develop a screening program for female relatives of boys with DMD. The program’s goal was to inform a woman of her chances of being a carrier based on serum markers as well as her family pedigree. Another question of interest is whether age should be taken into account in the analysis. Enzyme levels were measured in known carriers (75 samples) and in a group of non-carriers (134 samples). The serum marker creatine kinase ( ck) is inexpensive to obtain, while the marker lactate dehydrogenase ( ld) is very expensive to obtain. It is of interest to predict the value ld by using the level of ck, carrier status and age of patient.

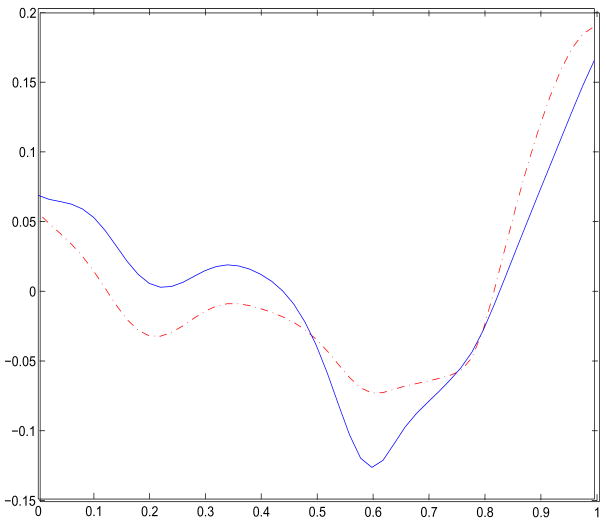
We consider the following model: Y = β₀ + β₁Z₁ + β₂Z₂ + g(U), where Z₁ = ck is measured with errors, and Z₂ = carrierstatus is exactly measured, U is age and Y denotes the observed level of lactate dehydrogenase. We justify the measurement error of Z₁ by regressing Z₁ on U. The estimates and associated standard errors based on the naive and proposed methods are as follows: β̂_0,naive = 4.6057(0.113), β̂_1,naive = 0.1509(0.027), β̂_2,naive = 0.2269(0.055); β̂_0,n = 4.4296(0.329), β̂_1,n = 0.1775(0.042), and β̂_2,n = 0.3702(0.050). The estimated curves of the nonparametric function g(u) are provided in Figure 1. Accounting for measurement errors, the estimate of β₁ increases about 17.2%, and the associated standard error also increases 55%. The estimate of β₂ also increases when measurement errors are taken into account. The patterns of the nonparametric curve are similar, and shows slight difference.

Figure 1.

Estimated curves of the nonparametric function for the DMD study. The solid, dotted lines were obtained using the naive and proposed method, respectively.

5 Discussion

We developed estimation and inference procedures for the SVCPLM when parts of the parametric components are unobserved. The procedures are derived by incorporating ancillary information to calibrate the mismeasured variables, and by applying the profile least-square-based principle.

In some case we may not have an auxiliary variable η, but we can observe two or more independent replicates of V. For instance, when two measurements V₁ and V₂, which satisfy that V₁ = ξ + u₁ and V₂ = ξ + u₂, and E(u₁|V₂) = 0 and E(u₂|V₁) = 0, are available, we can estimate ξ by

$$\widehat{\mathit{\xi }}(v)=\frac{{\sum }_{i=1}^n\{{\mathbf{V}}_{i1}{K}_h({\mathbf{V}}_{i2}-v)+{\mathbf{V}}_{i1}{K}_h({\mathbf{V}}_{i1}-v)\}}{{\sum }_{i=1}^n\{K_h({\mathbf{V}}_{i2}-v)+K_h({\mathbf{V}}_{i1}-v)\}}$$

because E(V₁|V₂ = υ) = E(V₂|V₁ = υ) = E(ξ|V = υ). The proposed procedure applies to this situation as well, and similar results to those presented in this paper can be obtained for the resulting estimator.

It is of interest to extend the proposed methodology to a more general semiparametric model:

$$E(Y\mid \mathbf{Z},\mathbf{X},U)=G\{{\mathbf{\Theta }}^{\text{T}}\mathbf{Z}+{\mathit{\alpha }}^{\text{T}}(U)\mathbf{X}\},$$

where G(·) is a link function. The study of this model with mismeasured components of Z needs further investigation and is beyond the scope of this paper.

Table 1.

Results of simulation study for scenario (i)

		β1				β2				β3
ϱ		Est.	SE	SD	COV	Est.	SE	SD	COV	Est.	SE	SD	COV
0	B	−0.000	0.030	0.027	0.912	−0.990	0.133	0.125	0.938	1.000	0.138	0.126	0.924
	P	−0.001	0.031	0.028	0.918	−0.990	0.133	0.125	0.936	1.000	0.139	0.126	0.930
	N	−0.001	0.026	0.024	0.904	−0.990	0.133	0.125	0.940	0.999	0.138	0.126	0.926
0.1	B	0.002	0.028	0.027	0.920	−0.890	0.139	0.126	0.910	1.003	0.129	0.126	0.936
	P	0.003	0.030	0.028	0.938	−0.890	0.139	0.126	0.912	1.003	0.129	0.126	0.938
	N	0.003	0.025	0.024	0.938	−0.890	0.140	0.126	0.912	1.004	0.129	0.126	0.938
0.2	B	0.000	0.029	0.027	0.936	−0.802	0.144	0.126	0.894	0.991	0.138	0.126	0.932
	P	−0.000	0.030	0.028	0.934	−0.802	0.145	0.126	0.898	0.991	0.138	0.126	0.940
	N	−0.001	0.027	0.024	0.912	−0.801	0.145	0.126	0.896	0.992	0.138	0.125	0.934
0.25	B	−0.001	0.029	0.027	0.930	−0.749	0.128	0.127	0.936	0.990	0.138	0.127	0.940
	P	−0.000	0.031	0.028	0.928	−0.748	0.129	0.127	0.938	0.990	0.139	0.127	0.938
	N	−0.000	0.024	0.024	0.948	−0.749	0.128	0.126	0.938	0.990	0.138	0.126	0.940
0.5	B	−0.002	0.029	0.027	0.926	−0.513	0.143	0.126	0.918	1.000	0.131	0.126	0.936
	P	−0.002	0.031	0.028	0.928	−0.513	0.143	0.126	0.920	1.001	0.131	0.126	0.936
	N	−0.001	0.026	0.024	0.926	−0.513	0.143	0.126	0.918	1.001	0.131	0.126	0.936
0.7	B	0.000	0.029	0.027	0.936	−0.299	0.140	0.127	0.916	0.996	0.138	0.127	0.924
	P	0.001	0.029	0.028	0.930	−0.298	0.140	0.127	0.920	0.997	0.138	0.127	0.926
	N	0.001	0.025	0.024	0.934	−0.299	0.140	0.126	0.914	0.996	0.138	0.126	0.926
1	B	0.001	0.030	0.027	0.934	0.002	0.137	0.127	0.942	1.008	0.144	0.127	0.908
	P	0.001	0.031	0.028	0.934	0.002	0.137	0.127	0.938	1.008	0.145	0.127	0.906
	N	0.001	0.026	0.024	0.928	0.002	0.138	0.127	0.938	1.007	0.144	0.127	0.908

Note: “Est” is the simulation mean; “SE” is the mean of the estimated standard error; “SE” is the mean of the estimated standard deviation; and “COV” is the coverage probability of a nominal 95% confidence interval. The methods used are “B” for the benchmark method, “P” for the proposed method, and “N” for the naive method.

Table 2.

Results of simulation study for scenario (ii)

		β1				β2				β3
ϱ		Est.	SE	SD	COV	Est.	SE	SD	COV	Est.	SE	SD	COV
0	B	0.000	0.034	0.033	0.920	−0.795	0.154	0.153	0.948	0.995	0.160	0.154	0.946
	P	0.001	0.036	0.035	0.922	−0.795	0.154	0.154	0.950	0.995	0.159	0.154	0.950
	N	0.000	0.030	0.029	0.928	−0.794	0.154	0.153	0.948	0.994	0.160	0.154	0.950
0.05	B	0.002	0.028	0.027	0.920	−0.790	0.139	0.125	0.910	1.003	0.129	0.126	0.936
	P	0.003	0.030	0.028	0.938	−0.790	0.139	0.125	0.908	1.004	0.129	0.126	0.938
	N	0.003	0.025	0.024	0.938	−0.790	0.140	0.125	0.908	1.004	0.129	0.126	0.938
0.1	B	0.000	0.029	0.027	0.936	−0.802	0.144	0.126	0.894	0.991	0.138	0.125	0.928
	P	−0.000	0.030	0.028	0.936	−0.802	0.144	0.126	0.898	0.991	0.138	0.126	0.938
	N	−0.001	0.027	0.024	0.916	−0.801	0.145	0.125	0.896	0.992	0.138	0.125	0.932
0.15	B	−0.001	0.029	0.027	0.932	−0.799	0.128	0.126	0.936	0.990	0.138	0.126	0.938
	P	−0.000	0.031	0.028	0.930	−0.798	0.128	0.126	0.938	0.990	0.138	0.126	0.938
	N	−0.000	0.024	0.024	0.950	−0.799	0.128	0.126	0.938	0.990	0.138	0.126	0.936
0.2	B	−0.002	0.029	0.027	0.926	−0.813	0.143	0.126	0.918	1.001	0.131	0.126	0.934
	P	−0.002	0.031	0.028	0.932	−0.813	0.143	0.126	0.918	1.001	0.131	0.126	0.934
	N	−0.001	0.026	0.024	0.924	−0.813	0.143	0.126	0.916	1.001	0.131	0.126	0.934
0.5	B	0.000	0.029	0.027	0.936	−0.799	0.140	0.126	0.916	0.996	0.138	0.126	0.924
	P	0.001	0.029	0.028	0.930	−0.798	0.140	0.126	0.922	0.997	0.138	0.127	0.926
	N	0.001	0.025	0.024	0.934	−0.799	0.140	0.126	0.914	0.996	0.138	0.126	0.926
0.7	B	0.001	0.030	0.027	0.932	−0.798	0.137	0.127	0.942	1.008	0.144	0.127	0.906
	P	0.001	0.031	0.028	0.934	−0.798	0.137	0.127	0.938	1.008	0.145	0.127	0.906
	N	0.001	0.026	0.024	0.930	−0.798	0.138	0.126	0.938	1.007	0.144	0.126	0.908

Table 3.

Results of simulation study for scenario (iii)

		β1				β2				β3
ϱ		Est.	SE	SD	COV	Est.	SE	SD	COV	Est.	SE	SD	COV
0	B	0.200	0.034	0.035	0.936	−0.995	0.154	0.162	0.956	0.995	0.160	0.163	0.964
	P	0.195	0.038	0.038	0.920	−0.995	0.158	0.167	0.958	0.994	0.163	0.168	0.958
	N	0.156	0.031	0.030	0.684	−0.995	0.158	0.160	0.952	0.995	0.165	0.160	0.946
0.05	B	0.202	0.028	0.029	0.948	−0.990	0.139	0.138	0.938	1.003	0.129	0.138	0.950
	P	0.197	0.032	0.032	0.944	−0.994	0.144	0.144	0.938	1.004	0.139	0.144	0.948
	N	0.159	0.026	0.025	0.602	−0.991	0.149	0.133	0.910	1.004	0.140	0.133	0.926
0.1	B	0.200	0.029	0.029	0.950	−1.002	0.144	0.138	0.924	0.991	0.138	0.138	0.956
	P	0.194	0.032	0.033	0.948	−1.005	0.151	0.144	0.922	0.991	0.147	0.144	0.954
	N	0.155	0.028	0.025	0.560	−1.004	0.153	0.133	0.904	0.991	0.148	0.133	0.912
0.15	B	0.199	0.029	0.029	0.950	−0.999	0.128	0.138	0.960	0.990	0.138	0.138	0.960
	P	0.194	0.033	0.032	0.938	−0.998	0.135	0.144	0.958	0.986	0.144	0.144	0.956
	N	0.155	0.025	0.025	0.542	−0.997	0.138	0.133	0.938	0.989	0.145	0.133	0.948
0.2	B	0.198	0.029	0.029	0.948	−1.013	0.143	0.138	0.942	1.001	0.131	0.138	0.958
	P	0.193	0.033	0.032	0.936	−1.012	0.148	0.144	0.938	0.997	0.136	0.144	0.954
	N	0.155	0.027	0.025	0.536	−1.016	0.154	0.133	0.920	0.998	0.141	0.133	0.932
0.5	B	0.200	0.029	0.029	0.956	−0.999	0.140	0.138	0.954	0.996	0.138	0.138	0.944
	P	0.195	0.032	0.032	0.952	−1.000	0.147	0.144	0.954	0.993	0.144	0.144	0.956
	N	0.157	0.026	0.025	0.582	−1.000	0.153	0.133	0.898	0.996	0.145	0.133	0.920
0.7	B	0.201	0.030	0.029	0.952	−0.998	0.137	0.139	0.958	1.008	0.144	0.139	0.938
	P	0.196	0.033	0.033	0.946	−0.997	0.143	0.145	0.962	1.008	0.146	0.145	0.956
	N	0.157	0.028	0.025	0.594	−1.000	0.146	0.134	0.932	1.006	0.151	0.134	0.912

Appendix

In this Appendix, we list assumptions and outline proofs of the main results. The following technical assumptions are imposed.

A.1 Assumptions

1. The random variable U has a bounded support . Its density function f_u(·) is Lipschitz continuous and bounded away from 0 on its support. The density function of random variable V, f_υ(v), is continuously differentiable and bounded away 0 and infinite on its finite support . {α_i(u), i = 1, 2, ···, q} have continuous second derivative.

2. The q × q matrix E(ZZ^T|U) is non-singular for each U ∈ 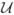. All elements of the matrixes E(ZZ^T|U), E(ZZ^T|U)⁻¹ and E(ZX^T|U) are Lipschitz continuous.

3. The kernel functions K(·) and L(·) are density functions with compact support [−1, 1].

4. There is an s > 2 such that E||Z||^2s < ∞ and E||X||^2s < ∞ and for some δ < 2 − s⁻¹ such that n^2δ−1h → ∞, n^2δ−1b_k → ∞ and $nh{b}_k^{(2r+2)}\to 0$, k = 1, 2, ···, p₁ where b_k is the bandwidth parameter in polynomial estimator ξ̂_k(·) of ξ_k(·).

   5. nh⁸ → 0 and nh²/(log n)² → ∞.

A.2 Preliminary Lemmas

Write $c_{n1}={\left(\frac{logh}{nh}\right)}^{1/2}+h^2,c_{n2}={\left(\frac{logb}{n{b}^d}\right)}^{1/2}+b^{r+1},c_n=c_{n1}+c_{n2}$.

Lemma A.1

Suppose that (Z_i, X_i, U_i), i = 1, 2, ···, n are i.i.d random vector. E|g(X, Z, U)| < ∞ and E[g(·, ·, u)|U = u] has continuous second derivative on u. Further assume that E(|g(X, Z, U)|^s|Z = z, X = x) < ∞. Let K be a bounded positive function with a bounded support, satisfying Lipschitz condition. Given that n^2δ−1h → ∞ for some δ < 1 − s⁻¹, then we have

$$\underset{u\in \mathcal{U}}{sup}\mid \frac{1}{n}\sum _{i=1}^n{K}_h(U_i-u){\left(\frac{U_i-u}{h}\right)}^{k}g(X_i,{\mathbf{Z}}_i,U_i)-f(u)E\{g(\mathbf{X},\mathbf{Z},u)\mid U=u\}{\mu }_k\mid =O(c_{n1})a.s.$$

Furthermore, Assume that E[ε_i|Z_i, X_i, U_i] = 0, E[|ε_i|^s|Z_i, X_i, U_i)] < ∞, then

$$\underset{u\in \mathcal{U}}{sup}\mid \frac{1}{n}\sum _{i=1}^n{K}_h(U_i-u)g({\mathbf{X}}_i,Z_i,U_i){\epsilon }_i\mid =O(c_{n1})a.s.$$

Proof

The first result follows an argument similar to that of Lemma A.2 of Fan and Huang (2005). The second result follows the first result and an argument similar to Xia and Li (1999).

Lemma A.2

Suppose that E[g(Z, X, u)|U = u] has continuous second derivative on u and E|g(X, Z, U)|^s < ∞. Under Assumptions 1–5, we have

$$\underset{u\in \mathcal{U}}{sup}\mid \frac{1}{n}\sum _{i=1}^n{K}_h(U_i-u){\left(\frac{U_i-u}{h}\right)}^{k}g({\mathbf{X}}_i,{\mathbf{Z}}_i,U_i){\widehat{\mathit{\xi }}}_i^{\text{T}}-f(u)E\{g(\mathbf{X},\mathbf{Z},u){\mathit{\xi }}^{\text{T}}\mid U=u\}{\mu }_k\mid =O(c_n)a.s.$$

and

$$\underset{u\in \mathcal{U}}{sup}\mid \frac{1}{n}\sum _{i=1}^n{K}_h(U_i-u)g({\mathbf{X}}_i,{\mathbf{Z}}_i,U_i)h({\widehat{\mathit{\xi }}}_i){\epsilon }_i\mid =O(c_n),$$

where h(·) is a twice continuous differentiable function.

Proof

Note that $\frac{1}{n}{\sum }_{i=1}^n{K}_h(U_i-u){\left(\frac{U_i-u}{h}\right)}^{k}g({\mathbf{X}}_i,{\mathbf{Z}}_i,U_i){\widehat{\mathit{\xi }}}_i^{\text{T}}$ can be decomposed as

$$\begin{array}{l}\frac{1}{n}\sum _{i=1}^n{K}_h(U_i-u){\left(\frac{U_i-u}{h}\right)}^{k}g({\mathbf{X}}_i,{\mathbf{Z}}_i,U_i){\mathit{\xi }}_i^{\text{T}}\\ +\frac{1}{n}\sum _{i=1}^n{K}_h(U_i-u){\left(\frac{U_i-u}{h}\right)}^{k}g({\mathbf{X}}_i,{\mathbf{Z}}_i,U_i){({\widehat{\mathit{\xi }}}_i-{\mathit{\xi }}_i)}^{\text{T}}.\end{array}$$

By Lemma A.1, the first term equals f_u(u)E{g(X, Z, u)ξ|U = u}μ_k + O(c_n1) uniformly on u ∈ 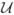in probability. Recalling the asymptotic expression given in (2.1) and using Lemma A.1, one can show that the second term is O(c_n2). This completes the proof of Lemma 2.

Lemma A.3

g(·, ·, u) has continuous second derivative on u and E|g(X, Z, U)| < ∞. Under Assumptions 1–5, $\mid \frac{1}{n}{\sum }_{i=1}^n({\widehat{\mathbf{Z}}}_i-{\mathbf{Z}}_i)g({\mathbf{X}}_i,{\mathbf{Z}}_i,U_i)\mid$ and $\mid \frac{1}{n}{\sum }_{i=1}^n({\widehat{\mathbf{Z}}}_i-{\mathbf{Z}}_i){\widehat{\mathbf{Z}}}_{i}g({\mathbf{X}}_i,{\mathbf{Z}}_i,U_i)\mid$ are of order O(c_n) a.s.

Proof

The proof follows from (2.1) and arguments similar to Lemma A.2.

Lemma A.4

Under Assumptions 1–5, we have

$$\begin{array}{l}{({\stackrel{\sim }{\mathbf{Z}}}^{\text{T}}\stackrel{\sim }{\mathbf{Z}})}^{-1}{\stackrel{\sim }{\mathbf{Z}}}^{\text{T}}(\mathbf{I}-\mathbf{S})\mathbf{Z}={\mathbf{\sum }}^{-1}(\frac{{\zeta }_1{S}_u^{-1}{c}_p{b}^{r+1}}{n(r+1)!}\sum _{i=1}^n\psi ({\mathbf{Z}}_i,{\mathbf{X}}_i,U_i)[{\{{\mathit{\xi }}^{(r+1)}({\mathbf{V}}_i)\}}^{\text{T}},\mathbf{0}]\\ +\frac{1}{n^2}\sum _{i=1}^n\sum _{j=1}^n\frac{1}{f_v({\mathbf{V}}_i)}\psi ({\mathbf{Z}}_i,{\mathbf{X}}_i,U_i)L_b({\mathbf{V}}_j-{\mathbf{V}}_i)({\mathbf{e}}_j^{\text{T}},\mathbf{0}))\{1+o(1)\}\end{array}$$

in probability.

Proof

We first prove that

$$\frac{1}{n}{\stackrel{\sim }{\mathbf{Z}}}^{\text{T}}\stackrel{\sim }{\mathbf{Z}}\to \mathbf{\sum }.$$ (A.1)

A direct calculation yields

$$D_u^{\text{T}}{W}_u{D}_u=n{f}_u(U)\mathrm{\Gamma }(U)\otimes \left(\begin{array}{cc}1& {\mu }_1\\ {\mu }_1& {\mu }_2\end{array}\right)\{1+O_P(c_{n1})\}.$$ (A.2)

On the other hand, Lemma A.3 implies

$$D_u^{\text{T}}{W}_u\widehat{\mathbf{Z}}=n{f}_u(U)\mathrm{\Phi }(U)\otimes {(1,{\mu }_1)}^{\text{T}}\{1+O_P(c_n)\}.$$ (A.3)

A combination of (A.2) and (A.3) implies

$$({\mathbf{X}}^{\text{T}},0){(D_u^{\text{T}}{W}_u{D}_u)}^{-1}{D}_u^{\text{T}}{W}_u\widehat{\mathbf{Z}}={\mathbf{X}}^{\text{T}}{\mathrm{\Gamma }}^{-1}(U)\mathrm{\Phi }(U)\{1+O_P(c_n)\},$$ (A.4)

and then

$${\stackrel{\sim }{\mathbf{Z}}}_i={\widehat{\mathbf{Z}}}_i-{\mathrm{\Phi }}^{\text{T}}(U_i){\mathrm{\Gamma }}^{-1}(U_i){\mathbf{X}}_i\{1+O_p(c_n)\},i=1,2,\cdots ,n.$$ (A.5)

It follows from these arguments that $n^{-1}{\stackrel{\sim }{\mathbf{Z}}}^{\text{T}}\stackrel{\sim }{\mathbf{Z}}=\frac{1}{n}{\sum }_{i=1}^n{\{\psi ({\mathbf{Z}}_i,{\mathbf{X}}_i,U_i)\}}^{\otimes 2}\{1+O_P(c_n)\}$, and (A.1) follows.

Note that ${\stackrel{\sim }{\mathbf{Z}}}^{\text{T}}(\mathbf{I}-\mathbf{S})(\mathbf{Z}-\widehat{\mathbf{Z}})={\mathbf{Z}}^{\text{T}}{(\mathbf{I}-\mathbf{S})}^{\text{T}}(\mathbf{I}-\mathbf{S})(\mathbf{Z}-\widehat{\mathbf{Z}})-{(\mathbf{Z}-\widehat{\mathbf{Z}})}^{\text{T}}{(\mathbf{I}-\mathbf{S})}^{\text{T}}(\mathbf{I}-\mathbf{S})(\mathbf{Z}-\widehat{\mathbf{Z}})\stackrel{\text{def}}{=}{J}_1-J_2$. The second term, J₂, is $O_P(c_n^2)$ by Lemma A.3. Write Z̃_* = (I − S)Z. We have $J_1={\stackrel{\sim }{\mathbf{Z}}}_{\ast }^{\text{T}}(\mathbf{Z}-\widehat{\mathbf{Z}})-{\stackrel{\sim }{\mathbf{Z}}}_{\ast }^{\text{T}}\mathbf{S}(\mathbf{Z}-\widehat{\mathbf{Z}})$. It follows from (2.1) that

$$\begin{array}{l}{D}_u{W}_u(\mathbf{Z}-\widehat{\mathbf{Z}})=\frac{{\zeta }_1{S}_u^{-1}{c}_p{b}^{r+1}}{(r+1)!}\sum _{i=1}^n\left(\begin{array}{cc}{K}_h(U_i-U){\mathbf{X}}_i{\mathit{\xi }}^{(r+1)}({\mathbf{V}}_i)& \mathbf{0}\\ K_h(U_i-U)h^{-1}(U_i-U){\mathbf{X}}_i{\mathit{\xi }}^{(r+1)}({\mathbf{V}}_i)& \mathbf{0}\end{array}\right)\\ +\frac{1}{n^2}\sum _{i=1}^n\sum _{j=1}^n{f}_v^{-1}(V_i)\left(\begin{array}{cc}{K}_h(U_i-U)L_b(V_j-V_i){\mathbf{X}}_i{\mathbf{e}}_j^{\text{T}}& \mathbf{0}\\ h^{-1}(U_i-U)K_h(U_i-U)L_b(V_j-V_i){\mathbf{X}}_i{\mathbf{e}}_j^{\text{T}}& \mathbf{0}\end{array}\right)\\ +o(b^{r+1}+log{b}^{-1}/\sqrt{nb}).\end{array}$$

By an argument similar to that of (A.5), we derive

$$\begin{array}{l}{\stackrel{\sim }{\mathbf{Z}}}_{\ast }^{\text{T}}\mathbf{S}(\mathbf{Z}-\widehat{\mathbf{Z}})=\frac{1}{n}\sum _{l=1}^n\stackrel{\sim }{\rho }({\mathbf{Z}}_l,{\mathbf{X}}_l,U_l)\sum _{i=1}^n\{\frac{{\zeta }_1{S}_u^{-1}{c}_p{b}^{r+1}}{(r+1)!}\left(\begin{array}{cc}{K}_h(U_i-U_l){\mathbf{X}}_i{\mathit{\xi }}^{(r+1)}({\mathbf{V}}_i)& \mathbf{0}\\ K_h(U_i-U_l)h^{-1}(U_i-U_l){\mathbf{X}}_i{\mathit{\xi }}^{(r+1)}({\mathbf{V}}_i)& \mathbf{0}\end{array}\right)\\ +\frac{1}{n}\sum _{j=1}^n{f}_v^{-1}(V_i)\left(\begin{array}{cc}{K}_h(U_i-U_l)L_b(V_j-V_i){\mathbf{X}}_i{\mathbf{e}}_j^{\text{T}}& \mathbf{0}\\ h^{-1}(U_i-U_l)K_h(U_i-U_l)L_b(V_j-V_i){\mathbf{X}}_i{\mathbf{e}}_j^{\text{T}}& \mathbf{0}\end{array}\right)\}\{1+o_P(1)\},\end{array}$$

where ρ̃(Z_l, X_l, U_l) can be expressed as

$$\begin{array}{l}\psi ({\mathbf{Z}}_l,{\mathbf{X}}_l,U_l)\{1+O_P(c_n)\}]({\mathbf{X}}_l^{\text{T}},\mathbf{0})\\ \times {\left\{f_u(U_l)\mathrm{\Gamma }(U_l)\otimes \left(\begin{array}{cc}1& {\mu }_1\\ {\mu }_1& {\mu }_2\end{array}\right)\{1+O_p(c_n)\}\right\}}^{-1}\\ =\frac{1}{f_u(U_l)}\{\psi {({\mathbf{Z}}_l,{\mathbf{X}}_l,U_l)}^{\text{T}}{\mathbf{X}}_l^{\text{T}},0\}\left\{{\mathrm{\Gamma }}^{-1}(U_1)\otimes {\left(\begin{array}{cc}1& {\mu }_1\\ {\mu }_1& {\mu }_2\end{array}\right)}^{-1}\right\}\{1+O_P(c_n)\}\\ =\frac{1}{f_u(U_l)({\mu }_2-{\mu }_1^2)}\{\psi ({\mathbf{Z}}_l,{\mathbf{X}}_l,U_l){\mathbf{X}}_l^{\text{T}}\}{\mathrm{\Gamma }}^{-1}(U_1)\otimes ({\mu }_2,-{\mu }_1)\{1+O_P(c_n)\}.\end{array}$$

Denote by ρ(Z_l, X_l, U_l) the main term of the right hand side of the above formula. Note that E{ρ (Z_l, X_l, U_l)|U_l} = 0. By Lemma 3 of Chen, Choi and Zhou (2005) we have

$$\frac{1}{n^3}\sum _{i=1}^n\sum _{j=1}^n\sum _{l=1}^n{K}_h(U_i-U_l)L_b(V_j-V_i)\rho ({\mathbf{Z}}_l,{\mathbf{X}}_l,U_l)\frac{{\mathbf{X}}_i{\mathbf{e}}_j^{\text{T}}}{f_v(V_i)}=O_P(c_n{n}^{-1/2}).$$ (A.6)

Furthermore, we can show, in a similar way as that for (A.6), that

$$\frac{{\zeta }_1{S}_u^{-1}{c}_p{b}^{2(r+1)}}{n^2(r+1)!}\sum _{i=1}^n\sum _{l=1}^n{K}_h(U_i-U_l)\rho ({\mathbf{Z}}_l,{\mathbf{X}}_l,U_l){\mathbf{X}}_i{\{{\mathit{\xi }}^{(r+1)}(V_i)\}}^{\text{T}}=O_P(c_n^2).$$

These arguments imply that

$$n^{-1}{\stackrel{\sim }{\mathbf{Z}}}_{\ast }^{\text{T}}\mathbf{S}(\mathbf{Z}-\widehat{\mathbf{Z}})=O_P(c_n^2).$$ (A.7)

We now deal with the term ${\stackrel{\sim }{\mathbf{Z}}}_{\ast }^{\text{T}}(\mathbf{Z}-\widehat{\mathbf{Z}})$. Note that ${\stackrel{\sim }{\mathbf{Z}}}_{\ast }^{\text{T}}(\mathbf{Z}-\widehat{\mathbf{Z}})$ equals ${\sum }_{i=1}^n\psi ({\mathbf{Z}}_i,{\mathbf{X}}_i,U_i)\{{({\mathit{\xi }}_i-{\widehat{\mathit{\xi }}}_i)}^{\text{T}},\mathbf{0}\}$, which can be further decomposed as

$$\begin{array}{l}\frac{{\zeta }_1{S}_u^{-1}{c}_p{b}^{r+1}}{(r+1)!}\sum _{i=1}^n\psi ({\mathbf{Z}}_i,{\mathbf{X}}_i,U_i)[{\{{\mathit{\xi }}^{(r+1)}(V_i)\}}^{\text{T}},\mathbf{0}]\\ +\frac{1}{n}\sum _{i=1}^n\sum _{j=1}^n\frac{1}{f_v(V_i)}\psi ({\mathbf{Z}}_i,{\mathbf{X}}_i,U_i)L_b(V_j-V_i)({\mathbf{e}}_j^{\text{T}},\mathbf{0})+o_P(c_n).\end{array}$$

This completes the proof of Lemma A.4.

Lemma A.5

Under Assumptions 1–5, we have Z̃^T(I −S)(I −S)^TZ̃/n → Σ in probability and Σ̂ = n(Z̃^TZ̃)⁻¹Z̃^T(I −S)(I −S)Z̃(Z̃^TZ̃^T)⁻¹ → Σ.

Proof

The proof of the first result can be finished by arguments similar to those of Lemmas A.2–A.4, while the second one can be proved by arguments similar to Lemma 7.3 of Fan and Huang (2005).

Lemma A.6

Under Assumptions 1–5, we have ${\stackrel{\sim }{\mathbf{Z}}}^{\text{T}}(\mathbf{I}-\mathbf{S})\mathbf{M}/n=O_p(c_n^2)$.

Proof

The proof follows (A.5) and an argument similar to that of Lemma 7.4 of Fan and Huang (2005).

Lemma A.7

g (·) and h(·) are two continuous function vectors. Under Assumptions 1–5, we have $\frac{1}{\sqrt{n}}{\sum }_{i=1}^n({\widehat{\mathbf{Z}}}_i-{\mathbf{Z}}_i)g({\mathbf{Z}}_i){\epsilon }_i\to 0$ and $\frac{1}{\sqrt{n}}{\sum }_{i=1}^n({\widehat{\mathbf{Z}}}_i-{\mathbf{Z}}_i){\mathbf{X}}_i^{\text{T}}h(U_i){\epsilon }_i\to 0$ in probability.

Proof

The proof follows from arguments similar to those of Lemma A.2.

Lemma A.8

Under Assumptions 1–5, we have ${\stackrel{\sim }{\mathbf{Z}}}^{\text{T}}(\mathbf{I}-\mathbf{S})\mathbf{\varepsilon }={\sum }_{i=1}^n\psi ({\mathbf{Z}}_i,{\mathbf{X}}_i,U_i){\mathbf{X}}_i\{1+o_P(1)\}{\epsilon }_i+o(n^{1/2})$, where ε= (ε₁, ···, ε_n)^T.

Proof

Note that ${\stackrel{\sim }{\mathbf{Z}}}^{\text{T}}(\mathbf{I}-\mathbf{S})\mathbf{\varepsilon }={\sum }_{i=1}^n{\stackrel{\sim }{\mathbf{Z}}}_i\{{\epsilon }_i-({\mathbf{X}}_i,0){(D_{u_i}{W}_{u_i}{D}_{u_i})}^{-1}{D}_{u_i}{W}_{u_i}\epsilon \}$. By the same argument as those for (A.3), we have

$$n^{-1}{D}_u^{\text{T}}{W}_u\mathit{\epsilon }=n^{-1}\sum _{i=1}^n\left(\begin{array}{c}{\mathbf{X}}_i\\ \frac{U_i-U}{h}{\mathbf{X}}_i\end{array}\right)K_h(U_i-U){\epsilon }_i=f_u(U)E(\mathbf{X}\mid U)O_P(c_n).$$

This formula along with (A.2) yields $({\mathbf{X}}^{\text{T}},0){(D_u^{\text{T}}{W}_u{D}_u)}^{-1}{D}_u{W}_u\mathit{\epsilon }={\mathbf{X}}^{\text{T}}{\mathrm{\Gamma }}^{-1}(U)E(\mathbf{X}\mid U)O_P(c_n)$. A combination of these arguments with Lemma A.7 finishes the proof of Lemma A.8.

A.3 Proof of Theorem 1

Note that Θ̂_n can be expressed as (Z̃^TZ̃)⁻¹Z̃^T(I −S)ZΘ+ (Z̃^TZ̃)⁻¹Z̃^T(I −S)M + (Z̃^TZ̃)⁻¹Z̃^T(I −S)ε. By Lemma A.8, the third term equals ${\mathbf{\sum }}^{-1}{n}^{-1}{\sum }_{i=1}^n\psi ({\mathbf{Z}}_i,{\mathbf{X}}_i,U_i){\epsilon }_i\{1+o_p(1)\}+o_P(n^{-1/2})$. The first term equals, via Lemma A.4,

$$\begin{array}{l}{\mathbf{\sum }}^{-1}[\frac{{\zeta }_1{S}_u^{-1}{c}_p{b}^{r+1}}{n(r+1)!}\sum _{i=1}^n\psi ({\mathbf{Z}}_i,{\mathbf{X}}_i,U_i){\{{\mathit{\xi }}^{(r+1)}(V_i)\}}^{\text{T}}{\mathit{\beta }}_0\\ +\frac{1}{n^2}\sum _{i=1}^n\sum _{j=1}^n\frac{1}{f_v(V_i)}\psi ({\mathbf{Z}}_i,{\mathbf{X}}_i,U_i)L_b(V_j-V_i){\mathbf{e}}_j^{\text{T}}{\mathit{\beta }}_0].\end{array}$$

By Lemma A.6 and (A.1), it follows that the second term of Θ̂_n’s expression is of order $O(c_n^2)$ in probability. These arguments imply that

$$\begin{array}{l}{\widehat{\mathbf{\Theta }}}_n-{\mathbf{\Theta }}_0={\mathbf{\sum }}^{-1}[\frac{{\zeta }_1{S}_u^{-1}{c}_p{b}^{r+1}}{n(r+1)!}\sum _{i=1}^n\psi ({\mathbf{Z}}_i,{\mathbf{X}}_i,U_i){\{{\mathit{\xi }}^{(r+1)}(V_i)\}}^{\text{T}}{\mathit{\beta }}_0\\ +\frac{1}{n^2}\sum _{i=1}^n\sum _{j=1}^n\frac{1}{f_v(V_i)}\psi ({\mathbf{Z}}_i,{\mathbf{X}}_i,U_i)L_b(V_j-V_i){\mathbf{e}}_j^{\text{T}}{\mathit{\beta }}_0\\ +\frac{1}{n}\sum _{i=1}^n\psi ({\mathbf{Z}}_i,{\mathbf{X}}_i,U_i){\epsilon }_i]\{1+o_p(1)\}.\end{array}$$

This completes the proof of Theorem 1.

A.4 Proof of Theorem 3

By the definition of Ψ̂ (u), we have

$$\begin{array}{l}\mathbf{H}\widehat{\mathbf{\Psi }}={(D_u^{\text{T}}{W}_u{D}_u)}^{-1}{D}_u^{\text{T}}{W}_u(Y-\widehat{\mathbf{Z}}{\widehat{\mathbf{\Theta }}}_n)\\ =I_1+{(D_u^{\text{T}}{W}_u{D}_u)}^{-1}{D}_u^{\text{T}}{W}_u(\mathbf{Z}-\widehat{\mathbf{Z}})\mathbf{\Theta }+{(D_u^{\text{T}}{W}_u{D}_u)}^{-1}{D}_u^{\text{T}}{W}_u\mathbf{Z}(\mathbf{\Theta }-{\widehat{\mathbf{\Theta }}}_n)+R_n,\end{array}$$

where $I_1={(D_u^{\text{T}}{W}_u{D}_u)}^{-1}{D}_u{W}_u(Y-\mathbf{Z}\mathbf{\Theta })$ and $R_n={(D_u^{\text{T}}{W}_u{D}_u)}^{-1}{D}_u{W}_u(\mathbf{Z}-\widehat{\mathbf{Z}})(\mathbf{\Theta }-{\widehat{\mathbf{\Theta }}}_n)$. It is easy to show that R_n = o(n^−1/2) in probability. Note that

$$\begin{array}{l}{D}_u^{\text{T}}{W}_u(\mathbf{Z}-\widehat{\mathbf{Z}})\mathbf{\Theta }=\{\frac{{\zeta }_1{S}_u^{-1}{c}_p{b}^{r+1}}{(r+1)!}\sum _{i=1}^n\left(\begin{array}{c}{K}_h(U_i-u){\mathbf{X}}_i{\{{\mathit{\xi }}^{(r+1)}(V_i)\}}^{\text{T}}\mathit{\beta }\\ K_h(U_i-u)h^{-1}(U_i-u){\mathbf{X}}_i{\{{\mathit{\xi }}^{(r+1)}(V_i)\}}^{\text{T}}\mathit{\beta }\end{array}\right)\\ \frac{1}{n}\sum _{i=1}^n\sum _{j=1}^n{f}_v^{-1}(V_i)\left(\begin{array}{c}{K}_h(U_i-u)L_b(V_j-V_i){\mathbf{X}}_i{\mathbf{e}}_j^{\text{T}}\mathit{\beta }\\ K_h(U_i-u)L_b(V_j-V_i)h^{-1}(U_i-u){\mathbf{X}}_i{\mathbf{e}}_j^{\text{T}}\mathit{\beta }\end{array}\right)\}\{1+o_P(1)\}\\ =I_1^{\prime }+I_2^{\prime }.\end{array}$$

It follows from (A.2) that

$$\begin{array}{r}{(D_u^{\text{T}}{W}_u{D}_u)}^{-1}{I}_1^{\prime }=\frac{{\zeta }_1{S}_u^{-1}{c}_p{b}^{r+1}}{(r+1)!}{\left\{f_u(u){\mathrm{\Gamma }}^{-1}(u)\otimes \left(\begin{array}{cc}1& {\mu }_1\\ {\mu }_1& {\mu }_2\end{array}\right)\right\}}^{-1}\\ \times \left[\sum _{i=1}^n\left\{\begin{array}{c}{K}_h(U_i-u){\mathbf{X}}_i{\{{\mathit{\xi }}^{(r+1)}(V_i)\}}^{\text{T}}\mathit{\beta }\\ K_h(U_i-u){\mathbf{X}}_i{h}^{-1}(U_1-u){\{{\mathit{\xi }}^{(r+1)}(V_i)\}}^{\text{T}}\mathit{\beta }\end{array}\right\}\{1+o_P(1)\}\right]\end{array}$$ (A.8)

and

$$\begin{array}{l}{(D_u^{\text{T}}{W}_u{D}_u)}^{-1}{I}_2^{\prime }=\frac{1}{n^2}\sum _{j=1}^n\sum _{i=1}^n{\left\{f_u(u)\mathrm{\Gamma }(u)\otimes \left(\begin{array}{cc}1& {\mu }_1\\ {\mu }_1& {\mu }_2\end{array}\right)\right\}}^{-1}\\ \times \left\{\begin{array}{c}{K}_h(U_i-u)E({\mathbf{X}}_i\mid V=V_j){\mathbf{e}}_j^{\text{T}}\mathit{\beta }\\ h^{-1}(U_i-u)K_h(U_i-u)E({\mathbf{X}}_i\mid V=V_j){\mathbf{e}}_j^{\text{T}}\mathit{\beta }\end{array}\right\}\{1+o_p(1)\}\\ =\frac{{\mathrm{\Gamma }}^{-1}(u)}{n{f}_u(u)({\mu }_2-{\mu }_1^2)}\sum _{i=1}^n{K}_h(U_i-u)E({\mathbf{X}}_i\mid V=V_i){\mathbf{e}}_i^{\text{T}}\mathit{\beta }\\ \otimes \left(\begin{array}{c}{\mu }_2-{\mu }_1(U_i-u)/h\\ (U_i-u)/h-{\mu }_1\end{array}\right)\{1+o_p(1)\}.\end{array}$$

Furthermore, (A.3) implies that

$$\begin{array}{l}{(D_u^{\text{T}}{W}_u{D}_u)}^{-1}{D}_u^{\text{T}}{W}_u\mathbf{Z}(\mathbf{\Theta }-{\widehat{\mathbf{\Theta }}}_n)={\left\{f_u(u)\mathrm{\Gamma }(u)\otimes \left(\begin{array}{cc}1& {\mu }_1\\ {\mu }_1& {\mu }_2\end{array}\right)\right\}}^{-1}\\ \{n{f}_u(u)\mathrm{\Phi }(u)\otimes {(1,{\mu }_1)}^{\text{T}}\}(\mathbf{\Theta }-{\widehat{\mathbf{\Theta }}}_n)\{1+o_P(1)\}\\ =\left\{{\mathrm{\Gamma }}^{-1}(u)\mathrm{\Phi }(u)\otimes {(1,0)}^{\text{T}}\right\}(\mathbf{\Theta }-{\widehat{\mathbf{\Theta }}}_n)\{1+o_P(1)\}.\end{array}$$ (A.9)

We therefore have $I_1={(D_u^{\text{T}}{W}_u{D}_u)}^{-1}{D}_u^{\text{T}}{W}_u{\mathbf{M}}_u+{(D_u^{\text{T}}{W}_u{D}_u)}^{-1}{D}_u^{\text{T}}{W}_u\mathit{\epsilon }$, where M_u = α(u)^TX.

By Taylor expansion and a direct simplification, we have

$$\begin{array}{l}\mathbf{M}=\left(\begin{array}{c}{\mathbf{X}}_1^{\text{T}}\mathit{\alpha }(u)+(U_1-u){\mathbf{X}}_1^{\text{T}}{\mathit{\alpha }}^{\prime }(u)+2^{-1}{(U_1-u)}^2{\mathbf{X}}_1^{\text{T}}{\mathit{\alpha }}^{″}(u)\\ ⋮\\ {\mathbf{X}}_1^{\text{T}}\mathit{\alpha }(u)+(U_n-u){\mathbf{X}}_n^{\text{T}}{\mathit{\alpha }}^{\prime }(u)+2^{-1}{(U_n-u)}^2{\mathbf{X}}_n^{\text{T}}{\mathit{\alpha }}^{″}(u)\end{array}\right)+o(h^2)\\ =D_u\left(\begin{array}{c}\mathit{\alpha }(u)\\ h{\mathit{\alpha }}^{\prime }(u)\end{array}\right)+\frac{1}{2}\left(\begin{array}{c}{(U_1-u)}^2{\mathbf{X}}_1^{\text{T}}{\mathit{\alpha }}^{″}(u)\\ ⋮\\ {(U_n-u)}^2{\mathbf{X}}_n^{\text{T}}{\mathit{\alpha }}^{″}(u)\end{array}\right)+o(h^2).\end{array}$$

Hence,

$$\begin{array}{l}{I}_1=\{\left(\begin{array}{c}\mathit{\alpha }(u)\\ h\mathit{\alpha }(u)\end{array}\right)+\frac{1}{2}{(D_u^{\text{T}}{W}_u{D}_u)}^{-1}{D}_u^{\text{T}}{W}_u\left(\begin{array}{c}{(U_1-u)}^2{\mathbf{X}}_1^{\text{T}}{\mathit{\alpha }}^{″}(u)\\ ⋮\\ {(U_n-u)}^2{\mathbf{X}}_n^{\text{T}}{\mathit{\alpha }}^{″}(u)\end{array}\right)\\ +{(D_u^{\text{T}}{W}_u{D}_u)}^{-1}{D}_u^{\text{T}}{W}_u\mathit{\epsilon }\}\{1+o_P(h^2)\}.\end{array}$$ (A.10)

It follows from (A.8)–(A.10) that $\sqrt{nh}\mathbf{H}\{\widehat{\mathbf{\Psi }}(u_0)-\mathbf{\Psi }(u_0)\}$ can be represented as

$$\begin{array}{l}\sqrt{nh}[\frac{b^{r+1}}{n(r+1)!}\frac{{\zeta }_1^{\text{T}}{S}_u^{-1}{c}_p}{({\mu }_2-{\mu }_1^2)f_u(u)}{\mathrm{\Gamma }}^{-1}(U)\sum _{i=1}^n{K}_h(U_i-u)\\ \otimes \left(\begin{array}{c}\{{\mu }_2={\mu }_1(U_i-u)/h\}{\mathbf{X}}_i{\{{\mathit{\xi }}^{(r+1)}(V_i)\}}^{\text{T}}{\mathit{\beta }}_0\\ \{(U_i-u)/h-{\mu }_1\}{\mathbf{X}}_i{\{{\mathit{\xi }}^{(r+1)}(V_i)\}}^{\text{T}}{\mathit{\beta }}_0\end{array}\right)\\ +\frac{{\mathrm{\Gamma }}^{-1}(U)}{2({\mu }_2-{\mu }_1^2)f_u(u)}\sum _{i=1}^n{K}_h(U_i-u)\otimes \left(\begin{array}{c}\{{\mu }_2-{\mu }_1(U_i-u)/h\}{(U_i-u)}^2{\mathbf{X}}_i{\mathbf{X}}_i^{\text{T}}{\alpha }^{″}(u)\\ \{(U_i-u)/h-{\mu }_1\}{(U_i-u)}^2{\mathbf{X}}_i{\mathbf{X}}_i^{\text{T}}{\alpha }^{″}(u)\end{array}\right)\\ +o(h^2+b^{r+1})+O(n^{-1/2})]\\ +\sqrt{nh}{(D_u^{\text{T}}{W}_u{D}_u)}^{-1}{D}_u^{-1}{W}_u\mathit{\epsilon }+\frac{\sqrt{nh}{\mathrm{\Gamma }}^{-1}(u)}{n{f}_u(u)({\mu }_2-{\mu }_1^2)}\sum _{i=1}^n{K}_h(U_i-u)E({\mathbf{X}}_i\mid V=V_i){\mathbf{e}}_i^{\text{T}}\mathit{\beta }\\ \otimes \left(\begin{array}{c}{\mu }_2-{\mu }_1(U_i-u)/h\\ (U_i-u)/h-{\mu }_1\end{array}\right)\{1+o_p(1)\}.\end{array}$$

By the similar argument of Lemma A.8, we have

$$\begin{array}{l}{(D_u^{\text{T}}{W}_u{D}_u)}^{-1}{D}_u^{-1}{W}_u\mathit{\epsilon }=\frac{{\mathrm{\Gamma }}^{-1}(u)}{n{f}_u(u)({\mu }_2-{\mu }_1^2)}\sum _{i=1}^n{K}_h(U_i-u){\mathbf{X}}_i{\epsilon }_i\\ \otimes \left(\begin{array}{c}{\mu }_2-{\mu }_1(U_i-u)/h\\ (U_i-u)/h-{\mu }_1\end{array}\right)\{1+o_p(1)\}.\end{array}$$

The proof of Theorem 3 is completed.

A.5 Proof of Theorem 5

The proof is similar to Theorems 3.1 and 3.2 of Fan and Huang (2005). We only give a sketch. We first prove that n⁻¹RSS₁ = σ²{1 + o_P (1)}.

By a similar procedure as that of Theorem 3.2 in Fan and Huang (2005), we can obtain that $n^{-1}RS{S}_{10}=n^{-1}{\sum }_{i=1}^n{(Y_i-{\widehat{M}}_{i0}-{\widehat{\mathbf{\Theta }}}^{\text{T}}{\mathbf{Z}}_i)}^2={\sigma }^2\{1+o_P(1)\}$, where M̂_i0 is the ith element of M̂₀ = S(Y −ZΘ̂). A direct calculation yields that

$$\begin{array}{c}{n}^{-1}(RS{S}_1-RS{S}_{10})=n^{-1}\sum _{i=1}^n{\widehat{\mathbf{\Theta }}}^{\text{T}}({\widehat{\mathbf{Z}}}_i-{\mathbf{Z}}_i)\{(Y_i-{\widehat{M}}_i-{\widehat{\mathbf{\Theta }}}^{\text{T}}{\widehat{\mathbf{Z}}}_i)+(Y_i-{\widehat{M}}_{i0}-{\widehat{\mathbf{\Theta }}}^{\text{T}}{\mathbf{Z}}_i)\}\\ +n^{-1}\sum _{i=1}^n({\widehat{M}}_i-{\widehat{M}}_{i0})\{(Y_i-{\widehat{M}}_i-{\widehat{\mathbf{\Theta }}}^{\text{T}}{\widehat{\mathbf{Z}}}_i)+(Y_i-{\widehat{M}}_{i0}-{\widehat{\mathbf{\Theta }}}^{\text{T}}{\mathbf{Z}}_i)\}.\end{array}$$ (A.11)

By (2.1), Theorem 2 and Jensen inequality, we know that the first term in the right-hand side of (A.11) is bounded by

$$\underset{1\le i\le n}{max}{\widehat{\mathbf{\Theta }}}^T\mid {\widehat{\mathbf{Z}}}_i-{\mathbf{Z}}_i\mid \left[{\left\{n^{-1}\sum _{i=1}^n{(Y_i-{\widehat{M}}_{i0}-{\widehat{\mathbf{\Theta }}}^{\text{T}}{\mathbf{Z}}_i)}^2\right\}}^{1/2}+\underset{1\le i\le n}{max}\{\mid {\widehat{M}}_i-{\widehat{M}}_{i0}\mid +{\widehat{\mathbf{\Theta }}}^T\mid {\widehat{\mathbf{Z}}}_i-{\mathbf{Z}}_i\mid \}\right],$$ (A.12)

which is o_p(1). A similar argument can show that the second term in the right-hand side of (A.11) is also o_p(1). We therefore have n⁻¹RSS₁ = σ²{1 + o_P (1)}.

Furthermore, RSS₀ can be decomposed as ${\{\mathbf{Y}-\widehat{\mathbf{M}}-\widehat{\mathbf{Z}}\widehat{\mathbf{\Theta }}+\stackrel{\sim }{\mathbf{Z}}(\widehat{\mathbf{\Theta }}-{\widehat{\mathbf{\Theta }}}_0)\}}^{\text{T}}\{\mathbf{Y}-\widehat{\mathbf{M}}-\widehat{\mathbf{Z}}\widehat{\mathbf{\Theta }}+\stackrel{\sim }{\mathbf{Z}}(\widehat{\mathbf{\Theta }}-{\widehat{\mathbf{\Theta }}}_0)\}\stackrel{\text{def}}{=}RS{S}_1+Q_1+Q_2+Q_3$, where Q₁= {Z̃(Θ̂ − Θ̂₀)}^T{Z̃(Θ̂ − Θ̂₀)}, Q₂= (Y − M̂ − ẐΘ̂) {Z̃(Θ̂ − Θ̂₀)}, Q₃={Z̃(Θ̂ − Θ̂₀)}^T(Y − M̂ − ẐΘ̂).

Recalling the expression of Θ̂₀ and the result given in (A.1), we know that n⁻¹Z̃^T Z̃ → Σ in probability, and $Q_1-n{\mathbf{\Theta }}^{\text{T}}{\mathbf{A}}^{\text{T}}{\{\mathbf{A}{\mathbf{\sum }}^{-1}{\mathbf{A}}^{\text{T}}\}}^{-1}\mathbf{A}\mathbf{\Theta }\to {\sigma }^2{\sum }_{i=1}^l{\omega }_i{\chi }_{i1}^2$ in distribution. In an analogous way, we can that show Q₂ and Q₃ are asymptotic negligible in probability. These statement along with the Slutsky theorem imply that $2T_n-n{\sigma }^{-2}{\mathbf{\Theta }}^{\text{T}}{\mathbf{A}}^{\text{T}}{\{\mathbf{A}{\mathbf{\sum }}^{-1}{\mathbf{A}}^{\text{T}}\}}^{-1}\mathbf{A}\mathbf{\Theta }\to {\sum }_{i=1}^l{\omega }_i{\chi }_{i1}^2$ in distribution. Finally, following the lines of Rao and Scott (1981), we can prove that the distribution of $\varrho n{\sum }_{i=1}^l{\omega }_i{\chi }_{i1}^2$ has the approximate distribution as ${\chi }_l^2$, and complete the proof of Theorem 5.