Abstract
Objective
To determine the magnitude and importance of declines in model performance associated with altering the source data and time frame from which comorbid conditions were identified in claims-based risk-adjustment among persons with hip fracture.
Study Design and Setting
Medicare claims data were used to identify incident hip fracture cases in 1999. Three risk-adjustment instruments were evaluated: one by Iezzoni, the Charlson Index (Romano adaptation), and the Clinical Classification Software (CCS). Several implementation strategies, defined by altering data source (MedPar and/or Part B claims) and time frame (index hospitalization and/or 1-year pre-period), were assessed for each instrument. Logistic regression was used to predict one-year mortality and model performance was compared.
Results
Each instrument had modest ability to predict 1-yr mortality following hip fracture. The CCS performed best overall (c = 0.76), followed by the Iezzoni (c = 0.73) and Charlson models (c = 0.72). Although each instrument performed most favorably when applied to both inpatient and outpatient claims and when comorbidities were considered during the pre-period, varying data source and time frame had trivial effects on model performance.
Conclusion
The similar predictive ability of the three risk adjustment instruments suggests that ease of implementation be a key consideration in choosing an approach for hip fracture populations.
Keywords: risk adjustment, hip fracture, Medicare, administrative data, prospective cohort, ROC analysis
“What’s New”.
Key Finding: Three distinct diagnosis-based risk adjustment instruments had similar ability to predict death among persons with hip fracture when applied claims from alternative care settings and over varying lengths of follow-back.
What This Research Adds: This research supports existing evidence that using increasing complicated algorithms for risk adjustment produces only marginal gains in model performance.
Implication: Ease of implementation should be considered alongside of performance when using diagnosis based risk-adjustment instruments in claims-based analysis of persons with hip fracture.
INTRODUCTION
Hip fracture is common among the elderly and is associated with considerable mortality, comorbidity, and health service utilization [1]. This disabling medical event can cascade into a series of adverse health consequences including infection[2, 3], heart failure[2], pneumonia[3, 4], depression[5], and functional dependency[6]. Nearly a third of all persons who experience a hip fracture die within one year[2], and increasingly, people who experience hip fracture become institutionalized following acute treatment in the hospital[7]. Hip fracture already taxes the U.S. healthcare system and its burden is expected to increase as the population ages[8]. Growing awareness of variation in practice and clinical outcomes associated with hip fracture, as well as the evolving link between reimbursement and performance measurement, make it more important than ever to understand the care received by persons with hip fracture.
The age and frailty of this population make risk-adjustment important as a way of removing potentially confounding effects of patients’ illness burden. When characterizing the health services received by persons with hip fracture, either for inter-provider comparisons of quality or when comparing patient outcomes, adequate risk-adjustment ensures that the observed populations are sufficiently similar, such that differences in outcome likely result from variations in the care that is provided and not the underlying level of illness among the patients.
Administrative claims data can be a useful tool for examining patterns of care associated with hip fracture. When applied to administrative data, many risk-adjustment instruments rely on patient diagnosis codes[9–12] or the use of specific health resources (e.g., prescription drugs[13–15]) to construct a comorbidity profile for each individual that is then used in statistical models to hold the effect of specific patient characteristics constant across observations, helping researchers and health managers make unbiased evaluations.
Risk-adjustment instruments and alternative strategies for implementation are evaluated according to their ability to predict patient outcomes, usually service utilization, expenditures, or mortality. Early approaches to risk-adjustment relied on relatively simple strategies for grouping diagnosis codes according to common chronic conditions[9, 10, 16, 17]. Recent efforts to enhance predictive power have led to development of increasingly sophisticated algorithms able to identify a broader range of coexisting diseases[18–20], draw on data from multiple care settings[11, 12] and alternative claim types[13–15], and more effectively account for disease severity[12, 21].
This progression in complexity is well documented. Fowles et al. found that diagnosis-based risk assessment was better able to predict future health expenditures than either simple demographic information or self-reported functional status[22]. Weiner and Allen argued that ambulatory data provide the best source of diagnostic information, by capturing coexisting disease among those not hospitalized[23]. By applying a diagnosis-based risk-adjustment instrument to Part B physician claims, Klabunde et al. identified substantially more persons with coexisting disease and more accurately predicted health service use and mortality than when the instrument was applied solely to hospital data[24]. Others have shown that supplementing diagnosis-based risk-adjustment instruments with pharmacy[25] and laboratory[26] data enhances predictive ability. Strukenborg, Wagner, and Conners reported a higher number of coexisting conditions per patient and consistently better model performance when they compared the Deyo[10] adaptation of the Charlson Index(17 categories of comorbid illness) with Elixhauser’s[19] method (30 categories of comorbid illness) [27]. Among persons who experienced myocardial infarction, Ash et al. found that increasing the complexity of the risk-adjustment model (i.e., using a series of risk-adjustment instruments, each of which was designed to identify more coexisting conditions than the previous) improved model performance[28].
In contrast to the ‘more is better’ approach, other researchers rally behind the use of simple measures to predict outcomes. Farley, Harley, and Devine found that simple counts of utilized health services compared favorably to several common diagnosis-based risk-adjustment strategies in predicting health outcomes [29]. Perkins et al. reported only marginal differences between relatively simple (e.g., counts of diseases and the Charlson Index) and more complex (Ambulatory Care Groups) risk-adjusters in their ability to predict total expenditures, physician visits, and mortality[30]. Melfi et al. reported that simple counts of coexisting diseases predicted mortality better than the more complicated Charlson Index[31]. Similarly, Ellis et al. found only modest benefit from combining outpatient and inpatient diagnoses in their ability to prospectively predict expenditures among Medicare beneficiaries, but substantial improvements when considering the severity of the patients’ illness burden[12]. These findings highlight an important trade-off between the predictive power of some complex risk-adjustment strategies and the ease of use and interpretation associated with simpler models.
We sought to examine how using different input data affected the adequacy of risk prediction among Medicare beneficiaries with hip fracture. Using Medicare inpatient and outpatient claims data, we examined the effects of altering the source data (MedPar vs. part B claims) and time frame (index event vs. the preceding year) used to identify comorbid conditions on the ability of three diagnosis-based risk-adjustment instruments to predict 1-year mortality following hip fracture. We chose the most robust instrument with the broadest input data as the reference risk-adjustment strategy and examined the decline in performance experienced with simpler strategies.
METHODS
Data were obtained from a 20% sample of the 1998–2000 MedPar and Part B evaluation and management (E/M) claims files. The eligible study population included Medicare enrollees who, at the time of the index fracture in 1999, were between the ages of 65 and 99, were eligible for Medicare parts A and B (individuals enrolled in a Medicare health maintenance organization were excluded), who were hospitalized with a primary diagnosis of hip fracture or who had evidence of surgical repair of hip fracture (N = 43,811). The index fracture was defined as the first hospitalization in 1999 with a primary diagnosis of hip fracture or any hospitalization in 1999 with evidence of surgical hip fracture repair. Comorbidity was assessed at the time of the index fracture or during the preceding 365 days (pre-period). One-year mortality following hip fracture was defined as death within 365 days of the index fracture admission date.
Risk Adjustment Instruments
In addition to adjustment for age, sex, and race (ASR) characteristics, three diagnosis-based risk-adjustment instruments were evaluated: one proposed by Iezzoni et al. [32], the Charlson Comorbidity Index (Romano adaptation)[17], and the Agency for Healthcare Research and Quality’s (AHRQ) Clinical Classification Software(CCS) [33]. All three are freely available, as either published or downloadable lists of diagnoses codes, and are fairly straightforward to translate into an electronic algorithm for implementation with datasets that contain ICD-9-CM diagnosis codes.
The instrument proposed by Iezzoni et al. was designed to identify severe forms of 13 chronic conditions common among the elderly [32]. An electronic algorithm assigns an indicator flag based on presence or absence of specific ICD-9-CM codes that represent the most severe cases of each comorbidity (e.g., diabetes with end-stage organ disease or nutritional deficiencies that require assistive feeding devices). We simplified Iezzoni’s instrument by combining the categories for cancer and metastatic cancer into a single category. The small number of comorbidities identified and relative ease of use make the Iezzoni instrument an attractive strategy for risk-adjustment in administrative data and for aged populations likely to have an elevated base level of illness.
Similar to Iezzoni, the Romano adaptation of the Charlson Comorbidity Index uses ICD-9-CM diagnosis codes to assign indicator flags for common chronic conditions, but adds codes for acute myocardial infarction. The Charlson Index also differs from the Iezzoni Index in two other important ways. First, a broader range of diagnosis codes are used to detect each chronic condition, giving it the potential to identify comorbidities in more patients than the Iezzoni instrument. Second, the Charlson Index also weights each comorbidity based on severity and assigns each individual an overall risk score representing the sum of their comorbidity weights. In our analysis, the Charlson’s tool was implemented first as an index (weighted sum of comorbidity indicators), and also as individual components (simply assigning an indicator based on the presence or absence of the comorbidity without assigning a weight and comorbidity score). This approach was taken because in several preliminary analyses, the Charlson index score produced predicted mortality probabilities with only a small degree of variation, making it difficult to group individuals based on their predicted risk of death.
The CCS is a ‘clinical grouper’ that classifies ICD-9-CM diagnosis codes into 259 clinically meaningful and mutually exclusive categories. Though not developed as a risk-adjuster, CCS performs well when used for this purpose with administrative data[28]. The CCS uses a broad definition for each disease and, unlike the Iezzoni and Charlson instruments, makes little distinction regarding disease severity when categorizing diagnosis codes. Individuals can receive a flag for as many CCS categories as their recorded diagnoses support. Because the CCS classifies diagnoses codes with a high degree of detail, we were concerned that several categories may represent complications of hip fracture-related care. We tested a modified version of the CCS that eliminated categories that were likely complications of fracture-related care (e.g., skin ulcers) and those irrelevant in an elderly population (e.g., categories related to child birth), but found no difference in predictive ability between the modified and original forms. We report only findings from the un-modified, original CCS. A complete list of CCS categories can be downloaded from AHRQ.
Strategies for Implementation
Each risk-adjustment instrument was applied to seven distinct data source and time-frame combinations. In order of increasing complexity, they are as follows: (1) MedPar alone at the index fracture, (2) MedPar alone during the pre-period, (3) MedPar alone at index and during the pre-period, (4) Part B during the pre-period, (5) MedPar at the index and Part B during the pre-period, (6) MedPar and Part B during the pre-period, and (7) MedPar at the index and during the pre-period and Part B during the pre-period. We applied a restriction to Part B claims, that a comorbid condition could be flagged during the pre-period only if it appeared two or more times at least 7 days apart. While such a restriction could limit identification of comorbid conditions among infrequent health services users, it reduces the number of falsely identified conditions and rules out diagnoses.
Data Analysis
The most complex risk prediction procedure considered in our analysis was application of CCS to MedPar at the time of the index fracture and to MedPar and Part B during the pre-period. This strategy allowed for the highest level of disease differentiation and took advantage of the broadest set of claims from which to identify comorbid conditions. We identified this combination a priori as the reference standard to which we would compare the other models.
Logistic regression was used to predict 1-year mortality following hip fracture. Adjustments for age, sex, and race were considered alone and then added to each of the other risk prediction strategies. In total, there were parameters added to each model for 19 distinct age(65–69, 70–74, 75–79, 80–84, 85+), sex (male, female), and race (black, non-black) combinations. White males age 65–69 were considered the reference and not identified with an indicator in the statistical models. Statistically insignificant or negative coefficients were not dropped.
Each risk prediction model was evaluated on its ability to predict death within 1 year of the index hip fracture. Model discrimination—the ability of each model to correctly distinguish individuals who died from those who did not—was assessed using c-statistics provided in standard statistical output. The c-statistic equals the area under the receiver operating characteristic (ROC) curve when applied to a binary outcome and measures the ability to correctly rank order any two randomly drawn individuals on their predicted likelihood of dying. C-statistics are valued from 0.5 – 1.0 with higher values signifying greater ability to accurately distinguish those with and without the outcome. C- values less than 0.7 are generally considered poor and those over 8 are considered good. Model performance was compared and tested for statistically significant differences using a method proposed by Hanley and McNeil to compare the area under ROC curves [34, 35]. Three comparisons were made: (1) to our reference standard model, (2) across risk-adjustment strategies for the same data source/time-frame combination, and (3) within the same risk-adjustment strategy but across data source/time-frame combinations. Results are presented in Table 2. Simple comparisons of the Akaike’s Information Criterion (AIC), a measure of relative goodness-of-fit that penalizes overfitting statistical models with superfluous parameters, were considered in secondary analyses and served as confirmatory tests of our primary findings.
Table 2.
C-Statistics Rating Model Performance for One-Year Mortality Following Hip Fracture among Medicare Beneficiaries
|
Adjustment Instruments |
||||
|---|---|---|---|---|
| Charlson
|
||||
| Implementation Strategy | CCS | Components | Index | Iezzoni |
|
|
|
|
||
| MedPar (index+pre-period) + Part B (pre-period) | 0.76 | 0.72*,‡ | 0.71*,‡ | 0.73*,‡ |
| MedPar (pre-period) + Part B (pre-period) | 0.72*,§ | 0.69*,‡,§ | 0.69*,‡,§ | 0.70*,‡,§ |
| MedPar (index) + Part B (pre-period) | 0.76 | 0.71*,‡ | 0.70*,‡ | 0.72*,‡ |
| Part B (pre-period) | 0.71*,§ | 0.68*,‡,§ | 0.68*,‡,§ | 0.70*,‡,§ |
| MedPar (index + pre-period) | 0.76 | 0.71*,‡ | 0.71*,‡ | 0.72*,‡ |
| MedPar (pre-period) | 0.69*,§ | 0.68*,‡,§ | 0.68*,‡,§ | 0.68*,‡,§ |
| MedPar (index) | 0.75*,§ | 0.70*,‡,§ | 0.69*,‡,§ | 0.71*,‡,§ |
Legend:
Models are arranged from most to least complex based on data source and time frame to which each was applied. All models adjusted for age, sex, and race differences.
Comparison 1 - denotes statistical difference (p < 0.05) from the reference standard model:
CCS - MedPar (index + pre-period) + Part B (pre-period).
Comparison 2 - denotes statistical difference (p < 0.05) from the model with the greatest number of parameters (CCS) across risk-adjustment strategies for the same data source and time-frame combination.
Comparison 3 - denotes statistical difference (p < 0.05) from the model with the broadest data source and time-frame combination [MedPar (index + pre-period) + Par B (pre-period)] within each risk-adjustment strategy.
Model performance was also evaluated among subjects with similar predicted mortality. Model calibration curves that plot observed and predicted mortality were constructed and evaluated using the Lemeshow and Hosmer chi-square test [36, 37]. This allowed us to visually identify the range of predicted mortality from which each model deviated from perfect prediction. Statistical analyses were performed using SAS version 9.1.3 (Cary, NC).
RESULTS
Characteristics of the hip fracture cohort are presented in Table 1. A cohort of 43,811 persons with hip fracture was identified. The cohort was predominantly female (77%), non-black (96%), and aged 75 or older (85%). The vast majority of patients were treated surgically (97%). One-year mortality was 27%.
Table 1.
Characteristics of the Hip Fracture Cohort
| Characteristic | N (%) |
|---|---|
| Age | |
| 65–74 | 6,615 (15) |
| 75–84 | 18,006 (41) |
| 85+ | 19,233 (44) |
| Female | 33,778 (77) |
| Black race | 1,665 (4) |
| One-year mortality | 11,512 (26) |
| Fracture surgically repaired | 42,365 (97) |
Controlling for age, sex, and race alone had poor predictive ability (c = 0.63). Overall, the predictive ability achieved among the prediction models considered here was modest, ranging from c = 0.68 for one implementation of the Charlson instrument to c = 0.76 for the CCS. Table 2 describes the performance of the three risk-adjustment instruments when applied to each data source and time-frame combination.
Comparison #1 tested for differences from our reference standard model (CCS applied to MedPar at index and MedPar + Part B during the pre-period: c = 0.76) which are denoted by “*” in Table 2. Almost all of the other prediction models underperformed compared to the reference standard, and most differences were statistically significant. The two exceptions were alternative implementations of the CCS which used MedPar data from the index hospitalization supplemented with either hospital claims (c = 0.76) or Part B (c = 0.76) data from the pre-period. Consideration of the AIC suggests that the CCS when applied to MedPar at index and Part B during the pre-period (AIC = 44,176), may even perform slightly better than the more complex reference standard model (AIC = 44,385).
Comparison #2 considered differences across risk-adjustment instruments when applied to the same data source and time-frame combination and is denoted by “‡” in Table 2. These comparisons indicate that the Iezzoni and Charlson instruments performed well overall, but showed significantly worse ability to predict mortality relative to the CCS. The magnitude varied across models, though on average, Iezzoni (4% difference from the CCS counterpart model) was preferable to the Charlson instrument implemented as a weighted index and as flagged components (6% difference from the CCS counterpart model − both implementations).
Comparison #3 tested the effect of varying the data source and time frame within each risk-adjustment instrument, with statistically significant differences denoted by “§” in Table 2. Altering data source and timeframe led to trivial changes in the performance. While all three instruments performed best when applied to a broad range of claims data, comparisons of c-statistics and the AIC within each risk-adjustment strategy suggest that application of each instrument to MedPar at index appeared to generate the largest degree of predictive power. Supplementing hospital claims from the index admission with data from the pre-period and from outpatient visits added marginal performance improvements that were nearly uniform in magnitude across instruments. While several implementations of the CCS were similar in their ability to predict mortality risk (similar c-statistics), this instrument had a large degree of variation, with a 10% difference between the most (c=0.76) and least (c=0.69) favorable implementations. The marginal benefit of adding additional input data was smaller for the Iezzoni (7% difference between the most and least favorable models) and Charlson instruments (6% difference).
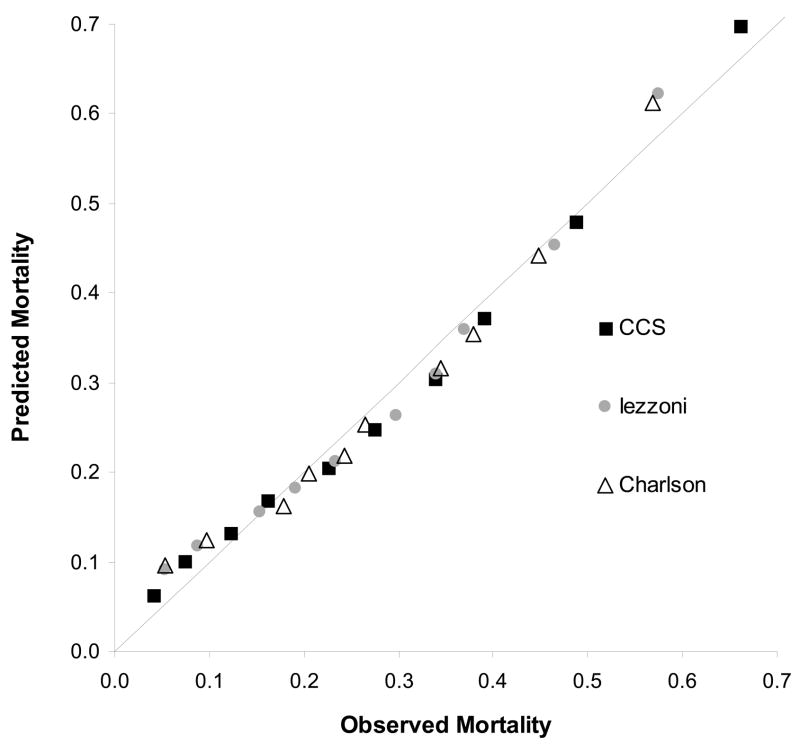
Figure 1 depicts observed mortality plotted against deciles of predicted mortality for our reference standard model. Table 3 shows the input values for this plot. The straight line represents a model with perfect discrimination (c = 1.0), e.g., the ability to perfectly distinguish those who died from those who did not. Several trends emerge from observation of this plot. First, all three instruments produced lower than expected risk estimates among persons at average risk of death and higher than expected risk estimates among persons with very high or very low risks of death. Second, the risk-prediction model derived from each instrument produces a unique range of predicted mortality among subjects. Not surprisingly, the large number of parameters in the CCS model generates the widest range of predicted mortality values, from close to zero to almost 1. The other instruments generate predicted mortality values in a much smaller range, clustering more patients with similar values. Though not shown, similar plots were generated for each of the prediction models examined. There was some variation in the range of predicted mortality values, but the general “U” shape remained, and similar conclusions could be drawn about the discriminative ability of each risk prediction model. The Lemeshow-Hosmer chi-square test indicated statistically significant differences between observed and predicted mortality across deciles for each of the instruments considered (LH χ2 statistic > 15.5 with 8 DF: p<0.001 for each model). However, it is unlikely that such differences are particularly meaningful since their magnitudes are small and overall model performance was good (c = 0.72 – 0.76).
Figure 1.
Calibration Curve Comparing the CCS, Iezzoni, and Charlson Instruments applied to MedpPar (index + Pre) + Pt. B (Pre)
Table 3.
Model Calibration by Decile of Predicted Mortality
|
Died |
Survived |
||||||
|---|---|---|---|---|---|---|---|
| Mortality Risk | Total Patients | Observed | Expected | Observed | Expected | Deviation | L.H. χ2 |
| CCS
| |||||||
| 0–8% | 4,381 | 178 | 278 | 4,203 | 4,103 | 39 | 166 |
| 8–12% | 4,381 | 323 | 440 | 4,058 | 3,941 | 34 | |
| 12–15% | 4,381 | 534 | 580 | 3,847 | 3,801 | 4 | |
| 15–19% | 4,381 | 707 | 737 | 3,674 | 3,644 | 1 | |
| 19–22% | 4,381 | 988 | 899 | 3,393 | 3,482 | 11 | |
| 22–27% | 4,382 | 1,201 | 1,090 | 3,181 | 3,292 | 15 | |
| 27–33% | 4,381 | 1,481 | 1,331 | 2,900 | 3,050 | 24 | |
| 33–42% | 4,381 | 1,705 | 1,631 | 2,676 | 2,750 | 5 | |
| 42–55% | 4,381 | 2,136 | 2,101 | 2,245 | 2,280 | 1 | |
| 55–100% | 4,381 | 2,895 | 3,062 | 1,486 | 1,319 | 30 | |
|
| |||||||
| Iezzoni
| |||||||
| 6–11% | 4,303 | 226 | 394 | 4,077 | 3,909 | 79 | 224 |
| 11–13% | 4,597 | 403 | 541 | 4,194 | 4,056 | 40 | |
| 13–18% | 3,492 | 538 | 545 | 2,954 | 2,947 | 0 | |
| 18–20% | 5,135 | 978 | 933 | 4,157 | 4,202 | 3 | |
| 20–23% | 4,232 | 989 | 895 | 3,243 | 3,337 | 13 | |
| 23–30% | 4,372 | 1,299 | 1,153 | 3,073 | 3,219 | 25 | |
| 30–32% | 4,537 | 1,539 | 1,401 | 2,998 | 3,136 | 20 | |
| 32–39% | 4,381 | 1,618 | 1,573 | 2,763 | 2,808 | 2 | |
| 39–51% | 4,372 | 2,034 | 1,984 | 2,338 | 2,388 | 2 | |
| 51–96% | 4,390 | 2,524 | 2,729 | 1,866 | 1,661 | 41 | |
|
| |||||||
| Charlson
| |||||||
| 7–11% | 4,285 | 230 | 413 | 4,055 | 3,872 | 90 | 209 |
| 11–14% | 4,498 | 436 | 555 | 4,062 | 3,943 | 29 | |
| 14–19% | 4,360 | 778 | 706 | 3,582 | 3,654 | 9 | |
| 19–20% | 5,611 | 1,152 | 1,115 | 4,459 | 4,496 | 2 | |
| 20–23% | 3,154 | 765 | 687 | 2,389 | 2,467 | 11 | |
| 23–28% | 4,331 | 1,146 | 1,097 | 3,185 | 3,234 | 3 | |
| 28–33% | 4,421 | 1,526 | 1,397 | 2,895 | 3,024 | 17 | |
| 33–39% | 4,396 | 1,669 | 1,560 | 2,727 | 2,836 | 12 | |
| 39–50% | 4,398 | 1,969 | 1,946 | 2,429 | 2,452 | 0 | |
| 50–97% | 4,357 | 2,477 | 2,671 | 1,880 | 1,686 | 36 | |
Legend:
Each risk-adjustment instrument applied to MedPar (index + pre-period) + Part B (pre-period).
Deviation = difference between observed and expected probabilities of death among deaths and survivors.
Calculated using: (Odeaths − Edeaths)2 / (total no. pt. in group)*(Edeaths/total pts in group)*(1 − (Edeaths/total patients in group))
L.H. = Lemeshow-Hosmer χ2 > 15.5, df = 8, p < 0.001 for each risk-adjustment strategy
DISCUSSION
Administrative claims data from the 1998–2000 CMS MedPar and Part B claims files were used to evaluate the performance of three freely-available diagnosis based risk-adjustment instruments. The Charlson Index, a method proposed by Iezzoni, and the CCS all predicted post-hip fracture mortality better than controlling for age, sex, and race alone. The CCS performed best overall, followed by the Iezzoni and Charlson instruments. The effect on model performance of varying the data source (MedPar vs. part B) and the time frame (index vs. pre-period) ranged from trivial to substantial, depending on which risk-adjustment instrument and implementation strategy was used.
Differences were detected both across risk-adjustment instruments when the data source and time frame were held constant and within risk-adjustment strategies when the source and time frame for input data varied. Although these differences were statistically significant, their practical implications are unclear. For example, there was a 4% loss in predictive ability between the CCS reference standard model and the Iezzoni counterpart when applied to the same input data (c = 0.76 vs. 0.73). However, when model performance was examined across subgroups for each of these models, they appeared similar in their ability to distinguish deaths from survivors, suggesting that the small predictive gain may not be worth the computational burden of the more complex risk adjustment strategy.
Regardless of risk-adjustment instrument or implementation strategy, most predictive power was derived from diagnoses captured using MedPar data from the index event. The addition of Part B data provided marginal predictive benefit for all three instruments considered. There was no difference between models that used MedPar at index and during the pre-period and models that used MedPar at index and MedPar and Part B during the pre-period. This finding gives further evidence that it may be important to consider the trade-off between a small loss of predictive power and the relative ease of coding an instrument to one dataset at one point in time. For example, the CCS gained little predictive power (about 1%) when applied to the most complex input data (MedPar at index + MedPar and Part B during the pre-period) compared to MedPar data alone at the index event. It is clear why so much predictive power comes from the index event—primary and secondary diagnoses are identified during the hospitalization and used for billing, among other purposes. Since payment is related to the accuracy of diagnostic coding, there is an incentive to be comprehensive. Still, evidence suggests that diagnostic coding for hospitalizations may be largely inaccurate [38].
The performance of the CCS relative to the Charlson and Iezzoni instruments suggests that it differentiates a greater number of pre-existing diseases during the index hospitalization than the other instruments, but raises concern about the identification of post-hip fracture complications. Although this can enhance the predictive power of the risk-adjustment instrument, particularly when mortality is the primary outcome and complications occurring in the hospital may represent near-death experiences[39], it may undermine our ability to detect poor quality when comparing post-fracture care across providers. For example, a hopspital’s post-hip fracture mortality rate is a prominent quality indicator. When pre-fracture health status is adequately controlled, higher post-fracture mortality rates are thought to reflect failure in post-surgical care processes[40]. A risk-adjuster that identifies post-surgical complications (e.g., pneumonia, skin ulcers, or infection) as pre-existing comorbidities, particularly complications that increase the risk of death but that may be related more to processes of care than to specific patient characteristics, as may erroneously lead to lower risk-adjusted mortality rates among hospitals that provide poor quality care.
In other settings, both the CCS and the Charlson indices have performed more favorably than shown here. When used to predict mortality among elderly myocardial infarction patients in Medicare claims data, they performed in the good to excellent range, with c-statistics of 0.74 and 0.82 for the Charlson and CCS indices, respectively [28]. This discrepant performance may result from differences in the illness burden among hip fracture patients compared to myocardial infarction patients.
Although our findings may be discouraging for researchers seeking a risk-adjustment instrument to use among persons with hip fracture, there may be few better alternatives for this population. Other risk-adjustment instruments used in hip fracture cohorts include the Chronic Disease Score (CDS) [41], the RAND Sickness at Admission Score[16, 42, 43], and the Acute Physiology and Chronic Health Evaluation (APACHE) score [42, 43 ]. As CDS uses prescription drug utilization to predict patient outcomes, it is difficult to apply to cohorts defined from Medicare claims, which have limited prescription drug data. The RAND and APACHE instruments perform well in predicting post-fracture locomotion, adverse events, and mortality, but require more detailed clinical information than are available from the standard diagnoses contained in administrative claims. Schwartz et al. have compared several measures of patient disease severity on ability to predict length of stay (LOS) among persons with hip fracture. Included were 14 severity measures that came from a wide range of input data, including diagnostic codes as well as observed clinical data. The authors reported that these measures of severity had little ability to explain variations in LOS across hospitals[44], while their clinical detail make these data difficult for hospitals, payers, and other decision makers to obtain.
Several limitations suggest that care should be taken when interpreting the results of this analysis. There is inherent difficulty in distinguishing complications from comorbidities when relying on diagnosis codes in administrative data [32, 38, 45]. This misclassification is particularly threatening when diagnoses are drawn from the index admission, but can be minimized by considering only those diagnoses present during the pre-period. This analysis evaluated model performance when diagnoses were drawn from the index admission, the pre-period alone, and from both simultaneously and found relatively little difference in most cases.
The CCS was designed to simply group diagnoses, not necessarily for risk-adjustment. While its ability to predict mortality has been validated in administrative data [28], its use may pose two distinct problems. First, many of its classification categories are irrelevant for an elderly population. Inclusion of these categories would likely weaken this instrument’s performance in a prediction model since many cohort members who do not have the outcome could potentially be flagged with comorbid conditions that do little to predict mortality. The second problem using the CCS poses is more serious, but again is related to the volume of disease categories that it defines. In this case, there is concern that some of the disease categories may represent complications of fracture-related care rather than pre-existing illness. Including these would likely increase the instrument’s ability to predict death since complications probably place an affected individual at greater risk of death. Considering diagnoses in these classification categories as comorbidities of hip fracture could confound our results and lead to erroneous conclusions regarding CCS’s predictive ability among hip fracture patients. With regard to each of these problems, the similarity between the modified and unmodified model results suggests these biases had little effect on our analyses and confirm the CCS’s admirable predictive ability.
Caution is needed when the performance of several risk-adjustment tools is compared, since each instrument identifies comorbid conditions based on a slightly different set of diagnostic codes[25]. We were able to make valid comparisons across instruments because we applied them to the same population, with a constant distribution of comorbid conditions.
Conclusion
Effective and freely available risk-adjustment strategies that are fairly straightforward to implement exist for claims-based analyses of individuals with hip fracture. Altering the source data (MedPar vs. Part B claims) and time frame (index event vs. the year preceding the index event) used to identify comorbid conditions offers only a marginal advantage for predicting one-year mortality among hip fracture patients. When predictive ability is similar for different risk-adjustment instruments, model performance should be weighed against complexity and ease of use.
Acknowledgments
This research was funded by a grant (AG12262) that is co-funded by the National Institute on Aging and the National Institute for Arthritis, Musculoskeletal and Skin Diseases.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.U.S. Department of Health and Human Services. Bone Health and Osteoporosis: A Report of the Surgeon General. Rockville, MD: U.S. Department of Health and Human Services, Office of the Surgeon General; 2004. [Google Scholar]
- 2.Roche JJ, Wenn RT, Sahota O, Moran CG. Effect of comorbidities and postoperative complications on mortality after hip fracture in elderly people: prospective observational cohort study. BMJ. 2005;331(7529):1374. doi: 10.1136/bmj.38643.663843.55. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Wehren LE, Hawkes WG, Orwig DL, Hebel JR, Zimmerman SI, Magaziner J. Gender differences in mortality after hip fracture: the role of infection. J Bone Miner Res. 2003;18(12):2231–7. doi: 10.1359/jbmr.2003.18.12.2231. [DOI] [PubMed] [Google Scholar]
- 4.Myers AH, Robinson EG, Van Natta ML, Michelson JD, Collins K, Baker SP. Hip fractures among the elderly: factors associated with in-hospital mortality. Am J Epidemiology. 1991;134(10):1128–37. doi: 10.1093/oxfordjournals.aje.a116016. [DOI] [PubMed] [Google Scholar]
- 5.Lenze EJ, Munin MC, Skidmore ER, Amanda Dew M, Rogers JC, Whyte EM, et al. Onset of depression in elderly persons after hip fracture: implications for prevention and early intervention of late-life depression. J Am Geriatr Soc. 2007;55(1):81–6. doi: 10.1111/j.1532-5415.2006.01017.x. [DOI] [PubMed] [Google Scholar]
- 6.Magaziner J, Hawkes W, Hebel JR, Zimmerman SI, Fox KM, Dolan M, et al. Recovery from hip fracture in eight areas of function. J Gerontol A Biol Sci Med Sci. 2000;55(9):M498–507. doi: 10.1093/gerona/55.9.m498. [DOI] [PubMed] [Google Scholar]
- 7.Gehlbach SH, Avrunin JS, Puleo E. Trends in hospital care for hip fractures. Osteoporos Int. 2007;18(5):585–91. doi: 10.1007/s00198-006-0281-0. [DOI] [PubMed] [Google Scholar]
- 8.Burge R, Dawson-Hughes B, Solomon DH, Wong JB, King A, Tosteson ANA. Incidence and Economic Burden of osteoporosis-related fractures in the United States, 2005–2025. J Bone Miner Res. 2007;22(3):465–75. doi: 10.1359/jbmr.061113. [DOI] [PubMed] [Google Scholar]
- 9.Charlson ME, Pompei P, Ales KL, MacKenzie CR. A new method of classifying prognostic comorbidity in longitudinal studies: development and validation. J Chronic Dis. 1987;40(5):373–83. doi: 10.1016/0021-9681(87)90171-8. [DOI] [PubMed] [Google Scholar]
- 10.Deyo RA, Cherkin DC, Ciol MA. Adapting a clinical comorbidity index for use with ICD-9-CM administrative databases. J Clin Epidemiol. 1992;45(6):613–9. doi: 10.1016/0895-4356(92)90133-8. [DOI] [PubMed] [Google Scholar]
- 11.Starfield B, Weiner J, Mumford L, Steinwachs D. Ambulatory care groups: a categorization of diagnoses for research and management. Health Serv Res. 1991;26(1):53–74. [PMC free article] [PubMed] [Google Scholar]
- 12.Ellis RP, Pope GC, Iezzoni L, Ayanian JZ, Bates DW, Burstin H, et al. Diagnosis-based risk adjustment for Medicare capitation payments. Health Care Financ Rev. 1996;17(3):101–28. [PMC free article] [PubMed] [Google Scholar]
- 13.Clark DO, Von Korff M, Saunders K, Baluch WM, Simon GE. A chronic disease score with empirically derived weights. Med Care. 1995;33(8):783–95. doi: 10.1097/00005650-199508000-00004. [DOI] [PubMed] [Google Scholar]
- 14.Gilmer T, Kronick R, Fishman P, Ganiats TG. The Medicaid Rx model: pharmacy-based risk adjustment for public programs. Med Care. 2001;39(11):1188–202. doi: 10.1097/00005650-200111000-00006. [DOI] [PubMed] [Google Scholar]
- 15.Kronick R, Dreyfus T, Lee L, Zhou Z. Diagnostic risk adjustment for Medicaid: the disability payment system. Health Care Financ Rev. 1996;17(3):7–33. [PMC free article] [PubMed] [Google Scholar]
- 16.Keeler EB, Kahn KL, Draper D, Sherwood MJ, Rubenstein LV, Reinisch EJ, et al. Changes in sickness at admission following the introduction of the prospective payment system. JAMA. 1990;264(15):1962–8. [PubMed] [Google Scholar]
- 17.Romano PS, Roos LL, Jollis JG. Adapting a clinical comorbidity index for use with ICD-9-CM administrative data: differing perspectives. J Clin Epidemiol. 1993;46(10):1075–9. doi: 10.1016/0895-4356(93)90103-8. [DOI] [PubMed] [Google Scholar]
- 18.Ash A, Porell F, Gruenberg L, Sawitz E, Beiser A. Adjusting Medicare capitation payments using prior hospitalization data. Health Care Financ Rev. 1989;10(4):17–29. [PMC free article] [PubMed] [Google Scholar]
- 19.Elixhauser A, Steiner C, Harris DR, Coffey RM. Comorbidity measures for use with administrative data. Med Care. 1998;36(1):8–27. doi: 10.1097/00005650-199801000-00004. [DOI] [PubMed] [Google Scholar]
- 20.Pope GC, Ellis RP, Ash AS, Liu CF, Ayanian JZ, Bates DW, et al. Principal inpatient diagnostic cost group model for Medicare risk adjustment. Health Care Financ Rev. 2000;21(3):93–118. [PMC free article] [PubMed] [Google Scholar]
- 21.Pope GC, Kautter J, Ellis RP, Ash AS, Ayanian JZ, Lezzoni LI, et al. Risk adjustment of Medicare capitation payments using the CMS-HCC model. Health Care Financ Rev. 2004;25(4):119–41. [PMC free article] [PubMed] [Google Scholar]
- 22.Fowles JB, Weiner JP, Knutson D, Fowler E, Tucker AM, Ireland M. Taking health status into account when setting capitation rates: a comparison of risk-adjustment methods. JAMA. 1996;276(16):1316–21. [PubMed] [Google Scholar]
- 23.Weiner JP, Dobson A, Maxwell SL, Coleman K, Starfield B, Anderson GF. Risk-adjusted Medicare capitation rates using ambulatory and inpatient diagnoses. Health Care Financ Rev. 1996;17(3):77–99. [PMC free article] [PubMed] [Google Scholar]
- 24.Klabunde CN, Potosky AL, Legler JM, Warren JL. Development of a comorbidity index using physician claims data. J Clin Epidemiol. 2000;53(12):1258–67. doi: 10.1016/s0895-4356(00)00256-0. [DOI] [PubMed] [Google Scholar]
- 25.Schneeweiss S, Wang PS, Avorn J, Glynn RJ. Improved comorbidity adjustment for predicting mortality in Medicare populations. Health Serv Res. 2003;38(4):1103–20. doi: 10.1111/1475-6773.00165. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Pine M, Jordan HS, Elixhauser A, Fry DE, Hoaglin DC, Jones B, et al. Enhancement of claims data to improve risk adjustment of hospital mortality. JAMA. 2007;297(1):71–6. doi: 10.1001/jama.297.1.71. [DOI] [PubMed] [Google Scholar]
- 27.Stukenborg GJ, Wagner DP, Connors AF., Jr Comparison of the performance of two comorbidity measures, with and without information from prior hospitalizations. Med Care. 2001;39(7):727–39. doi: 10.1097/00005650-200107000-00009. [DOI] [PubMed] [Google Scholar]
- 28.Ash AS, Posner MA, Speckman J, Franco S, Yacht AC, Bramwell L. Using claims data to examine mortality trends following hospitalization for heart attack in Medicare. Health Serv Res. 2003;38(5):1253–62. doi: 10.1111/1475-6773.00175. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Farley JF, Harley CR, Devine JW. A comparison of comorbidity measurements to predict healthcare expenditures. Am J Manag Care. 2006;12(2):110–9. [PubMed] [Google Scholar]
- 30.Perkins AJ, Kroenke K, Unutzer J, Katon W, Williams JW, Hope C, et al. Common comorbidity scales were similar in their ability to predict health care costs and mortality. J Clin Epidemiol. 2004;57(10):1040–8. doi: 10.1016/j.jclinepi.2004.03.002. [DOI] [PubMed] [Google Scholar]
- 31.Melfi C, Holleman E, Arthur D, Katz B. Selecting a patient characteristics index for the prediction of medical outcomes using administrative claims data. J Clin Epidemiol. 1995;48(7):917–26. doi: 10.1016/0895-4356(94)00202-2. [DOI] [PubMed] [Google Scholar]
- 32.Iezzoni LI, Daley J, Heeren T, Foley SM, Fisher ES, Duncan C, et al. Identifying complications of care using administrative data. Med Care. 1994;32(7):700–15. doi: 10.1097/00005650-199407000-00004. [DOI] [PubMed] [Google Scholar]
- 33.Healthcare Cost and Utilization Project (HCUP) Clinical Classifications Software (CCS) Rockville, MD: Agency for Healthcare Quality and Research; 1999. [Google Scholar]
- 34.Hanley J, McNeil B. The Meaning and Use of the Area under a Receiver Operating Characteristic (ROC) Curve. Radiology. 1982;143(1):29–36. doi: 10.1148/radiology.143.1.7063747. [DOI] [PubMed] [Google Scholar]
- 35.Hanley J, McNeil B. A Method of Comparing the Areas under Receiver Operating Characteristic Curves Derived from the Same Cases. Radiology. 1983;148(3):839–43. doi: 10.1148/radiology.148.3.6878708. [DOI] [PubMed] [Google Scholar]
- 36.Lemeshow S, Hosmer DW., Jr A review of goodness of fit statistics for use in the development of logistic regression models. Am J Epidemiol. 1982;115(1):92–106. doi: 10.1093/oxfordjournals.aje.a113284. [DOI] [PubMed] [Google Scholar]
- 37.Shwartz M, Ash AS. Evaluating Risk-Adjustment Models Empirically. In: Iezzoni L, editor. Risk Adjustment for Measuring Health Care Outcomes. Chicago: Health Administration Press; 2003. pp. 231–73. [Google Scholar]
- 38.Romano PS, Chan BK, Schembri ME, Rainwater JA. Can administrative data be used to compare postoperative complication rates across hospitals? Med Care. 2002;40(10):856–67. doi: 10.1097/00005650-200210000-00004. [DOI] [PubMed] [Google Scholar]
- 39.Iezzoni L. Coded Date from Administrative Sources. In: Iezzoni L, editor. Risk Adjustment for Measuring Health Care Outcomes. Vol. 3. Chicago: Health Administration Press; 2003. pp. 83–138. [Google Scholar]
- 40.AHRQ Quality Indicators. Guide to Inpatient Quality Indicators: Quality of Care in Hospitals - Volume, Mortaltiy, and Utilization [version 3.1] Rockville (MD): Agency for Healthcare Research and Quality (AHRQ); Mar 12, 2007. 2007. [Google Scholar]
- 41.Chan KA, Andrade SE, Boles M, Buist DS, Chase GA, Donahue JG, et al. Inhibitors of hydroxymethylglutaryl-coenzyme A reductase and risk of fracture among older women. Lancet. 2000;355(9222):2185–8. doi: 10.1016/S0140-6736(00)02400-4. [DOI] [PubMed] [Google Scholar]
- 42.Hannan EL, Magaziner J, Wang JJ, Eastwood EA, Silberzweig SB, Gilbert M, et al. Mortality and locomotion 6 months after hospitalization for hip fracture: risk factors and risk-adjusted hospital outcomes. JAMA. 2001;285(21):2736–42. doi: 10.1001/jama.285.21.2736. [DOI] [PubMed] [Google Scholar]
- 43.Halm EA, Magaziner J, Hannan EL, Wang JJ, Silberzweig SB, Boockvar K, et al. Frequency and impact of active clinical issues and new impairments on hospital discharge in patients with hip fracture. Arch Intern Med. 2003;163(1):108–13. doi: 10.1001/archinte.163.1.107. [DOI] [PubMed] [Google Scholar]
- 44.Shwartz M, Iezzoni LI, Ash AS, Mackiernan YD. Do severity measures explain differences in length of hospital stay? The case of hip fracture. Health Serv Res. 1996;31(4):365–85. [PMC free article] [PubMed] [Google Scholar]
- 45.Ghali WA, Quan H, Brant R. Risk adjustment using administrative data: impact of a diagnosis-type indicator. J Gen Intern Med. 2001;16(8):519–24. doi: 10.1046/j.1525-1497.2001.016008519.x. [DOI] [PMC free article] [PubMed] [Google Scholar]