The Curtius Rearrangement of Cyclopropyl- and Cyclopropenoyl Azides. A Combined Theoretical and Experimental Mechanistic Study

Abstract

A combined experimental and theoretical study addresses the concertedness of the thermal Curtius rearrangement. The kinetics of the Curtius rearrangements of methyl 1-azidocarbonyl cycloprop-2-ene-1-carboxylate and methyl 1-azidocarbonyl cyclopropane-1-carboxylate were studied by ¹H NMR spectroscopy, and there is close agreement between calculated and experimental enthalpies and entropies of activation. Density Functional Theory (DFT) calculations (B3LYP/6-311+G(d,p)) on these same acyl azides suggest gas phase barriers of 27.8 and 25.1 kcal/mol. By comparison, gas phase activation barriers for the rearrangement of acetyl, pivaloyl and phenyl azides are 27.6, 27.4 and 30.0 kcal/mol, respectively. The barrier for the concerted Curtius reaction of acetyl azide at the CCSD(T)/6-311+G(d,p) level exhibited a comparable activation energy of 26.3 kcal/mol. Intrinsic reaction coordinate (IRC) analyses suggest that all of the rearrangements occur by a concerted pathway with the concomitant loss of N₂. The lower activation energy for the rearrangement of methyl 1-azidocarbonyl cycloprop-2-ene-1-carboxylate relative to methyl 1-azidocarbonyl cyclopropane-1-carboxylate was attributed to a weaker bond between the carbonyl carbon and the three-member ring in the former compound. Calculations on the rearrangement of cycloprop-2-ene-1-oyl azides do not support π–stabilization of the transition state by the cyclopropene double bond. A comparison of reaction pathways at the CBS-QB3 level for the Curtius rearrangement versus the loss of N₂ to form a nitrene intermediate provides strong evidence that the concerted Curtius rearrangement is the dominant process.

Introduction

The transformation of an acyl azide into an isocyanate — the Curtius rearrangement — is a broadly useful method for the synthesis of amine derivatives from carboxylic acids (Eq 1).¹ The mechanism of the Curtius rearrangement has been a question of longstanding interest. The rearrangement of acyl azides to isocyanates represents a classic example of a 1,2 nucleophilic shift where the migrating group carries a pair of electrons, and the migration terminus is an atom with a formal open sextet. While early mechanistic proposals for the Curtius rearrangement invoked the intermediacy of acylnitrenes,² experimental studies suggested that the thermal rearrangement is a concerted process^3,4 that occurs with retention of configuration.^4b Most notably, extensive experimental studies by Lwowski and coworkers^4c–4e failed to intercept pivaloylnitrene upon pyrolysis of pivaloyl azide. Pivaloylnitrene, generated photolytically from pivaloyl azide did not rearrange to pivaloyl isocyanate, and both singlet and triplet pivaloylnitrene were excluded as intermediates in both thermal and photo-induced Curtius rearrangement of pivaloyl azide.^4c–e Resonance interactions in phenyl substituents are known to influence the aryl migration rate. It has also been established that electron releasing groups in the meta position of benzoyl azides increase the rate of rearrangement while all para substituents decrease the rate.^1c,5

(1)

In theoretical studies⁶, Hadad, Platz and coworkers studied the Curtius rearrangements of acetyl azide at several levels of theory (B3LYP/6-31+G**, CCSD(T), and CBS-QB3).⁷ Acyl azides can exist as both syn and anti conformations with respect to the C-N bond. We refer to these conformations as syn_C-N and anti_C-N, respectively. DFT and CBS-QB3 calculations suggest that the conformer of MeC(O)N₃ with the syn_C-N relationship between the carbonyl and azide group is 4.5–4.8 kcal/mol more stable than the anti_C-N conformer⁷. This is an important distinction because rearrangements of syn_C-N acyl azides have been calculated to proceed by a concerted mechanism while the higher energy anti_C-N conformers tend to follow the stepwise pathways that produce acylnitrene intermediates.^7,8 It was concluded that the syn_C-N conformer of acetyl azide rearranges by a concerted mechanism to methylisocyanate with a barrier of ~27 kcal/mol, whereas the calculated barrier for the formation of acetylnitrene, with the attendant loss of N₂, was calculated to be higher (32 kcal/mol) leading to the suggestion that a free nitrene is not produced in the pyrolysis of acetyl azide. However, it was recognized that the relative barriers for concerted versus stepwise Curtius rearrangement could be sensitive to the substituent on the carbonyl group. It was shown that for methoxycarbonyl azide the stepwise process to generate the free nitrene was favored over concerted rearrangement, an observation that is consistent with accompanying experimental studies of alkoxycarbonyl azides that do produce trappable nitrenes upon thermolysis.⁷ Although an experimental study on acetyl azide is not available for direct comparison, the calculated barrier for the concerted rearrangement of acetyl azide is in reasonable agreement with the experimentally determined barriers for thermal Curtius rearrangements of other acyl azides.^1c,3c,5

A subsequent DFT study on the Curtius rearrangement was conducted by Zabalov and Tiger at the PBE/TZ2P level of theory.⁸ The barriers to concerted rearrangement of several syn_C-N and anti_C-N acyl azide conformers, versus the loss of N₂ and formation of the corresponding nitrene, were reported for formyl azide (28.0 vs 34.6 kcal/mol), acetyl azide (32.9 vs 32.9 kcal/mol), and benzoyl azide (34.5 vs 32.3 kcal/mol), respectively.⁸ Because of the additional barrier associated with the subsequent rearrangement of the acylnitrenes to the isocyanates (20.9, 18.9 and 13.6 kcal/mol, respectively) in a two-step process, these authors concluded that overall concerted pathways would be predominant. Thus, calculated relative activation barriers suggest that rearrangement of acyl azides by the one-step concerted mechanism is preferable to the two-step process involving formation of acylnitrene.⁸

However, in a more recent computational study at the Moller Plesset ((MP2)(full)/6-31G*) level of theory, it was proposed that the thermal rearrangements of acetyl azide and benzoyl azide are stepwise processes that proceed via acylnitrene intermediates.⁹ The activation energies for the formation of acetylnitrene was calculated to be 39.2 kcal/mol, and the transition state for the conversion of the nitrene into methylisocyanate was 55.6 kcal/mol relative to the acyl azide ground state. Similarly, unusually large activation energies were calculated for the formation of benzoylnitrene (47.8 kcal/mol) and phenylisocyanate (64.6 kcal/mol) relative to the benzoyl azide ground state. By contrast, a single transition state was located for the rearrangement of formyl azide to isocyanate with an activation energy of 37.5 kcal/mol.

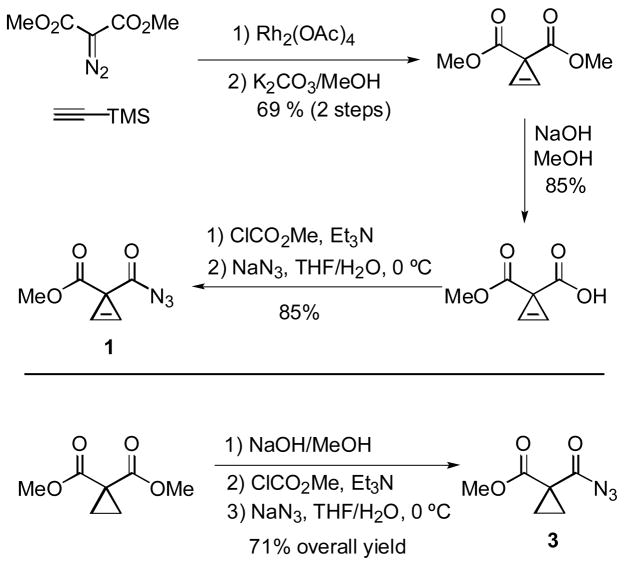
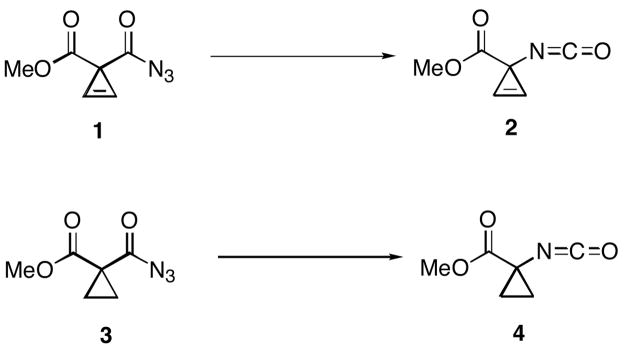
In light of these conflicting conclusions regarding the thermal Curtius rearrangement, we considered that a combined theoretical and experimental study might provide additional insight into the mechanism. In the course of our studies on the synthesis and application of cyclopropene α-amino acids,¹⁰ we noticed that acyl azides of cyclopropene-bis-carboxylic acids undergo Curtius rearrangement with unusual facility. Thus, cycloprop-1-enoyl azide 1 undergoes rearrangement to isocyanate 2 to >90% conversion within 24 h at room temperature, whereas elevated temperatures have been reported for similar rearrangements of acyl azides derived from malonic acid.¹¹ As a control, we synthesized the cyclopropane analog 3, and noted that a significantly higher reaction temperature was required for conversion into isocyanate 4 within a similar timeframe. An intriguing explanation for the accelerated rearrangement of 1 relative to 3 would invoke π–stabilization of the transition state(s) for rearrangement of the former by involvement of the π-bond of the highly strained alkene. Alternatively, a simpler explanation would invoke the differing C-C bond strengths¹² of the acyl bonds to cyclopropenes and cyclopropanes as discussed below. An accurate theoretical method should be capable of affirming the origin of this reactivity trend.

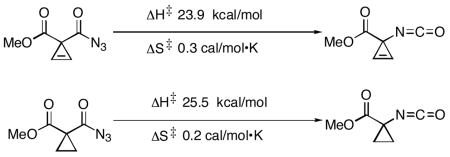
Given the unusual reactivity of 1, we considered that this rearrangement might deviate from the generic Curtius rearrangement pathway. Herein, it is shown that the activation energies calculated by Density Functional Theory (DFT) are in close agreement with experimentally measured free energies of activation for the rearrangements of 1 (23.8 kcal/mol by experiment; 25.1 kcal/mol by calculation) and 3 (25.5 kcal/mol by experiment; 27.8 kcal/mol by calculation). In both rearrangements, small entropies of activation were measured (0.3 and 0.2 cal/mol•K for 1 and 3, respectively). These measurements are consistent with the calculated entropies (3.1 cal/mol•K for 1, 3.7 cal/mol•K for 3), and the location of early transition states in which N₂ bond breakage is not far advanced. Calculations were also carried out on the rearrangements of acetyl azide, benzoyl azide, and pivaloyl azide. In each case, concerted rearrangement to the isocyanate was observed with barriers of 27.6, 30.0 and 27.4 kcal/mol, respectively.

Results and Discussion

Experimental Results

Acyl azide 1 was prepared from dimethyl diazomalonate as shown in Scheme 2. Dimethyl cycloprop-2-ene-1, 1-bis-carboxylic ester was synthesized with a modification of Gevorgyan’s protocol,¹³ and subsequent conversion into 1 was accomplished with a modified version of Wheeler and Ray’s procedure.¹⁴ Analogously, acyl azide 3 was prepared from dimethyl cyclopropane-1, 1-bis-carboxylic ester (Scheme 2).

Scheme 2.

Synthesis of acyl azides 1 and 3

Kinetic measurements

NMR spectroscopy was used to monitor reactions for the disappearance of 1 and 3. The peaks assigned to the methyl esters of 1 (3.38 ppm) and of 3 (3.34 ppm) were integrated, depending on the rate of rearrangement, every 20 to 144 seconds over the entire course of the reaction. This in situ method allows for the collection of many data points, as is desired for accurate rate determination. First order rate constants were measured in duplicate runs by monitoring the disappearance of 1 at 30, 40 and 50 °C, and the disappearance of 3 at 50, 61 and 71 °C. The Arrhenius equation was used to calculate the activation energies, and Eyring analyses were used to determine the free energies of activation, the enthalpies of activation, and the entropies of activation for the Curtius rearrangements of 1 and 3. The kinetic data is summarized in Table 1.

Table 1.

Kinetic measurements on Curtius rearrangements of 1 and 3

Temp	k	t1/2	Ea 24.5 (1.3) kcal/mol
30 °C	4.58 (0.22)a × 10−5	252 min	ΔG‡ 23.8 (1.8) kcal/mol
40 °C	1.75 (0.14) × 10−4	66 min	ΔH‡ 23.9 (1.3) kcal/mol
50 °C	5.65 (0.33) × 10−4	20 min	ΔS‡ 0.3 (7.1) cal/mol•K
Temp	k	t1/2	Ea 26.2 (1.4) kcal/mol
50 °C	3.95 (0.09) × 10−5	292 min	ΔG‡ 25.5 (2.0) kcal/mol
61 °C	1.51 (0.14) × 10−4	76 min	ΔH‡ 25.5 (1.4) kcal/mol
71 °C	4.77 (0.38) × 10−4	24 min	ΔS‡ 0.2 (7.3) cal/mol•K

^aThe sample standard deviation is listed in parenthesis.

The Curtius rearrangements of 1 and 3 proceed in high yield as determined by analysis of the crude NMR spectra: 3 and 4 are both formed in >95% purity. The free energy of activation for the rearrangement of 1 was measured to be 23.8 kcal/mol. The free energy of activation energy for the rearrangement of 3 was 25.5 kcal/mol. Small, positive entropies of activations (0.2–0.3 cal/mol•K) were measured both for the rearrangements of 1 and 3. At 50 °C, the relative rates of Curtius rearrangements for 1 and 3 could be directly compared: the rearrangement of 1 is 14 times faster than that of 3.

Theoretical results

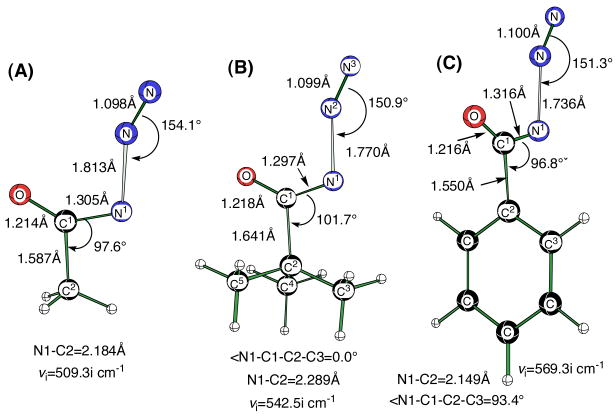
In order to establish reliable theoretical activation barriers for the Curtius rearrangement of 1 and 3, we first revisited the calculated activation barriers for several more simple acyl azides. In this manner, it was possible to establish the accuracy of our DFT calculations relative to the earlier studies described above.^7–9 The calculated DFT activation barrier (Figure 1) for the concerted Curtius rearrangement on acetyl azide was 27.6 kcal/mol [B3LYP/6-311+G(d,p)]. This barrier is comparable to that reported earlier for syn_C-N acetyl azide at CBS-QB3 (27 kcal/mol), and significantly lower than the reported barrier for the formation of the corresponding nitrene (32 kcal).⁷

Figure 1.

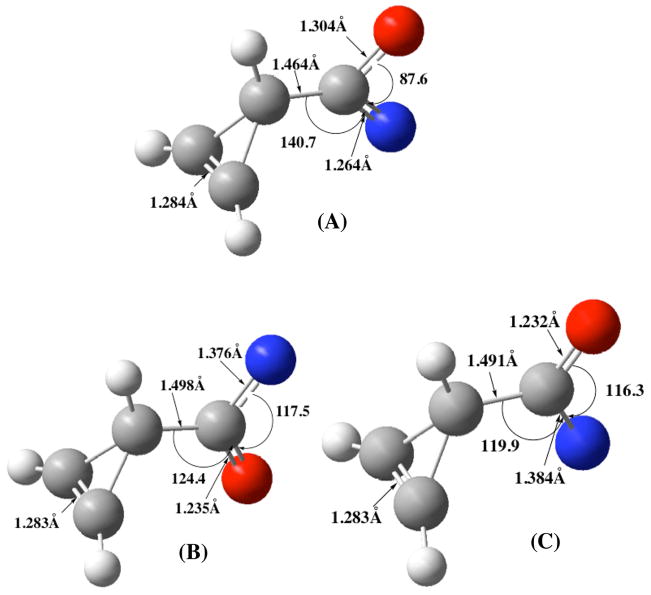
Transition structures for the Curtius rearrangement on syn_C–N conformers of acetyl azide, pivaloyl azide and benzoyl azide. Transition structures were optimized at the B3LYP/6-311+G(d,p) level of theory. (A) Δ(E+ZPVE)^‡ =27.6 kcal/mol. (B) Δ(E+ZPVE)^‡ =27.4 kcal/mol. (C) Δ(E+ZPVE)^‡ =30.0 kcal/mol.

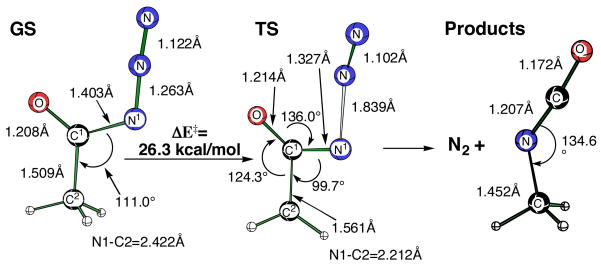
These Curtius rearrangement barriers did not change significantly with a higher degree of electron correlation. The CCSD(T)/6-311+G(d,p) activation energy for this concerted exothermic (ΔE = 53.9 kcal/mol) loss of N₂ from acetyl azide was ΔE^‡ = 26.3 kcal/mol (Figure 2).

Figure 2.

Activation barrier for concerted acetyl azide rearrangement at the CCSD(T)/6-311+G(d,p) level. Total reaction exothermicity for the formation of methylisocyanate is ΔE = −53.9 kcal.

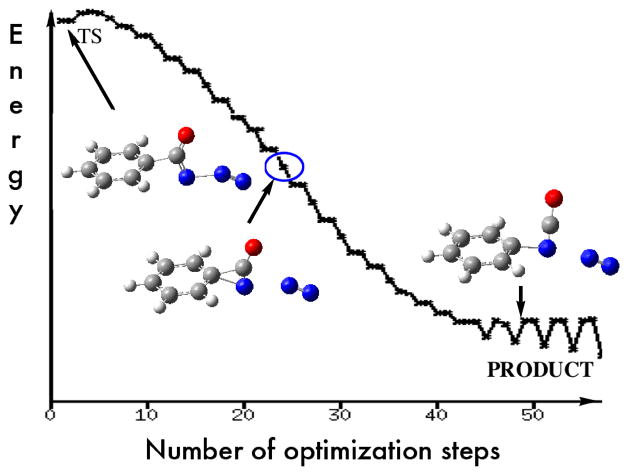
Steric factors do not seem to play a measurable role in the Curtius reaction because concerted 1,2-migration of the t-butyl group in pivaloyl azide (Figure 1) had essentially the same barrier as that for CH₃ migration with the acetyl group. A slightly larger activation energy was calculated for phenyl migration (30.0 kcal/mol). A possible reason for the higher barrier is that the phenyl and the carbonyl groups of benzoyl azide are conjugated in the ground state, but not in the transition state of the rearrangement where the benzene ring is essentially orthogonal to the C=O group.⁵ An IRC analysis supports the concerted rearrangement mechanism with bonding of the benzene ipso-carbon atom to the nitrogen atom at the migration terminus with concomitant loss of N₂ as suggested by several snapshots along the reaction pathway (Figure 3). Examination of the molecular orbitals in this transition state also shows a definite overlap of the ipso carbon atomic p-orbital overlapping with both the carbonyl carbon and the nitrogen terminus in the HOMO-3 orbital (∠N₁-C₁-C₂-C₃ = 93.4°, Figure 1). Thermal decomposition of benzoyl azide in toluene and in n-heptane exhibited enthalpies of activation of 27.1 and 31.6 kcal/mol^1c in excellent agreement with our gas phase calculations.

Figure 3.

Snapshots along the reaction pathway from the transition state to product for the Curtius reaction of benzoyl azide.

Additional evidence that these are indeed concerted rearrangements comes from an analysis of the potential energy surface (PES) for acetyl azide. Concerted rearrangement is evidenced by an IRC calculation (DFT) that proceeds from the transition state down to methylisocyanate with the N₂ molecule weakly bound to the developing NCO central carbon atom as depicted in Figure 2 for the CCSD surface. Along the 1,2-methyl migration pathway, the N–C–C bond angle in the transition state (Figure 2, 99.7°) contracts to about 70° as the 1,2-methyl migration to nitrogen takes place. At no point on the PES is expansion of the N–C–C angle observed, as would be required for formation of a singlet nitrene (141.5°). Similarly, the N-C-O angle in the transition state (136.0°) continues to expand as it approaches 180° and shows no sign of contracting to the 86.6° in acylnitrene.

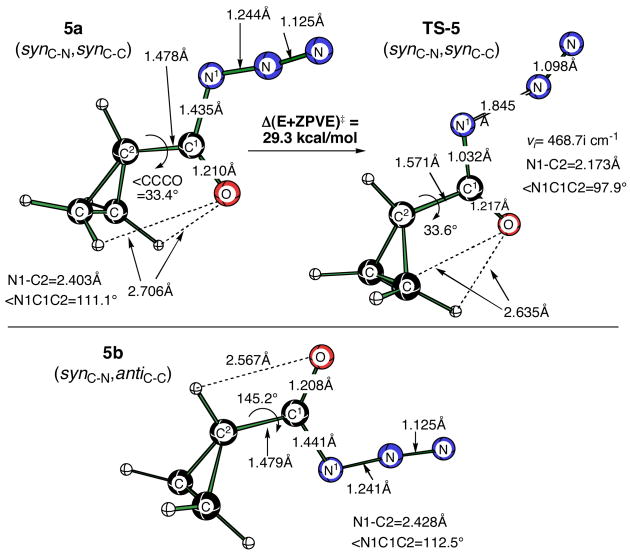
DFT calculations were also performed for a series of model cyclopropyl compounds that are related to those that were examined experimentally. The simplest cyclopropanoyl azide can exist as four basic conformers [B3LYP/6-311+G(d,p)] that include both syn and anti relationships of the carbonyl oxygen with respect to the azide group and the cyclopropyl ring. These stereochemical relationships are referred to as syn_C-N/anti_C-N and syn_C-C/anti_C-C, respectively. The current study was restricted to the syn_C-N conformation that is required for concerted Curtius rearrangement. Calculations were performed for both syn_C-C and anti_C-C conformations. The syn_C-N, syn_C-C conformer 5a is 1.06 kcal/mol lower in energy than syn_C-N, anti_C-C conformer 5b (Figure 4). Similarly, the concerted TS-5(syn_C-N, syn_C-C) for the Curtius rearrangement is 2.2 kcal/mol lower in energy than TS-5(syn_C-N, anti_C-C) (not shown). TS-5(syn_C-N, syn_C-C) exhibits an activation barrier with ZPE corrections of 29.3 kcal/mol (ν_i= 468.7i cm⁻¹), a barrier that is 1.7 kcal/mol higher than that calculated for the simplest acyl azide, acetyl azide.

Figure 4.

Minima of the (syn_C-N, syn_C-C) and (syn_C-N, anti_C-C) conformers of cyclopropanoyl azide (5a and 5b), and TS-5(syn_C-N, syn_C-C) (ΔE^‡ =29.3 kcal/mol) optimized at the B3LYP/6-311+G(d,p) level of theory.

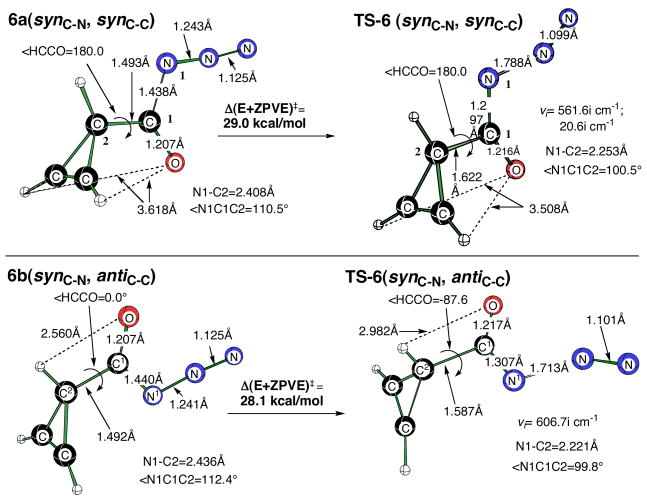
In an effort to better understand the origin of the more facile Curtius rearrangement attributed to the presence of a carbon-carbon double bond in 1, we next calculated rearrangement barriers with the corresponding cyclopropene derivatives. The syn_C-N, syn_C-C isomer of the parent cycloprop-1-enoyl azide 6a is slightly more stable (0.26 kcal/mol) than the syn_C-N, anti_C-C isomer 6b (Figure 5). The syn_C-N, syn_C-C activation barrier of 29.0 kcal/mol (ν_i= 561.5i cm⁻¹) for this cyclopropene derivative is 0.9 kcal/mol higher than TS-6(syn_C-N, syn_C-C) (ν_i= 606.8i cm⁻¹).

Figure 5.

Minima of the (syn_C-N, syn_C-C) and (syn_C-N, anti_C-C) conformers of cycloprop-1-enoyl azide (6a and 6b) and the corresponding transition structures [TS-6(syn_C-N, syn_C-C) – a second-order saddle point and TS-6(syn_C-N, anti_C-C)] optimized at the B3LYP/6-311+G(d,p) level of theory.

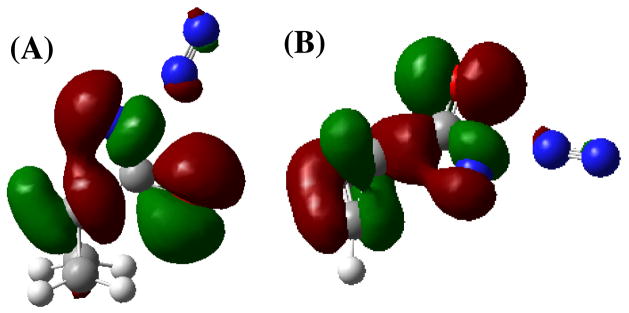
If there is any π–stabilization of TS-6(syn_C-N, anti_C-C) by the cyclopropene double bond, it is only a modest effect. In TS-6(syn_C-N, anti_C-C) the distance to N¹ appears to be too great for extensive interaction with the π-bond. More importantly, the effect of the alkene results in only a 1.2 kcal/mol reduction in activation energy relative to that of cyclopropyl TS-5(syn_C-N, syn_C-C). Attempts to locate a syn-syn TS, where the geometry precludes π–stabilization, resulted in a second-order saddle point that is only 0.9 kcal/mol higher in energy than that of first-order saddle point, TS-6(syn_C-N, anti_C-C). Re-optimization of the second order saddle point TS-6(syn_C-N, syn_C-C) (Figure 5) led to TS-6(syn_C-N, anti_C-C), with a dihedral angle between the C=C bond and the N-C=O fragment of essentially zero (< C-C-N-O = 0.92°). Based on these observations, it is plausible that the C=C π-bond of TS-6(syn_C-N, anti_C-C) may offer a small stabilization to the N-C=O π-system by a through-space interaction. Nonetheless, we conclude that the energetics simply do not support a meaningful π–interaction in the transition state. Additional support for a concerted Curtius rearrangement for syn_C-N acyl azides comes from plotting the HOMO orbitals for TS-5(syn_C-N, syn_C-C)and TS-6(syn_C-N, anti_C-C) that clearly evidences an overlap of the migrating carbon atom and the nitrogen atom of the migration terminus (Figure 6).

Figure 6.

HOMO orbitals for (A) TS-5(syn_C-N, syn_C-C) and (B) TS-6(syn_C-N, anti_C-C)

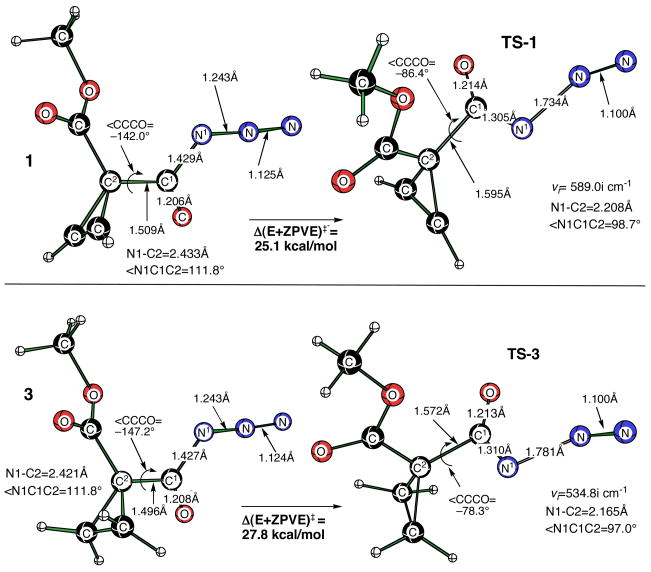
In order to examine the effect of the ester group on the reaction rate we also carried out calculations on the Curtius reactions for 1 and 3 (Figure 7). The activation barrier for saturated cyclopropyl derivative, TS-3 (27.8 kcal/mol, ν= 534.8 cm⁻¹) was reduced by 1.5 kcal/mol relative to the parent cyclopropanoyl TS-5(syn_C-N, syn_C-C) as a consequence of adding the ester functionality. More importantly, the barrier for the unsaturated cycloprop-1-enoyl ester (TS-1) was 2.65 kcal/mol lower than that of the saturated ester (TS-3) in good agreement with the experimental energy difference (ΔE_a= 1.7 kcal/mol). When the role of solvent (toluene) was examined using the CPCM (Cosmo) solvent model we observed a comparable ΔΔE^‡=2.53 kcal/mol for these two transition states. An IRC analysis starting from both transition states in the forward direction clearly showed migration of the cyclopropyl carbon to the migration terminus (nitrogen) with the concomitant loss of N₂, while the reverse IRC pathway generated ground state acyl azides. We also examined TS-1 and TS-3 with a different DFT variant (mPW1PW/6-31G(d)) that has been reported to treat both covalent and noncovalent interactions quite satisfactorily.¹⁸ We again found a comparable ΔΔE^‡=2.86 kcal/mol for the two transition states (see Supporting Information).

Figure 7.

Structures of 1, 3 minima and their corresponding transition structures, TS-1 and TS-3, optimized at the B3LYP/6-311+G(d,p) level of theory.

DFT calculations support the conclusions reached thus far about the concerted nature of the Curtius rearrangement of syn_C–N acyl azides. To support these conclusions, energy refinement calculations were carried out on selected key acyl azides at the CBS-QB3 level of theory. Platz and coworkers used this method to check the ground state electronic configuration of several acylnitrenes because DFT theory sometimes improperly assigned singlet versus triplet ground states for acylnitrenes.⁷ If acylnitrenes could potentially form along the reaction pathway, then the correct assignment for the electronic state is of primary importance. Additionally, the CBS-QB3 method provides a level of accuracy comparable to that of G3 theory that typically provides geometries within experimental accuracy.²⁰

Studies were focused on the rearrangement of cycloprop-2-enoyl azide 6. This acyl azide was chosen for study because it rearranges with the lowest barrier, and might therefore be most likely to deviate from a concerted mechanism. A striking observation is that the syn_C-C–cycloprop-1-enoylnitrene [corresponding to 6a (Figure 5)] does not exist as a minimum on the singlet surface. The syn_C-C–singlet nitrene immediately rearranges to the corresponding isocyanate precluding the formation of a discrete singlet nitrene intermediate from this conformer on the PES. The anti_C-C singlet nitrene (Figure 8a) exhibits the relatively closed N-C-O angle (87.6°) alluded to above. That same angle for the triplet nitrenes is much wider. On the triplet surface both syn_C-C and anti_C-C–nitrenes exist as minima, with the syn_C-C–arrangement of the cyclopropenoyl ring with respect to the carbonyl group being preferred by 0.31 kcal/mol. More importantly, at the CBS-QB3 level the anti_C-C singlet nitrene is predicted to be the ground state (ΔE = 2.50 kcal/mol) as suggested by earlier calculations by Platz and coworkers⁷ on related nitrenes. These data provide confidence that the above transition structures on the singlet surface are adequately represented by DFT theory.

Figure 8.

Cycloprop-2-enoyl anti_C-C singlet nitrene (A), syn_C-C triplet nitrene (B), and anti_C-C triplet nitrene (C) at the CBS-QB3 level of theory.

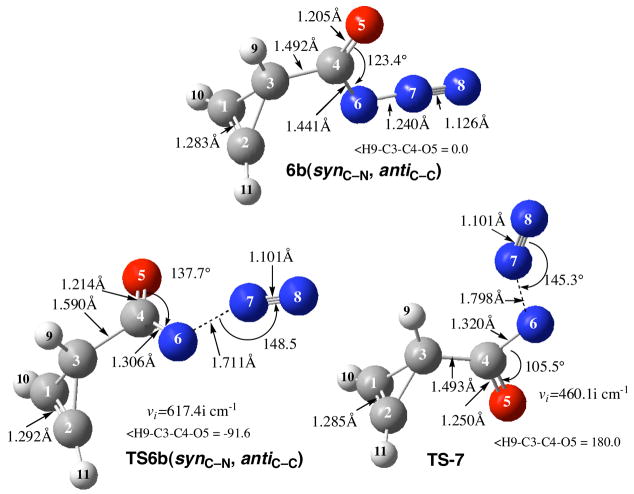
Interestingly, the anti_C-N, anti_C-C conformer of cycloprop-1-enoyl azide (not shown) does not exist as a minimum but rotates about the C-C bond to produce syn_C-N-anti_C-C-cycloprop-1-enoyl azide 6b. We have therefore located the transition state for the Curtius rearrangement of the syn_C-N, anti_C-C isomer of cycloprop-1-enoyl azide 6b at the CBS-QB3 level of theory (Figure 9). Again, it was observed that the N-C-O fragment was twisted by nearly 90° in TS-6b(syn_C-N, anti_C-C) (<H⁹-C³-C⁴-O⁵ = −91.6°) and the activation barrier (ΔE^‡ = 29.3 kcal/mol) was quite comparable to that at the DFT level (Figure 5). Perhaps of more relevance to the primary question at hand, the degree of concertedness of the rearrangement, animation of the single imaginary frequency (v_i= 617.4i cm⁻¹) for TS-6b(syn_C-N, anti_C-C) clearly evidenced involvement of the cycloprop-1-enoyl moiety including the vinyl hydrogens. The migration terminus nitrogen (N⁶) was oscillating between the cyclopropene carbon (C³) and the departing nitrogen (N⁷). Although the largest contribution to the vector comes from breaking the N⁶-N⁷ bond, the C³-C⁴-N⁶ and C³-C⁴-O⁵ bond angles were clearly involved. It is concluded that this is a concerted process with alkyl migration in concert with the loss of N₂ and formation of the isocyanate.

Figure 9.

Minimum [6b(syn_C-N, anti_C-C)] and transition structure [TS-6b(syn_C-N, anti_C-C)] for the Curtius rearrangement, and the transition state for loss of N₂ (TS-7) to form cycloprop-2-enoylnitrene at the CBS-QB3 level of theory.

For comparison, we also located the transition state for loss of N₂ from 6b to form the cycloprop-2-enoylnitrene that provided further support for the concerted nature of the Curtius rearrangement. Although the TS-7 (syn_C-N, anti_C-C) (Figure 9) was only 2.9 kcal/mol higher in energy than the Curtius transition state [TS-6b(syn_C-N, anti_C-C], there is a mechanistic difference between the two pathways. Animation of the single imaginary frequency for this transition state (v_i=−460.1i cm⁻¹) showed that it contained essentially no contribution from the cyclopropene moiety and was comprised largely of N⁶-N⁷ bond breaking and a modest contribution from the N⁶-C⁴-O⁵ angle that disclosed a wagging of the carbonyl oxygen as the N₂ departed. The <H⁹-C³-C⁴-O⁵ dihedral angles (180.0° and −91.6°) for these two transition states also clearly distinguish the two mechanisms.

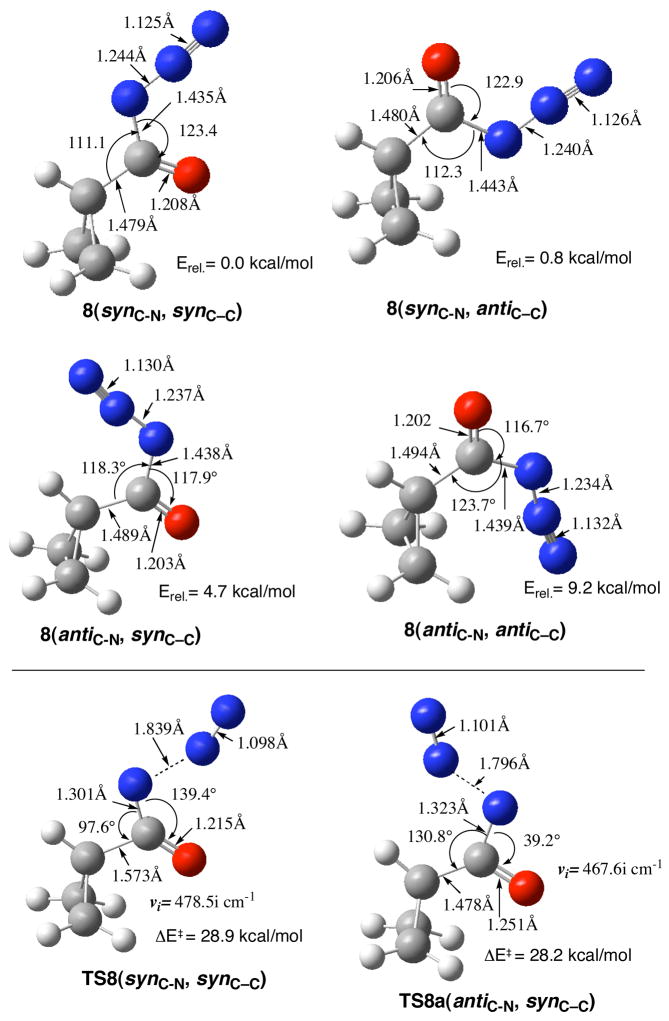
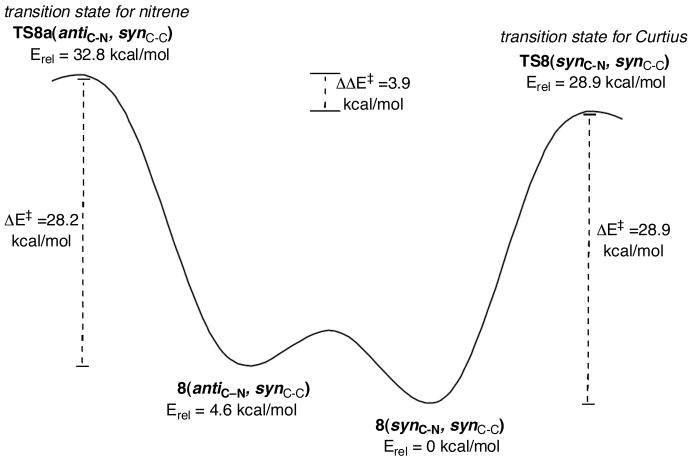
A very similar picture emerged when we examined the transition structures for rearrangement versus loss of N₂ from the cyclopropanoyl azides at the CBS-QB3 level. First, we provide the relative energies of four of the potential conformers involved in the rearrangement. The ground state conformer of cyclopropanoyl azide 8(syn_C-N, syn_C-C) undergoes the Curtius rearrangement with an activation barrier of 28.9 kcal/mol, a value very close to that predicted above at the DFT level for TS-5 (ΔE^‡ = 29.3 kcal/mol). The loss of N₂ from an acyl azide requires the anti orientation of the azide functionality with respect to the C=O group. The cyclopropanoyl azide 8(anti_C-N, syn_C-C) is 4.5 kcal/mol lower in energy than the more sterically hindered anti_C-N, anti_C-C conformer (Figure 10) and its barrier for loss of N₂ from 8(anti_C-N, syn_C-C) to produce the cyclopropanoyl nitrene is actually 0.7 kcal/mol lower in energy (ΔE^‡ = 28.2 kcal/mol) than the Curtius transition state. However, 8(anti_C-N, syn_C-C) is 4.6 kcal/mol higher in energy than 8(syn_C-N, syn_C-C), and this is a classic Curtin-Hammett equilibration where the barrier for ground state rotation is much lower than either activation barrier (Figure 11). Because TS-8a(anti_C-N, syn_C-C) is 3.9 kcal/mol higher in energy relative to TS-8(syn_C-N, syn_C-C), it is the concerted rearrangement to isocyanate that is favored.

Figure 10.

Conformers of cyclopropanoyl azides: 8(syn_C-N, syn_C-C) and 8(syn_C-N, anti_C-C), 8(anti_C-N, syn_C-C) and 8(anti_C-N, anti_C-C), TS-8(syn_C-N, syn_C-C) for Curtius rearrangement, and TS-8a(anti_C-N, syn_C-C) for the loss of N₂ to produce cyclopropanoylnitrene.

Figure 11.

Curtin-Hammett equilibrium between 8(anti_C-N, syn_C-C) (which leads to nitrene formation) and 8(syn_C-N, syn_C-C) (which gives concerted Curtius rearrangement). Because TS8a(anti_C-N, syn_C-C) is 3.9 kcal/mol higher in energy relative to TS8(syn_C-N, syn_C-C), it is the concerted rearrangement to isocyanate that is favored.

Animation of the single imaginary frequencies for the above TSs (Figure 10) closely mirrored those for the cycloprop-1-enoyl transition states (Figure 9). The vectors for Curtius rearrangement TS-8 had a large contribution from the cyclopropane ring that was essentially absent from TS-8a that largely involved N-N bond breaking attending the loss of N₂. In TS-8 and TS-8a, the H⁹-C³-C⁴O⁵ dihedral angles are 180°. This stands in contrast to TS-6b (Figure 9), where the H⁹-C³-C⁴O⁵ dihedral angle is −91.6°. This observation reinforces the earlier comment that the double bond of the cyclopropene does exert an influence on the geometry of the Curtius transition state, but not necessarily on the energetics of the transition state.

From this series of calculations on the Curtius reaction it is evident that both the alkene and the ester functionalities each make a small contribution to the rate enhancement noted for 1 relative to 3. However, calculations suggest that it is unlikely that the primary role of the alkene is π–stabilization by the C=C in the transition state. A more likely explanation lies in the differing strengths of C-C bonds to cyclopropane and to the allylic position of cyclopropene. The bond dissociation energy (BDE) of the C-C single bond in methylcyclopropane is 8.8 kcal/mol higher than the corresponding bond in 3-methylcyclopropene (Table 2). Analogously, we feel that the lower barrier for the rearrangement of 1 relative to 3 is attributable to a weaker bond between the carbonyl carbon and the three-member ring in the former compound.

Table 2.

C–C bond dissociation energies of selected compounds.

compound	Experimental	calculated	method
C2H6	90.412b	90.812b	G2
Me-cyclopropane		99.5a	CBS-APNO
Me-cyclopropene		90.7a	CBS-APNO
Me-Phe	87.622
neopentane	78.723	87.7a	G3

^abond dissociation energy calculated in the present study.

Of course, BDE is not the only consideration that determines the activation energy for the Curtius rearrangement. For example, the BDE for Ph–CH₃ in toluene (~90 kcal/mol) is relatively weak (Table 2), but the activation energy for the Curtius rearrangement of benzoyl azide (30.0 kcal/mol) is higher than that of an alkyl group. As explained earlier, stereoelectronic factors can influence the high barrier for the transformation of benzoyl azide to phenylisocyanate. However, we feel that the comparison of BDE’s is appropriate for structurally similar systems, as is the case for the acyl azides of cyclopropene and cyclopropane.

CONCLUSIONS

In summary, we conclude on the basis of theoretical studies that the Curtius rearrangements of a series of syn acyl azides are concerted in nature. The kinetics of the Curtius rearrangements of methyl 1-azidocarbonyl cycloprop-2-ene-1-carboxylate (1) and methyl 1-azidocarbonyl cyclopropane-1-carboxylate (3) were studied by ¹H NMR spectroscopy, and there is close agreement between calculated and experimental enthalpies and entropies of activation. The lower activation energy for the rearrangement of 1 relative to 3 was attributed to a weaker bond between the carbonyl carbon and the three-membered ring in the former compound. The calculations on 1 are not consistent with π–stabilization of the transition state by the C=C bond of the alkene. A comparison of reaction pathways at the CBS-QB3 level for the Curtius rearrangement versus the loss of N₂ to form a nitrene intermediate provides strong evidence that the concerted Curtius rearrangement is the dominant process. This combined study places the concerted mechanism of the thermal Curtius reaction and very likely the closely related Schmidt, Hofmann, Lossen and Beckman reactions on a sound mechanistic basis corroborating both earlier experimental^1c,3–5 and theoretical studies⁷.

Computational Methods

Quantum chemistry calculations were carried out using the Gaussian98 and Gaussian03 program system¹⁵ utilizing gradient geometry optimization.¹⁶ The Becke three-parameter hybrid functional combined with the Lee, Yang and Parr (LYP) correlation functional, denoted B3LYP,¹⁷ was employed in the calculations using density functional theory (DFT). In some calculations, we used the hybrid meta-RMPW1PW91¹⁸ DFT method. In this study we used 6-31G(d) and 6-311+G(d,p) basis sets.¹⁹ Selected geometries were optimized at the CCSD(T)/6-31G(d) CCSD(T)/6-311+G(d,p) levels to further check the relative energies of potential TSs versus intermediates. Zero-point energy corrections are not possible in the CCSD calculations because analytical frequencies are not yet available for this method in Gaussian. Additionally, we used The CBS-QB3 method, which utilizes a B3LYP/6-31G* geometry optimization and zero-point energy. Energy refinements include single point corrections at MP2/6-311+G(3d2f,2df,2p) with CBS extrapolation; MP4(SDQ)/6-31+G(d(f), p) and QCISD(T)6-31+G′.20a,b Corrections for solvation and optimizations in dielectric medium with the toluene dielectric constant (ε=2.379) were made using the CPCM model^20c,d implemented in Gaussian 03. Most of calculations were performed using GridChem computational resources and services, Computational Chemistry Grid.²¹ (www.gridchem.org).

Experimental Section

Dimethyl cycloprop-2-ene-1, 1-dicarboxylate

The following is a modification of a procedure described by Gevorgyan.¹³ A solution of dimethyl diazomalonate²⁴ (15.48 g, 97.95 mmol) dissolved in trimethylsilylacetylene (3 mL) was added by a syringe pump (0.5 mL/h) to a suspension of Rh₂(OAc)₄ (267 mg, 0.604 mmol, 0.6 mol%) in trimethylsilylacetylene (52 mL) at room temperature. After the addition was complete, the reaction mixture was allowed to stir at room temperature overnight. The majority of unreacted trimethylsilylacetylene was recovered by short path distillation from the reaction mixture at atmospheric pressure. The residue was passed through a short plug of silica gel (7″ × 6″). Ethyl acetate was used as the eluent and filtrate was again concentrated under reduced pressure. The crude product was dissolved in THF (100 mL), and the solution was cooled by ice-water bath (0 °C) and allowed to stir. To this solution was added dropwise 160 mL of an aqueous solution of K₂CO₃ (16.24 g, 117.5 mmol). After the addition was complete, the solution was allowed to warm to room temperature and stir for 1 h. The reaction mixture was concentrated under reduced pressure. The aqueous phase was extracted with ethyl acetate (4 × 150 mL). The combined organic layers were dried (MgSO₄), filtered and concentrated under reduced pressure. Flash column chromatography (5–20% EtOAc in hexane) furnished 10.54 g (67.50 mmol, 69%) of dimethyl cycloprop-2-ene-1, 1-dicarboxylate as pale brown oil along with 1.27 g (5.56 mmol, 5.7 %) of 2-methoxy-3-methoxycarbonyl-4-trimethylsilyl furan as pale brown oil. Spectroscopic data for these compounds (¹H, ¹³C NMR) matched those described previously.¹³

Methyl 1-azidocarbonyl-cycloprop-2-ene-1-carboxylate (1)

Note: In one preparation, a sample of 1 decomposed violently. Although the preparation below describes the isolation of 1, we strongly recommend that 1 should be handled only in solution. Methyl cyclopropene-1, 1-dicarboxylate was prepared from dimethyl cycloprop-2-ene-1, 1-dicarboxylate by the procedure of Wheeler and Ray.¹⁴

A solution of methyl cyclopropene-1, 1-dicarboxylate (0.82 g, 5.8 mmol) in THF (50 mL) was cooled by a cold bath (acetone/dry ice, −35 °C). The solution was allowed to stir, and triethylamine (1.23 mL, 8.66 mmol) was added dropwise. After ca. 10 min., methyl chloroformate (0.67 mL, 8.7 mmol) was added dropwise. The reaction mixture was allowed to stir while warming to 0 °C over a period of 2.5 h in the same cold bath. Acetone/dry ice bath was then replaced by an ice/water bath. Sodium azide (1.13 g, 17.3 mmol) was dissolved in H₂O (5 mL) and added dropwise. After the addition was complete, the reaction mixture was allowed to stir at 0 °C for 40 min. The crude reaction mixture was concentrated on the rotary evaporator. Water was added and the mixture was extracted with ethyl acetate (3 × 70 mL). The combined organics were dried (MgSO₄), filtered and concentrated under reduced pressure to provide 0.82 g (4.9 mmol, 85%) of 1 as pale brown oil. By the time an NMR spectrum was acquired, 10% of 1 had rearranged to isocyanate 2. As the Curtius rearrangement took place at room temperature, it was not possible to obtain a sample of 1 that was free of the isocyanate. ¹H NMR (CDCl₃, 400 MHz, δ): 6.89 (s, 2H), 3.74 (s, 3H); ¹³C NMR (CDCl₃, 100 MHz, δ): 177.8 (C), 170.3 (C), 102.2 (CH), 52.6 (CH₃), 32.0 (C); IR (neat, cm⁻¹): 2143, 1730, 1712, 1437, 1282, 1214, 1133, 1008, 773, 710, 639.

Methyl 1-isocyanato-cycloprop-2-ene-1-carboxylate (2)

In a 10 mL round bottomed flask fitted with reflux condenser, methyl 1-azidocarbonyl-cycloprop-2-ene-1-carboxylate (190 mg, 1.14 mmol) was dissolved in anhydrous benzene (3 mL). The solution was heated to reflux for 30 min. The reaction mixture was then concentrated under reduced pressure to provide 142 mg (1.02 mmol, 90%) of 2. Compound 2 was further characterized by reaction with ^tBuOH (Ti(ⁱOPr)₄, reflux, 50%) to give Methyl 1-[(tert-Butoxycarbonyl)amino] cycloprop-2-enecarboxylate, which was spectroscopically identical to that reported by Wheeler and Ray.¹⁴ Spectral properties of 2: ¹H NMR (CDCl₃, 400 MHz, δ): 7.12 (s, 2H), 3.73 (s, 3H); ¹³C NMR (CDCl₃, 100 MHz, δ): 172.7 (C), 126.3 (C), 108.7 (CH), 53.4 (CH₃), 38.8 (C); IR (neat, cm⁻¹): 2244, 1730, 1439, 1280, 1215, 1051, 754.

Methyl 1-azidocarbonyl-cyclopropane-1-carboxylate (3)

Note: Low molecular weight acyl azides present explosion hazards (see preparation of 1). Although compound 3 was isolated in the preparation below, we recommend that 3 should not be isolated in pure form, and should only be handled in solution.

A solution of methyl cyclopropane-1, 1-dicarboxylate²⁵ (1.15 g, 8.0 mmol) in THF (35 mL) was cooled by a cold bath (acetone/dry ice, −35 °C). The solution was allowed to stir, and triethylamine (1.36 mL, 9.6 mmol) was added dropwise. After ca. 10 min., methyl chloroformate (0.74 mL, 9.6 mmol) was added dropwise. The reaction mixture was allowed to stir while warming to 0 °C over a period of 2.5 h in the same cold bath. The acetone/dry ice bath was then replaced by an ice/water bath. Sodium azide (1.56 g, 23.9 mmol) was dissolved in H₂O (5 mL) and added dropwise. After the addition was complete, the reaction mixture was allowed to stir at 0 °C for 1 h. The crude reaction mixture was concentrated on the rotary evaporator. Water was added and the mixture was extracted with ethyl acetate (3 × 70 mL). The combined organic layers were dried (MgSO₄), filtered and concentrated under reduced pressure. Flash column chromatography (3–5% diethyl ether in hexane) furnished 1.13 g (6.68 mmol, 84%) of 3 as colorless oil. ¹H NMR (CDCl₃, 400 MHz, δ): 3.75 (s, 3H), 1.57–1.54 (m, 4H); ¹³C NMR (CDCl₃, 100 MHz, δ): 176.4 (C), 169.4 (C), 52.8 (CH₃), 30.1 (C), 18.2 (CH₂).

IR (neat, cm⁻¹): 2145, 1730, 1712, 1695, 1334, 1298, 1130, 1063, 1015

Methyl 1-isocyanato-cyclopropane-1-carboxylate (4)

In a 10 mL round bottomed flask fitted with reflux condenser, methyl 1-azidocarbonyl-cyclopropane-1-carboxylate (100 mg, 0.59 mmol) was dissolved in anhydrous benzene (2 mL). The solution was heated to reflux for 50 min. The reaction mixture was then concentrated under reduced pressure to provide 73 mg (0.52 mmol, 87%) of the title compound. ¹H NMR (C₇D₈, 400 MHz, δ): 3.26 (s, 3H), 1.07–1.04 (m, 2H), 0.71–0.68 (m, 2H). ¹³C NMR (C₇D₈, 100 MHz, δ): 171.8 (C), 52.5 (CH₃), 36.9 (C), 16.8 (CH₂). IR (neat, cm⁻¹): 2262, 1731, 1441, 1328, 1230, 1196, 1069, 1040, 747, 730. HRMS-CI (NH₃) m/z: [M+H], calcd for C₆H₇NO₃, 142.0504; found 142.0504.

NMR Kinetic Experiments

NMR studies were carried out in duplicate with 20 mg sample of acyl azides 1 and 3 that were dissolved in toluene-d₈. Analyses of 1 were carried out at 303 K, 313 K and 323 K. Analyses of 3 were carried out at 323 K, 334 K and 344 K. Each kinetic run consisted of 90–220 ¹H NMR experiments, with 2–4 scans in each experiment, and a time interval of 20–144 sec between two successive experiments. All reactions were monitored to 75% conversion except for the reaction of 3 at 323 K, which was carried out to 52% conversion. After all the experiments in a kinetic run were finished, they were all integrated serially at the same time. The singlet corresponding to the methoxy group in the starting material in the first experiment of the series was normalized to 100%. The singlet peak appearing at the same chemical shift in the following experiments was measured against the one that was normalized to 100% in the first experiment. The residual solvent peaks from toluene-d₈ served as an internal standard for this analysis: the combined integrals for the product and starting material methoxy singlets were constant relative to the toluene-d₈ methyl group over the course of the reaction.

Integration values were plotted against time to create a curve that indicated the disappearance of the starting material as the time progressed. The first order rate constants (k) were obtained from a plot of time vs Ln [Integration]. Error analysis was conducted by plotting the combined data from duplicate runs: a straight line was fit to each plot using the Origin^® software package. The sample standard deviation for each rate constant was calculated from the standard error of the mean associated with each line fit. The error from the rate was propagated in straightforward fashion for the calculations of ΔH, ΔG^‡ and E_a. The values for ΔS^‡ reported in Table 1 are averages from the solutions of the Erying equation at three temperatures. The variance in ΔS^‡ was estimated by sum of squares analysis.

Supplementary Material

1_si_001. Supporting Information Available.

Total energies and Cartesian coordinates. This material is available free of charge via the Internet at http://pubs.acs.org

Scheme 1.

Curtius rearrangements of cycloprop-1-enoyl azide 1 and cyclopropanoyl azide 3