Making the right decision: Benjamin Franklin's son dies of smallpox in 1736

Benjamin Franklin in his autobiography said:

“In 1736 I lost one of my sons, a fine boy of four years old, by the smallpox taken in the common way. I long regretted bitterly and still regret that I had not given it to him by inoculation. This I mention for the sake of the parents who omit that operation, on the supposition that they should never forgive themselves if a child died under it; my example showing that the regret may be the same either way, and that, therefore, the safer should be chosen.”¹

Good medical care requires making the right decisions—to test, treat or do nothing—in the face of uncertainty.² Franklin came to believe he made the wrong decision to forgo smallpox inoculation for his son in 1736. We have enough information about Franklin's decision, made over a quarter of a millennium ago, to evaluate his choice.

Benjamin Franklin was born in Boston in 1706. He worked as an apprentice to his brother James in a printing business in 1716 before moving to Philadelphia in 1723.³,⁴ During this era smallpox came periodically to these isolated commercial towns perhaps by way of an infected person on a merchant ship and swept through the town. Those who had been infected in the past and survived were immune. Most of the rest took smallpox “in the natural way” and lived or died from it. A few escaped the contagion all together. For about a decade afterwards, the town was immune to smallpox. A new generation of children were born and new people moved in. With time the unprotected proportion of the population grew. With each passing year without smallpox the risk of a new epidemic grew greater and the cycle would repeat itself. Boston had such epidemics in 1721, 1730, 1752, 1764, 1776, 1778 and 1792.⁵

As we have described in this series, Onsemus, an African servant of the clergyman Cotten Mather in Boston, explained the use of smallpox inoculation in West Africa. Mather noted this down and later convinced a local doctor, Zabdial Baylston, to try this method in the Boston smallpox outbreak of 1721.⁶,⁷ He did so. Mortality for inoculated and non‐inoculated people were counted and compared to demonstrate the lower death rate for inoculation: 2% versus 15% taken in the natural way. Inoculation became the state of the art treatment prior to Jenner's discovery of the more effective and lower risk cowpox vaccination, which was published in 1798.

The Franklin brothers' Boston newspaper was critical of smallpox inoculation in 1721. Inoculation used a string which had been drawn through the pustule of a smallpox victim. The string was dried out and saved. For inoculation, an incision was made and the string was drawn through it to infect the recipient with attenuated smallpox. The recipient would more often get a milder form of smallpox with a lower risk of death. During that period the recipient would be contagious to others. (This would not be the case for Jenner's later cowpox vaccine, an important improvement.)

Quality improvement and decision analysis

• Quality improvement and clinical decision analysis are not the same thing. Decision analysis can guide the right choice for a patient and family. Quality improvement can be used to increase the likelihood that such informed decisions are made.

• Showing that a new drug is better than today's care calls for a randomised trial. Expert consensus is required to develop best practice guidelines. Good clinical decision making requires data on probabilities and patient preferences. Quality improvement is about getting that beneficial drug to all the right patients. It is about implementing best practices for all. It is about making sure that patient choices are informed.

• In our example, the town of Boston throughout the 1700s collected outcome data on its smallpox epidemics, treatment choices, and outcomes. So that town's people could make their own informed decisions. They did such a good job that we can evaluate these choices today.

Franklin's decision

Decisions in medicine would be easy if they consisted of this choice: take treatment and you will live; don't and you will die. Unfortunately, Franklin's choice was not so simple. Franklin's son could die if either choice was made. If there was no risk of smallpox then “do nothing” made sense. Inoculation became a relevant option when smallpox arrived in town. The key to the decision was the probability that Franklin's son would become infected in the natural way. If this risk was high enough, then at some point inoculation with its 2% mortality would be justified.

Decision analysis: key concepts and symbols

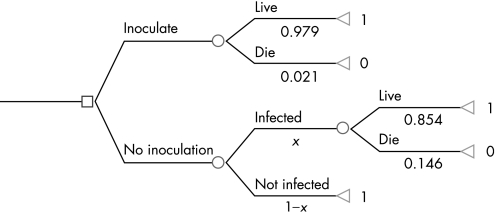
A decision tree can be used to analyse Franklin's choice (fig 1 and table 1). The square box is a choice node. The box refers to a decision and decision maker. In this case Franklin's choice is to inoculate his son or not. Branches to the right indicate the two choices. The circles are chance nodes. Each circle indicates the consequences of a choice which have a probability of occurrence. There are two such uncertain consequences of this decision: The probability of infection and the probability of living or dying. Chance nodes have probabilities attached to each branch to the right of the chance node. These probabilities must add up to 1.00.

Figure 1 Smallpox, Boston 1721: population 10 700. Decision tree: inoculate or not.

Table 1 Smallpox, Boston 1721: population 10 700. Decision: inoculate or not.

Path name	Path probability	Number of people
Inoculate and live	0.979	281
Inoculate and die	0.021	6
No inoculation, infected and live	(x)(0.854)	4917
No inoculation, infected and die	(x)(0.146)	842
No inoculation, not infected and live	(1–x)	4654
Total population		10 700

In 1721, 287 people were inoculated by Boylston. Of these, 281 lived (281/287 = 0.979) and six died (6/287 = 0.021). Thus, the two probabilities associated with the inoculation chance node add up to 1.00 (0.979 + 0.021 = 1.00)

Branches in sequence are “paths”. Each path has an “outcome” associated with it. Paths have probabilities of occurring, which are obtained by multiplying the branch probabilities together. The upper branch (inoculate) probabilities we know from the data. The lower branch (do not inoculate) has two chance nodes. The first is the probability of infection in the natural way without inoculation. We start off by deciding we do not know what this probability is. So we call it x which can range in value from 0 (no chance of infection) to 1.00 (certainty of infection.) By the rules of decision analysis we know that if the probability of infection is x then the probability of not being infected is 1–x (x plus 1–x adds up to 1).

The larger the value of x the better inoculation looks as a choice. This decision tree has three paths to the right of the choice to do nothing. The probabilities associated with these paths are obtained by multiplying the probabilities along the path (table 2). These probabilities add to 1.00. The path probabilities to the right of each choice node add to 1.00. Outcomes are numerical and are associated with each path. In this case “live” is given the value of 1 and “death” is given the value of 0. More complex medical decisions relate to quality of life, different life expectancies and costs.

Table 2 Smallpox, Boston 1721. Decision: inoculate or not (contd).

Path name	Path probabilities
Infected and live	(x)(0.854)
Infected and die	(x)(0.146)
Not infected	(1–x)
Sum	1.00

What should Franklin do with that unknown x?

Two possibilities come to mind. The Boston population figures shown in fig 1 allows us to make an estimate of the probability of being infected without inoculation, (4917+842)/(4654+4917+842)  = 0.553. The probability of being infected in the natural way in Boston in 1721 was 0.553. If we give x this value we can give Franklin an answer. This is done by multiplying the path probabilities by the outcomes and adding these up for each choice to compare them. For the inoculation choice this is (0.979×1) + (0.021×0)  = 0.979. This expected value is the same as the probability of surviving this treatment. What about the do nothing choice where x is replaced by 0.553? The expected value of the “do nothing” choice is 0.919 (table 3), which is less than the expected value of inoculation (0.979).

Table 3 Smallpox, Boston 1721. Decision: inoculate or not (contd).

Path names	Path probabilities times outcomes
Do nothing, infected, live	(0.553)(0.854)(1)  = 0.472
Do nothing, infected, death	(0.553)(0.146)(0)  = 0. 0
Do nothing, not infected	(1−0.553)(1)  = 0.447
Expected value of do nothing	0.919

The rule in decision analysis is, if the tree structure, probabilities and outcomes are correct, the choice should be made which has the best expected value, in this case—inoculation. If you have followed us this far, we hear you saying “now wait a minute”. From your list of concerns, let us pick one. The probability of being infected of 0.553 is not realistic. Of the 4654 Bostonians who were not infected many of them were not infected because they were not at risk, having had smallpox in the past and survived. This is information we would like to have, but cannot and can never know. So what should we do? We can do two things, which come under the broad heading of sensitivity analysis.

This bias in our data implies that for Bostonians without exposure to smallpox, the risk of becoming infected in the natural way was greater than 55.3%. The greater the risk of infection above 55.3%, the better and better inoculation looks as a choice. So this bias will not change our decision and, therefore, we can still choose inoculation.

The other approach is to ask how low does the probability of infection have to be to give these two choices equal expected values? Knowing this probability will give us the “indifference point” where the expected values are the same. This probability can be found with a bit of algebra. Set the two expected outcomes equal to each other and solve for x (see table 4).

Table 4 Smallpox, Boston 1721. Decision: inoculate or not (contd).

Expected survival with inoculation		Expected survival—do nothing
0.979	=	(x)(0.854)(1) + (x)(0.146)(0) + (1−x)(1)
0.979	=	(0.854)(x) + (1–x)
x–(0.854)(x)	=	1−0.979
(0.146)(x)	=	0.021
x	=	0.021/0.146
x	=	0.144

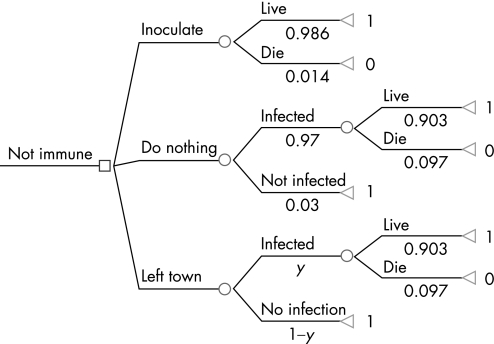
If the probability of becoming infected in the natural way is less than 0.144 then it is best to do nothing. If the probability is greater than 0.144 then inoculation is a better choice. Now wait just another minute—your analysis assumes just two choices. Are there other choices? Actually there were: “head for the hills” or leave town. Data on this choice are reported for the Boston smallpox epidemic of 1752; too late for Franklin's 1736 decision (fig 2 and table 5). In 1752 Boston was a bigger town with 15 684 people of whom 5998 were recorded as immune to smallpox. Thus 9686 Bostonians were at risk of infection. They made one of three choices, inoculation, do nothing or leave town:

Figure 2 Smallpox, Boston 1752: population 15 684. The decision tree: inoculate, do nothing or leave town.

Table 5 Smallpox, Boston 1752. Decision: inoculate or not.

Path name	Path probabilities	Outcomes	Number of people
Inoculate and live	(0.986)	1	2094
Inoculate and die	(0.014)	0	30
Do nothing infected and live	(0.97)(0.903)	1	5006
Do nothing infected and die	(0.97)(0.097)	0	539
Do nothing NOT infected and live	(0.03)	1	174
Left town infected and live	(y)(0.903)	1	1762
Left town infected and die	(y)(0.097)	0	26
Left town not infected and live	(1−y)	1	55
Not at risk of infection, immune			5998
Total population			15 684

• 2124 people chose inoculation of whom 30 died (0.014);

• 5719 people chose to do nothing. Of these 97% were infected and 539 died;

• 1843 left town to escape infection in the more isolated countryside. We do not know how many of these people died.⁵

Note that in 1721, 2.7% of the total population took inoculation. In 1752, 13.5% of the total population and 21.9% of the at‐risk population chose inoculation, showing a slowly greater public acceptance of this beneficial treatment. More inoculated, and therefore infectious, people could have increased the risk of infection for the do nothing group. We can calculate the expected values in 1752. The probability of surviving inoculation was 0.986. For at‐risk people, doing nothing led to a high risk of infection (0.97) and an expected outcome of (1)(0.903)(0.97) + (0)(0.097)(0.97) + (1)(0.03)  = 0.906.

Inoculation with its higher survival rate is the better choice between these two. What about the “leaving town” choice? To be worth choosing, it should have a better survival rate than the 0.986 resulting from inoculation. All we know about the “leave town” group is that 1843 susceptible people made this choice. For this choice to be better than inoculation with its 98.6% survival, there would have to be fewer than 26 deaths in this group of 1843 people. This is 26/1843 = 0.0141 mortality compared to the inoculation mortality of 0.014. We do not know the probability of becoming infected in the leave town group. Therefore we give it a value of y. If the value of y is low enough, leave town could be the best choice. What value of y would make us indifferent between the leave town, and the next best choice, which is inoculation? We can find this out by setting the two expected outcomes equal to each other and solving for y (table 6).

Table 6 Smallpox, Boston 1752. Decision: inoculate or not (contd).

Expected value of leaving town  =  (probability of living)		Expected value of inoculation (probability of living)
(y)(0.903)(1) + (y)(0.097)(0) + (1−y)(1)	=	0.986
(y)(0.903) + 1 − (y)	=	0.986
y	=	0.144

If the probability of being infected is less than 14.4% the best choice is to leave town. If the probability of being infected is greater than 14.4%, inoculation is the best choice. This probability of infection times the mortality times the number of Bostonians' who left town ((0.144)(0.097)(1843)) equals 25.7, just below the 26 deaths that makes this our preferred choice in the short run. Short run, because these people will continue to be at risk when the next epidemic comes in 1764, when they will have to choose again.

You now know the basic ideas of clinical decision analysis. It can be seen as the logic of medical decision making. Decision analysis was developed by Howard Raiffa⁸ and others in the 1960s. It was applied to real clinical problems in the 1970s in two books Clinical decision analysis⁹ and Costs, risks and benefits of surgery,¹⁰ and in an entire issue of the New England Journal of Medicine.¹¹ There is now an active Society for Medical Decision Making with its own journal Medical Decision Making.