Statistical Approaches for Modeling Radiologists’ Interpretive Performance

Abstract

Although much research has been conducted to understand the influence of interpretive volume on radiologists’ performance of mammography interpretation, the published literature has been unable to achieve consensus on the volume standards required for optimal mammography accuracy. One potential contributing factor is that studies have used different statistical approaches to address the same underlying scientific question. Such studies rely on multiple mammography interpretations from a sample of radiologists; thus, an important statistical issue is appropriately accounting for dependence, or correlation, among interpretations made by (or clustered within) the same radiologist. This manuscript aims to increase awareness about differences between statistical approaches used to analyze clustered data. We review statistical frameworks commonly used to model binary measures of interpretive performance, focusing on two broad classes of regression frameworks: marginal and conditional models. While both frameworks account for dependence in clustered data, the interpretations of their parameters differ; hence, the choice of statistical framework may (implicitly) dictate the scientific question being addressed. Additional statistical issues that influence estimation and inference are also discussed, together with their potential impact on the scientific interpretation of the analysis. This work was motivated by ongoing research being conducted by the Breast Cancer Surveillance Consortium; however, the ideas are relevant to a broad range of settings where researchers seek to identify and understand sources of variability in clustered binary outcomes.

INTRODUCTION

Despite improvements in the technical quality of mammography since the implementation of the Mammography Quality Standards Act (MQSA) of 1992 (1), radiologists’ interpretive performance of mammography has remained highly variable in the United States (2). Much research has been conducted toward understanding the role of patient, radiologist, and facility characteristics in explaining this variation (3-7). Notwithstanding this large body of work, substantial unexplained variability in interpretative performance remains.

A recent topic of interest is evaluating the influence of radiologists’ mammographic annual interpretive volume on performance, which could help inform whether current certification requirements should be changed (2). Conflicting study findings, however, have defied consensus on whether and how interpretive volume influences performance (2, 4-6, 8-12). Although these studies shared the common goal of understanding the influence of volume on performance, they differed in several important ways, including the study populations, time frames, choice of performance indices used as the primary outcomes, definitions of interpretive volume, and selection of adjustment variables. Studies also differed in the statistical approaches and modeling strategies used to characterize and estimate the associations of interest. To achieve consensus on the answer to a specific scientific question such as the influence of interpretive volume on interpretative performance, it is important to place into context differences in statistical methodologies and how they may influence results. A recent Institute of Medicine report on improving breast imaging quality standards underscored the need “to establish the implications, advantages, and disadvantages of statistical approaches to evaluating the influence of volume on interpretive performance” (2).

Motivated by this, we review commonly used statistical approaches for modeling the influence of radiologist characteristics on interpretive performance. Evaluating radiologist interpretive performance relies on observing multiple interpretations for each radiologist. This type of data is often referred to as repeated measures or clustered data, because outcomes (i.e., interpretations) are clustered within the interpreting radiologist. While researchers have a broad range of statistical methods at their disposal for analyzing clustered data, the focus here is on regression-based modeling approaches, because they permit adjustment for possible differences in case mix shown to affect interpretive performance (3-6). Two broad classes of regression model formulations have been used to study interpretive performance: marginal and conditional models. We compare and contrast these approaches, focusing on the scientific interpretation of their parameters. We also outline various scientific and statistical issues that should be considered when deciding on the specific modeling approach to use or when interpreting the results of an analysis. We emphasize that the choice of the statistical method may (often implicitly) dictate the scientific question being addressed, and that modeling assumptions, and violation of these assumptions, have important implications for achieving consensus across studies that have a common scientific goal.

Throughout this paper, we illustrate concepts using mammography interpretive performance data collected by the Breast Cancer Surveillance Consortium (BCSC) (13). The National Cancer Institute (NCI)-funded BCSC is a consortium of seven mammography registries that has collected information on 7.5 million mammography examinations interpreted by over 1,000 radiologists at 243 radiology facilities in seven states across the United States (http://breastscreening.cancer.gov). Each mammography registry annually links women in their registry to a state tumor registry or regional Surveillance Epidemiology and End Results (SEER) program that collects population-based cancer data. Five of the seven registries also link to pathology databases to supplement cancer registry information and collect information about benign disease. All data are sent to the BCSC’s central Statistical Coordinating Center (SCC) for pooled analysis. Each BCSC registry, as well as the SCC, received institutional review board (IRB) approval either for active or passive consenting processes or for a waiver of consent to enroll women who obtained mammograms at BCSC sites, to link data, and to perform analytic studies. All procedures are HIPAA-compliant, and all registries and the SCC received a Federal Certificate of Confidentiality that protects the identities of research subjects including radiologists (14).

The remainder of the paper is organized as follows. We begin by outlining some design considerations, concentrating on issues associated with the choice of primary outcomes and predictor definitions. We then provide an overview of marginal and conditional models and discuss differences in the interpretation of their model parameters. We give brief description of additional statistical issues which will often be encountered in the analysis of clustered binary data and conclude with a discussion and some recommendations for analytic strategies. Although this paper is motivated by challenges in modeling the interpretive performance of mammography, the ideas are relevant to a broad range of settings where researchers seek to understand sources of variability in clustered binary outcomes—beyond both mammography and radiologist interpretive performance.

DESIGN CONSIDERATIONS

Before we address the implications of differences in statistical methods for achieving consensus across studies with a common scientific goal, we must consider how studies differ in their outcome and predictor definitions. These choices dictate the mechanism a study is trying to understand, i.e., the underlying process by which a predictor variable such as interpretive volume influences interpretive performance. We cannot expect to achieve consensus from studies exploring different mechanisms.

Choice of Outcome

When designing a study to investigate interpretive performance, a researcher may choose from a variety of clinically meaningful outcome measures. In this paper, we focus on the assessment of radiologist interpretive performance on the basis of a binary interpretation of no recall or recall, possibly conditional on disease status. Let Y_ij = 0 or 1 denote the binary no recall/recall outcome of the j^th examination interpreted by the i^th radiologist, and let D_ij = 0 or 1 denote a binary indicator of disease status. For mammography studies, disease is typically defined as a breast cancer diagnosis within 1 year of the mammography examination (15). Throughout this manuscript, we use π to denote a generic performance measure of interest, which may depend on a set of radiologist and/or case-specific predictors or covariates X_ij. Commonly used measures of interpretive performance include:

• Recall rate (or abnormal interpretation rate): the probability of recall for additional work-up, P(Y_ij = 1 | X_ij)

• Sensitivity: the probability of recall among those with disease, P(Y_ij = 1| D_ij = 1, X_ij)

• Specificity: the probability of no recall among those without disease, P(Y_ij = 0| D_ij = 0, X_ij)

• Positive predictive value of recall (PPV₁): the probably of disease among patients recalled, P(D_ij = 1| Y_ij = 1, X_ij)

• Cancer/disease detection rate (or diagnostic yield): the proportion of examinations with detected disease, P(D_ij = 1 AND Y_ij = 1 | X_ij).

Choice of predictor

Annual interpretive volume is essentially a continuous variable with variability among radiologists. Prior studies have discretized this volume into a few categories for analysis. For example, Barlow and colleagues (2004) studied volume in a single year based on a self-report assessment using three categories; ≤1000, 1001–2000 and >2000. In contrast, Smith-Bindman and colleagues (2005) considered the average observed annual volume over a 5-year period, categorized into six volume groups. They also considered the ratio of screening to diagnostic mammograms (categorized into two groups at a threshold of 5.0). Although both studies examined interpretive volume, they reflect different mechanisms by which volume influences interpretive performance and hence address different questions.

Separation of between- and within-cluster predictor effects

In addition to the specific choice of predictor, another important consideration when analyzing clustered data is the potential for both within- and between-cluster effects of predictors. To illustrate this, suppose interest lies in the (unadjusted) association between some performance measure π and annual interpretive volume, X_ij. Here, the predictor of interest is denoted with a radiologist-specific index, i, and mammography case-specific index, j, to acknowledge that volume may vary both between and within radiologists. Figure 1 illustrates how annual interpretive volume can vary both between and within radiologists using data from five BCSC radiologists. Radiologists 1 and 2 have higher average volume over the time period while radiologists 4 and 5 have low volume. Radiologists 2 and 4 have large changes in volume over time, while radiologist 5’s volume remains fairly stable.

Figure 1.

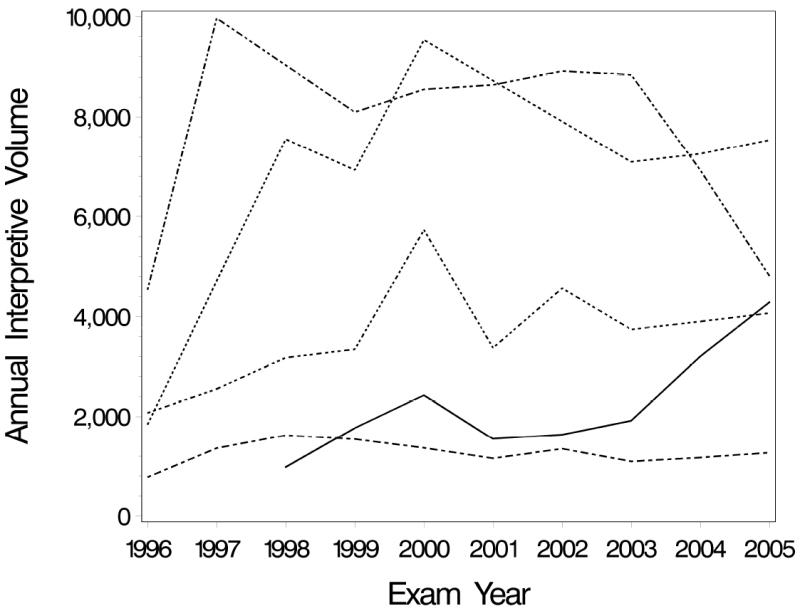
Annual interpretive volume from 1996 to 2005 for five radiologists who participate in the Breast Cancer Surveillance Consortium.

To address the question of whether interpretive volume influences performance, one might adopt the following logistic regression model:

$$\mathrm{logit}\pi (X_{\mathit{ij}})={\beta }_0+X_{\mathit{ij}}{\beta }_1.$$ (1)

The slope parameter β₁ refers to the change in log-odds of a positive response associated with a unit change in annual interpretive volume X. As noted above, a “unit change” in X may correspond to one of two potential contrasts: (i) a between-radiologist change, comparing two different groups of radiologists with different volumes; or (ii) a within-radiologist change, assessing how an individual’s performance changes over time (e.g., as their annual volume increases).

In many instances, both types of “change” occur within the study population and time-frame facilitating the assessment of both cross-sectional (between-radiologist) and longitudinal (within-radiologist) predictor effects. One might, however, anticipate the impact of the two changes on interpretive performance to differ. For example, consider two populations of radiologists, one that interprets 1,000 mammograms per year and another that interprets 5,000 per year. The difference in performance between these two populations of radiologists may differ from the impact of increasing an individual radiologist’s annual interpretive volume from 1,000 mammograms per year to 5,000 mammograms per year. The model given by (1), however, assumes the impact on performance is the same for these between- and within-radiologist comparisons. As an alternative to making this restrictive assumption, Neuhaus and Kalbfleisch (16) proposed decomposing the predictor variable into two components: the cluster-level predictor mean X̄_i and deviations of each observation from that mean X_ij − X̄_i. This decomposition leads to a modification of model (1):

$$\mathrm{logit}\pi (X_{\mathit{ij}})={\beta }_0^{\ast }+{\overline{X}}_i{\beta }_1^b+(X_{\mathit{ij}}-{\overline{X}}_i){\beta }_1^w.$$ (2)

In model (2), the regression parameter β₁^b denotes the between-radiologist effect and β₁^w the within-radiologist effect of the predictor X. Note that when the between- and within-radiologist effects are equal, i.e., β₁^b = β₁^w, model (2) reduces to model (1). Whether β₁^b and β₁^w are equal could be assessed with a hypothesis test. In addition, for some applications, it may be more reasonable to include an interaction of the between- and within-radiologist effects. For example, high-volume radiologists may not experience much change in performance with changes in their interpretive volume from year to year, whereas low-volume radiologists may experience improvements in performance if they increase their interpretive volume.

REGRESSION APPROACHES FOR CLUSTERED DATA

A key feature of clustered data is the potential for dependence between interpretations made by the same radiologist. Intuitively, observations for the same radiologist are more “similar” than those for another radiologist. This dependence arises because of heterogeneity across radiologists: differences in skill levels, thresholds for recalling patients, patient populations, and/or practice or facility characteristics (4-6, 17, 18). One can account for such between-radiologist differences by including appropriate, radiologist-specific covariates into a regression model; however, in many instances unexplained heterogeneity, and hence dependence, will remain.

Statistical models that assess predictors of interpretive performance must take into account the potential dependence among multiple interpretations made by the same radiologist. Naïve methods that ignore clustering, such as the traditional chi-square test or logistic regression, yield biased standard error estimates. These methods rely on the data being a sample of independent observations, while clustered data are inherently dependent. This dependence typically lessens the amount of statistical information about parameters of interest below what the overall sample size would suggest. For example, consider a study consisting of 50,000 mammography examinations interpreted by 10 radiologists. It is tempting to think 50,000 independent observations are available for analysis; however, the effective number of independent observations is closer to 10 (i.e., the number of radiologists). Therefore, naïve standard error estimates will be too small and inference based on confidence intervals and p-values will be statistically invalid.

Two broad classes of regression models have been used to account for potential dependence in the analysis of interpretive performance: marginal and conditional models (19-21). Historically, the two approaches were developed specifically to account for dependence in clustered or longitudinal data. While both approaches achieve this goal, careful consideration of the model assumptions highlight important differences in the interpretation of the model results; a consequence of these differences is that the two modeling approaches address different scientific hypotheses. Indeed, the approaches are distinguished by the labels “marginal” and “conditional” because of implicit differences in the interpretations of the component parameters.

Conditional or cluster-specific models

Dependence among observations within a cluster can be induced by between-radiologist heterogeneity that is not explained by measured covariates. Conditional or cluster-specific models are a general class of regression models that approach the problem of accounting for dependence within clusters by introducing cluster-specific parameters directly into the model specification. These parameters serve to capture unmeasured between-cluster heterogeneity. An example of a cluster-specific logistic regression model for a performance measure, say recall rate, is

$$\mathrm{logit}{\pi }^C(X_{\mathit{ij}},b_i)={\beta }_0^C+X_{\mathit{ij},1}{\beta }_1^C+\cdots +X_{\mathit{ij},p}{\beta }_p^C+b_i,$$ (3)

Where b_i is a radiologist-specific parameter, and π^C(X_ij,b_i) is the conditional probability of recall given the covariates X_ij = (X_ij,1, …, X_ij,p) and the radiologist-specific parameter b_i. Intuitively, the radiologist-specific effect b_i induces dependence across the multiple observations from the i^th radiologist, because a large positive value of b_i indicates that each mammogram-specific probability of being recalled, given by (3), will be high, while a large negative value of b_i indicates that each mammogram-specific probability of recall will be low. In more general conditional models, the single radiologist-specific effect b_i can be replaced with a vector of effects, potentially depending on observed covariates.

Inspection of model (3) reveals that estimation is required for p+1+N parameters: β₀^C, β₁^C, …, β_p^C, b₁, …, b_N, where p is the number of covariates and N is the number of radiologists. Thus, the number of parameters in model (3) is directly linked to the sample size; the number of radiologist-specific effects increases with the number of radiologists. In such settings, traditional estimation methods (such as maximum likelihood) can break down (22). One way to overcome this problem is to use conditional logistic regression (23). This approach, which has its roots in the analysis of matched case-control studies, takes the N radiologist-specific effects to be nuisance parameters and uses the statistical technique of conditioning to eliminate them from the likelihood. As a result, the task of estimation is concentrated on the p+1 regression parameters. An additional consequence of the conditioning, however, is that one is no longer able to estimate the effect of any covariate that varies solely between radiologists, such as gender or average annual interpretive volume. In such settings, an alternative to removing the N radiologist-specific effects from the task of estimation is to impose some distributional assumptions on how the radiologist-specific effects vary across the population of radiologists. A common distributional assumption, for example, is that the b_i are normally distributed, with zero mean and constant variance, σ². In this case, the task of estimation reduces to p+2 parameters: the p+1 β^C regression coefficients and the unknown variance term, σ². With this approach, the b_i are treated as random variables and distinguished from the fixed model terms (i.e., the β^C regression coefficients). As such, the combination of model (3) with distributional assumptions concerning the b_i parameters is often referred to as a random effects or hierarchical model.

In observational, community-based settings such as the BCSC, mammography cases are typically interpreted by one or two radiologists. Multiple-reader multiple-case (MRMC) studies provide researchers with a potentially more efficient design where each case is interpreted by multiple radiologists, thereby reducing one source of study variability-- differences across the cases (24). While several random effects models have been proposed for analyzing continuous performance measures collected from MRMC studies (24), extending the framework outlined above to analyze a binary performance measure is straightforward. Specifically, equation (3) could be modified to include an additional random effect corresponding to the case number, to account for correlation among multiple interpretations made on the same case.

Marginal or population-averaged models

An alternative approach to incorporating a radiologist-specific parameter into the mean model to account for dependence within clusters is to model the population mean as a function of covariates only, as in case of independent data, and then adjust for the dependence within clusters in the calculation of the standard errors. Consider a model for a performance measure π_ij based solely on the observed X_ij:

$$\mathrm{logit}{\pi }^M(X_{\mathit{ij}})={\beta }_0^M+X_{\mathit{ij},1}{\beta }_1^M+\cdots +X_{\mathit{ij},p}{\beta }_p^M.$$ (4)

A common technique for estimating the parameters in model (4) is that of generalized estimation equations (GEE) (25). Specifically, an estimate of the vector of marginal regression coefficients β^M = (β₀^M, β₁^M, …, β_p^M) is obtained by solving the estimating equations

$$\mathrm{U}({\mathbf{\beta }}^M)=\sum _{i=1}^N{\mathbf{D}}_i^T{\mathbf{V}}_i^{-1}\left[{\mathbf{Y}}_i-{\pi }^M({\mathbf{X}}_i)\right]=0,$$ (5)

where D_i is the first derivative of the vector π^M (X_i) with respect to the regression parameters β^M and V_i is the assumed variance-covariance matrix for the vector of observed outcomes for the ith radiologist Y_i. Intuitively, the solution to the estimating equations, β̂^M, is the value of the regression parameters β^M, that provides the closest correspondence between the observed outcomes, Y_i, and what is expected under the assumed model, π^M (X_i). Provided the mean model (4) is correctly specified, the estimating equations (5) are unbiased (i.e., have zero expectation) regardless of the specific choice of the assumed variance-covariance V; hence, the corresponding regression parameter estimates β̂^M are consistent (asymptotically unbiased).

Estimation of standard errors that take into account the dependence within clusters is straightforward. The sandwich or robust variance estimator is most commonly used and is well-known to be robust in the sense that valid inference is obtained for the marginal regression coefficients even if the variance-covariance matrix is misspecified. That is, the sandwich variance estimator accounts for arbitrary dependence among observations within a cluster, thereby ensuring valid inference (25). GEE methods that use standard software have also been proposed for non-nested clusters or crossed studies, such as MRMC studies, where the same cases are interpreted by multiple radiologists (8, 26).

Interpretation of regression parameters

The nomenclature adopted to distinguish the two regression-based approaches for analyzing clustered data (conditional and marginal) arose from differences in the interpretation of their component parameters. To illustrate this, consider the interpretation of the conditional and marginal log-odds ratios β₁^C and β₁^M from models (3) and (4) respectively. The interpretation of both parameters relate to differences in performance (on the log-odds scale) between two populations of mammograms (the unit of analysis here); the two populations differ in terms of their covariates X_ij,1, while all other remaining components are held constant. Suppose, for example, we are interested in the effect of a binary measure of annual interpretive volume X_ij,1 which takes the value of 1 if the i^th radiologist had a high volume (based on some criteria) during the year the mammogram was interpreted and 0 otherwise, after adjusting for patient age X_ij,2. From (3), the interpretation of the conditional log-odds ratio can be derived via

$${\beta }_1^C=\mathrm{logit}{\pi }^C(X_{\mathit{ij},1}=1,X_{\mathit{ij},2},b_i)­\mathrm{logit}{\pi }^C(X_{\mathit{ij},1}=0,X_{\mathit{ij},2},b_i).$$ (7)

Hence, in addition to holding patient age (X_ij,2) constant, interpreting the conditional log-odds ratio β₁^C requires holding constant, or conditioning on, the value of the radiologist-specific effect, b_i. Consequently β₁^C is referred to as a “conditional” or “cluster-specific” parameter. In contrast, the interpretation of the marginal log-odds ratio, derived via

$${\beta }_1^M=\mathrm{logit}{\pi }^M(X_{\mathit{ij},1}=1,X_{\mathit{ij},2})­\mathrm{logit}{\pi }^M(X_{\mathit{ij},1}=0,X_{\mathit{ij},2}),$$ (8)

does not require conditioning on anything beyond the two measured predictor variables. In particular, the interpretation of the marginal log-odds ratio does not require conditioning on the radiologist-specific effect b_i; hence β₁^M describes differences in performance between two populations of mammograms, averaging across all radiologists. Consequently, β₁^M is referred to as a “population-averaged” or “marginal” parameter. Here, the term “marginal” is a statistical term referring to marginalizing (integrating or averaging) over the distribution of a random variable (in this instance, the random variable is the radiologist-specific effect b).

Connections between the two models

Although the two regression frameworks are presented separately, and have differing interpretations, the marginal and conditional means are connected mathematically via the convolution equation

$${\pi }^M(X_{\mathit{ij}})=\underset{b}{\int }{\pi }^C(X_{\mathit{ij}},b)dG(b).$$ (9)

In this expression, G(b) is the distribution of the random effects across clusters, often taken to be Normal with zero mean and a constant variance. Examination of this expression reveals that the marginal mean is equal to the average of the conditional mean, averaging with respect to the distribution of the random effect b.

The relationship between the marginal and conditional means, given by equation (9), indicates that both are well-defined in any given context. That is, given specification of the random effects distribution G(b), the two associations could be considered simultaneously. In practice, one typically decides which of the models is of primary scientific interest, and the modeling framework is chosen accordingly.

Numerical differences in conditional and marginal regression parameters

Comparing equations (7) and (8) indicates that the crucial difference in interpreting the two types of regression parameters is whether or not one conditions on the radiologist-specific random effect, b_i. For linear regression and ANOVA models for analyzing continuous performance measures collected from MRMC studies (27-32), the marginal and conditional regression coefficients can be shown to be numerically equivalent. However, for logistic regression models, such as those considered here, the values of the marginal and conditional odds ratios will typically not be numerically equivalent. Exceptions include when the random effects have no variability across clusters or the true value of the conditional log-odds ratio β₁^C equals zero and the variability of the random effect distribution does not depend on the covariate X_ij,1 (in which case the marginal log-odds ratio β₁^M also equals zero).

In most settings, the numerical difference between the marginal and conditional regression coefficients depends on the various components of the model as well as the underlying variation (magnitude and shape) of the distribution of the radiologist-specific random effects in the population. If the random effects are normally distributed with constant variance (specifically, if the variance does not depend on the covariate X_ij,1), the marginal odds ratio will be attenuated toward 1.0 compared to the conditional odds ratio (16, 20). Figure 2 shows a hypothetical example that illustrates this attenuation. The solid line represents the average radiologist-specific effect of volume on sensitivity of mammography for a hypothetical conditional odds ratio of 2.0 measuring the increased odds of an abnormal mammogram among women with cancer corresponding to an increase in volume of 2,000 and a radiologist-specific effect standard deviation of 2.0. The dashed line shows the relationship for the corresponding marginal odds ratio of 1.5, which is attenuated relative to the conditional effect.

Figure 2.

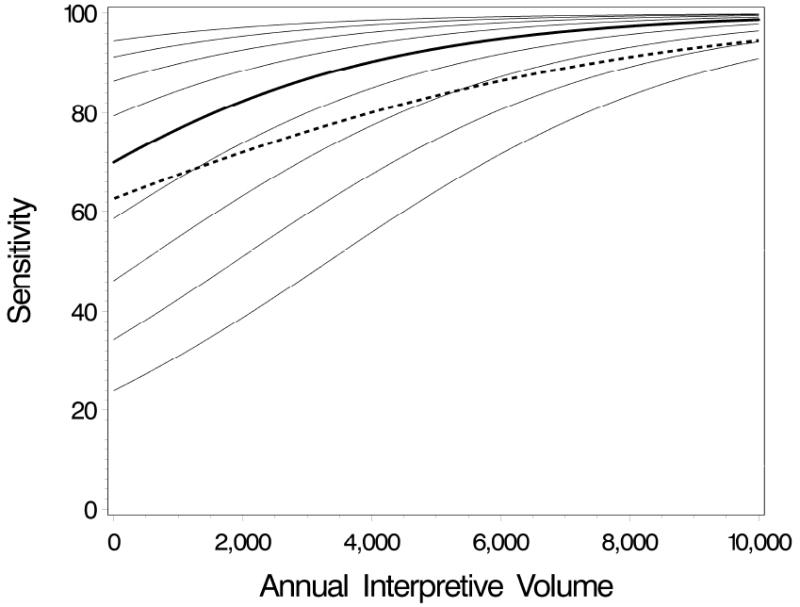
Hypothetical radiologist-specific (solid lines) and population-averaged (dashed line) curves showing the effect of annual interpretive volume on sensitivity. The thick solid line is the radiologist-specific sensitivity by volume for an average radiologist, i.e., a radiologist with a random effect of zero. The thin solid lines are the radiologist-specific curves for radiologists with random effects ranging from -1 to 1 standard deviation at increments of 0.25.

The dashed line is the population-averaged (marginal) sensitivity by volume, which represents an averaging of the radiologist-specific curves over the random effect distribution. The odds ratio measuring the effect of increasing volume by 2000 on the odds of an abnormal mammogram among women with breast cancer is 2.0 for the conditional model and 1.5 for the marginal model.

More generally, the value of one parameter given the other and the distributional assumptions of the radiologist-specific random effects can be derived via the relationship given by equation (9). Table 1 shows how the numerical values of the conditional and marginal odds ratios, exp(β₁^C) and exp(β₁^M), differ under various conditions in the simple setting of a single binary predictor. As noted above, when the random effect variance does not depend on the predictor X, the marginal odds ratio is attenuated toward 1.00, with the extent of the attenuation depending on the value of the conditional odds ratio, the intercept, and the random effects standard deviation. For example, when the conditional odds ratio is 2.00, the overall baseline mean is 0.50, and the random effects standard deviation is 0.50 in both the X=0 and X=1 groups, then the marginal odds ratio is 1.93. If the (common) standard deviation is 2.00, the attenuation is greater and the marginal odds ratio is 1.52.

Table 1.

Marginal odds ratios for various values of the conditional odds ratio, the conditional intercept (β₀^C) and corresponding mean response when X=0 (π₀^C), and the standard deviation (SD) of the normally distributed radiologist-specific effects.

			Marginal odds ratio, exp(β1M)
Conditional odds ratio, exp(β1C)	SD for X=1	SD for X=0	β0C = −2.2 (π0C = .10)	β0C = −1.1 (π0C = .25)	β0C = 0 (π0C = .50)	β0C = 1.1 (π0C = .75)	β0C = 2.2 (π0C = .90)
1.00	0.50	0.50	1.00	1.00	1.00	1.00	1.00
		1.00	0.79	0.88	1.00	1.13	1.26
		2.00	0.48	0.69	1.00	1.45	2.09
	1.00	0.50	1.26	1.13	1.00	0.88	0.79
		1.00	1.00	1.00	1.00	1.00	1.00
		2.00	0.61	0.78	1.00	1.28	1.65
	2.00	0.50	2.09	1.45	1.00	0.69	0.48
		1.00	1.65	1.28	1.00	0.78	0.61
		2.00	1.00	1.00	1.00	1.00	1.00
2.00	0.50	0.50	1.96	1.93	1.93	1.95	1.97
		1.00	1.55	1.70	1.93	2.21	2.50
		2.00	0.94	1.33	1.93	2.82	4.12
	1.00	0.50	2.32	2.03	1.78	1.60	1.48
		1.00	1.83	1.79	1.78	1.81	1.88
		2.00	1.11	1.40	1.78	2.32	3.10
	2.00	0.50	3.26	2.22	1.52	1.06	0.76
		1.00	2.57	1.95	1.52	1.21	0.96
		2.00	1.56	1.53	1.52	1.54	1.59

In contrast, if the radiologist-specific effect variability depends on X, the marginal odds ratio can be either attenuated or increased relative to the conditional odds ratio. In some cases, the marginal effect can even be in the opposite direction as the conditional effect. For example, when the conditional odds ratio is 2.00, the overall baseline mean is 0.10, and the random effects standard deviation is 2.00 when X=0 and 0.50 when X=1, then the marginal odds ratio is 0.94. Last, it is also important to note that if a covariate has no conditional effect (i.e., the conditional odds ratio is 1.00), the marginal odds ratio could be different from 1.00 if the variability of the radiologist-specific effect depends on X. In other words, if high-volume radiologists have the same conditional performance as low-volume radiologists, but high-volume radiologists are less variable in their interpretations, they will have a larger marginal performance than low-volume radiologists for performance measures with means above 50%.

For binary covariates, differences between the numerical values of the conditional and marginal parameters do not depend on the covariate distribution (i.e., the prevalence of the binary covariate). While we have focused here on a binary covariate, for continuous covariates the differences between the two parameters may depend on the covariate distribution, in addition to the factors considered in Table 1. In addition, in the case of a continuous covariate, it is important to note that both the marginal and conditional effects of that covariate will not be linear on the same scale (e.g., logit), unless the random effects are assumed to follow a specific distribution called a bridge distribution (33, 34).

Implications for science

Given the possible differences in the magnitude and direction of the conditional and marginal effects, it is important to consider carefully whether inference should be made at the radiologist or population level before analyzing clustered data with nonlinear regression models. For instance, the question of whether interpretive volume influences radiologists’ interpretive performance can be thought of in two ways. First, we may be interested in whether the sensitivity and specificity of mammography examinations interpreted by high-volume radiologists in the United States are better than these performance measures for mammography examinations interpreted by low-volume radiologists. This is a population-level question comparing the performance of mammography examinations interpreted by two different types of radiologists. In contrast, we may want to know whether an individual radiologist’s interpretive performance improves when his or her interpretive volume increases, controlling for other traits of that radiologist that influence performance. This is a radiologist-specific question that examines changes in an individual’s performance when one condition is changed but everything else about that radiologist remains constant. Both questions may be of interest, for example, to policy makers considering whether to increase the current interpretive volume requirements for certification. If the current requirement of ≥960 mammograms over the prior 2 years was increased to 2,000 mammograms, radiologists with 2-year volumes below 2,000 would have to either (a) stop interpreting mammography, leaving these mammograms to be interpreted by the group of remaining high-volume radiologists (the effect of this on the performance of mammography in the United States is estimated from the marginal model) or (b) increase their annual volume to meet the new guidelines (the effect of this on an individual radiologists-performance is estimated from the conditional model).

ADDITIONAL STATISTICAL CONSIDERATIONS

A variety of additional statistical issues that can influence estimation and inference, and therefore potentially affect the interpretation of the analysis, should be considered when choosing a regression formulation. In this section, we focus on statistical issues, and hence statistical bias in the regression parameter estimates and/or the standard error estimates that is specifically introduced by decisions concerning the statistical analyses. It should be noted, however, that traditional epidemiologic biases, such as selection bias and confounding, also require consideration.

Sample size

For clustered data, such as those in studies of mammography interpretive performance, one can identify two sample sizes: the number of clusters (e.g., radiologists) and the number of observations per cluster (e.g., mammography examinations). For estimation of marginal regression parameters, standard error estimates from GEE have been shown to be underestimated when the number of clusters is small (e.g., <50) (35, 36). The impact is that confidence intervals are too narrow, p-values are too small, and one will generally reject null hypotheses more often than the nominal type I error rate (i.e., α level) would suggest. In such settings, Mancl and DeRouen (36) proposed a simple correction that scales the variance by N/N-P, where N is the number of clusters and P is the number of regression parameters. This correction performs well as long as the number of clusters is not extremely small (say, <15 or <20). Note that by default, the Stata statistical software scales the robust variance by N/N-1, which may not provide a sufficient correction for regression models that include covariates (37). For studies with a very small number of clusters, one should consider an approach other than GEE to adjust for dependence within clusters.

Estimation of conditional parameters typically suffers less in the case of a small number of clusters. Estimation of random effects models, for example, builds on the structure imposed by assumptions concerning the distribution of the random effects, G(b), and, therefore, does not suffer as much when the number of clusters is small. A challenge with this, however, is that the model assumes the distribution of the random effects is correctly specified. If this is not the case, bias can result, especially when the cluster sizes are small.

Additional consideration should be given in settings where the cluster size itself may be correlated with the random effects (38-40). The assessment of interpretive volume is an example of this, where one might hypothesize that radiologists with high volume (i.e., large cluster sizes) have superior performance. Simulations have shown that the marginal intercept, and hence the predicted values and group means, can be biased in this case, but any biases of the odds ratios are small (38-40).

Distributional assumptions for cluster-specific effects

As noted above, conditional logistic regression does not rely on distributional assumptions about radiologist-specific effects, b_i; these effects are treated as fixed nuisance parameters and are conditioned out of the likelihood. In contrast, random effects models rely on the correct specification of the random effects distribution, G(b). While random effects are typically assumed to be normally distributed, simulations have shown that if the shape of the true underlying distribution does not follow that of a normal distribution (e.g., is not symmetric), there is little bias in the estimated regression coefficients (21, 41). It is also common to assume a constant mean and variance across all clusters, after adjusting for covariates. However, if the mean and/or variance of the true underlying distribution depend on covariates, then bias in the odds ratio estimates can result (40, 41). The case of the random effect mean depending on covariates is similar to the issue of confounding. High-volume radiologists may have better performance if radiologists who are good at mammography tend to specialize in breast imaging and interpret relatively large numbers of mammograms. In this case, estimates of within-radiologist effects may more accurately reflect the effect of changing volume on an individual radiologist’s performance (40); however, it may also be of scientific interest to determine whether there are between-radiologist effects of volume on performance, even if these differences are due to innate differences between radiologists who choose to interpret high volumes of mammograms.

The assumption that variability of the random effects does not depend on covariates is particularly important for our interests here, because it is reasonable to expect that radiologist variability among radiologists in their performance could depend on their characteristics. For example, we might expect more experienced radiologists to perform more similarly and thus have smaller between-radiologist variability than less experienced radiologists. To illustrate this, Figure 3 shows the variability in recall rate for mammograms interpreted in the BCSC from 1996 to 2005 by 46 radiologists with ≤1 year of experience and 46 radiologists with 20 years of experience. Recall rates for more experienced radiologists are clearly less variable that those for the less experienced radiologists. The variance of the radiologist-specific effect distribution is double for radiologists with ≤1 year of experience than that for radiologists with 20 years of experience (0.56 vs. 0.29).

Figure 3.

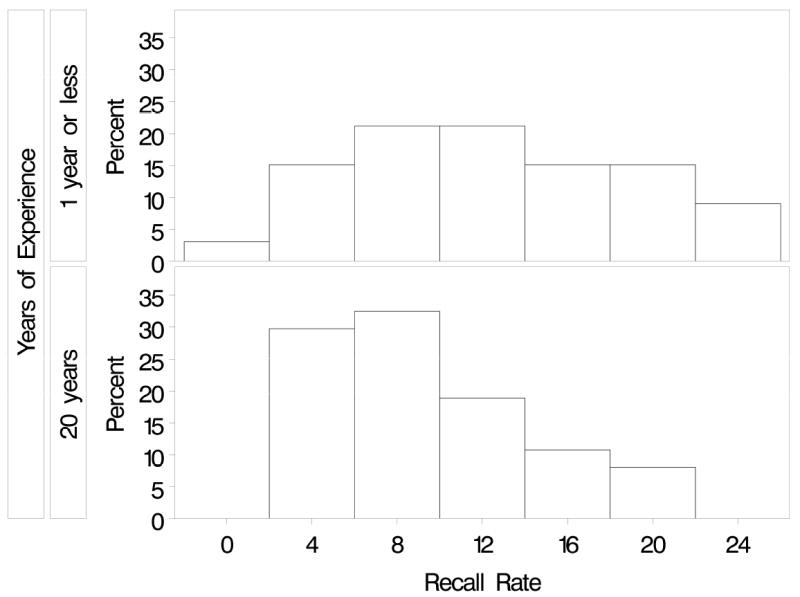
Variability in recall rate for mammograms interpreted in the BCSC from 1996-2005 by 46 radiologists with ≤1 year of experience and 46 radiologists with 20 years of experience. The variance of the radiologist-specific effect distribution is 0.56 for radiologists with 1 or fewer years experience and 0.29 for radiologists with 20 years of experience.

To relax the assumption of a constant variance, and reduce the potential for bias, it is possible to extend the traditional random intercepts model to allow the standard deviation to depend on covariates by including multiple random effects or by building a separate regression model for the standard deviation. One approach is to model the random effect standard deviation as a function of covariates using a log-link to constrain the standard deviation to be positive:

$$\begin{array}{c}\mathrm{logit}{\pi }^C(X_{\mathit{ij}})={\beta }_0^C+X_{\mathit{ij},1}{\beta }_1^C+\dots +X_{\mathit{ij},p}{\beta }_p^C+{\sigma }_{\mathit{ij}}{z}_j\\ \mathrm{logit}{\sigma }_{\mathit{ij}}(X_{\mathit{ij}})={\alpha }_0+X_{\mathit{ij},1}{\alpha }_1+\dots +X_{\mathit{ij},p}{\alpha }_p\\ z_j\sim N(0,1)\end{array}$$ (10)

This model can be fit in SAS using PROC NLMIXED (SAS institute; Carey, NC).

Missing data

Full likelihood-based approaches such as random effects models typically provide valid inference when observations are missing at random, i.e., the missing data mechanism is conditionally independent of the unobserved data given the observed data (42). In other words, likelihood-based procedures will typically provide valid inference even if the probability of an observation missing an outcome or covariate values depends on either the observed outcomes, such as the radiologist’s performance, or the observed covariates, such as the radiologists’ interpretive volume. However, GEE and conditional logistic regression require the more stringent condition of data being missing completely at random, i.e., the probability of data being missing does not depend on either the observed or missing outcomes or covariates. For GEE, weighting may be used to correct for bias when data are missing at random, but this requires determining the correct weights to use (43, 44). Bias-correction methods have also been proposed for conditional logistic regression (45).

DISCUSSION AND RECOMMENDATIONS

We have reviewed commonly used approaches for analyzing clustered data and, in particular, for estimating the influence of covariates such as radiologist interpretive volume on radiologist performance. We emphasize three key points. First, for the analysis of clustered data, one should consider whether the covariates of interests potentially vary within a radiologist, between radiologists, or both. In settings where both types of variability occur, one should consider whether or not the effects are the same, and model any differences appropriately. Second, conditional (radiologist-specific) and marginal (population-averaged) statistical modeling approaches answer different scientific questions, with the underlying parameters potentially having different numerical values. Consequently, caution should be taken when choosing a statistical methodology, and one should ensure that careful consideration of the scientific objectives drives the choice. Last, modeling assumptions need to be considered carefully because violations of assumptions that are likely to occur with radiologist performance data may lead to clinically significant biases in results. These issues have important implications for achieving consensus on the role of interpretive volume or the influence of an intervention or new technology on radiologist interpretive performance.

The distinction in the interpretations of marginal and conditional parameters is closely related to the notion of non-collapsibility of non-linear models (46). Non-collapsibility is most-often encountered in settings where the estimate of a covariate effect changes with the inclusion of an adjustment variable, and yet the adjustment variable is not a confounder. Therefore, the difference in the values of the estimate cannot be attributed to confounding, and one must acknowledge that the stratum-specific parameter (i.e., where one has included the adjustment variable) has a different numerical value than the marginal parameter (i.e., where one does not include the adjustment variable).

Despite the vast literature on the importance of taking clustering into account in statistical analyses, naïve approaches are still commonly used in the analysis of radiologist performance. For example, several recent papers published in the radiology literature used standard chi-square tests to compare the interpretive performance of two groups of radiologists, ignoring clustering among examinations interpreted by the same radiologist (47, 48). In other words, they analyzed the data as if each examination were interpreted by a different radiologist as opposed to the small number (N=10) of radiologists in the study. Given that these studies made between-radiologist comparisons based on a large number of mammography interpretations for each radiologist, the naïve chi-square test is expected to be liberal, resulting in p-values that are too small and possibly rejecting the null hypothesis too often.

Based on our review of the literature, we offer several recommendations. First, if interest lies solely in the conditional effect of changing a covariate within radiologists, such as the effect of an intervention, we recommend considering the use of conditional logistic regression, because it relies on fewer model assumptions. However, in this case, one must take care to ensure that variability of the response across radiologists does not depend on the predictor under study. Second, if interest is in marginal effects, and the number of clusters is not small (e.g., <20), an advantage of using GEE is that it is robust to misspecification of the covariance matrix. However, for cluster sizes between 20 and 50, it is important to correct for potential bias in the standard errors, which can be easily done by scaling the variance by N/N-P, where N is the number of clusters and P is the number of regression parameters (36). For cases with a small number of clusters, one could fit a random effects model and calculate the marginal effect induced by that model or directly model the marginal effect using a likelihood-based marginalized model (33, 34, 49, 50). Another advantage of using likelihood-based marginalized models is that their flexibility with respect to the random effect variance model permits an exploration and assessment of the underlying mechanism that generated marginal effect. Last, random effects models are particularly useful in several settings: (i) to estimate the conditional effect of a covariate that varies between radiologists, (ii) to quantify variation in mammography performance, across radiologists, and (iii) to estimate or predict adjusted radiologist-specific performance measures. However, we suggest exploring whether the variance of the random effects depends on covariates of interest. Not taking into account any dependences could lead to clinically meaningful bias in odds ratios estimates (41). In addition, we believe it is often of scientific interest to understand whether covariates influence the variability in radiologist performance. It is our hope that the careful consideration of the statistical issues discussed in this paper will help studies with a common scientific goal, such as determining the influence of interpretive volume on interpretive performance, achieve consensus.