Exploratory Structural Equation Modeling of Resting-state fMRI: applicability of group models to individual subjects

Abstract

The extension of group-level connectivity methods to individual subjects remains a hurdle for statistical analyses of neuroimaging data. Previous group analyses of positron emission tomography data in clinically depressed patients, for example, have shown that resting-state connectivity prior to therapy predicts how patients eventually respond to pharmacological and cognitive-behavioral therapy. Such applications would be considerably more informative for clinical decision making if these connectivity methods could be extended into the individual subject domain. To test such an extension, 46 treatment-naïve depressed patients were enrolled in an fMRI study to model baseline resting-state functional connectivity. Resting-state fMRI scans were acquired and submitted to exploratory structural equation modeling (SEM) to derive the optimal group connectivity model. Jackknife and split sample tests confirm that group model was highly reproducible, and path weights were consistent across the best five group models. When this model was applied to data from individual subjects, 85% of patients fit the group model. Histogram analysis of individual subjects’ paths indicate that some paths are better representative of group membership. These results suggest that exploratory SEM is a viable technique for neuroimaging connectivity analyses of individual subjects’ resting-state fMRI data.

Introduction

Structural equation modeling (SEM) is an increasingly popular technique for assessing the effective connectivity of neurocognitive systems. SEM has been used to model diverse cognitive networks, including those mediating visual perception (Büchel et al., 1999; McIntosh et al., 1994), motor control (Rowe et al., 2005; Solodkin et al., 2004; Toni et al., 2002), language function (Cabeza et al., 1997; Fu et al., 2006; Holland et al., 2008), associative learning (Fletcher et al., 1999; McIntosh and Gonzalez-Lima, 1998), and pain processing (Craggs et al., 2007). Unlike correlative connectivity techniques, SEM allows the inference of both magnitude and direction of functional influence, thus permitting the testing of sophisticated hypotheses of neural connectivity. Yet despite the growing prevalence of SEM, two developing areas of functional MRI (fMRI) research could further benefit from SEM analysis: resting-state functional connectivity and the extension of group level analyses to individual subjects.

Several methodological factors have impeded these applications, including the complexity of modeling nonrecursive systems (i.e. models with reciprocal “feedback” paths between two regions), a priori selection of the optimal network model (to capture the influence of mediating variables), and the uncertain contribution of individual-specific variance (e.g. physiological noise) to the group derived model. Simulation work suggests the application of SEM to individuals to be viable; models generated from 100 observations are as equally valid and reliable as models generated from 10,000 observations (Boucard et al., 2007). fMRI’s high temporal resolution of 20–30 data acquisitions per minute allows the acquisition of 100–200 datapoints in a 5–7 minute run.

The interpretation of resting-state neuroimaging connectivity models is further confounded by the frequent inability to derive a clear biological etiology for neurological and psychiatric illness. For some illnesses, such as Parkinson’s disease, the symptoms clearly originate from the loss of striatal dopaminergic cells, which manifests biologically as a reduction in glucose and DOPA uptake on positron emission tomography (PET) (Brooks et al., 1990; Eidelberg et al., 1990; Rougemont et al., 1984) and frontostriatal hypometabolism (Lozza et al., 2004). For other illnesses, such as epilepsy, PET can localize the focus of epileptogenic activity, but techniques with greater temporal resolution (like electroencephalography (EEG) and fMRI) are needed to detect perturbations in connectivity (Henry et al., 1990; Symms et al., 1999; Waites et al., 2006). And for many illnesses, such as schizophrenia, neuroimaging has revealed no consistent anatomic etiology or functional consequence (Leonard et al., 1999; Lewine et al., 1982; Seaton et al., 1999).

Despite these limitations, progress has been made at characterizing individual differences in neuroimaging data with SEM. One of the earliest neuroimaging applications of SEM showed a correlation between individual’s learning rates and the path weight from posterior parietal to inferotemporal cortex for a network model of visuo-spatial learning (Buchel et al., 1999). Mechelli and colleagues (2002) expanded upon this work by building a “network of networks” – that is, by modeling individuals as separate networks (connected by a node representing stimulus onsets) – for a pseudoword discrimination task. By iteratively freeing up one path across subjects while constraining all other paths to a constant group value, Mechelli used model fits to assess which paths significantly differed when allowed to vary across individuals. Unfortunately, the large number of ROIs modeled by their approach (m ROIs × n subjects + 1) makes it ill suited for the exploratory adaptation of SEM described in this work and elsewhere (see below; Zhaung, 2005).

Theoretically derived models constructed from resting-state data (primarily PET) have provided an additional starting point for individual-level analyses of resting state fMRI data using SEM techniques. Seminowicz and colleagues developed a structural model for resting-state PET data acquired from a multisite sample of depressed patients prior to treatment (Seminowicz et al., 2004). Alterations among the model’s path loadings corresponded with patients’ therapeutic outcome. But the paucity of PET data per patient constrained this analysis to group-level interpretations. Resting state analyses with fMRI, taking advantage of the modality’s high temporal resolution, should provide the necessary power for structural equation modeling of individual subjects.

We present several optimizations of SEM for its extension toward both resting-state data and individual-level analyses. We started with the most frequently cited structural equation model for resting state data – a 7 node model of limbic-frontal connectivity in major depressive disorder (Seminowicz et al., 2004). Seminowicz and colleagues chose the nodes based on a metanalysis of regions associated with consistent antidepressant treatment response. We applied this model to a sample of depressed patients, since this model had previously only been applied to depression.

The transition from PET to fMRI substantially increases the observation size, which in turn increases our statistical power – i.e. our ability to reject the null hypothesis when it is false (Agresti and Finlay, 1997). The null hypothesis for structural equation modeling is that the model fits the data, and our fit criteria test if we can reject the null hypothesis. A model that fits the relatively underpowered PET data may not fit fMRI data. Thus, we subjected this base model to an exploratory adaptation of SEM (Zhuang et al., 2005) to optimally tailor the model to fit our sample of depressed patients. Exploratory SEM calculates and ranks all possible subsets of the base model to find the model with the optimal fit – thus obviating the need for a priorii model selection.

Additionally, the increased number of observations per subject permits cross-validation approaches for assessing model reliability. The best model’s reliability was assessed with jackknife and split-sample approaches to characterize the influence of subject outliers on the model. We next performed confirmatory SEM to assess how reliably the optimal group model fit data from individual subjects. The extension of these group-level analyses toward individual subjects allows us to better capture sample homogeneity and heterogeneity.

Materials and Methods

Subjects

Forty-six (22 male; mean ± sd age = 42 ± 12 years old) never treated patients meeting DSM IV criteria for a current major depressive episode were recruited in accordance with Emory University Institutional Review Board policy. Patients provided verbal and written informed consent to participate in this study. To qualify for inclusion, participants must be ages 18–65 years old, of any ethnicity or gender, have a DSM IV diagnosis of Major Depressive Episode as determined by the SCID IV structured interview (with MDD as the primary diagnosis and no co-morbid disorders except anxiety disorders), have a 17 question score Hamilton-D ≥ 18 at screening and ≥ 15 at baseline (day of scanning), and be able to understand and provide written consent. Table 1 provides sample demographics, and Appendix A provides our rigorous list of exclusion criteria used to generate our sample of never-before treated MDD patients.

TABLE 1.

Sample Demographics

Age: Mean(sd)	42 (12) years
Gender	48% male
Race	76% Caucasian
	17% African-American
	7% Multiethnicity
Episode Duration: mean(sd)	60 (110) months
Episode Duration: chronic (episode lasting over 24 months)	50%
HAMD-17 at baseline: mean(sd)	22 (3.3)
HAMD at scan: mean(sd)	20 (3.8)
Recurrent vs First Episode	53% Recurrent MDD
	47% First Episode MDD
Family History	35% with family history of MDD
Concurrent Axis I Anxiety Disorder	35% with comorbid anxiety

Equipment, Procedure and Preprocessing

MRI data acquisition was performed using a 3.0T Siemens Magnetom Trio scanner (Siemens Medical Solutions USA; Malvern PA, USA) with the Siemens 12-channel head matrix coil. Anatomic images were acquired at 1×1×1 mm³ resolution with an MPRAGE sequence using the following parameters: FOV 224×256×176 mm, TR 2600ms, TE 3.02ms, FA 8°. Functional data were acquired with a z-saga sequence to minimize ablation of orbitofrontal cortex signal due to sinal cavities (Heberlein and Hu, 2004). The z-saga sequence used scan parameters of FOV 220×220×80 mm, 20 axial slices, TR 2020ms, TE¹/TE² 30ms/66ms, FA 90° for 210 acquisitions across 7.2 minutes at 3.4×3.4×4.0mm resolution. Although z-saga has reduced anatomic coverage compared to standard echo-planar sequences, its usage was necessary to capture orbitofrontal cortex activity, an essential region in this model.

For functional scans, participants were instructed to passively view a fixation cross while “clearing their minds of any specific thoughts”. The fixation cross helped prevent brain activity from eye movement and helped prevent subjects from falling asleep. Since we have no direct measure of compliance, subjects were asked following scanning if they performed the task as instructed. All subjects reported performing the task. In-house automated Perl scripts operating SPM5 (Friston et al., 1995) performed data processing. The anatomical images were simultaneously segmented and normalized to the ICBM462 normalized brain atlas using the SPM5 program “spm_preproc.m”. Functional data were motion corrected, slice time corrected, written to ICBM452 space using the parameters calculated from the corresponding anatomical imaging, spatially smoothed using a 6mm FWHM Gaussian kernel, and bandpass filtered (0.008 < f <0.09Hz). Anatomic gray matter masks were also transformed to MNI space using each subject’s MNI transformation matrix.

ROI selection

Regions of interest (ROIs) were generated from an in-house mask of 14 ROIs implicated in depression from PET, fMRI, and DTI studies (Craddock, 2008). ROIs were defined by a clinically trained neuroanatomist (HSM) as 6mm radius spheres using the anatomy of the ICBM452 anatomic template. When faced with ambiguity in placing the ROIs (particularly large cortical areas such as prefrontal cortex), ROI placement was additionally guided by a resting-state connectivity analysis using a posterior cingulate (PCC) seed, a 6mm radius sphere centered on MNI coordinates 0, 50, 25. AFNI (Cox, 1996) was used to generate PCC seed maps for each of 25 healthy control subjects. A two-tailed one-sample t-test assessed voxelwise if individuals’ seed map correlations significantly differed from zero (false detection rate threshold of q=0.05). This group map was used to guide placement of the 14 ROIs (each 6mm radius spheres), of which the 7 ROIs from the Seminowicz study were a subset. For bilateral ROIs, only the right hemisphere ROI was included to avoid issues of multicollinearity. Figure 1 depicts the ROIs overlaid atop the ICBM452 anatomic template, and Table 2 provides the MNI coordinates for the centers of the 6mm spheres representing these 7 ROIs. These ROIs were subsequently resampled from anatomic resolution (1×1×1mm³) to functional resolution (3.4×3.4×4mm³) using AFNI’s 3dfractionize program. If the resampled voxel included two neighboring ROIs – for example, included high-resolution voxels from amygdala and hippocampus – then it was assigned to whichever ROI composed the largest percentage of its volume.

Figure 1.

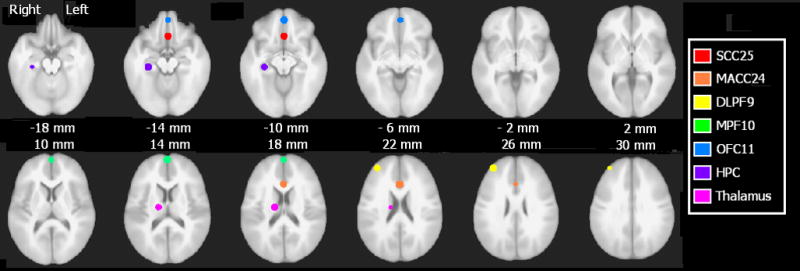
ROIs overlayed atop the ICBM452 anatomic template. Images shown in radiological convention (subject’s left is viewer’s right). SCC25, subanterior cingulate, red; MACC24, midanterior cingulate, orange; DLPF9, dorsolateral prefrontal cortex, yellow; MPF10, medial prefrontal cortex, green; OFC11, orbitofrontal cortex, blue; HPC, hippocampus, indigo; Thalamus, violet.

Table 2.

ROI center coordinates for Base Model.

	Talairach Coordinates
Region of Interest	x	y	z
Subgenual cingulate	1	24	−10
Midanterior cingulate	1	17	−34
Dorsolateral prefrontal cortex	34	48	27
Medial prefrontal cortex	1	62	14
Orbitofrontal cortex	1	49	−10
Hippocampus	29	−24	−12
Anterior thalamus	15	−11	17

Analysis

An additional 15 subjects (not reported in demographics above) were enrolled but excluded due to claustrophobia, excessive head motion (greater than 1mm), technical difficulties with data reconstruction, or uncorrectable scanner artifact. Timecourses for each individual were extracted by multiplying the resampled ROI mask by the subject’s MNI-transformed gray matter mask to capture only gray matter voxels, then averaging voxels within each ROI to obtain a mean gray matter timecourse per ROI. ROI timecourses were further cleaned by using AFNI’s 3dDeconvolution to regress out the influence of the 6 motion parameters (acquired from SPM5’s spm_“realign.m”) and the global mean timecourse (mean signal intensity at each timepoint). ROI timecourses were normalized as z-scores for each participant, then concatenated across participants within group to produce a matrix of ROI (7) columns and subject × timepoints (46×210) rows. Subject number and image number were also added as additional columns.

Exploratory SEM was performed using in-house programs written in Matlab 7.4.0 (The MathWorks, 2007). Testing all possible submodels of the 17 path base model took approximately 19 hours with a 2.5 GHz processor running Linux Redhat Enterprise version 4.0. Note that paths in the base model were constrained to established human and non-human primate anatomy (Seminowitc et al., 2005); therefore, all submodels tested by this method are likewise constrained to established anatomy. The Matlab program determined which paths to model from an input matrix, generated the corresponding Lisrel 8.80S.spl file (Jöreskog and Sörbon, 2006), executed Lisrel in a Linux environment, and extracts the goodness of fit indices from Lisrel output. Lisrel analyzed the data’s correlation matrix (as opposed to covariance matrix) so that the inputs to Lisrel were standardized to a unit variance across all variables. Extracted fit criteria include 35 fit indices, the lowest path-weight t-score, the greatest Psi variable t-score (see below), the greatest multiple squared correlation, and coefficients along the estimated covariance matrix diagonal not equaling one. The script also calculated and saved a binary variable describing model recursiveness (Maruyama, 1998).

Several optimizations have been introduced since previous implementations of this method (Zhuang et al., 2005). First, the code has been streamlined for user friendliness: the user inputs a matrix of 1s and 0s describing viable paths in the full model, from which the Matlab code generates its Lisrel syntax. Due to the fact that the data are already centered (raw data are standardized scores), the Alpha matrix is constrained to 0 by setting each variable’s Alpha matrix mean and variance to 0. Since the Alpha matrix is no longer being estimated, this modification also frees up degrees of freedom, thus increasing the complexity of identifiable models. Third, we ensured that the standardized Beta matrix would be interpretable as correlations by excluding models with squared multiple correlations (R²) exceeding 1 (over-parameterized models).

Ranking

Appendix B describes the exploratory SEM approach and the fit indices described below. Ranking began with removal of nonviable models. Previously published exclusion criteria for this method were failure to converge after 240 iterations, a parsimonious goodness of fit (PGFI) less than 0.10, and nonsignificant path weights (i.e. path loadings whose 90% confidence intervals included 0) (Zhuang et al., 2005). The latter criterion is justified since this approach tests all models; this method tests both the model in question and an identical model lacking the nonsignificant path(s). Three additional exclusion criteria were used. First, models with a squared multiple correlation (R²) score exceeding 1 were excluded, as these should be statistically impossible. Second, models with a probability of close fit (PCLOSE) less than or equal to 0.05 were excluded, as this is indicative of a root mean squared error of approximation (RMSEA) significantly differing from zero. Third, applying covariance structure models to a correlation matrix can alter the reconstruction of that matrix, as indicated by values other than 1.00 along the correlation matrix diagonal (Cudeck, 1989). Models with such reconstruction errors were also excluded.

We propose that the best model is the one that explains the most variability within the dataset and introduce a new metric for ranking the non-excluded models: Psi t-scores. Each ROI of a given model is accompanied by a variable Psi that describes how much of that ROI’s variance is explained. In other words, the PSI matrix is the variance-covariance matrix of the error terms (i.e. the residuals) of the structural equation linear model. We assume this matrix is diagonal, i.e., the covariance terms are zero, so the only remaining terms for our modeling are the variance of the residuals for each ROI. A highly significant Psi score represents a similar lack of fit to the model as the significance that would be assigned to standardized residuals in a linear regression analysis. So as Psi becomes increasingly significant, the model explains less of the corresponding ROI’s variance. We calculated the maximum Psi t-score per model, and then ranked models from least to most significant Psi t-score. The Psi score rankings typically showed a bimodal distribution with a gap of several points between the top 4–8 models and remaining models.

The top models with the lowest maximum Psi t-score (i.e., the smallest amount of unexplained variance) were subsequently ranked by the following criteria, in order of importance. First, we ranked the models by the number of ROIs in the model (described by saturated AIC). The justification is that, when choosing between two models that capture equal amounts of variance, the model that incorporates more ROIs allows for richer interpretations of network interactions. We next ranked the models by lowest to highest standardized root mean square residual (stRMR). Finally, we ranked models by highest to lowest adjusted and parsimonious goodness of fit (AGFI and PGFI, respectively).

Jackknife and Borda counts

The potential influence of subject outliers upon the respective group models was assessed using a combination of jackknife tests and Borda counts (Dym et al., 2002; Zwicker, 1991). We generated every possible subset of the group data with exclusion of 1–5 subjects. For example, our sample of 46 patients was resampled as 46 subsets with exclusion of 1 subject, 1,035 subsets with exclusion of 2 subjects, etc. For each subsample, we ranked how well each of the top 5 models fit that subsample using the same ranking criteria described above. Models were ranked on a scale of 1–5, with 5 being the best-fitting model. We then calculated the mean ranking of each model for each number of excluded subjects.

Split-sample analysis

For additional assessment of replicability, the sample of 46 depressed patients was randomly split into 2 groups of 23 patients each. The optimal model for each group (again determined with exploratory SEM) was compared to the best model for the full sample.

Individual

We then assessed how well individual patients fit the group model. We selected the probability of close fit (PCLOSE) from the many fit indices available to assess model fit. PCLOSE is the probability that RMSEA is significantly greater than zero. The null hypothesis for this comparison is that RMSEA does not differ from zero. PCLOSE is the p-value for rejecting the null hypothesis that the model fits the individual subject’s data; a PCLOSE value less than 0.05 indicates that RMSEA is greater than zero, and therefore the model does not fit.

Results

Group Models

All of the viable patient models had Psi t-scores exceeding 68, suggesting that all of the models retained large portions of unexplained variability (Table 3). Without a clear Psi cut-off threshold, the top 10 models were selected for subsequent sorting. Interestingly, the model with the marginally better Psi score (111436) also had the lowest stRMR of the surviving models with 5 ROIs (0.016 vs 0.023+). The fit indices for this model meet common criteria for a good fit (stRMR<0.05, PCLOSE≫0.05, low AIC, high AGFI and PGFI).

Table 3.

Fit indices for top 5 models (all subjects) and best models for each sample half.

Model	Subjects Included	Standard RMSEA	PCLOSE	Standard RMR	AIC	AGFI	PGFI	Min path t-score	Max PSI t-score
111436	ALL	0.025	1.00	0.016	68.77	1.00	0.40	3.51	68.07
110924	ALL	0.034	1.00	0.023	109.50	0.99	0.47	3.88	69.49
37212	ALL	0.032	1.00	0.023	110.63	0.99	0.53	2.17	69.49
46412	ALL	0.034	1.00	0.023	112.52	0.99	0.47	3.44	69.49
107340	ALL	0.036	1.00	0.025	118.06	0.99	0.47	1.69	69.49
111436	Half1	0.008	1.00	0.010	35.67	1.00	0.40	2.03	47.69
103260	Half2	0.040	0.95	0.026	82.65	0.99	0.40	2.05	32.16

The full base model (Figure 2, left) did not meet our criteria for a good model. It failed to converge after 240 iterations, had squared multiple correlation scores exceeding 1 in magnitude, and could not provide an estimate of Psi or path t-scores. The best model for this prospectively recruited group of depressed patients differs strikingly from the base model (Figure 2, right).

Figure 2.

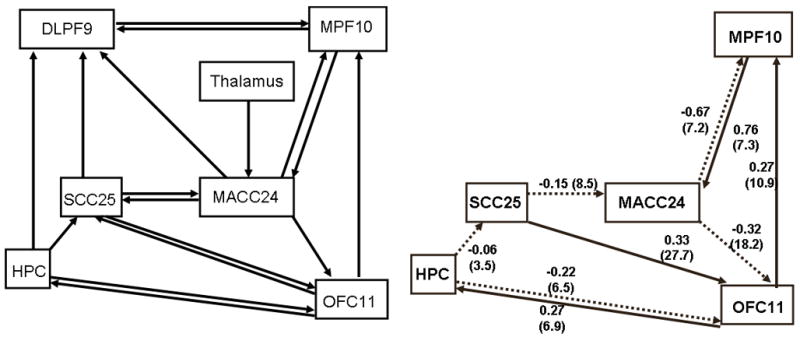
Comparison of the base causal model (left) and best model for 46 depressed patients. Depressed patients lack the reciprocal interactions between subgenual and midanterior cingulate. Additionally, patients lack the involvement of the dorsolateral prefrontal cortex. Dashed lines indicate negative path coefficients. SCC25: subgenual cingulate. MACC24: midanterior cingulate. HPC: hippocampus. DLPF9: dorsolateral prefrontal cortex. MPF10, medial prefrontal cortex. OFC11: orbitofrontal cortex.

Model stability and reproducibility

Table 4 reflects consistency among the path coefficients for the 5 best patient models. Some path coefficients show remarkable consistency. For example, the path from MACC24 to OFC11 ranges in magnitude from −0.21 to −0.32, and the path from OFC11 to MAC24 ranges 0.20 to 0.28. Some paths (such as OFC11 to HPC) have varying weights whose magnitudes appear correlated with other paths (in this case, the reciprocal path of HPC to OFC11). And other paths have more spurious coefficients (MPF10-MACC24, SCC25-OFC11) that retain consistent signs among the top models. Although beyond the scope of the presented work, future endeavors could characterize how path weight consistency influences overall model fit – i.e. if the most consistent paths also explain the greatest amount of sample variance.

Table 4.

Path coefficients for top 5 models (using all patients) and top models (using half of patients).

A	B	C	D	E	F	G	H	I	J	K	L	M
111436	ALL	--	−0.32	−0.67	−0.15	0.33	0.76	--	0.27	0.27	−0.06	−0.22
110924	ALL	--	−0.22	--	−0.07	0.36	0.04	--	0.20	0.43	−0.11	−0.35
37212	ALL	--	−0.23	--	--	0.06	0.04	0.28	0.20	0.39	--	−0.35
46412	ALL	−0.06	−0.21	--	--	0.36	0.04	--	0.20	0.39	−0.10	−0.32
107340	ALL	--	−0.30	−0.69	−0.15	0.31	0.79	--	0.28	0.03	0.02	--
103620	Half1	--	−0.37	−0.74	−0.24	0.28	0.86	0.10	0.31	0.34	--	−0.34
111436	Half2	--	−0.29	−0.75	−0.06	0.30	0.83	--	0.28	0.20	−0.07	−0.12

^A=Model

^B=Subjects Included

^C=MACC24→SCC25

^D=MACC24→OFC11

^E=MACC24→MPFC10

^F=SCC25→MACC24

^G=SCC25→OFC11

^H=MPFC10→MACC24

^I=OFC11→SCC25

^J=OFC11→MPFC10

^K=OFC11→HPC

^L=HPC→SCC25

^M=HPC→OFC1

To further assess model stability, we repeated our analysis method using split samples of the full dataset. Path coefficients for each of the best split sample models are comparable to the path coefficients for the best full sample model (Table 4). The two paths differing between the split samples (OFC11 to SCC25 and HPC to SCC25) are of negligible magnitude (respectively 0.10 and −0.07).

The ranking with Borda counts shows the best model to be resilient against the influence of subject outliers (Table 5). The best model consistently retained the greatest mean ranking (as summarized with Borda counts) with removal of 1, 2, 3, or 4 patients. Removal of more than four subjects becomes computationally intractable. However, the Borda counts show a distinct trend for the top model to win compared to rival models.

Table 5.

Borda counts for ranking of top 5 models with removal of 1–5 depressed subjects.

		Mean Ranking by Model
Subjects Removed	Number of Combinations	111436	110924	37212	46412	107340
1	46	5.00	3.98	2.48	2.46	1.09
2	1,035	5.00	3.93	2.22	2.57	1.28
3	15,180	5.00	3.89	2.08	2.58	1.45
4	163,185	5.00	3.69	2.20	2.70	1.41
5	1,370,754	Becomes computationally intractable

Individual

The ideal application of this method is to characterize how well individual subjects fit the group model. Using PCLOSE as the fit criteria, 85% (39/46) of patients fit the optimal group model. This high percentage of fit further reinforces that the group model is applicable to individual subjects.

The path coefficients distributions for the 46 individual subjects fit to the optimal group model are perhaps more informative, as they describe the relationships between these regions on an individual level. Histograms for subjects’ path coefficients (constrained from −1 to 1) are plotted for each of the 9 paths in Figure 3. For N=46, the Lilliefors composite goodness of fit test is insufficiently powerful to determine if the distributions are non-Gaussian; as such, we relied upon visual inspection to qualitatively infer Gaussianity. (Note that qualitative assessments such as visual inspection are prone to experimenter bias; however, the small sample size offers no alternative.) The path coefficient histograms that best approximate a Gaussian distribution (MACC24-OFC11, OFC11-MPF10) are also the most stable paths for the top 5 group models and the best split-half models. Likewise, the paths that least resemble a Gaussian distribution (MACC24-MPFC and MPFC-MACC24) have the most variable path coefficients.

Figure 3.

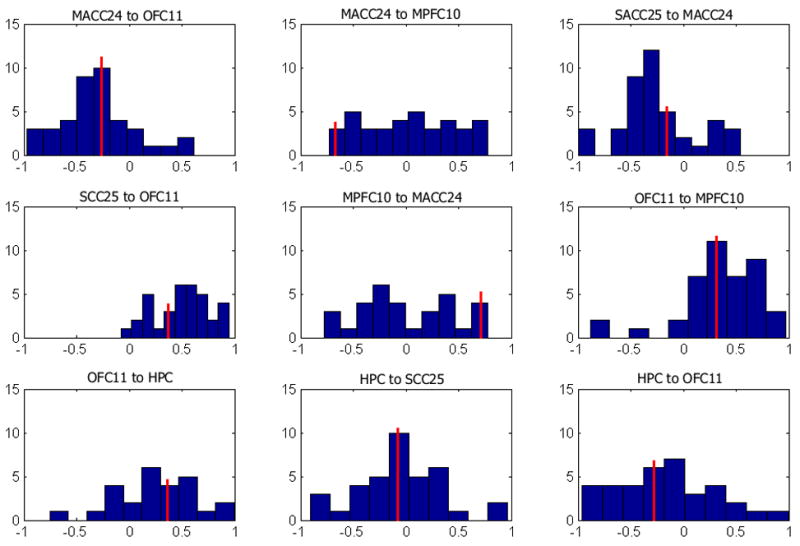
Histograms for path coefficients generated by fitting group model to individual subjects. The red line indicates group path coefficient value. Most path coefficients assume a Gaussian distribution centered about the group value. X-axis is path coefficient value (excluding values with absolute magnitude exceeding 1), and y-axis is number of subjects with coefficients of this value.

Discussion

We have shown the group model to be highly reproducible for group subsamples and applicable to the majority of individuals in our sample. While this group model appears to characterize this group of depressed patients most generally, it may not yet be optimal to explain the deviations in neural connectivity patterns underlying potential depression subtypes. Two converging lines of evidence suggest that our group analysis could benefit from additional refinement. First, the starting 7-node base model may be suboptimal. Anatomic and functional neuroimaging studies have implicated the posterior cingulate’s and amygdala’s involvement with this resting state emotional network (Anand et al., 2005; Johansen-Berg et al., 2008) – two regions not included in the Seminowicz model due to power issues. Independent diffusion tensor imaging (DTI) studies show another anatomic connection, inferred from the white matter tract between subgenual cingulate and medial prefrontal cortex (Fonteijn et al., 2008), not included in the base model. Inclusion of these additional nodes and paths would likely improve the validity of the base model.

Second, the patient sample contains a mix of therapy responders and nonresponders to whom’s status the authors are blind until completion of the ongoing study. A larger dataset (currently being collected) will be necessary to fully differentiate between these subpopulations. The large amount of variance not captured by our “optimal” model and the presence of path weights with negligible magnitude (i.e. −0.06 for hippocampus to subgenual cingulate) further suggests that a better model may exist. Nonetheless, we have presented a viable technique for identifying such an optimal model given a refined starting model that could conceivably characterize depression subtypes with implications for treatment response prediction based on individual baseline fMRI measures of activity or connectivity.

The most notable difference between the base model and best patient model is the lack of dorsolateral prefrontal involvement. One potential behavioral interpretation of this model is that DLPFC involvement reflects modulation of the core emotional network, and its absence in depressed patients indicates an inability to self-regulate one’s mood state. However, several pragmatic considerations overshadow this speculative interpretation. ROI selection for the DLPFC was the most problematic of ROIs in this study, given the region’s large size and functionally diverse subregions (see below). Diffusion tractography or other structural techniques would be necessary to more accurately select the optimal DLPFC ROI. Such approaches would also indicate if intermediate regions, such as the dorsal raphe or dorsomedial thalamus, should be included within this model. Furthermore, the small sample size severely curtails the implications that could be drawn between DLPFC activity and clinical variables. Future work with a better refined model and larger sample size will address the interpretation of regional activity and symptom.

Additionally, the reciprocal feedback of midanterior cingulate to subgenual cingulate is missing. Additional reciprocity is seen between midanterior cingulate and medial prefrontal, perhaps to stabilize the system in the absence of subgenual to midanterior cingulate reciprocity. While the two regions share a direct anatomic connection, we stress that anatomic connectivity implies neither functional nor effective connectivity. For example, Broca’s and Wernicke’s areas are strongly correlated during both overt reading but not during tongue movement tasks (He et al, 2003), despite their connection through the arcuate fasciculus. Following Wright’s rules (Wright, 1934), our model suggests that subgenual cingulate can directly influence midanterior cingulate, but midanterior cingulate does not directly influence subgenual cingulate. While midanterior can affect subgenual cingulate through an indirect path (midanterior to orbitofrontal to hippocampus to subgenual), the composite path loading for this influence (−0.32 * −.22 * −.06 = −0.004) is negligible.

This “one-way” effective connectivity is surprising, especially given the reciprocating effective connectivity influences between subgenual and midanterior cingulate shown in the original Seminowicz model. An important caveat is that the original model, while valid, is not necessarily the most optimal model, whereas our exploratory SEM approach specifically searches all possible models to find the model with the best goodness of fit indices and explaining the most variance. We are hesitant to make inferences about depression from this model, as the starting model can be improved with inclusion of subcortical regions with anatomic connections to both subgenual and midanterior cingulate, namely caudate and ventral striatum. We believe the inclusion of these regions will further elucidate the complex functional interactions along the cingulate.

It is not surprising that the optimal model does not incorporate thalamus. The thalamic ROI is modeled as an exogenous variable with only 1 path through which to explain its variance. Consequently, models incorporating the thalamic ROI had considerably greater Psi t-scores than models not incorporating thalamus. Since these models could not adequately explain thalamic variance, they were excluded by the sorting criteria. As with DLPFC, the thalamic ROI may require further refinement as other core members of the model are identified.

Our usage of Psi represents another criterion by which to gauge model fit. The significance of the PSI score represents a similar lack of fit to the model as the significance that would be assigned to standardized residuals in a linear regression analysis. One purpose of the analysis of residuals in linear regression can be to identify observations that may be overly influencing the results of the regression. However, the size of the residuals can also be indicators of overall lack of fit with a measure such as R²= 1−(SSres/SStotal), which is small when there is a large amount of variance which is not accounted for by the model (i.e., the sum of all residual terms SSres, is large). In our multivariate setting, the maximum significance value of all measures (ROIs) gives us an indication of the maximum lack of fit or the largest amount of unexplained variance due to one node for that particular model. Thus, our use of the PSI significance (t scores) allows us to identify models for which the residuals are large, i.e. there is a large amount of unexplained variance. Given a subsequent choice between models with the same number of parameters and equivocal goodness of fit indices, the model with the smaller amount of unexplained variance would be preferred regardless of the particular reason for the lack of fit (outlying observations, misspecification of the model). We feel that this is a reasonable and statistically sound criterion to use.

We chose to define ROIs as 6mm radius spheres placed upon the group’s mean standardized anatomic MRI. Using static, spherical ROIs may be less optimal than defining ROIs for each individual, given anatomic variability across subjects and issues with linear transformations of anatomic scans to standardized space (Crivello et al, 2002). But defining ROIs for each individual is a double-edged sword; while potentially increasing ecological validity, misplacement of a subject’s ROI(s) introduces an additional source of error. In the interest of consistency, we chose to use ROIs defined from group mean anatomy, then use the jackknife “leave N out” approach to assess deviations in individual fit from the group model. If anatomic variability causes an ROI to be poorly placed for a given subject, then excluding that subject with the jackknife approach would show the group model to be inferior to its rival models. Since the group model consistently wins against its rivals with the exclusion of 1–4 subjects, we can be confident that the group-defined ROIs are sufficient for all subjects.

In the absence of a functional localizer task, we used a group-level correlational analysis with a posterior cingulate (PCC) seed to guide ROI placement. PCC was selected because some of the regions of interest (medial prefrontal cortex and subgenual cingulate) have been shown to be correlated with PCC during rest (Greicius et al., 2003). DLPF9 was the most challenging ROI to place due to broad area covered by this anatomic region. In retrospect, a seed map generated from one of the ROIs in our model may have been more suitable. However, t-test analyses show the mean group correlation of DLPF9 to significantly differ from zero (all p < 0.0001) for SCC25 (r = −0.16), HPC (r = −0.18), MACC24 (r = 0.28), and OFC11 (r = −0.23). These significant correlations suggest that placement of the DLPF9 ROI, while arguably serendipitous, is nonetheless valid.

Even if DLPF9 was excluded from the model due to suboptimal ROI placement, this is not an indictment of our modeling approach. On the contrary, we want a method that eliminates models that incorporate erroneous ROIs. This is exactly what our usage of PSI scores does, and represents an improvement over previous implementations (wherein an ROI would be included regardless of how much of that variable’s variance was explained by the model). Every model only approximates reality, and models can err in being over- or under-inclusive of relevant variables. We have chosen to pursue a modeling approach that aims at parsimony (minimize Type 1 error) while accepting increased risk of missing relevant regions (Type 2 error).

Usage of the z-saga sequence was necessary to retain signal from the orbitofrontal cortex, an essential region in the Seminowicz model. Z-saga has reduced anatomic coverage compared to standard echo planar images, although whole brain coverage is possible with a TR of 3000ms. The mean variance of the orbitofrontal cortex ROI (4.91) across subjects was comparable to variances of other ROIs (subgenual cingulate, 4.19; thalamus, 4.09). Ventromedial prefrontal had the greatest variance of all ROIs (9.30) while hippocampus had the least (1.92). Regardless, our usage of correlation (rather than covariance) matrices ensures that all ROIs are expressed as standardized variance units, so these variance differences across ROIs do not influence our results.

Our most novel application of SEM is the assessment of individual subjects’ fit to the group model. 85% of patients fit the group model, showing that this model represents the patient sample well. The histogram analysis illustrates that the path coefficients that are most stable among the top group models are also the most Gaussian-distributed across individuals. These paths may be indicative of group commonality – i.e. how individuals of the group are similar.

Conversely, the path weights varying most across subjects may convey nuanced information of responder/nonresponder subtype membership that is lost in the group model. By example, the MACC24-MPFC10 path (and its reciprocal) have flat, non-Gaussian distributions across individuals. These regions have previously been associated with relapse vulnerability (Gemar et al., 2007) and with changes in pre- and post-treatment activation as a function of treatment strategy (Goldapple et al., 2004). Within this context, DLPFC’s absence from the optimal model may not be surprising; Seminowicz and colleagues showed path loadings to this region to differ between cognitive-behavioral therapy responders and medicine responders (via the HPC-DLPF9 path) as well as between medicine responders and nonresponders (via the SCC25-DLPF9 path) (Seminowicz et al., 2004).

Figure 4 plots the non-Gaussian path coefficients (midanterior cingulate to medial prefrontal and its reciprocal path) by subject. For most subjects, these path coefficients have comparable magnitude but opposite sign. This relationship can be viewed as a negative feedback loop; an increase in A leads to an increase in B, which in turn induces a decrease in A. Subjects that did not fit the model (denoted by Xs) have path coefficients that are skewed toward the right of the histogram (in the opposite direction of the group path coefficients). Subjects with path weights closer to the group model (i.e. with negative MACC24-MPF10 and positive MPF10-MACC24 path weights) are more likely to fit the group model than those subjects with path weights in the opposite direction. However, numerous subjects with path weights opposite of the group model still have a good statistical fit. The reciprocal relationship suggests that the values of these path pairs are not as important for model stability as the paths being commensurate and opposing. The incorporation of additional patient characteristics (i.e. responder subtype) with a larger sample will help elucidate the relative contribution of Gaussian-distributed path coefficients and non-Gaussian, reciprocating path coefficients toward overall model fit.

Figure 4.

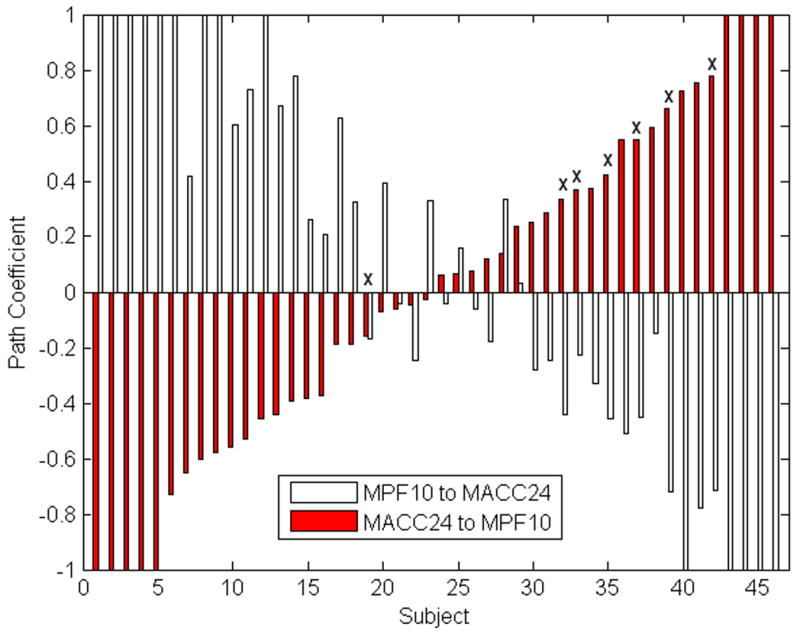
Path coefficients for two paths without Gaussian distributions, by subject and with outliers. For most subjects (38 of 46), the midanterior cingulate to medial prefrontal path has an opposite sign as its reciprocal medial prefrontal to midanterior cingulate path. Subjects who do not fit the model (denoted by Xs) are skewed away from the group model path weight (−0.67 and 0.76, toward the left of bar chart).

Conclusions

Our extensions to exploratory SEM result in highly stable and replicable group models for describing resting state connectivity. The best group model is resilient to the effect of outliers and reductions in sample size. Individuals’ data fit the group model well, and the distributions of individual-level path coefficients provide insight into which paths offer the most critical contribution to the group model. Our refinements to exploratory SEM are suitable for future exploration and characterization of individual resting-state functional MRI data.

Appendix A: Exclusion criteria

Patients were excluded if they had

• Current psychosis, dementia, eating or dissociative disorder.

• History of bipolar disorder (I and II) or schizophrenia

• Alcohol or drug dependence within 12 months or abuse within 3 months of baseline visit (excluding nicotine and caffeine) as assessed by history and urine drug screen

• Need for concurrent neuroleptic or mood stabilizer therapy

• Presence of any acute or chronic medical disorder that would likely affect or preclude completion of the trial.

• Medical contraindications which would preclude treatment with escitalopram or duloxetine.

• Presence of practical issues that would likely prevent the patient from completing the 12 weeks of the study (e.g. planned geographical relocation)

• Pregnant or breast-feeding women

• Women of child-bearing potential not using a medically approved form of contraception and/or double barrier methods.

• Contraindications for MRI: pacemaker, aneurysm clips, neurostimulators, cochlear implants, metal in eyes, steel worker, or other implants.

• Contraindications for Dex-CRF test: Uncontrolled hypertension; significant abnormalities in EKG, anemia, known allergies against CRF.

• Any (lifetime) prior exposure to Lexapro (escitalopram), Celexa (citalopram) or Cymbalta (duloxetine)

• Any (lifetime) prior treatment with Cognitive Behavioral Therapy (CBT), Interpersonal Therapy (IPT) or Behavioral Marital Therapy for depressive symptoms for >4 sessions.

• Any (lifetime) adequate medication treatment (≥4 weeks at minimal effective dose) for major depression or dysthymia.

• Treatment with an inadequate dose of an antidepressant for any reason for > 4 weeks for during the current episode.

• Use of fluoxetine within 8 weeks of the screening visit.

• Use of any psychotropic medication within 1 week of the screening visit.

Appendix B. Exploratory SEM and fit indices

We include this appendix to offer additional insight into the exploratory adaptation of SEM detailed elsewhere (Zhuang, 2005) and justification for the fit criteria used to sort models. We recommend Raykov and Marcoulides (2000 chapter 1) or Maruyama (1998) for more comprehensive descriptions of SEM.

SEM is confirmatory approach used to infer causality among variables. Like all confirmatory approaches, the investigator is testing how well a pre-defined model fits the observed data. Model fit is assessed by comparing the variance-covariance matrix predicted from the model to the variance-covariance matrix observed from the data. The predicted covariance matrix can also be expressed in terms of model parameters (i.e. path weights and variables’ unexplained error). SEM programs such as LISREL iteratively adjust the model parameters to minimize the difference between the predicted and observed variance-covariance matrices (in our work, using the Maximum Likelihood Estimate). The iterative adjustment of parameters continues until the improvement in model fit is negligible (convergence) or the process exceeds a preset maximum number of iterations (non-convergence). Then model fit criteria are calculated to describe differences in the predicted and observed covariance matrices

For our exploratory adaptation of SEM, we are using a brute-force method to iteratively test every possible sub-model of the starting base model. Then we evaluate which model is best by ranking the models by their fit criteria. Below, we described the fit criteria and provide justification for their use in ranking models.

Many of these indices are derived from the chi-squared (χ²) goodness of fit T=(N−1)F_min, where N= # observations and F_min=minimal value for the fit function used. χ² is rarely used, since the multiplication by sample size inflates its significance value.

The Goodness of Fit Index (GFI) expresses the proportion of variance that the proposed model explains. For MLE, GFI = 1 − [Tr((C⁻¹(S−C))²)/Tr((C⁻¹S)²)] where C and S are the predicted and observed covariance matrices and TR is the trace of the matrix.

Adjusted and Parsimonious GFI (AGFI, PGFI) are GFI respectively corrected for number of parameters and sample size. For all three indices, the expression in brackets approaches 0 as the difference between C and S diminishes, so that a perfect solution would have a GFI of 1. A common threshold for GFI is to exceed 0.90. However, AGFI and PGFI are more conservative estimates. We chose to exclude models with PGFI ≤ 0.10, as these models represent the very worst fitting models. Higher thresholds were considered but ultimately rejected; our strategy was to use exclusion criteria to reject the unquestionably bad models, then rank the remaining non-excluded models.

Estimated path coefficients were accompanied by a standard deviation and t-statistic. We excluded models with any path |t-statistic| ≤ 1.64 (corresponding to a two-tailed 90% confidence interval. We justify the exclusion of these models with non-significant paths because the identical model without these paths was also testing (since our brute force approach testing every possible model).

The amount of each variables’ variance explained by the model is described as the matrix Psi. The Psi matrix is also accompanied by a standard error and t-statistic. A significant t-statistic for a variable’s Psi score indicates that the model cannot explain a significant portion of that variable’s variance. To clarify our Methods, we used the highest Psi score of all variables as that model’s Psi score. For example, a model with the Psi t-scores:

$$var1\text{t}=4.03var2\text{t}=2.05var3\text{t}=37.28var6\text{t}=9.51$$

would be assigned a PSI t-score of 37.28

Note that variables not included in the model (var4, var5 and var7) are not contributing to the overall solution due to LISREL’s “SE” command – an additional improvement over previous implementations of this method.

PCLOSE (or “P-value for Test of Close Fit”) is a p-value for the null hypothesis that the root mean squared error of approximation (RMSEA) is no greater than 0.05. RMSEA is ((χ²/((n−1)df))−(df/((n−1)df)))*.5, where n=sample size and df=degrees of freedom. RMSEA < 0.10 indicates an adequate fit and <0.05 indicates a good fit. Likewise, a significant PCLOSE (i.e. p<0.05) indicates that RMSEA > 0.05 (and therefore, not a good model). We excluded models with a significant PCLOSE (providing statistical evidence that RMSEA > 0.05) rather than RMSEA directly, since RMSEA with a narrow distribution could be close to but still significantly different from 0.05.

Standardized root mean residual (stRMR) is the mean difference between predicted and observed variances, divided by the standard error of the differences. StRMR <0.10 indicate an adequate fit and <0.05 indicate a good fit.

Akaike Information Criterion (AIC) is a χ² adjusted for model complexity. AIC is uninterpretable for a single model, but rather compares models drawn from the same dataset (i.e. models including the same ROIs). Lower AIC indicate better fit between model and data. AIC is interpretable for Table 3 since all models include the same 5 ROIs, even though the paths between these ROIs differ.

Saturated AIC (satAIC) is n*(n+1), where n is the number of ROIs in the model. satAIC is used in our ranking to represent the number of ROIs in the model.