Experimental Health Insurance Estimates for Low-Income and Demographic Groups by State

Abstract

Objective

To assess the quality of new modeled estimates of health insurance based on a federal survey.

Data Sources/Study Setting

The study uses data from the Annual Social and Economic Supplements to the Current Population Survey (CPS ASEC), calendar years 2001–2003. Health insurance estimates for low-income populations are analyzed.

Study Design

To assess a method for making estimates for uninsured low-income persons, survey estimates of low-income children are compared with modeled estimates. Inferences can be drawn from this comparison and the method is extended to account for demographic groups.

Data Collection

Data for 2001–2002 CPS ASEC were self-tabulated for low-income children aged 0–17. A special tabulation of the CPS ASEC was used to categorize the numbers of uninsured by age, race, sex, and Hispanic origin by low income at the state level. This special tabulation was the underlying data for the model.

Principal Findings

The modeled estimates reduce the variance and margin of error substantially compared with the survey estimates.

Conclusions

These health insurance estimates are credible and increase the precision for the low-income uninsured population. They have broad uses for policy makers and program administrators who focus on the uninsured in special populations.

Since 1987, the Census Bureau has published state uninsured rates as part of the Current Population Reports series. Estimates for children under age 19 who are at or below 200 percent of the federal poverty level, all children aged 0–17, people under 65, and all ages are published on the website (Census Bureau 2007a). The Census Bureau's Small Area Health Insurance Estimates (SAHIE) program published county-level modeled estimates of the number of uninsured by age (0–17 and total) and, at the state level, number of uninsured by sex, age, race/ethnicity, and income-to-poverty ratios (Census Bureau 2007b).

Data on health insurance coverage for all counties are not available elsewhere because the Census 2000 does not ask this question. The American Community Survey contains questions on this topic as of the 2008 survey. However, those data are not available yet. National surveys, such as the Annual Social and Economic Supplement (ASEC) of the Current Population Survey (CPS), do not have sufficient sample size or full representation in all counties to provide survey estimates at the county level.

The limited state-level sample size in the CPS ASEC direct survey estimates means that partitioning age groups further into race, sex, and ethnicity categories results in unacceptably high variance. The SAHIE program publishes small area estimates for health insurance that incorporate age, race, sex, and Hispanic origin by income-to-poverty ratios.

This project is partly funded by the Centers for Disease Control and Prevention's (CDC) National Breast and Cervical Cancer Early Detection Program (NBCCEDP). The main criteria of eligibility of the early detection program are that women are uninsured and have a low income. The CDC program will be enhanced by precise estimates for participation rates and identification of underserved populations at the state and the county level.

One of the motivations for creating these estimates is to provide small area estimates for health insurance similar to the Small Area Income & Poverty Estimates (SAIPE) program. The SAIPE program has model-based estimates of poor persons by age. The geographies include states, counties, and school districts. The Department of Education uses these estimates to allocate Title 1 funds. Before the SAIPE estimates, the state estimates varied substantially and the county and school district estimates were only available from the decennial census. The goal of the SAHIE program is to produce similar estimates for the low-income uninsured population.

When there are no alternative estimates of health insurance coverage for a small area, any of the small area techniques will give estimates of coverage rates for specific areas. This paper describes the usefulness of a particular small areas approach that is beneficial because it is consistent across states. These estimates fill a need for accurate uninsured estimates for states (Blewett and Davern 2006) as well as estimates by age, race, sex, and ethnicity. The focus on the state-level model, as opposed to the county-level model, is because of its capability to produce uninsured estimates by income groups.

Need For Health Insurance Estimates

The primary emphasis of this paper is to offer estimates to describe the characteristics of the uninsured for policy administration. Small area estimation techniques can provide state policy makers with the ability to identify areas with higher and lower levels of need, using a common methodology. Czajka and Jabine (2002) showed that direct survey estimates for uninsured low-income children are relatively imprecise for allocation of funds for the State Children's Health Insurance Program (SCHIP) and modeling the data was recommended, with caveats.

Like the SAIPE program, modeled estimates of health insurance coverage have greater precision of estimates that lend themselves for use in funding allocations or participation rate analyses. Programs can appropriately target populations and subpopulations that are underserved. When a new policy is implemented within a small area to foster increased insurance coverage, small area estimates can help determine whether the policy initiative was successful.

Having more refined estimates for small areas and subpopulations can increase the general awareness of the uninsured across more sectors of the population. For example, county estimates can provide a local point of view about the size of the uninsured population. Because much of public policy occurs at the local level, estimates can keep the community better informed. The initial county-level heath insurance estimates by the SAHIE program partly met this need.

Federal Programs Need Estimates

The Government Performance and Results Act of 1993 emphasized the need for appropriate data to evaluate performance and inform spending decisions. As a result, government agencies have annual performance reports that require measurable outcomes of individual programs. Many federal programs provide health insurance or health service benefits based on the number of uninsured people by specific characteristics such as age or sex.

In 2002, the National Research Council evaluated available data sources to determine data sufficiency concerning the SCHIP. They concluded that current survey estimates were insufficient to evaluate program performance (although the CPS is sufficient to allocate funds). The first recommendation of the panel was “developing more uniform ways of estimating eligibility and health insurance coverage among the states.”

Other federal programs also need accurate estimates of the uninsured population. For instance, the CDC's NBCCEDP provides screening services for breast and cervical cancer to low-income, uninsured, and underserved women. At the national level, the program can be evaluated using survey estimates. At the state level, the confidence interval on the number of eligible women at risk is unreliable for funding decisions for many states (O’Hara et al. 2006). The NBCCEDP, SCHIP, and other programs related to health insurance are constrained in measuring success with survey estimates.

State, Local, and Private Programs Need Estimates

Estimates are equally important in evaluating the need for funds at the state and local levels, and in the private sector. For instance, the State Medicaid Director may want to fund outreach efforts in counties that have the most uninsured, low-income children. States can further use information to determine the potential cost for implementing SCHIP or Medicaid expansions/waivers. Accurate estimates would allow a state to make informed decisions on whether to offer health insurance to people with higher incomes (Glied and Gould 2005) or parents (Dubay and Kenney 2003).

More detailed estimates of the number of uninsured are also needed when states consider the cost of implementing new health insurance coverage programs. The State of Illinois has implemented a program called “All Kids” (All Kids 2007). The goal of the program is to fill the insurance gap for children who have family incomes greater than the SCHIP eligibility criteria but still have low family incomes. To predict costs, Illinois could use the number of uninsured children by income groups.

Local information can improve other programs that are related to health services such as reallocating local resources to a clinic (National Research Council 2003). These local data are not available in sufficient detail for most counties or states (Luck et al. 2006).

Public/private ventures are becoming a common way of meeting needs at a local level. Nonprofits often fill the gaps by paying fees and premiums for public health insurance. For example, Eblen Children's Healthcare Initiative pays for enrollment fees for SCHIP in North Carolina (Eblen 2007). Caring for Children (2007) are state-based charities, sponsored by Blue Cross/Blue Shield, which provide health insurance for low-income children who do not qualify for Medicaid. Without a sense of the number of eligible children, applying for adequate funding from grant organizations or program evaluation is guesswork.

Methods

The SAHIE program constructs statistical models that relate health insurance coverage, as measured by survey estimates from the CPS ASEC, to population estimates and administrative records. These are then combined to provide estimates and standard errors for the geographic areas of interest. In this paper, this is called a modeled estimate.

Data Sources

The CPS ASEC provides survey estimates of the proportions of people with health insurance coverage within each income-to-poverty category by demographic characteristics. The data are pooled and averaged from three survey years: 2000, 2001, and 2002. The proportion of people in an income-to-poverty category (by age, race, sex, and Hispanic origin) and the proportion of people in an income-to-poverty category by insurance coverage (by age, race, sex, and Hispanic origin) are the dependent variables.

The CPS ASEC data are categorized into demographic groups, consisting of four ages (0–17, 18–39, 40–49, 50–64), three races (white, black, other), two sexes (male, female), and Hispanic origin (Hispanic, non-Hispanic). The race/ethnicity is further collapsed into four categories: non-Hispanic white, non-Hispanic black, non-Hispanic other, and Hispanic. This categorization was established to provide as many race/ethnicities as possible with a reasonable population size to be estimated.

There are three income-to-poverty categories (0–200, 201–250, >250 percent) per demographic group; the model is flexible enough to accept any three categories. All of these categories are cross-classified, giving 96 demographic and income-to-poverty categories per state. The model can be run for various levels of low-income groups. It would only take an adjustment of the underlying data to produce other low-income groups, such as 200 and 300 percent of poverty, or other age groups. This is an important feature because policy makers may be interested in other income-to-poverty ratios.

Because the independent variables must have broad coverage of counties and states, administrative data from local programs that have national coverage are needed. Administrative data are aggregated to the county and the state level. These data include the following: tax exemptions tabulated by age and income-to-poverty ratios, and a tax-to-income distribution and its variance (from the Internal Revenue Service 1040 Individual Master File aggregated before the data are released to SAHIE); the number of food stamp enrollees (from the Food and Nutrition Service); the number of Medicaid enrollees by age and sex (from the Centers for Medicare and Medicaid Services Medicaid Statistical Information System); and the number of SCHIP enrollees (from the SCHIP Annual Reports).

The model also uses Census 2000 data in the form of estimates of people in the demographic groups by income-to-poverty ratios. Finally, Census Bureau population estimates, by demographic groups, are used to transform the predicted proportions into numbers.

Data Limitations

Recently, the Census Bureau revised the CPS ASEC numbers on health insurance because there was a flaw in the processing of the data that affected coverage from employer-provided and directly purchased health insurance in families (Census Bureau 2007c). This research uses unrevised numbers because historical Census Bureau numbers on health insurance are used. When the SAHIE program produces the next round of estimates, the revised data will be used. However, preliminary analysis indicates that it should have little impact on the model. Besides the data revision, the CPS has potential problems measuring health insurance. There is evidence that Medicaid coverage in the CPS is lower than that indicated by administrative records (Davern, Klerman, and Ziegenfussi 2007).

The incidence and method of imputation are relevant because they can bias the state count of the uninsured. All of the CPS imputations are conducted at the national level, not at the state level. Therefore, the imputations are unbiased at the national level and probably biased at the state level. Davern et al. (2004) have shown that the state count of the uninsured is in fact biased. Although the modeled estimates have this imputation problem, the model uses auxiliary data that should minimize this imputation bias.

The CPS data could be biasing the number of uninsured estimates because of the imputation procedures at the national level. There were fewer persons having employer-provided and direct purchased health insurance data in the imputed cases than the nonimputed cases in the unrevised 2004 CPS estimates. The imputation bias affects married people and children (Davern et al. 2007). The revised estimates should ameliorate this problem. However, this research was conducted using the data before the revision, and thus contains this bias. Results should be viewed accordingly.

The administrative data have the regular caveats, particularly with tax data as well as Medicaid and Food Stamps data. Tax data lack information on people who do not file, and there may differ by geography. The expectation is that people aged 65 and older (i.e., less likely to have a filing requirement) and poor persons with no earned income (i.e., not qualified or unaware of the Earned Income Tax Credit) are the nonfilers.

Medicaid participants in the administrative records who had limited coverage are excluded from the final dataset because these participants do not meet the CPS definition of insured. Medicaid data poorly report race and ethnicity and this information is not used. In some states the SCHIP participants are included with the Medicaid participants; SCHIP participants are excluded for constancy across states. The quality of the Medicaid data will also vary because the likelihood that income verification and administrative practices differ from state to state is high (SHADAC 2005). The last caveat is that there are known anomalies in the data that need to be “corrected” (CMS 2007).

Food stamp participation rates for states differ substantially (Cunnyngham, Castner, and Schirm 2007). This is a limitation in using the variable because differing participation rates will influence the states’ estimated uninsured rate. Similar to Medicaid, the issue of differing state practices in administering the food stamps program will affect the estimates.

Statistical Model

The modeled estimates use Bayesian hierarchical methods (Ghosh et al. 1998) with an uninformative prior. The model estimates the number of insured in categories defined by demographic categories and income-to-poverty ratios at the state level, resulting in 4,896 estimates for the nation. Estimates can be aggregated to be more inclusive of a demographic characteristic. For instance, adding up race/ethnicity and sex creates a new estimate of age group by income-to-poverty ratios (with new variances).

The model is decomposed into two levels, representing the number of people in income-to-poverty categories (level 1) and the number of people, given the income-to-poverty category, with insurance coverage (level 2). Once the number of people in an income-to-poverty category who are insured is estimated, calculating the uninsured is a matter of simple subtraction. For technical details, refer to Fisher and Riesz (2006).

Evaluation Approach

This study relies on the coefficient of variation (CV) and the margin of error (the half-width of the length of the confidence interval) for determining the quality of an estimate. The CV is the standard error divided by its mean and is a typical measure of goodness of fit for this type of model. A CV is standardized, which allows comparison of different estimates. The CV is also related to the margin of error; smaller CVs coincide with smaller margins of error and better estimates.

It is also an important criterion because many statistical agencies determine whether a statistic can be released based on CVs; surveys have different thresholds for the CVs depending on the precision needed for the main estimate produced. For the National Center for Health Statistics, estimates are not released if the CV is above 30 percent. For the Census Bureau, the rules concerning CVs are more complex. If the median CV of key survey estimates is less than 30 percent, the estimates can be released without caveats (Census 2007d).

It is difficult to evaluate whether a modeled estimate is statistically different from a survey estimate. Tests of comparing two percentages are not applicable because (1) modeling error is not accounted for, which underestimates the “true variance,” and (2) the correlation of the survey and modeled estimates is unknown because the dependence of the model on the underlying survey estimates is unknown.

A variety of “tests” between the two estimates are conducted to measure the plausibility of the modeled estimates. The first test is whether the modeled estimate falls within the survey estimates’ confidence interval; this test assumes that the modeled estimate has no variance and functions as a plausibility test. The second test is the traditional test for difference in means with a variety of correlations assumed. Presumably, there is a positive correlation between the two estimates because they share the same underlying data. However, this correlation is unknown. These two tests allow for a range in assumptions.

Findings

Although estimates are available for demographic groups by income-to-poverty categories, the analyses presented will be on low-income uninsured children aged 0–17. The first section compares survey estimates for uninsured low-income children with these experimental modeled estimates. The second section presents demographic modeled estimates for low-income non-Hispanic black children with CVs and confidence intervals. All estimates presented are percents, not numbers.

Uninsured Low-Income Children

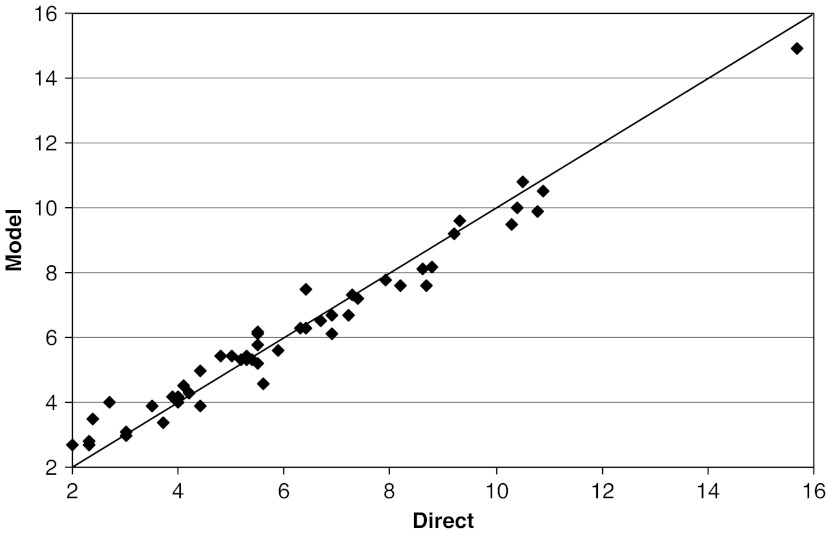
Figure 1 compares CPS ASEC survey and modeled estimates of uninsured low-income children. The x-axis is the direct estimate of the percent of low-income uninsured children and the y-axis is the modeled estimate. The 45° line represents equality of the two estimates. Each point on Figure 1 represents a state. Deviation from the 45° line indicates a larger differential. The states where the direct and modeled estimate stands out are for the lowest uninsured rates. With one exception (North Dakota), states with the lowest uninsured rates for low-income children (Massachusetts, Missouri, Rhode Island, Vermont, Wisconsin) have the largest percent increase in the modeled estimates. Otherwise, the states have roughly similar uninsured rates.

Figure 1.

Direct versus Modeled for Percentage of Uninsured Children at or below 200 Percent of the Income-to-Poverty Ratio.

Source: Estimates are based on unadjusted numbers from CPS ASEC 2000–2002.

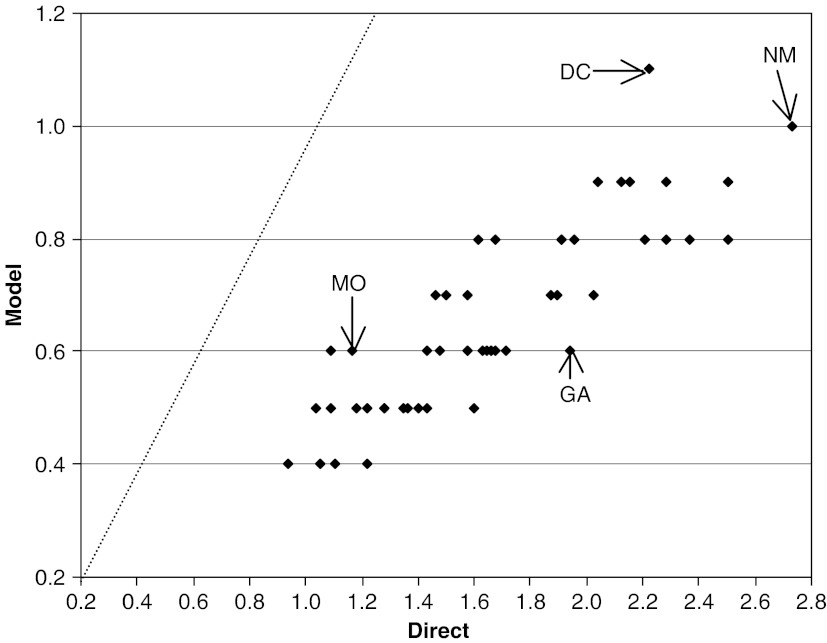
A widely used “test” of quality is the margin of error (the half-width on the confidence interval); a smaller margin of error indicates a better estimate. Figure 2 shows the margin of error of the percent for the direct estimates (x-axis) and the modeled estimates (y-axis). By this metric, all states have lower margins of error from modeling, as evidenced by each point's location below the 45° line. Modeling incorporates auxiliary data to increase the reliability of the percentage uninsured estimates and the variances. Smaller states benefit the most from modeling.

Figure 2.

The Margin of Error (1.645 SE) of Direct and Modeled Estimates of the Percentage of Uninsured Children at or below 200 Percent of the Income-to-Poverty Ratio.

Source: Estimates are based on unadjusted numbers from CPS ASEC 2000–2002.

At the extreme, Georgia has the highest percent change from the 45° line, a margin of error of 1.9 percentage points with direct estimates and 0.6 with modeling. The highest point on the figure is DC (2.2 versus 1.1, respectively). The rightmost point is New Mexico (2.7 versus 1.0, respectively). The model has the advantage of smoothing the estimates to give increased stability from year to year and state to state. The state that was least improved in terms of the margin of error was Missouri (1.2 versus 0.6, respectively). The figure can also be interpreted vertically or horizontally; when the direct estimate of the margin of error is 1.0 percent, the modeled estimate is between 0.4 and 0.5.

Table 1 summarizes the effect of the variety of assumptions between the two percentages presented in Figure 1. These tests are basic comparisons to establish the face value of the modeled estimates. The first test is whether a modeled estimate falls within the confidence interval of the direct estimates. The estimates for Missouri alone failed this simple test.

Table 1.

Tests for Differences between Survey and Modeled Estimates

		Mean Difference Test
States	“Plausibility Test” Model Estimate Falls into the CI of the Survey Estimate	ρ=1	ρ=0.5	ρ=0
Missouri	X	X	X	—
Rhode Island	—	X	X	—
Vermont	—	X	—	—

For the test that accounts for the variances in both estimates, three correlations were chosen: one (100 percent correlation), half, and zero. When the correlation is one, Missouri, Rhode Island, and Vermont have modeled estimates that are statistically different from the survey estimates. When there is a 0.5 correlation, Missouri and Rhode Island have survey and modeled estimates that are statistically different. When the correlation is zero, which is necessarily false, no states are statistically different. In each of these states, the modeled estimates of the percent uninsured low-income children had the largest absolute percent increase (48.1, 45.8, 35.0 percent, respectively). The next highest percent increase was Wisconsin at 21.7 percent. Each of these states was in the lowest deciles for uninsured low-income children.

In general, the state-modeled estimates are reasonable because they have estimates of uninsured low-income children similar to that of the survey estimates but are more precise.

Uninsured Low-Income Non-Hispanic Black Children

The model can generate race/Hispanic categories for each state. Only low-income, non-Hispanic black children are presented here to demonstrate the improved reliability in a group that is measured with high variance in survey estimates.

Table 2 displays the modeled estimates, CVs, and the margins of error of uninsured non-Hispanic black children at or below 200 percent of poverty by state. The lowest estimates of the percent uninsured are for Hawaii, Delaware, and Massachusetts (3.5, 4.8, and 5.0 percent, respectively). The highest estimates of the uninsured are for Louisiana, Florida, and Texas (12.6, 14.1, and 14.9 percent, respectively). However, CVs need to be considered to know the quality of the point estimates. Florida and Texas have the lowest CVs (0.07), indicating that the estimates (and the confidence intervals) are reliable for those states. Hawaii has the highest CV at 0.23. This is somewhat expected because estimates of the variance become larger as the estimate for the uninsured goes to zero.

Table 2.

Percentage of Non-Hispanic Black Children Aged 0–17 Uninsured, at or below 200 Percent of Poverty, by State

ST	%	CV	Margin of Error	ST	%	CV	Margin of Error
AL	10.6	0.10	1.8	MT	10.1	0.19	3.1
AK	7.6	0.17	2.1	NE	7.9	0.17	2.2
AZ	8.5	0.16	2.2	NV	9.1	0.15	2.3
AR	11.0	0.12	2.1	NH	6.6	0.19	2.1
CA	7.7	0.11	1.4	NJ	6.4	0.13	1.4
CO	7.8	0.16	2.0	NM	10.0	0.17	2.8
CT	7.4	0.14	1.7	NY	7.7	0.10	1.3
DE	4.8	0.19	1.5	NC	11.1	0.09	1.6
DC	6.1	0.14	1.4	ND	7.0	0.21	2.4
FL	14.1	0.07	1.5	OH	8.0	0.12	1.6
GA	9.0	0.09	1.3	OK	11.7	0.14	2.6
HI	3.5	0.23	1.3	OR	7.2	0.19	2.2
ID	8.4	0.18	2.5	PA	7.8	0.12	1.6
IL	10.6	0.09	1.5	RI	5.3	0.22	1.9
IN	10.4	0.12	2.0	SC	7.3	0.14	1.7
IA	6.2	0.21	2.1	SD	10.3	0.15	2.6
KS	7.7	0.17	2.1	TN	5.7	0.17	1.6
KY	9.7	0.15	2.4	TX	14.9	0.07	1.7
LA	12.6	0.09	1.8	UT	6.6	0.19	2.0
ME	7.3	0.20	2.4	VT	5.3	0.22	1.9
MD	7.2	0.12	1.4	VA	9.1	0.10	1.5
MA	5.0	0.18	1.5	WA	7.2	0.16	1.9
MI	6.1	0.14	1.4	WV	9.7	0.16	2.6
MN	7.1	0.17	2.0	WI	5.9	0.20	1.9
MS	10.4	0.11	1.8	WY	9.9	0.18	2.9
MO	6.3	0.17	1.8

Source: Estimates are based on unadjusted numbers from CPS ASEC 2000–2002.

Is Hawaii's CV unreliable for uninsured low-income, non-Hispanic black children? When compared with the highest CV for the survey estimates of low-income uninsured children (0.28), Hawaii is deemed reliable. This indicates that these experimental estimates for non-Hispanic black children do not exceed the implied CV standards set by the survey estimates for all races. The choice of non-Hispanic black children may also call the reliability of the modeled estimates for Hawaii into question.

DISCUSSION

The Census Bureau is in the process of producing estimates of the number and percentage of uninsured, as well as CVs and confidence intervals, by age, race, sex, and Hispanic origin categories by various low-income levels. Although the model only accommodates three income levels, the definition of those levels can be changed. If smaller margins of error are desirable, then the modeled estimates are preferable to the direct estimates. Policy makers and analysts can readily use these estimates to evaluate, administer, and allocate funds for private organizations as well as all levels of government. However, many policy makers are interested in details that these small area estimates cannot accommodate. For instance, there is state variation on eligibility for the SCHIP program regarding income levels and income disregards.

The models seem to fit well overall, given available comparisons. The resulting estimates have substantial reductions in variance relative to the survey estimates. While these estimates can be improved, the results here indicate that the state-level modeled estimates are reliable and useful particularly when demographic estimates are needed. Producing small area estimates for counties by low-income levels is planned in future research.

A limitation in the current model is that it models all insured. If the model incorporated public and private insurance separately, a better estimate would likely be the case. This could lead to confusion among policy makers. Comparisons between public and private insurance (and their interactions) will be investigated in the future.

The 2008 American Community Survey (ACS) will include a 12-month rolling average of health insurance status. This new data source will improve on the CPS ASEC direct and modeled estimates by allowing lower levels of geography and subpopulations to be analyzed. The ACS offers county- and state-based estimates of health insurance coverage. By the release of the 2008 ACS (usually in August of the following survey year), the SAHIE program should be able to produce ACS-based county estimates for all counties while the ACS direct estimates will have estimates on counties that have populations 65,000 and over.

The experience with the SAIPE program is useful toward understanding the process of changing from CPS to ACS. When that program tested the ACS for accuracy of the survey versus the modeled estimates, it was concluded that the states and counties were substantially improved (as measured by the margin of error) for all but the largest geographies. The SAIPE model benefited from the ACS because it simplified assumptions and had more data to base the model on. It is expected that the SAHIE comparisons of CPS ASEC with 2008 ACS will yield similar results. With the richness of the ACS, other types of modeling will be possible, including the ability to distinguish between public and private insurance.