The emergence of lineage-specific chromosomal topologies from coordinate gene regulation

Abstract

Although the importance of chromosome organization during mitosis is clear, it remains to be determined whether the nucleus assumes other functionally relevant chromosomal topologies. We have previously shown that homologous chromosomes have a tendency to associate during hematopoiesis according to their distribution of coregulated genes, suggesting cell-specific nuclear organization. Here, using the mathematical approaches of distance matrices and coupled oscillators, we model the dynamic relationship between gene expression and chromosomal associations during the differentiation of a multipotential hematopoietic progenitor. Our analysis reveals dramatic changes in total genomic order: Commitment of the progenitor results in an initial increase in entropy at both the level of gene coregulation and chromosomal organization, which we suggest represents a phase transition, followed by a progressive decline in entropy during differentiation. The stabilization of a highly ordered state in the differentiated cell types results in lineage-specific chromosomal topologies and is related to the emergence of coherence—or self-organization—between chromosomal associations and coordinate gene regulation. We discuss how these observations may be generally relevant to cell fate decisions encountered by progenitor/stem cells.

The convergence of biological questions and mathematical approaches has encouraged the characterization of complex cellular processes. Our understanding of the regulation of gene activity, for example, has been aided by in silico modeling—exploring genetic associations from the standpoint of Boolean networks or cellular automata (1, 2). Similarly, more recent developments in graph theory—particularly the description of small-world and scale-free networks—have uncovered a scarcity of randomness in biological systems (3). The shared insight from these different approaches is that biological processes are inclined to self-organize, in which a network of localized interactions yields an emergent structure that subsequently feeds back on and strengthens the original network (4). With this conceptual framework, cellular organelles can be viewed as the spatial organization of dynamic cellular tasks. Therefore, it is not surprising that perturbing the function of an organelle—such as the Golgi apparatus' processing of polypeptides—results in the loss of its 4-dimensional form (5, 6).

Current evidence indicates that genes and chromosomes are nonrandomly localized within the nucleus. For example, several gene loci have been shown to be positioned at the periphery when inactive and then relocalized to the nuclear center upon their developmentally regulated activation (7, 8). Also, various chromosomal attributes, including gene density, size (base pair length), and coregulated gene activity, have been indicated in their organization in mammalian nuclei (9–11). Given the growing evidence for deterministic nuclear organization, identifying its origin and structure has become increasingly important. We have previously shown that during the in vitro differentiation of a murine hematopoietic progenitor to derived erythroid and neutrophil cell types, there is a correlation between the nonrandom organization of the genome and coordinate gene regulation (11). We observed that genes that are coregulated during differentiation have a significant tendency to be proximally distributed along chromosomes. In turn, we found that the frequency at which homologous chromosomes associate is related to the number of coregulated genes they possess. We have therefore suggested that coordinate gene regulation during cellular differentiation may yield lineage-specific nuclear topologies that facilitate gene coregulation (7). Moreover, we have hypothesized that the process of self-organization is responsible for the emergence of these topologies (12).

Here, we directly test our idea that chromosomes self-organize during differentiation according to coordinate gene regulation. To do so, we first made the assumption that a full understanding of nuclear organization necessitates the view that it is a dynamical system. For example, capturing a snapshot of genomic gene expression at any one point in time during differentiation reveals a static regulatory network; however, a genetic network actually evolves over time, with groups of genes coupling or decoupling their expression to the overall coregulated gene set. Furthermore, based on our previous analysis, we propose that this evolving regulatory network is manifested spatially at the level of chromosomal organization, with all chromosomes—both homologs and heterologs—associating according to their overall coregulation. Our analysis focuses on determining the collective similarity between gene regulatory and chromosomal association networks by expressing them as matrices. To construct the matrices, we measure the relative entropy—or “distance”—among nodes within networks as well as between networks during differentiation, allowing us to assay shared global properties and the emergence of lineage-specific relationships. In addition, using the theoretical concept of coupled oscillators, we can determine whether the evolving nature of these relationships is reflected in an increase in coherence, i.e., self-organization. Our analysis demonstrates that the networks of coregulated gene expression and chromosomal association are indeed mutually related during differentiation, resulting in the self-organization of lineage-specific chromosomal topologies.

Results

To test our hypothesis of dynamical genome organization, we first analyzed how coordinate gene expression evolves along a previously reported time course of differentiation from a hematopoietic progenitor (FDCPmixA) to derived erythroid and neutrophil cell types (7 time points, 0, 4, 8, 16, 24, 48, and 72 h) (11, 13). We expressed these individual coregulated gene expression networks as matrices whose cells represent nodes that are linked together with relative strengths (refer to Dynamics of Networks in Methods for an elaboration on the concept of a network). Changes among nodes over time can occur in many fashions, including differences in periodicities and amplitudes that are the same or inverted (Fig. 1A, a and c). We consider these 2 examples as the basic forms of coregulation in our analysis of dynamical gene expression, representing activation and silencing, respectively. To describe the overall evolution of coregulated gene expression networks during the differentiation of the progenitor to erythroid and neutrophil cell types, we constructed a N × N distance matrix of the total coregulated gene set for each lineage (N = 1,720 for erythroid, 2,113 for neutrophil, and 3,833—their sum—for the progenitor) and for each time point using the raw expression score with each gene compared with all others. The distance (relative entropy) between gene profiles was established by using symmetrized Kullback–Leibler distances (SKL) (Fig. 1 B and C) (14–16):

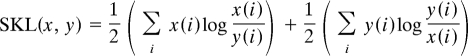where x(i) and y(i) are the expression levels of genes x and y at time i. Next, we used hierarchical clustering (17) to find the similarity or dissimilarity for every gene-by-gene comparison, thereby capturing the total organization of the distance matrix. A dendogram of the gene expression at the starting time point—the progenitor state—reveals that there is a very large set of genes that are expressed similarly, creating a giant component (GC). A GC is the core of a network, the connected set of nodes that characterizes its overall behavior or direction. At a given time point, order can therefore be defined as the fraction of genes residing in the GC relative to the total gene set. By following the genes that dynamically entrain with or diverge from the expression pattern represented in the GC, we can determine the change in order as the system evolves, i.e., differentiation occurs. Surprisingly, our analysis indicates that the degree of order represented in the progenitor state decreases as the differentiation program initiates, indicating a phase transition from a defined cell type into one that is amenable to subsequent reorganization (Fig. 1D). As the disordered progenitor eventually commits to either the erythroid or neutrophil lineage, there is a concomitant increase in order, eventually stabilizing at a level greater than that of the original multipotent progenitor (Fig. 1D). Therefore, we argue that during the differentiation of a progenitor to derived cell types, cellular potential decreases as gene regulatory order increases.

Fig. 1.

The order of coregulated gene expression networks increases during differentiation. (A) Potential differences between the expression patterns of 2 genes over time. (B) Pick any 2 genes (x and y) and measure the pairwise distance (relative entropy) during differentiation. (C) Example of a portion of the N × N distance matrix consisting of all pairwise comparisons at one time point. (D) Order is the fraction of genes at any given time point (0, 4, 8, 16, 24, 48, and 72 h) that are coregulated, thereby residing in a GC that reflects their hierarchical clustering. As genes entrain with or diverge from the expression pattern of the GC during the course of differentiation, the change in order as the system evolves can be determined. In the progenitor state (time 0), the GC corresponds to 84% of coregulated genes, is reduced to as low as 70% at 4 h, and reaches a maximum of 91% in the fully differentiated state. Red and black lines represent erythroid and neutrophil lineages, respectively.

As indicated above, we have previously demonstrated that coregulated gene expression is correlated with the increased proximity of homologous chromosomes, determined in pairwise analysis between chromosomes and the total association of all chromosomes depicted in prometaphase rosettes (Fig. 2A; see Methods for a description of our measurement of chromosomal associations) (11). By expressing the frequency of chromosome associations in rosettes as a 19 × 19 symmetric matrix (sex chromosomes are not included in our analysis), denoted A (Methods) (Fig. 2B), we can now analyze the chromosomal association network in its entirety, looking at the relationship among all homologs and heterologs. To make the comparison between chromosomal associations and gene expression among the progenitor, erythroid, and neutrophil cell types, we must first convert each of the larger coregulated gene expression matrices to a comparable 19 × 19 matrix, denoted B, by mapping the coregulated genes onto their respective chromosomes (Fig. 2C). We define an element (b_kl) in B where k,l represent any 2 of the 19 autosomal chromosomes as follows:

where (x, y) ranges over all gene pairs. If k ≠ l, gene x is on chromosome k and gene y is on chromosome l, whereas if k = l, gene x and gene y are on the same chromosome. If gene coregulation is related to the overall proximity of chromosomes, then the 2 types of matrices should be inversely related: The rosette data are an actual frequency count with a larger number indicating greater overall physical proximity; the expression data are a measure of the distance between genes' expression profiles, with smaller values revealing less distance and therefore indicating coregulation. To test this relationship we computed the symmetrized Stein distance (SSD) (Methods) (15) between A and the inverse of B as follows:

where d = 19 is the size of the matrices (Methods).

implies that A and B⁻¹ are identical, having maximum mutual information. For the comparison in each lineage, the distance between matrices is close to zero, indicating that gene coregulation is in fact manifested in overall chromosomal organization (Table 1). In support of the lineage specificity of these relationships, comparing the chromosomal matrix (A) from one cell type to the gene expression (B) of another yields SSD values closer to 1 (Table 1). To determine the statistical significance of these results, we performed a permutation test, keeping the chromosomal association matrix constant and permuting the rows and columns of the coregulated gene expression matrix elements while maintaining their symmetry. After each permutation of the coregulated gene expression matrix (10,000×) we computed the SSD(A,B⁻¹). We then compared the observed value of SSD(A,B⁻¹) to this permutation distribution to obtain a P value for its significance. Each of the 3 lineages demonstrates a significant difference from the permutation, whereas the interlineage comparisons do not (Table 1). Therefore, the overall organization of chromosomes at the onset and conclusion of differentiation is a reflection of the unique expression pattern of each cell type.

Fig. 2.

Coregulated gene expression and chromosomal association networks are related. (A) Example of an erythroid rosette with each chromosome identified by using spectral karyotyping (SKY). (B) The chromosomal association network represented as a 19 × 19 frequency matrix counting all possible chromosome associations. (C) The larger coregulated gene expression network compressed to a 19 × 19 chromosomal association matrix, using the mean of coregulated genes found on each chromosome.

Table 1.

Distances between chromosomal association and coregulated gene expression matrices

Comparison	Distance (AB−1)	P
AP:BP	0.064	0.0015
AE: BE	0.025	0.0024
AN:BN	0.036	0.0052
AP:BE	0.316	0.3425
AP:BN	0.294	0.2115
AE:BP	0.338	0.2463
AN:BP	0.341	0.2725
AE:BN	0.271	0.2061
AN:BE	0.294	0.2134

A and B denote rosette and expression matrices, and subscripts P, N, and E indicate progenitor, neutrophil, and erythroid lineages. We compute the distance between matrix A and B⁻¹, where B⁻¹is the inverse of the 19 × 19 transformed coregulated gene expression network. The closer a value is to zero, the greater the shared mutual information. The first 3 rows depict the results for comparisons between matrices derived from the same lineage (intra), whereas the last 6 rows make interlineage comparisons. The P values are the result of a permutation test described in the text.

Having demonstrated that the coregulated gene expression data can be visualized as rosette-based chromosomal association matrices, we next asked how overall chromosomal organization evolves during differentiation. To do this, we used the coregulated gene expression matrices from the remaining 5 time points (Fig. 1) and converted each to a 19 × 19 matrix (B), as we did for the progenitor and derived cell types above, and then transformed these matrices to a corresponding chromosomal association matrix (A) (where A ≃ B⁻¹). With these distance matrices based on gene regulation, we determined the change in relative entropy (SSD) among chromosomes, comparing the matrix of the progenitor to each successive time point (e.g., D6 is the difference in entropy between the progenitor and the differentiated cell types) (Methods) (Fig. 3A). This analysis reveals that there is decreased entropy in chromosomal organization at defined stages of differentiation to the erythroid and neutrophil lineages (Fig. 3A). Importantly, the initial decrease in entropy coincides with the increasing reordering of gene expression (compare with Fig. 1D). We also determined the overall entropy (15) at each time point, which supports the observation that cellular commitment leads to decreased entropy (Fig. 3B). In both types of analysis, the overall order of chromosomes is greater in the differentiated cell types than the progenitor. Therefore, chromosomes can be viewed as reorganizing according to differential gene expression, creating a new higher-order state or attractor than that in the progenitor.

Fig. 3.

The organization of chromosomal associations increases during differentiation. (A) Graph of the relative entropy of chromosomal associations as computed from the SSDs for the progenitor against successive time points. (B) The general entropy (15) for each time point in the differentiation, normalized between 0 and 1. (C) Strength of chromosomal contribution to the chromosomal association network during differentiation. (Left) The front elevation at 0 h (the progenitor). (Right) The elevation from 72 h (erythroid). (Center) The total chromosomal contributions over time. Representative chromosomes 1, 6, 11, and 17 are indicated as green, blue, red, and dark blue, respectively.

To determine the evolving role of each individual chromosome to the overall organization of the network during differentiation, we computed a centrality measure for each chromosome at each time point with the vertex strength s_i defined as

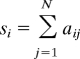(18), where a_ij is the ijth entry of the matrix A. This quantity measures the importance of vertices (i.e., chromosomes) in terms of the total weight of their connections, and it is therefore a natural measure of the importance or centrality of a given chromosome i in the network. Our analysis demonstrates that chromosomes contribute differently over the time course of differentiation (Fig. 3C). In Fig. 3C Center, we have depicted the relative strengths for each chromosome during the differentiation, arbitrarily highlighting 4 chromosomes (1, 6, 11, and 17) for elucidation. In the Fig. 3C Left and Right sides of the total time course, we focus on the progenitor and erythroid lineages, respectively, illustrating the change in contribution of the 4 chromosomes from the beginning and end states. The erythroid state also reveals that many of the chromosomes (indicated by x) have collapsed onto each other in terms of their relative strengths, representing increased coherence. Moreover, because the centrality measure of all chromosomes is greater at the end than the beginning, the overall organization of chromosomes increases during differentiation. Therefore, paralleling our results with gene expression, cellular potential is lost as chromosomal order is gained.

The analysis above suggests that coregulated gene expression and chromosome association networks are mutually related during cellular differentiation. Genomic organization proceeds from an unstable ordered to a disordered state during the commitment of the progenitor and ultimately reaches a highly ordered state in the differentiated cell types. This evolving nature of genomic order prompted us to use a mathematical framework to model the interrelated behaviors of gene regulation and chromosome association as a dynamical system. The cooperative phenomenon of mutual entrainment is well described by the classical Kuramoto model (4, 19–21), in which a collection of globally coupled phase oscillators exhibit a transition from incoherence to a coherent state as the coupling strength increases past a critical threshold. Therefore, the Kuramoto framework is an ideal mathematical model with which to demonstrate the organized behavior of the complex dynamical reorganization of the genome during differentiation. A generalized form of this mathematical model can be written as

Here, θ_i and ω_i denote, respectively, the phase and intrinsic frequency of oscillator i and N is the number of oscillators (19). The matrix A_ij(t) is the time-dependent network architecture of oscillators, assumed to be symmetric. To characterize the degree of self-organization in the network, we used a global order parameter (R) that ranges between 0 and 1, with 0 meaning uniform incoherence and 1 meaning complete self-organization (19, 22). To apply this framework to the dynamic mutual relationship between chromosomal organization and coregulated gene expression during differentiation, we rendered each of the 19 chromosomes as an oscillator by first mapping the coregulated gene set onto their respective chromosomal positions. Therefore, we will be measuring how each chromosome associates with all other chromosomes (i.e., oscillates) in the rosettes as a function of its share of the coregulated gene set. The initial conditions for parameters θ_i and ω_i of the oscillators were obtained from s_i as previously defined for the progenitor state (see Fig. 1), and A_ij(0) is derived from the progenitor state chromosomal association matrix A (see Fig. 2). By following the relationship through time (the differentiation), we can capture whether coordinate gene regulation and chromosomal organization are integrated. In support of this hypothesis, the numerical simulations show that the behavior of R initially decreases in order, after which a highly ordered state emerges [Fig. 4A (R1–R3) and B]. Furthermore, the chromosome association network of the differentiated state is similar to the model predicted network structure. Therefore, these simulation results reveal that coregulated gene expression and chromosome association networks are mutually related and lead to deterministic nuclear self-organization (Fig. 4C). We believe our approach provides a simple mathematical framework for further investigation of the dynamics of genome organization during cellular differentiation and other cell fate decisions.

Fig. 4.

Chromosomes self-organize according to coordinate gene regulation. (A) Geometric interpretation of the chromosomal network, where the phases of θ_i are plotted on the unit circle. Three snapshots during differentiation are represented, where R1 is the distribution of the network representing the progenitor state, R2 the phase transition, and R3 the erythroid differentiated cell type. (B) Schematic illustration of the evolution of the order parameter (R) seen in numerical simulations of the chromosomal oscillator model for a specific coupling strength equation (19). (C) Schematic illustration for the mechanics of self-organization, with local interactions (gene coregulation) leading to chromosomal associations that emerge cooperatively in a cell-specific organization of the nucleus, which in turn feeds back to strengthen the local associations.

Discussion

The nucleus is compartmentalized according to the various functions it performs. For example, a subnuclear body, such as the nucleolus, represents the spatial localization of the components necessary to carry out its particular activities, rDNA transcription and ribosomal biogenesis (5, 7). The process of self-organization provides an attractive model by which to understand the relationship between nuclear form and function (4). The key feature of a self-organizing system is the emergence of a structure that both results from and subsequently supports localized interactions (Fig. 4C). Evidence indicates a role for this phenomenon in the genesis of nuclear bodies. For example, it has been shown that the DNA damage response can be initiated in the absence of damage by the localization of components of the repair machinery to a particular genomic site (23). Moreover, a recent study has directly demonstrated features of self-organization in the de novo formation of Cajal bodies, involved in the processing of small nuclear ribonucleoproteins, by the nonhierarchical localization of constituent proteins (24).

Beyond the organization of specific activities into nuclear bodies, the nucleus also demonstrates a general compartmentalization of transcriptional activity. One example of this is gene loci assuming developmentally regulated positions within the nucleus (7). We have reasoned that if this behavior was extended over the total complement of genes that are regulated during the differentiation of a specific cell type, then lineage-specific nuclear topologies may occur (12). In testing this idea, we have previously shown that the genome—in both the linear distribution of genes and the association of homologous chromosomes—is organized according to coregulated gene expression during the in vitro differentiation of a hematopoietic progenitor (FDCPmixA cells) to derived erythroid and neutrophil cell types (11). We have therefore suggested that the genome—at the level of chromosomes—may self-organize to facilitate coordinate gene regulation during cellular differentiation. Here, we present a test of this hypothesis, applying the mathematical approaches of distance matrices and coupled oscillators to our datasets of gene expression and chromosomal associations (in the form of rosettes) from the differentiation of the progenitor to the erythroid and neutrophil lineages.

A major difficulty in comparing total coordinate gene expression with total chromosomal association patterns is finding similarities embedded in high-dimensional datasets. In our current study, we have found a solution to this problem by depicting the networks of gene expression and chromosomal associations as matrices, allowing us to compare them in their entirety to uncover shared features. We believe this approach may be useful for a broad range of biological questions dealing with information-rich datasets. Our analysis determined that coordinate gene expression undergoes a phase transition—characterized by an increase in entropy—upon commitment of the progenitor. As differentiation continues, there is a gradual loss of entropy, culminating in a highly ordered state in the differentiated cell types (Fig. 1). The coregulated gene sets of the semiordered progenitor and ordered erythroid and neutrophil lineages are significantly correlated with lineage-specific chromosomal association patterns (Fig. 2 and Table 1). Furthermore, by transforming the gene expression networks along the time course to corresponding chromosomal association matrices, we demonstrated that chromosomal topologies change dynamically during differentiation but, as with gene expression, result in a more highly ordered state in the differentiated cell types (Fig. 3). Finally, we modeled this relationship by employing nonlinear dynamical systems theories (i.e., the concept of coupled oscillators), revealing the mutual entrainment—or self-organization—of coordinate gene regulation and chromosomal associations (Fig. 4).

That the genome self-organizes according to gene coregulation may be broadly relevant for cell fate decisions, in particular those of progenitor/stem cells. The phase transition we observe upon commitment of the hematopoietic progenitor suggests 2 salient features of a multipotent state: (i) a progenitor/stem cell is a defined cell type in terms of its genomic organization; and (ii) this semiordered state must be disrupted for a subsequent identity or higher-order state to be established. Additionally, our demonstration that terminal differentiation coincides with the stabilization of this highly ordered state indicates that cellular potential is inversely related to genomic order. A hallmark of stem cells is their ability to undergo asymmetric division, allowing both self-renewal and commitment to a differentiation pathway. We suggest that this process may be related to our observation of a phase transition: A daughter cell that commits to a program of differentiation will have a marked increase in genomic entropy, whereas the self-renewing cell will not. Recent studies have demonstrated bivalent chromatin marks underscoring the “primed” expression profile of stem cells, in particular ES cells (25, 26). The resolution of this bivalency and subsequent differentiation may require a brief increase in disorder for the establishment of a pattern of chromatin modifications that potentiates a given differentiation pathway. Based on our results, we would further suggest that this reordering would be manifested in a discernable chromosome topology. Future work comparing gene expression analyses and chromatin compartments both in silico and in situ will be necessary to validate these claims.

Although asymmetric division of a stem cell was once thought to be unidirectional, resulting in the irreversible commitment of a daughter cell, recent evidence indicates that it is possible to induce pluripotent stem (iPS) cells from differentiated cell types (27, 28). Because these strategies rely heavily on the expression of transcription factors to induce pluripotency, it is likely that the changes leading to iPS cells are reflected in nuclear organization. Our demonstration of dynamic genomic reorganization through a phase transition may provide a means to refine iPS strategies for a wide variety of differentiated cell types. For example, by identifying the GC of gene expression during the differentiation of a particular cell lineage, we can determine the gene set that drives the phase transition and thereby reverse-engineer the genetic network to that critical juncture. Knowing the GC of a given differentiation program permits the identification of the transcriptional regulatory factors significant in the process, either by analysis of functionally characterized regulatory elements and/or the alignment and description of shared domains. These factors could then be ectopically expressed to drive a differentiated cell back to the disordered state of the phase transition wherein it is amenable to multiple pathways. Beyond a possible role in the asymmetric cell division of stem cells or iPS cell strategies, our demonstration of nuclear self-organization may be of importance to any feature of the nucleus representing a dynamical system.

Methods

Symmetrized Kullback-Leibler (SKL) Divergence.

For any two points x and y of Δ⊆ℝ^d, the Bregman divergence B_f (.,.): Δ↦ℝ of x to y, corresponding to a strictly convex and differentiable function F, is defined as

where ∇F is the gradient of F and 〈.,.〉 the inner product. SKL divergence can be derived by substituting the convex function: F(x) = $\sum _i$ x(i)log x(i) (14, 16). We define SKL (x,y) = 1/2 B_F (x,y) + 1/2 B_F (y,x), then

Note that x and y should be nonnegative. It can be shown that SKL(x,y) is always nonnegative, 0 ≤ SKL(x,y), and SKL(x,y) = 0 iff x = y (16).

Chromosomal Association Analysis.

As reported previously (11), total chromosomal organization was analyzed in prometaphase rosettes from progenitor, erythroid, and neutrophil cells. At least 30 rosettes were examined for each cell type. Briefly, chromosome identity was determined through spectral karyotyping (SKY) and a pattern recognition algorithm was used to assay chromosomal associations in the rosette. The relative proximity of each chromosome to all others was measured. Chromosomes were considered to be associated if they were removed by no more than 2 chromosomes. Results from rosettes were verified in the interphase nucleus (11).

SSD.

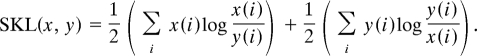which is invariant under both matrix scale transformations and matrix inversion. Note especially that SSD(X,Y) = 0 if X = Y (16). The distance between X and Y⁻¹ is:

This distance measure is designed to test our main hypothesis: If gene coregulation is related to the overall proximity of chromosomes, then the 2 types of matrices should be inversely related. The relative entropy difference is standardized with respect to the first time point and is defined as follows:

where D₆ is the difference in entropy between the progenitor and the differentiated cell state. We performed all calculations using the MATLAB software package.

Dynamics of Networks.

The complexity of a network depends on topological structure, network evolution, node connectivity and diversity, and/or dynamical evolution. The evolving nature of a network is determined by both the dynamical rules governing the nodes and the flow occurring along each link. Mathematically, a network can be represented by a graph, recalling that a graph is an ordered pair of disjoint sets (V,E) such that E is a subset of the set of unordered pairs of V. V is the set of vertices and E is the set of edges. Most computations of graph properties are accomplished by representing the graph in the form of a matrix, called the adjacency matrix A; A is a n × n symmetric matrix, where n is the number of vertices in the network. The matrix A has the elements a_ij : a_ij = 1 if the node i is connected to the node j and a_ij = 0 otherwise. The A is symmetric if there is an edge between i and j there is also an edge between j and i (3, 18). For a weighted network, a_ij has a numerical value, which represents the weight on the edge connecting the nodes i and j. Thus, a weighted network can be represented mathematically by an adjacency matrix with entries that are not simply 0 or 1, but are equal instead to the weights on the edges. Note that distance matrices are related to adjacency matrices, with the difference that an entry of the distance matrix is smaller if 2 elements are closer, whereas “close” (connected) vertices yield larger entries in an adjacency matrix. The evolving nature of the network is given by:

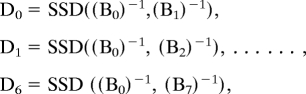where x_i = [x_i, y_i, z_i,…]^T ∈ ℝ^N is the state vector of node i for i = 1,2,…,n and describes the node equations as f : ℝ^N → ℝ^N. If we assume that the first components of each node are connected to each other, then h_j(x_j) : ℝ → ℝ is the output of the node j, C = [1,0,…,0]^T, and a_ij is as described above (22). The above model becomes the Kuramoto model when it is used to describe a network of phase oscillators.