Determination of Kinetic Parameters of Enzyme-Catalyzed Reaction A + B + C → Products with the Minimum Number of Velocity Measurements

Abstract

Rapid-equilibrium rate equations are derived for the five different mechanisms for the enzymatic catalysis of A + B + C → products using a computer. These rate equations are used to determine the minimum number of velocities required to estimate the values of the kinetic parameters. The rate equation for the completely ordered mechanism involves four kinetic parameters, and the rate equation for the completely random mechanism involves eight kinetic parameters. Therefore, the four to eight kinetic parameters can be estimated by determining four to eight velocities and solving four to eight simultaneous equations. General recommendations are made as to the choices of triplets of substrate concentrations {[A], [B], [C]} to be used to determine the velocities. The effects of 5% errors in the measured velocities, one at a time, are calculated and are summarized in tables. Calculations of effects of experimental errors are useful in choosing the triplets of substrate concentrations to be used to obtain the most accurate values of the kinetic parameters. When the kinetic parameters for A + B + C → products are to be determined for the first time, it is recommended that the program for the completely random mechanism be used because it can identify the mechanism and determine the kinetic parameters in one operation.

Introduction

This article is concerned with the possible rapid-equilibrium rate equations for enzyme-catalyzed reactions of the type A + B + C → products. Many reactions of this type are found among the oxidoreductases, and most ligase reactions are of this type.(1) Four examples of these reactions are shown in Table 1. The fact that the change in binding of hydrogen ions Δ_rN_H of the forward reaction is positive suggests that one or more hydrogen ions are bound in the rate-determining reaction.(2) The effects of pH in rapid-equilibrium enzyme kinetics have been discussed recently,(3) and the relation between Δ_rN_H and the integer number n of hydrogen ions consumed in the rate-determining reaction has been derived for A + B → products.

Table 1. Changes in Binding of Hydrogen Ions Δ_rN_H in Enzyme-Catalyzed Reactions as a Function of pH at 298.15 K.

	pH 5	pH 6	pH 7	pH 8	pH 9
EC 1.4.1.1	pyruvate + NADred + ammonia = alanine + NADox + H2O
ΔrNH	1.00	1.00	1.01	1.05	1.36
EC 1.4.1.2	+ NADred + ammonia = glutamate + NADox + H2O
ΔrNH	1.00	1.00	1.01	1.05	1.36
EC 6.3.5.4	aspartate + ATP + glutamine = asparagine + glutamate + AMP + PPi
ΔrNH	1.83	1.27	0.92	0.67	0.17
EC 6.4.1.5	succinate + ATP + CoA = succinylCoA + ATP + Pi
ΔrNH	0.44	0.66	0.32	0.48	0.89

There are five possible rapid-equilibrium rate equations for the enzyme-catalyzed reaction A + B + C → products, with mechanisms from the completely ordered mechanism to the completely random mechanism. The completely ordered mechanism involves four kinetic parameters, and the completely random mechanism involves eight kinetic parameters. Rapid-equilibrium rate equations are derived for each of these five mechanisms using a computer. These rate equations can be used to determine the kinetic parameters with the minimum number of measured velocities.(4) The concept that N kinetic parameters can be calculated from N velocity measurements was introduced by Duggleby(5) in 1975. Before that, Frieden,(6) in an article about malate dehydrogenase, showed that it was possible to determine the four kinetic parameters (V_AB, K_A, K_B, and K_AB) in the rate equation v = V_AB/(1 + K_A/[A] + K_B/[B] + K_AB/[A][B]) with four velocity measurements. This article is concerned with rapid-equilibrium rate equations because they are the simplest possible rate equations. Steady-state rate equations have more terms, but the concept of determining the kinetic parameters with the minimum number of velocity measurements also applies.

Rapid-equilibrium rate equations can be derived with a computer because Mathematica, Maple, and MatLab have the operation Solve that solves sets of simultaneous polynomial equations. General recommendations are made here as to the choice of triplets of substrate concentrations {[A],[B],[C]} to be used to determine velocities. The objective is to use triplets of substrate concentrations that reduce the effects of experimental errors on the estimated kinetic parameters.

Derivations of Rapid-Equilibrium Rate Equations for A + B + C → Products

When the rapid-equilibrium assumption is used, all of the reactions up to the rate-determining reaction are in equilibrium. When a system of reactions is at equilibrium, not only are the reactions used in the calculation at equilibrium, but all reactions that can be obtained by adding and subtracting these reactions are also at equilibrium. This makes it possible to calculate dissociation constants (Michaelis constants) for this larger set of reactions. For example, the determination of 8 velocities for the completely random mechanism makes it possible to calculate 12 dissociation constants (Michaelis constants). The number N′ of reactants in the completely random mechanism is 11; these reactants are E, A, B, C, EA, EB, EC, EAB, EBC, EAC, and EABC. The total number of dissociation reactions is 12

These reactions are not all independent. The number of independent reactions R′ can be calculated(2) by using N′ = C′ + R′, where the number of components C′ is 4 (E, A, B, and C), and there are 11 reactants in eqs 1−12. The number of independent reactions is given by R′ = N′ − C′ = 11 − 4 = 7; thus, only 7 of the dissociations in eqs 1−12 are independent. Seven is also the number of dissociation reactions in the completely random mechanism. These seven reactions are the ones for which numerical values have been arbitrarily assigned in eqs 1−5, 7, and 10 so that rapid-equilibrium velocities can be calculated. Other choices of independent variables can be made. The equilibrium constants for these 7 reactions can be used to calculate the equilibrium constants for the other 5 dissociation reactions, but we will take a different path here and discuss the estimation of all 12 equilibrium constants by determining the minimum number of velocities for the 5 mechanisms for A + B + C → products.

There are two ways that the pH can affect the rate of an enzyme-catalyzed reaction calculated using the rapid-equilibrium assumption. The more familiar way is through the pKs of the substrates, enzymatic site, and enzyme−substrate complexes. The less familiar way is through the consumption of hydrogen ions in the rate-determining reaction,^7,8 which introduces a factor of 10^npH into the expression for the velocity. When one hydrogen ion is consumed, n = −1 because of the convention in thermodynamics that the stoichiometric numbers of reactants are negative. The fact that there are oxidoreductase reactions for which the limiting velocity V_fexp is proportional to 10^npH over a wide range of pHs is an argument for the rapid-equilibrium assumption. Only the consumption of hydrogen ions in the rate-determining reaction can give rise to the 10^npH factor over a range of pHs. For the calculations in this paper, V_fexp is taken to be 1, and the effects of pH are not investigated further.

Determination of the Kinetic Parameters V_fexp, K_A, K_AB, and K_ABC for Mechanism I

Completely ordered mechanism I is made up of the reactions in eqs 1, 4, 10, and

where the limiting velocity V_fexp is equal to k_f[E]_t, where k_f is the rate constant for the production of products and [E]_t is the total concentration of enzymatic sites.

It is important to check the number of independent equilibrium expressions used in the derivation of the reaction velocity v. The number N′ of reactants in mechanism I is seven (E, A, EA, B, C, EAB, and EABC). The number of components C′ is four (E, A, B, and C). The number of independent equilibrium equations R′ is three, and therefore, N′ = C′ + R′ is 7 = 4 + 3. To obtain the expression for the equilibrium concentration of EABC, three equilibrium equations and one conservation equation are used in Solve. This operation is shown in the . The rapid-equilibrium velocity of the reaction A + B + C → products is given by v = k_f[EABC]. Therefore, the [E]_t in the expression for [EABC] obtained using Solve is replaced by V_fexp, and the symbol for the limiting velocity in the forward direction is V_fexp = k_f[E]_t. In Mathematica, V_fexp is represented by vfexp because capital letters are used for operations. The rapid-equilibrium velocity for mechanism I obtained in this way is

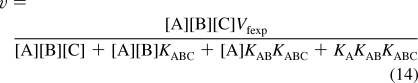An advantage in deriving the rapid-equilibrium rate equation with a computer is that the equation is in computer-readable form. If v is measured at four triplets of substrate concentrations {[A],[B],[C]}, the four versions of rate equation 14 can be solved for the four kinetic parameters. Since there are experimental errors in the measured velocities, the triplets of substrate concentrations used should be chosen so as to reduce the effects of these experimental errors on the calculated kinetic parameters. There are also experimental errors in the concentrations of the substrates, but these errors are independent of the choices of substrate concentrations. The effects of 5% errors in substrate concentrations are 5% errors in Michaelis constants. There are other possible errors in velocity measurements that have to be discussed for specific enzyme kinetic studies.

The effects of choices of substrate concentrations have been discussed for A + B → products.(4) Therefore, the calculations here on mechanism I have been made with the following triplets of substrate concentrations {[A],[B],[C]}: {200,200,200}, {0.5,200,200}, {200,0.5,200}, and {200,200,0.5}. The concentration 200 is hopefully significantly higher than the largest Michaelis constant, and the 0.5 is hopefully significantly lower than the smallest Michaelis constant. The velocity for the first triplet has the predominate effect in determining V_fexp. The velocity for the second triplet has the predominate effect in determining K_A. The velocity for the third triplet has the predominate effect in determining K_AB. The velocity for the fourth triplet has the predominate effect in determining K_ABC. The velocities for the four triplets of substrate concentrations calculated using eq 14 with the specified values of V_fexp and the Michaelis constants (see eqs 1, 4, and 10) are v₁ = 0.8383, v₂ = 0.7313, v₃ = 0.1198, and v₄ = 0.01279. Since v₄ is very low, it may be necessary to raise [E]_t.

The Mathematica program calckinparsABC1 for calculating the four kinetic parameters in mechanism I from four measured velocities is given in the . This program is based on the Solve operation. The effects of 5% errors in the four measured velocities, one at a time, calculated using this program, are given in Table 2.

Table 2. Effects of 5% Errors in Four Measured Velocities for Mechanism I.

	Vfexp	KA	KAB	KABC
no errors	1.00	5.0	20.0	35.0
1.05 × v1	1.06	6.6	20.0	37.1
1.05 × v2	1.00	3.1	20.2	35.0
1.05 × v3	1.00	5.3	18.7	35.2
1.05 × v4	0.99	5.0	21.1	32.8

Increasing the high substrate concentrations and reducing the low substrate concentrations at which velocities are calculated will reduce these errors somewhat. Calculations with 5% errors are arbitrary, and the errors can be increased without changing the general conclusions.

Determination of the Kinetic Parameters V_fexp, K_A, K_B, K_AB, and K_ABC for Mechanism II

For mechanism II, reaction 2 is added to the reactions in mechanism I. The number N′ of reactants is eight. The number of components C′ is four (E, A, B, and C). The number of independent equilibrium equations R′ is four, and therefore, N′ = C′ + R′ is 8 = 4 + 4. To calculate the equilibrium concentration of EABC using Solve, four equilibrium equations and one conservation equation are used. This yields the following expression for the rapid-equilibrium velocity.

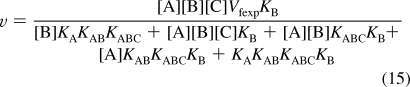When v is measured at five triplets of substrate concentrations {[A],[B],[C]}, the five versions of rate eq 15 can be solved for the five kinetic parameters. The calculations here for mechanism II have been made with the following triplets of concentrations {[A],[B],[C]}: {200,200,200}, {0.5,200,200},{200,0.5,200},{200,200,0.5}, and {0.5,0.5,200}.

The velocities for the five triplets calculated using eq 15 and the specified values of V_fexp and the Michaelis constants involved are v₁ = 0.8322, v₂ = 0.2054, v₃ = 0.1196, v₄ = 0.01224, and v₅ = 0.01224. Since v₄ and v₅ are very low, it may be necessary to raise [E]_t for these two measurements.

The program calckinparsABC2 (not in the ) was written to calculate the five kinetic parameters from five measured velocities. This program has the same structure as calckinparsABC1 given in the , but there are five lines, which are different versions of eq 15. The effects of 5% errors in velocities, one at a time, were calculated using this program, and they are summarized in Table 3.

Table 3. Effects of 5% errors in 5 measured velocities for mechanism II.

	Vfexp	KA	KAB	KB	KABC
no errors	1.00	5.0	20.0	10.0	35.0
1.05 × v1	1.06	5.0	20.2	9.8	37.1
1.05 × v2	1.00	5.0	19.9	10.7	35.1
1.05 × v3	1.00	5.3	18.8	10.1	35.2
1.05 × v4	0.99	5.0	21.2	10.0	32.7
1.05 × v5	1.00	4.7	20.0	9.4	35.0

Three of the reactions in mechanism II almost form a cycle; they are reactions 1, 2, and 4.

This cycle is completed with EB + A = EAB. Therefore, the value of K_BA can be calculated from values of K_A, K_B, and K_AB determined using the five measured velocities.

Equations of this type are well-known in enzyme kinetics.^9,10 Thus, when the enzyme-catalyzed reaction follows mechanism II and there are no experimental errors, K_BA = 5 × 20/10 = 10. The values of K_BA when there are 5% errors in the velocities, one at a time, are given later in Table 7. This is the first illustration here of the fact that when a system of reactions is at equilibrium, not only the reactions used to calculate the equilibrium composition are at equilibrium, but also any reaction that can be obtained by adding and subtracting the reactions used to calculate the equilibrium concentrations is also at equilibrium.

Table 7. Effects of 5% Errors in Velocities on the Five Dependent Equilibrium Constants for Mechanism V.

	no errors	1.05 × v1	1.05 × v2	1.05 × v3	1.05 × v4	1.05 × v5	1.05 × v6	1.05 × v7	1.05 × v8
KBA	10.0	10.0	10.1	10.0	10.9	10.0	10.1	9.9	9.0
KCA	8.3	8.4	8.5	9.2	8.4	7.0	8.8	8.2	8.3
KACB	28.0	30.0	27.9	26.1	27.7	28.2	27.9	28.3	28.0
KCB	20.0	20.1	21.8	20.8	20.1	16.7	21.3	19.9	19.7
KBCA	23.3	24.0	21.5	23.3	22.6	23.7	23.1	21.6	26.2

Determination of the Kinetic Parameters V_fexp, K_A, K_B, K_C, K_AB, and K_ABC for Mechanism III

For mechanism III, reaction 3 is added to the reactions in mechanism II. The number N′ of reactants is nine. The number of components C′ is four (E, A, B, and C). The number of independent equilibrium relations R′ is five, and therefore, N′ = C′ + R′ is 9 = 4 + 5. To calculate the equilibrium concentration of EABC using Solve, five equilibrium equations and one conservation equation are used. This yields the following expression for the rapid-equilibrium velocity

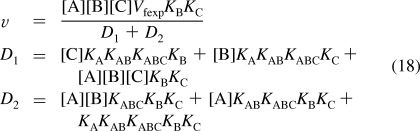When v is measured at six triplets of substrate concentrations {[A],[B],[C]}, the six versions of rate equation 18 can be solved for the six kinetic parameters. The calculations for mechanism III have been made with the following triplets of concentrations: {200,200,200}, {0.5,200,200},{200,0.5,200},{200,200,0.5}, {5,5,50}, and {5,5,5}. The reason for the particular sixth triplet is that [A] and [B] should be low so that the enzymatic site is not saturated with A or B so that reaction 3 is significant. The previous article(4) has shown that it is when the concentration of a reactant is low (in comparison with its Michaelis constant) that the velocity is most sensitive to the change in concentration of that reactant. However, {0.5,0.5,0.5} yields an extremely low velocity. Therefore, all three concentrations are increased, and {5,5,5} is used for the sixth triplet. The velocities for the six triplets calculated using eq 18 and the specified values of V_fexp and the Michaelis constants are v₁ = 0.8281, v₂ = 0.1389, v₃ = 0.9353, v₄ = 0.01224, v₅ = 0.05545, and v₆ = 0.01145. Mathematica program calckinparsABC3 was written to calculate the six kinetic parameters from six measured velocities. This program has the same structure as calckinparsABC1 given in the , but there are six lines, which are different versions of eq 18. The effects of 5% errors in velocities, one at a time, were calculated using this program, and they are summarized in Table 4.

Table 4. Effects of 5% Errors in Six Measured Velocities for Mechanism III.

	Vfexp	KA	KAB	KB	KC	KABC
no errors	1.00	5.0	20.0	10.0	15.0	35.0
1.05 × v1	1.06	4.9	20.1	9.7	14.7	37.1
1.05 × v2	1.00	5.3	19.9	11.7	15.8	35.2
1.05 × v3	1.00	5.8	18.4	10.8	16.1	35.3
1.05 × v4	0.99	5.1	21.2	10.1	15.2	32.7
1.05 × v5	1.00	4.7	20.8	9.0	16.1	34.7
1.05 × v6	1.00	4.4	19.7	8.8	12.3	35.1

Determination of the Kinetic Parameters V_fexp, K_A, K_B, K_C, K_AB, K_AC, and K_ABC for Mechanism IV

For mechanism IV, reaction 5 is added. The number N′ of reactants is 10. The number of components C′ is four (E, A, B, and C). The number of independent equilibrium relations R′ is six, and therefore, N′ = C′ + R′ is 10 = 4 + 6. To calculate the equilibrium concentration of EABC using Solve in Mathematica, six equilibrium equations and one conservation equation are used. This yields the following expression for the velocity

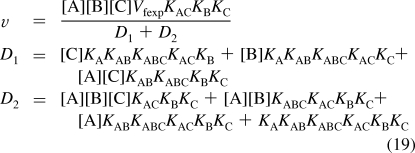When v is measured at seven triplets of substrate concentrations {[A],[B],[C]}, the seven versions of the rate equation can be solved for the seven kinetic parameters. The calculations for mechanism IV have been made with the following triplets of concentrations: {200,200,200}, {0.5,200,200}, {200,0.5,200}, {200,200,0.5}, {5,5,50}, {5,5,5}, and {200,5,5}. The velocities calculated with these seven triplets are v₁ = 0.7421, v₂ = 0.1362, v₃ = 0.1500, v₄ = 0.01222, v₅ = 0.04231, v₆ = 0.01076, and v₇ = 0.02332. Mathematica program calckinparsABC4 was written to calculate the seven kinetic parameters from seven measured velocities. This program has the same structure as calckinparsABC1 given in the , but there are seven lines, which are different versions of eq 19. The effects of 5% errors in velocities, one at a time, were calculated using this program, and they are summarized in Table 5.

Table 5. Effects of 5% Errors in Seven Measured Velocities for Mechanism IV.

	Vfexp	KA	KAB	KB	KC	KABC	KAC
No errors	1.00	5.0	20.0	10.0	15.0	35.0	25.0
1.05 × v1	1.07	4.9	20.0	9.8	14.8	37.4	25.0
1.05 × v2	1.00	5.3	19.9	11.7	15.8	35.2	25.0
1.05 × v3	0.99	4.9	20.2	10.2	14.5	34.7	26.9
1.05 × v4	0.99	4.9	21.5	10.0	15.0	32.7	25.4
1.05 × v5	1.00	5.0	20.1	9.2	17.4	34.8	24.9
1.05 × v6	1.00	4.2	20.1	8.6	11.9	35.1	25.2
1.05 × v7	1.00	5.8	18.3	10.8	16.2	35.3	22.8

Three of the reactions in this mechanism almost form a cycle; they are reactions 1, 3, and 5.

Therefore, values of K_CA can be calculated from experimental values of K_A, K_AC, and K_C.

Thus, when the enzyme-catalyzed reaction follows mechanism IV and there are no experimental errors, K_CA = 5 × 25/15 = 8.333. The values of K_CA when there are 5% errors in the velocities, one at a time, are given later in Table 7.

Another three reactions in this mechanism almost form a cycle; they are reactions 4, 5, and 10.

Therefore, values of K_ACB can be calculated from experimental values of K_AB, K_AC, and K_ABC.

Thus, when the enzyme-catalyzed reaction follows mechanism IV and there are no experimental errors, K_ACB = 20 × 35/25 = 28. The values of K_ACB when there are 5% errors in the velocities, one at a time, are given later in Table 7.

Determination of the Kinetic Parameters V_fexp, K_A, K_B, K_C, K_AB, K_AC, K_BC, and K_ABC for Mechanism V

For the completely random mechanism V, reaction 7 is added to the mechanism. The number N′ of reactants is 11. The number of components C′ is four (E, A, B, and C). The number of independent equilibrium relations R′ is seven, and therefore, N′ = C′ + R′ is 11 = 4 + 7. To calculate the equilibrium concentration of EABC using Solve, seven equilibrium equations and one conservation equation are required. This yields the following expression for the velocity

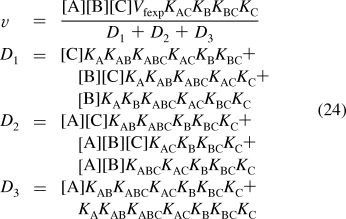When v is measured at eight triplets of substrate concentrations {[A],[B],[C]}, the eight versions of rate equation 24 can be solved for the eight kinetic parameters.

The calculations here for mechanism V have been made with the following triplets of substrate concentrations: {200,200,200}, {0.5,200,200}, {200,0.5,200}, {200,200,0.5}, {5,5,50}, {5,5,5}, {200,5,5}, and {5,200,5}. The velocities calculated with these eight triplets are v₁ = 0.7113, v₂ = 0.03260, v₃ = 0.1498, v₄ = 0.02221, v₅ = 0.03851, v₆ = 0.01050, v₇ = 0.02329, and v₈ = 0.03830. A program calckinparsABC5 was written to calculate the eight kinetic parameters from eight measured velocities. This program has the same structure as calckinparsABC1 given in the , but there are eight lines, which are different versions of eq 24. The effects of 5% errors in velocities, one at a time, were calculated using this program, and they are summarized in Table 6.

Table 6. Effects of 5% Errors in Eight Measured Velocities for Mechanism V.

	Vfexp	KA	KAB	KB	KC	KABC	KBC	KAC
no errors	1.00	5.0	20.0	10.0	15.0	35.0	30.0	25.0
1.05 × v1	1.07	5.0	20.0	9.9	14.8	37.6	30.1	25.0
1.05 × v2	1.00	5.0	20.0	9.8	14.7	34.8	32.5	25.0
1.05 × v3	0.99	4.9	20.3	9.9	14.3	34.7	30.1	26.9
1.05 × v4	0.99	4.9	21.5	9.6	14.7	32.6	31.0	25.4
1.05 × v5	1.00	5.3	20.0	10.5	18.6	35.0	29.5	24.8
1.05 × v6	1.00	4.0	20.1	8.0	11.5	35.0	30.5	25.2
1.05 × v7	1.00	5.9	18.3	10.8	16.3	35.3	29.9	22.8
1.05 × v8	1.00	5.2	19.9	11.6	15.8	35.2	26.7	25.0

Mechanism V provides the opportunity to calculate K_CB and K_BCA in addition to the rate parameters in Table 6. The value of K_CB can be calculated from experimental values of K_B, K_C, and K_CB.

Thus when the enzyme-catalyzed reaction follows mechanism V and there are no experimental errors, K_CB = 10 × 30/15 = 20. The values of K_CB when there are 5% errors in the velocities, one at a time, are given later in Table 7.

The value of K_BCA can be calculated from values of K_AB, K_AC, and K_ABC obtained from velocity measurements.

Thus, when the enzyme-catalyzed reaction follows mechanism V and there are no experimental errors, K_BCA = 20 × 35/30 = 23.333.

The equilibrium constants in Table 6 can be used to calculate the equilibrium constants and effects of 5% errors in velocities for the five dependent equilibrium constants (K_BA, K_CA, K_ACB, K_CB, and K_BCA). These calculations are summarized in Table 7. This table shows that equilibrium constants and the effects of 5% errors in velocities can be calculated for reactions 1−12 from velocity measurements on a reaction following mechanism V.

The determinations of equilibrium constants from the rate equations for the five mechanisms can be summarized as follows:

I: K_A, K_AB, K_ABC

II: K_A, K_B, K_AB, K_ABC, and indirectly K_BA

III: K_A, K_B, K_C, K_AB, K_ABC, and indirectly K_BA

IV: K_A, K_B, K_C, K_AB, K_AC, K_ABC, and indirectly K_BA, K_CA, and K_ACB

V : K_A, K_B, K_C, K_AB, K_AC, K_BC, K_ABC, and indirectly K_BA, K_CA, K_ACB, and K_CB, K_BCA

Use of calckinparsABC5 to determine the Mechanism When A + B + C → Products Is Studied for the First Time

An earlier article(4) has shown that more general programs for calculating kinetic parameters can be used to determine the kinetic parameters for mechanisms with fewer kinetic parameters. This is demonstrated here by applying calckinparsABC5 to velocities calculated using the completely ordered mechanism I. To do this, four more velocities have to be measured on A + B + C → products with the completely ordered mechanism in order to use calckinparsABC5. These additional velocities are v{5,5,50} = 0.1370, v{5,5,5} = 0.01563, v{5,5,50} = 0.2725, and v{5,5,50} = 0.1064. The first four velocities are given in the description of Table 2. The effects of 5% errors in velocities, one at a time, were calculated using calckinparsABC5, and they are summarized in Table 8.

Table 8. Effects of 5% errors in 8 velocities when calckinparsABC5 is applied to velocities for the completely-ordered mechanism.

	Vfexp	KA	KAB	KB	KC	KABC	KBC	KAC
no errors	1.00	5.0	20.0	−8 × 104	7 × 103	35.0	19.7	−2 × 105
1.05 × v1	1.06	5.0	20.0	3 × 103	2 × 103	37.1	88.0	6 × 104
1.05 × v2	1.00	5.0	20.0	3 × 104	5 × 103	35.0	−3.5	−2 × 105
1.05 × v3	1.00	5.0	20.0	−2 × 105	2 × 103	35.0	2.4	−3 × 105
1.05 × v4	0.99	4.9	21.5	4 × 102	5 × 103	32.7	−190	−1 × 104
1.05 × v5	1.00	5.1	20.0	−1 × 104	−4 × 102	35.0	−6.1	1 × 104
1.05 × v6	1.00	4.3	20.0	1 × 103	3 × 102	35.0	−46.7	−1 × 104
1.05 × v7	1.00	5.7	18.5	−3 × 103	−6 × 103	35.3	−334.	2 × 103
1.05 × v8	1.00	5.1	20.0	−3 × 102	2 × 104	35.1	−208.	−3 × 105

This table shows that when the program for the completely random mechanism (calckinparsABC5) is applied to experimental data for the completely ordered mechanism, the expected values are obtained for V_fexp, K_A, K_AB, and K_ABC, but unreasonable values are obtained for K_B, K_C, K_BC, and K_AC. This is the way the program communicates that the velocity data is for the completely ordered mechanism. The fact that K_B, K_C, K_BC, and K_AC are unreasonable is also shown by the sensitivity of these four kinetic parameters to 5% errors in measured velocities. Other more general programs can be used in this way. For example, calckinparsABC4 can be applied to experimental data for mechanism I. Application of less general programs to velocity data on more complicated mechanisms involves dropping measured velocities and does not provide useful information.

Discussion

The determination of kinetic parameters using the minimum number of velocity measurements makes it possible to study the kinetics of more complicated enzyme-catalyzed reactions. This method has already been illustrated with A + B → products(4) when the experimental data follows rapid-equilibrium rate equations. Another advantage of deriving rate equations with a computer is that complicated rate equations are obtained in computer-readable form so that they do not need to be typed into the computer. The effects of experimental errors in velocities on the kinetic parameters are smaller when the substrate concentrations are chosen according to the general recommendations given here. The objective in this article is not to find the best set of triplets of substrate concentrations but to apply some general principles that indicate what can be done.

When the kinetic parameters for A + B + C → products are to be determined for the first time, it is recommended that the program for the completely random mechanism be used because it can identify the mechanism and determine the kinetic parameters in one operation. When the enzyme catalysis follows the completely random mechanism, all of reactions 1−12 reactions are at equilibrium, not just those in the mechanism used to calculate the equilibrium concentration of EABC.

When the values of kinetic parameters have been calculated with one minimal set of measured velocities, it is recommended that the calculation be repeated with a second set of substrate concentrations to be sure the same values (within the expected experimental errors) are obtained. The precision of kinetic parameters can be improved by making replicate measurements of the velocities.

The steady-state rate equation for ordered A + B + C → products has seven terms in the denominator,(9) but the rapid-equilibrium rate equation for the completely random mechanism has eight terms in the denominator. The number of terms in the denominator is useful in distinguishing between the five mechanisms discussed here. Usually, rapid-equilibrium rate equations have fewer denominator terms than steady-state rate equations. Cornish-Bowden(10) gives a good discussion of reactions with three or more substrates and calls attention to the fact that Frieden(11) was the first to call attention to the importance of the missing terms in the denominator of a rate equation.

The calculations in this paper support the following conclusions:

1. Computer programs using the minimum number of velocities can be used to calculate kinetic parameters for five rapid-equilibrium mechanisms of the reaction A + B + C → products.

2. The effects on the kinetic parameters of experimental errors in the velocities and substrate concentrations can be calculated, one at a time.

3. Equilibrium constants can be calculated for reactions not included in the mechanism used to derive the rapid-equilibrium rate equation.

4. More general computer programs can be used to identify a simpler mechanism and determine the kinetic parameters for the simpler mechanism.

Appendix

For mechanism I, the expression for the equilibrium concentration of EABC is derived by applying Solve in Mathematica to the three equilibrium equations and the conservation equation for enzymatic sites.

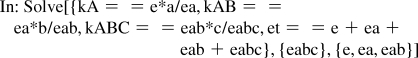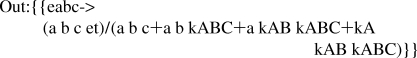Lower case type is used for equilibrium constants and concentrations of reactants because in Mathematica the name of a command like Solve begins with a capitol letter. In order to obtain the expression for the velocity v1, it is necessary to replace et with vfexp.

The velocity of A + B + C → products with specified kinetic parameters is given by

In order to calculate the four kinetic parameters for the completely ordered mechanism from the minimum number of velocity measurements, velocities are calculated for the following four triplets of substrate concentrations {a,b,c}: {200,200,200}, {0.5,200,200}, {200,0.5,200}, and {200,200,0.5}.

In:

The following program uses Solve to calculate the kinetic parameters from four velocity measurements for mechanism I:

calckinparsABC1[v1_,a1_,b1_,c1_,v2_,a2_,b2_,c2_,v3_,a3_,b3_,c3_,v4_,a4_,b4_,c4_]:=Module[{},(*This program calculates vfexp, kA, kAB, and kABC from four experimental velocities for the completely ordered mechanism of A + B + C → products at four triplets of substrate concentrations on the assumption that the mechanism is ordered, with A bound first, B bound second, and C bound last. The first velocity is at high [A], high [B], and high [C], the second velocity is at low [A], high [B] and high [C], the third velocity is at high [A], high [B] and low [C], and the fourth velocity is at high [A], high [B], and low[C].*)

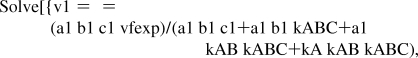The full set of calculations for this article is freely available at MathSource (http://library.wolfram.com/infocenter/MathSource).

Funding Statement

National Institutes of Health, United States