The Meaning and Use of the Volume Under a Three-Class ROC Surface (VUS)

Abstract

Previously, we have proposed a method for three-class receiver operating characteristic (ROC) analysis based on decision theory. In this method, the volume under a three-class ROC surface (VUS) serves as a figure-of-merit (FOM) and measures three-class task performance. The proposed three-class ROC analysis method was demonstrated to be optimal under decision theory according to several decision criteria. Further, an optimal three-class linear observer was proposed to simultaneously maximize the signal-to-noise ratio (SNR) between the test statistics of each pair of the classes provided certain data linearity condition. Applicability of this three-class ROC analysis method would be further enhanced by the development of an intuitive meaning of the VUS and a more general method to calculate the VUS that provides an estimate of its standard error. In this paper, we investigated the general meaning and usage of VUS as a FOM for three-class classification task performance. We showed that the VUS value, which is obtained from a rating procedure, equals the percent correct in a corresponding categorization procedure for continuous rating data. The significance of this relationship goes beyond providing another theoretical basis for three-class ROC analysis—it enables statistical analysis of the VUS value. Based on this relationship, we developed and tested algorithms for calculating the VUS and its variance. Finally, we reviewed the current status of the proposed three-class ROC analysis methodology, and concluded that it extends and unifies decision theoretic, linear discriminant analysis, and psychophysical foundations of binary ROC analysis in a three-class paradigm.

I. Introduction

PREVIOUSLY, we have developed a three-class decision model which produces a 2-D receiver operating characteristic (ROC) surface in a 3-D ROC space. The volume under the three-class ROC surface (VUS) was proved to be a figure-of-merit (FOM) for three-class task performance [1]. Having explored the decision theoretic and linear discriminant analysis (LDA) foundations of three-class ROC analysis [2], [3], this paper aims at exploring the psychophysical foundation of this proposed three-class ROC analysis, which is inspired by the two-alternative forced-choice (2AFC) procedure and its relationship to binary ROC analysis [4], [5]. This relationship provides the psychophysical foundation for binary ROC analysis, and will be extended in a three-class paradigm in the present paper. The significance of the extension of this relationship goes beyond providing another theoretical basis for three-class ROC analysis—it enables statistical analysis of VUS value. We present and test algorithms for calculating VUS and its variance. At the end of this paper, we provide a short discussion of the current status of the proposed three-class ROC methodology.

II. Background

As a method to evaluate binary classification task performance, conventional ROC analysis has been extensively studied [4]-[11]. A binary classification task can be performed using two procedures: a rating procedure, whose performance is described by area under an ROC curve (AUC), or a 2AFC procedure, whose performance is described by the percent correct. We briefly introduce these two procedures and their relationship.

A medical diagnostic task is often modeled as a classification task using a rating procedure. In such a procedure, the observer is presented with one of two mutually exclusive alternatives (e.g., signal-present image versus signal-absent image) at one time. In other words, the rating procedure has one observation interval [5]. The observer is then asked to rate his confidence level of which alternative is presented. Any number of responses may be used to rate the confidence level. For example, in a human observer signal detection task, a set of five confidence level responses is often used. Alternatively, an observer might be asked to use a continuous rating scale. An ROC curve is then traced out by calculating the sensitivity/specificity (TPF/TNF) pair for each confidence level. The area under this ROC curve gives the AUC value, which serves as a figure-of-merit for describing the task performance using a rating procedure.

A forced-choice design is a psychophysical procedure that can be used to avoid the problem of determining the observer's criterion (or confidence level) [5]. In a 2AFC procedure, two observation intervals are provided, i.e., two images, one from each alternative, are shown at the same time, e.g., a signal-absent image and a signal present image. The observer is instructed to categorize one of the images as signal-present and the other as signal absent. Note that since there are only two classes, this is equivalent to selecting which of the images has the signal present. The probability of correctly identifying which of the two stimuli is “signal-present” and which is “signal-absent” is defined as the percent correct.

In a binary classification task, Green and Swets showed the percent correct of a forced-choice procedure equals the AUC value in a rating procedure [5], [6]. This equivalence is of particular importance in binary ROC analysis [4]. It indicates that, for a given data source, the performance of a binary classification task could be identically determined using either a rating procedure or a 2AFC procedure. Further, both procedures result in the same scalar value that summarizes classification performance. In particular, when an investigator calculates the AUC value from a rating procedure, “he is in fact, or at least in mathematical fact, reconstructing random pairs of images, one from a diseased subject and one from a normal subject, and using the reader's separate ratings of these two images to simulate what the reader would have decided if theses two images had in fact been presented together as a pair in a 2AFC experiment” [4]. Bamber showed that this “probability of correctly ranking a (normal, abnormal)” pair is connected with the quantity calculated in the Wilcoxon or Mann–Whitney (M-W) statistical test [6]. As a result, the extensively-studied properties of M-W test can be used to predict the statistical properties of the area under a ROC curve.

Furthermore, this relationship enables us to study the AUC value and its properties without assumptions either on the distributions of the data or on the properties of the decision variable. Therefore, the AUC value obtained from a nonideal and non-Hotelling observer, e.g., a human observer, is interpretable in the sense of 2AFC.

III. Theory

Scurfield has previously investigated “n-event, m-dimensional” forced-choice tasks [12]. In that work, Scurfield first reformulated the two-class decision rules by introducing, for mathematical convenience, two dummy parameters which do not play a role in the observer's decision. As a natural extension of the reformulated two-class decision rules, a three-class decision rule was introduced which also added dummy parameters that do not play a role in the observer's decision. The resulting decision space is 2-D, and the decision structure has the same shape as the decision structure we derived under the ideal observer framework [1]. Scurfield proved that the volume under a 123-ROC surface (i.e., a surface in the 3-D space with axes T1F, T2F, and T3F, where TiF is the probability of correctly classifying the ith class, or the sensitivity of the ith class) equals the percent correct of an I₃A₆ (three interval, six-alternative) task. Since Scurfield's decision structure is identical to the decision-theory based one we have previously proposed, Scurfield's proof can be applied readily to this work. However, Scurfield's proof is very hard to follow, and it is not couched in terms that are familiar to the imaging community.

In the following, we first define a forced-choice procedure in a three-class paradigm; we then introduce the three-class decision model that has been proved to extend and unify the decision theoretic and LDA foundations of binary ROC analysis [1]-[3]. Next, we elaborate on the underlying connections between the proposed decision model and a three-class categorization procedure, and prove the equivalence of the percent correct and VUS in a different, and, we believe, more easily understood way. Based on this relationship, we propose methods and algorithms for calculating the VUS value and its standard deviation.

In the following, scalar variables are denoted with italic fonts, and functions are in regular fonts. For example, in T1F = T1F (x, y), T1F is a variable, and T1F is a function.

A. Definition of the Three-Class Categorization Procedure

We now define a three-class categorization procedure that is analogous to the 2AFC procedure. In this procedure, three randomly sampled objects, one from each of the three distinct classes, are presented to the observer simultaneously. The observer's task is to categorize the three objects into each of the three hypotheses. The observer is said to make a correct decision when, and only when, all three objects are correctly categorized.

B. Decision Model for Three-Class ROC Analysis

We have derived the optimal decision variables and decision rules for practical three-class ROC analysis using a rating procedure [1]. For a given data vector $\stackrel{\rightharpoonup }{g}$, two decision variables (rating values), LR₁₃, and LR₂₃, are computed, i.e.,

$$\log L{R}_{13}=\log \frac{\mathrm{f}(\stackrel{\rightharpoonup }{g}\mid H_1)}{\mathrm{f}(\stackrel{\rightharpoonup }{g}\mid H_3)}$$

and

$$\log L{R}_{23}=\log \frac{\mathrm{f}(\stackrel{\rightharpoonup }{g}\mid H_2)}{\mathrm{f}(\stackrel{\rightharpoonup }{g}\mid H_3)}$$ (1)

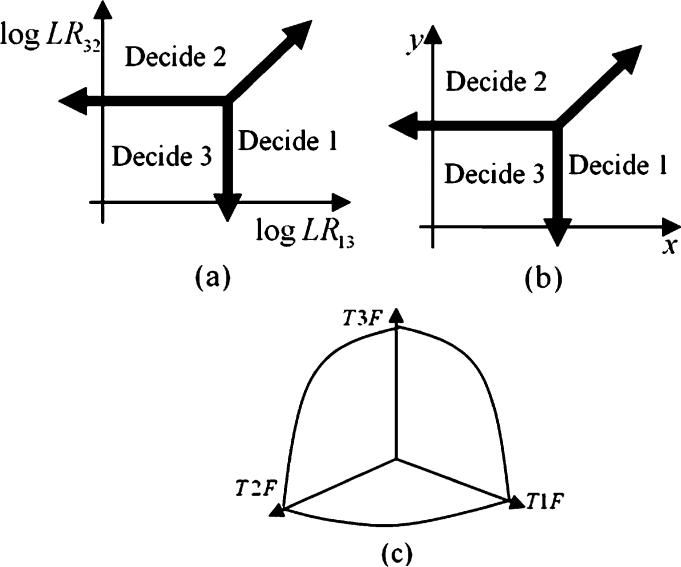
where H_i (i = 1, 2, 3) denotes the ith hypothesis, $\stackrel{\rightharpoonup }{g}$ is the data vector, and $\mathrm{f}(\stackrel{\rightharpoonup }{g}\mid H_i)$ is the likelihood of the data vector $\stackrel{\rightharpoonup }{g}$ under the ith hypothesis, H_i. To make a decision, a pair of ratings are calculated and compared to a decision structure centered on a critical point, which is determined by prior information (i.e., the decision utilities and prior probabilities of the classes, or predetermined sensitivity pairs). Fig. 1(a) shows the three-class decision plane and decision structure that was proved to be optimal under certain decision criteria in two previous papers [1], [2].

Fig. 1.

Decision plane of the three-class decision model and a three-class ROC surface. (a) Decision plane spanned by (log LR₁₃, log LR₂₃). (b) Decision plane spanned by (x, y). (c) Example of three-class ROC surface.

In order to relate the decision model to a corresponding categorization procedure, where any pairs of decision variables might be used, we provide the following mathematical treatment for the decision model. Since the result to be presented in this paper does not depend on the use of the decision variables, we replace log LR₁₃ and log LR₂₃ with a pair of general decision variables, x and y, as shown in Fig. 1(b). The general decision variables, (x, y), might be any pair of possible decision variables representing a pair of ratings assigned to each object. Note that for the same classification problem, if the decision variables that span the decision plane are different, the distributions on the decision plane would also be different.

The rating pair distributions of the three classes on this general decision plane can thus be represented by f₁(x, y), f₂(x, y), and f₃(x, y), respectively. Fig. 1(c) shows a typical ROC surface. The volume under the ROC surface is given by

$$VUS={\int }_0^1{\int }_0^{1}T1FdT2FdT3F$$ (2)

where TiF(i = 1, 2, 3) is the probability that class i can be correctly classified. It can be seen that TiF is a function of x and y, i.e.,

$$TiF=\mathrm{TiF}(x,y).$$ (3)

C. Mathematical Treatment of the Three-Class Categorization Procedure

In order to relate the three-class categorization procedure to the rating procedure described above, we now analyze the categorization procedure mathematically as a three-step process.

• Step 1) Present a triplet of randomly grouped class 1, class 2, and class 3 objects to the observer.

• Step 2) Rate each object independently as in a rating procedure, resulting in a rating pair, (x, y), for each object as in the rating procedure.

• Step 3) Test the three rating pairs associated with each object to see if the differences among the rating pairs lead to them being correctly categorized according to the decision rules suggested by the decision structure in Fig. 1. That is to say, a triplet can be correctly classified if there exists a decision structure position (defined by a critical point) such that all three rating pairs are correctly classified. Note here that the outcome of this test depends only on the relative positions of the rating pairs on the decision plane.

The described procedure is illustrated graphically in Fig. 2, where the triangle, square, and disk represent the randomly sampled objects, with one from each rating pair distributions f₁(x, y), f₂(x, y), and f₃(x, y), respectively. Fig. 2(a) illustrates a case when at least one decision structure position exists that results in correctly categorizing these three rating pairs, and Fig. 2(b) illustrates a case when no such position exists. Note that the underlying assumption here is that the rating procedure and the categorization procedure use the same decision structure and decision variables. By repeating this procedure and computing the ratio of correct to total trials, we can thus estimate the percent correct for this categorization procedure from the rating data produced by a rating procedure.

Fig. 2.

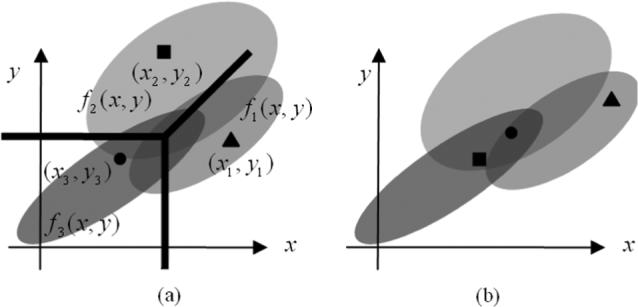
Illustration of a mathematical treatment of the categorization procedure that is equivalent to a rating procedure. Ellipses with different shadings schematically represent the distributions of decision variables for the three classes. Triangle is a random sample from class 1, the square is a random sample from class 2, and the disk represents a random sample from class 3. (a) Illustration of a case where the triplet can be correctly categorized. (b) Illustration of a case where correct categorization is not possible for any position of the proposed decision structure.

D. Equivalence of VUS in a Rating Procedure and Percent Correct in a Categorization Procedure

Given the above mathematical treatment, we can compute the percent correct (PC) as the integration of the product of the probability distributions of the rating pairs for the three classes over all the combinations that can give correct decisions. The formulation of PC is thus obtained by finding a strategy such that a complete set of correctly classified triplets is obtained without counting any triplet more than once, and then integrating the probabilities of all possible correct classifications. In the Appendix, we prove that such a formulation of percent correct leads to the same expression for VUS, i.e.,

$$VUS=PC.$$ (4)

Note that the proof is done for continuous rating data. In other words, samples of rating values from the continuous distributions cannot give rise to rating triplets at identical positions in the decision space.

IV. Statistical Analysis

Given the equivalence of VUS and percent correct, we now propose methods for statistical analysis of VUS value.

A. Calculation of the VUS Value

Since, as described above and proved in the Appendix, the VUS equals the percent correct in the corresponding three-class categorization task, we can thus estimate PC as a substitute for estimating the VUS. With sample sizes of n₁, n₂, and n₃ from continuous class 1, class 2, and class 3 distributions, respectively, the rating procedure will result in n_k rating pairs for class k (where k = 1, 2, 3). We denote each rating pair as ${\stackrel{\rightharpoonup }{p}}_{ki}=(x_{ki},y_{ki})$, where i = 1 ... n_i refers to the ith sample in the kth class. The corresponding categorization procedure, at least conceptually, consists of making all possible n₁ · n₂ · n₃ comparisons among the ratings from the three classes and summing the score, $\mathrm{U}({\stackrel{\rightharpoonup }{p}}_{1l},{\stackrel{\rightharpoonup }{p}}_{2m},{\stackrel{\rightharpoonup }{p}}_{3n})$, for each comparison according to the rule

$$\mathrm{U}({\stackrel{\rightharpoonup }{p}}_{1l},{\stackrel{\rightharpoonup }{p}}_{2m},{\stackrel{\rightharpoonup }{p}}_{3n})=\{\begin{array}{cc}1,\hfill & \text{correct categorization}\hfill \\ 0,\hfill & \text{otherwise}\hfill \end{array}\phantom{\}}.$$ (5)

where l, m, and n are the lth, mth, and nth samples from classes 1, 2, and 3, respectively. In (5), correct categorization is said to occur when there exists a critical point (this is a position for the decision structure) such that ${\stackrel{\rightharpoonup }{p}}_{1l}$ falls into the area for a class 1 decision, ${\stackrel{\rightharpoonup }{p}}_{2m}$ falls into the area for a class 2 decision, and ${\stackrel{\rightharpoonup }{p}}_{3n}$ falls into the area for a class 3 decision. The percent correct, PC, is then estimated by averaging the {U} over all n₁ · n₂ · n₃ comparisons, i.e.,

$$\widehat{PC}=\frac{1}{n_1\cdot n_2\cdot n_3}\sum _1^{n_1}\sum _1^{n_2}\sum _1^{n_3}\mathrm{U}({\stackrel{\rightharpoonup }{p}}_{1l},{\stackrel{\rightharpoonup }{p}}_{2m},{\stackrel{\rightharpoonup }{p}}_{3n})$$ (6)

where the caret above PC indicates that it is an estimate. Given the equivalence between the VUS and PC, VUS can be evaluated using (6).

Equation (5) is very similar to its counterpart in the 2AFC procedure, as described in [4]. In the binary case, when discrete rating data are used, it is possible for two samples from different classes to be identical, and the decision rule will assign a value of 0.5 for percent correct calculation [4]. One may note (5) does not include a contingency for the case where some of the ratings are the same. This is because, in this paper we only proved VUS = PC for a continuous rating scale, where we do not need to consider the case where random samples of the ratings are identical. The possible relationship between VUS and PC for three-class discrete rating scale is more complicated than in the binary case and is beyond the scope of this paper.

B. Estimation of the Variance of the VUS Value

We have implemented two methods for variance estimation. The first method is based on Dreiseitl's extension [13] of Lehmann's nonparametric approach [14]. In Dreiseitl's work, algorithms for estimating the volume under the surface value and its variance were proposed for Mossman's three-class decision model. Dreiseitl's algorithms for volume-under-the-surface estimation are very similar to (5) and (6). The only difference lies in the definition of correct categorization in (5). This is because Mossman's decision model uses different decision structures, requiring a different correct categorization test. However, this difference does not affect the formulation for VUS and its variance, and Dreiseitl's variance calculation algorithm can be readily applied to this work as explained below.

In this method, the variance is given by [13]

$$\begin{array}{cc}\hfill \mathrm{var}\left(VUS\right)& =\mathrm{cov}(VUS,VUS)\hfill \\ \hfill & =\frac{1}{n_1^2{n}_2^2{n}_3^2}\hfill \\ \hfill & \times \sum _i\sum _j\sum _k\sum _I\sum _J\sum _K\mathrm{cov}(U_{ijk},U_{IJK}).\hfill \end{array}$$ (7)

In (7), $U_{ijk}=\mathrm{U}({\stackrel{\rightharpoonup }{p}}_{1i},{\stackrel{\rightharpoonup }{p}}_{2j},{\stackrel{\rightharpoonup }{p}}_{3k})$, cov(U_ijk, U_mnl) = E(U_ijkU_mnl) - θ², where E() is the expectation operation, $U_{ijk}=\mathrm{U}({\stackrel{\rightharpoonup }{p}}_{1i},{\stackrel{\rightharpoonup }{p}}_{2j},{\stackrel{\rightharpoonup }{p}}_{3k})$, and θ = E(U_ijk), which is the true percent correct. Note that E(U_ijkU_mnl) is the probability that both U_ijk and U_mnl are 1. Expanding (7), as described in [13] results in the following formula for variance of the VUS

$$\begin{array}{cc}\hfill & \mathrm{var}\left(VUS\right)\hfill \\ \hfill & =\frac{1}{n_1{n}_2{n}_3}\{\theta (1-\theta )+(n_3-1)[\mathrm{E}\left(U_{ijk}{U}_{ijK}\right)-{\theta }^2]\hfill \\ \hfill & +(n_1-1)(n_2-1)[\mathrm{E}\left(U_{ijk}{U}_{IJk}\right)-{\theta }^2]\}\hfill \\ \hfill & +\frac{1}{n_1{n}_2{n}_3}\{(n_2-1)[\mathrm{E}\left(U_{ijk}{U}_{iJk}\right)-{\theta }^2]\hfill \\ \hfill & +(n_1-1)[\mathrm{E}\left(U_{ijk}{U}_{Ijk}\right)-{\theta }^2]\}\hfill \\ \hfill & +\frac{1}{n_1{n}_2{n}_3}\{(n_2-1)(n_3-1)[\mathrm{E}\left(U_{ijk}{U}_{iJK}\right)-{\theta }^2]\hfill \\ \hfill & +(n_1-1)(n_3-1)[\mathrm{E}\left(U_{ijk}{U}_{IjK}\right)-{\theta }^2]\}.\hfill \end{array}$$ (8)

Note that the elements in each expectation in (8) have at least one identical subscript, e.g., the two elements in E(U_ijkU_IJk) have subscripts ijk and IJk, respectively. E(U_ijkU_IJk) is de fined as

$$\mathrm{E}\left(U_{ijk}{U}_{IJk}\right)=\sum _i\sum _j\sum _k\sum _{I\ne i}\sum _{J\ne j}\left(U_{ijk}{U}_{IJk}\right).$$ (9)

Other expectations in (8) have analogous definitions.

The calculation of each E(U_ijkU_mnl) in (8) requires four or five nested loops, which, as will be demonstrated later, takes a long time when the number of rating pairs is large. Therefore, we propose to implement a second method using a bootstrap approach [15], [16] to estimate the variance. The steps involved in this method are as follows.

• Step 1) Formulate three empirical probability rating pair distributions, ${\tilde{\mathrm{f}}}_i(x,y)$, to estimate the real rating pair distribution, ${\mathrm{f}}_i(x,y)$, where I represents the ith class. For a standard Bootstrap approach, ${\tilde{\mathrm{f}}}_i(x,y)$ is expressed as a discrete distribution such that each of the n_i samples from ${\tilde{\mathrm{f}}}_i(x,y)$ from class i has a probability of 1/n_i. Despite the fact that ${\tilde{\mathrm{f}}}_i(x,y)$ is discrete, each rating pair is a sample from the continuous rating distribution, f_i(x, y). In cases where the sample size is small, one might want to fit the distribution of the data with a normal distribution as is done in binary ROC analysis. However, we have not yet been able to derive a three-class counterpart of the binormal ROC curve fitting. Thus we provide an alternative approach using a simple parametric Bootstrap method, where the available experimental samples are used to fit bivariate Gaussian distributions to estimate ${\tilde{\mathrm{f}}}_1(x,y)$, ${\tilde{\mathrm{f}}}_2(x,y)$ and ${\tilde{\mathrm{f}}}_3(x,y)$, respectively. To be specific, using the experimentally obtained rating pairs of the ith class, we compute the mean, variance and the covariance of x and y, and then use these parameters to formulate the empirical probability distribution of the rating pairs of the ith class. Note that the parametric bootstrap approach is not essential, but does have the advantage of handling the case for discrete ratings and, to the extent the data are described by bivariate Gaussian distributions, more precise estimates of the VUS and its variance.

• Step 2) Take n₁ random samples from ${\tilde{\mathrm{f}}}_1(x,y)$, n₂ random samples from ${\tilde{\mathrm{f}}}_2(x,y)$, and n₃ random samples from ${\tilde{\mathrm{f}}}_3(x,y)$ with replacement.

• Step 3) Make all possible n₁ · n₂ · n₃ comparisons among the random samples from each class. Calculate the fraction, Γ, of the samples of comparisons that result in a correct categorization using (5)-(6).

• Step 4) Repeat Steps 2 and 3 B times, to create B bootstrap samples. This results in a set of estimates of the percent correct Γ₁, Γ₂, Γ₃, ..., Γ_B.

• Step 5) The distribution of Γ estimates the distribution of PC, which estimates the distribution of the VUS value. The variance of the VUS is estimated by the variance of Γ.

V. Experiments

We have implemented the algorithms for estimating the VUS and its variance. To test the algorithms, we used a set of data from a previous experiment on dual-isotope myocardial perfusion SPECT (MPS) image quality evaluation described in [17], [18], where the rest-stress MPS images were obtained from a simulated population of normal patients and patients with reversible or fixed defects. For each of the three classes, a total of 432 rating pairs were generated. Fig. 3(a) shows the decision plane and Fig. 3(b) shows the corresponding three-class ROC surface.

Fig. 3.

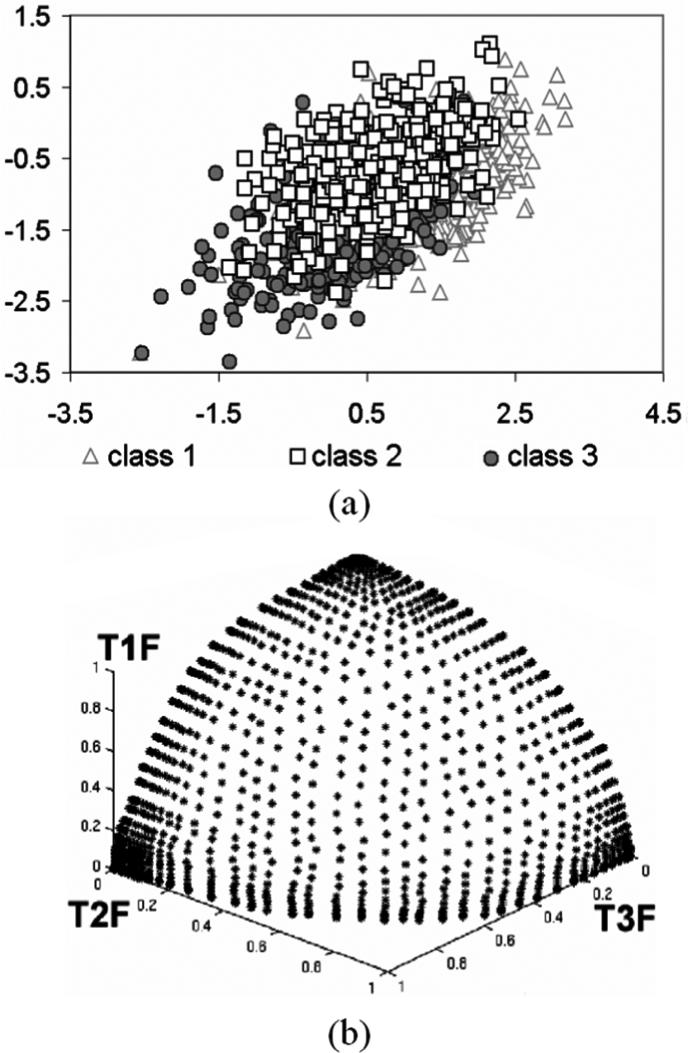
Decision planes and the ROC surface obtained for simulated dual-isotope MPS images. (a) Decision plane. (b) ROC surface traced out by moving the decision structure on the decision plane and compute the sensitivity triplets.

To validate the VUS calculation algorithm proposed, we developed an ad hoc VUS calculation algorithm, as illustrated in Fig. 4. The rating pair distributions were sampled on a grid with very small grid spacing [Fig. 4(a)]. In the ROC space, a relatively large bin size was defined on the (T1F, T2F) plane [Fig. 4(b)]. Moving the decision structure in the decision plane with very small grid spacing produced several T3F values in each of the (T1F, T2F) bin in the ROC space. For each (T1F, T2F) bin in the ROC space, we average the T3F values to produce an ROC histogram. An estimate of the VUS value was obtained by averaging the histogram for all (T1F, T2F) bins. The accuracy of the VUS can be increased by decreasing the grid spacing.

Fig. 4.

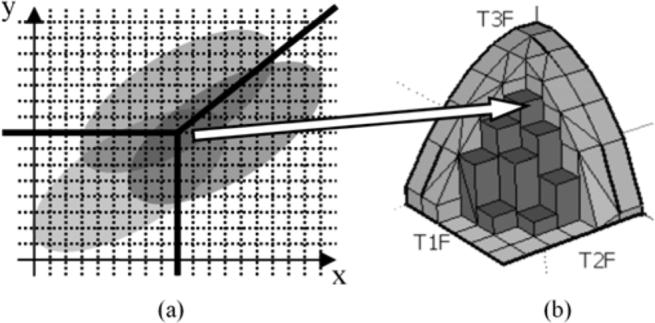
Calculation of the VUS. (a) Sample the distributions with very small grid spacing in the decision plane. (b) For each (T1F, T2F) bin in the ROC space, we average the T3F values to produce an ROC histogram.

The experimentally obtained data were too sparse to enable small grid spacing in the experimental decision plane. We thus fit the three rating pair distributions to bivariate Gaussian distributions for the ad hoc algorithm. This was done based on our previous unpublished study of the normality of the rating pairs. Note that the ad hoc method is a very coarse method, its resulting VUS value is affected by the bin sizes on both the decision plane and the histogram. We developed this ad hoc method only to obtain a rough idea of the magnitude of the VUS value to test whether the theoretical method provides a VUS that is similar. For the method based on (6), we did not use the bivariate Gaussian fitting. Table I shows the parameters of the fitted bivariate Gaussian distributions for the three classes. To validate the variance calculation, we simply compared the estimate from Dreiseitl's extension [13] in (8) and the proposed Bootstrap method. We also compared the computational times for (8) and the Bootstrap method.

TABLE I.

Parameters of the Fitted Bivariate Gaussian Distributions for the Three Classes

	μ x	σ x	μ y	σ y	ρ
Class 1	1.340	0.643	−0.878	0.386	0.532
Class 2	0.688	0.520	−0.642	0.328	0.492
Class 3	0.187	0.557	−1.358	0.390	0.528

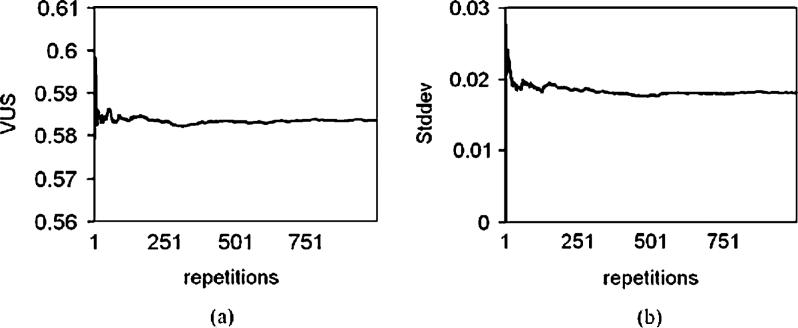
Since the data were obtained from 432 triplets of rating values, we used n₁ = n₂ = n₃ = 432 in calculating VUS using (6). The results are shown in Table II, where we see that methods based on VUS = PC agreed well with the ad hoc method for estimating the VUS value. To calculate the variance using the Bootstrap method, we used B = 1000 repetitions. It can be seen from Fig. 5 that VUS and its variance were well-converged after 200 repetitions. The resulting standard deviation using the Bootstrap method after 1000 iterations was 0.181 (Fig. 5), which is in the same order as the one obtained using (8). However, the algorithm for obtaining standard deviation using (8) took approximately eight days. This is because, as described above, each E(U_ijkU_mnl) in (8) involves a nested summation loop four or five levels deep [an example is given in (9)]. The five level deep loops dominate the computational time. Thus, when n = n₁ = n₂ = n₃, the nested summation loops result in a computational time that is roughly proportional to n⁵. For example, using a 2.13 GHz AMD Opteron processor, when n = 100, it took 418 s to compute the variance, while when n = 200, it took 13, 358 s, approximately 31.96 times longer. In our study, with n = 432, the computational time was about eight days. The Bootstrap method, on the other hand, required only 15 min for 200 repetitions, as shown in Table II.

TABLE II.

Resulting VUS Values and the Standard Deviations Using Different Approaches

	VUS = PC method			Ad hoc method
	Bootstrap		Eqn. (6)-(8)
	1000 repetitions	200 repetitions
VUS	0.5835	0.5835	0.5830	0.5815
Standard deviation	0.0181	0.0189	0.0182	N/A
Computational time	75min	15min	∼8 days	N/A

Fig. 5.

Convergence of VUS (a) and its standard deviation (b) using the Bootstrap method.

VI. Discussion

Current Status of the Proposed Three-Class ROC Analysis

Binary ROC analysis has been a standard method for assessing diagnostic performance. However, there are an increasing number of diagnostic tasks of interest for which binary classification is not sufficient. In particular, in many cases diagnosing disease using imaging techniques requires both detection and characterization of the disease instead of disease detection alone; analysis of these cases requires ROC analysis techniques for analyzing multi-class diagnoses. However, multiclass ROC analysis is a theoretical problem whose solution has been eluded the community ever since the introduction of the binary ROC in the 1950s [19], [20]. Much work has been devoted to understanding the nature of a multiclass classification problem, and many metrics have been proposed to assess the performance of a multiclass classification task [12], [13], [19]-[32].

Motivated by the medical problem of cardiac perfusion defect evaluation using simultaneous dual-isotope myocardial perfusion SPECT (MPS), where the assessment of a three-class diagnostic task is required to evaluate and optimize MPS imaging techniques, we have carried out a series of studies on the theoretical foundations for a practical three-class ROC analysis method. The present paper results in both an additional theoretical justification for the proposed method, and a practical method to calculate its figure of merit, the volume under a three-class ROC surface. In the following, we review the previous developments in order to present a more complete picture of the theoretical framework.

Model Development

We first developed an optimal three-class decision model that maximizes the expected utility under decision theory by assuming that incorrect decisions have equal utilities under the same hypothesis (the equal error utility assumption). This decision model produces a 2-D ROC surface in a 3-D ROC space and the volume under this surface (VUS) is a figure-of-merit for three-class task performance. We have compared the proposed three-class ROC analysis with conventional binary ROC analysis and concluded that they share many similar properties and that three-class ROC analysis reduces to binary ROC analysis for certain special cases [1].

Decision Theoretic Foundation

We thoroughly investigated the decision theoretic foundations of the proposed three-class ROC analysis and proved the optimality of the three-class ideal observer (3-IO) according to several decision theoretic criteria. In particular, we found that the 3-IO and the proposed decision model maximizes the expected utility (MEU) under equal error utility assumption, maximizes the probability of making correct decisions, provides the maximum likelihood (ML) decision, and satisfies the Neyman-Pearson (N-P) criterion in the sense that, given the sensitivities of two classes, the sensitivity of the third class is maximized [2]. We believe that the optimality with respect to N-P criterion is of particular importance for clinical applications, as explained in [2] and [3].

Linear Discriminant Analysis (LDA) Foundation

We then investigated the LDA foundation of three-class ROC analysis. We have shown that the conventional multiclass extension of LDA has significant limitations. In particular, the L-class Hotelling trace, which has been used as a figure-of-merit for multiclass task performance, cannot distinguish cases where all classes are perfectly classified from cases where only one of the classes can be correctly classified [33]. Using the proposed three-class ROC analysis method, we have found that when the data follow multivariate Gaussian distribution with equal covariance matrices, in addition to the optimality mentioned above, the proposed three-class decision model maximizes the SNR between each pairs of the classes, and likelihood ratios can be computed using a linear observer, i.e., the three-class Hotelling observer (3-HO) [3]. When the data are not Gaussian distributed, we have shown that 3-HO still maximizes the SNR between each pair of the classes given a certain data linearity condition [3].

Psychophysical Foundation

In this paper, we have investigated the relationship between a three-class rating procedure and the corresponding categorization procedure. The equivalence of VUS and the percent correct extends the psychophysical foundation of binary ROC analysis to the proposed three-class ROC analysis.

From the above, we conclude that the proposed three-class ROC analysis method extends and unifies the decision theoretic, linear discriminant analysis, and psychophysical foundations of binary ROC analysis in a three-class paradigm. The proposed three-class ROC methodology is practical mathematically in the sense that a figure-of-merit (FOM) was proposed along with practical numerical methods to obtain the FOM and its statistical properties [1]-[3]. Additionally, the proposed methodology might also prove to be a reasonable model of clinical decision making, as described in [2] and [3].

VII. Conclusion

In this paper, we investigated the psychophysical foundation of a previously-proposed three-class ROC methodology by presenting an intuitive meaning for the VUS value, i.e., the percent correct in a three-class categorization procedure for continuous rating data. This equivalence is neither dependent on the decision variables used, nor dependent on the actual distributions of the three classes. In other words, no matter what decision variables are used, the VUS obtained always equals the percent correct in a corresponding three-class categorization procedure when using the decision rules defined by the decision structure used in this work. Based on this psychophysical foundation, we developed and tested algorithms for calculating the VUS and its variance.

In light of this connection to the proposed psychophysical task, we reviewed the current status of the proposed three-class ROC analysis methodology, and concluded that it extends and unifies decision theoretic, linear discriminant analysis, and psychophysical foundations of binary ROC analysis in a three-class paradigm.

Appendix

We denote the rating pair distributions as f₁(x, y), f₂(x, y), and f₃(x, y) for each of the three classes, respectively, and the corresponding true class fractions as

$$T1F=\mathrm{T}1\mathrm{F}(x,y)={\int }_x^{\infty }{\int }_{-\infty }^{y-x+x^{\prime }}{\mathrm{f}}_1(x^{\prime },y^{\prime })d{y}^{\prime }d{x}^{\prime }$$ (A1)

$$T2F=\mathrm{T}2\mathrm{F}(x,y)={\int }_y^{\infty }{\int }_{-\infty }^{y^{\prime }-y+x}{\mathrm{f}}_2(x^{\prime },y^{\prime })d{x}^{\prime }d{y}^{\prime }$$ (A2)

and

$$T3F=\mathrm{T}3\mathrm{F}(x,y)={\int }_{-\infty }^x{\int }_{-\infty }^y{\mathrm{f}}_3(x^{\prime },y^{\prime })d{y}^{\prime }d{x}^{\prime }.$$ (A3)

Note that scalar variables are represented using italic fonts while functions are in regular fonts. In the following, we prove the equivalence of the VUS and the PC with respect to a categorization procedure.

A. Preparing Necessary Partial Derivatives and Three Lemmas

Before proving the equivalence of the VUS and the PC in a categorization procedure, we first introduce three lemmas and derive the partial derivatives of T2F(x, y) and T3F(x, y), which will be used later in the proof.

1) The Three Lemmas

Lemma 1

The purpose of Lemma 1 is to change the bound of the integrals, and is expressed as

$${\int }_b^{\infty }{\int }_a^{y-b+a}\mathrm{f}(x,y)dxdy={\int }_b^{\infty }{\int }_a^{\infty }\mathrm{f}(x,y+x-a)dxdy.$$ (A4)

Proof:

$${\int }_b^{\infty }{\int }_a^{y-b+a}\mathrm{f}(x,y)dxdy={\int }_b^{\infty }{\int }_a^{\infty }\mathrm{f}(x,y)\Theta (y-b+a-x)dxdy.$$

where Θ is the Heaviside step function. Now let y′ = y - x + a

$$\begin{array}{cc}\hfill {\int }_b^{\infty }& {\int }_a^{\infty }\mathrm{f}(x,y)\Theta (y-b-a-x)dxdy\hfill \\ \hfill & ={\int }_b^{\infty }{\int }_a^{\infty }\mathrm{f}(x,y^{\prime }+x-a)\Theta (y^{\prime }-b)dxd{y}^{\prime }\hfill \\ \hfill & ={\int }_b^{\infty }{\int }_a^{\infty }\mathrm{f}(x,y^{\prime }+x-a)dxd{y}^{\prime }.\hfill \end{array}$$

Let y = y′

$${\int }_b^{\infty }{\int }_a^{\infty }\mathrm{f}(x,y^{\prime }+x-a)dxd{y}^{\prime }={\int }_b^{\infty }{\int }_a^{\infty }\mathrm{f}(x,y+x-a)dxdy.$$

Lemma 2

Lemma 2 is very similar to Lemma 1, and is expressed as

$${\int }_b^{\infty }{\int }_{y-b+a}^{\infty }\mathrm{f}(x,y)dxdy={\int }_b^{\infty }{\int }_a^{\infty }\mathrm{f}(x+y-b,y)dxdy.$$ (A5)

Proof:

$${\int }_b^{\infty }{\int }_{y-b+a}^{\infty }\mathrm{f}(x,y)dxdy={\int }_b^{\infty }{\int }_{-\infty }^{\infty }\mathrm{f}(x,y)\Theta (x-y+b-a)dxdy$$

where Θ is the Heaviside step function, let x′ = x - y + b

$$\begin{array}{cc}\hfill {\int }_b^{\infty }& {\int }_{-\infty }^{\infty }\mathrm{f}(x,y)\Theta (x-y+b-a)dxdy\hfill \\ \hfill & ={\int }_b^{\infty }{\int }_{-\infty }^{\infty }\mathrm{f}(x^{\prime }+y-b,y)\Theta (x^{\prime }-a)d{x}^{\prime }dy\hfill \\ \hfill & ={\int }_b^{\infty }{\int }_a^{\infty }\mathrm{f}(x^{\prime }+y-b,y)d{x}^{\prime }dy\hfill \end{array}$$

Let x = x′

$${\int }_b^{\infty }{\int }_a^{\infty }\mathrm{f}(x^{\prime }+y-b,y)d{x}^{\prime }dy={\int }_b^{\infty }{\int }_a^{\infty }\mathrm{f}(x+y-b,y)dxdy.$$

Lemma 3

The purpose of Lemma 3 is to change the order of the double integral, and is expressed as

$${\int }_{-\infty }^{\infty }\mathrm{f}\left(y\right)\left[{\int }_y^{+\infty }\mathrm{g}\left(y^{\prime }\right)d{y}^{\prime }\right]dy={\int }_{-\infty }^{+\infty }\mathrm{g}\left(y^{\prime }\right)\left[{\int }_{-\infty }^{y^{\prime }}\mathrm{f}\left(y\right)dy\right]d{y}^{\prime }.$$ (A6)

Proof:

$$\begin{array}{cc}\hfill {\int }_{-\infty }^{\infty }\mathrm{f}\left(y\right)\left[{\int }_y^{+\infty }\mathrm{g}\left(y^{\prime }\right)d{y}^{\prime }\right]& dy\hfill \\ \hfill =& {\int }_{-\infty }^{\infty }\mathrm{f}\left(y\right)\left[{\int }_{-\infty }^{+\infty }\mathrm{g}\left(y^{\prime }\right)\Theta (y^{\prime }-y)d{y}^{\prime }\right]dy\hfill \end{array}$$

where Θ (y) is the Heaviside step function. Now the order of the integration can be changed.

$$\begin{array}{cc}\hfill & {\int }_{-\infty }^{\infty }\mathrm{f}\left(y\right)\left[{\int }_{-\infty }^{+\infty }\mathrm{g}\left(y^{\prime }\right)\Theta (y^{\prime }-y)d{y}^{\prime }\right]dy\hfill \\ \hfill & ={\int }_{-\infty }^{\infty }{\int }_{-\infty }^{+\infty }\mathrm{f}\left(y\right)\mathrm{g}\left(y^{\prime }\right)\Theta (y^{\prime }-y)dyd{y}^{\prime }\hfill \\ \hfill & ={\int }_{-\infty }^{+\infty }\mathrm{g}\left(y^{\prime }\right)\left[{\int }_{-\infty }^{y^{\prime }}\mathrm{f}\left(y\right)dy\right]d{y}^{\prime }.\hfill \end{array}$$

2) Partial Derivatives of T2F (x, y)

For a decision structure centered on (x, y), T2F(x, y) is expressed in (A2), and the partial derivative of T2F(x, y) with respect to x is thus

$$\frac{\partial \mathrm{T}2\mathrm{F}(x,y)}{\partial x}={\int }_y^{\infty }{\mathrm{f}}_2(y^{\prime }-y+x,y^{\prime })d{y}^{\prime }.$$ (A7)

To calculate the partial derivative of T2F(x, y) with respect to y, we note that T2F(x, y) is an integral over a region bounded below by a horizontal ray extending from the origin of the decision structure to -∞ and a second ray from the origin of the decision structure along the 45° line from the origin of the decision structure toward (∞, ∞). We use the observation above to rewrite T2F(x, y) as

$$\begin{array}{cc}\hfill \mathrm{T}2\mathrm{F}(x,y)={\int }_y^{\infty }{\int }_{-\infty }^x{\mathrm{f}}_2& (x^{\prime },y^{\prime })d{x}^{\prime }d{y}^{\prime }\hfill \\ \hfill & +{\int }_y^{\infty }{\int }_x^{y^{\prime }-y+x}{\mathrm{f}}_2(x^{\prime },y^{\prime })d{x}^{\prime }d{y}^{\prime }.\hfill \end{array}$$ (A8)

Applying Lemma 1 in (A4) to the second term of (A8), T2F(x, y) can be expressed as

$$\begin{array}{cc}\hfill \mathrm{T}2\mathrm{F}(x,y)=& {\int }_y^{\infty }[{\int }_{-\infty }^x{\mathrm{f}}_2(x^{\prime },y^{\prime })d{x}^{\prime }\phantom{]}\hfill \\ \hfill & \phantom{[}+{\int }_x^{\infty }{\mathrm{f}}_2(x^{\prime },y^{\prime }-x+x^{\prime })d{x}^{\prime }]d{y}^{\prime }.\hfill \end{array}$$ (A9)

Using this we find that

$$\frac{\partial \mathrm{T}2\mathrm{F}(x,y)}{\partial y}=-{\int }_{-\infty }^x{\mathrm{f}}_2(x^{\prime },y)d{x}^{\prime }-{\int }_x^{\infty }{\mathrm{f}}_2(x^{\prime },y-x+x^{\prime })d{x}^{\prime }.$$ (A10)

3) Partial Derivatives of T2F(x, y)

For a decision structure centered on (x, y), T3F(x, y) is given by (3). Its partial derivatives with respect to x and y are thus

$$\frac{\partial \mathrm{T}3\mathrm{F}(x,y)}{\partial x}={\int }_{-\infty }^y{\mathrm{f}}_3(x,y^{\prime })d{y}^{\prime }$$

and

$$\frac{\partial \mathrm{T}3\mathrm{F}(x,y)}{\partial y}={\int }_{-\infty }^x{\mathrm{f}}_3(x^{\prime },y)d{x}^{\prime }.$$ (A11)

B. Strategy for Computing the Percent Correct

We now describe the strategy for computing percent correct; a full mathematical derivation based on this strategy will be given in the next section. The percent correct on a three-class categorization procedure is given by

$$\begin{array}{cc}\hfill & PC=\iint \iint \iint \{{\mathrm{f}}_1(x_1,y_1){\mathrm{f}}_2(x_2,y_2){\mathrm{f}}_3(x_3,y_3)\hfill \\ \hfill & \times \mathrm{c}(x_1,y_1,x_2,y_2,x_3,y_3)\}d{x}_{1}d{y}_{1}d{x}_{2}d{y}_{2}d{x}_{3}d{y}_3\hfill \end{array}$$ (A12)

where c = c(x₁, y₁, x₂, y₂, x₃, y₃) is 1 if there exists a position of the decision structure such that the triplet of rating pairs ((x₁, y₁), (x₂, y₂), (x₃, y₃))can be correctly classified, and is 0 otherwise. Rearranging (A12), we obtain

$$\begin{array}{cc}\hfill PC=& \iint {\mathrm{f}}_3(x_3,y_3)\{\iint {\mathrm{f}}_2(x_2,y_2)\phantom{\}}\hfill \\ \hfill & \times \left[\iint {\mathrm{f}}_1(x_1,y_1)\mathrm{c}(x_1,y_1,x_2,y_2,x_3,y_3)d{x}_{1}d{y}_1\right]\hfill \\ \hfill & \phantom{\{}\times d{x}_{2}d{y}_2\}d{x}_{3}d{y}_3.\hfill \end{array}$$ (A13)

Examination of (A13) reveals that the outermost double integral can be expressed as

$$PC=\iint {\mathrm{f}}_3(x_3,y_3)\mathrm{p}(c=1\mid x_3,y_3)d{x}_{3}d{y}_3$$ (A14)

where

$$\begin{array}{cc}\hfill \mathrm{p}& (c=1\mid x_3,y_3)\hfill \\ \hfill & =\iint {\mathrm{f}}_2(x_2,y_2)[\iint {\mathrm{f}}_1(x_1,y_1)\phantom{]}\hfill \\ \hfill & \phantom{[}\times \mathrm{c}(x_1,y_1,x_2,y_2,x_3,y_3)d{x}_{1}d{y}_1]d{x}_{2}d{y}_2.\hfill \end{array}$$ (A15)

Here, p(c = 1|x₃, y₃) is the probability density for a correct classification over all possible (x₁, y₁) and (x₂, y₂) combinations for the given (x₃, y₃). Similarly, p(c = 1|x₃, y₃) can be expressed as

$$\begin{array}{cc}\hfill \mathrm{p}(c=1\mid x_3,y_3)=& \iint \{{\mathrm{f}}_2(x_2,y_2)\hfill \\ \hfill & \times \mathrm{p}(c=1\mid x_2,y_2,x_3,y_3)\}d{x}_{2}d{y}_2\hfill \end{array}$$ (A16)

where p(c = 1|x₂, y₂, x₃, y₃) is the probability density for correct classification over all possible (x₁, y₁) for the given (x₂, y₂) and (x₃, y₃) combination, and is expressed as

$$\begin{array}{cc}\hfill \mathrm{p}& (c=1\mid x_2,y_2,x_3,y_3)\hfill \\ \hfill & =\iint {\mathrm{f}}_1(x_1,y_1)\mathrm{c}(x_1,y_1,x_2,y_2,x_3,y_3)d{x}_{1}d{y}_1.\hfill \end{array}$$ (A17)

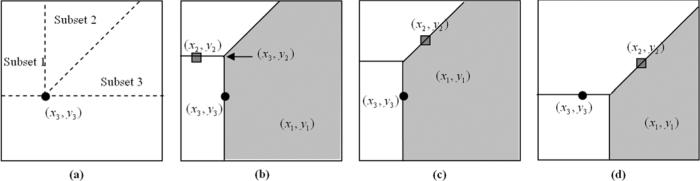
Equations (A14), (A16), and (A17) provide a natural strategy to evaluate the six-dimensional integral in (A12). We first select a (x₃, y₃) pair. Next, we recognize that all (x₂, y₂) for which correct classifications are possible will necessarily have y₂ > y₃, as seen in Fig. 6(a). For such pairs, the maximum region containing (x₁, y₁) that is correctly classifiable will be obtained if the decision structure is positioned such that the selected (x₂, y₂) and (x₃, y₃) lie on the rays comprising the decision structure. For a given (x₃, y₃), there are three subsets of (x₂, y₂) for which correct classification is possible, as described in Table III and shown in Fig. 6(b)–(d), depending on which of the rays the two pairs of decision variables are located on. Thus, what we need to do is to add the probability density for correct classification for each of these subsets. Integrating over all the (x₂, y₂) pairs for a given (x₃, y₃) and then over all the (x₃, y₃) will give the percent correct.

Fig. 6.

For a particular (x₃, y₃), (a)–(d) illustrates the strategies for finding correctly classifiable triplet. (a) We divide all (x₂, y₂) that may form a correct classification with (x₃, y₃), i.e., y₂ > y₃, into three mutually exclusive subsets, Subset 1, Subset 2, and Subset 3, respectively. Here, (b)–(d) shows examples of the set of (x₁, y₁), indicated by the shaded region, which will result in correct classification for the particular (x₃, y₃) and a (x₂, y₂) from each subset, respectively.

TABLE III.

Definition of the Three Subsets

Subset 1	{x2 < x3, y2 > y3}
Subset 2	{x2 ≥ x3, y2 > y3, y2 - x2 ≥ y3 - x3}
Subset 3	{x2 ≥ x3, y2 > y3, y2 - x2 < y3 - x3}

C. Computing the Percent Correct

First consider p(c = 1|x₃, y₃) for a particular (x₃, y₃). Note that

$$\mathrm{p}(c=1\mid x_2,y_2,x_3,y_3)=0\text{for}{y}_2\le y_3.$$ (A18)

Thus, (A16) can also be written as

$$\begin{array}{cc}\hfill \mathrm{p}(c=1\mid x_3,y_3)=& {\iint }_{y_2>y_3}{\mathrm{f}}_2(x_2,y_2)\mathrm{p}\hfill \\ \hfill & \times (c=1\mid x_2,y_2,x_3,y_{3}l)d{x}_{2}d{y}_2\hfill \end{array}$$ (A19)

where the double integral is over the half plane where y₂ > y₃. As described above, there are three nonintersecting subsets of (x₂, y₂) that satisfy y₂ > y₃, defined by their relative locations; we label these Subset 1, Subset 2 and Subset 3, respectively, as shown in Table III and illustrated in Fig. 6(a).

Given the subsets defined in Table III, (A19) is expressed as

$$\begin{array}{cc}\hfill \mathrm{p}& (c=1\mid x_3,y_3)\hfill \\ \hfill & ={\iint }_{\text{Subset}1}{\mathrm{f}}_2(x_2,y_2)\mathrm{p}(c=1\mid x_2,y_2,x_3,y_3)d{x}_{2}d{y}_2\hfill \\ \hfill & +{\iint }_{\text{Subset}2}{\mathrm{f}}_2(x_2,y_2)\mathrm{p}(c=1\mid x_2,y_2,x_3,y_3)d{x}_{2}d{y}_2\hfill \\ \hfill & +{\iint }_{\text{Subset}3}{\mathrm{f}}_2(x_2,y_2)\mathrm{p}(c=1\mid x_2,y_2,x_3,y_3)d{x}_{2}d{y}_2.\hfill \end{array}$$ (A20)

Fig. 6 provides an intuitive illustration of the three subsets [Fig. 6(a)] and the corresponding strategies for identifying p(c = 1|x₂, y₂, x₃, y₃) for a (x₂, y₂) sampled from each subsets [Fig. 6(b)–(d)]. In particular, Fig. 6(b) shows the strategy for identifying p(c = 1|x₂, y₂, x₃, y₃) for a (x₂, y₂)sampled from Subset 1. We wish to find all (x₁, y₁) that may be correctly classified with this particular (x₂, y₂) and (x₃, y₃). To accomplish this, the decision structure should be moved toward x = -∞, y = +∞ to include as many (x₁, y₁)as possible. However, as shown in Fig. 6(b), the vertical line of the decision structure should not exceed x = x₃, and the horizontal line should not exceed y = y₂. Otherwise, incorrectly classified triplets will be counted. As a result, the shaded area in Fig. 6(b) includes all (x₁, y₁) that form correct classification triplet with the particular (x₂, y₂), and (x₃, y₃) shown in Fig. 6(b). For this particular (x₂, y₂) and (x₃, y₃), p(c = 1|x₂, y₂, x₃, y₃) is obtained by integrating f₁(x₁, y₁) in the shaded area. Fig. 6(c)–(d) illustrate the strategies for identifying for p(c = 1|x₂, y₂, (x₃, y₃) for (x₂, y₂) belonging to Subsets 2 and 3, respectively. It can be seen that the first, second and third term in (A20) are the probability densities for correct classification given a (x₃, y₃) for each of the three subsets of potentially-correctly-classifiable (x₂, y₂). In the following, we consider the computation of each of the three terms in (A20).

Let the first term be

$$\mathrm{A}(x_3,y_3)={\iint }_{\text{Subset}1}{\mathrm{f}}_2(x_2,y_2)\mathrm{p}(c=1\mid x_2,y_2,x_3,y_3)d{x}_{2}d{y}_2.$$ (A21)

Now note that the true class 1 fraction, T1F(x, y), when the decision structure is located at (x, y) is equal to p(c = 1|x₂, y₂, (x₃, y₃), i.e.,

$$\begin{array}{cc}\hfill & \text{if}(x_2,y_2)\in \text{Subset}1\hfill \\ \hfill & \mathrm{p}(c=1\mid x_2,y_2,x_3,y_3)=\mathrm{T}1\mathrm{F}(x_3,y_2).\hfill \end{array}$$ (A22)

Thus, referring to Fig. 6(b) for the computation of A(x₃, y₃), we see that A(x₃, y₃) can be expressed as

$$\mathrm{A}(x_3,y_3)={\int }_{y_3}^{+\infty }{\int }_{-\infty }^{x_3}{\mathrm{f}}_2(x_2,y_2)\mathrm{T}1\mathrm{F}(x_3,y_2)d{y}_{2}d{x}_2.$$ (A23)

Rearranging (A23) gives

$$\mathrm{A}(x_3,y_3)={\int }_{y_3}^{+\infty }\left[{\int }_{-\infty }^{x_3}{\mathrm{f}}_2(x_2,y_2)d{x}_2\right]\mathrm{T}1\mathrm{F}(x_3,y_2)d{y}_2.$$ (A24)

Similarly, the second term in (A20), is

$$\mathrm{B}(x_3,y_3)={\iint }_{\text{Subset}2}{\mathrm{f}}_2(x_2,y_2){\mathrm{p}}_{\mathrm{c}}(x_2,y_2,x_3,y_3)d{x}_{2}d{y}_2.$$ (A25)

Referring to Fig. 6(c) and again recognizing the true class 1 fraction, we see that we can rewrite this as

$$\begin{array}{cc}\hfill \mathrm{B}(x_3,y_3)={\int }_{y_3}^{\infty }& {\int }_{x_3}^{y_2-y_3+x_3}{\mathrm{f}}_2(x_2,y_2)\hfill \\ \hfill & \times \mathrm{T}1\mathrm{F}(x_3,y_2-x_2+x_3)d{x}_{2}d{y}_2.\hfill \end{array}$$ (A26)

We now apply Lemma 1 [given in (A2)] to change the bounds of the integrals in B(x₃, y₃), obtaining

$$\begin{array}{cc}\hfill \mathrm{B}(x_3,y_3)={\int }_{y_3}^{\infty }& \left[{\int }_{x_3}^{\infty }{\mathrm{f}}_2(x_2,y_2+x_2-x_3)d{x}_2\right]\hfill \\ \hfill & \times \mathrm{T}1\mathrm{F}(x_3,y_2)d{y}_2.\hfill \end{array}$$ (A27)

Thus, the sum of the first two terms of (A20) is

$$\begin{array}{cc}\hfill \mathrm{A}& (x_3,y_3)+\mathrm{B}(x_3,y_3)\hfill \\ \hfill & ={\int }_{y_3}^{+\infty }[{\int }_{-\infty }^{x_3}{\mathrm{f}}_2(x_2,y_2)d{x}_2\phantom{]}\hfill \\ \hfill & \phantom{[}+{\int }_{x_3}^{\infty }{\mathrm{f}}_2(x_2,x_2+y_2-x_3)d{x}_2]\mathrm{T}1\mathrm{F}(x_3,y_2)d{y}_2.\hfill \end{array}$$ (A28)

Comparing (A28) and (A10) reveals that the line integral inside the square brackets in (A28) is equivalent to the negative of the partial derivative of T2F with respect to y₂.

Similarly, referring to Fig. 6(c), the third term in (A20) can be expressed as

$$\begin{array}{cc}\hfill \mathrm{C}& (x_3,y_3)\hfill \\ \hfill & ={\iint }_{\text{Subset}3}{\mathrm{f}}_2(x_2,y_2){\mathrm{p}}_{\mathrm{c}}(x_2,y_2,x_3,y_3)d{x}_{2}d{y}_2\hfill \\ \hfill & ={\int }_{y_3}^{\infty }{\int }_{y_2-y_3+x_3}^{\infty }{\mathrm{f}}_2(x_2,y_2)\mathrm{T}1\mathrm{F}(y_3-y_2+x_2,y_3)d{x}_{2}d{y}_2.\hfill \end{array}$$ (A29)

Applying Lemma 2 [given in (A3)] to change the limits of integration, (A29) becomes

$$\begin{array}{cc}\hfill \mathrm{C}(x_3,y_3)={\int }_{x_3}^{\infty }& \left[{\int }_{y_3}^{+\infty }{\mathrm{f}}_2(y_2-y_3+x_2,y_2)d{y}_2\right]\hfill \\ \hfill & \times \mathrm{T}1\mathrm{F}(x_2,y_3)d{x}_2.\hfill \end{array}$$ (A30)

Inside the square brackets is the line integral of f₂(x, y) along the line of identity in Fig. 6(d), and function T1F is an area integration of f₁(x, y) over the shaded area. Comparing (A30) and (A7) reveals that the line integral inside the bracket in (A30) is the partial derivative of T2F with respect to x₂.

Substituting the partial derivatives of T2F given in (A7) and (A10), p(c = 1|x₃, y₃) in (A20) is given by

$$\begin{array}{cc}\hfill \mathrm{p}& (c=1\mid x_3,y_3)\hfill \\ \hfill & =-{\int }_{y_3}^{+\infty }\frac{\partial \mathrm{T}2\mathrm{F}(x_3,y_2)}{\partial y_2}\mathrm{T}1\mathrm{F}(x_3,y_2)d{y}_2\hfill \\ \hfill & +{\int }_{x_3}^{\infty }\frac{\partial \mathrm{T}2\mathrm{F}(x_2,y_2)}{\partial x_2}\mathrm{T}1\mathrm{F}(x_2,y_3)d{x}_2.\hfill \end{array}$$ (A31)

Substituting (A31) into (A14), we obtain an expression for PC, i.e.,

$$\begin{array}{cc}\hfill PC& =\hfill \\ \hfill & -{\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }{\mathrm{f}}_3(x_3,y_3)\hfill \\ \hfill & \times {\int }_{y_3}^{\infty }\frac{\partial \mathrm{T}2\mathrm{F}(x_3,y_2)}{\partial y_2}\mathrm{T}1\mathrm{F}(x_3,y_2)d{y}_{2}d{x}_{3}d{y}_3\hfill \\ \hfill & +{\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }{\mathrm{f}}_3(x_3,y_3)\hfill \\ \hfill & \times {\int }_{x_3}^{\infty }\frac{\partial \mathrm{T}2\mathrm{F}(x_2,y_2)}{\partial y_2}\mathrm{T}1\mathrm{F}(x_2,y_3)d{x}_{2}d{x}_{3}d{y}_3.\hfill \end{array}$$ (A32)

Equation (A32) shows that the percent correct is a sum of two terms. For notational simplicity, we replace all the x₃ with x, y₃ with y, x₂ with x′, and y₂ with y′. We first rewrite the first term as

$$-{\int }_{-\infty }^{\infty }\left[{\int }_{-\infty }^{\infty }{\mathrm{f}}_3(x,y){\int }_y^{\infty }\frac{\partial \mathrm{T}2\mathrm{F}(x,y^{\prime })}{\partial y^{\prime }}\mathrm{T}1\mathrm{F}(x,y^{\prime })d{y}^{\prime }dy\right]dx.$$ (A33)

Applying the Lemma 3 [given in (A4)] to the expression inside the square bracket in, (A33) becomes

$$\begin{array}{cc}\hfill -{\int }_{-\infty }^{\infty }& [{\int }_{-\infty }^{\infty }\frac{\partial \mathrm{T}2\mathrm{F}(x,y^{\prime })}{\partial y^{\prime }}\mathrm{T}1\mathrm{F}(x,y^{\prime })\phantom{]}\hfill \\ \hfill & \times \phantom{[}\left({\int }_{-\infty }^{y^{\prime }}{\mathrm{f}}_3(x,y)dy\right)d{y}^{\prime }]dx.\hfill \end{array}$$ (A34)

Comparing (A11) and (A34) reveals that the term inside the parentheses is the partial derivative of T3F with respect to x. Substituting (A11) into (A34), gives

$$-{\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }\mathrm{T}1\mathrm{F}(x,y^{\prime })\frac{\partial \mathrm{T}2\mathrm{F}(x,y^{\prime })}{\partial y^{\prime }}\frac{\partial \mathrm{T}3\mathrm{F}(x,y^{\prime })}{\partial x}d{y}^{\prime }dx.$$ (A35)

Applying Lemma 3 and the expression for the partial derivative of T3F in (A11) to the second term of (A32) in a similar fashion gives

$${\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }\mathrm{T}1\mathrm{F}(x^{\prime },y)\frac{\partial \mathrm{T}2\mathrm{F}(x^{\prime },y)}{\partial x^{\prime }}\frac{\partial \mathrm{T}3\mathrm{F}(x^{\prime },y)}{\partial y}d{x}^{\prime }dy.$$ (A36)

For notational simplicity, we rewrite (A35) and (A36) so that they are both integrals of x and y. Thus, (A32) becomes

$$PC={\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }\mathrm{T}1\mathrm{F}(x,y)\mid \begin{array}{cc}\hfill \frac{\partial \mathrm{T}2\mathrm{F}(x,y)}{\partial x}\hfill & \hfill \frac{\partial \mathrm{T}2\mathrm{F}(x,y)}{\partial y}\hfill \\ \hfill \frac{\partial \mathrm{T}3\mathrm{F}(x,y)}{\partial x}\hfill & \hfill \frac{\partial \mathrm{T}3\mathrm{F}(x,y)}{\partial y}\hfill \end{array}\mid dydx.$$ (A37)

Inspection of (A37) reveals that the determinant is the Jacobian for the change of variables from (T2F, T3F) to (x, y). Noting that these fractions become 0 and 1, respectively, as the rating values move from -∞ to ∞, we thus have

$$PC={\int }_0^1{\int }_0^{1}T1FdT3FdT2F$$ (A38)

where T1F, T2F, and T3F are defined in (A1). Equation (A38) is the expression for VUS, and we thus have that

$$PC=\mathrm{VUS}.$$ (A39)