Identifying Small Pulsatile Signals within Noisy Data: A Fluorescence Application

Abstract

One of the most challenging scientific data analysis quandaries is the identification of small intermittent irregularly spaced pulsatile signals in the presence of large amounts of heteroscedastic experimental measurement uncertainties. We present an application of the use of AutoDecon to a typical fluorescence and/or spectroscopic data sampling paradigm, which is to detect a single fluorophore in the presence of high background emission. Our calculations demonstrate that single events can be reliably detected by AutoDecon with a signal-to-noise ratio of 3/20. AutoDecon was originally developed for the analysis of pulsatile hormone-concentration time-series data measured in human serum. However, AutoDecon has applications within many other scientific fields, such as fluorescence measurements where the goal is to count single analyte molecules in clinical samples.

1. Introduction

There are numerous cases in the scientific literature where the ability to identify small pulsatile signals of a magnitude comparable to the concomitant measurement errors is critical. One typical example of this would be detection of a low concentration of fluorophores in a flow cell or detection of a small number of fluorophores on a surface. The fluorescence might also originate from monitoring a single fluorescence molecule within the sample. The flow cell might be attached to the output of a chromatography column or any of a near infinity number of other types of experimental apparatus. Additionally, a wide variety of bioaffinity surfaces are used in genomic and proteomic analysis.

The basic data processing concepts presented here do not depend upon the specifics of the experiment other than the size and shape of the pulsatile signal or the properties of the concomitant measurement errors. Consequently, the current discussion will emphasize irregularly spaced approximately Gaussian-shaped pulsatile events of variable size and the typical Poisson distributed measurement uncertainties that originate from photo counting experiments. One example of this approach to signal analysis could be the counting of single analyte molecules in biological samples which may display high background emission. Single molecule counting (SMC) assays would represent the ultimate in high sensitivity detection. However, the basic mathematical approach presented here is not specific to this application nor to Gaussian events or Poisson noise. This work presents a fluorescence monitoring application of a data analysis algorithm that was originally developed for identifying pulsatile events in the hormone-concentration time-series that are observed in human serum ( Johnson et al., 2009).

2. Methods

The general approach to be presented here is to generate a large number of simulated data sets with specific signal and measurement error characteristics. The advantage of simulated data is that the locations and sizes of the simulated pulsatile events within the data series are known a priori. The ability of the AutoDecon algorithm to identify small, irregularly timed events within noisy experimental data can then be evaluated by how well it can identify the events within these simulated data time-series. One example could be the photon counts from a single fluorophore flowing past a detector.

The specific event detection criteria utilized here are the: True-Positives, the fraction of identified events that correctly identified; False-Positives, the fraction of identified events that it incorrectly identified; False-Negatives, the fraction of simulated events that were not identified; and Sensitivity, the fraction of simulated events that were correctly identified. For an event to be correctly identified it must occur within a specific time window of a corresponding simulated event in the specific simulated data sets.

2.1. The simulated data

The data is simulated to mimic typical data that could be obtained from many different types of experiments. Specifically, each simulated data set consists of 1000 data points equally spaced in time units with three additive parts: (1) The background number of photons, typically 20 per unit time; (2) Several sparsely occurring Gaussian-shaped events of various heights and widths; and (3) Poisson distributed pseudo random measurement errors based upon the total number of counts within each unit of time. One thousand data sets were simulated for each example presented in this work. The results are independent of the specific units of time.

The number of Gaussian-shaped events within each data set was randomly selected between 1 and 5 with an even distribution. The temporal locations of these events were also selected based upon an even distribution with two caveats: no events were assigned within the first and last hundred data points, and the events could not occur within two standard deviations of the Gaussians. The first of these was intended to exclude the end effects of partial events at either end of the simulated data set. The second was to enforce the restriction that multiple events cannot be nearly simultaneous in time and thus indistinguishable.

The Poisson distributed measurement errors, that is, the experimental noise, were generated from the total number of background and event counts by the POIDEV procedure (Press et al., 1986).

2.1.1. AutoDecon procedure

AutoDecon was originally developed for the analysis of the pulsatile hormone-concentration secretory events that are observed in serum. This deconvolution procedure functions by developing a mathematical model for the time course of the pulsatile event and then fitting this mathematical model to the experimentally observed time-series data with a weighted nonlinear least-squares algorithm. It implements a rigorous statistical test for the existence of pulsatile events. The algorithm automatically inserts presumed pulsatile events, then tests the significance of presumed events, and removes any events that are found to be nonsignificant. This automatic algorithm combines three modules: a parameter fitting module, an insertion module that automatically adds presumed events, and a triage module which automatically removes events which are deemed to be statistically nonsignificant. No user intervention is required subsequent to the initialization of the algorithm.

It is interesting to note that the mathematical form of hormone-concentration time-series data is the same mathematical form as expected in time-domain fluorescence lifetime measurements. Specifically, this mathematical model (Johnson and Veldhuis, 1995; Veldhuis et al., 1987) is:

$$C(t)=\underset{-\infty }{\overset{t}{\int }}S(\tau )E(t-\tau )\text{d}\tau$$ (13.1)

where C(t) is the hormone-concentration as a function of time t, S(τ) is the secretion into the blood as a function of time and is typically modeled as the sum of Gaussian-shaped events, and E(t−τ) is the one- or two-exponential elimination of the hormone from the serum as a function of time. For the time-domain fluorescence lifetime experimental system, the S(t) function corresponds to the lamp function (i.e., the instrument response function) and the E(t−τ) corresponds to the fluorescence decay function.

For the current study it was assumed that the elimination half-time was short compared with the width of the Gaussian-shaped events to be detected. In this limit, the shape of the events detected by AutoDecon will approach a Gaussian profile. This allowed the existing algorithm and software to detect the simulated Gaussian-shaped events without modification.

2.1.2. AutoDecon fitting module

The fitting module performs weighted nonlinear least-squares parameter estimations by the Nelder–Mead Simplex algorithm (Nelder and Mead, 1965; Straume et al., 1991). In the present example, it fits Eq. (1) to the experimental data by adjusting the parameters of the Gaussian-shaped events function such that the parameters have the highest probability of being correct. The module is based upon the Amoeba routine (Press et al., 1986) which was modified such that convergence is assumed when both the variance-of-fit and the individual parameter values do not change by more than 2 × 10⁻⁵ or when 15,000 iterations have occurred. This is essentially the original Deconv algorithm ( Johnson and Veldhuis, 1995; Veldhuis et al., 1987) with the exception that the Nelder–Mead Simplex parameter estimation algorithm (Nelder and Mead, 1965; Straume et al., 1991) is used instead of the damped Gauss–Newton algorithm which was previously utilized as the Nelder–Mead algorithm simplifies the software since it does not require derivatives.

The AutoDecon fitting module constrains all of the events to have a positive amplitude by fitting to the logarithm of the amplitude instead of the amplitude. The fitting module also constrains all of the events to have the same standard deviation.

2.1.3. AutoDecon insertion module

The insertion module inserts a presumed event at the location of the maximum of the Probable Position Index (PPI).

$$\text{PPI}(t)=\{\begin{array}{cc}-\frac{\partial [\text{Variance}-\text{of}-\text{fit}]}{\partial H_z}& \text{if}\frac{\partial [\text{Variance}-\text{of}-\text{fit}]}{\partial H_z}<0\\ 0& \text{if}\frac{\partial [\text{Variance}-\text{of}-\text{fit}]}{\partial H_z}\ge 0\end{array}$$ (13.2)

The parameter H_z is the amplitude of a presumed Gaussian-shaped event at time z. The index function PPI(t) will have a maximum at the data point position in time where the insertion of an event will result in the largest negative derivative in the variance-of-fit versus event size. It is important to note that the partial derivatives of the variance-of-fit with respect to an event size can be evaluated without any additional weighted nonlinear least-squares parameter estimations or without even knowing the size of the presumed event, H_z. Using the definition of the variance-of-fit given in Eq. (3), the partial derivative with respect to the addition of an event at time z is shown in Eq. (4) where the summation is over all data points,

$$[\text{Variance}-\text{of}-\text{fit}]=\sum _i{\left(\frac{Y_i-C(t_i)}{w_i}\right)}^2=\sum _i{R}_i^2$$ (13.3)

$$\begin{array}{l}\frac{\partial [\text{Variance}-\text{of}-\text{fit}]}{\partial H_z}=\sum _i\left[\frac{2}{w_i^2}\left(Y_i-C(t)\right)\frac{\partial C(t)}{\partial H_z}\right]\frac{\partial C(t)}{\partial H_z}\\ =\left[exp\left(-\frac{1}{2}{\left(\frac{t-z}{\text{Secretion}\text{SD}}\right)}^2\right)\right]E(t)\end{array}$$ (13.4)

where w_i corresponds to the weighting factor for the ith data point, and R_i corresponds to the ith residual. The inclusion of these weighting factors is the statistically valid method to compensate for the heteroscedastic properties of the experimental data. For the present case it was assumed that these weighting factors were equal to the square-root of the number of photon counts at any specific time.

2.1.4. AutoDecon triage module

The triage module performs a statistical test to ascertain whether or not a presumed secretion event should be removed. This test requires two weighted nonlinear least-squares parameter estimations, one with the presumed event present and one with the presumed event removed. The ratio of the variance-of-fit resulting from these two parameter estimations is related to the probability that the presumed event does not exist, P, by an F-statistic, as in Eq. (5). For most of the present examples a probability level of 0.01 was used.

$$\frac{\text{Variance}-\text{of}-{\text{fit}}_{\text{removed}}}{\text{Variance}-\text{of}-{\text{fit}}_{\text{present}}}=1+\frac{2}{\mathit{ndf}}F-\text{statistic}(2,\mathit{ndf},1-P)$$ (13.5)

This is the F-test for an additional term (Bevington, 1969) where the additional term is the presumed event. The 2’s in Eq. (5) are included since each additional event increases the number of parameters being estimated by 2, specifically the location and the amplitude of the event. The number of degrees of freedom, ndf, is the number of data points minus the total number of parameters being estimated when the event is present. Each cycle of the triage module performs this statistical test for every event in an order determined by size, from smallest to largest. If an event is found to be not statistically significant it is removed and the triage module is restarted from the beginning (i.e., a new cycle starts). Thus, the triage module continues until all nonsignificant events have been removed. Each cycle of the triage module performs m + 1 weighted nonlinear least-squares parameter estimations where m is the current number of events for the current cycle: one where all of the events are present and one where each of the events has been removed and individually tested.

2.1.5. AutoDecon combined modules

The AutoDecon algorithm iteratively adds presumed events, tests the significance of all events, and removes nonsignificant events. The procedure is repeated until no additional events are added. The specific details of how this is accomplished with the insertion, fitting, and triage modules are outlined here.

For the present study, AutoDecon was initialized with the background set equal to zero, the elimination half-life set to a small value (specifically three time units), the standard deviation of the events set to the specific simulated value, and zero events. It is possible, but neither required nor performed in this study, that initial presumed event locations and sizes be included in the initialization. Initializing the program with event position and amplitude estimates might produce faster convergence and thus decrease the amount of computer time required.

The next step in the initialization of the AutoDecon algorithm is for the fitting module to estimate only the background. The fitting module then estimates all of the model parameters except for the elimination half-life and the standard deviation of the secretion events. If any secretion events have been included in the initialization, the second fit will also refine the locations and sizes of these secretion events. Next, the triage module is utilized to remove any nonsignificant events. At this point the parameter estimations that are performed within the triage module will estimate all of the current model parameters except for the elimination half-life and the standard deviation of the secretion events.

The AutoDecon algorithm next proceeds with Phase 1 by using the insertion module to add a presumed event. This is followed by the triage module to remove any nonsignificant events. Again, the parameter estimations performed within the triage module during Phase 1 will estimate all of the current model parameters with the exception of the elimination half-life and the standard deviation of the secretion events. If during this phase the triage module does not remove any secretion events, Phase 1 is repeated to add an additional presumed event. Phase 1 is repeated until no additional events are added in the insertion followed by triage cycle.

For the current example, Phase 2 repeats the triage module with the fitting module estimating all of the current model parameters but this time including the standard deviation of the secretion events and not the elimination half-life.

Phase 3 will repeat Phase 1 (i.e., insertion and triage) utilizing the parameter estimations that are performed by the fitting module within the triage module estimating all of the current model parameters again including the standard deviation of the secretion events but not the elimination half-life. For the present example, the elimination half-life is never estimated. Phase 3 is repeated until no additional events have been added in the insertion followed by triage cycle.

2.1.6. Concordant secretion events

Determining the operating characteristics of the algorithms requires a comparison of the apparent event positions from the AutoDecon analysis of a simulated time-series with the actual known event positions upon which the simulations were based. This process must consider whether the concordance of the peak positions is statistically significant or whether it is a consequence of a simply random position of the apparent and simulated events. Specifically, the question could be posed: given two time-series with n and m distinct events, what is the probability that j coincidences (i.e., concordances) will occur based upon a random positioning of the distinct events within each of the time-series? The resulting probabilities are dependent upon the size of the specific time window employed for the definition of coincidence. This question can easily be resolved utilizing a Monte-Carlo approach. One hundred thousand pairs of time-series are generated with the n and m distinct randomly timed events, respectively. The distribution of the expected number of concordances can then be evaluated by scanning these pairs of random event sequences for coincident peaks where coincidence is defined by any desired time interval.

Obviously, as the coincidence interval increases so will the expected number of coincident events. The expected number of coincident events will also increase with the numbers of distinct events, n and m. Thus, the coincidence interval should be kept small.

3. Results

The procedure to demonstrate the functionality of AutoDecon for the detection of small events within noisy time-series involves simulating and then analyzing one thousand time-series which have between one and five events temporally assigned at random between data points 100 and 900. These are analyzed via AutoDecon and the results compared with the known answers upon which the simulations were based. If an observed event is within a concordance window of 20 data points from a simulated event then it is considered a true-positive, if an observed event is not within 20 data points of an actual simulated event it is a false-positive, etc. However, an initial question is how many true-positive events are expected based simply upon the random locations of the events. For a specific data set containing one simulated event there is a 0.05 probability that a coincidence will be randomly coincident to within ±20 data points. For each specific data set with five simulated events randomly located within 800 data points there is a 0.71 probability that one or more coincident events will be randomly coincident to within ±20 data points, a 0.26 probability of two or more coincident events, a 0.04 probability of three or more coincident events, a 0.0024 probability of four or more coincident events, and less than a 0.0001 probability that five or more will be randomly located. However, when combining 1000 independent data sets these probabilities are raised to the 1000th power. Thus, the probability of observing five or more randomly coincident events in 1000 data sets is less that 10⁻⁴⁰⁰⁰.

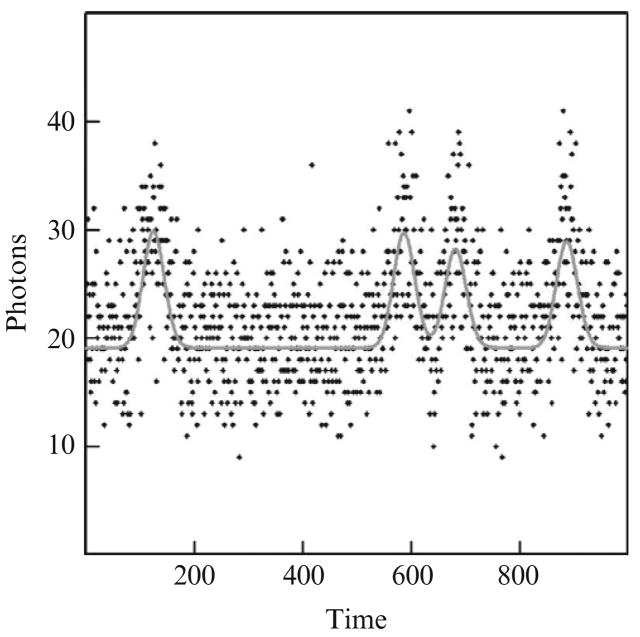
Figure 13.1 presents the analysis of the first of a 1000 data sets that were simulated with between 1 and 5 noncoincident events between data points 100 and 900 of a total of 1000 data points in the time sets. The simulated number of photons at each data point was a Poisson distributed random deviate with a mean based upon Gaussian-shaped randomly occurring noncoincident events with a standard deviation (i.e., half-width/2.354) of 20 data points and a height of 10 photons and a background, that is, dark current, of 20 photons. The probability of randomly observing these four events correctly to within ±20 data points is less than 0.0001.

Figure 13.1.

A simulated case where four simulated events were correctly identified. Background is 20 photons, simulated Gaussian event standard deviations are 20 time units and the event heights are 10 photons. The points are the simulated noisy photon counts and the curve represents the best estimated values.

Table 13.1 presents the operating characteristics of the AutoDecon algorithm when applied to 1000 time-series analogous to Fig. 13.1. The mean, median, and interquartile distances are given because the operating characteristic distributions do not always follow Gaussian distributions. For this simulation the sensitivity is ~98% for finding the event locations to within ±10 time units when the half-width of the simulated events is ~50 time units (~2.354 SD). Obviously this simulation, where the events heights are 50% of the dark current and event standard deviation is equal to the dark current, represents a comparatively easy case. For an analogous simulation (not shown) where the standard deviation of the event is decreased to half of the dark current sensitivity increases to 99.1 ± 0.2% and the false-positive % increases slightly to 4.0 ± 0.04%.

Table 13.1.

Operating characteristics of AutoDecon for 1000 data sets simulated as in Fig. 13.1

	Median	Mean ± SEM	Interquartile range
±20 Data point concordance
True-positive%	100.0	98.6 ± 0.2	0.0
False-positive%	0.0	1.4 ± 0.2	0.0
False-negative%	0.0	0.1 ± 0.1	0.0
Sensitivity%	100.0	99.9 ± 0.1	0.0
±15 Data point concordance
True-positive%	100.0	98.3 ± 0.2	0.0
False-positive%	0.0	1.7 ± 0.2	0.0
False-negative%	0.0	0.4 ± 0.1	0.0
Sensitivity%	100.0	99.6 ± 0.1	0.0
±10 Data point concordance
True-positive%	100.0	96.8 ± 0.4	0.0
False-positive%	0.0	3.2 ± 0.4	0.0
False-negative%	0.0	2.0 ± 0.3	0.0
Sensitivity%	100.0	98.0 ± 0.4	0.0

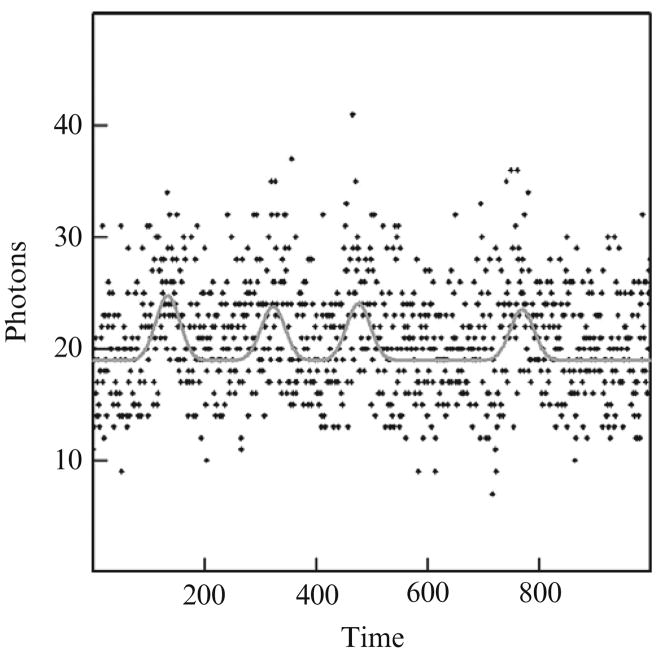
Figure 13.2 and Table 13.2 present a somewhat more difficult case. This simulation is identical to the previous simulation except that the simulated event height is only 5 photons. Here the events are half the size of the previous simulations. For this simulation the AutoDecon algorithm was still able to accurately find the event locations to within ±15 time units.

Figure 13.2.

A second simulated case where four simulated events were correctly identified. Background is 20 photons, simulated Gaussian event standard deviations are 20 time units and the event heights are 5 photons.The points are the simulated noisy photon counts and the curve depicts the best estimated values.

Table 13.2.

Operating characteristics of AutoDecon for 1000 data sets simulated as in Fig. 13.2

	Median	Mean ± SEM	Interquartile range
±20 Data point concordance
True-positive%	100.0	97.1 ± 0.3	0.0
False-positive%	0.0	2.9 ± 0.3	0.0
False-negative%	0.0	2.6 ± 0.3	0.0
Sensitivity%	100.0	97.4 ± 0.3	0.0
±15 Data point concordance
True-positive%	100.0	94.7 ± 0.5	0.0
False-positive%	0.0	5.3 ± 0.5	0.0
False-negative%	0.0	4.8 ± 0.5	0.0
Sensitivity%	100.0	95.2 ± 0.5	0.0
±10 Data point concordance
True-positive%	100.0	84.7 ± 0.8	25.0
False-positive%	0.0	15.3 ± 0.8	25.0
False-negative%	0.0	14.8 ± 0.8	25.0
Sensitivity%	100.0	85.2 ± 0.8	25.0

It is instructive to examine the median values found in Tables 13.1 and 13.2. In every case the medians are either 100% or 0%. This indicates that the AutoDecon algorithm correctly located all of the simulated events to within ±10 time units for more than half of the simulated data sets. Furthermore, for the instances where the interquartile distance is also 0.0 the AutoDecon algorithm correctly located all of the simulated events in more than 75% of the simulated data sets.

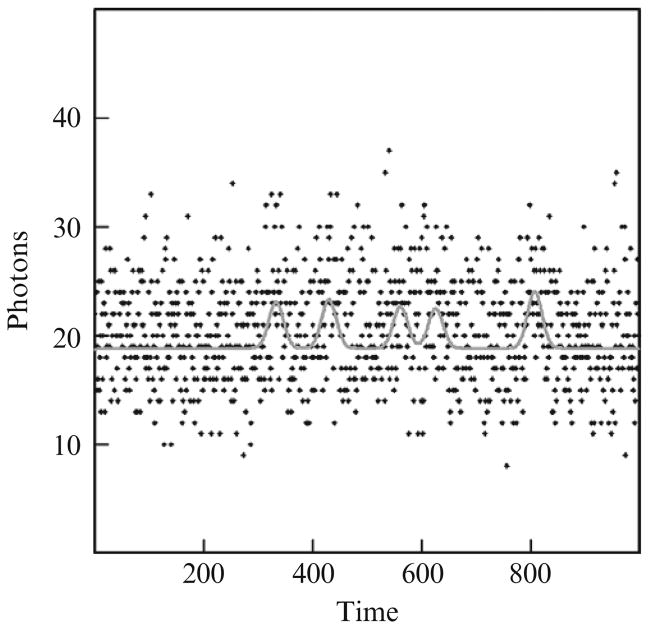
Figure 13.3 and Table 13.3 takes the simulations presented in Figs. 13.1 and 13.2 and Tables 13.1 and 13.2 to the next logical step where the standard deviation is 20 data points and a height of 3 photons and a background of 20 photons. In Fig. 13.3, five events were correctly identified within ±20 data points. When all 1000 simulated time-series are examined the false-positive% for event identification to within ±20 data points is 6.8 ± 0.6% and the corresponding false-negative% is 28.5 ± 1.0%. This is clearly a very difficult case where the Autodecon algorithm performs surprisingly well.

Figure 13.3.

A third simulated case where five simulated events were correctly identified. Background is 20 photons, simulated Gaussian event standard deviations are 20 time units and the event heights are 3 photons.The points are the simulated noisy photon counts and the curve depicts the best estimated values.

Table 13.3.

Operating characteristics of AutoDecon for 1000 data sets simulated as in Fig. 13.3

	Median	Mean ± SEM	Interquartile range
±20 Data point concordance
True-positive%	100.0	89.0 ± 0.8	0.0
False-positive%	0.0	6.8 ± 0.6	0.0
False-negative%	20.0	28.5 ± 1.0	50.0
Sensitivity%	80.0	71.5 ± 1.0	50.0
±15 Data point concordance
True-positive%	100.0	81.1 ± 1.0	33.3
False-positive%	0.0	14.7 ± 0.9	25.0
False-negative%	33.3	34.2 ± 1.0	60.0
Sensitivity%	66.7	65.8 ± 1.0	60.0
±10 Data point concordance
True-positive%	66.7	65.5 ± 1.2	50.0
False-positive%	20.0	30.3 ± 1.1	50.0
False-negative%	50.0	46.1 ± 1.1	75.0
Sensitivity%	50.0	53.9 ± 1.1	75.0

In Table 13.1, the false-positive percentages are substantially higher than the corresponding false-negative percentages. They are of a comparable size in Table 13.2, while in Table 13.3 the false-positive percentages are substantially lower than the corresponding false-negative percentages. Clearly, these percentages are both expected and observed to be a function of the relative height of the events. But the false-negative percentages are more sensitive to the relative event heights than are the false-positive percentages. These percentages are also a function of the probability level within the triage module, see Eq. (5). Table 13.4 presents the results from the analysis of the same simulated data sets that were used for Table 13.3 where the only difference is that a probability level of 0.05 was used in Eq. (5). With the probability level of 0.05 the false-positive and false-negative percentages are approximately equal for simulated event sizes of three photons.

Table 13.4.

Operating characteristics of AutoDecon for 1000 data sets simulated as in Fig. 13.3

	Median	Mean ± SEM	Interquartile range
±20 Data point concordance
True-positive%	100.0	83.6 ± 0.8	33.3
False-positive%	0.0	15.6 ± 0.7	33.3
False-negative%	0.0	13.5 ± 0.7	25.0
Sensitivity%	100.0	86.5 ± 0.7	25.0
±15 Data point concordance
True-positive%	83.3	76.8 ± 0.9	40.0
False-positive%	16.7	22.4 ± 0.8	40.0
False-negative%	0.0	20.1 ± 0.9	33.3
Sensitivity%	100.0	79.9 ± 0.9	33.3
±10 Data point concordance
True-positive%	66.7	61.6 ± 1.0	56.3
False-positive%	33.3	37.6 ± 1.0	50.0
False-negative%	33.3	35.3 ± 1.1	60.0
Sensitivity%	66.7	64.7 ± 1.1	56.3

The probability level 0.05 was used in Eq. (5) for this table.

4. Discussion

The Autodecon algorithm functions by: (1) creating a mathematical model for the shape of an event, (2) using the derivative of the variance-of-fit with respect to the possible existence of events, predicts where the next presumptive event should be added, (3) performing a least-squares parameter estimation to determine the exact event locations and sizes, and (4) using a rigorous statistical test to determine if the events are actually statistically significant. Steps 2–4 are repeated until no additional events are added.

AutoDecon is a totally automated algorithm. For the current examples the algorithm was initialized with a probability level of 0.01 and an approximate standard deviation for the Gaussian-shaped events of 20 time units. The algorithm then automatically determined the number of events, their locations, and sizes.

The algorithm does not assume that the events occur at regular intervals. However, if they did occur at regular intervals the algorithm could be modified to include this assumption and would then perform even better.

Similarly the algorithm does not assume that the secretion events have the same height. If the events had a constant height this could also be included in a modified algorithm to obtain even better performance.

The Autodecon algorithm is also somewhat independent of the form of the noise distribution. In the present example, the simulated data contained Poisson distributed simulated measurement uncertainties while the current Autodecon software assumes that the measurement error distribution follows Gaussian distribution.

The Autodecon algorithm functions by performing a series of weighted nonlinear regressions. The weighting factors employed here are proportional to the square-root of the observed number of photons at each simulated data point. This is consistent with the procedure commonly employed for experimental photon counting protocols. A consequence of this is that the statistical weight assigned to a data point with n too many photons is less than the statistical weight of a data point with n too few photons. This introduces an asymmetrical bias into the weighting of the data points. The major consequence of this is that the baseline levels in Figs. 13.1–13.3 are ~19 photons instead of the simulated value of 20 photons.

The relative values of the false-positive and false-negative percentages are adjustable within the Autodecon algorithm. Tables 13.3 and 13.4 present an example of how the probability level within the algorithm’s triage module can be manipulated so that the false-positive and false-negative percentages are approximately equal. The optimal value for the probability level is a complex function of the relative sizes of the events and the baseline values as well as many other variables. Thus, the optimal probability level cannot be predicted a priori but it can be determined by computer simulations which include the specific experimental details.

The Concordance and Autodecon algorithms are part of our hormone pulsatility analysis suite. They can be downloaded from www.mljohnson.pharm.virginia.edu/pulse_xp/.