Negative autoregulation linearizes the dose–response and suppresses the heterogeneity of gene expression

Abstract

Although several recent studies have focused on gene autoregulation, the effects of negative feedback (NF) on gene expression are not fully understood. Our purpose here was to determine how the strength of NF regulation affects the characteristics of gene expression in yeast cells harboring chromosomally integrated transcriptional cascades that consist of the yEGFP reporter controlled by (i) the constitutively expressed tetracycline repressor TetR or (ii) TetR repressing its own expression. Reporter gene expression in the cascade without feedback showed a steep (sigmoidal) dose–response and a wide, nearly bimodal yEGFP distribution, giving rise to a noise peak at intermediate levels of induction. We developed computational models that reproduced the steep dose–response and the noise peak and predicted that negative autoregulation changes reporter expression from bimodal to unimodal and transforms the dose–response from sigmoidal to linear. Prompted by these predictions, we constructed a “linearizer” circuit by adding TetR autoregulation to our original cascade and observed a massive (7-fold) reduction of noise at intermediate induction and linearization of dose–response before saturation. A simple mathematical argument explained these findings and indicated that linearization is highly robust to parameter variations. These findings have important implications for gene expression control in eukaryotic cells, including the design of synthetic expression systems.

Genetically identical cells may be very different in their protein content (1–7) because of stochastic biochemical events underlying gene expression (8, 9), random partitioning of molecules during cell division (10), or different cellular responses to environmental factors (11). This heterogeneity is commonly known as “gene expression noise,” and can be either disadvantageous and subject to reduction (12) or beneficial and evolutionarily maintained (13, 14) depending on the biological role of the affected pathways.

Because essentially all genes are parts of transcriptional networks (15), the characteristics of gene expression depend on regulatory motifs present in network topology (16). For example, negative autoregulation is abundant in gene regulatory networks (17) and possibly subject to evolutionary selection (16, 18) because of its ability to reduce gene expression noise (19–21) to speed up gene response times (22), to induce oscillatory gene expression (23, 24), or to reduce the metabolic cost of protein production by the minimization of mRNA usage (18). Despite these findings, the effects of negative feedback (NF) on gene expression are not fully understood. For example, it was suggested that NF alters the shape of the dose–response curve in transcriptional cascades (22, 25, 26), but this effect has never been explored in detail. Such knowledge is vital for the rational design and characterization of increasingly complex transcriptional networks via bottom-up approaches in synthetic biology (27–30).

Our goal was to determine how NF regulation affects the characteristics of gene expression in synthetic transcriptional cascades. We first constructed a TetR-based transcriptional cascade with no feedback in Saccharomyces cerevisiae and measured the noise and mean of gene expression at various inducer concentrations. Based on the experimentally measured dose–response, we estimated the biochemical reaction rates and developed a computational model that reproduced the experimentally observed sigmoidal dose–response and noise peak at intermediate levels of induction. The computational model predicted that introducing negative autoregulation into the cascade reduces the heterogeneity of reporter gene expression and linearizes the dose–response before saturation. We verified these predictions by gene expression measurements in a “linearizer” gene circuit built by introducing TetR autoregulation into the original transcriptional cascade. Additional gene constructs using different TetR-repressible promoters indicate that this gene circuit is highly robust in producing a linear dose–response and eliminating gene expression heterogeneity at a wide range of inducer concentrations.

Results

Transcriptional Cascade Without Autoregulation.

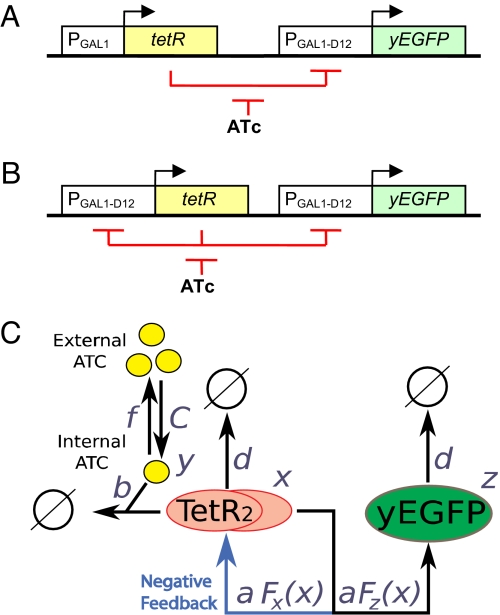
We built a negative-regulatory (NR) gene circuit consisting of chromosomally integrated, separate regulator and reporter parts (Fig. 1A). The regulator part of this cascade was the TetR repressor (31) expressed constitutively from the native yeast GAL1 promoter (P_GAL1) in the presence of galactose. The DNA-binding activity of the TetR repressor can be controlled through the extracellular concentration of anhydrotetracycline (ATc) that associates with TetR and blocks its binding to target promoters, thereby enabling the expression of target genes. The reporter part of the NR cascade consisted of the yEGFP gene under the control of the P_GAL1-D12 promoter (9, 14, 32), which can be repressed by TetR binding to 2 tetO₂ sites downstream from the TATA box.

Fig. 1.

Diagram of the gene constructs and the corresponding simplified model scheme. (A) NR cascade, consisting of the yEGFP reporter and the constitutively expressed tetR repressor. (B) Cascade with NF, consisting of the yEGFP reporter and the tetR repressor that also regulates its own expression. (C) Simplified model of dose–response in the constructs from A and B. ATc (y) enters the cell at an influx determined by external ATc concentration (C), and leaves through outflux and binding to free TetR molecules (x). Free TetR is eliminated by binding to ATc and spontaneous degradation/dilution. TetR affects its own and yEGFP (z) production via a repressory Hill function. yEGFP is eliminated through spontaneous degradation/dilution.

We measured reporter (yEGFP) expression means at increasing ATc concentrations across yeast cell populations using flow cytometry and observed a sigmoidal (nonlinear) dose–response, with a steep increase at intermediate induction levels (Fig. 2A). The gene expression noise (measured as the coefficient of variation; standard deviation divided by the mean) also peaked at intermediate levels of ATc (50–90 ng/mL), whereas it diminished at low and high levels of ATc (Fig. 2C), as observed previously (9, 32). Analysis of population-distribution histograms revealed that at intermediate ATc concentrations, cells switched to the high expression state nonuniformly, giving rise to highly heterogeneous (bimodal) yEGFP expression and high levels of noise (Fig. 2D). This represents a potential problem for synthetic gene expression systems that require tight and graded control over a wide range of expression levels (33).

Fig. 2.

Linearization and noise reduction due to NF. (A) Experimental and simulated dose–response curves for the constructs in Fig. 1. For theoretical curves, the parameters are a = 50 nM h⁻¹, b = 3.6 nM⁻¹ h⁻¹, C = 0.6 [ATc] h⁻¹, d = 0.12 h⁻¹, f = 1.2 h⁻¹, θ = 0.44, n = 4, F_x ≡ 1.5 for NR strains, and F_x = F_z for NF strains (B) Experimental, background-corrected dose–response for the NF cascade and the corresponding linear fit plotted on log–log scale, showing that linearity holds from very small to saturating ATc concentrations (0.1–60 ng/mL). Error bars corresponding to standard deviations (from 3 replicates) are smaller than the symbols. (C) Experimentally measured and simulated gene expression noise for the NR and NF gene circuits. (D and E) Experimental fluorescence histograms for the NR (D) and the NF (E) strains at increasing ATc concentrations (0–500 ng/mL).

To better understand the experimentally observed behavior of the NR cascade, we developed a computational model based on a biochemical reaction scheme that incorporates both regulator and repressor synthesis [see supporting information (SI) Appendix and Figs. S1–S8 for a full description of the model, gene constructs, and controls, and experimental data]. Using this model, we ran stochastic simulations to estimate the gene expression noise for various ATc concentrations. The simulated gene expression mean and noise agreed well with the experimental data (Fig. 2 A and C). Our simulations suggest that the noise peak at intermediate ATc concentrations is due to high repressor noise, further amplified by the sharp dose–response of the downstream promoter (5) and coupled with slow promoter dynamics (14, 34). In addition, basal expression lowers the noise (5) as the promoter approaches the fully repressed state at ATc = 0. The model also suggests that ATc binds and inactivates free intracellular TetR molecules before interacting with DNA-bound TetR and relieving repression. This gives rise to the sharp increase in dose–response near the lowest ATc concentration that completely depletes free intracellular TetR (Fig. 2A).

Transcriptional Cascade with Negative Autoregulation (Linearizer).

The computational model allowed us to predict the effect of incorporating feedback into the regulatory part of the cascade. Keeping the reaction rates unchanged, we incorporated regulator self-repression into our model (section 5 in SI Appendix), such that the reporter and the repressor were transcribed from identical promoters. Based on published experimental data (32), the only rate change compared with the no-feedback cascade was a 30% decrease in regulator transcription rate at full induction. Stochastic simulations of this modified system predicted a dose–response curve that was linear up to 90% saturation and lower noise levels at all inducer concentrations (Fig. 2 A–C).

To verify these computational predictions experimentally, we constructed the linearizer NF cascade by replacing the upstream P_GAL1 promoter with the P_GAL1-D12 promoter, thereby introducing negative autoregulation into the cascade (Fig. 1B). Measuring yEGFP expression, we indeed observed a linear dose–response (R² = 0.99, L1-norm = 6.5 × 10⁻², see section 6 in SI Appendix and Figs. S6, S7 for the definition of these measures and comparison with the NR strain) over a wide range of ATc concentrations, from no induction (0 ng/mL) up to 90% saturation (≈60 ng/mL), confirming our computational predictions (Fig. 2A). Flow cytometry over additional low ATc concentrations (starting at 0.1 ng/mL) ruled out nonlinearity in the beginning of the dose–response curve and the possibility that linearity could arise from the leftward shift of a Hill curve (Fig. 2B and section 6 in SI Appendix and Fig. S8). Furthermore, as predicted computationally, the distribution of yEGFP expression in the NF strain was unimodal and narrow, maintaining a low level of noise throughout all inducer concentrations (Fig. 2 C and E). Compared with earlier findings of noise reduction by NF (20), the effect here is much more pronounced (up to 7-fold at intermediate inducer concentrations).

To verify that reporter gene expression acts as a readout (mimics the dose–response of the upstream regulator, TetR), we also built a single-gene NF system, placing the tetR::yEGFP fusion construct under the control of P_GAL1-D12 promoter. As expected, the dose–response of the single-gene autoregulatory circuit was also linear, and its noise level was comparable with the NF cascade after rescaling (section 2 in SI Appendix).

Simple Mathematical Model Explains Linearization and Noise Reduction.

After reducing the number of biochemical reactions used for stochastic simulations and assuming mass action kinetics (section 5.3 in SI Appendix), we arrived at a set of differential equations that can be used to mathematically explain dose–response linearization in the cascade with NF:

where the variables x, y, and z correspond to free intracellular repressor, inducer, and reporter concentration, respectively, and C is a control parameter proportional to extracellular inducer concentration. Other parameters are a (protein synthesis rate), b (inducer–repressor association rate), d (rate of dilution due to cell growth), and f (combined rate of inducer dilution, outflux, and degradation). Inducer dissociation from the repressor occurs at much slower time scale than the other processes we considered (35), and thus, for the sake of mathematical tractability, it was not included in this model. The functions F_x and F_z describe the repressor dependence of protein synthesis from the upstream and downstream promoters, respectively. Because repression by TetR is generally cooperative (5), we used the same Hill function to describe the repressor dependence of the 2 identical promoters in the NF strain:

where θ is the induction threshold and n is the Hill coefficient. The set of Eqs. 1 also describes the cascade without feedback (NR) after setting F_x = 1.

The steady-state solution of Eqs. 1 includes a quasi-linear function z(C), confirming that NF linearizes the dose–response (Fig. 2A). This can be understood by considering that below saturation, association with free repressor is the dominant source of decay for both inducer and free repressor, implying that the terms dx and fy are negligible compared with bxy. Therefore, setting dx ≈ fy ≈ 0 in the first 2 equations for the NF strain at steady state results in

Here, F_x⁻¹ is the inverse function of F_x, indicating that x (free repressor concentration) is a predistorted function of C. At the reporter level we obtain

demonstrating that the reporter's promoter redistorts the function x(C), resulting in the linear dependence z = C/d. Therefore, provided F_z and F_x are related via a linear transformation

the dose–response will be well approximated by the linear function z = (sC + sϕ + l)/d, where the factors s, l, and ϕ stretch and move F_x vertically or horizontally (the values s = 1, l = 0, and ϕ = 0 correspond to identical up- and downstream promoters, F_x ≡ F_z).

In summary, linearization in the NF cascade requires that the predistortion at the regulator level be redistorted at the reporter level. Therefore, this simple argument predicts a linear dose–response if the repressor dependences F_x and F_z of upstream and downstream promoter activities are related via a linear transformation (section 5.3 in SI Appendix).

Linearization of Dose–Response Does Not Depend on the Number of Repressor Sites.

To confirm linearization via pre- and redistortion, we constructed 3 additional linearizers (section 4.2 in SI Appendix and Figs. S1, S3), using identical up- and downstream promoters with 1 (P_GAL1-S1), 2 (P_GAL1-D12), or 3 (P_GAL1-T123) tetO₂ sites (32). Importantly, the open-loop (NR) dose-response of the P_GAL1-S1 promoter was twice as steep as that of the other two promoters, while the peak noise level increased with the number of tetO₂ sites in these promoters (32). We combined these promoters in pairs to govern the expression of a tetR::mCherry fusion as repressor and yEGFP::zeoR as reporter. As expected, the ATc dependence of gene expression noise and mean in the strain harboring 2 P_GAL1-D12 promoters was almost identical to that of the original linearizer after rescaling (sections 3.3 and 4.2 in SI Appendix and Fig. S2). More importantly, in accordance with the mathematical prediction that NF linearizes the dose–response if the repressor-dependencies F_z and F_x of up- and downstream promoters are linear transformations of each other, we found that all 3 promoter pairs produced linear dose–responses (R² = 0.99, L1-norms = 2.1 × 10⁻², 5.7 × 10⁻², and 3 × 10⁻², respectively) of nearly identical slopes over a wide range of inducer concentrations, independent of promoter strength, and regardless of the number of tetO₂ sites present in the promoters.

As a control, we have also replaced the P_GAL1-D12 promoter in the original linearizer with different downstream promoters [P_GAL1-S1 and P_GAL1-T123 (section 4.3 in SI Appendix)]. Comparing the dose–response of these downstream promoters to that of P_GAL1-D12 in cascades with no feedback (32) we concluded that the repressor dependence of P_GAL1-S1 is markedly different, whereas that of P_GAL1-T123 is quasi-identical to P_GAL1-D12 after linear rescaling (Fig. 3A). In accordance with the mathematical prediction, we found by flow cytometry that, compared with the construct with 2 identical P_GAL1-D12 promoters, the promoter combination P_GAL1-D12–P_GAL1-T123 had steeper but still linear dose–response (R² = 0.99, L1-norm = 7.9 × 10⁻²), whereas the dose–response of the P_GAL1-D12–P_GAL1-S1 cascade deviated from linearity (R² = 0.93, L1-norm = 14.7 × 10⁻²) (Fig. 3C and section 6.2 in SI Appendix). This departure from linearity for the latter construct confirms that a NF cascade is a linearizer if the repressor dependencies of upstream and downstream promoters are related via a linear transformation as in Eq. 5.

Fig. 3.

Confirmation of linearization in alternative NF cascades. (A) Linear transformations of best fits to the dose–response curves of P_GAL1-S1, P_GAL1-D12, and P_GAL1-T123 promoters plotted against the P_GAL1-D12 promoter, based on the data from ref. 32. (B) Experimental dose–response curves and respective linear fits up to saturation levels for 3 different linearizers based on P_GAL1-S1 (1 tetO₂ site); P_GAL1-D12 (2 tetO₂ sites); and P_GAL1-T123 (3 tetO₂ sites). (C) Experimental dose–response curves and the corresponding linear fits up to saturation for the NF constructs with P_GAL1-D12 promoter upstream and the promoters P_GAL1-S1, P_GAL1-D12, and P_GAL1-T123 downstream, respectively.

Finally, we also observed efficient noise reduction for all promoter combinations with NF (sections 4.2 and 4.3 in SI Appendix), suggesting that noise suppression and dose–response linearization are independent properties of our constructs. Overall, these experimental findings confirmed the predictions of the mathematical model, suggesting that linearization in our constructs results from predistortion at the regulator followed by redistortion at the reporter level (Fig. 3).

Discussion

Using a chromosomally integrated gene expression system, we studied the effect of NF on the characteristics of eukaryotic gene expression over a broad range of induction. This is important, because of the “fundamentally different logic of gene regulation” (36) and the different sources and characteristics of gene expression noise in eukaryotes versus prokaryotes (9). Indeed, we observed a massive (7-fold) reduction of noise compared with prokaryotic systems (20) at intermediate induction. Noise reduction at intermediate and high ATc levels might be explained by differences in regulator (free TetR) fluctuations in the 2 different strains (section 5.2.9 in SI Appendix).

Importantly, we have also demonstrated that introducing negative autoregulation into a transcriptional cascade can linearize the dose–response before saturation. Currently, no known alternatives exist to linearize the dose–response in eukaryotic gene expression systems. For example, reducing the number of repressor binding sites can result in steeper dose–response, depending on the location of the operator sites (32). Moreover, even when the desired reduction of steepness is obtained, it is accompanied by a drastic increase in basal expression (32). Although to the best of our knowledge, a systematic study of linearization by a gene circuit has not previously been undertaken, similar effects have been widely known and applied in electronics, control theory, and even neuroscience. For example, NF increases the linearity (reduces distortion) in electronic amplifiers, and may play a role in the “spike-frequency adaptation” of neurons (37), converting nonlinear instantaneous firing rate responses to linear at steady state (38).

A set of gene circuits similar to ours have recently been studied in Escherichia coli (26), and NF was shown to reduce noise at a wide range of inducer concentrations. However, noise had a U-shaped dependence on inducer concentration in the bacterial construct corresponding to our NF cascade, and there was no noise peak in the bacterial construct corresponding to our NR cascade. The U-shaped inducer dependence of noise was explained by plasmid copy number variation acting as a source of extrinsic noise (7), which is suppressed most efficiently at intermediate inducer concentrations by NF (39). On the other hand, gene copy number variation did not play a role in our single-copy, chromosomally integrated constructs, eliminating this source of extrinsic noise. The presence of a noise peak observed for the NR cascade, and other similar constructs (9, 32, 40), is explained by bimodal yEGFP distributions occurring only at intermediate inducer concentrations, whereas the reporter expression in the corresponding bacterial system was already bimodal even without induction (26). This could be a result of higher tetR expression in our constructs, which could increase the steepness of the dose–response curve and shift the induction threshold higher in the absence of feedback. Thus, the specifics of the bacterial and yeast system can account for the different inducer dependence of the gene expression noise and mean in these studies.

The architecture of the linearizer gene circuit closely resembles inducible bacterial operons with repressor control (41) with the exception that bacterial effectors frequently catalyze biochemical reactions or encode transport proteins that affect inducer levels creating additional feedbacks (42). Thus, natural gene circuits with completely identical architecture and linear dose–response might not exist at all. However, the ability of linearizers to convert sigmoidal dose–responses to linear and to eliminate bimodality could have wide-ranging applications for building reliable synthetic transcriptional networks. Based on our results, introducing NF will improve the performance of current gene expression systems by reducing cellular heterogeneity, and by allowing the experimenter to fine-tune the expression of any gene along a linear dose–response curve. This seems particularly important considering the nonlinear dose–response of many artificial transcription activation elements (33), and the wide use of tet gene expression systems in bacteria (20, 26, 40), yeast (5, 14, 32), insects (43), and mammalian cells (31). In summary, the precise control of gene expression mean accompanied by noise reduction are attractive features that should make the linearizer gene circuit a highly useful tool in synthetic biology.

Materials and Methods

Strains and Media.

The haploid S. cerevisiae strain YPH500 (α, ura3-52, lys2-801, ade2-101, trp1Δ63, his3Δ200, leu2Δ1) (Stratagene) was used as a parental strain. First, the reporter part of the cascade was integrated into the native GAL1-GAL10 locus, followed by the integration of regulatory parts into the ampR gene of the first integrant. Modified lithium acetate procedure was used for transformation (44). The number of integrations for each construct was verified by PCR and flow cytometry, selecting only the strains with single integrations. Cultures were grown in synthetic drop-out medium with the appropriate supplements to maintain selection (all reagents from Sigma) and supplemented with sugars as described below.

Construction of Cascades.

The yeast integrative plasmid pRS4D1 (9, 14) carrying a P_GAL1-D12 promoter (pGAL1* in refs. 9 and 14, and D12 in ref. 32) with 2 tetO₂ sites and selectable TRP1 marker was used as the template for all subsequent plasmids in this work. The tetracycline repressor gene (tetR) present in the original pRS4D1 plasmid under the control of GAL10 promoter was replaced with nonfunctional fragment inserted between SacI and SpeI sites. The genetic constructs were then generated in 2 steps. First, in the reporter part, the region of plasmid containing transcriptional terminators flanking P_GAL1-D12 promoter and downstream yEGFP gene were amplified by PCR and inserted into the pRS403 shuttle vector (Stratagene) between 2 PvuII sites, producing pDN-G1Gh plasmid with HIS3 selectable marker. Second, in the regulator parts, the functional tetR gene was amplified by PCR and placed between BamHI and XhoI sites under the control of either P_GAL1-D12 (NF) or P_GAL1 (NR) promoters, producing the pDN-G1Tt and pDN-NG1Tt plasmids, respectively. The pDN-NG1Tt was engineered, replacing the P_GAL1-D12 with the native P_GAL1 promoter restoring the original sequence between AgeI and BamHI sites, by using the pESC-Leu (Stratagene) as a template. All cloning procedures were performed in E. coli XL-10 Gold strain (Stratagene) by using selection by ampicillin (Sigma). All constructs were sequenced in the insert regions with double coverage. Oligonucleotides used in the study can be found in SI Appendix.

Flow Cytometry.

Single cell colonies were picked from the plate and incubated overnight in synthetic drop-out medium supplemented with glucose 2% at 30 °C. Cell suspension was diluted 1:6, and 100 μL was used to inoculate synthetic drop-out medium supplemented with 2% galactose and increasing concentrations of ATc (0 to 500 ng/mL; ACROS Organics). Cultures were then grown at 30 °C for another 16 h and read on the FACScan flow cytometer (Becton Dickinson) or MoFlo flow cytometer (DAKO North America).

Data Analysis, Computational Models, and Simulations.

Flow cytometry data were analyzed using R (R Development Core Team, Vienna). The original log-binned fluorescence intensity values were transformed (by raising 10 to the power of each log bin), and the mean and standard deviation of the resulting values were calculated for each sample within a small forward and side scatter gate to reduce variability in cell size and shape (4). Cells with log fluorescence deviating >3 standard deviations from the geometric mean were considered outliers and were discarded from the analysis. The noise (coefficient of variation) was computed for each sample as the standard deviation divided by the mean. Linearity was assessed by using a linear regression and the L1-norm (see SI Appendix for details).

Computational models were developed based on chemical mass action kinetics, and the resulting analytical formulas were fitted in Matlab (MathWorks) to the average of 3 experimental replicates the NR strain by using the fminsearch (Nelder–Mead) algorithm. Stochastic simulations based on the Gillespie algorithm were performed in Dizzy (45) and analyzed with Octave (University of Wisconsin, Madison). The detailed description of the computational model and the sensitivity of the results to various parameters can be found in SI Appendix and Table S1.