Abstract
We present a theory for protein folding stability and cooperativity for helix bundle proteins. We treat the individual helices with a Schellman-Zimm-Bragg-like approach, using nucleation and propagation quantities, and we treat the hydrophobic and van der Waals contacts between the helices as a binding equilibrium. Predictions are in good agreement with experiments on both thermal and urea-induced transitions of: (1) molecules that can undergo single helix-to-coil transitions, for various chain lengths, and (2) 3-helix-bundle proteins A and α3C. The present model addresses a problem raised by Kaya and Chan, that proteins fold more cooperatively than previous models predict. The present model correctly predicts the experimentally observed two-state cooperativities, ΔHvan’tHoff/ΔHcal ≈ 1, for helix-bundle proteins. The predicted folding cooperativity is greater than that of helix formation alone, or collapse alone, because of the nonlinear coupling between the tertiary interactions and the helical interactions.
I. INTRODUCTION
We present here a theory of protein stability and cooperativity. We focus on helix-bundle proteins. Protein folding involves both secondary structure formation and collapse. Historically, two types of models have been prominent in explaining conformational cooperativity in proteins and polymers. First, helix-coil models treat the sharp transition that some polymers undergo from a disordered random coil state to a single helix1–7. Such processes are dominated by the local interactions among nearest neighbors in the chain. Helix-coil experiments are typically well described in terms of the two parameters of helix-coil theory: σ, a nucleation parameter and s, a helix propagation parameter8. Second, polymer collapse theories treat the sharp condensation collapse transition of hydrophobic polymers in water9–17. Collapse processes are dominated by nonlocal interactions – the solvent-mediated contacts among pairs of monomers that need not be adjacent in the chain sequence. While both types of models have given important insights, a deeper understanding of the folding cooperativity of proteins requires an approach that treats both local and nonlocal interactions within the same theoretical framework.
The underpinnings of cooperativity has recently been of considerable interest. Chan and coworkers have been at the forefront of protein folding cooperativity by comparing different theoretical models17–21. This question has also been the subject of experimental controversy in the matter of whether or not proteins undergo downhill folding, with no barrier22–27. It is a challenge for experiments to determine the density of states, with the exception of some recent work using NMR24 or FRET27 studies. Hence, there remains a need for a microscopic statistical mechanical model of the density of states and folding cooperativity.
There is also an experimental challenge in understanding protein folding cooperativity because a given protein differs from the next in non-systematic ways: different proteins have different chain lengths, different secondary structures, different numbers of hydrogen bonds and hydrophobic interactions, and different packing densities. There is no simple single variable (i.e., “knob”) that can systematically vary the folding cooperativity of a protein. In contrast, our understanding of helix-coil processes was considerably advanced because of experiments that have systematically explored the effects of changing the chain length N and the propagation parameter s8,28,29. And, unlike helix-coil or collapse processes in simple model polymers, the chain length of a protein is seldom the most important variable controlling its folding cooperativity.
However, there is a class of proteins in which, in principle, cooperativity can be studied systematically. These are helix-bundle proteins. Modern methods now allow for the synthesis of simple repeating helical sequences of various numbers and lengths that can be connected by loops into bundles. Experiments by Hecht30,31, Degrado32 and others33, for example, show that it is straightforward to design helix bundle folds: you mainly need hydrophobic residues on the inside and polar ones (for solubility) on the outside. Moreover, foldable helix-bundle polymers have also been made using non-biological backbones, such as in peptoids34,35. Despite these possibilities, however, as far as we know there are not yet systematic investigations of folding stability and cooperativity of experimental model helix-bundle systems.
Here, we develop an analytical theory for the equilibrium properties of helices and helix-bundle proteins. We first describe below our treatment of a single helix, since the helix-bundle models that follow rely upon it. Our helix-coil treatment here differs slightly from most earlier models, such as Schellman’s1, the Zimm-Bragg model2, or the Lifson-Roig model4. In those classical models, the only entropy that is treated explicitly is the “combinatoric entropy”, which is the count of the number of different locations where helical residues can be located in the sequence. For example, three consecutive helical units can occur in a chain of 5 monomers in three ways, CCHHH, CHHHC, and HHHCC, where C represents a segment of chain that is in a coil configuration and H represents a helical bond. However, this combinatoric entropy is only one of the contributors to the entropy of a polymer chain. Another important entropy – the chain conformational entropy – is not treated explicitly in the classical helix-coil models. Our approach keeps the chain entropy explicit, because: (1) it is essential for more complex helix-bundle treatment that follows, (2) it gives insights into the temperature dependences, and (3) it allows for predictions of observables such as the radius of gyration, which are not otherwise available from helix-coil theories.
In recent years, a key focus of helix-coil models has been on predicting how helical stability depends on the amino acid sequence of a protein. To treat such dependences, such theories typically utilize transfer matrices. For example, the Zimm-Bragg and Lifson-Roig models use the 1-dimensional Ising matrix method. Such matrix treatments are also useful for treating multiple non-interacting helical stretches within a longer chain; that was particularly important in the early years for the proof of principle of helix-coil cooperativity in poly-benzyl glutamate chains having 1500 monomers2. However, for treating the lengths of helices found in globular proteins, which are typically less than about 20 monomers long, much simpler models are possible, and, for applications of interest to us, more desirable. Here, we make this “single-helix” simplification.
We start with a Schellman-like partition function for a helix-coil process; then introduce terms into the statistical physics that account for the interactions among pairs of helices in order to understand 2-helix-bundle (2hb) and 3-helix-bundle (3hb) molecules.
II. THE PARTITION FUNCTION FOR A SINGLE HELIX
Consider a chain molecule that can have a maximum number N of helical bonds, and for which z is number of rotameric configurations accessible to each backbone virtual bond. M is number of amino acid residues in the protein molecule. These quantities are related by N = M − 4 since residue i forms a helical hydrogen bond with i + 4. In this section, we consider a molecule that undergoes a transition from coil to a single helix. We call this a 1-helix molecule, to distinguish it from 2-helix and 3-helix bundles below. We factorize the total partition function, qtot
| (1) |
into a product of two terms. The first term, qp, is the total count of all the polymer chain conformations,
| (2) |
The factor of z is the total number of conformations of the virtual bonds in one helical turn, one conformation of which is helical and (z − 1) of which are coil conformations. The second term, which accounts for the combinatorics, can be expressed as a sum of Boltzmann factors over all the helical and coil states of a chain that can form a single helix (see Figure 1):
| (3) |
where s is the equilibrium constant for forming each helical bond relative to a coil unit, and σ is the nucleation parameter, i.e. the equilibrium constant for forming the first H after a string of C’s. The first term (1) in Equation 3 is the statistical weight for the coil state, i.e., it counts all the chain conformations that have all C’s and no helix. The second term, Nσs expresses that there are N different locations in the chain that can have a single helical bond. The third term, (N − 1)σs2 expresses that there are N − 1 locations in the chain sequence at which an HH pair can appear in a string of N monomers. The factor of σ accounts for the difficulty of nucleating the helix, i.e. forming the first H. The factor of s2 is an equilibrium constant for having 2 consecutive H’s in the helix. Each term in the partition function is made up from factors in this way. This model is essentially identical to the model originally introduced many years ago by Schellman1, which makes the “single-helix” approximation, except that we treat the temperature dependence a little differently, as indicated below. To make explicit the full temperature dependence, we express the helix-propagation equilibrium constant s, or unit partition function, in terms of its energetic and entropic parts
FIG. 1.
Different conformations considered in the partition sum for a single-helix. A1 denotes complete coil, A2 is for partially formed helix and A3 denotes fully formed helix.
| (4) |
where εhb > 0 is the interaction energy increase upon breaking one helical bond, k is Boltzmann’s constant and T is the absolute temperature. This expression for s shows that: (a) there is an entropic cost (the factor of z − 1 in the unit equilibrium constant) when the chain forms a helical bond from among the possible coil conformations, and (b) there is an energetic advantage for forming the helix. Helix-coil theories usually treat σ as being a temperature independent equilibrium coefficient, and thus as resulting from an entropy. Here, we treat it more broadly as a free energy, since helix nucleation appears to be thermally activated, hence:
| (5) |
The enthalpic barrier is εnuc and the entropic component cost is (z − 1)2 because the first bond of a helix points in an arbitrary direction and the second and third virtual bonds must then be restricted to the correct orientation to form a helix. Now, to compute the properties of this helix-coil model, we need the probabilities of the various states. From the model, the probability that a chain has i ≠ 0 helical contacts is
| (6) |
and . Several experimental properties are of interest for individual helices and for helix bundles, including the average fractional helicity, Θ, the average energy 〈E〉 and the heat capacity Cv. We get these quantities from the model using standard expressions38:
| (7) |
| (8) |
| (9) |
When computing 〈E〉 and Cv, we substitute the combinatoric part, qc, for q in equations 8 and 9 since qp does not depend on temperature.
We are interested in how the helix-coil equilibrium is affected by temperature and in how the helix-coil equilibrium is affected by denaturing and stabilizing solvents. For example, for denaturants, we adopt the standard expression 36–38 that the interaction strength ε is a linear function of the urea concentration
| (10) |
where represents the interaction energy in the absence of urea, and [c] is the concentration of urea. For some types of denaturant, higher-order terms may be needed at high concentrations.
A. Predictions for the single helix-to-coil process
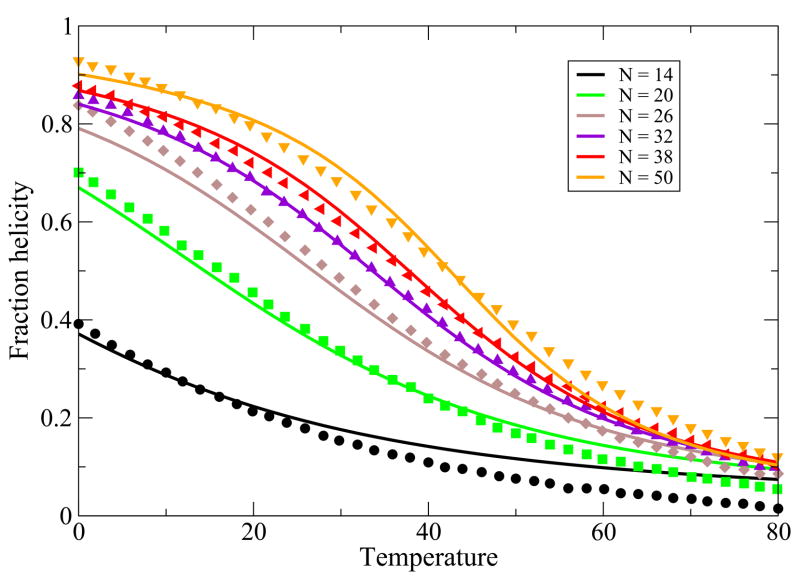
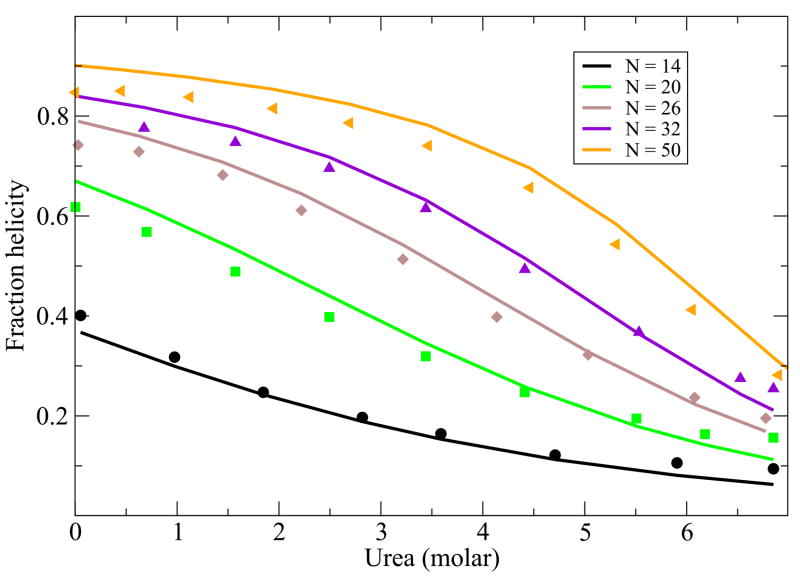
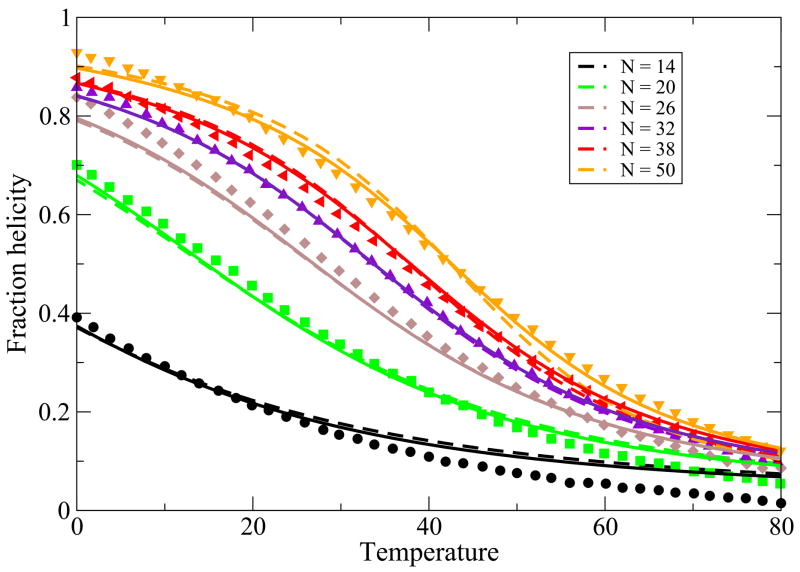
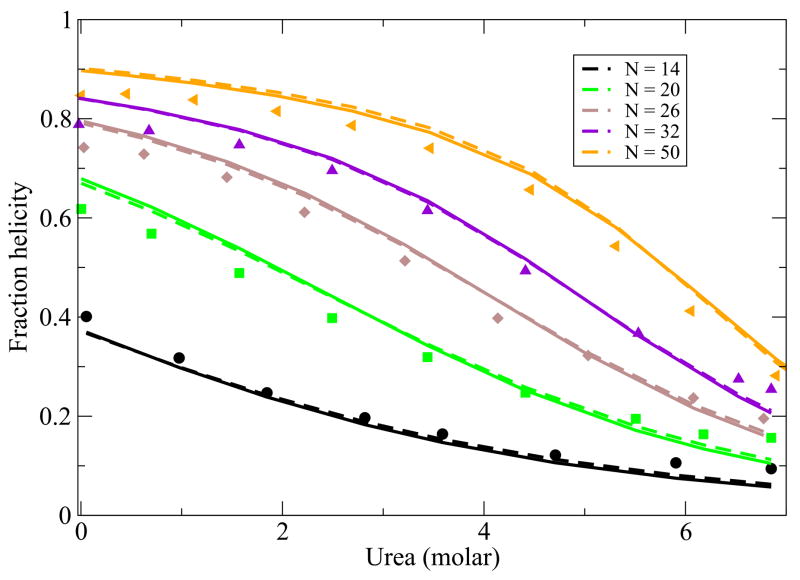
While the main point of this paper is to treat helix-bundle proteins, described below, we first validate that this simple Schellman-like 1-helix model adequately describes the transition between a single helix and its coil states. There is much more data now than when Schellman first developed this kind of model. Here is how we apply it. First, for a given peptide, we know the chain length, N and the temperature T. A particular chain sequence will be characterized in our model by three parameters: a nucleation parameter εnuc that is averaged over the different types of sequence monomers, an average chain flexibility z, and an average helical turn energy εht. This is the same number of parameters that would be used in other helix-coil models, such as the Zimm-Bragg model, when the temperature dependence is of interest. For a given monomer sequence, we take these three quantities and m to be fit parameters. Figure 2 and Figure 3 show the model predictions are in good agreement with the experimentally observed temperature and urea denaturation for different lengths of a given peptide sequence39,40. The fits for the thermal denaturation data and urea denaturation data for different chain lengths were obtained from a single set of parameter values.
FIG. 2.
Thermal denaturation data from 39, vs. theory. In the model, we use z = 6.83, εhb = 1.14 Kcal/(mol-residue), εnuc = 1.08Kcal/mol-residue. Different colors are for different chain lengths
FIG. 3.
Urea denaturation from Schotlz etal40. In the model, we use z = 6.83, εhb = 1.14 Kcal/(mol-residue), εnuc = 1.08Kcal/mol-residue and m = 0.028 kcal/M. Different colors are for different chain lengths.
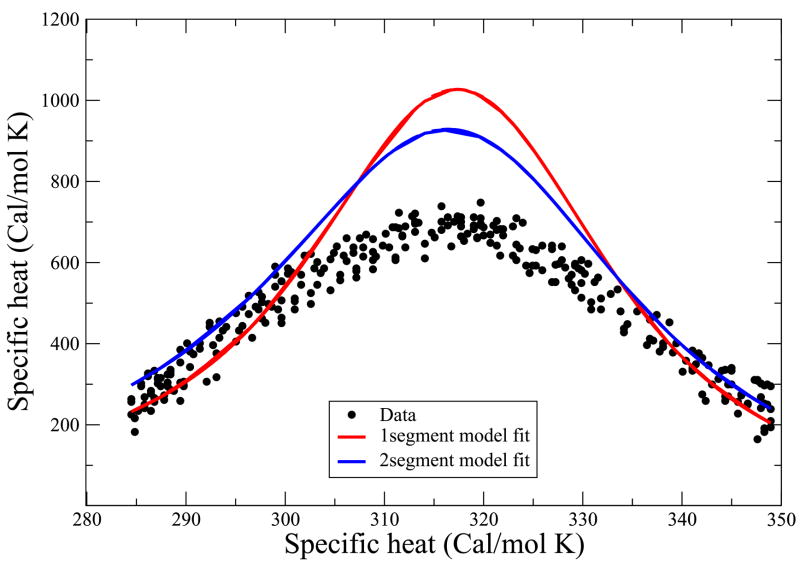
We also use this model to predict the specific heat vs. temperature. Figure 6 compares the predictions with experimental data on Baldwin’s peptide41 using the same parameters that were used for the thermal and urea denaturation curves.
FIG. 6.
Heat capacity data from Scholtz etal41. This data was not used to obtain the best fit parameter values. Solid line is the theoretical prediction while data points are shown in filled circle. Red curve is produced using single helical sequence approximation with the parameter values z = 6.83, εhb = 1.14 kcal/(mol-residue), εnuc = 1.08kcal/mol-residue whereas the blue curve was produced by using two helical sequence approximation with the parameter values z = 7.43, εhb = 1.2 kcal/(mol- residue), εnuc = 1.0 kcal/mol-residue.
Because the model described above does not fit the heat capacity data accurately, we first explore an improved version before treating helix bundles. In particular, we now explore the two-helix approximation (2ha): a molecule can have a maximum of two helices anywhere in the chain.
B. Single-helix protein again, now in the two helical-segment approximation
In the two-helix approximation (2ha), the partition sum is given by
| (11) |
where s and σ have the same definitions as before. The first term represents the complete coil, the second term represents all conformations containing a maximum of a single helix, and the third term represents all conformations having two helical segments (j and k helical bonds each). The fractional helicity (Θ) and specific heat Cv are found by substituting q1c,2h into equations 7 and 9.
Relative to the single-helix approximation, the two-helix approximation leads to a small change in the best-fit parameters (see Figures 2 and 3). The best-fit value of the hydrogen bond parameter changes by 6% and the z parameter changes by 9%. While the predictions in figures 4 and 5 are only slightly improved, the predicted specific heat improves more significantly using the two-helix approximation than the single-helix approximation (see Figure 6). This calculation shows the nature of the errors made by these approximations. We take the simpler single-helix approximation to be sufficient for the purpose of treating helix-bundles below.
FIG. 4.
Thermal denaturation of peptides of different length from Scholtz etal40. Symbols represent experimental data, lines with -- denote bestfit lines using model with single helical approximation where as solid lines represent bestfit using two helical segment model. In this model, we use z = 7.43, εhb = 1.2 kcal/(mol-residue), εnuc = 1.0 kcal/mol-residue.
FIG. 5.
Urea denaturation of peptides of different length from Scholtz etal40. Symbols represent experimental data, lines with -- denote bestfit lines using model with single helical approximation where as solid lines represent bestfit using two helical segment model. In this model, we use z = 7.43, εhb = 1.2 kcal/(mol-residue), εnuc = 1.0 kcal/mol-residue and m = 0.029 kcal/M.
III. PARTITION FUNCTION FOR TWO-HELIX-BUNDLE PROTEINS
In this section, we treat two-helix-bundle (2hb) molecules. Now, in addition to the local interactions within each helix, we also treat the nonlocal interactions that occur when the two helices are packed adjacent to each other. As before, we factorize the total partition function q2t for the 2-helix bundle into its (z − 1)2(N2+2) chain conformations and its combinatoric factor q2c
| (12) |
where q2c is expressed as
| (13) |
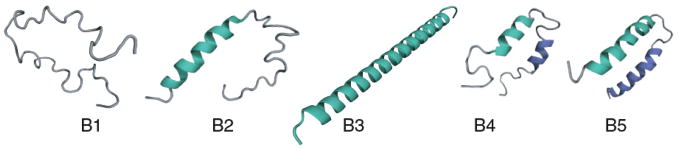
These equations are based on the following parsing of terms. q1c is the partition sum for each individual helical sequence of the chain, given by equation 3. Hence the first term in equation 13 (2-independent-arm term) accounts for all the ways that each helical arm can have at least one helical turn, where the helices do not interact with each other. The factor of z4 accounts for the minimum of three virtual bonds connecting the two helices and the fact that the second helix can orient in any possible direction compared to the three-bond linker. Subtracting unity from q1c ensures that we count only non-coil states, i.e., all the states in which there is at least one helical bond. The second term in equation 13 2-helix-bundle term is a sum over all the states in which one helix is partially formed to any degree and the second helix is formed to any degree and the two helices are in contact and interact with each other (see Figure 7). Each helix-helix contact has a contact energy εhh, corresponding to an equilibrium constant r = exp(εhh/kT). This contact term operates between helical turns and hence the sum is over number of helical turns, rather than over helical bonds. We regard these as helix-helix interactions as primarily hydrophobic and packing interactions. We have also assumed that only the configuration with maximum helix-helix interactions contribute to the partition sum and hence we have the term min(i, j). The other configurations which are responsible for forming contacts less than min(i, j) between two helices have been ignored because the statistical weight of those terms will be negligible. Thus the first component in equation 12 accounts for all combinations of two segments where helical turns nucleate into two helices (B4 and B5 in Figure 7). The final term single-helix term, given in equation 12, accounts for the possibility that instead of a 2-helix bundle, the whole chain simply forms a single long helix of any degree of helicity (including the all-coil state; see Figure 7). N1 is the maximum number of helical bonds that can be formed if the chain had a complete single helix conformation. Thus, 2N2 + 10 = M and N1 = M − 4 where for the two helix conformations we assume a three linker between the two helices. The expression of N2 is derived from the fact there are M − 1 bonds of which 3 of them contribute to the linker and rest of the bonds are equally distributed in each helix, and maximum number of helical bonds is always 3 less than the total number of bonds available because i, i + 4 nature of the helical cotacts. Thus N2 = (M − 4)/2 − 3 which gives M = 2N2 + 10. As above, added denaturant will diminish the hydrophobic interactions approximately linearly,
FIG. 7.
Different conformations considered in the partition sum for a 2-helix bundle protein. B1, B2, B3 denote all the components of a single helix conformation while B4 shows all possible configurations with two partially formed helices interacting with each other. B5 represents fully formed two helices, the native state of a 2-helix bundle protein.
| (14) |
where is the interhelical contact formation energy in the absence of denaturant. We use the same value of m as was used for the hydrogen bond strength dependence on denaturant concentration.
IV. PARTITION FUNCTION FOR THREE-HELIX BUNDLE PROTEINS
Finally, we treat three-helix bundles in a similar way. Following previous notation, we use q3tot = (z − 1)3(N3+2)q3c and q3c is the combinatoric factor for the three-helix partition sum.
| (15) |
where q3c is expressed as
| (16) |
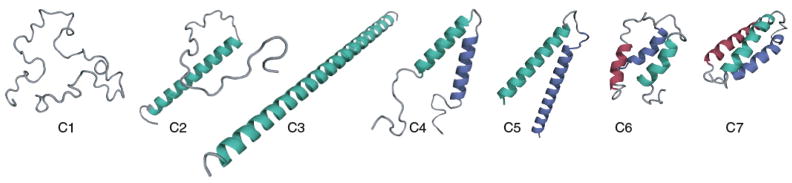
The logic behind different terms follows much the same way as before, q1c(N3, T) is the partition function for a single helix having a total of N3 bonds, given by equation 3. Hence, the first term in equation 16 (3-independent-arm-term) accounts for all conformations having three fully or partially formed helices throughout the chain where helices do not interact with each other. The factor of z8 accounts for the minimum of three virtual bonds connecting helices and the second and third helix can orient in any possible direction with respect to the three-bond linker. Subtracting unity from q1c ensures that we count only non-coil states, i.e., all the states in which there is at least one helical bond. The second term in equation 16 3-helix-bundle term is a sum over all the states in which one helix is partially formed to any degree and the second and third helices are formed to any degree and the three helices are in contact and interact with each other. Each helix-helix contact has a contact energy εhh (hydrophobic and packing interaction), corresponding to an equilibrium constant r = exp(εhh/kT) as before. This contact term operates between helical turns and hence the sum is over number of helical turns, rather than over helical bonds. It is important to note that the interaction is still two body and hence we get a factor of three in the exponent of r. Once again, we assume the most dominant contribution to the partition sum arises due to three helices (with i,,j and k number of turns) having min(i, j, k) number of contacts and the configurations with less number of contacts have been ignored. Thus, the first component in equation 15 accounts for all combinations of three segments where helical turns nucleate into three helices (see Figure 8). The final term 2-helix term in equation 15 includes all possible conformations that the protein molecule could adopt if it were in a two-helix bundle conformation (see C1,C2,C3,C4,C5 in Figure 8). This has already been derived explicitly in equation 12 and accounts for single-helix term as well as all complete coil state. There are a maximum of 3N3 helical bonds with each helix having N3 bonds for a 3-helix configuration. N3 is related to the total number of amino acids M by M = 3N3 + 16 using same argument used for two-helix bundle protein and assuming each helix has a 3 linker spacing as before. N2 is the number of bonds in each helix for 2-helix bundle conformation and it is related to total number of amino acids M as before, M = 2N2 + 10.
FIG. 8.
Different conformations considered in the partition sum for a 3-helix. C1,C2,C3,C4,C5 shows all the components for a full 2-helix bundle partition sum. C6 denotes structures where helices in three helical-arms are partially formed and C7 is the three helix bundle native structure with completely formed helices.
A. Results
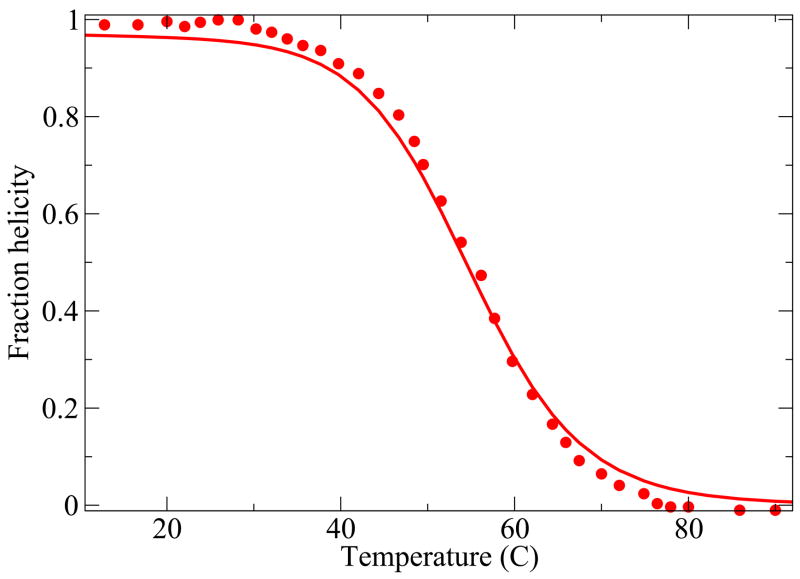
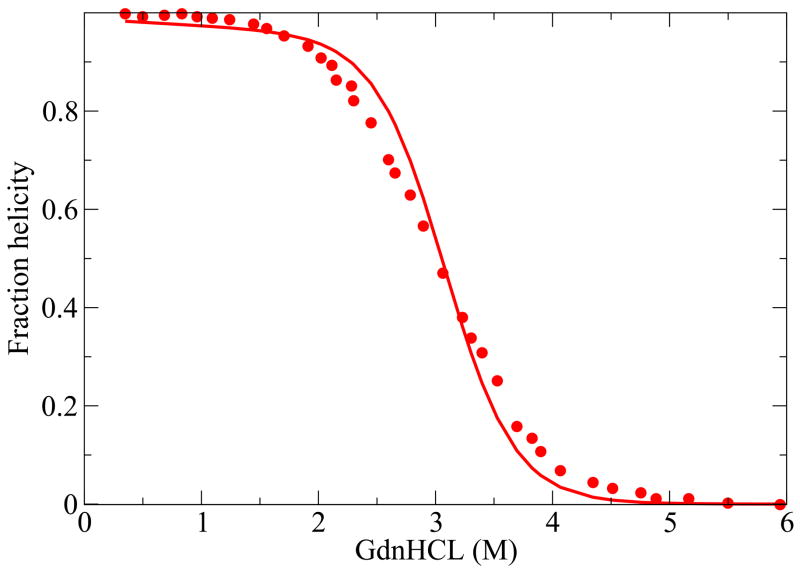
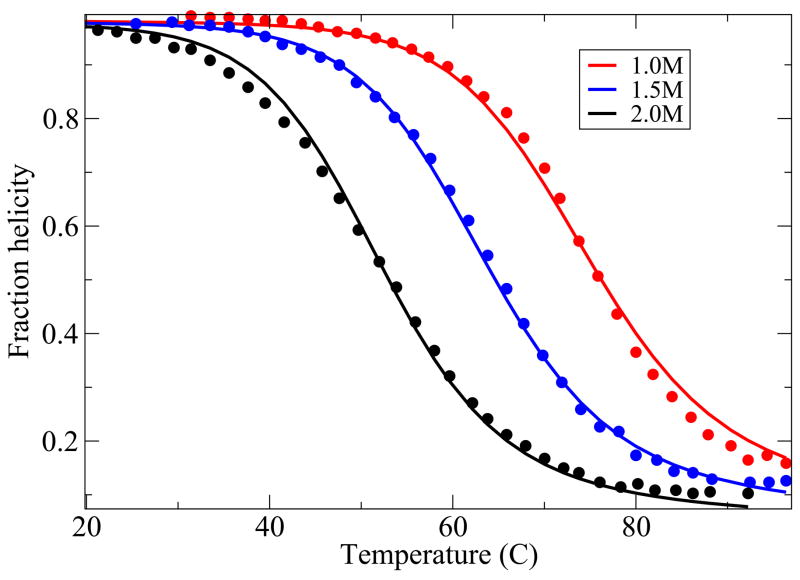
Here we compare the predictions from the model with experiments on two 3-helix-bundle proteins. Because of the extensive experimental data available, we study the thermal and denaturant-induced unfolding of Protein A42 (see Figures 9 and 10), with a single set of parameters, and the thermal denaturation for three different values of denaturant concentration of the protein Alpha3C43 (see Figure 11). For these cases, although the agreement is not perfect, it is quite good. A deeper test of the theory would be if our model helix-coil parameters were known for the individual helices from independent experiments, but they are not in these cases, as far as we know. Our parameter values are given in table I.
FIG. 9.
Protein A thermal denaturation data42. The values of the parameters used are, z = 3.73, εhb = 0.73 Kcal//(mol-residue), εhh = 2.38Kcal/mol-residue and m = 0.04 kcal/M and εnuc = 6.33 Kcal/mol.
FIG. 10.
Protein A GdnHcl denaturation42. The values of the parameters used are, z = 3.73, εhb = 0.73 kcal//(mol-residue), εhh = 2.38kcal/mol-residue and m = 0.04 kcal/M and εnuc = 6.33 kcal/mol
FIG. 11.
Alpha3C thermal denaturation data43. The values of the parameters used are, z = 3.43, εhb = 0.64 kcal//(mol-residue), εhh = 1.31kcal/mol-residue and m = 0.04 kcal/M and εnuc = 3.6kcal/mol.
TABLE I.
Values of fitted parameters
| Protein name | z | εhb (kcal) | εhh (kcal) | εnuc (kcal) | σ(T=298) | m(kcal/M) |
|---|---|---|---|---|---|---|
| Ala-Glu-Ala-Ala-Lys 1 helix | 6.83 | 1.14 | 1.08 | 0.17 | 0.028 | |
| Protein A(3 helix) | 3.73 | 0.73 | 2.38 | 6.33 | 0.00003 | 0.04 |
| α3C (3 helix) | 3.43 | 0.64 | 1.31 | 3.6 | 0.002 | 0.04 |
V. THE NATURE OF THE COOPERATIVITY IN HELIX-BUNDLE FOLDING
Kaya and Chan and their colleagues21 have argued that previous models of protein folding underpredict the high cooperativities that are observed in experiments. Small single-domain globular protein molecules tend to fold in a two-state manner: i.e., at the transition midpoint, there is a negligible population of intermediate states. Experiments reflect this either when specific measurements are made of the individual chain populations, or through the observation that the ratio of the van’t Hoff enthalpy(HvH) to the calorimetric enthalpy (Hcal) is experimentally found to be very close to one. Theoretical models, in contrast, tend to predict a value of this ratio that is smaller than one. As noted by Kaya and Chan21, even Go models, which are nonphysical models that are designed to be highly cooperative, give ratios of this quantity that are too small.
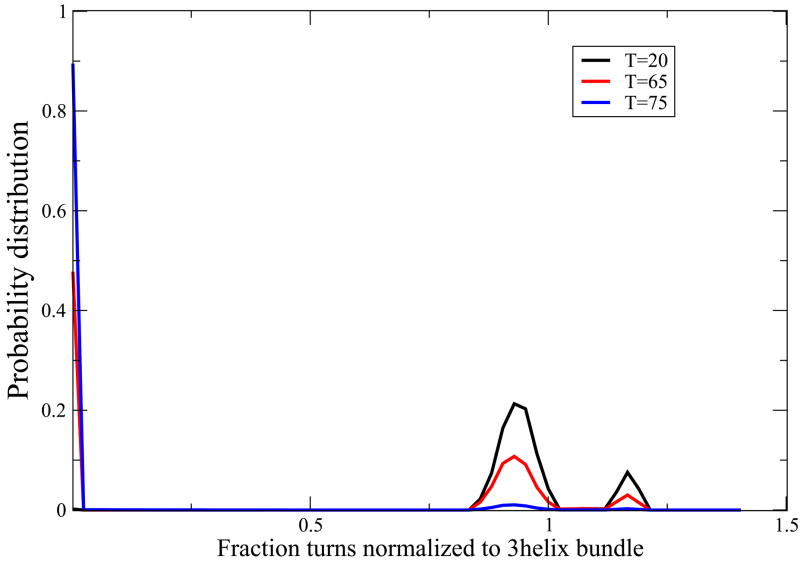
To explore the cooperativity predicted by our model for 3-helix bundles, we computed conformational populations at the transition midpoint, and we computed the ratio of enthalpies. We find that this model predicts two-state cooperativity. For protein A and Alpha3C, we evaluate the density of states at three different temperatures. At high temperatures, the model predicts a peaked unimodal distribution around the denatured states. At low temperatures, it predicts a peaked unimodal distribution around the native state, however there is a very small peak at the two-helix conformation as well predicted by our mean-field model. And, at the midpoint temperature, the model predicts a predominantly bimodal distribution but with a small population of the two-helix-bundle intermediate conformation. Our model predicts a high cooperativity for Protein A and moderately high cooperativity for Alpha3C (see Figure 12, 13).
FIG. 12.
Protein A folds with a two-state transition. Blue curve shows the population of different states at high temperature (T=75) denaturing condition with a major peak near coil-like conformation regime. The distribution of states at low temperature (T=20) is shows in black which shows a peak near the 3-helix bundle native state with a very small peak near two-helix bundle conformation as well. Red curve, predicting distribution of states at intermediate temperature near melting (T=65) shows an approximate 2-state behavior with two peaks near i) the coil like state and ii) the three helix bundle native state and with a slight population near the two-helix bundle state. These curves were generated using the parameter values z = 3.73, εhb = 0.73 kcal//(mol-residue), εhh = 2.38kcal/mol-residue and m = 0.04 kcal/M and εnuc = 6.33 kcal/mol
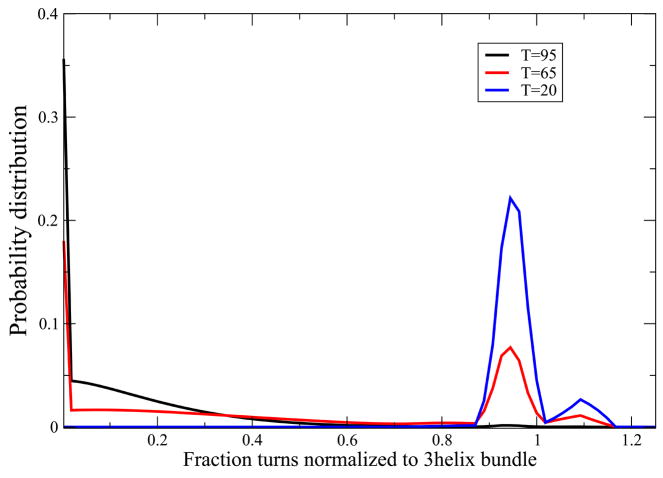
FIG. 13.
Protein Alpha3C folds with a two-state transition. Black curve shows the population of different states at high temperature (T=95) denaturing condition with a major peak near coil-like conformation regime. The distribution of states at low temperature (T=20) is shown in blue which shows a peak near the 3-helix bundle native state with a very small peak near two-helix bundle conformation as well. Red curve, predicting distribution of states at an intermediate temperature near melting (T=65) shows an approximate 2-state behavior with two peaks i) the coil like state and ii) the three helix bundle native state with a slight population at the two-helix bundle state as well. These curves were generated using the parameter values z = 3.43, εhb = 0.64 kcal//(mol-residue), εhh = 1.31kcal/mol-residue and m = 0.04 kcal/M and εnuc = 3.6kcal/mol.
In addition, we tested the prediction for the calorimetric behavior. We define ΔHcal as the enthalpy difference between the fully unfolded state and the native state. The van’t Hoff enthalpy HvH is defined as21,44
| (17) |
where we take K(T) to be
| (18) |
and where 〈i〉, which serves as an order parameter, is the average number of helical turns in the protein at temperature T, iu is the average number of helical turns in the unfolded state and ins is the number of helical turns in the native state. We define δ as the ratio of these two enthalpies,
| (19) |
For any system, it must be true that δ ≤ 1. δ = 1 only for a two-state transition44. Thus, the quantity δ is a measure of how well a model captures the two-state cooperativity observed in proteins. In Table 1, we show predictions of the model for these two 3-helix-bundle proteins. In the same table, we also show the cooperativities of the individual helices (if the full protein molecule assumes a completely long helix) taken alone computed at the experimentally observed melting temperature, predicted from the model. Our model predicts that protein A should have near two-state cooperativity, but that α3C is less cooperative. We are not aware of calorimetric data for these particular proteins. We also find that the individual component helices of these proteins are not by themselves sufficiently cooperative to account for the folding cooperativity of the full protein. Hence, this model indicates that the process of both forming helices and the association and packing of multiple helices together is more cooperative than the helix formation process alone. This indicates how protein folding may be so highly cooperative.
VI. CONCLUSIONS
We study a simple analytical model for a single polymer chain transition from a large denatured ensemble to either a single helix or to compact helix bundle conformations. First, at the single helix level, this model is among the simplest possible versions of classical helix-coil theory, and it performs well on a substantial body of data on thermal and solvent-induced denaturation vs. chain length. We find that the single-helix approximation is adequate for short polymers, except when predicting the heat capacity, in which case the two-helix approximation is needed. Because of the simplicity of this model, we can then also treat helix-bundle proteins analytically. Even though we use mean-field treatment, this helix-bundle model gives a good accounting of the experimental data on denaturation and cooperativity. The model predicts two-state cooperativity for helix bundle proteins. The two-state behavior arises because the cooperativity in the helix-coil process is enhanced by the process of the tertiary packing of helices upon each other. This model for cooperativity may generalize to the folding of other small globular proteins, and provides a simple tractable model of protein stability.
TABLE II.
The cooperativities of different proteins and their component helices
| Protein name | δ (1 helix at Tm) | δ (3 helix at Tm) | Tm(K) |
|---|---|---|---|
| Protein A (2.2 M) | 0.36 | 0.91 | 327.3 |
| α3C (2.0M) | 0.33 | 0.72 | 326 |
Acknowledgments
We thank Hue Sun Chan, Adam Lucas, Bruce Kerwin and David Brems for helpful discussions. This research was supported by UC discovery grant from Amgen and NIH Grant GM 34993.
References
- 1.Schellmann J. J Phys Chem. 1958;62:1485–1494. [Google Scholar]
- 2.Zimm B, Bragg J. J Chem Phys. 1958;28:1246–1247. [Google Scholar]; J Chem Phys. 1959;31:526–535. [Google Scholar]
- 3.Zimm BH, Doty P, Iso K. Proc Natl Acad Sci. 1959;45(11):1601–1604. doi: 10.1073/pnas.45.11.1601. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Lifson S, Roig A. J Chem Phys. 1961;34:1963–1974. [Google Scholar]
- 5.Polan D, Scheraga H. Theory of Helix-Coil Transitions in Biopolymers. Academic Press; New York: 1970. [Google Scholar]
- 6.Munoz V, Serrano L. Nature Struct Bio. 1994;1:399–409. doi: 10.1038/nsb0694-399. [DOI] [PubMed] [Google Scholar]
- 7.Munoz V, Serrano L. Curr Op Biotech. 1995;6:382–386. doi: 10.1016/0958-1669(95)80066-2. [DOI] [PubMed] [Google Scholar]
- 8.Scholtz JM, Baldwin RL. Ann Rev Biophy and Biom Struc. 1992;21:95–118. doi: 10.1146/annurev.bb.21.060192.000523. [DOI] [PubMed] [Google Scholar]
- 9.Dill K. Biochemistry. 1985;24:1501–1509. doi: 10.1021/bi00327a032. [DOI] [PubMed] [Google Scholar]
- 10.Dill K, Stigter D. Adv Prot Chem. 1995;46:59–104. doi: 10.1016/s0065-3233(08)60332-0. [DOI] [PubMed] [Google Scholar]
- 11.Finkelstein A, Shakhnovich E. Biopolymers. 1989;28:1667–1680. doi: 10.1002/bip.360281003. [DOI] [PubMed] [Google Scholar]
- 12.Saven JG, Wolynes PG. J Mol Biol. 1996;257:199–216. doi: 10.1006/jmbi.1996.0156. [DOI] [PubMed] [Google Scholar]
- 13.Saven JG, Wolynes PG. Physica D. 1997;107:330–337. [Google Scholar]
- 14.Grosberg AYu, Khokhlov AR. Statistical Physics of Macromolecules. AIP Press; New York: 1994. [Google Scholar]
- 15.Pande VS, Grosberg AY, Tanaka T. Rev Mod Phys. 2000;72:259–314. [Google Scholar]
- 16.Lucas A, Huang L, Joshi A, Dill KA. J Am Chem Soc. 2007;129:4272–4281. doi: 10.1021/ja067153s. [DOI] [PubMed] [Google Scholar]
- 17.Moghaddam MS, Shimizu S, Chan HS. J Am Chem Soc. 2005;127:303–316. doi: 10.1021/ja040165y. [DOI] [PubMed] [Google Scholar]
- 18.Knott M, Chan H. Chem Phys. 2004;307:187–199. [Google Scholar]
- 19.Chan H, Shimizu S, Kaya H. Methods Enzymol. 2004;380:350–379. doi: 10.1016/S0076-6879(04)80016-8. [DOI] [PubMed] [Google Scholar]
- 20.Chan H. Proteins: Struct Funct Genet. 2000;40:543–571. doi: 10.1002/1097-0134(20000901)40:4<543::aid-prot20>3.0.co;2-o. [DOI] [PubMed] [Google Scholar]
- 21.Kaya H, Chan HS. Proteins: Struct Funct Genet. 2000;40:637–661. doi: 10.1002/1097-0134(20000901)40:4<637::aid-prot80>3.0.co;2-4. [DOI] [PubMed] [Google Scholar]
- 22.Kelly JW. Nature. 2006;442:255–256. doi: 10.1038/442255a. [DOI] [PubMed] [Google Scholar]
- 23.Zhou Z, Bai YW. Nature. 2007;445:E16–E17. doi: 10.1038/nature05644. [DOI] [PubMed] [Google Scholar]
- 24.Sadqi M, Fushman D, Munoz V. Nature. 2006;442:317–321. doi: 10.1038/nature04859. [DOI] [PubMed] [Google Scholar]
- 25.Sadqi M, Fushman D, Munoz V. Nature. 2007;445:E17–E18. [Google Scholar]
- 26.Ferguson N, Sharpe TD, Johnson CM, Schartau PJ, Fersht AR. Nature. 2007;445:E14–E15. doi: 10.1038/nature05643. [DOI] [PubMed] [Google Scholar]
- 27.Huang F, Sato S, Sharpe TD, Ying L, Fersht AR. Proc Natl Acad Sci. 2007;104:123–127. doi: 10.1073/pnas.0609717104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Huyghues-Despointes Beatrice MP, Scholtz JM, Baldwin RL. Protein Science. 1993;2:80–85. 1604–1611. doi: 10.1002/pro.5560020108. [DOI] [PMC free article] [PubMed] [Google Scholar]; Huyghues-Despointes Beatrice MP, Klingler TM, Baldwin RL. Biochemistry. 1995;34:13267–13271. doi: 10.1021/bi00041a001. [DOI] [PubMed] [Google Scholar]
- 29.von Dreele PH, Poland D, Scheraga HA. Macromolecules. 1971;4:396–407. [Google Scholar]; von Dreele PH, Lotan N, Ananthanarayanan VS, Andreatta RH, Poland D, Scheraga HA. Macromolecules. 1971;4:408–417. [Google Scholar]; Ananthanarayanan VS, Andreatta RH, Poland D, Scheraga HA. Macromolecules. 1971;4:417–424. [Google Scholar]; Platzer KEB, Ananthanarayanan VS, Andreatta RH, Scheraga HA. Macromolecules. 1972;5:177–187. [Google Scholar]
- 30.Kamtekar S, Schiffer JM, Xiong HY, Babik JM, Hecht MH. Science. 1993;262:1680–1685. doi: 10.1126/science.8259512. [DOI] [PubMed] [Google Scholar]
- 31.Brunet AP, Huang ES, Huffine ME, Loeb JE, Weltman RJ, Hecht MH. Nature. 1993;364:355–358. doi: 10.1038/364355a0. [DOI] [PubMed] [Google Scholar]
- 32.Regan L, Degrado WF. Science. 1988;241:976–978. doi: 10.1126/science.3043666. [DOI] [PubMed] [Google Scholar]; Bryson J, Betz S, Lu H, Suich D, Zhou H, Oneil K, Degrado W. Science. 1995;270:935–941. doi: 10.1126/science.270.5238.935. [DOI] [PubMed] [Google Scholar]
- 33.Johansson JS, Gibney BR, Skalicky JJ, Wand AJ, Dutton PL. J Am Chem Soc. 1998;120:3881–3886. [Google Scholar]
- 34.Burkoth T, Beausoleil E, Kaur S, Tang D, Cohen F, Zuckermann R. Chem Biol. 2002;9:647–654. doi: 10.1016/s1074-5521(02)00140-0. [DOI] [PubMed] [Google Scholar]
- 35.Lee YC, Zuckermann RN, Dill KA. J Am Chem Soc. 2005;127:10999–11009. doi: 10.1021/ja0514904. [DOI] [PubMed] [Google Scholar]
- 36.Dill KA, Alonso DOV. Biochemistry. 1991;30:5974–5985. doi: 10.1021/bi00238a023. [DOI] [PubMed] [Google Scholar]
- 37.Greene RF, Jr, Pace CN. J Biol Chem. 1974;249:5388–5393. [PubMed] [Google Scholar]
- 38.Dill KA, Bromberg S. Molecular Driving forces. Garland Science; [Google Scholar]
- 39.Scholtz JM, Qian H, York EJ, Stewart JM, Baldwin RL. Biopolymers. 1991;31:1463–1470. doi: 10.1002/bip.360311304. [DOI] [PubMed] [Google Scholar]
- 40.Scholtz JM, Barrick D, York EJ, Stewart JM, Baldwin RL. Proc Natl Acad Sci. 1995;92:185–189. doi: 10.1073/pnas.92.1.185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Scholtz JM, Marqusee S, Baldwin RL, York EJ, Stewart JM, Santoro M, Bolen DW. Proc Natl Acad Sci. 1991;88:2854–2858. doi: 10.1073/pnas.88.7.2854. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Dimitriadis G, Drysdale A, Myers JK, Arora P, Radford SE, Oas TG, Smith DA. Proc Natl Acad Sci. 2004;101:3809–3814. doi: 10.1073/pnas.0306433101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Bryson JW, Desjarlais JR, Handel TM, Degrado WF. Prot Sci. 1998;7:1404–1414. doi: 10.1002/pro.5560070617. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Lumry R, Biltonen R, Brandts JF. Biopolymers. 1966;4:917–944. doi: 10.1002/bip.1966.360040808. [DOI] [PubMed] [Google Scholar]