Quantitative Ultrasound Assessment of the Rat Cervix

Abstract

Objective

The purpose of this research was to detect cervical ripening with a new quantitative ultrasound technique.

Methods

Cervices of 13 nonpregnant and 65 timed pregnant (days 15, 17, 19, 20, and 21 of pregnancy) Sprague Dawley rats were scanned ex vivo with a 70-MHz ultrasound transducer. Ultrasound scatterer property estimates (scatterer diameter [SD], acoustic concentration [AC], and scatterer strength factor [SSF]) from the cervices were quantified and then compared to hydroxyproline and water content. Insertion loss (attenuation) was measured in 3 rats in each of the 6 groups. Discriminant analysis was used to predict gestational age group (cervical ripening) from the ultrasound variables SD, SSF, and AC.

Results

Differences were observed between the groups (SD, AC, and SSF; P < .0001). Quantitative ultrasound measures changed as the cervix ripened: (1) SD increased from days 15 to 21; (2) AC decreased from days 15 to 21; and (3) SSF was the greatest in the nonpregnant group and the least in the day 21 group. Cervix hydroxyproline content increased as pregnancy progressed (P < .003) and correlated with group, SD, AC, and SSF (P < .001). Discriminant analysis of ultrasound variables predicted 56.4% of gestational group assignment (P < .001) and increased to 77% within 2 days of the predicted analysis. Cervix insertion loss was greatest for the nonpregnant group and least for the day 21 group.

Conclusions

Quantitative ultrasound predicted cervical ripening in the rat cervix, but before use in humans, quantitative ultrasound will need to predict gestational age in the later days of gestation with more precision.

The underlying mechanisms preceding labor are not yet fully understood. Preterm birth is the second leading cause of infant mortality in the United States.¹ Among the survivors, 20% to 25% have a major disability,² and it is estimated that just the initial neonatal care costs $6 billion annually.³ The preterm birth rate was 12.5% in 2004, and the 16% increase in the incidence of preterm birth in the United States between 1990 and 2004 is an indication of the seriousness of this problem.⁴ Reducing the preterm birth rate to 7% in the United States is a goal of the Healthy People 2010 initiative.⁵

As early as 1947, Danforth⁶ described the corpus of the uterus (mainly smooth muscle and contractile) and the cervix (mainly connective tissue and noncontractile) as histologic and functionally different structures. Interventions to delay preterm birth have focused on modifying the final phase of extensive uterine contractions (smooth muscle) and have not addressed the phasic nature of labor, which involves a long period of cervical ripening before the active phase of extensive uterine contractions and cervical dilatation. Without a ripe cervix, uterine contractions alone cannot accomplish the work of labor and birth.^7–9 Clinical and research efforts to modify cervical ripening have been limited by the lack of a reliable, valid, and noninvasive technique to measure cervical ripening. This research tested a new application of a noninvasive ultrasound technique, quantitative ultrasound (QUS), to determine cervical ripening in the rat.

Conventional B-mode ultrasonographic images are derived from backscattered radio frequency (RF) echo signals.¹⁰ The RF echoes contain frequency-dependent information about the smaller-scale structures (less than the wavelength of sound) in the tissues.¹¹ B-mode processing removes the frequency-dependent information. To quantify smaller-scale structures in tissues, the frequency-dependent information must be used.^11,12

Scatterer property estimates related to tissue microstructure can be made from the ultrasound backscatter RF signals.¹³ When an acoustic wave propagates through tissues, the spatially varying impedance differences cause acoustic waves to be scattered.¹⁴ Acoustic scattering theories for biological tissues assume that the tissues can be modeled as either discretely or continuously varying distributions of mass density and bulk compressibility.¹⁵ Scattering models from simple shapes (spheres and cylinders) have been solved analytically.¹⁶ To estimate 3 unique tissue-based parameters (scatterer diameter [SD], scatterer acoustic concentration [AC], and scatterer strength factor [SSF]), it is necessary to assume a geometric model (called a form factor) for the scatterers. These parameters were estimated by modeling the tissues as scatterers with a Gaussian form factor. The Gaussian form factor assumes that the scatterers do not have sharp discontinuities in acoustic impedance with the surrounding tissues (like glass beads in agar) but have more of a gradual change in impedance with surrounding tissues. The Gaussian form factor model was theorized to be appropriate for cervix tissue because this form factor has been shown to be a good predictor of scattering in many soft tissues.^17–21 The Gaussian form factor was chosen from several other available form factors because it gave the smallest χ² value relative to the scattered spectra. Furthermore, the properties of the spherical Gaussian model allowed rapid processing because it could be linearized in log space.¹²

The scatterer property estimates are made by comparing the backscatter power spectrum from a region of interest (ROI) in the tissues being evaluated, to a theoretical backscattered power spectrum. The backscattered power spectrum is parameterized to yield 3 quantifiable tissue-based parameters: SD, AC, and SSF. Scatterer diameter is related to the correlational length of the underlying structure. Scatterer AC is the number of scatterers per unit volume times the square of the relative impedance difference between scatterer and background. Scatterer strength factor is a combination of scattering size and scatterer AC. A further explanation of calculating the scatterer property estimates can be found in previous publications.^12,22,23

The cause of scattering has been hypothesized to be related to the amount of collagen in the tissues^24–26 and to the structure and function of the extracellular matrix.²⁷ The cervix is mainly composed of collagen (70% type I collagen, 30% type III collagen, and a small amount of type IV collagen) and only 5% to 10% smooth muscle cells.²⁸ In the cervix, collagen fibrils are 53 to 58 ± 3 nm in diameter, average about 2100 to 2200 ± 200 nm in length, and are packed in bundles.²⁹ During pregnancy, the total collagen content of the cervix increases, whereas the concentration of collagen decreases.^29–32 As the cervix ripens, the collagen fibrils become disorganized, and more space is created between the fibrils; thus, the concentration of collagen decreases.^29,30,32 Hydroxyproline is an amino acid unique to collagen and is used to measure the collagen content of tissues.³³ Hydroxyproline provides stability to the triple-stranded helical structure of collagen by forming hydrogen bonds.³³ The space in between the collagen fibrils is occupied by hyaluronan, decorin, water, and enzymes, which act synergistically to ripen the cervix in preparation for labor.³⁴ The hyaluronan content of the cervix increases with cervical ripening, creating a cell-free space, which allows substances and cells (fibroblasts, white cells, and smooth muscle cells) to move, divide, and migrate in the extracellular matrix.³⁵ Hyaluronan has a high capacity to bind water molecules, leading to loosening collagen fibrils and softening elastin.^36,37 Decorin is a proteoglycan that binds to the collagen fibrils regulating the interfibrillary distance, and increased expression results in collagen disorganization.³² Thus, this study’s hypothesis was that QUS will detect the changes in the microstructure of the rat cervix associated with ripening (collagen content and concentration).

Materials and Methods

Animals

The cervices of Sprague Dawley rats (Harlan, Indianapolis, IN) were scanned prospectively in 13 nonpregnant virgin rats and 65 timed pregnant rats (13 each at days 15, 17, 19, 20, and 21 of pregnancy). Rats were randomized into 6 groups (n = 13 rats per group). Power analysis for SD indicated that a sample size of 13 rats in each group would detect an effect size of 0.23 with a power of 0.90, using 1-way analysis of variance (2-tailed test) and α = .05 (nQuery Advisor; Statistical Solutions, Saugus, MA). A small effect size was chosen for this study because group intervals between scans (1–2 days) were small, and it was judged important not to waste the animal resources on an underpowered study. The experimental protocol was approved by the Institutional Animal Care and Use Committee at both the University of Illinois at Urbana-Champaign and the University of Illinois at Chicago and satisfied all campus and National Institutes of Health rules for the humane use of laboratory animals.

Procedure

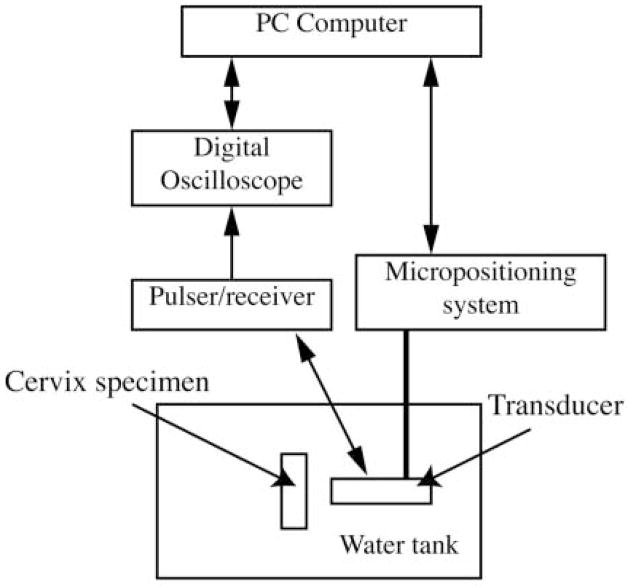
Before the rats were humanely euthanized, the experiment was prepared by placing degassed water (20°C–22°C) in a scanning tank (Figure 1). Ultrasonic scanning was accomplished with a custom-fabricated 70-MHz lithium niobate transducer (National Institutes of Health Transducer Resource Center, University of Southern California, Los Angeles, CA) and a Panametrics (Waltham, MA) 5900 pulser/receiver. The water temperature was recorded for each scan. Each rat was weighed before necropsy, and the cervix was dissected, trimmed, weighed, and then immediately sealed in plastic wrap and taped to the holder (Figure 2A) that would be placed in the tank of degassed water (Figure 2B). The cervix specimen in the holder was placed at the approximate focal length of 6.75 mm, and fine adjustments were made with the computer-controlled micropositioning system (Daedal, Inc, Harrisburg, PA) until a maximum-amplitude echo signal from the tissue was obtained on the oscilloscope. Each cervix specimen was scanned 7 mm longitudinally in the middle of the cervix and 5 mm transversely at the superior margin near the internal os of the cervix. Only 2 scans of each cervix were conducted because of the time required for data acquisition (20 minutes per scan) and concern for tissue integrity due to the time that the tissue was ex vivo. A B-mode image of each specimen was generated from the RF echoes of the longitudinal scan to ensure that the tissue was in the field’s depth of focus.

Figure 1.

Experimental setup.

Figure 2.

A, Cervix specimen wrapped in plastic wrap and placed in the holder. B, Cervix specimen in the holder in the scanning tank of degassed water with a 70-MHz lithium niobate transducer placed at focal zone to the specimen (6.5 mm).

A backscatter power spectrum was then calculated for each scan line by gating the time signal corresponding to the chosen ROI. The total power spectrum for the ROI was determined by averaging the power spectra from each individual scan line corresponding to the ROI. The optimal size of each ROI was 10 times the wavelength axially and 5 times the beam width laterally.²² Estimates of SD, AC, and SSF were obtained for each ROI by comparing the total power spectrum with the theoretical power spectrum. Three parameterized values (SD, AC, and SSF) for each cervix specimen were determined by averaging each of them from the processed longitudinal and transverse ROIs. The average number of ROIs per scan was 350 (range, 153–567). The size of each ROI was 400 × 400 μm (5 beam widths laterally by 12 pulse lengths axially).²² The number of ROIs per scan depended on the thickness of the cervix tissue. These ultrasound measures would be compared to 1 mean hydroxyproline and water value for each cervix.

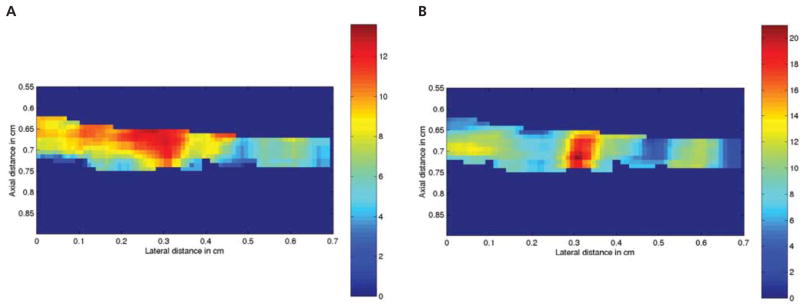
The loss of energy in the ultrasound beam as ultrasound propagates through tissue, insertion loss (or attenuation), is a function of tissue properties and the frequency of ultrasound.³⁸ Tissue-specific attenuation is essential in calculating the ultrasound backscatter measures of SD, AC, and SSF. Corrections to the total backscatter power spectrum were made for tissue-specific insertion loss for each gestational age (GA) group as well as for the attenuation of the plastic wrap. Insertion loss was estimated by comparing the signal when the sample was inserted into the ultrasound beam relative to when the sample was not present.²⁷ Each ROI was converted into a color-coded pixel that represented the average SD and SSF (Figure 3). All processing of ultrasound data was conducted with MATLAB software (The MathWorks, Natick, MA).

Figure 3.

Quantitative ultrasonographic images of rat 64 cervix (day 19 of pregnancy). A, Image of SD where each pixel represents 1 mean ROI in micrometers (range, 2–12 μm). B, Image of SSF where each pixel represents 1 mean ROI in negative decibels (range, −2 to −20 dB).

Cervical Tissue Processing

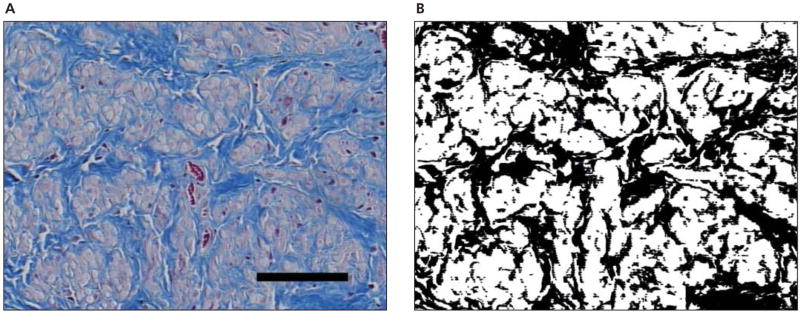
After the cervix specimen was scanned, one fifth of the cervix was dissected freehand, placed in formalin, embedded in paraffin, sectioned, mounted on a glass slide, and stained with Masson trichrome stain. To quantify the distribution of collagen, a transverse and longitudinal section of each specimen was photographed at ×20 magnification using a Nikon microscope imaging workstation (Nikon Instruments Inc, Melville, NY) and saved as digital images that were colorized in Photoshop (Adobe Systems Inc, San Jose, CA). The blue-stained collagen areas on the histologic slide were colorized to black, and the rest of the tissue was colorized to white (Figure 4). The black and white pixels were counted with a MATLAB program to quantify the collagen in each histologic slide.

Figure 4.

A, Masson trichrome-stained histologic slide (original magnification ×20) of a longitudinal section of the cervix of rat 64 (day 19 of pregnancy). Collagen is stained blue, and smooth muscle is pink/red. The solid bar represents 100 μm. B, Colorized histologic slide. Collagen was colorized black, and the rest of the tissue was white. The ratio of collagen pixels to white pixels (averaging cross and longitudinal sections) was 0.45.

The remainder of the specimen was flash frozen in liquid nitrogen until a solid pellet was formed, wrapped, and placed in a plastic bag in a −70°C freezer until all the samples could be analyzed at the same time. Before chemical analysis at the University of Illinois at Urbana-Champaign, Department of Animal Sciences, samples were ground under liquid nitrogen. Water, nitrogen, and hydroxyproline contents of the specimens were analyzed by methods 934.01, 992.15, and 990.26, respectively, of the Official Methods of Analysis of the Association of Official Analytical Chemists.³⁹ The nitrogen content of the cervix was measured to produce a crude protein value for each cervix. Hydroxyproline was calculated as a portion from the crude protein. To obtain water content, a sub-sample of each specimen was placed in previously dried crucibles, weighed, dried in a 105°C oven overnight, and weighed again. The percentage of dry matter was calculated by subtracting the wet weight in the crucible from the dry weight and multiplying by 100 (method 934.01) with an accuracy of ±0.4 mg.³⁹ The sensitivity to detect a difference in water percentage was ±0.01%.³⁹ After the water content was determined, these specimens were used to determine total nitrogen via combustion using a Leco FP2000 analyzer (Leco Corporation, St Joseph, MN) (method 992.15). Another sub-sample of each specimen was hydrolyzed in 6-N hydrochloric acid for 16 hours in a 105°C oven; water was added to the test tube and mixed; and the aliquot was filtered through Whatman 541 filter paper (Whatman Inc, Florham Park, NJ) with activated charcoal (method 990.26).³⁹ The filtrate aliquot was then diluted by a factor of 10, and 2 mL of chloramine T (oxidant solution) was added to each tube. After 20 minutes, 1 mL of 4-dimethylaminobenzaldehyde (color reagent) was added to each tube, and the tubes were incubated for 15 minutes in a 60°C water bath. The tubes were cooled under running water for 3 minutes and then read with a spectrophotometer at 558 nm.³⁹ The accuracy of the method to detect a difference in hydroxyproline was a hydroxyproline concentration of 1.2 to 4.8 μg/mL. The laboratory conducting the compositional analyses was blinded to the GA group of the specimens.

Statistical Analysis

The data were analyzed with SPSS 13.0 software (SPSS Inc, Chicago, IL), tested for normality, linearity, and outliers. Descriptive statistics were calculated for all the variables and analyzed by group. One-way analysis of variance (F ratio, between-groups degrees of freedom, followed by within-groups degrees of freedom) with Tukey post hoc tests (to determine between group differences) were conducted for age of the rats, duration of the experiment, pre-experiment and post-experiment cervix weight, percentage of water/cervix, percentage of hydroxyproline/cervix, SD, AC, and SSF to determine significant differences by GA group. Pearson correlations (r statistic: + for a positive relationship and − for a negative relationship) were conducted to determine the relationship between the following variables: GA group, hydroxyproline, SD, AC, SSF, and collagen-stained pixels. Discriminant analysis was used to predict GA group from the ultrasound variables SD, SSF, and AC, as well as to build a statistical prediction model for future use. Discriminant analysis was used rather than regression analysis because of the colinearity of SD, AC, and SSF with each other. Colinearity would violate an important assumption of independence of the variables for regression analysis.⁴⁰ The level for statistical significance was P < .05.

Results

Complete data were collected on 78 Sprague Dawley rats, including 65 timed pregnant rats and 13 virgin nonpregnant Sprague Dawley rats. The 13 nonpregnant rats were a group of rats that were scheduled to be euthanized from another investigator’s study and thus were considerably older than the timed pregnant rats purchased specifically for this study. In addition to data being acquired for all 78 rats, insertion loss data were collected on 3 rats in each group for the last 18 rats in the study. Table 1 lists rat and pup characteristics.

Table 1.

Characteristics of the Sample by Groups

Characteristic	n	Nonpregnant	Day 15	Day 17	Day 19	Day 20	Day 21	Statistics
Rat age, d*	78	215 (25)	108 (14)	108 (14)	108 (14)	110 (13)	111 (11)	F5,72 = 93.61; P < .0001
Rat weight, g	78	301 (17)	286 (15)	298 (16)	323 (39)	349 (24)	353 (36)	F5,72 = 14.86; P < .0001
No. of pups	65	0	13	12	11	13	13	F4,60 = 0.84; P = .51
Pup weight, g	65	0	0.4 (0.1)	1.1 (0.2)	2.7 (0.4)	4.2 (0.3)	5.4 (0.6)	F4,60 = 5.26; P < .0001
Duration of experiment, min†	78	99 (51)	90 (10)	95 (33)	108 (53)	88 (32)	105 (37)	F5,72 = 0.50; P = .77
Rat cervix weight, mg	78	66 (13)	74 (10)	88 (11)	97 (11)	99 (18)	114 (23)	F5,72 = 17.33; P < .0001
Cervix length, mm	78	5.9 (0.6)	6.4 (0.5)	6.7 (0.6)	6.8 (0.8)	5.8 (0.8)	5.9 (0.7)	F5,72 = 5.26; P < .0001
Cervix width, mm	78	3.0 (0.4)	3.1 (0.5)	3.4 (0.4)	3.3 (0.6)	3.3 (0.5)	3.7 (0.6)	F5,72 = 3.28; P = .01
Cervix depth, mm	78	4.4 (0.4)	4.7 (0.5)	4.7 (0.7)	4.7 (0.7)	5.1 (0.4)	6.1 (1.1)	F5,72 = 9.82; P < .0001

Values are expressed as mean (standard deviation); n = 13 rats in each group.

^*Age was not significantly different among pregnant groups; F_4,60 = 0.14; P = .96.

^†Time from euthanasia until the cervix specimen was frozen.

For each sample, the mean SD, AC, and SSF values were determined. Figure 3 shows that for 2 of these parameters, there was heterogeneity as a function of position. Table 2 lists the ultrasound and compositional measures of the cervix by group. Except for the day 17 group, which had the largest SD, there was a trend of increasing SD from the day 15 group toward day 21 of pregnancy (Table 2). Except for the day 17 group, which had the least AC, the AC decreased from the non-pregnant group to the day 21 group. Scatterer strength factor was the greatest in the nonpregnant group and the least in the day 21 group. Day 17 SSF was almost as low as the day 21 SSF. There was a significant linear decrease in the percentage of hydroxyproline (P < .0001) and an increase in the micrograms of hydroxyproline per cervix (P < .003) from the day 15 group to the day 21 group (Table 2). These findings suggest that, as pregnancy progresses, the total hydroxyproline content per cervix increases, whereas the concentration of hydroxyproline decreases.

Table 2.

Sonographic and Compositional Measures of the Cervix

GA of Rat	n	SD, μm*	AC, dB/mm3†	SSF, dB/mm3‡	Hydroxyproline/Cervix, %§	Hydroxyproline/Cervix, μg/mg||	Water/Cervix, %	Ratio of Collagen Pixels¶
Nonpregnant	13	10.4 (0.6)#	−118 (6)#**	2.8 (1)#**	0.88 (0.1)#**	568 (75)#**	68 (5)	0.83 (0.3)
Day 15	13	8.2 (1.3)#**	−130 (7)**	−1.5 (1)	0.72 (0.1)#**	532 (83)**	69 (8)	0.69 (0.3)
Day 17	13	11.2 (0.8)#	−144 (7)#	−2.3 (2)	0.68 (0.1)	603 (103)	68 (5)	0.61 (0.2)
Day 19	13	8.6 (1.2)	−130 (5)**	−1.2 (1)	0.62 (0.1)#	605 (75)#	69 (6)	0.69 (0.2)
Day 20	13	8.8 (1.0)	−136 (8)	−2.2 (2)	0.64 (0.1)#	640 (131)#	69 (4)	0.58 (0.2)
Day 21	13	10.0 (1.7)#	−141 (11)#	−2.7 (2)	0.62 (0.1)#	707 (153)#	68 (6)	0.70 (0.3)
Statistic		F5,72 = 10.72; P < .0001	F5,72 = 19.47; P < .0001	F5,72 = 26.47; P < .0001	F5,72 = 107.45; P < .0001	F5,72 = 4.09; P < .003	F5,72 = 0.24; P = .24	F5,72 = 1.6; P = .17

Values are expressed as mean (standard deviation)

^*Scatterer diameter = correlational length of the scatterer; differences among groups.

^†Acoustic concentration = number of scatterers/mm³ − (average impedance of scatterers)².

^‡Scatterer Strength Factor = AC × (average radius of scatterers)⁶.

^§Concentration of hydroxyproline per cervix, wet weight.

^||Content of hydroxyproline per total cervix, wet weight.

^¶Ratio of collagen-stained pixels compared with stained cells (smooth muscles and white cells) per digital histologic slide at ×20 magnification.

^#**Tukey post hoc tests to determine between-group differences:

^#P < .01 versus day 15 group;

^**P < .01 versus day 21 group.

The percentage of water per cervix (P = .24) and the ratio of collagen-stained pixels on the histologic slides (P = .17) were not significantly different among the groups (Table 2). The percentage of hydroxyproline was significantly correlated with group (r = −0.70; P < .001). The ratio of collagen-stained pixels on the histologic slides was significantly correlated with AC (r = +0.39) and SSF (r = +0.35; P < .001).

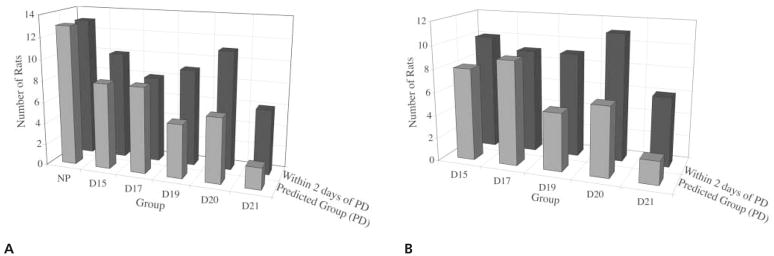
To predict the day of gestation, and thus cervical ripening, from the ultrasound variables, discriminant analysis was used. Two discriminant analysis models were calculated to predict group classification: 1 that included the nonpregnant group with the pregnant groups and 1 that only included the pregnant groups.

The first discriminant analysis model, which included the nonpregnant and pregnant groups, determined that SD, AC, and SSF significantly predicted group assignment (Wilks λ = 0.187; χ²[15] = 121.6; P < .0001), with 70% of the variance explained by the model. Scatter strength factor contributed most to the model (r = +0.98), followed by AC (r = +0.73) and SD (r = +0.23). With all the ultrasound variables entered into the model, the following discriminant function equation was calculated to predict GA group: GA = 1.20 × SSF − 0.28 × AC + 0.16 × SD. Overall, this model correctly predicted group membership for 56.4% of the cases (Figure 5A). Predicting the exact day of gestation is difficult in any biological model. Therefore, the model was analyzed within 2 days of the predicted gestational day as well (Figure 5A). The number of correct gestational day classifications increased from 56.4% in the predicted model to 77% within 2 days of prediction analysis. The model predicted 100% of the nonpregnant group and performed the poorest in the day 21 group.

Figure 5.

A, Discriminant analysis group classification for the nonpregnant (NP) and pregnant groups, using the ultrasound measures of SD, AC, and SSF for the predicted group (Wilks λ = 0.187; χ²[15] = 121.6; P < .0001) and within 2 days of the predicted group; n = 13 per group. B, Discriminant analysis group classification for the pregnant groups only, using the ultrasound measures of SD, AC, and SSF for the predicted group (Wilks λ = 0.451; χ ²[12] = 47.8; P < .0001) and within 2 days of the predicted group; n = 13 per group. D indicates day of pregnancy; and PD, predicted day of gestation.

Because the nonpregnant group SD, AC, and SSF were so different from those of the pregnant groups, a second discriminant analysis was conducted considering only the pregnant groups in the model. The model was again found to be significant (Wilks λ = 0.451; χ²[12] = 47.84; P < .0001), with 86% of the variance explained by the model. In this model, SD contributed most to the model (r = +0.96), followed by AC (r = +0.75) and SSF (r = −0.30). The following discriminant function equation was calculated to predict GA group: GA = 1.26 × SD − 0.787 × SSF + 0.594 × AC. Again, most of the errors in classification were within 2 days of the predicted group. Correct classification of groups increased from 46% in the predicted model to 69% within 2 days of the predicted model (Figure 5B). The model predicted the day 15 and 17 groups the best and the day 21 group the least.

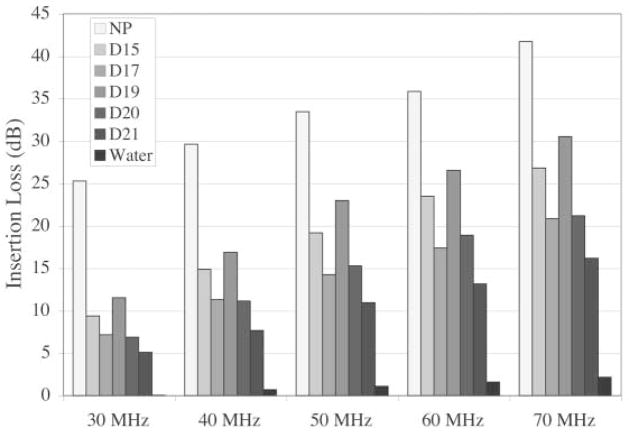
Insertion loss was the greatest for the nonpregnant group and the least for the day 21 group across the frequency range between 30 and 70 MHz (Figure 6). Insertion loss for the water path of the ultrasound beam was given as a reference point.

Figure 6.

Mean insertion loss in decibels for cervix samples by groups (temperature, 21.8°C) compared with insertion loss of water (temperature, 22°C) for frequency ranges of 30 to 70 MHz; n = 3 per group. D indicates day of pregnancy; and NP, nonpregnant.

Discussion

In this study, QUS was used to examine the microstructural changes in the cervix throughout pregnancy. Based on previous work,^24,25,27 it was hypothesized that ultrasound scattering was related to the organization and content of collagen in tissues. As pregnancy progressed, the total collagen content of the cervix increased, whereas the concentration decreased as fibers disorganized and more space was created between the collagen fibers.³² In a study of cervical ripening in pregnant rats, Feltovich and coworkers²⁹ found little change in the diameter of the collagen fibrils (53 ± 3 nm control, 58 ± 3 nm after ripening) but significantly more space between fibrils as the cervix ripened. In our study, SD varied little during pregnancy, whereas AC decreased significantly as pregnancy progressed. This suggests that the scattering size did not markedly change, but the concentration of the scatterers in the cervix tissue did decrease as pregnancy progressed. There was a significant correlation between the ratio of collagen pixels on the colorized histologic slides and AC and SSF, giving further evidence to suggest a relationship between scattering and collagen. Future research is warranted to relate interfibrillary distance of collagen fibrils to SD, AC, and SSF. However, our study did determine significant correlations between the hydroxyproline percentage and content of the cervix specimens with GA group, AC, and SSF.

The day 17 group presented a different pattern for SD, AC, and SSF. The data were analyzed for outliers, and the standard deviations were very similar to those of the other groups. The differences between the day 17 group and the other groups cannot be explained by differences in methods. Around day 17 or 18 in the rat pregnancy, marked changes occurred with collagen content and glycosaminoglycan content and distribution in the ripening cervix.^30,32 It is possible that the day 17 pattern of SD, AC, and SSF showed these morphologic changes, heralding the onset of cervical ripening.

The cervical water content did not significantly vary among groups. All animals were allowed food and water ad libitum before scanning. A previous report³⁰ noted only a 3% increase in cervix water content from the nonpregnant state until term, and proteoglycans have been found to be the main component in the extracellular matrix during ripening.³⁴

The marked GA differences in insertion loss of the cervix were unexpected findings. Tissue-specific attenuation is essential in calculating the ultrasound backscatter measures of SD, AC, and SSF. Insertion loss in tissues has been related to the structure of tissue⁴¹ and the type of tissue.²⁵ In tissues such as the cervix, where dynamic structural changes occur with cervical ripening, it is important to use a measured insertion loss rather than a value that is a tissue average. The non-pregnant cervix had the highest insertion loss, and the day 21 pregnant cervix had the least. In this study, insertion loss was only measured in 3 rats in each group to obtain a mean attenuation coefficient for each GA group. Refining the methods by measuring insertion loss for each animal and using that unique value in the calculation of QUS may improve detection of cervical ripening.

In summary, this article reports the use of QUS to detect GA changes in the cervix. Although the discriminant function analysis significantly predicted GA group using the ultrasound parameters of SD, AC, and SSF, for this technology to be useful in humans, it must predict the later days of pregnancy with more precision. We anticipate that we can improve the prediction of cervical ripening with QUS by (1) making the measurements in vivo; (2) measuring insertion loss in each individual case; and (3) using the unique insertion loss measurement for each case to calculate SD, AC, and SSF. Before this technology can be used with humans, the following must occur: (1) the frequency that best shows the microstructural changes in the cervix associated with cervical ripening must be determined; (2) the content and distribution of collagen from histologic slides must be validated with QUS; and (3) an in vivo scanning method must be developed in the animal model. The computer processing of QUS could be automated, thus making it user-friendly and fast. Quantitative ultrasound could be an added feature to commercial ultrasound systems available to clinicians. This technology has the potential to affect the care of pregnant women by providing a non-invasive technique to detect cervical ripening.

Abbreviations

AC

acoustic concentration

GA

gestational age

QUS

quantitative ultrasound

RF

radio frequency

ROI

region of interest

SD

scatterer diameter

SSF

scatterer strength factor