Abstract
Previous work on pure tone intensity discrimination in school-aged children concluded that children might have higher levels of internal noise than adults for this task [J. Acoust. Soc. Am. 120, 2777–2788 (2006)]. If true, this would imply that psychometric function slopes are shallower for children than adults, a prediction that was tested in the present experiment. Normal hearing children (5–9 yr) and adults were tested in a two-stage protocol. The first stage used a tracking procedure to estimate 71% correct for intensity discrimination with a gated 500 Hz pure tone and a 65 dB sound pressure level standard level. The mean and standard deviation of these tracks were used to identify a set of five signal levels for each observer. In the second stage of the experiment percent correct was estimated at these five levels. Psychometric functions fitted to these data were significantly shallower for children than adults, as predicted by the internal noise hypothesis. Data from both stages of testing are consistent with a model wherein performance is based on a stable psychometric function, with sensitivity limited by psychometric function slope. Across observers the relationship between slope and threshold conformed closely to predictions of a simple signal detection model.
INTRODUCTION
School-aged children perform more poorly than adults in a wide range of psychoacoustic paradigms including simple tasks, such as detection of a tone (Fior, 1972; Maxon and Hochberg, 1982; Allen and Wightman, 1994), frequency discrimination (Maxon and Hochberg, 1982; Jensen and Neff, 1993), and gap detection (Irwin et al., 1985; Wightman et al., 1989; Trehub et al., 1995), as well as more complex tasks, such as speech recognition under challenging listening conditions (Elliott, 1979; Nabelek and Robinson, 1982) and informational masking (Allen and Wightman, 1995; Oh et al., 2001; Wightman et al., 2003; Hall et al., 2005). While there have been many reports documenting this poorer performance, there is little consensus regarding the underlying cause of elevated thresholds in school-aged children.
Whereas the auditory peripheral physiology is thought to be functionally mature well before the school-aged years (e.g., Abdala and Folsom, 1995), there is evidence of continued development in auditory cortex (Moore and Linthicum, 2007) and more general cognitive development not specifically related to auditory processing (e.g., Gomes et al., 2000) throughout this period. A wide range of nonsensory factors has been proposed to account for the poor psychoacoustic data of school-aged children. Some are based on general cognitive development, such as central noise due to fluctuations in attention, unstable decision criteria or memory limitations (e.g., Allen et al., 1998; Wightman et al., 1989; Allen and Nelles, 1996). Others may be more specific to auditory processing, including an inability to optimally combine or switch among sensory cues (Allen et al., 1989), immature sound source determination (Leibold and Neff, 2007), reduced listening efficiency (Hall and Grose, 1991; 1994), inability to listen in a frequency selective manner (Allen and Wightman, 1994; Stellmack et al., 1997; Lutfi et al., 2003), poor temporal focus of attention (Sutcliffe and Bishop, 2005), and relatively ineffective combination of information distributed over time (Schneider and Trehub, 1992).
Whereas any one or more of these interrelated factors could affect thresholds of school-aged children, some researchers conclude that general developmental factors nonspecific to auditory processing fail to explain the developmental effects observed. For example, Schneider et al. (1989) argued that the relative stability of thresholds over time and the small effects of changing the task reward structure indicate that motivation and inattention play little, if any, role in the poorer performance of child observers. While the combination of sensory cues almost certainly plays a role in the performance of young children under some listening conditions, the data of Willihnganz et al. (1997) suggest that maturation of listening strategy cannot account for developmental effects observed under complex listening conditions.
Several previous studies have proposed that increased internal noise could account for the reduced sensitivity in psychoacoustic tasks for child observers as compared to adult observers. For example, Schneider and co-workers (1989; 1992) proposed that the sensitivity with which child observers are able to detect a tone in a masking noise could be limited by internal noise. They tested this hypothesis by estimating percent correct for detection of a tone masked by a 1∕3-octave band of noise. If higher levels of internal noise were responsible for threshold elevation, this should be reflected in shallower psychometric function slopes. Contrary to initial predictions, psychometric functions from group data in that study failed to provide compelling evidence of shallower psychometric functions for children as compared to adults (Schneider et al., 1989). Other studies have estimated psychometric functions for individual observers and found the expected increase in slope with age (Allen and Wightman, 1994; Bargones et al., 1995). Whereas the literature is somewhat inconclusive regarding the role of internal noise in the detection of a tone, the present study set out to delineate the role of internal noise for intensity discrimination for a suprathreshold tonal signal.
A recent study by Buss et al. (2006a) argued that the poor intensity discrimination thresholds obtained in school-aged children is consistent with increased internal noise. The phrase internal noise is sometimes used in a very broad sense, describing any source of inaccuracy in processing that might account for deviations from optimal performance, including factors specific to auditory processing, such as jitter in peripheral encoding of sounds, and other more general functions related to cognitive processing, such as transient attention to the task or variable strategy in utilizing the available sensory cues. Buss et al. (2006a) hypothesized that the poor performance of child observers and the inferred elevation of internal noise could be due to variability in the neural representation of intensity rather than nonauditory factors. Briefly, that study showed that stimulus variability within or across intervals affected intensity discrimination thresholds of adults to a greater extent than those of children. This finding is broadly consistent with a simple model incorporating higher levels of internal noise for child than adult observers and predicts that psychometric function slope for intensity discrimination should be shallower for child than adult observers. If this is the case, then the data of children should conform to the basic assumptions of signal detection theory, and, in particular, the assumption that a single psychometric function accurately describes performance over time. In contrast, if variable response strategies or transient inattention were responsible for poor performance, then this would be reflected in greater variability in behavioral data over time.
Stability of the psychometric function underlying performance was assessed in the present study in two ways. The first stage of testing used an adaptive procedure to estimate threshold, incorporating two interleaved tracks that converged on a single value (71% correct). This general strategy was proposed by Leek et al. (1991) to identify shifts in the psychometric function characterizing performance over time; using this method, a shift in the psychometric function within a block of trials results in increased statistical dependence across pairs of interleaved tracks. That is, trials from both tracks occurring in close temporal proximity should reflect a slow shift in psychometric function, and therefore be highly correlated. A second approach was to compare replicate estimates of percent correct, with the expectation that variability around those estimates would be elevated if the psychometric function underlying performance shifted over the course of multiple blocks of trials. In both cases, variability of child and adult data was expected to be comparable. If that were not the case, and child data were more variable, this result would undermine the psychometric function fit and complicate interpretation of the slope parameter.
Internal noise in the present study was estimated based on the slope of the psychometric function. Because intensity discrimination for a pure tone signal is thought to be limited by internal noise, the slope of the function directly reflects the magnitude of that noise (Jesteadt et al., 2003). Therefore, if poorer performance of child observers is due to higher levels of internal noise, then this should be reflected in proportionally shallower psychometric function slopes.
METHODS
Observers
The child group included 16 observers, 6 males and 10 females, ages 4.9–9.4 yr (mean 7.1 yr). The adult group included 11 observers, 5 males and 6 females, ages 19.0–55.2 yr (mean 26.7 yr). All observers had pure tone thresholds equal to or better than 15 dB HL for octave frequencies 250–8000 Hz in the test ear (ANSI, 1996). None of the observers had a history of hearing or ear-related problems.
Stimuli
The stimulus was a 500 Hz pure tone, gated on for 500 ms including 50 ms ramps computed as one-half of the period of a raised cosine. In the standard intervals this tone was presented at 65 dB sound pressure level (SPL), and in target intervals it was more intense. The intensity increment in the target interval was defined in units of 10 log(ΔI∕I).
Procedures
Stimuli were presented in a three-alternative forced-choice procedure, with one randomly selected interval containing the target stimulus. Intervals were separated by 600 ms. An animated sequence marked the three listening intervals, after which the observer was prompted to select the target interval via associated buttons on a touch-screen computer monitor. After each correct answer, a small portion of a cartoon picture was revealed, in the style of a puzzle piece. A progress bar at the top of the screen reflected progress through the run. At the end of a run, the cartoon picture was fully revealed, and it performed a brief animation. Data collection was completed in a single 1 h session for adults, whereas child observers took two 1 h sessions.
Testing included two stages. In the first stage an adaptive 2-down, 1-up tracking paradigm was used to estimate the 71% correct point on the psychometric function (Levitt, 1971). Following the procedures proposed by Leek et al. (1991), there was a single tracking rule for all trials up to the second track reversal, wherein the signal level was adjusted in relatively large steps of 4 dB. After the second reversal, the track split into two interleaved tracks, and the stepsize for signal level adjustment was reduced to 2 dB. From that point on, one track determined the course of even numbered trials and the other determined the course of odd numbered trials. These two tracks continued until both had achieved six or more reversals and there was an equal number of trials in both tracks. Thresholds were calculated as the mean level at reversals 3–6 of each track. The standard deviation across those reversal levels was also recorded for each track. This procedure was performed twice, for a total of four estimates of threshold (m) and four associated standard deviations (s).
Estimates obtained in the first procedure were averaged for each observer, resulting in an overall estimate of threshold and average standard deviation . These values were interpreted as initial estimates of the 71% correct point and psychometric function slope, respectively. A set of five signal levels was computed for each observer based on these results, defined as , , , , and . Percent correct was then estimated at each of these five signal levels. Data were collected in ten blocks of 40 trials; within a block there were eight presentations of each of the five signal levels, with those signal levels presented in random order.
RESULTS
Prior to data analysis all variables were assessed for normality using a one-sample Komogorov–Smirnov test, both in the aggregate and for the two groups separately. For all parametric statistics reported below, this test failed to reject the null hypothesis that data were normally distributed (p⩾0.10). These criteria of normality were also met for statistics on derived parameters (e.g., estimates of psychometric function slope). Data from the adaptive track procedure were analyzed in units of 10 log(ΔI∕I), the same units used to adjust signal level. Units of ΔL were used in analysis of the percent correct data in order to facilitate comparison with previous results of Buss et al. (2006a). While the best units for representing intensity discrimination is a topic of debate (Buus and Florentine, 1991; Moore et al., 1999), the choice between 10 log(ΔI∕I) and ΔL was of little consequence in the present case; repeating analyses in each of these units did not affect the general conclusions of the study.
Statistics below were performed excluding the data of one child observer (C4) whose results were notably poorer than those of her peers. While these data may accurately reflect this observer’s psychophysical performance, it was decided to consider the trends exhibited by the other 15 children. Results of the outlier child observer are indicated in the data figures with a filled symbol except where values fell outside reasonable axis limits.
Thresholds based on adaptive tracks
Intensity discrimination thresholds obtained in the first stage of testing were higher for child than adult observers, with respective means of 0.20 and −4.96 dB [10 log(ΔI∕I)]. This group difference was significant (t24=5.54, p<0.0001). Within the child data, a regression analysis of the threshold on age resulted in a significant trend for improvement with age (β=−0.86, t12=2.20, p<0.05 one-tailed). These results confirm that intensity discrimination is different in adults as compared to school-aged children, with evidence of significant improvement between 5 and 9 yr of age.
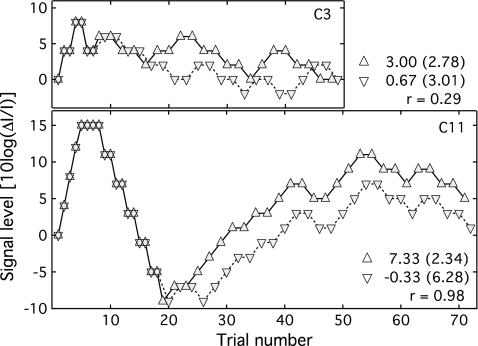
Because the adaptive runs split into two interleaved tracks after the second track reversal, it is possible to test the hypothesis that threshold elevation in child observers is due to the instability of the underlying psychometric function, such as might occur with fluctuations in attention or changes in response strategy. Figure 1 shows the example tracks from the child dataset, with signal intensity plotted as a function of trial number. The top panel shows the second adaptive track for observer C3, a 5.7 yr old. In this example, the first phase of the track, characterized by a single track trajectory and large stepsize, lasted for seven trials; after this point, signal level was controlled by the two interleaved tracks. These data reflect some improvement as a function of trial number, but the interleaved tracks are not uniformly parallel, consistent with the interpretation that performance is relatively free from shifts in attention or listening strategy over the course of the trial. The bottom panel shows the second adaptive track for C11, a 7.9 yr old. In this track the signal level rose to the ceiling of 15 dB, fell precipitously, and then gradually increased; the two tracks split apart after the 18th trial but remained largely parallel. It seems likely that this child was confused about the task demands at the outset of the track, adopted a more effective strategy for trials 8–20 and then reverted to a less optimal approach to the task at the end of the track. While the data of C11 are consistent with cognitive dependencies rather than purely auditory limits to performance, this pattern of results was unique among child observers, with the remaining datasets more closely resembling C3 with respect to the relationship of performance across tracks.
Figure 1.
Signal intensity is plotted as a function of trial number for two observers. The top panel shows data for C3, which is representative of the child data. The bottom panel shows data for C11, a unique case where the two interleaved tracks were highly correlated. Symbols reflect the two tracks, which do not diverge until after the second track reversal. The legend shows the mean and standard deviation associated with each track, as well as the correlation between tracks.
The statistical dependence of pairs of interleaved tracks was assessed by comparing the correlation between signal levels in pairs of interleaved tracks for child and adult observers. If instability in the psychometric function were responsible for poor performance in children, and if fluctuations in that function spanned two or more trials, then the intertrack correlation should be greater for child than adult observers. Data were retrieved from disk for the second adaptive run of each observer excluding the last two child observers run on the experiment; files for these two observers were lost due to computer error. For each dataset, the initial trials using a large stepsize and a single tracking trajectory were excised, leaving only trials in which the small stepsize and the interleaved tracking procedures were used. The first trial from each track was omitted, to allow the two tracks to diverge, and the resulting arrays were used to calculate the Pearson product correlation across tracks. Units of 10 log(ΔI∕I) were adopted for this analysis.
The median intertrack correlation was r=−0.11 for adults (spanning r=−0.44 to 0.58) and r=0.01 for children (spanning r=−0.88 to 0.98). If the processing underlying performance is variable over the course of a run, this could be reflected in a relatively high correlation across tracks. A t-test assuming unequal variance failed to reject the null hypothesis of equal correlation (t22=0.42, p=0.68). Within the child group there was no correlation between child age and track correlation (r=−0.47, p=0.10). These results can be summarized as showing no reliable age effect for intertrack correlation, either across age groups or within the child group, a result that is consistent with comparable stability of the underlying psychometric function over the course of trials.
Psychometric function fits
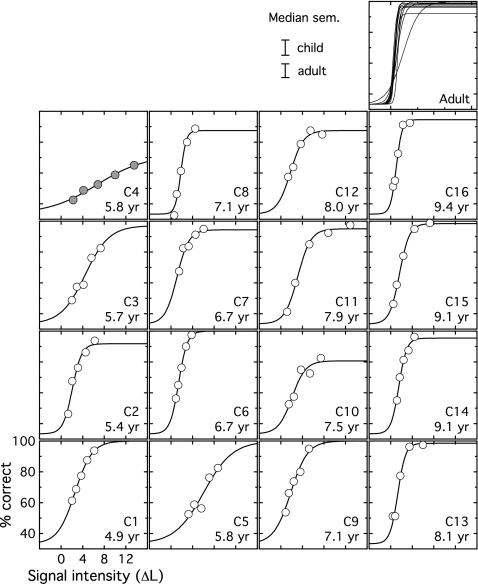
In the second stage of testing, percent correct was measured for a set of five fixed signal levels, based on the mean threshold and standard deviation of each observer’s data from the first stage. Results are shown in Fig. 2, where percent correct is plotted as a function of signal intensity in units of ΔL. Circles indicate estimates of percent correct, with 80 trials at each level. Each child observer’s data appear in a separate panel, with age of the observer indicated in the lower right corner. The median standard error of the mean (sem) for each group of observers is shown in the legend of Fig. 2. The relationship between sem of child and adult estimates was assessed statistically by applying an arcsine transform to all estimates of percent correct and computing the sem across the ten replicate estimates at each signal level. The resulting values were submitted to a repeated measures analysis of variance (ANOVA), with two levels of GROUP (child, adult) and five levels of SIGNAL (the five signal levels unique to each observer). This analysis revealed a main effect of SIGNAL (F4,96=4.67, p<0.05), no effect of GROUP (F1,24=0.19, p=0.66) and no interaction between GROUP and SIGNAL (F4,96=2.15, p=0.08). This result confirms that the variability in percent correct data of child and adult observers was comparable.
Figure 2.
Percent correct data are shown for individual child observers, plotted in percent correct as a function of intensity increment in units of ΔL. The circles show data, and the lines show data fits. Observer age is indicated in each panel, and panels are arranged with child age increasing from left to right. All adult data fits are shown in the upper right panel. The legend indicates the median standard error of the mean for each group. The filled symbols in the upper left panel highlight the fact that results of observer C4 are markedly poorer than those of other observers, as discussed in the text.
A least squares procedure was used to fit the percent correct data of each observer with a Logit function of the form
where p is the proportion correct (0-1), n is the probability of inattention on any given trial, x is the signal level in ΔL, μ is the midpoint of the function, and k is the slope, with larger values representing shallower functions.1 Psychometric function fits were good, accounting for 89%–100% of variance in child data and 95%–100% of variance in adult data. Fitted functions are shown with the data for individual child observers, and all adult functions are shown in the upper right panel of Fig. 2. The median value of n was 0.07 for children and 0.02 for adults, associated with upper asymptotes of 95% and 99% correct, respectively. Fitting the data a second time holding n constant at zero reduced the median variance accounted for by 2% in the child dataset and by less than 1% in the adult dataset. Looking across individual data, including the n variable did not significantly increase the quality of the fit for any observer (p<0.1, uncorrected), a finding which can be interpreted as a failure to find reliable evidence of random lapses of attention in these data. The decision to retain the variable n in data fits was made to ensure that possible differences in asymptotic performance would not lead to an overestimate of the parameter k (i.e., an excessively shallow fit, as discussed by Allen and Wightman, 1994). Models of inattention and the relationship between inattention and estimated slope will be considered in more detail in Sec. 4.
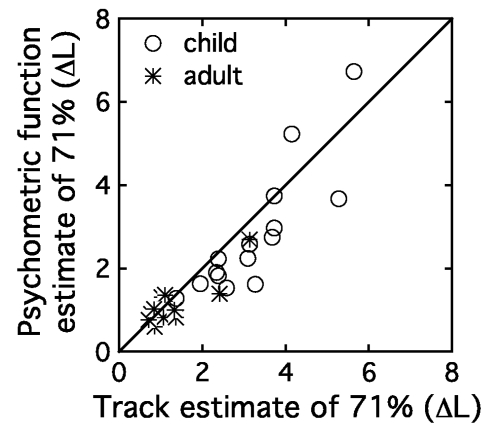
Consistency of performance over the two stages of testing was systematically evaluated by comparing the 71% point on fitted psychometric functions and 71% thresholds estimated in the adaptive tracking. Figure 3 shows thresholds calculated from psychometric function fits plotted as a function of thresholds based on the adaptive track, both in units of ΔL. Each symbol corresponds to an individual observer’s data, as indicated in the legend, and the diagonal line shows a perfect correspondence between thresholds obtained using the two methods. Thresholds estimated in the two stages of testing are highly correlated when evaluated across all data (r=0.89, p<0.0001) or just within the child observer group (r=0.86, p<0.0001). Thresholds were submitted to a repeated measures ANOVA, with two levels of GROUP (child, adult) and two levels of EST (pc, track). There was a main effect of GROUP (F1,24=17.46, p<0.0001) and a main effect of EST (F1,24=5.77, p<0.05), but no interaction (F1,24=1.11, p=0.30). Thresholds based on psychometric function fits were on average 0.3 dB lower than those based on the adaptive tracking procedure; simulations indicate that at least part of this effect could be attributed to the choice of units used to adaptively vary signal level in the track. More important in the present analysis is the fact that there was no interaction between threshold estimation procedure and group. This result supports the assumption that data from these two paradigms both reflect the age effect of interest. Threshold estimates based on psychometric function fits will be used as an index of sensitivity in further analyses, as these estimates are based on a greater number of trials.
Figure 3.
Threshold estimates based on psychometric function fits are plotted as a function of thresholds estimated in the initial tracking procedure both in units of ΔL. The circles show child data, and the stars indicate adult data. The diagonal line indicates perfect correspondence between these two estimates of 71% correct.
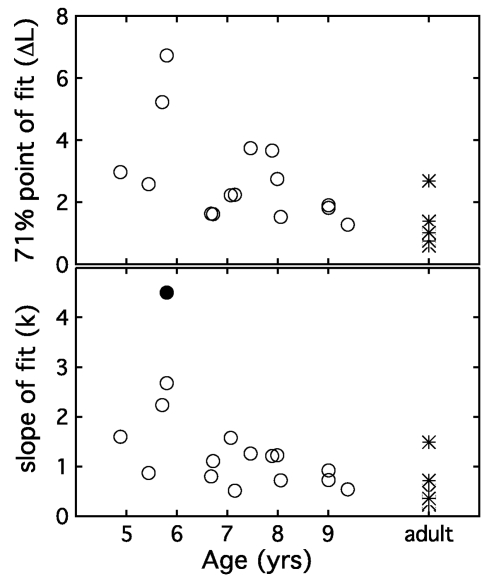
Figure 4 shows two parameters based on psychometric function fits plotted as a function of observer age, with adult data plotted at a single arbitrary point on the abscissa. The top panel shows estimates of 71% correct. Child thresholds fall as a function of age, suggesting improvement in performance between 4.9 and 9.4 yr of age. This trend is significant (β=−0.56, t13=2.14, p<0.05 one-tailed). The bottom panel of Fig. 4 shows individual estimates of psychometric function slope. Fitted values of slope differ across groups by an average of 0.72, a difference that is significant (t24=3.45, p<0.01). This effect of age on slope is also evident within the child observer group (β=0.26, t13=2.59, p<0.05 one-tailed). We also examined the association between slope and the standard deviation of the track reversal values obtained in the first phase of testing, as it is possible that both could be affected by a common underlying factor. However, the correlation between these metrics did not approach significance (r=0.001, p=0.99), indicating that this track statistic serves as a very poor predictor of function slope under conditions tested here.
Figure 4.
Two parameters of the fitted psychometric function are plotted with circles as a function of child observer age, with the filled circle indicating the slope estimate of the outlier child observer C4. The threshold value for C4 is not shown because it is greater than the 8 dB axis limit. Adult values are plotted with stars at an arbitrary point on the abscissa. The top panel indicates thresholds for 71% correct in units of ΔL, and the bottom panel shows results for function slope (k).
Slope as a predictor of threshold
One motivation for the present study was to determine whether psychometric functions for intensity discrimination conform to the prediction of shallower slope in child than adult observers. Buss et al. (2006a) modeled intensity discrimination thresholds and found some evidence for greater internal noise in school-aged children than adults; greater spread in the cue underlying the intensity discrimination task would elevate thresholds and produce a shallower psychometric function. As shown in the Appendix, the standard deviation of the underlying cue distribution (σ), reflecting internal noise, can be estimated based on the fitted Logit function slope (k) and then used to generate threshold predictions.
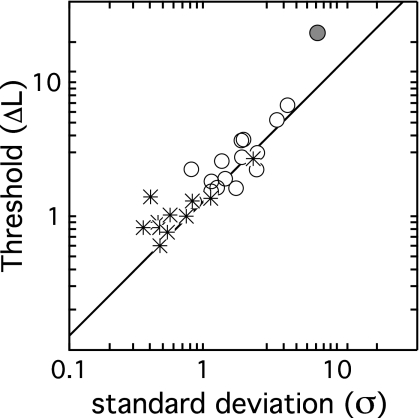
Figure 5 shows thresholds based on psychometric function fits plotted as a function of σ, with symbols indicating individual observer’s results. The line shows predicted thresholds. Estimates of σ differed significantly across groups (t24=3.46, p<0.01), with average values of 0.76 and 1.91 for adults and children, respectively. Threshold predictions were relatively accurate, accounting for 85% of the variance in both child and adult data (F1,24=136.34, p<0.0001). This fell to 79% when considering just child data (F1,13=49.88, p<0.0001).
Figure 5.
Thresholds in ΔL are plotted as a function of the standard deviation of the underlying cue distribution (σ), estimated for each observer based on psychometric function slope. Child data are shown with circles, and adult data are shown with stars. The solid line indicates the threshold predicted based on σ, as described in the Appendix.
Characterizing the outlier
Apart from very high thresholds, the data of the omitted outlier (C4) are very similar to those of other observers. Despite very poor performance, the sem associated with each estimate of percent correct was not unusually large, with values near the 65th percentile relative to other child observers’ data. The psychometric function fit was also quite good for this observer, accounting for 98.6% of the variability across the five estimates of percent correct. The relatively low values of percent correct shown in Fig. 2 for this observer stem from a deviation from the testing protocol: adaptive thresholds were judged to be unreasonably high, so signal levels adopted for the second stage of testing were lowered to more typical values in this special case. Assuming the fitted slope estimate of k=4.5 is accurate for this observer, internal noise would be estimated as σ=7.18, corresponding to a threshold prediction of 9.2 dB (ΔL). This result is of interest because, whereas this observer’s performance is quite poor, there are no other features of the data that suggest unreliable or unstable underlying psychometric function.
DISCUSSION
The first stage of testing showed a group difference in intensity discrimination thresholds, as well as an effect of age within the child group. Intensity discrimination has previously been reported to be poorer in school-aged children than adults (Fior, 1972; Maxon and Hochberg, 1982; Buss et al., 2006a), though age effects have not been found in all studies (Jensen and Neff, 1993). Examination of the signal levels visited by the interleaved tracks generally supported the assumption that child observers were adopting a reliable listening strategy and using that strategy consistently over the course of an entire track, with one notable exception: the interleaved tracks associated with C11 were highly correlated, highlighting the utility of this procedure. Across observers, however, child data were no more likely to be correlated than those of adults, and the correlation across tracks was not a predictor of threshold. This result is evidence that variability in the psychometric function over the course of a threshold estimation track is probably not responsible for the poor performance of child observers. Previous comparisons of adaptive tracking data of adult and school-aged children also support this conclusion (Allen et al., 1989; Wightman et al., 1989). One caveat to this conclusion is that this method is sensitive only to shifts in the underlying psychometric function which span two or more trials within a track: if these effects were independent across sequential trials, then variability would not be evident in intertrack correlation.
The most interesting aspect of the present data was the finding of shallower psychometric function slopes in child as compared to adult observers. Function fits were quite good in both groups, and variability around each underlying estimate of percent correct was comparable for child and adult observers. These findings are consistent with a simple signal detection model, wherein each observer’s performance can be modeled in terms of a single, stable function. Stability of the psychometric function underlying performance over the experiment was further corroborated by the comparison between estimates of 71% correct from the two stages of testing; estimates based on adaptive methods and psychometric function fits were highly correlated both within and across observer groups. The finding of shallower slopes for intensity discrimination in school-aged children than adults is consistent with the shallower slopes for signal detection reported in some (Allen and Wightman, 1994) but not all previous studies (Schneider et al., 1989).
The psychometric function estimates of both threshold and slope were significantly different across groups and were significantly correlated with age within the child observer group. Psychometric function slope in units of ΔL was used to estimate internal noise and generate threshold predictions. These results were broadly consistent with the previous estimates of internal noise determined under comparable stimulus conditions (Buss et al., 2006a). That study reported internal noise estimates of 0.99 and 2.45 dB for intensity discrimination in adult and school-aged child observers, respectively. Estimates based on the present data were 0.76 and 1.91 dB, respectively. Threshold predictions based on estimates of internal noise for individual observers fitted the data quite closely despite substantial individual differences across child observers (see Wightman and Allen, 1992). This result supports the hypothesis that increased internal noise in child observers is responsible for elevated intensity discrimination thresholds, as reflected in shallower psychometric function slopes. The relative stability of performance over time in child data indicates that this age effect is not likely to be due to increased variability in listening strategy or motivation.
One potential difficulty in measuring psychometric function slope is the confounding effect of inattention. Inattention is often modeled as a random, “all-or-none” process. In this model the observer is said to respond randomly without respect to the stimulus on some proportion of randomly distributed trials (n), and on the remainder of trials (1−n) to respond according to the psychometric function characterizing sensitivity (e.g., Wightman et al., 1989; Green, 1995). This model produces an upper asymptote below 100% correct. Attempting to fit a function with an asymptote at 100% to data that asymptote below 100% can result in an inaccurately shallow slope estimate as well as threshold elevation (e.g., Wightman et al., 1989; Wightman and Allen, 1992; Allen and Wightman, 1994). Estimates of n for the present data are consistent with upper asymptotes of 95% and 99% correct for child and adult observers, respectively. These values are consistent with those previously observed under comparable experimental conditions for a detection task (Buss et al., 2001), supporting the use of a three-parameter fit even in the absence of a significant improvement over the two-parameter fit with no inattention (n=0). To the extent that the three-parameter fit accounts for individual differences in asymptotic performance, estimates of slope reported here are not affected by all-or-none lapses in attention. Using psychometric function fits with an asymptote at 100% (n=0) to estimate internal noise results in larger estimates, with mean values of 0.81 and 2.50 dB for child and adult observers, respectively; this result suggests that any effect of all-or-none inattention may have contributed to, but was not wholly responsible for, the age effect observed in the dataset of Buss et al. (2006a).
Wightman and Allen (1992) hypothesized that the psychometric functions characterizing the quality of sensory cues available to adults and children are identical, and that group differences in behavioral thresholds are due solely to random, all-or-none inattention. Modeling in that report indicated that inattention could account for performance if child observers’ responses were unrelated to sensory input on about 50% of trials. Pursuing a similar analysis on the present data, psychometric functions fitted to adult data were hypothesized to also characterize sensitivity of child observers, with differences in performance across groups due solely to differences in inattention. For this analysis, values of μ and k were based on mean values fitted to adult data assuming consistent levels of attention (n=0, μ=1.04, and k=0.51). The value of n was then adjusted to fit the mean child threshold of 2.79 dB. This procedure generated an estimate of n=0.42, consistent with an upper asymptote of 72% correct [n∕3+(1−n)]. Data shown in Fig. 2 are inconsistent with this magnitude of inattention, with the possible exception of observer C4, for whom the best performance measured was 65% correct. This analysis supports the conclusion that all-or-none inattention is insufficient to account for the developmental effects observed in the present experiment. This model also fails to account for the differential development effects observed across auditory tasks (Jensen and Neff, 1993; Dawes and Bishop, 2008).
Several investigators have argued that inattention is unlikely to be random with respect to signal level. A more realistic model might incorporate reduced probability of inattention with increasing signal level (Schneider and Trehub, 1992; Viemeister and Schlauch, 1992; Allen and Wightman, 1994). Whereas signal-dependent attentional effects might be difficult to distinguish from other sources of internal noise (e.g., variability in the neural representation of intensity), it has been argued that signal-dependent inattention could play a larger role in adaptive tracking data than in measurements of percent correct for randomly interspersed signal levels (Schneider and Trehub, 1992; Viemeister and Schlauch, 1992). For example, a series of several “difficult” trials clustered together in time could reduce motivation or confidence in the listening strategy for child observers. If signal-dependent inattention is responsible for the developmental effects in intensity discrimination, and if threshold estimation procedures influence the probability of this type of inattention, then developmental effects might be expected to vary for the two procedures used in the present experiment. Comparison of thresholds across procedures reveals a relatively constant developmental effect, however, a result that fails to support an effect of signal-dependent inattention.
Despite this failure to find evidence of inattention as a source of internal noise, previous work suggests that threshold elevation for intensity discrimination in school-aged children is due to central, nonsensory factors. In a review of the literature, Werner and Marean (1996) argued that the wide variability across individual children and the good performance of some very young observers suggests very early maturation of the sensory representation of intensity cues and implicates nonsensory factors in developmental behavioral effects in school-aged children. This hypothesis is bolstered by the results of Berg and Boswell (2000), who reported adultlike intensity discrimination under some conditions by 3 yr of age. In the present data, the very poor performance of observer C4 is also consistent with nonsensory factors: if a threshold of 9.2 dB were an accurate reflection of sensitivity, one might expect this observer to have significant auditory processing difficulties with naturally occurring sound stimuli, which is not the case. Progressive development of nonsensory factors affecting auditory processing over the school-aged population is supported by both behavioral and physiological studies. A recent paper by Moore and Linthicum (2007) reviews the physiological evidence that, whereas the peripheral auditory system is fully developed early in life, continued maturation of the auditory cortex spans 6–12 yr of age, a process involving plastic changes in response to sensory stimulation and auditory learning. Analogous developmental trends are also evident in the extended developmental effects observed psychophysically (e.g., Dawes and Bishop, 2008). Nonauditory attention also develops extensively over this same age range, with many factors not captured by the all-or-none or even the signal-dependent inattention model considered in analyses of the present data (Gomes et al., 2000).
One aspect of the present paradigm that could highlight the development of nonsensory limits to performance is the choice of a gated stimulus presentation. Durlach and Braida (1969) hypothesized that nonsensory sources of internal noise for gated intensity discrimination can be characterized in terms of memory. For the present three-interval task, an observer might maintain a detailed auditory memory of the stimuli in all three intervals, comparing those memories at the end of the trial; alternatively, the stimulus on each interval could be compared to an internal template of the standard, with the final response based on the interval with stimulus judged to be more intense than the template. It is reasonable to hypothesize that developmental memory effects could limit performance using either of these strategies. If this is the case, then presenting a continuous (as opposed to a gated) standard tone should reduce the developmental effects for intensity discrimination; changing the task in this way would significantly reduce the memory load, whether child performance was limited by auditory memory for each interval or memory for the standard template. This expectation is consistent with the adultlike performance of 3 yr old observers for intensity discrimination with a continuous standard stimulus observed by Berg and Boswell (2000). Contrary to this expectation, however, initial data suggest that presenting the standard tone continuously may not reduce the developmental effect (Buss et al., 2006b). While memory or some other cognitive factor may play a role in performance, more work is needed to clarify its contribution to the developmental effects observed here.
CONCLUSIONS
The present results replicate previous findings of a developmental effect in pure tone intensity discrimination in school-aged children. Psychometric function slopes were shallower in children than adults, consistent with the hypothesis that this age effect is related to internal noise. Predicting performance based on estimates of slope provides a good fit to the data and comparable estimates of internal noise to those published previously (Buss et al., 2006a). Stability of the psychometric function underlying performance appears to be comparable across groups when assessed both via correlation across interleaved adaptive tracks and variability across sequential estimates of percent correct, a result interpreted as showing that fluctuations in attention or listening strategy over blocks of trials is not responsible for the poorer performance of child observers. Future work will evaluate other possible sources of greater internal noise in young school-aged children, including limits to the fidelity of sensory coding as well as memory and signal-dependent attentional factors.
ACKNOWLEDGMENTS
This work was supported by a grant from NIH, R01 DC00397. We thank Lori Leibold for helpful discussions of this work. Ruth Litovsky, Marjorie Leek, and two anonymous reviewers provided helpful comments on a previous draft of this manuscript.
APPENDIX
Many studies report psychometric function slopes in terms of the k-parameter of a Logit fitted to psychophysical estimates of percent correct. The Logit can be defined as
where μ is the midpoint of the function, k is the slope parameter, and x is the signal level. In comparison, the cumulative normal distribution can be defined as
where M is the mean of the distribution, σ is the standard deviation of the distribution, and x is the signal level. The Logit is often offered as an approximation of the cumulative normal distribution. Based on Gilchrist et al. (2005), the relation between slopes quantified using these two functions can be evaluated as
As discussed in more details elsewhere (Jesteadt et al., 2003; Buss et al., 2006a), the standard deviation of the underlying cue distribution can be used to generate an estimate of observer sensitivity. Sensitivity is defined as
Because this experiment estimated thresholds for 71% correct using a three-alternative forced-choice task, threshold (Δ) is predicted as
Footnotes
References
- Abdala, C., and Folsom, RC. (1995). “The development of frequency resolution in humans as revealed by the auditory brain-stem response recorded with notched-noise masking,” J. Acoust. Soc. Am. 10.1121/1.414350 98, 921–930. [DOI] [PubMed] [Google Scholar]
- Allen, P., and Nelles, J. (1996). “Development of auditory information integration abilities,” J. Acoust. Soc. Am. 10.1121/1.416290 100, 1043–1051. [DOI] [PubMed] [Google Scholar]
- Allen, P., and Wightman, F. (1994). “Psychometric functions for children’s detection of tones in noise,” J. Speech Hear. Res. 37, 205–215. [DOI] [PubMed] [Google Scholar]
- Allen, P., and Wightman, F. (1995). “Effects of signal and masker uncertainty on children’s detection,” J. Speech Hear. Res. 38, 503–511. [DOI] [PubMed] [Google Scholar]
- Allen, P., Jones, R., and Slaney, P. (1998). “The role of level, spectral, and temporal cues in children’s detection of masked signals,” J. Acoust. Soc. Am. 10.1121/1.423882 104, 2997–3005. [DOI] [PubMed] [Google Scholar]
- Allen, P., Wightman, F., Kistler, D., and Dolan, T. (1989). “Frequency resolution in children,” J. Speech Hear. Res. 32, 317–322. [DOI] [PubMed] [Google Scholar]
- ANSI (1996). ANSI S3-1996, American National Standards Specification for Audiometers (American National Standards Institute, New York: ). [Google Scholar]
- Bargones, J. Y., Werner, L. A., and Marean, G. C. (1995). “Infant psychometric functions for detection: Mechanisms of immature sensitivity,” J. Acoust. Soc. Am. 10.1121/1.414446 98, 99–111. [DOI] [PubMed] [Google Scholar]
- Berg, K. M., and Boswell, A. E. (2000). “Noise increment detection in children 1 to 3 years of age,” Percept. Psychophys. 62, 868–873. [DOI] [PubMed] [Google Scholar]
- Buss, E., Hall, J. W., and Grose, J. H. (2006a). “Development and the role of internal noise in detection and discrimination thresholds with narrow band stimuli,” J. Acoust. Soc. Am. 10.1121/1.2354024 120, 2777–2788. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buss, E., Hall, J. W., and Grose, J. H. (2006b). “Processing of intensity in children,” paper presented at the Association for Research in Otolaryngology, Baltimore, MD.
- Buss, E., Hall, J. W., Grose, J. H., and Dev, M. B. (2001). “A comparison of threshold estimation methods in children 6–11 years of age,” J. Acoust. Soc. Am. 10.1121/1.1337960 109, 727–731. [DOI] [PubMed] [Google Scholar]
- Buus, S., and Florentine, M. (1991). “Psychometric functions for level discrimination,” J. Acoust. Soc. Am. 10.1121/1.401928 90, 1371–1380. [DOI] [PubMed] [Google Scholar]
- Dawes, P., and Bishop, D. V. (2008). “Maturation of visual and auditory temporal processing in school-aged children,” J. Speech Lang. Hear. Res. 51, 1002–1015. [DOI] [PubMed] [Google Scholar]
- Durlach, N. I., and Braida, L. D. (1969). “Intensity perception. I. Preliminary theory of intensity resolution,” J. Acoust. Soc. Am. 10.1121/1.1911699 46, 372–383. [DOI] [PubMed] [Google Scholar]
- Elliott, L. L. (1979). “Performance of children aged 9 to 17 years on a test of speech intelligibility in noise using sentence material with controlled word predictability,” J. Acoust. Soc. Am. 10.1121/1.383691 66, 651–653. [DOI] [PubMed] [Google Scholar]
- Fior, R. (1972). “Physiological maturation of auditory function between 3 and 13 years of age,” Audiology 11, 317–321. [DOI] [PubMed] [Google Scholar]
- Gilchrist, J. M., Jerwood, D., and Ismaiel, H. S. (2005). “Comparing and unifying slope estimates across psychometric function models,” Percept. Psychophys. 67, 1289–1303. [DOI] [PubMed] [Google Scholar]
- Gomes, H., Molholm, S., Christodoulou, C., Ritter, W., and Cowan, N. (2000). “The development of auditory attention in children,” Front. Biosci. 5, D108–D120. [DOI] [PubMed] [Google Scholar]
- Green, D. M. (1995). “Maximum-likelihood procedures and the inattentive observer,” J. Acoust. Soc. Am. 10.1121/1.412390 97, 3749–3760. [DOI] [PubMed] [Google Scholar]
- Hall, J. W., and Grose, J. H. (1991). “Notched-noise measures of frequency selectivity in adults and children using fixed-masker-level and fixed-signal-level presentation,” J. Speech Hear. Res. 34, 651–660. [DOI] [PubMed] [Google Scholar]
- Hall, J. W., and Grose, J. H. (1994). “Development of temporal resolution in children as measured by the temporal modulation transfer function,” J. Acoust. Soc. Am. 10.1121/1.410474 96, 150–154. [DOI] [PubMed] [Google Scholar]
- Hall, J. W., III, Buss, E., and Grose, J. H. (2005). “Informational masking release in children and adults,” J. Acoust. Soc. Am. 10.1121/1.1992675 118, 1605–1613. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Irwin, R. J., Ball, A. K., Kay, N., Stillman, J. A., and Rosser, J. (1985). “The development of auditory temporal acuity in children,” Child Dev. 10.2307/1129751 56, 614–620. [DOI] [PubMed] [Google Scholar]
- Jensen, J. K., and Neff, D. L. (1993). “Development of basic auditory discrimination in preschool children,” Psychol. Sci. 4, 104–107. [Google Scholar]
- Jesteadt, W., Nizami, L., and Schairer, K. S. (2003). “A measure of internal noise based on sample discrimination,” J. Acoust. Soc. Am. 10.1121/1.1610456 114, 2147–2157. [DOI] [PubMed] [Google Scholar]
- Leek, M. R., Hanna, T. E., and Marshall, L. (1991). “An interleaved tracking procedure to monitor unstable psychometric functions,” J. Acoust. Soc. Am. 10.1121/1.401930 90, 1385–1397. [DOI] [PubMed] [Google Scholar]
- Leibold, L. J., and Neff, D. L. (2007). “Effects of masker-spectral variability and masker fringes in children and adults,” J. Acoust. Soc. Am. 10.1121/1.2723664 121, 3666–3676. [DOI] [PubMed] [Google Scholar]
- Levitt, H. (1971). “Transformed up-down methods in psychoacoustics,” J. Acoust. Soc. Am. 10.1121/1.1912375 49, 467–477. [DOI] [PubMed] [Google Scholar]
- Lutfi, R. A., Kistler, D. J., Oh, E. L., Wightman, F. L., and Callahan, M. R. (2003). “One factor underlies individual differences in auditory informational masking within and across age groups,” Percept. Psychophys. 65, 396–406. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maxon, A. B., and Hochberg, I. (1982). “Development of psychoacoustic behavior: Sensitivity and discrimination,” Ear Hear. 10.1097/00003446-198211000-00003 3, 301–308. [DOI] [PubMed] [Google Scholar]
- Moore, J. K., and Linthicum, F. H., Jr. (2007). “The human auditory system: A timeline of development,” Int. J. Audiol. 46, 460–478. [DOI] [PubMed] [Google Scholar]
- Moore, B. C., Peters, R. W., and Glasberg, B. R. (1999). “Effects of frequency and duration on psychometric functions for detection of increments and decrements in sinusoids in noise,” J. Acoust. Soc. Am. 10.1121/1.428207 106, 3539–3552. [DOI] [PubMed] [Google Scholar]
- Nabelek, A. K., and Robinson, P. K. (1982). “Monaural and binaural speech perception in reverberation for listeners of various ages,” J. Acoust. Soc. Am. 10.1121/1.387773 71, 1242–1248. [DOI] [PubMed] [Google Scholar]
- Oh, E. L., Wightman, F., and Lutfi, R. A. (2001). “Children’s detection of pure-tone signals with random multitone maskers,” J. Acoust. Soc. Am. 10.1121/1.1371764 109, 2888–2895. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schneider, B. A., and Trehub, S. E. (1992). “Sources of developmental change in auditory sensitivity,” Developmental Psychoacoustics (American Psychological Association, Washington, DC: ), pp. 3–46. [Google Scholar]
- Schneider, B. A., Trehub, S. E., Morrongiello, B. A., and Thorpe, L. A. (1989). “Developmental changes in masked thresholds,” J. Acoust. Soc. Am. 10.1121/1.398604 86, 1733–1742. [DOI] [PubMed] [Google Scholar]
- Stellmack, M. A., Willihnganz, M. S., Wightman, F. L., and Lutfi, R. A. (1997). “Spectral weights in level discrimination by preschool children: analytic listening conditions,” J. Acoust. Soc. Am. 10.1121/1.419479 101, 2811–2821. [DOI] [PubMed] [Google Scholar]
- Sutcliffe, P., and Bishop, D. (2005). “Psychophysical design influences frequency discrimination performance in young children,” J. Exp. Child Psychol. 91, 249–270. [DOI] [PubMed] [Google Scholar]
- Trehub, S. E., Schneider, B. A., and Henderson, J. L. (1995). “Gap detection in infants, children, and adults,” J. Acoust. Soc. Am. 98, 2532–2541. [DOI] [PubMed] [Google Scholar]
- Viemeister, N. F., and Schlauch, R. S. (1992). “Issues in infant psychoacoustics,” Developmental Psychoacoustics (American Psychological Association, Washington, DC: ), pp. 191–209. [Google Scholar]
- Werner, L. A., and Marean, G. C. (1996). “Factors related to threshold in noise: Intensity, frequency, and temporal resolution,” in Human Auditory Development (Westview, Boulder, CO: ), pp. 89–131. [Google Scholar]
- Wightman, F., and Allen, P. (1992). “Individual differences,” Developmental psychoacoustics (American Psychological Association, Washington, DC: ), pp. 113–133. [Google Scholar]
- Wightman, F., Allen, P., Dolan, T., Kistler, D., and Jamieson, D. (1989). “Temporal resolution in children,” Child Dev. 10.2307/1130727 60, 611–624. [DOI] [PubMed] [Google Scholar]
- Wightman, F. L., Callahan, M. R., Lutfi, R. A., Kistler, D. J., and Oh, E. (2003). “Children’s detection of pure-tone signals: Informational masking with contralateral maskers,” J. Acoust. Soc. Am. 10.1121/1.1570443 113, 3297–3305. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Willihnganz, M. S., Stellmack, M. A., Lutfi, R. A., and Wightman, F. L. (1997). “Spectral weights in level discrimination by preschool children: Synthetic listening conditions,” J. Acoust. Soc. Am. 10.1121/1.419478 101, 2803–2810. [DOI] [PubMed] [Google Scholar]