Towards intra-operative computerized planning of prostate cryosurgery

Abstract

Background

As part of ongoing efforts to develop computerized planning tools for cryosurgery, the current study provides a comparison between two recently developed methods for planning, known as bubble packing and force-field analogy.

Methods

For the purpose of comparison, four 3D prostate models were reconstructed from ultrasound imaging. The quality of planning for each method was evaluated based on bioheat transfer simulations.

Results

Both methods are shown to be robust planning tools in 3D. Typical results show at least 75% of the target region volume having temperatures below a target temperature isotherm for planning. While the force-field analogy method yields superior planning results, it comes at the expense of an order of magnitude longer run time, with only moderate improvement.

Conclusions

Due to time constraints in a clinical setup, bubble packing alone may be considered adequate for computerized planning. Furthermore, only bubble packing is demonstrated to be adequate for intra-operative planning. Copyright © 2007 John Wiley & Sons, Ltd.

Introduction

Cryosurgery is the destruction of undesired tissue by freezing. Minimally invasive cryosurgery is performed by means of cryoprobes, each having the shape of a long hypodermic needle with a sharp pointed tip. During surgical operation, a cooling sink is created at the tip of the cryoprobe, either by the effect of liquid nitrogen boiling, or by the effect of Joule–Thomson cooling (i.e. the cooling effect associated with a sudden change in pressure of a gas flowing through a nozzle). Prostate cryosurgery was the first minimally invasive cryosurgical procedure to pass from the experimental stage to become a routine surgical treatment (1). The minimally invasive approach created a new level of difficulty in surgery planning, in which a predefined three-dimensional (3D) region of tissue must be treated with an array of cryoprobes, while minimizing the damage to the surrounding healthy tissue.

The success of the cryoprocedure relies on four critical steps of the medical operation: (a) reconstruction of the target region; (b) planning the optimal cryoprobe layout within the target region; (c) insertion of the cryoprobes according to the planned layout; and (d) operation of the cryoprobe array in concert. It is the planning of the optimal cryoprobe layout that is the focus of the current study. While planning is affected by the cryoprobe specification and the number of cryoprobes applied – both are considered to be hardware constraints in the current study – it is the optimal spatial distribution of the cryoprobes in the target region that is the main objective in the current study. The need to find an optimal cryoprobe layout has also been acknowledged by others, and efforts to develop computerized means for planning are reported in the literature (2-4). While the most important set of cryosurgery parameters to be optimized is still open for debate, to combine geometrical consideration with the thermal history in the target region is widely accepted for the purpose of planning. Prior reports, however, did not offer an efficient means for cryosurgical planning that could be utilized in a clinically relevant time frame, neither could they be applied efficiently in an intra-operative mode.

As a part of ongoing efforts to develop planning tools for cryosurgery, the current research group has recently presented a two-phase planning approach, combining the so-called techniques of bubble packing (5) and force-field analogy (6). Bubble-packing (Phase I) originated as an efficient method for finite element meshing (7-9), and has been modified to assist in uniform volumetric distribution of cryoprobes in the target region (5). The force-field analogy method (Phase II) has been developed as an iterative technique, based on a series of bioheat transfer simulations of the cryoprocedure (6). At the end of each simulation, defective regions are identified, where a defect region is defined as either cryoinjured tissue exterior to the target region, or insufficiently cryotreated tissue interior to the target region. In an analogy between the thermal field and a force field, defective regions apply forces onto the cryoprobes, and displace them to better locations between every two consecutive bioheat transfer simulations. This process of bioheat simulations and cryoprobe displacements repeats until no additional improvement can be found.

A proof of concept for the two-phase planning scheme has been demonstrated recently in two dimensions (2D) (5). However, migrating the planning scheme to the general 3D case required the following preparation steps: (a) developing an efficient numerical scheme for 3D bioheat simulations (10); (b) developing a bubble-packing technique for ellipsoidal bubbles (11); and (c) evaluating the quality of bubble packing in 3D by means of bioheat transfer simulations (11). Based on four prostate models reconstructed from ultrasound imaging, it has been demonstrated that the cryoprobe layout found by bubble packing alone typically leads to cooling of 75% of the prostate volume below a target temperature threshold of −22°C (5,11).

The current study integrates the two-phase scheme of planning – bubble packing (Phase I) with force-field analogy (Phase II) – in 3D. The contribution of Phase II to cryosurgery planning is further evaluated in this study. For this purpose, the force-field analogy technique has been modified from 2D to 3D. Finally, an intra-operative planning procedure is demonstrated, where replanning is being executed for the remaining cryoprobes after each cryoprobe localization, due to uncertainty in cryoprobe placement of the already localized cryoprobes.

Computational methods

Procedure of intra-operative planning

The long-term goal in this line of research is to develop an efficient planning tool for cryosurgery, which can be executed in minutes, while the patient is lying on the operating table as part of the same surgical session. Preplanning at a preceding session – as would be required if planning is not time-efficient – is not feasible for the prostate, which may change its geometry and orientation over time. Figure 1 illustrates integration of the proposed planning tool into the cryoprocedure. First, the target area is scanned using an imaging device (most frequently ultrasound imaging in the case of prostate cryosurgery), and the organ to be treated is reconstructed and registered. Next, the planning software is executed subject to pre-defined clinical constraints, such as the number of cryoprobes available for operation and the specifications of each cryoprobe (diameter, active length, cooling power, etc.). Finally, based on the simulated thermal history of the target region, and with the aid of a visualization interface, the cryosurgeon either accepts or rejects the plan.

Figure 1.

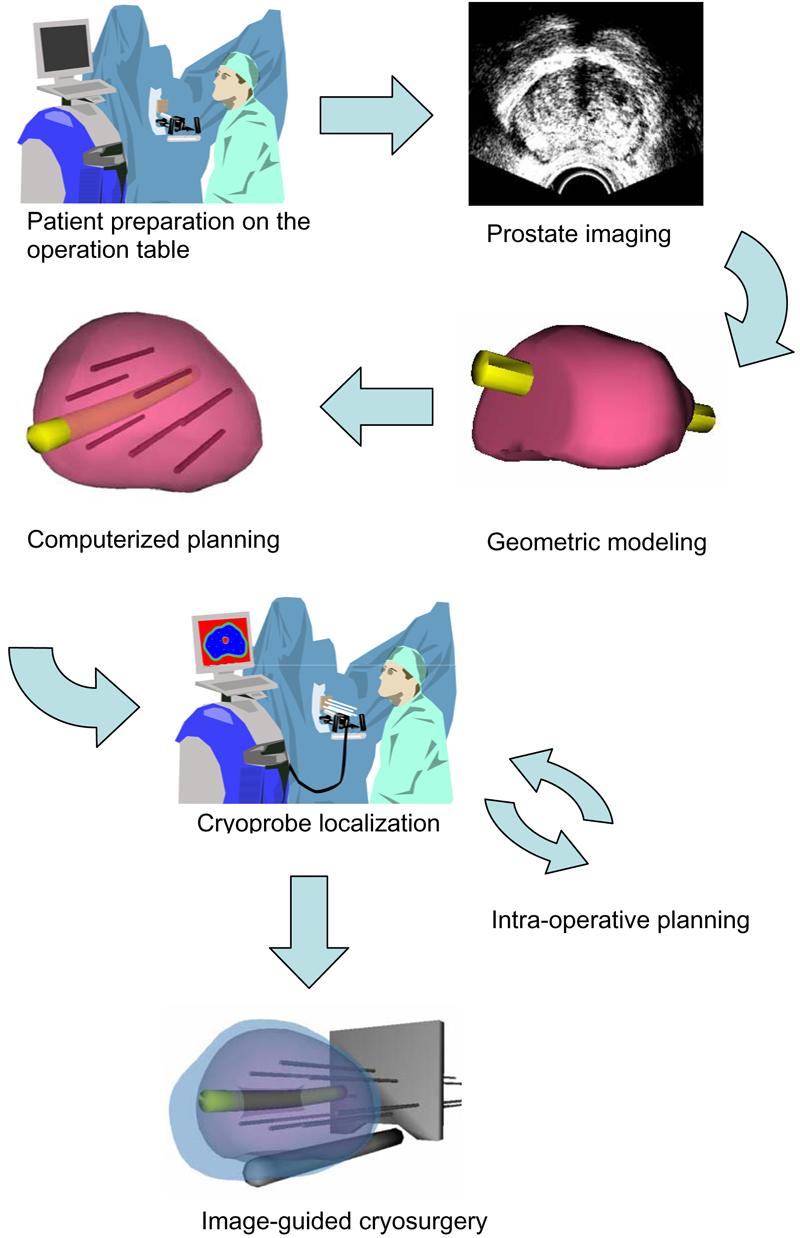
Illustration of the application of computerized planning in cryosurgery

Cryoprobe insertion is a challenging task, and cryoprobe localization may not be as precise as one would hope. Reasons for cryoprobe misplacement include: cryoprobe bending (due to cryoprobe strength or tissue stiffness); movement of the patient; movement of the organ due to cryoprobe penetration; and the experience of the clinician. While computerized planning cannot increase the precision of cryoprobe localization, it can assist in continuous modification of planning to compensate for cryoprobe misplacement, i.e. the intra-operative mode. In this mode, a replanning of the remaining cryoprobes is executed after the insertion of each additional cryoprobe. Here, the location of an already inserted cryoprobe is verified through imaging and taken as a constraint in the next step of replanning. Replanning with an ever-increasing number of constraints, and an ever-decreasing number of cryoprobes to be localized, continues until the last cryoprobe is inserted.

Intra-operative planning is demonstrated in the current study as a proof of concept, towards the end of the Discussion, after all the key algorithms of planning are presented: prostate-shape reconstruction, bioheat transfer simulation, bubble packing and force-field analogy.

Geometric modelling: prostate shape reconstruction

In the proposed method, the 3D shape of a prostate is reconstructed, based on manual segmentation of ultrasound images. The user selects a series of good-quality ultrasound images of a transverse cross-section, from the apex to the base of the prostate (Figure 2a). On each cross-section, the user identifies the contour of the prostate as a sequence of points, the points having a denser distribution for a high-curvature part of the contour. Next, the points are connected to form a polyline, which is then approximated as a piecewise cubic Bezier curve. In order to form a smooth contour, two adjacent curves are forced to share the same end point. Furthermore, two additional control points are added, so that the slopes of the two adjacent curves become continuous. This procedure is repeated for all the selected cross-sections, resulting in a series of transverse contours (Figure 2b).

Figure 2.

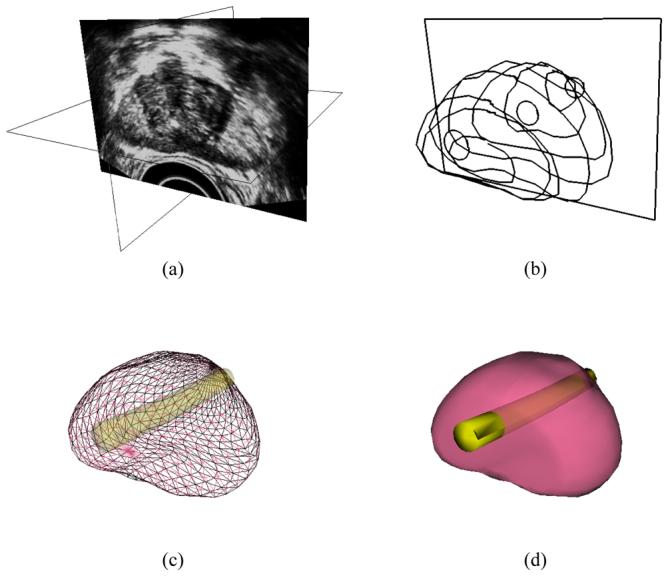
Reconstruction of the prostate model from ultrasound images: (a) selection of good-quality ultrasound cross-sections; (b) generation of the prostate contour on each cross-section, including illustration of the urethral warmer; (c) generation of polygonal mesh based on cubic Bezier surface interpolation; and (d) surface rendering of the prostate

Once a series of transverse contours is generated, a series of longitudinal cross-sections is defined, intersecting perpendicularly with all the transverse contours. Points from all the intersected transverse contours are connected along each longitudinal cross-section to form a series of longitudinal polylines running from the apex to the base of the prostate. In a similar manner to the process of generating the transverse contours, each longitudinal polyline is approximated as a piecewise cubic Bezier curve, and continuity of position and slope is forced at the end of each curve to ensure the smoothness of the contour. Finally, the surface of the prostate is presented with a polygonal mesh based on bicubic Bezier surface interpolation (Figure 2c).

Consistent with current prostate-cryosurgery practice, a urethral warmer is assumed in the prostate, although not originally present in the ultrasound image data. This warmer, embedded in a catheter, is ordinarily inserted into the urethra to keep its temperature above freezing, and thereby to reduce post-cryosurgery complications (12). In the current study, the geometry of the urethral warmer is modelled as a 6 mm diameter tube, having the same centreline as the urethra, as identified from ultrasound images; its shape is modelled by connecting 6 mm diameter circles from each image, in a similar manner to the outer prostate surface reconstruction.

Physical modelling: bioheat transfer simulation

The quality of cryosurgery planning is evaluated by means of bioheat transfer simulations and the concept of defect region. The classical bioheat equation is used to model bioheat transfer in the prostate (13):

$$C\frac{\partial T}{\partial t}=\nabla (k\nabla T)+{\stackrel{.}{w}}_b{C}_b(T_b-T)$$ (1)

where C is the volumetric specific heat of the tissue, T is the temperature, t is the time, k is the thermal conductivity of the tissue, ẇ_b is the blood perfusion rate, C_b is the volumetric specific heat of the blood, and T_b is the blood temperature entering the thermally-treated area (core body temperature). The current study uses the typical model properties listed in Table 1. Note that the metabolic heat generation can be neglected during cryosurgery (14), and therefore it is omitted from Equation (1). The numerical scheme applied in the current study has been developed recently to meet the specific requirement for short run time for clinical applications, and is presented elsewhere (10).

Table 1.

Representative thermophysical properties of biological tissues used in the current study (20-21)

Thermophysical property	Value
Thermal	0.5	273K < T
conductivity, k,	15.98 − 0.0567 × T	251K < T < 273K
W/m-K	1005 × T−1.15	T < 251K
Volumetric	3.6	273K < T
specific heat, C,	880 − 3.21 × T	265K < T < 273K
MJ/m3-K	2.017 × T − 505.3	251K < T < 265K
	0.00415 × T	T < 251K
Blood perfusion,	40	273K < T
wbCb, kW/m3-K	0	T ≤ 273K

Data from (19,20,21).

The current planning tool aims at maximizing cryodestruction internal to the target region, while minimizing cryoinjury external to the target region, for a given number of cryoprobes selected by the cryosurgeon. The target region in this study is defined as the prostate region, excluding the urethra. The concept of the so-called ‘lethal temperature’ is widely accepted by clinicians as a threshold temperature below which maximum cryodestruction is achieved. Since currently accepted values for the lethal temperature are in the range of −50 °C to −40 °C (15,16), and since cryodamage is assumed to progress gradually between the onset of crystal formation, around 0 °C, and the lethal temperature threshold, the isotherm of −22 °C has been selected here for planning, splitting this temperature range by half. For the purpose of planning, a defect region is defined as either area interior to the target region having temperatures above that isotherm for planning, or exterior area having temperatures below the same temperature threshold. The total defect area, which is the objective function of planning to be minimized, is given by:

$$\begin{array}{cc}\hfill G& =\frac{1}{V_t}{\int }_{V_s}w{\mathit{dV}}_s;\hfill \\ \hfill w& =\{\begin{array}{ccc}\hfill 1\hfill & \hfill -22°\mathrm{C}<T\hfill & \hfill \text{interior to the target region}\hfill \\ \hfill 0\hfill & \hfill T\le -22°\mathrm{C}\hfill & \hfill \text{interior to the target region}\hfill \\ \hfill 1\hfill & \hfill T\le -22°\mathrm{C}\hfill & \hfill \text{exterior to the target region}\hfill \\ \hfill 0\hfill & \hfill -22°\mathrm{C}<T\hfill & \hfill \text{exterior to the target region}\hfill \end{array}\phantom{\}}\hfill \end{array}$$ (2)

where V_s is the volume of the entire simulated domain (including both the target and external regions), V_t is the volume of the target region, and w is a spatial weight defect function, determined by the local temperature distribution. The tool developed in this study is based on the underlying assumption that relocation of a cryoprobe is considered to be an improvement if the value of the objective function, G, decreases.

Cryosurgery planning algorithms

When thermo-physical properties and blood perfusion rate are assumed to be uniform throughout the simulated domain, the shape of the frozen region is expected to be a function of the cryoprobe layout (for given cryoprobe specifications). One may assume that an evenly-spaced layout of cryoprobes would result in a good plan, potentially leading to the optimum layout, with the incorporation of an optimization technique. Consequently, a two-phase planning scheme is outlined, where Phase I aims at evenly distributing cryoprobes within the prostate domain by the application of the bubble-packing method, while Phase II further advances planning in search of a minimum of the objective function [Equation (1)].

Phase I: bubble packing

Bubble packing is a physically-based approach to search for an even distribution of a given number of points inside a given geometrical domain. The bubble-packing scheme first generates spherical elements (or bubbles) inside the domain, the centres of which are the points to be distributed. Next, van der Waals'-like forces are simulated to move these bubbles, until a minimum-force configuration is found. Generally, the van der Waals' model represents coupled attraction and repulsion forces between every two elements in the domain, where attraction forces become dominant at far distance and repulsion forces become dominant at short distance. It is the combined forces between all the bubbles in the domain that dictates the final distances between them and the resulting layout, i.e. the equilibrium layout. Once bubbles are defined (or seeded) in the domain, their forced motion is simulated until equilibrium is reached. In the current study, the van der Waals' model is simplified as:

$$f\left(l\right)=\{\begin{array}{cc}\alpha l^3+\beta l^2+\gamma l+\epsilon \hfill & 0\le l\le 1.5l_0\hfill \\ 0\hfill & 1.5l_0<l\hfill \end{array}\phantom{\}}$$ (3)

having the following boundary conditions:

$$f\left(l_0\right)=f\left(1.5l_0\right)=0,f^{\prime }\left(0\right)=0,f^{\prime }\left(l_0\right)=-{\kappa }_0$$ (4)

where l is the distance between two interacting bubbles, l₀ is the equilibrium distance if only two isolated bubbles are interacting, k₀ is the a linear spring constant at distance l₀, and α, β, γ and ε are the coefficients of the simplified van der Waals' attraction–repulsion force function.

The motion of bubbles towards inter-bubble force equilibrium is simulated as a relaxation process:

$$m_i\frac{d^2{x}_i\left(t\right)}{{\mathit{dt}}^2}+c_i\frac{{\mathit{dx}}_i\left(t\right)}{\mathit{dt}}=f_i\left(t\right),i=1\dots n$$ (5)

where x_i is the location of the ith bubble and m_i and c_i are the mass and damping coefficient of the ith bubble, respectively. Note that m_i and c_i are assumed from computational convergence considerations, but their actual value has no physical meaning in the context of cryosurgery. Further note that f_i(t) is the sum of all interbubble forces acting on bubble i. Equation (5) is numerically integrated using a fourth-order Runge–Kutta method (17).

Finally, the volume of the bubbles is adjusted to minimize both gaps and overlaps between bubbles as relaxation progresses with the change in bubble size. One possible criterion for the optimal bubble size is the amount of overlap between a bubble and its neighbours (7):

$${\alpha }_i=\frac{2}{d_i}\underset{j=0}{\overset{n}{\Sigma }}(d_i+\frac{d_j}{2}-\stackrel{‒}{x_i{x}_j}),$$ (6)

where α_i measures the overlap ratio for the ith bubble, the index j represents a neighbour bubble, d is the diameter, x is the location and n is the number of neighbour bubbles. The overlap ratio for an ideal, tightly-packed configuration of bubbles in a 3D problem is 12. In the current study, the size of the bubbles is adaptively adjusted to bring the overlap ratio as close as possible to the ideal value. Once the system reaches equilibrium of interbubble forces for a given size of bubbles, the overlap ratio is calculated and the diameter of the bubbles is modified according to:

$$d_{\mathit{updated}}=\frac{\alpha }{{\alpha }_{\mathit{ideal}}}\cdot d_{\mathit{current}}.$$ (7)

The change in the diameter causes changes in the inter-bubble forces, which leads to a consecutive force relaxation procedure. The sequence of bubble size modification and force relaxation continues until the bubble size converges to a finite value.

The developing frozen region in the case of a single cryoprobe operation forms an elongated egg-like shape, which could be first order-approximated by an ellipsoid. Consistent with this observation, bubble packing is improved by assuming ellipsoidal bubbles, rather than spherical bubbles, where the axis ratio of the ellipsoid is derived from bioheat transfer simulations around a single cryoprobe (11). Here, the ellipsoidal axis ratio was taken at the location of the −22 °C isotherm (the target isotherm for planning) at the end of 500 s of simulation, which is considered to be a reasonable duration for cryosurgery. Similar axis parameters for a wide selection of freezing conditions are also available in the literature (14). It is acknowledged that in a multi-cryoprobe operation, frozen regions around the cryoprobes eventually fuse to form a large unified frozen region, which cannot be represented with bubble packing. Therefore, the ellipsoidal bubble ratio can only be regarded as a first-order approximation of the early stage of the procedure. Nevertheless, this approximation leads to remarkable results in terms of planning, as discussed below.

Phase II: force-field analogy

The force-field analogy technique has been published elsewhere (6) and is presented here in brief, for completeness and for the purposes of discussion. A single bioheat simulation is executed at the end of Phase I to study the quality of bubble packing. The simulation is terminated at the point at which a minimum defect region is found for that particular layout, as calculated using Equation (2). Next, through an analogy between the resulting temperature field at the end of the specific simulation and forces, a set of force vectors is defined:

$${\stackrel{\rightharpoonup }{F}}_{\mathit{nT}}=\underset{m}{\Sigma }\frac{C_1}{{\left|{\stackrel{\rightharpoonup }{r}}_{\mathit{mn}}\right|}^2}{w}_m{V}_m\Delta T_m{\stackrel{\rightharpoonup }{u}}_{\mathit{mn}}$$ (8)

where F⃑_nT is the net force vector applied to cryoprobe n by all of the defective regions, C₁ is a constant to scale the force, w_m is the weight function that switches off the force from the non-defective regions [Equation (2)], V_m is the volume associated with grid point m, r⃑_mn is a vector from grid point m to the cryoprobe n, u⃑_mn is a unit vector in the direction of r⃑_mn, and ΔT_m is the difference between the isotherm for optimization and the calculated temperature at grid point m (ΔT_m = −22 °C − T_m in the current study). For the region outside the prostate, ΔT_m is positive, while for internal defects it is negative, corresponding to a repulsive force for an external defect and an attractive force for an internal defect. The force applied by each defect is inversely proportional to the square of the distance from the defect to the cryoprobe. Thus, the force decreases rapidly with distance, so that defects near a cryoprobe apply greater force than defects farther away. The rationale is that the cryoprobes nearest a defect are likely to have the greatest influence on that defect. The force applied by a defect is also proportional to temperature difference, ΔT_m, which allows defective regions with more significant temperature differences to apply larger forces, with the goal being to accelerate the optimization process. In order to prevent congestion of too many cryoprobes at the same location, a short-acting repulsive force is further applied between cryoprobes:

$${\stackrel{\rightharpoonup }{F}}_{\mathit{nP}}=\underset{j}{\Sigma }\frac{C_2}{{\left|{\stackrel{\rightharpoonup }{r}}_{\mathit{jn}}\right|}^3}{\stackrel{\rightharpoonup }{u}}_{\mathit{jn}}$$ (9)

where F⃑_nP is the net force vector applied to cryoprobe n by all of the other cryoprobes, j is the cryoprobe index, C₂ is a constant, and r⃑_jn is a vector from cryoprobe j to cryoprobe n. This force is inversely proportional to the cube of the distance between cryoprobes, so that the force is negligible unless the cryoprobes are very close together.

At the end of the bioheat transfer simulation, the forces on the cryoprobes are computed and one or more cryoprobes are moved accordingly, yielding a modified cryoprobe layout. The process of bioheat transfer simulations, followed by cryoprobes relocation based on force-field analogy, repeats until no improved layout is found. If the total defect area is larger than one-eighth of the target region, all cryoprobes are allowed to be relocated simultaneously. From convergence considerations (6), however, once the total defect area becomes smaller than one-eighth of the target region, only one cryoprobe is moved at a time, i.e. the cryoprobe with the largest force. If the latter relocation does not yield a better layout, the program switches into the so-called ‘backtracking mode’, in which an attempt is made to relocate each cryoprobe to a better location, in a descending force magnitude order. Backtracking may be significantly time consuming, and it is important to acknowledge this step for the purpose of discussion, below. It should be noted that, while it may always result in a superior layout, the relative improvement of backtracking is frequently insignificant (6).

Results and discussion

Computerized planning is demonstrated on four prostate models, reconstructed from ultrasound images. Available ultrasound data included a greyscale array of pixels for each model, having an average size of 813 (longitudinal) × 413 × 336. About 10 transverse cross-sections were generated from each array, and about 10–15 points were used to mark the contour on each transverse cross-section. Generation of a prostate model took about 10 min. The resulting volume and length of each prostate is listed in Table 2 for reference, having an average volume of 50.6 cm³ and an average length of 46.8 mm. Consistent with previous numerical work (10), the simulated domain was selected to have a transverse cross-sectional area of 3.5 times larger than the largest cross-sectional area of the specific prostate model; the length of the domain was selected to be 1.5 times that of the prostate model. These dimensions satisfy an underlying assumption that the human body behaves as an infinite domain in the thermal sense, when compared with the prostate size. The domain was discretized with variable grid intervals for the purpose of numerical simulations, as discussed in (10).

Table 2.

Planning results for eight and 14 cryoprobes on four prostate models, where V_i and L_i are the volume and length of each model

		Bubble packing			Force-field analogy
Number of cryoprobes	Prostate model (Vi cm3, Li mm)	Total defect (%)	Run time (s)	Bioheat simulation run time (s)	Total defect (%)	Run time (h)
8	A (42.8, 47.0)	29.7	26	376	27.6 (2.1)	1.2
	B (73.6, 52.9)	27.4	26	792	27.4 (0.0)	3.3
	C (23.0, 37.2)	32.7	29	182	28.7 (4.0)	0.3
	D (62.8, 49.9)	29.8	31	480	27.2 (2.6)	2.1
	Average (50.6 ± 22.4, 46.8 ± 6.8)	29.9 ± 2.2	28 ± 2.4	458 ± 255	27.7 ± 0.7 (2.1 ± 1.7)	1.7 ± 1.3
14	A (42.8, 47.0)	32.6	6	196	26.7 (5.9)	1.1
	B (73.6, 52.9)	25.7	7	302	24.0 (1.7)	2.2
	C (23.0, 37.2)	31.3	6	116	29.1 (2.2)	1.3
	D (62.8, 49.9)	30.2	7	306	27.9 (2.3)	1.2
	Average (50.6 ± 22.4, 46.8 ± 6.8)	30.0 ± 3.0	6.5 ± 0.6	230 ± 91	26.9 ± 2.2 (3.0 ± 1.9)	1.5 ± 0.5

For cryosurgery simulation, the temperature of each cryoprobe was assumed to decrease linearly with time, starting with an initial temperature of 37 °C, and reaching −145 °C in 30 s; the cryoprobe temperature was assumed to be constant thereafter (typical parameters for a Joule–Thomson-based cryoprobe using argon). Case studies included 4–14 cryoprobes, where all cryoprobes are operated simultaneously. A diameter of 1.3 mm and an active length of 25 mm were assumed for each cryoprobe. The active length can play a significant role in cryosurgery planning, as has been demonstrated previously (11). However, further study of the active-length effect is deemed unnecessary for the scope of the current proof-of-concept report. It has been suggested previously (11) that the optimum insertion depth is at about 0.6 of the prostate length, when measured from its apex and when all cryoprobes are inserted to the same depth; this value is taken as a rule of thumb in the current study.

All run time results listed in Table 2 and discussed later are based on an AMD Athlon (TM) XP 3000+ computer, having a 2.1 GHz processor, 400 MHz front side bus and 1 GB of PC3200 DDR memory. The computerized planning was implemented with Visual C++. NET, and executed using Windows XP Professional.

Consistent with common belief, prior work on 2D models suggested that increasing the number of cryoprobes decreases the overall defect area (18). In the 3D case however, this expectation was found to be inconclusive (11). The current study further suggests that increasing the number of cryoprobes is not necessarily superior in terms of the total defect region, as can be seen from Table 2 for cases of eight and 14 cryoprobes. The increasing number of cryoprobes, however, decreases the size of the internal defect area, as can be seen from Figure 3.

Figure 3.

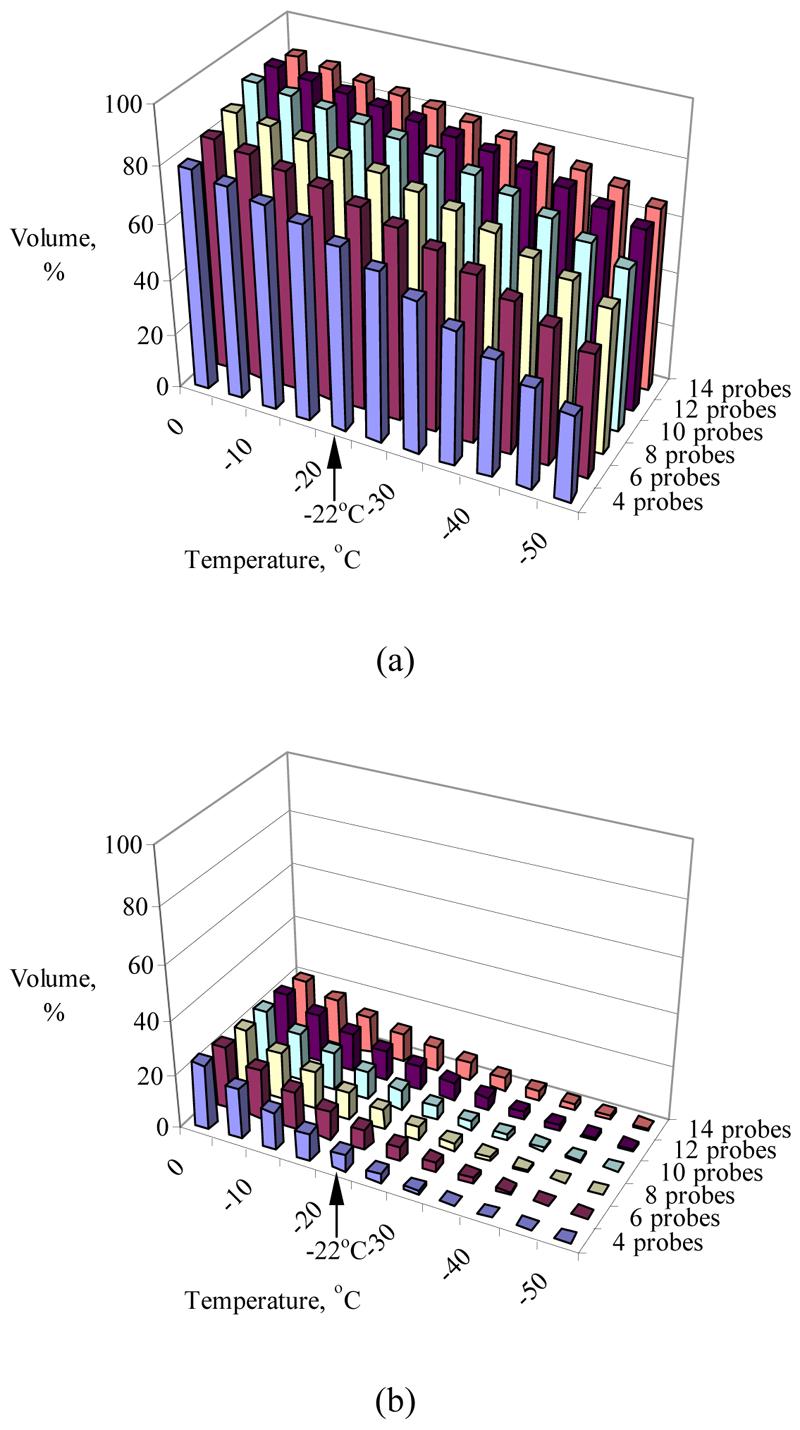
Temperature volume histogram of the target region (a) and the external region (b), where the volume is normalized with respect to the prostate volume (prostate model A, Table 2)

As shown in Table 2, the force-field method (Phase II of planning) reduces the total defect region in the range 0–6%, when compared with initial planning based on bubble packing alone (Phase I). On average, Phase II reduced the total defect region by 2.1% and 3% for the cases of eight and 14 cryoprobes, respectively. The magnitude of the total defect area is about 30%, and an improvement of about 3% in this value may be regarded as a minor contribution to optimal planning. For eight cryoprobes, an average run time of 28 s is required for bubble packing, and an additional average run time of 458 s is required for one bioheat transfer simulation (necessary to verify the quality of bubble-packing planning), yielding an average overall run time of 8.1 min for Phase I. In comparison, an average of 1.8 h was required for a complete two-phase optimization procedure. While 8.1 min may be considered a clinically-relevant time frame, improving planning by 2.1% at the expense of extending run time by an order of magnitude makes the cost : benefit ratio of Phase II planning debatable for the studied cases. In the case of the 14 cryoprobes, Phase I of planning required an average of 4 min, while two-phase planning required 1.6 h. Optimization of the parameters of the bubble-packing algorithm may further decrease the need in Phase II.

Figure 3 displays representative temperature volume histograms (TVHs) of the prostate model A (Table 2) in the target region and in the external region. All volume calculations are normalized with respect to the volume of the target region. It can be seen from Figure 3 that more than 75% of the target volume has temperatures below the isotherm for planning, −22 °C, while less than 10% of the external volume has temperatures below the same temperature threshold. Similar results were obtained for the other prostate models listed in Table 2.

Figure 4 displays the temperature field plotted on the contour of the target region, for prostate model C, using eight cryoprobes. It can be seen from Figure 4 that areas having temperatures as low as the lethal temperatures are found on the contour of the target region, indicating a significant risk for cryoinjury to the surrounding healthy tissue. It is again emphasized that the value of the target isotherm for planning (−22 °C) is selected in this study for demonstration purposes only, while its actual value may be modified according to the surgeon's own experience and preference. It can be further modified in an interactive manner, while evaluating planning results; the surgeon can repeat planning with a modified isotherm for planning, in order to reach acceptable safety margins.

Figure 4.

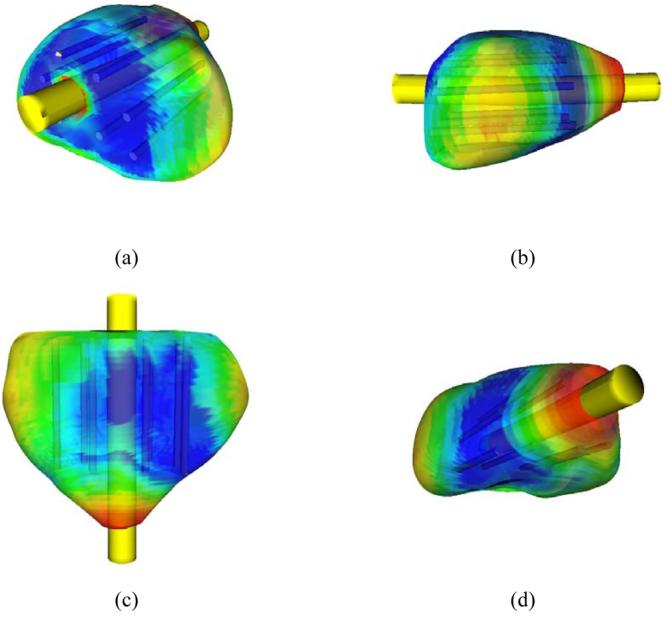
Temperature field illustrated on the target region contour, where blue represents areas with the temperature below −45 °C, green represents 0 °C, and red represents 37 °C. (a) View from the base; (b) sagittal view; (c) coronal view; (d) view from the apex

It can be seen from Figure 4 that a significantly large area in the lateral and apex regions was not simulated to be adequately cryotreated. Neither phases of planning placed a cryoprobe in the lateral and apex regions, due to the requirement of minimum on the total defect. If this region were considered critical to the success of the cryoprocedure, several actions could have been taken: (a) replanning with a combination of different cryoprobe lengths; (b) replanning with variable insertion depths; and (c) applying the so-called ‘pull-back’ procedure, in which some cryoprobes are reactivated in a second cycle of freezing, after axial relocation. These three alternatives represent ongoing research activities by the current research group.

To demonstrate the intra-operative capabilities of the new planning techniques, the following computerized experiment has been conducted on prostate model A, using eight cryoprobes. A localization uncertainty of 2 mm was assumed for the insertion of each cryoprobe, but only on the lateral plane. All other cryosurgery parameters remained unchanged from previous experiments. At the end of Phase I, one cryoprobe was randomly selected to be localized, but was randomly placed at a 2 mm radius from its planned location. Next, Phase I planning was repeated with the first cryoprobe fixed in space, while the remaining cryoprobes were free to move to potentially better locations (due to the less-than-optimal location of the first cryoprobe). Then, a second cryoprobe was randomly selected, randomly placed in a radius of 2 mm from its planned location in the last cycle of planning, and replanning for the remaining cryoprobes was conducted. This process was repeated until all cryoprobes were simulated to be inserted. A bioheat transfer simulation was executed at each stage, to evaluate the quality of planning.

Table 3 lists bubble-packing run time results for replanning after each cryoprobe insertion, and also notes the resulting total defect region. As expected, replanning run time decreases with the decreasing number of remaining cryoprobes; on average it is a reduction of 6 s/cryoprobe. During this process, the total defect region increased by 1.3% from the initial defect of 29.7% (Table 2). Comparable results were obtained for the other prostate models, and when subjected to a range of numbers of cryoprobes. To put these numbers in context, it was necessary to carry out a bioheat heat transfer simulation to evaluate the quality of replanning after each insertion, where the run time for eight cryoprobes is about 7.6 min (Table 2). However, it is not necessary to repeat all the above bioheat simulations in a clinical case, where run time is a significant issue, and when replanning yields moderate changes from the original plan. In the latter case, only the first bioheat transfer simulation would have a critical role on the procedure, when the surgeon must decide whether to accept or reject the computerized planning layout altogether. In the following replanning steps, bubble packing alone is expected to be adequate to cope with the uncertainties of insertion.

Table 3.

Results for intra-operative planning, for prostate model A (Table 2) and eight cryoprobes

Number of inserted cryoprobes	Replanning run time (s)	Total defect at the end of replanning
1	43	29.9
2	37	30.6
3	31	30.6
4	25	31.2
5	20	30.7
6	14	31.0
7	8	31.0

Finally, while replanning was demonstrated for the case of cryoprobe localization uncertainty, replanning can take into account other effects, such as deformation of the target region due to forces associated with the cryoprobe insertion, provided that rapid 3D reconstruction means are available.

Summary and conclusions

As part of ongoing efforts to develop computerized planning tools for cryosurgery, the current study focuses on two recently developed methods for planning, known as bubble packing and force-field analogy. A proof of concept for a two-phase planning scheme has been demonstrated recently in 2D, combining bubble packing and force-field analogy. For the purpose of upgrading the two-phase technique to the general 3D case, prior work included three preparation steps: (a) developing an efficient numerical scheme for 3D bioheat simulations; (b) developing a bubble-packing technique for ellipsoidal bubbles; and (c) evaluating the quality of bubble packing in 3D by means of bioheat transfer simulations. The current study also includes 3D reconstruction of four prostate models, based on ultrasound imaging.

Results of this study indicate that – contrary to common belief, and inconsistent with 2D studies – the increasing of number of cryoprobes does not necessarily improve the quality of planning. Results indicate that both planning algorithms are robust, while force-field analogy leads to superior planning results. However, due to the dramatically longer run time, and the relatively minor improvement of planning using force-field analogy, its clinical application is debatable in comparison with bubble packing. Typical bubble-packing results lead to cooling more than 75% of the target volume below the isotherm for planning, −22 °C, while less than 10% of the external volume resulted in temperatures below the same temperature threshold. The isotherm for planning can be adjusted by the surgeon to control the extent of the safety margins, either exterior or interior to the target region.

An intra-operative planning procedure is demonstrated, where cryoprobe insertion is subject to a localization uncertainty of 2 mm, and replanning is repeatedly done before the next insertion, given the actual locations of the already-inserted cryoprobes. This intra-operative mode is only feasible with bubble packing. The intra-operative mode can take other effects into account, such as deformation of the target region due to forces associated with the cryoprobe insertion, provided that rapid 3D reconstruction means are available.

Finally, the methodology presented in this study is based on the concept of the defect region, which refers to either an insufficiently cooled internal region or an excessively cooled external region. For demonstration purposes, a uniform weight was assigned to all defect regions in this study. A clinical application of this methodology, however, could be expanded to include additional anatomical information, with the example of attributing a higher weight to defects in the rectal area.