Fast Pressure Jumps Can Perturb Calcium and Magnesium Binding to Troponin C F29W

Abstract

We have used rapid pressure jump and stopped-flow fluorimetry to investigate calcium and magnesium binding to F29W chicken skeletal troponin C. Increased pressure perturbed calcium binding to the N-terminal sites in the presence and absence of magnesium and provided an estimate for the volume change upon calcium binding (-12 mL.mol^-1). We observed a biphasic response to a pressure change which was characterized by fast and slow reciprocal relaxation times of the order 1000 s^-1 and 100 s^-1. Between pCa 8-5.4 and at troponin C concentrations of 8-28 μM, the slow relaxation times were invariant indicating that a protein isomerization was rate-limiting. The fast event was only detected over a very narrow pCa range (5.6-5.4). We have devised a model based on a Monod-Wyman-Changeux cooperative mechanism with volume changes of -9 and +6 mL/mol for the calcium binding to the regulatory sites and closed to open protein isomerization steps respectively. In the absence of magnesium, we discovered that calcium binding to the C-terminal sites could be detected, despite their position distal to the calcium sensitive tryptophan, with a volume change of +25 mL/mol. We used this novel observation to measure competitive magnesium binding to the C-terminal sites and deduced an affinity in the range 200 - 300 μM (and a volume change of +35 mL/mol). This affinity is an order of magnitude tighter than equilibrium fluorescence data suggest based on a model of direct competitive binding. Magnesium thus indirectly modulates binding to the N-terminal sites, which may act as a fine-tuning mechanism in vivo.

Troponin and tropomyosin act together as a calcium sensitive regulator of myosin-actin binding in striated muscle. At low calcium concentration (<0.1 μM), as is typically found in the resting sarcomere,(1) troponin-tropomyosin sterically blocks myosin binding to the thin filament (2). Calcium binding to troponin induces a change in conformation of troponin-tropomyosin which results in a shift in the average position of tropomyosin on the thin filament, as observed by cryo-electron microscopy (3-6) and using Förster Resonance Energy Transfer (7, 8). Troponin consists of three subunits C, I and T which function as calcium binding, inhibitory and tropomyosin binding subunits respectively. Troponin C (TnC)¹ acts as the calcium sensor for the thin filament and has four EF-hand metal binding sites numbered I to IV starting at the N-terminus. The C-terminal sites (III & IV) have a high affinity for calcium (50-80 nM) (9, 10) and are generally thought to be constitutively occupied in vivo. They are thus termed ‘structural’ binding sites as the primary role is assumed to be in structural stability. Note that the structural binding sites also bind magnesium, though at a rather weak affinity (~2 mM) which has led to the suggestion that when calcium concentrations are low, magnesium can replace calcium in the structural binding sites (10). Although calcium-magnesium exchange in the sarcomere is still a contentious issue, (1, 11) evidence has been accumulating in favor of this hypothesis (12, 13) and suggests a role for magnesium in stabilizing the troponin complex under relaxing conditions (12, 14). The N-terminal binding sites display lower calcium affinities (1.6 – 3.2 μM), are thought to be calcium specific (10, 13, 15-18) and are the regulatory binding sites (10, 14, 19, 20).

The published data can be considered using the following scheme of calcium and magnesium binding to TnC (Scheme 1).

Scheme 1. Competitive calcium/magnesium binding to TnC F29W.^a.

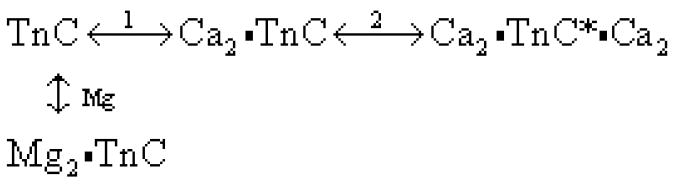
^aCa₂•TnC and Mg₂•TnC have the appropriate metals bound to their structural binding sites (III and IV) whereas Ca₂•TnC*•Ca₂ has both sets of sites filled with calcium. The asterisk on the fully filled state is included to indicate the binding state which exhibits enhanced fluorescence in TnC F29W that we used in our experiments (18).

In this scheme each step describes two second order binding equilibria, each with affinities measured in molar units. Each of these steps depicts the binding of two metal ions cooperatively and is thus simply described using the Hill equation (21):

$$\alpha =\frac{{\left[\mathrm{M}\right]}^{{\mathrm{n}}_{\mathrm{H}}}}{{\left[\mathrm{M}\right]}^{{\mathrm{n}}_{\mathrm{H}}}+K^{{\mathrm{n}}_{\mathrm{H}}}}$$ (1)

where α is the fractional occupancy of the binding sites, [M] is the free metal ion concentration and n_H is the Hill cooperativity parameter. Scheme 1, as drawn, implies that magnesium binding to the C-terminal sites competitively inhibits calcium binding to the C-terminal sites and thus indirectly inhibits calcium binding to the N-terminal sites. It is possible to envisage other states of metal binding, e.g. mixed states such as MgCa•TnC or Mg₂•TnC•Ca₂. We have found that such states are not necessary to explain the available data so they are not included, in accordance with the principle of parsimony (see Discussion).

Studies of metal binding to TnC have commonly employed engineered fluorophores (e.g. W29, W105 or fluorophores covalently bound to engineered cysteine residues) to report metal ion binding. These experiments are in broad agreement, though there is some disparity between work on different TnC constructs (e.g. in the double mutant F29W-F105W both pK₁ and pK₂ were about half a pCa unit tighter than in F29W (13)). Techniques such as NMR or atomic absorption spectroscopy have also been used on native/wild type protein, mostly with similar results. Values for the Hill parameter are not always quoted, but where they are available, estimates of n_H for calcium binding to the regulatory sites are mostly within the range 1.5 – 2.0 (13, 15, 18). Values of n_H for the structural sites are closer to 2 (9, 13, 18). The observation that magnesium binds to the structural sites is long established, (10) although this aspect of metal binding to TnC has since received relatively little attention. When the magnesium affinity has been measured it has mostly been detected using competitive binding effects, with values for K_Mg in the region of 2 mM (10, 22). The standard model of competitive binding that is used in the literature is simplified, in that it takes no account of the cooperative nature of metal binding to TnC:

$$K_{\mathrm{Ca}}^{\mathrm{APP}}=K_{\mathrm{Ca}}.\left(1+\left[\mathrm{Mg}\right]/K_{\mathrm{Mg}}\right)$$ (2)

where K_Ca^APP is apparent calcium affinity, K_Ca is the actual calcium affinity, K_Mg is the magnesium affinity and [Mg] is the magnesium concentration.

In this work we used a full length construct of chicken skeletal TnC containing a single tryptophan close to site I, TnC F29W (18). TnC F29W is not entirely native-like in its behavior principally because of a T130I mutation that weakens the calcium affinity of the C-terminal sites by ~half a pCa unit (9). Nevertheless, this construct is commonly used because it provides a large (~3 fold) fluorescence increase upon binding calcium to the N-terminal sites (18). We have measured pressure induced perturbations of calcium binding to TnC F29W, confirming that pressure favors the calcium bound state but with a smaller volume change than previously found for a similar reaction (15).

An unexpected finding from this pressure jump study was that we could also perturb calcium binding to TnC F29W at low calcium concentrations (7 > pCa > 6) in the absence of magnesium, implying that calcium binding to the C-terminal sites can also be measured using pressure jump. Investigating this further, we titrated magnesium competitively into this reaction and found that the affinity of magnesium for the C-terminal sites is an order of magnitude tighter than previous data suggested.

This work uses novel kinetic measurements to show that calcium binding to the regulatory sites can be explained using a classical Monod-Wyman-Changeux (MWC) scheme (23) with volume changes of opposite sign for calcium binding (-9 mL.mol^-1) and the closed to open protein isomerization steps (+6 mL.mol^-1). We have shown, for the first time, that calcium binding to the structural binding sites causes a change that can be detected using an engineered probe (W29) in the regulatory binding site. We have demonstrated that magnesium binding to the structural binding sites inhibits calcium binding to the regulatory sites. The improved quality of the data on calcium displacement allowed us to confirm that calcium binds to the regulatory sites sequentially. These studies demonstrate that experiments using single tryptophan mutants in combined fast perturbation and rapid mixing experiments are capable of resolving novel details of the mechanisms of action. Some of this work was presented previously at the Biophysical Society Annual Meeting in 2006 (24).

MATERIALS AND METHODS

Pressure jump technique

A change in pressure can alter the free energy of a reaction (ΔG°) in which there is a difference in volume (ΔV°) between the reactants and products. If the volume of the reactants is V and the volume of the products is V + ΔV°, then the forward reaction must do enthalpic work (given by P.ΔV°) against the external pressure to proceed. The pressure perturbation function is thus given by the differential of the work done with respect to pressure:

$$\mathrm{\Delta }V°=-\mathit{RT}.\frac{\partial \ln K}{\partial P}$$ (3)

Therefore, experiments can utilize pressure as a thermodynamic variable either at equilibrium (or steady state) or for transient kinetic measurements by imposing a fast step-change in pressure, as we do here using the pressure jump technique.

Pressure jump is often able to selectively perturb steps on a reaction pathway that other kinetic and equilibrium based approaches cannot (e.g. (25, 26)). Where second order (i.e. binding) events are being measured, this process can be modulated by changing the concentration of one of the binding partners, altering both the observed exponential inverse time constant and the amplitude (i.e. the relative concentration change resulting from the pressure jump).

Pressure Jump Equipment

The pressure jump apparatus is an improved version of the equipment described earlier (27). The new measurement unit (supplied by G. Holtermann, MPI, Dortmund) consists of a cylindrical sapphire sample cell (3 mm × OD 8 mm ×ID 3 mm) with a deformable polyimide membrane at one end that is in contact with a piston under the control of a piezoelectric stack. Compared to the earlier equipment, this system features a shorter column of liquid - enabling larger pressure steps to be achieved - and a third window so that both absorbance and fluorescence/light scattering measurements may be made. The electronics (supplied by TgK Scientific Ltd, Bradford-on-Avon, UK) are based on a HiTech Stopped-Flow Control Unit with an extra amplifier (range = 1x to 80x) and a digital voltage display for real time monitoring of the signal level. Signal conditioning filter circuits are user selectable between 3.3 μs up to 100 ms. The light source (100 W Hamamatsu Xe/Hg arc lamp), A/D board (DAS-50, Keighley Instruments) and software were unchanged from the previous configuration.

The performance of the equipment is illustrated in Fig. 1, where the upper panels (A-B) show the pressure increase (A) and decrease (B) applied to a 1 μM solution of fluorescein in imidazole buffer, together with the resulting change in fluorescence averaged over 500 consecutive pressure jumps (panels C-D). After the 0.2 ms pretrigger recording, the piezo stack was triggered, resulting in an initial pressure rise of 44.5 MPa (445 atmospheres) in less than 100 μs. This was followed by a slight ripple that decayed within 0.5 ms and reached a steady level of 47.0 MPa. The fluorescence transient followed a near identical profile to the pressure transient. The final fluorescence level of ~2.1 % is consistent with a simple compression effect (given by the bulk compliance of water, 0.0461 %/MPa). Upon reversal, the pressure returned to its original level over a similar timescale but with only a single slight ripple in the pressure transient that was also seen in the fluorescence transient.

Figure 1.

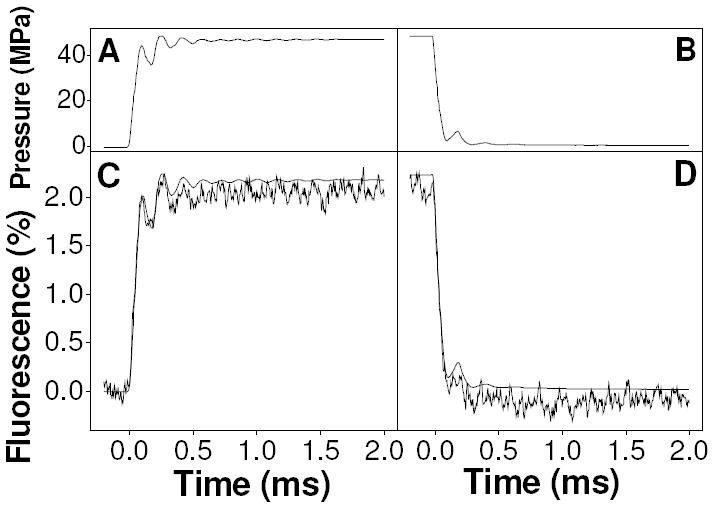
Example applied pressure transient (panels A-B) together with the associated fluorescence transient (panels C & D, the product of 500 averages) for 1 μM fluorescein in 20 mM imidazole buffer at pH 9.82. The smooth curve in panels C-D is calculated from the pressure trace, for comparison with the measured fluorescence transient.

Materials

Chicken fast skeletal muscle TnC F29W was prepared according to (18) which involved cloning into a pET3a plasmid and expression in BL21(DE3)pLysS cells. The clone was a gift from Jonathan P. Davis (Ohio State University). The protein was dialyzed into a standard buffer containing 100 mM KCl, 20 mM MOPS, 1 mM NaN₃ at pH 7. The samples were assayed spectrophotometrically at 280 nm in 6 M guanidinium HCl, pH 6.5, using an extinction coefficient of 5960 M^-1cm^-1, calculated using the ExPASY tool online (28). The protein was used in pressure jump experiments at a concentration of 10 μM, unless otherwise stated. Standard buffer with various concentrations of free calcium were prepared by diluting stock solutions of 100 mM calcium-EGTA and 100 mM EGTA to a final EGTA concentration of 1 mM unless stated otherwise. The free calcium concentrations were calculated using the Maxchelator Lite (v 1.15) website (29). The constants used for these calculations come from the National Institute of Standards and Technology scientific and technical database. Solutions for pressure jump were made up with 1-2 mM dithiothreitol added to stabilize the protein against photobleaching.

Pressure Jump Experiments

Tryptophan fluorescence was excited at 297 nm (± bandwidth 1.8 nm) using light from a Hg/Xe arc lamp and collected onto a photomultiplier via a WG320 cutoff filter to remove stray/scattered excitation light. Transients of 50 ms duration + 5 ms pretrigger were collected in sequences of 100 averages each (an observation lasting ~ 11 sec) and later averaged together to produce a final transient of at least 500 repeats. The DAS-50 A/D card collects at 1 MHz and signal oversampling was used to reduce the final number of points to 500 for each 50 ms transient (+ 50 pretrigger). In these experiments 35.0 MPa pressure steps were used, unless otherwise stated.

Stopped-Flow Experiments

Rapid-Mixing experiments were carried out using a High-Tech SF-61 Stopped-Flow apparatus. Displacement by pCa jump was measured by mixing TnC at pCa 4 with buffer at pCa 6.2 to achieve a final pCa of 5.8. All traces were the result of averaging at least six individual transients followed by subtraction of a buffer blank and normalization to the level of fluorescence observed at the ends of the transients. A protein concentration of 5 μM (post mixing) was used for these experiments. The filter time constant was manually set to 10 μs in order to ensure that any fast processes were not the result of electronic filter induced artifacts.

Data Analysis

Fluorescence transients resulting from pressure jump experiments were calculated as percent change in relative fluorescence (F(t)) using the following formula:

$$F(t)=100.\left\{\frac{B-S(t)}{B-S(0)}-1\right\}$$ (4)

where B is the signal measured using buffer, S(t) is the signal measured at time t, and S(0) is the signal averaged over the pre-trigger time before the jump was initiated. Exponential decay functions of the following form were fitted to the pressure jump and stopped-flow data:

$$F(t)=F_{\infty }+\sum _{\mathrm{i}}^{\mathrm{i}=\mathrm{n}}{A}_{\mathrm{i}}\left(1-\exp (-t/{\mathrm{\tau }}_{\mathrm{i}})\right)$$ (5)

where F(t) is the fitted fluorescence function, F_∞ is the end-point, A_i and τ_i are the amplitude and relaxation time of the ith phase respectively, and where larger subscript numbers indicate slower processes. Phase number zero is reserved for an instantaneous response (i.e. too fast to resolve using this technique) and therefore consists of only an amplitude (A₀). The phase 0 amplitude was determined from the difference between the pretrigger fluorescence and the beginning of the exponential curve fit. Fitting of exponential decay functions to the transients only included clearly defined exponential phases so, in Fig. 3 pCa 5.2 is shown fitted to a single exponential, ignoring the small fast lag component, whereas the pCa 5.5 transient is fitted to a double exponential function. The small artifact apparent in the pressure release of some of the transients was not included in the fitting (see pCa 7.0 in Fig. 3).

Figure 3.

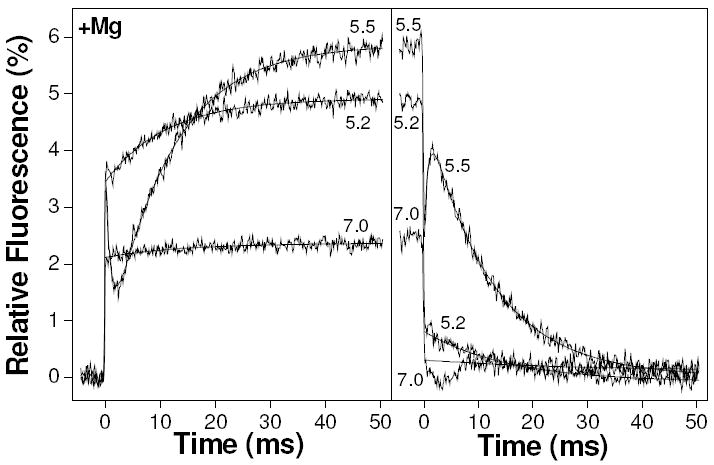
Example transients from the pressure jump showing the results of 35 MPa pressure jumps on 10 μM TnC F29W containing various concentrations of free calcium (indicated as pCa values, adjacent to appropriate curves), in the presence of 2 mM magnesium. The left panel is the result of pressure increase whilst the right panel is the result of pressure release.

Equilibrium fluorescence values (B - S(0)) resulting from the raw pressure jump transients were normalized to the low calcium (pCa 9) value and fitted to the following logistic sigmoid curve (30) which is equivalent to the normalized Hill isotherm (eq 9) but is not biased by the large dynamic range present in calcium concentrations:

$$F(\mathrm{Ca})=1+\frac{(Q-1)}{1+{10}^{n_H(\mathit{pCa}-\mathit{pK})}}$$ (6)

where F(Ca) is the normalized fluorescence, Q is the fractional increase in fluorescence upon binding calcium, pK is the −log of the binding constant K, pCa is the negative log of the calcium concentration and n_H is the apparent Hill cooperativity coefficient.

RESULTS

Pressure Jump Transients

The effect of rapid pressure jumps on TnC F29W was examined at pCa 5.6, close to the published value for the binding constant where classical perturbation theory predicts the largest amplitude of perturbation can be expected to occur. An example pressure jump transient (averaged over 600 - 1500 repeats) obtained using 10 μM TnC F29W at pCa 5.6 in the presence of 2 mM magnesium, is shown in Fig. 2 (A-D). Upon pressure application to 35.0 MPa (curves marked ‘35.0’ in the Fig.), there was an instantaneous enhancement in fluorescence of ~ 7.7 % (phase 0) which was followed by a transient that was well-fitted by two exponentials. The exponentials consisted of a fast quench (phase 1; A₁ = -2.05 %, 1/τ₁ = 1110 s^-1) followed by a slower large enhancement (phase 2; A₂ = +5.76 %, 1/τ₂ = 90 s^-1). Upon pressure release, the fluorescence followed essentially the reverse of the pressure increase profile, i.e., there was an instantaneous quench followed by two slower phases of opposite sign, after which the fluorescence returned to its original level. The equilibrium fluorescence level was stable between sets of repeat measurements on the same sample, i.e. over a time scale of 5-10 minutes, implying that there was no slow degradation of the sample e.g. photobleaching. Note that the large phase 0 amplitudes seen here were typical of the preparation used for this set of experiments but varied by as much as a factor of two from preparation to preparation. All other aspects of the response were reproducible when repeated using another protein preparation (see later section and Fig. 3 & 4).

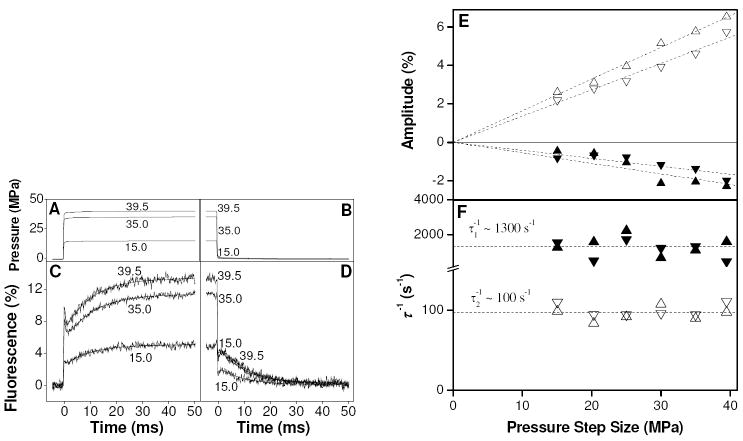
Figure 2.

(A-D) Example transients from the pressure jump showing the results of repeated fast 15.0, 35.0 and 39.5 MPa jumps on 10 μM TnC F29W at pCa 5.6, including 2 mM magnesium. Panels A-B show the pressure transients for this sample (single measurement each). Panels C-D show fluorescence transients (averaged over 600-1500 repeats), with double exponential fits superimposed. (E-F) Effect of pressure step size on amplitude (E) and inverse time constant (F) of fluorescence response. The amplitudes of phases 1 and 2 were linear in pressure step. The slopes for phase 1 were -0.05 ± 0.006 and -0.04 ± 0.003 %.MPa^-1 for pressure increase (▲) and pressure decrease (▼), respectively. The slopes for phase 2 were 0.165 ± 0.002 and 0.144 ± 0.003 %.MPa^-1 for pressure increase (△) and pressure decrease (▽), respectively. The inverse time constants were invariant (1/τ₁ ~ 1300 ± 150 s^-1 and 1/τ₂ = 97 ± 2 s^-1) within the accuracy of the measurements.

Figure 4.

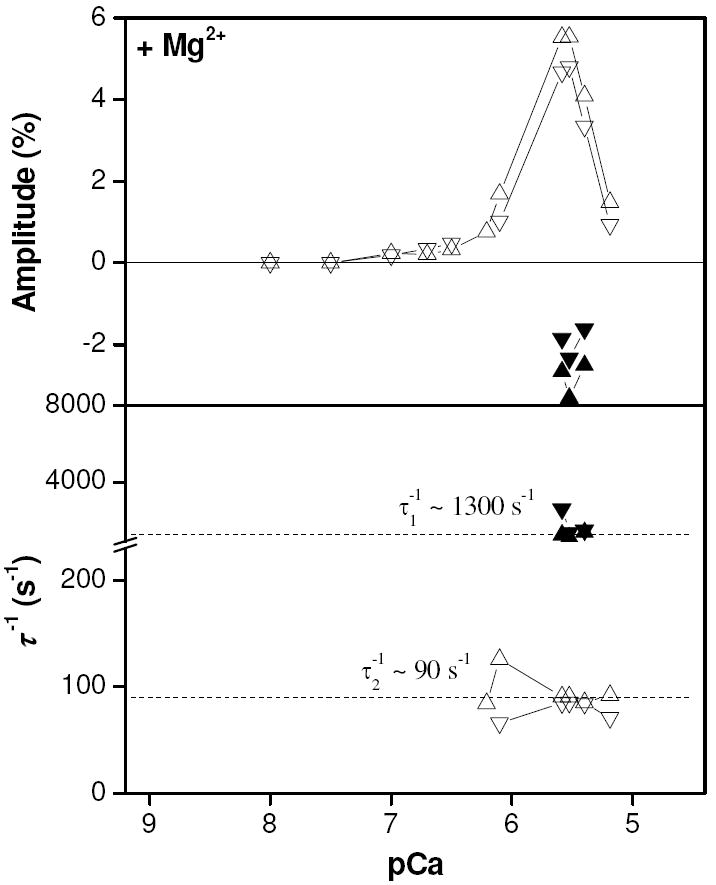
Amplitude plot of results of exponential fitting to pressure jump data as a function of pCa (upper). Plot of inverse relaxation times from exponential fitting to pressure jump transients (lower). Upward pointing triangles (phase 1 = ▲, phase 2 = △) indicate results from pressure application whilst downward pointing triangles (phase 1 = ▼, phase 2 = ▽) indicate results from pressure release.

We investigated the effect of changes in the size of the pressure step on the amplitude and inverse time constant of phases 1 and 2 in order to ensure that the relative concentration changes were small. Perturbation theory requires that for a “small” perturbation the amplitude of the perturbation should be linearly dependent on the size of the applied pressure step while the relaxation times should be independent of the size of the pressure step. The results are shown in Fig. 2 (E-F). The amplitude of phase 2 (Fig. 2E, positive quadrant) was linear in pressure step size up to steps of 40 MPa (slope = 0.165 & 0.144 %.MPa^-1 for pressure application and release, respectively) and the inverse time constant (Fig. 2F) was essentially invariant over this pressure range, within the accuracy of this experiment (1/τ₂ ~ 100 s^-1). Similarly, the amplitude of phase 1 (Fig. 2E, negative quadrant) was linear in pressure step size (slope = -0.05 & -0.04 %.MPa^-1 for pressure application and release, respectively) and the inverse time constant (Fig. 2F) was also invariant over this pressure range (1/τ₁ ~ 1300 s^-1). The combination of good fits to exponential decay functions, lack of apparent pressure dependence of the inverse time constants and linear dependence of the amplitudes on the pressure step size together indicate that the 35.0 MPa pressure steps used in the subsequent pressure jump experiments resulted in only small changes in concentration between different species compared to the total concentrations present. This means that the approximation to exponential decay implicit in these measurements is valid and that ΔV° is effectively invariant over this range of pressure.

Calcium Dependence of Pressure Jump Relaxation

We investigated the sensitivity of the phases observed in Fig. 2 to calcium concentration over the range pCa 8 - 5. Phase 0 was present at all calcium concentrations and will be considered in a later section. Phases 1 and 2 displayed calcium dependent amplitudes. Phase 1 was only clearly observable over a very narrow range (pCa 5.6 - 5.4) whereas phase 2 was reasonably well-defined over a broader range (pCa 6.2 - 5.2) near the midpoint of the calcium binding isotherm.

Example fluorescence transients obtained at a range of pCa values are shown in Fig. 3. The fluorescence transient at pCa 5.5 was similar to the transient shown earlier at pCa 5.6 (Fig. 2) with 3 phases. The phase 0 amplitude of ~ 3.5 % was followed by a slower biphasic exponential response (A₁ = -3.3 %, 1/τ₁ = 1100 s^-1; A₂ = 5.5 %, 1/τ₂ = 91 s^-1). At pCa 5.2 A₀ was the same as at pCa 5.5 but phase 1, if present, was too small to measure. Phase 2 at pCa 5.2 had a smaller amplitude than at pCa 5.5 but 1/τ₂ remained virtually unchanged (A₂ = 1.5 %, 1/τ₂ = 90 s^-1). At pCa 7.0 the amplitude of phase 0 was smaller than at higher calcium concentrations (2.4 %) and there was no observable phase 1. The amplitude of phase 2 at pCa 7.0 had declined to a level that was barely observable. Upon pressure release, the fluorescence was essentially reversed except for the presence of a small artifact between 0-10 ms after pressure release.

Plotting the amplitudes of the exponential fits as functions of pCa (Fig. 4 - upper) indicates that phase 1 was observable over a very narrow range of pCa values close to 5.5 (pCa 5.6 - 5.4), troughing at ~ -3 %. We observed no pCa dependence of the inverse relaxation time, with values over this narrow pCa range all close to 1300 s^-1 (Fig. 4 - lower). Phase 2 was present over a broader pCa range than phase 1 with an effectively invariant inverse relaxation time of ~90 s^-1 over this range of calcium concentrations. The main peak of about 5 % was centered about pCa 5.6 (as was the case for phase 1) and had a half-height peak width of 0.68 pCa units.

Effect of TnC Concentration on the Pressure Jump Relaxation

The inverse time constant of a putative second order binding reaction after a small perturbation depends linearly on the free concentrations of the reacting species:

$${\tau }^{-1}=k_{\mathrm{on}}\left\{\left[{\mathrm{Ca}}^{2+}\right]+\left[\mathrm{TnC}\right]\right\}+k_{\mathrm{off}}$$ (7)

Buffering of the free calcium concentration by EGTA has the effect of buffering the total free concentration over a pCa series. We therefore repeated the measurement at pCa 5.5 (in the absence of magnesium) over a range of concentrations of TnC in order to determine whether the invariance of the inverse time constants was due to this buffering effect. Fig. 5 shows the results of fitting to single exponential functions (phase 1 was not well-enough defined for analysis), plotted as a function of initial concentration of TnC. Both the amplitude and inverse relaxation times were invariant over the range shown (8 – 28 μM). This observation, combined with the invariance of the inverse relaxation times in previous measurements indicates that a protein isomerization is rate-limiting in these pressure jump experiments.

Figure 5.

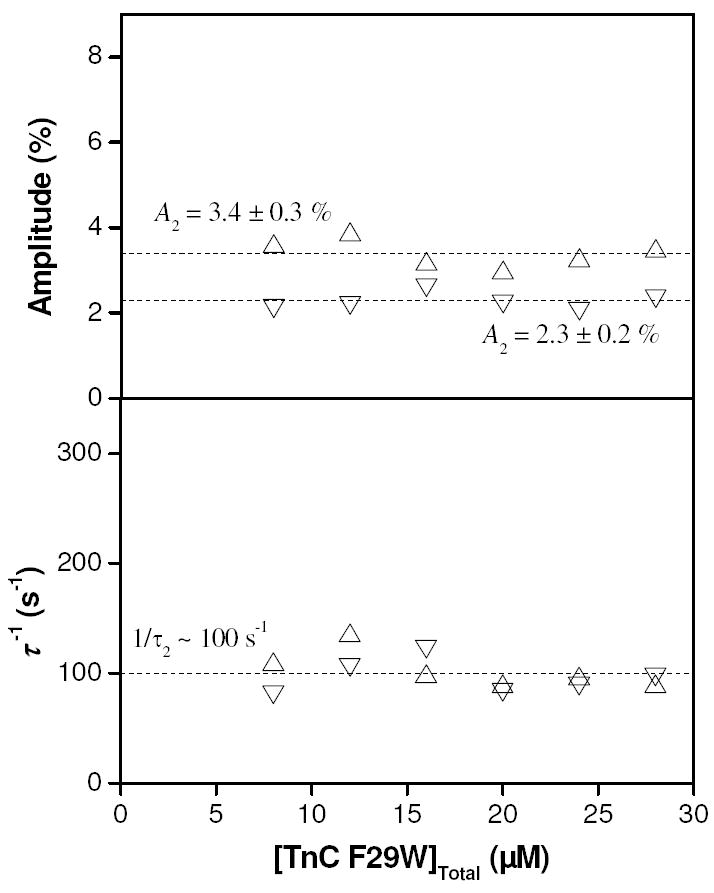
Results of varying the concentration of TnC F29W in pressure jump experiments at pCa 5.5, in the absence of magnesium. Upper panel shows the amplitude of phase 2 was unaffected by total protein concentration. Lower panel shows that the reciprocal relaxation time was also unaffected by total concentration of TnC F29W in the sample, within the range 8 – 28 μM. Upward pointing triangles (△) indicate results from pressure application whilst downward pointing triangles (▽) indicate results from pressure release.

Calcium Dissociation Experiments

We tested the rate-limiting-step of calcium release from TnC F29W by measuring the rate constant for calcium dissociation. This was carried out using displacement with a pCa jump from 4 to 5.8 by mixing with buffer at pCa 6.2. Jumping to pCa 5.8 avoids significant dissociation from the structural sites, which may complicate the interpretation. The presence of residual calcium means that some rebinding may occur contributing to the observed rate constant, which is therefore regarded as an upper estimate. The result of this experiment is shown in Fig. 6. The upper panel of Fig. 6 shows the residuals resulting from single exponential (n = 1) and double exponential (n = 2) fitting to these data for comparison. There is a large deviation associated with the residuals resulting from the single exponential fit compared to the double; therefore a double exponential was required to achieve a reasonable fit to the data. An F-test confirmed that adding the extra fitting parameters was statistically valid (p < 0.01). The results of this double exponential fit (as shown superimposed on the data curve) were a fast enhancement (A₁ = +89 %, k₁ = 338 s^-1) followed by a slower quench (A₂ = -195 %, k₂ = 155 s^-1). Note that a control experiment under identical conditions mixing a large excess of ATP with skeletal myosin S1 were fit convincingly using a single exponential (data not shown), as previously reported (31), ruling out a machine-based artifact as the origin of the fast phase.

Figure 6.

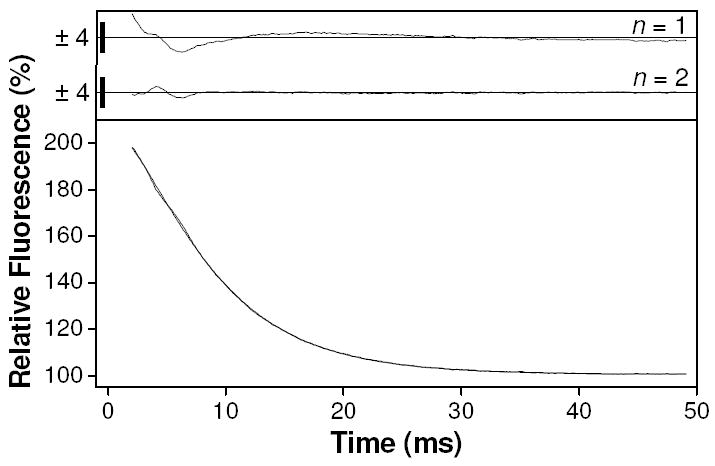
Results of calcium displacement reaction in stopped-flow. Lower panel shows Fluorescence transient resulting from a pCa jump experiment by mixing 10 μM TnC F29W at pCa 4 with pCa 6.2 buffer, leading to a final pCa value of ~5.8. Fitting to a double exponential gave amplitudes of +89 and -195 % and observed rate constants of 338 and 155 s^-1. Upper panel shows residuals from fits where n refers to the number of exponentials. Size of residuals are indicated by y-axis scale bars (%).

This surprising result was indicative of consecutive steps since the direction of the fluorescence change in the fast phase was reversed compared to the slower phase. Such a lag-phase is diagnostic of the accumulation of an optically silent on-pathway intermediate, as in the following scheme:

In the case of a two-step, consecutive reaction scheme, with a change in the optical signal on the second step, the ratios of the amplitudes and observed rate constants are related according to the following equation (32):

$$-\frac{A_1}{A_2}=\frac{{\lambda }_2}{{\lambda }_1}$$ (8)

where arabic numerals serve to distinguish the amplitudes (A₁ and A₂) and observed rate constants (λ₁ and λ₂) of the fast (1) and slow (2) phases from the intrinsic rate constants due to the individual steps (k_-I and k_-II). These observed rate constants and amplitudes are given by functions of the intrinsic rate constants because the flux through both steps affects the availability of substrate (see supplementary information, section S3 for further details). Making this comparison using the data from Fig. 6 ‘Ca’, -A₁/A₂ = 0.456 and k₂/k₁ = 0.459 which are identical within error. These observations are consistent with sequential calcium release from TnC F29W that is not rate-limited by the same protein isomerization as was apparently the case in the pressure jump experiments. We also modeled this scheme using Berkeley-Madonna software and obtained the same result.

Effect of Magnesium on the Pressure Jump Relaxation

The pressure jump data shown in Figs 2-4 were collected in the presence of 2 mM magnesium in line with previous publications (10, 33). In order to evaluate any contribution from the structural binding sites we reinvestigated the effect of calcium on the pressure induced relaxation, in the absence of magnesium. In the absence of magnesium, phase 0 was again present at all calcium concentrations in the range pCa 9 - 4. Phase 1 was also present as a small quench over a narrow range of pCa values (6.0 - 5.5). Phase 2 was well-defined over a broad range of calcium concentrations (pCa 7.0 - 5.0) but surprisingly the direction of phase 2 reversed to a quench on pressure application above pCa 6.1.

Fig. 7 shows example pressure jump fluorescence transients obtained over a range of pCa values in the absence of magnesium. In Fig. 7A-B, where calcium concentrations were at or above 1 μM, the transients were qualitatively similar to the results found in the presence of 2 mM magnesium. Upon pressure increase at pCa 6, there was a phase 0 enhancement of around 1.5 - 2 % followed by an apparent phase 1 that was smaller than -1 % and too small and fast to be sensibly included in the fit. The phase 2 amplitude was 1.5 % with 1/τ₂ = 122 s^-1. At pCa 5.6, A₀ was ~2.8 % which was followed by two phases (A₁ = -1.3 %, 1/τ₁ = 1660 s^-1; A₂ = 3.5 %, 1/τ₂ = 119 s^-1), reaching 5.1 % at the end-point. At higher calcium still (pCa 4.6), there was a strong phase 0 response (A₀ ~ 4.8 %) to pressure application but there were no measurable slow responses. All of these transients were essentially reversed upon release of pressure (Fig. 7B).

Figure 7.

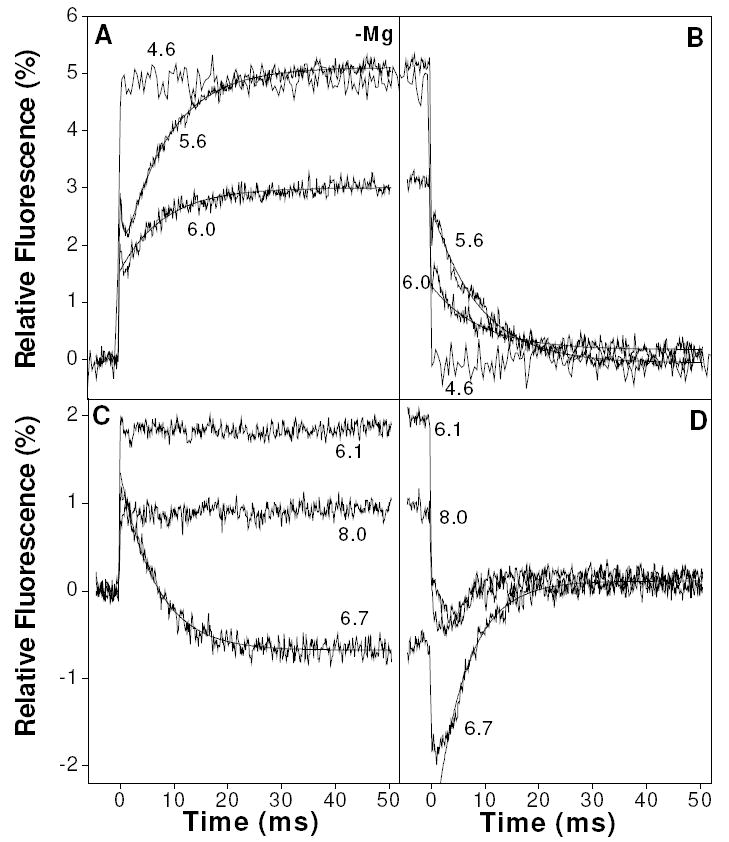
Example transients from the pressure jump showing the averaged results (fluorescence) of repeated fast 35 MPa jumps on 10 μM TnC F29W containing various concentrations of free calcium in the absence of magnesium. A-B shows results obtained in high concentrations of calcium while C-D shows results obtained at pCa > 6.

In Fig. 7C-D, where calcium concentrations were below 1 μM, the results are strikingly different. At pCa 6.1 there was a 1.8 % enhancement (phase 0) upon pressure increase with no subsequent slower processes. At pCa 6.7 there was a 1.3 % enhancement (phase 0) followed by a -2 % quench (phase 2) with 1/τ₂ = 150 s^-1. At pCa 8.0 this quench was no longer evident and phase 0 had declined to about 0.9 %. Upon pressure release, these transients were reversed but the fluorescence artifact seen on pressure release in Fig. 3 in the 0 - 10 ms time window was again evident. At pCa 6.7 this artifact takes the form of a lag phase in the pressure release transient that was not present either in the pressure application transient or at pCa < 6.

The plot of amplitude as a function of pCa (Fig. 8 - upper) again shows the presence of a fast quench (phase 1) over a narrow range of pCa values, this time troughing closer to pCa 6 (pCa 6.0 - 5.5). The values of 1/τ₁ are less clearly defined than in the presence of magnesium and appear to be considerably faster - in the region of 2500 s^-1 (Fig. 8 - lower). Phase 2 in this amplitude plot extends over a broader range of pCa values than it did in the presence of magnesium, peaking at pCa 5.5. The sign of the amplitude reverses below pCa 6.1, at which pCa the response was flat (see Fig. 7) and phase 2 troughs at pCa 6.5. The values for 1/τ₂ (Fig. 8 - lower) were marginally faster in the absence of magnesium, with a mean value for the pressure application data of 130 s^-1. Whilst the 1/τ₂ values derived from fits to the pressure application data did not vary systematically with pCa, the values from pressure release data seemed to decline with increasing calcium concentration. A systematic effect on these inverse time constants due to changing pCa values cannot be ruled out, but it is more likely that the presence of the 0 - 10 ms fluorescence artifact in much of the fluorescence data upon pressure release has systematically biased the results of exponential fitting to these data.

Figure 8.

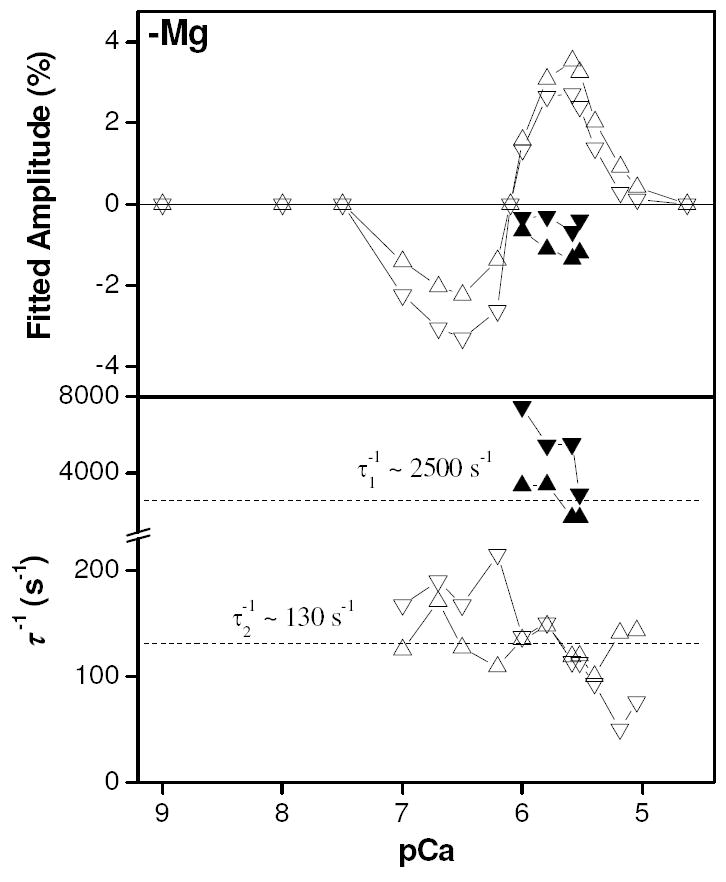
Amplitude plot of results of exponential fitting to pressure jump data obtained in the absence of magnesium as a function of pCa (upper). Plot of inverse relaxation times from exponential fitting to pressure jump transients (lower). Upward pointing triangles (phase 1 = ▲, phase 2 = △) indicate results from pressure application whilst downward pointing triangles (phase 1 = ▼, phase 2 = ▽) indicate results from pressure release.

Phase Zero Amplitudes and Calcium Titration

The values of equilibrium fluorescence (derived from the pressure jump measurements) were normalized to the value at pCa 9 and are shown in Fig. 9A. Both plus and minus magnesium data can be fitted to normalized Hill binding isotherms:

Figure 9.

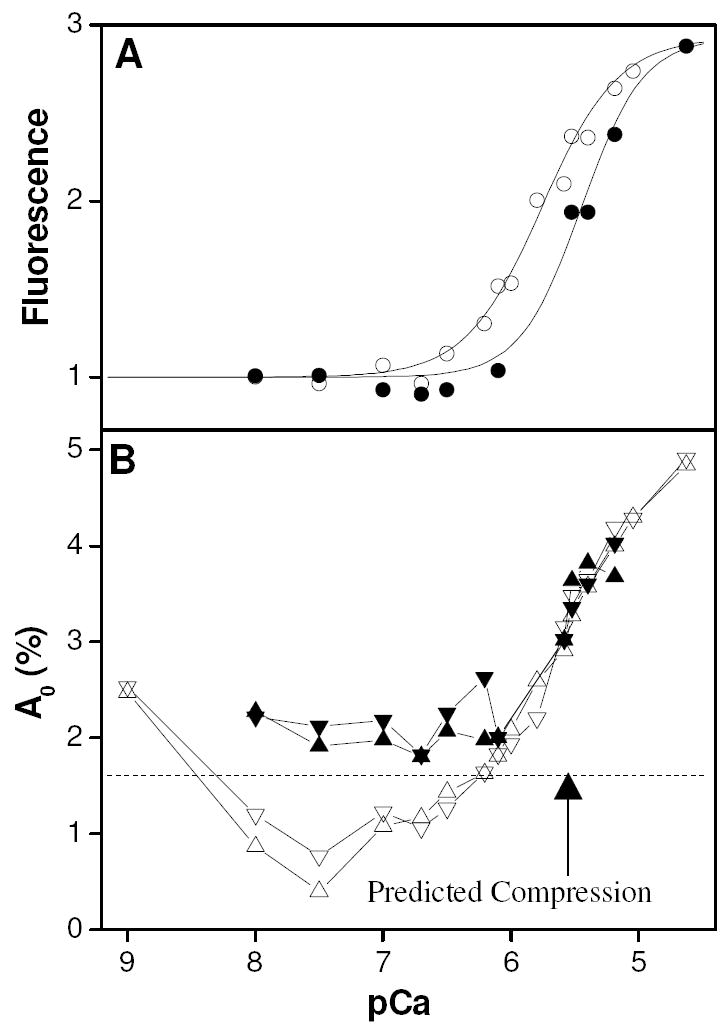
Panel A shows equilibrium fluorescence results from pressure jump experiments. Hill curves have amplitudes of 2.9, pK values of 5.76 and 5.45 and cooperativity parameter values of 1.46 and 1.8 for the no magnesium and 2 mM magnesium cases, respectively. Panel B shows the amplitude of the instantaneous change in fluorescence resulting from the same set of experiments. Empty symbols (○, △, ▽) indicate experiments done in the absence of magnesium, whereas filled symbols (●, ▲, ▼) indicate experiments done in the presence of 2 mM magnesium. Upward pointing triangles (+Mg = ▲, -Mg = △) indicate results from pressure application whilst downward pointing triangles (+Mg = ▼, -Mg = ▽) indicate results from pressure release.

$$F(\mathrm{Ca})=1+(Q-1).\frac{{\left[\mathrm{Ca}\right]}^{{\mathrm{n}}_{\mathrm{H}}}}{{\left[\mathrm{Ca}\right]}^{{\mathrm{n}}_{\mathrm{H}}}+K^{{\mathrm{n}}_{\mathrm{H}}}}$$ (9)

where Q is the fractional increase in fluorescence upon binding calcium, K is the binding constant, [Ca] is calcium concentration and n_H is the Hill cooperativity coefficient. In both cases, Q was 2.9 within the error of the measurement, indicating that the presence of magnesium did not alter the fluorescence of the sample either under low or saturating calcium conditions. The calcium half-saturation value (pK) was 5.45 ± 0.03 with an apparent Hill value of 1.8 ± 0.3, which is in line with published results. In the absence of magnesium, the apparent calcium binding constant became tighter (pK = 5.76 ± 0.02) as is predicted if magnesium competes for a subset of calcium binding sites and the apparent Hill parameter was 1.46 ± 0.09.

The amplitude of the phase 0 response is shown in Fig. 9B. At higher calcium concentrations (pCa < 6.1) the data in the presence and absence of magnesium are superimposable and follow the calcium binding isotherm from the +Mg data (c.f. Fig. 9A). This suggests that phase 0, under these conditions, is probably reporting a local conformational perturbation that is only observed when calcium is bound to the regulatory sites. At lower calcium concentrations (pCa > 6.1), the two cases (+ or - magnesium) look quite different. In the presence of magnesium, there is a small excess over the calculated compression effect (1.6 %, indicated by broken line) which indicates that with magnesium in the structural sites there is still some small response. By contrast, in the absence of magnesium the residual effect at pCa > 6.1 is negative (except at pCa 9).

Magnesium Titration Experiment

We further investigated the trough in the pressure jump amplitudes observed at low calcium concentrations (pCa ~ 6.5) that was only apparent in the absence of magnesium. The pressure jump experiment at pCa 6.5 was repeated, but this time magnesium was titrated into the mixture between repeat measurements. A logarithmically distributed range of magnesium concentrations was used between 1 μM and 1 mM. The results of this experiment are shown in Fig. 10. The amplitudes of phase 2 were fitted to Hill curves with [Mg]₅₀ values of 350 ± 20 μM for pressure application and 430 ± 20 μM for pressure release. In both cases, the values for the apparent Hill coefficients were close to 2 (1.96 and 1.88 respectively, ± 0.2). These results suggest that magnesium, binding cooperatively, competes for the structural binding sites with a half inhibition value of 430 μM at pCa 6.5, abolishing the signal from calcium binding that is visible in pressure jump in the absence of magnesium. The inverse time constants appear to increase at high magnesium concentrations. This is most likely due to the small amplitudes under these conditions making fits to single exponential functions increasingly under determined.

Figure 10.

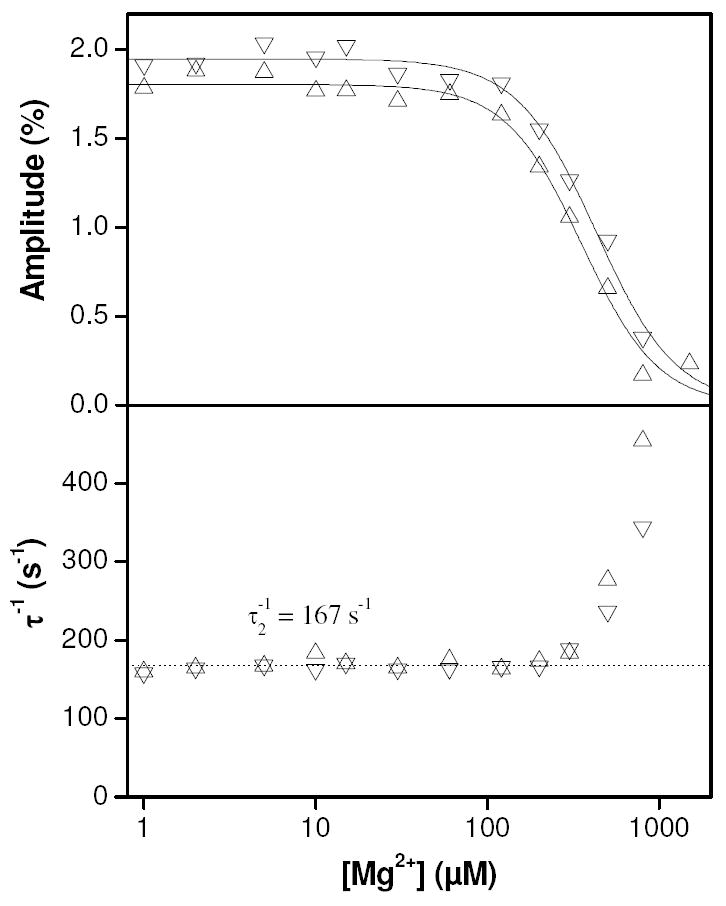
Results of titrating magnesium into 10 μM TnC F29W at pCa 6.5 in the pressure jump. At low magnesium concentrations (< 100 μM), the results were similar to the observations made in the absence of magnesium (Fig. 8). At higher magnesium concentrations the amplitudes of phase 2 (upper panel) declined to the point where they were no longer measurable (~ 1 mM). The amplitudes were fitted to Hill curves for respective pressure application and release with amplitudes of 1.80 and 1.95, half maximal magnesium concentrations of 350 and 430 μM and Hill parameters of 1.96 and 1.88. The reciprocal relaxation times (lower panel) were constant (mean = 167 s^-1) below ~200 μM magnesium above which they increased approximately exponentially. Upward pointing triangles (△) indicate results from pressure application whilst downward pointing triangles (▽) indicate results from pressure release.

This experiment was carried out at pCa 6.5, well below the calcium binding affinity for the regulatory sites but close to the half saturation value for the structural sites, which means we can calculate the magnesium affinity for the structural binding sites using the equivalent of eq 2 applied to calcium competition for magnesium:

$$K_{\mathrm{Mg}}^{\mathrm{APP}}=K_{\mathrm{Mg}}.\left(1+\left[\mathrm{Ca}\right]/K_1\right)$$ (10)

where K_Mg^APP is the apparent magnesium affinity, K_Mg is the actual magnesium affinity, K₁ is the calcium affinity to the structural sites and [Ca] is the magnesium concentration. Since, at half saturation [Ca] ~ K₁, the values for the magnesium affinity to the structural sites can be obtained by dividing the K_Mg^APP values by two, i.e. the affinities can be estimated at 175 and 215 μM for pressure application and release. We checked the validity of this method by modeling metal binding to the C-terminal sites as fully cooperative (i.e. no significantly populated intermediate states) and conducting simulations in Berkeley Madonna software. The result of this simulation was a titration curve following the disappearance of Ca₂•TnC with added magnesium. The curves could be fitted to Hill curves with n_H values close to but less than 2.0 and used actual magnesium affinities of 230 and 284 μM for pressure application and release respectively. This indicates that the simple calculation based on eq 2 provides a reasonable estimate for the true magnesium affinity.

The two Hill curves for pressure application and release were reasonably well separated, with clear differences between the fits. The pressure dependent difference between the affinities means that we can also estimate the apparent volume change for magnesium replacing calcium binding to the structural sites using eq 3, based on a value for ∂ln(K_Mg)/∂P of +5.9×10^-3 MPa^-1 which is the same whichever affinity estimates are used because the proportional change in affinity with pressure is not affected by the absolute values used. The value we obtain is ΔV^APP_Mg = +14 ± 7 mL.mol^-1.

DISCUSSION

Fast Pressure Jumps Can Perturb Calcium Binding to TnC F29W

TnC F29W responds to calcium binding with a 2.9-fold increase in tryptophan fluorescence (Fig. 9A) which is most simply described by a cooperative binding curve with a pK of 5.76 and a Hill coefficient of 1.46 in the absence of magnesium. The application of pressure of 35 MPa induces a fluorescence increase consistent with increased calcium binding. The total pressure induced change in fluorescence (+5.1 %) measured at pCa 5.6, close to the mid-point of the binding isotherm, (which is where we would expect the amplitude of the fluorescence change to be maximal) allows us to make an estimate of the apparent increase in calcium affinity induced by pressure and hence the molar volume change for calcium binding. Rearranging eq 9 implies that a +5.1 % increase in fluorescence translates to a shift in the midpoint of the Hill isotherm of +0.081 pCa units, which for a 35 MPa pressure jump leads to a value for ∂ln(K₂)/∂P of +5.3×10^-3 MPa^-1. Substituting this value into eq 3 leads to an estimate of ΔV°₂ = -13 mL.mol^-1 for the total volume change associated with calcium binding to TnC F29W. This assumes a simple single step calcium binding model and treats the protein as if all four calcium binding sites were identical. However, the three-phase relaxation kinetics imply a more complex mechanism (see next section).

The two structural binding sites located on the C-terminal lobe of TnC are known to have a much tighter calcium affinity than the N-terminal sites (pK₁ ~ 6.7 (13, 17, 18) whereas pK₂ lies in the range 5.8 – 5.5 (13, 16-18, 22, 30)). The calcium dependence of the peak fluorescence amplitude for phase 2 (peak amplitude = 5.6, Fig. 8), together with the location of the calcium sensitive probe (W29) in site I on the N-terminal lobe, indicates that phase 2 is dependent upon binding to the N-terminal sites. Whilst this may be exclusive to site I, it is well documented that EF-hand pairs commonly exhibit cooperative binding, mediated by a short section of shared β-sheet (34). It is thus safest to assume that the origin of phase 2 is related to cooperative binding to the N-terminal (regulatory) calcium binding sites. The peak fluorescence amplitude in Fig. 8 therefore provides an alternate estimate of the calcium affinity to the regulatory binding sites (i.e. pK₂ = 5.6); a value that is reasonably consistent with previously published values (13, 16-18, 22, 30).

Calcium binding to the N-Terminal sites of TnC F29W can be described by an MWC Mechanism

A rapid increase in pressure resulted in a 3-phase response in the fluorescence transient, an instantaneous response (phase 0) and two phases that were well described by exponentials of opposite amplitude. Phase 0 is very fast and is assigned to a local perturbation around W29 which is only observed when calcium is bound and is not coupled to the other two events (Fig. 9). The amplitudes of both phase 1 and 2 were maximal at the mid point of the calcium binding isotherm which clearly indicates that these processes depend on calcium binding. However, neither relaxation time showed any sign of calcium concentration dependence (Fig. 4 and Fig. 8) which is expected for a second order process (eq 7). The absence of calcium dependence of the relaxation time might be explained by the tendency of the Ca-EGTA buffering system to also buffer the total concentration of the free reactive species over a concentration range. However, we eliminated this possibility by measuring over a range of TnC concentrations where we still observed no concentration dependence of the relaxation times (Fig. 5). These data therefore require a more complex model, including both calcium binding and isomerization events.

We can postulate a simple two-step mechanism, in which (presumably fast) calcium binding is followed by an isomerization that is rate-limiting. A mechanism of this sort could give rise to a biphasic response, but the fast quench that we observed is only possible if there is a signal change on the calcium binding step. This mechanism is unlikely, since it is already well known that the fluorescence of W29 is dependent on the open-closed conformational change of the binding pocket (15). A further alternative would be a two-step mechanism in which calcium can only bind to or be released from an open pocket. Such a mechanism could explain the biphasic pressure jump results we observed but predicts a slow apparent second order binding constant if most of the TnC is in its closed form, which has not been observed in practice (22, 35). This scheme is also incapable of reproducing the apparent two-step dissociation mechanism we saw in the pCa jump experiments (Fig. 6).

We have determined that the simplest model that can account for our observations is a cooperative Monod-Wyman-Changeux calcium binding model (Scheme 3). An MWC model assumes that ligand binding promotes a conformational change that, in turn favors ligand binding (23). We assign this conformational change to the closed to open transition and therefore explicitly assume that this is the origin of the fluorescence enhancement seen on calcium binding. This model is limited to describing the events at the N-terminal regulatory sites. The C terminal binding sites are dealt with in the next section.

Scheme 3. MWC based calcium binding to the N-terminal sites of TnC.^c.

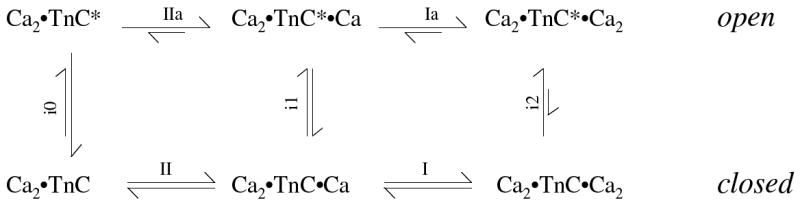
^csteps i0, i1, and i2 refer to the isomerization sensed by W29 and the number of calcium ions bound at the N-terminus (defined in the direction K_in = k_+in/k_-in = [open]/[closed]). The calcium binding steps in roman numerals refer to the N-terminal sites, whilst the letter ‘a’ included on the top line refers to the N-terminal lobe being in its high fluorescence state, which was identified as the ‘open’ state by NMR (15, 36-38). The model does not specify in which order calcium binds to the N-terminal sites, but we have chosen to label them in accordance with the previous finding that calcium binds site II before site I (39).

In terms of the original MWC paper, L = K_i0, which we set to 0.1, and the value of c (the ratio of the binding constants in the two conformations) was set to 10. These values constrain the values of K_i1 and K_i2 to 1 (Lc) and 10 (Lc²) respectively. The second-order rate constant for calcium binding was set to a value of 7.5 × 10⁷ M^-1s^-1 with values for the dissociation rate constant of 75 s^-1 in the open state and 750 s^-1 in the closed state implied by the combination of equilibrium and rate constants. The value for the closed to open isomerization rate constant was set to 375 s^-1 independent of the calcium bound state (i.e. k_+i0 = k_+i1 = k_+i2 =375 s^-1), which means that the reverse isomerization is dependent on the number of calcium ions bound (i.e. k_-i0 = 3750 s^-1, k_-i1 = 375 s^-1 and k_-i2 = 37.5 s^-1).

We used scheme 3 to model a 35 MPa pressure increase on 10 μM TnC F29W at pCa 5.52 using Berkeley Madonna software (see supplementary data section S1). We initially assumed that the volume change should coincide with the isomerization as observed previously in F29W 1-90 (15), but this was not capable of producing the double exponential we observed. Instead, the simulation was capable of reproducing the data well if both the calcium binding and closed-open isomerization steps exhibited volume changes (-9 and +6 mL.mol^-1, respectively) and also if the microscopic change in fluorescence upon isomerization was a factor of 4 (which leads to the observed calcium dependent fluorescence enhancement by a factor of 2.9, because neither the open nor closed form is ever fully occupied). The sum of these volume changes going from apo-closed to fully calcium bound-open configuration is -12 mL.mol^-1 which is close to the estimate of -13 mL.mol^-1 obtained earlier using the total change in fluorescence. Note that the inverse relaxation times cannot be assigned to individual steps in this model, instead representing eigenvalues resulting from the flux through scheme 3.

Studies using the TnC F29W 1-90 construct concluded that the isomerization into the open conformation is accompanied by a volume change of -25.4 mL.mol^-1 (15). In the TnC F29W 1-90 construct, however, the F29W mutation was shown to have a profound effect on the pressure and temperature sensitivity (40). This probably results from a lack of the stabilizing influence of the structural calcium/magnesium binding domain rather than from the introduction of a single tryptophan residue and may therefore account for this apparent discrepancy in the measured volume changes.

Examination of the relative magnitudes of the rate constants, mass balance and the directions of the volume changes on the individual steps in scheme 3 suggest that phase 1 is mostly due to the fast isomerization into the closed state, upon pressure application (resulting in a fast quench) whereas phase 2 is due to slower calcium binding, which causes an increase in fluorescence because in the calcium-bound states, the open state is preferred. Using a value for pK₂ of 5.76 (n_H = 1.46) and the observed amplitude of phase 2 (+3.5 %), we can estimate the shift in the binding isotherm of +0.055 pCa units which is equivalent to a volume change of -8.8 mL.mol^-1 for calcium binding during phase 2. This is close to the value of -9 mL.mol^-1 for calcium binding we obtained from modeling using scheme 3.

Using stopped-flow, we have determined the apparent rate constants for calcium dissociation from the regulatory binding sites (338 and 155 s^-1) using pCa jump. The ratios of the amplitudes and rate constants provide evidence that calcium dissociation proceeds stepwise as has been shown previously by NMR (39). Previous published work showing the results of measurements of calcium dissociation from the regulatory binding sites by rapid mixing with excess EGTA did not observe evidence of sequential dissociation (16, 22, 30). Re-examination of the published transients, in the light of these new measurements, hints at the presence of small lag-phases in these cases as well. Advances in instrumentation mean that the signals we were able to measure exhibited less random noise than the earlier work so these authors were not unreasonable in fitting their transients to single exponential functions. We tested the MWC model (scheme 3) to see if this could explain these results (see Supplementary Data – section S1). The precise mix of rate constants in the model was not sufficient to reproduce the observed fluorescence transient, however it did reproduce a double-exponential decay that satisfied the condition of eq 8, i.e. that the ratios of the amplitudes and observed rate constants are equal – which is usually considered diagnostic of a sequential scheme. In this case, since the unbinding of the first calcium is optically silent, we can infer that the open to closed isomerization step in the fully occupied state (Ca₂•TnC*•Ca₂) is slow by comparison to the calcium dissociation rate constant – a factor we have built into the values we used for the MWC model (scheme 3).

Magnesium Binds Competitively to the Structural Binding Sites

We have observed a further pressure induced response at low calcium concentrations (7 > pCa > 6), that we assign to the structural binding sites with pK₁ = 6.5, in good agreement with published data for this construct (pK₁ = 6.66, (18)). This response was abolished by the addition of magnesium at 2 mM. Titratation of magnesium into this mix at pCa 6.5 determined the magnesium affinity to the structural binding sites (K_Mg = 215 - 230 μM, n_H = 1.88) which is an order of magnitude tighter than published estimates based on assumed direct competitive binding using equilibrium measurements (10, 22). This may be affected by the presence of the T130I mutation present in many TnC F29W constructs which is known to weaken the calcium affinity (9). Magnesium and calcium affinities are commonly positively correlated in EF-hand proteins (41). It is thus likely that any such effect would be to also weaken the magnesium affinity, so that native TnC may bind magnesium even tighter to its structural sites. The difference between our pCa 6.5 magnesium titration curves at high (35 MPa) and low pressure (0.1 MPa) provided a means of estimating the apparent volume change for magnesium binding to the structural binding sites (ΔV^APP_Mg = +14 mL.mol^-1). We had initially modeled competitive magnesium binding from the equilibrium titration data assuming that it was directly competitive (i.e. magnesium binds to at least one of the regulatory sites with an affinity ~ 2 mM). However, the results of this magnesium titration suggested that magnesium binding to the regulatory sites was unnecessary, as scheme 1 was capable of explaining both sets of results. Thus, the simplest assumption consistent with these findings is that magnesium binds to the C-terminal sites exclusively and, by reducing the availability of competent N-terminal binding sites, effectively competes with calcium for these sites as well. This mechanism of magnesium inhibition is plausible given that magnesium binding to the C-terminal sites has been shown to induce a conformational change distinct from either the apo or calcium bound states (42). This mechanism of competitive magnesium binding is explicit in scheme 1 (see introduction) so we have applied this model to our data (see Supplementary Data - section S2). Using a modified Hill equation based on scheme 1, we were able to fit the equilibrium binding isotherms. The values we obtained were Q = 2.96, pK₂ = 5.76 and n₂ = 1.22, where pK₁ = 6.5 and n₁ = 2 are built-in to the model The value of n₂ represents the ‘true’ cooperativity of binding to the N-terminal sites and is much lower than the simple Hill fit value (n_H = 1.46 – see results section). Fitting to the data obtained in the presence of magnesium, using the values obtained in the absence of magnesium as fixed values yielded a value of 5.62 for the apparent pK₁ which implies (via eq 2) that K_Mg = 300 μM. This is in good agreement with the value obtained from the magnesium titration in the pressure jump (230 μM) and supports scheme 1 as a model of competitive magnesium binding to TnC F29W. This approach also reproduced the apparent increase in cooperativity evident upon addition of magnesium (an increase from 1.46 to 1.8) without making any change to the actual cooperativity of binding; this effect is thus entirely due to the shift in the apparent equilibrium constant for calcium binding to the C-terminal sites.

Using eq 3 we were able to make adjustments to the values of the metal binding constants obtained from the fits to the equilibrium data in order to model the amplitude data obtained from pressure jump experiments (see Supplementary Data - section S2). The model exhibited interdependency between these volume changes so the volume change for calcium binding to the N-terminal sites resulting in increasing fluorescence was set to ΔV°2 = -12 mL.mol^-1, in line with the results of MWC modeling (see previous section). Adjusting the other values by hand to optimize the fit resulted in volume change estimates of +25 mL.mol^-1 for calcium binding to the C-terminal sites (ΔV°₁), and +35 mL.mol^-1 for magnesium binding (ΔV°_Mg). This value is much larger than the apparent value of +14 mL.mol^-1 that was estimated from the pressure dependence of the magnesium titration curves. The value of +14 mL.mol^-1 probably reflects the difference between the two volume changes affecting binding to the C-terminal binding sites, i.e. ΔV^APP_Mg = ΔV°_Mg − ΔV°₁ and is therefore within the margins of experimental error. Recent work based on pressure and urea induced unfolding of TnC F105W and TnC F105W 88-162 in the presence and absence of magnesium and calcium yielded a value for ΔV°₁ of +27.6 mL.mol^-1 which was virtually identical to our estimate of +25 mL.mol^-1 (43). By contrast, the value they obtained for magnesium binding was ΔV°_Mg = +6 mL.mol^-1, which is much smaller than our estimate of +35 mL.mol^-1. The difference between these values may be due to differences in sequence in the C-terminus (F105W, T130I), or possibly the higher pressures these authors used (0.1-100 MPa). However, the similarity in the estimates for calcium binding suggests that the volume changes associated with metal binding are intrinsically similar in these two constructs. A high concentration of magnesium (44 mM) was used in their experiments in order to ensure complete occupancy of the magnesium binding sites. It is thus possible that the smaller value these authors reported is due to incomplete dissociation of magnesium from the unfolded state, i.e. the existence of Mg₂•TnC in an unfolded state.

Concluding Remarks

This work demonstrates that fast pressure perturbation can be used to measure calcium and magnesium dependent processes in TnC F29W. Surprisingly, although the engineered tryptophan residue is located in the N-terminal lobe of the molecule, calcium binding to the C-terminus was also sensed using this technique – a finding that is explained by the coupled metal binding model shown in scheme 1, which was able to reproduce the pCa 6.5 amplitude trough and its apparent disappearance upon addition of 2 mM magnesium (Fig. S4, supplementary information). The effect of magnesium on the equilibrium calcium titration was accounted for by this model, including the apparent increase in cooperativity upon addition of magnesium (Fig. S3, supplementary information). The physical nature of the communication between the two lobes of TnC has yet to be elucidated. It is intriguing to note, however, that in the presence of an N-terminal fragment of TnI, an X-ray (44) structure corresponding to the Ca₂•TnC state shows TnC in a folded conformation with an exposed hydrophobic patch in the structural lobe and the regulatory and structural lobes making direct contact. A similar open type structure for the calcium occupied C-terminal lobe was observed by NMR (45). We may speculate that a similar structure is formed transiently in solution and that this contact between the N- and C-terminal lobes is the basis of this communication between the two lobes of TnC.

The multi-exponential fluorescence transients resulting from the pressure jump experiments also allowed us to propose an MWC based model of calcium binding to the N-terminal sites (scheme 3) and to derive estimates of the volume changes for the individual steps.

The results presented here are of interest in relation to the effects of pressure on contracting muscle fibers. Ranatunga and Geeves (46) showed that elevated pressure (~10 MPa) depressed the tension generated by an intact muscle fiber when it was maximally calcium activated by tetanic stimulation. However, the maximum tension achieved during a single twitch was substantially elevated. While a major part of the twitch activation was thought to be due to effects on the calcium release and uptake from the sarcoplasmic reticulum, Fortune et al. (47) established (using chemically skinned muscle fibers in which the membrane components have been removed) that a component of the pressure induced response was due to activation of the thin filament. Rapid pressure jumps applied to this system revealed a force component that was activated by elevated pressure with a maximum amplitude at the mid-point of the force vs pCa curve, similar to the profiles shown here (Figs 4 and 8). Therefore it seems probable that the pressure effects reported here on isolated TnC may well be apparent in the thin filament complex (Actin.Tropomyosin.Troponin). The effects reported here can be expected to be modulated by the interaction of TnC with the other components of the thin filament. Nevertheless, this work establishes that our approach may be used to dissect out the communication pathway between TnC and ultimately the actin-myosin interaction in muscle.

The finding that magnesium inhibition is indirect, mediated via tight binding to the C-terminal portion of TnC F29W, supports the idea that magnesium exchanges with calcium in these binding sites under relaxing conditions (10, 12-14). Magnesium levels may fluctuate in the sarcomere in response to external stimuli (e.g. fatigue or ischemic hypoxia may induce depletion of ATP which strongly chelates magnesium) – indeed, in cardiac myocytes ATP depletion can increase the magnesium concentration by 2.5 fold above a resting concentration of 0.73 mM (48). Taken together, these facts suggest that magnesium plays a role in fine-tuning of the calcium response. Thus the C-terminal calcium binding sites may also act as magnesium based molecular switches in addition to their structural role.

The pressure jump apparatus in our laboratory uses small quantities of material with a fast turnaround. The use of oversampling and averaging means that it is a sensitive technique that provides additional information (e.g. molar volume change, access to intermediate steps on a reaction pathway) that is difficult to obtain any other way. We could therefore use pressure jump to investigate the effect of further mutations or TnC binding drugs on the calcium, magnesium and pressure sensitivity of TnC.

Supplementary Material

1_si_002. SUPPORTING INFORMATION AVAILABLE.

Simulation of cooperative N-terminal binding (section S1), fitting and simulation of calcium/magnesium competitive effects (section S2), notes on consecutive reactions (section S3). This material is available free of charge via the internet at http://pubs.acs.org.

Scheme 2. Sequential release of calcium from the N-terminal binding sites of TnC.^b.

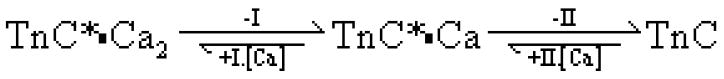
^bTnC*•Ca₂ is the high fluorescence calcium bound TnC, TnC*•Ca is the intermediate with the same fluorescence as the fully calcium bound version and TnC is the low fluorescence calcium free species.