Substituent Effects in the Benzene Dimer are Due to Direct Interactions of the Substituents with the Unsubstituted Benzene

Abstract

The prevailing views of substituent effects in the sandwich configuration of the benzene dimer are flawed. For example, in the polar/π model of Cozzi and co-workers (J. Am. Chem. Soc. 1992, 114, 5729), electron-withdrawing substituents enhance binding in the benzene dimer by withdrawing electron density from the π-cloud of the substituted ring, reducing the repulsive electrostatic interaction with the non-substituted benzene. Conversely, electron-donating substituents donate excess electrons into the π-system and diminish the π-stacking interaction. We present computed interaction energies for the sandwich configuration of the benzene dimer and 24 substituted dimers, as well as sandwich complexes of substituted benzenes with perfluorobenzene. While the computed interaction energies correlate well with σ_m values for the substituents, interaction energies for related model systems demonstrate that this trend is independent of the substituted ring. Instead, the observed trends are consistent with direct electrostatic and dispersive interactions of the substituents with the unsubstituted ring.

There has been dramatic growth in the use of π-stacking interactions in materials science,¹ template-directed synthesis,² and even enzyme design.³ Vital to such applications is the ability to tune these interactions through substituent effects. The sandwich configuration of the benzene dimer has long been used as a model for substituent effects in general π-π interactions.

Substituent effects in the sandwich configuration of the benzene dimer⁴ are often rationalized in terms of a simple electrostatic model:⁵ electron-withdrawing substituents enhance the π-stacking interaction by withdrawing π-electron density from the substituted benzene, reducing the electrostatic repulsion with the other benzene. Electron-donating substituents diminish π-stacking interactions by the opposite mechanism.

Such simple electrostatic models have recently come under fire.^6,7 Computational results of Sherrill and co-workers,^6,8,9 Lee et al.,¹⁰ and Grimme et al. ¹¹ indicate enhanced interactions for all substituted benzene dimers relative to the unsubstituted case. Also, the finding of Ringer et al. ¹² that binding energies increase linearly with the number of substituents is inconsistent with these models, since one would expect an attenuation of substituent effects in multiply-substituted dimers if the polarization of the π-system was the dominant factor.

We present binding energies for the sandwich configuration of a diverse set of 24 substituted benzene-benzene and benzene-perfluorobenzene dimers, computed at the M05-2X/6-31+G(d) level of theory¹³ using NWChem.^14,15 We have previously shown¹⁶ that M05-2X/6-31+G(d) accurately reproduces the relative stacking interaction energies of Sherrill and co-workers,⁹ but at a drastically reduced computational cost. Equilibrium interring distances (R_e) were located by scanning the distance between ring centers at 0.05 Å intervals while holding the monomers fixed at their respective optimized geometries. In the case of the p-xylene-benzene dimer, freezing the monomers alters the binding energy by less than 0.05 kcal mol⁻¹. Substituents considered range from electron donors such as NHCH₃ (σ_m = −0.30) to strong electron acceptors (e.g.: NO₂, σ_m = 0.71).

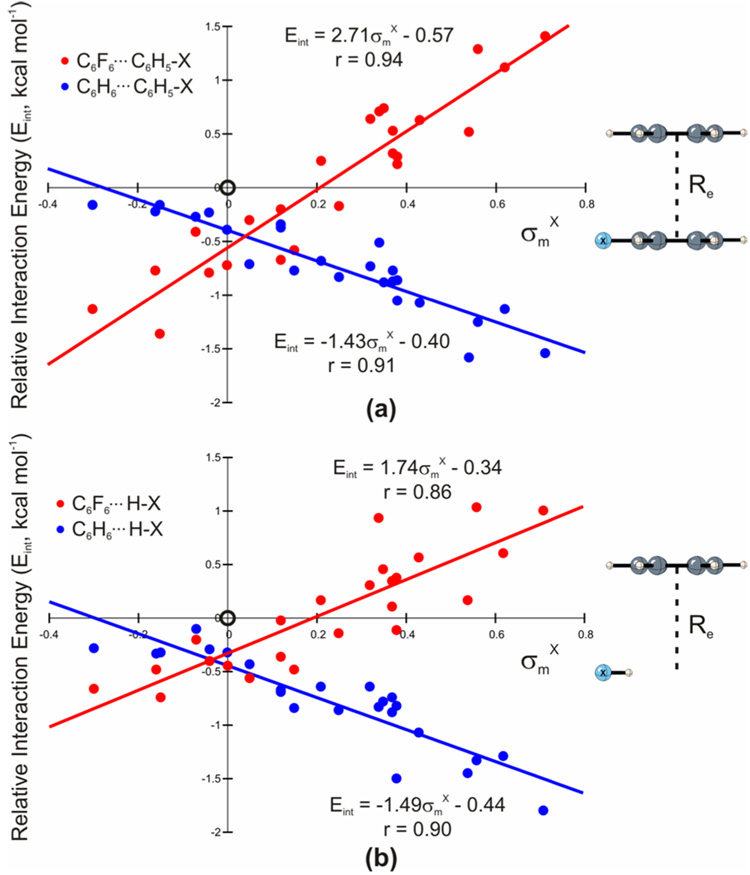
Computed interaction energies [E_int(X) = E_dimer − E_monomers − E_int(X = H)] for sandwich dimers of substituted benzenes (C₆H₅–X) and benzene, relative to the unsubstituted case (X = H), are plotted in Fig. 1(a) (blue dots) as a function of the Hammett sigma meta constants,¹⁷ σ_m ^X. σ_m constants provide a measure of the inductive electron-withdrawal or donation by the substituent. There is a correlation between E_int and σ_m, indicating that the trend in the substituent effects can be qualitatively understood in terms of the electron-donating or withdrawing character of the substituents. Sherrill’s observation⁶ that all substituents enhance π-stacking interaction energies relative to the unsubstituted benzene dimer is also reproduced—all of the predicted relative interaction energies are more strongly attractive than the unsubstituted case. The unsubstituted benzene dimer, marked by the open circle at the origin in Fig 1, is an apparent outlier.

Figure 1.

Interaction energies (kcal mol⁻¹), relative to the unsubstituted case (X = H), versus σ_m ^X for (a) the sandwich dimer of C₆H₅–X with benzene (blue) and C₆F₆ (red); (b) the dimer of H–X and benzene (blue) and C₆F₆ (red) at the equilibrium separation distances (R_e) of the corresponding substituted dimers in (a). The open circles at the origins correspond to X = H, and were not included in the least squares fits.

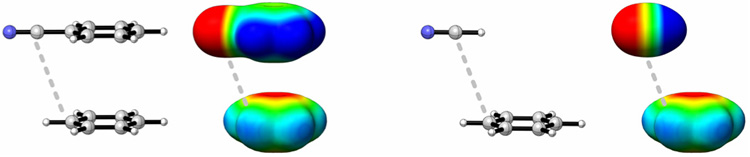
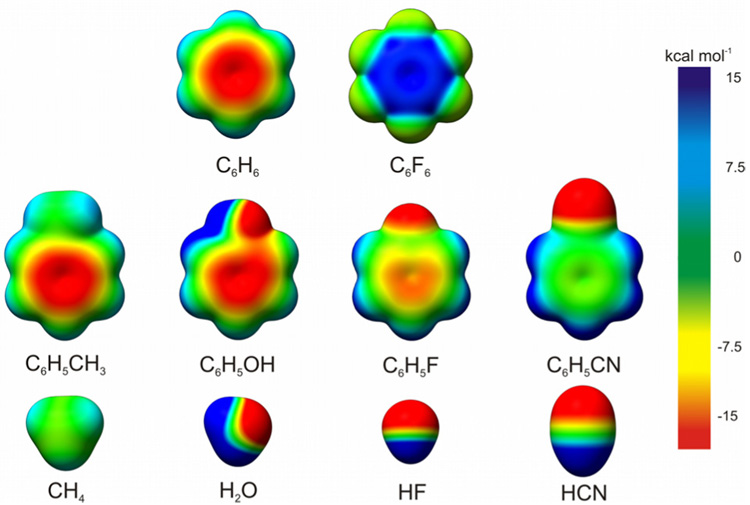
The red dots in Fig. 1(a) depict the relative dimerization energies of the same 24 substituted benzenes with C₆F₆. As previously observed,^18,19 the correlation with σ_m is now reversed. This is attributed to the reversal in sign of the electrostatic potential (ESP) in C₆F₆ relative to C₆H₆ (see Fig. 2).

Figure 2.

Electrostatic potential plots of benzene, perfluorobenzene, and representative monosubstituted benzenes and the corresponding substituents capped with hydrogen, computed with B3LYP/6-31G(d).

Least squares fit lines for both sets of dimerization energies in Fig. 1(a) exhibit non-zero y-intercepts. The case of X = CH₂OH is particularly instructive, since σ_m = 0.00 and thus this substituent is neither electron-donating nor withdrawing. For the benzene-benzene and benzene-C₆F₆ dimers, substitution by CH₂OH enhances the interaction by 0.4 and 0.7 kcal mol⁻¹, respectively. This stabilization is consistent with the y-intercepts of the best-fit lines shown in Fig. 1(a), and can be interpreted as a typical contribution to E^int that is not due to the electron withdrawing character of the substituent. This σ_m-independent shift in interaction energies for substituted benzene dimers, relative to the unsubstituted case, underlies Sherrill’s observation that all substituents enhance binding in the benzene dimer.^6,8,9 This shift is most readily explained by dispersive interactions between the substituent and the other aromatic ring. This is supported by the symmetry-adapted perturbation theory results⁸ of Sinnokrot and Sherrill for selected substituted benzene dimers [see Supporting Information (SI), Fig. S1]. This contribution clearly varies for different substituents, but, on average, dispersion preferentially stabilizes substituted benzene dimers relative to the unsubstituted case.

To further unravel the origin of the substituent effects in the benzene dimer, a simple model was constructed by replacing the carbon and hydrogen atoms of the substituted benzene (at the equilibrium separation of the corresponding substituted dimer) with a hydrogen atom. This hydrogen was placed along the C–X bond and the distance optimized while holding the remainder of the system fixed. Remarkably, this exceedingly crude model of substituted benzene sandwich dimers results in the same trend in relative interaction energies [see blue dots, Fig. 1(b)]. Moreover, while relative interaction energies for H–X⋯C₆H₆ and C₆H₅-X⋯C₆H₆ differ for individual substituents, the two sets of energies are strongly correlated (r = 0.91, see SI Fig. S2). The origin of substituent effects in the benzene dimer clearly does not involve the π-system of benzene, but instead must be attributed to direct interactions of the substituents with the unsubstituted ring.

Results for a related model, in which the hydrogen is replaced by a fluorine still gives the same trend relative to the X = H case (see SI Fig. S3), indicating an insensitivity of this model to the electronegativity of the capping atom and further supporting direct interactions of the substituents with the non-substituted ring as the dominant cause of substituent effects in the benzene dimer.

For perfluorobenzene, replacing the substituted benzene ring with a hydrogen atom reduces the slope of the best fit line [red dots, Fig 1(b)]. The intercept remains unchanged, however, in accord with postulated dispersive interactions of the substituents with the perfluorobenzene ring. The difference between the interaction energies for H–X and C₆H₅-X with perfluorobenzene correlates with σ_p ^X (r = 0.89), suggesting that in this case there is an additional appreciative substitutent effect related to polarization of the π-system of the substituted ring. Such effects are apparently negligible in the substituted benzene dimers.

Substituent effects in benzene dimers are often discussed in terms of computed electrostatic potentials for the substituted rings (Fig. 2). Specifically, that ESP values above the substituted ring roughly parallel observed trends in interaction energies has been noted.¹⁸ However, since the substituted benzene is not necessary to yield the observed trends, any changes in the ESP of benzene upon substitution are apparently outweighed by the ESP of the substituents themselves. Alternatively, rather than arising from changes in quadrupole-quadrupole interactions, these substituent effects can be understood qualitatively in terms of interactions between the quadrupole moment of the unsubstituted benzene and local dipoles introduced by the substituents.

Substituent effects in the sandwich configuration of the benzene dimer do not involve the π-system of the substituted benzene. The correlation of stacking interactions with σ_m arises from direct electrostatic interactions between the substituents and the unsubstituted ring. Additional dispersive interactions between the substituents and the other ring preferentially stabilize most substituted benzene dimers. This new model of substituent effects in the benzene dimer drastically alters our understanding of the effects operative in this model system, with far-reaching implications for the role of π-stacking interactions in materials, host-guest systems, and the interaction of drugs with receptors.

Supplementary Material

SI. Supporting Information Available.

Full citation for Ref. 14; E_int and σ_m constants plotted in Fig 1; Cartesian coordinates and electronic energies of computed structures; additional plots.