Distinct expressions of contrast gain control in parallel synaptic pathways converging on a retinal ganglion cell

Abstract

Visual neurons adapt to increases in stimulus contrast by reducing their response sensitivity and decreasing their integration time, a collective process known as ‘contrast gain control.’ In retinal ganglion cells, gain control arises at two stages: an intrinsic mechanism related to spike generation, and a synaptic mechanism in retinal pathways. Here, we tested whether gain control is expressed similarly by three synaptic pathways that converge on an OFF α/Y-type ganglion cell: excitatory inputs driven by OFF cone bipolar cells; inhibitory inputs driven by ON cone bipolar cells; and inhibitory inputs driven by rod bipolar cells. We made whole-cell recordings of membrane current in guinea pig ganglion cells in vitro. At high contrast, OFF bipolar cell-mediated excitatory input reduced gain and shortened integration time. Inhibitory input was measured by clamping voltage near 0 mV or by recording in the presence of ionotropic glutamate receptor (iGluR) antagonists to isolate the following circuit: cone → ON cone bipolar cell → AII amacrine cell → OFF ganglion cell. At high contrast, this input reduced gain with no effect on integration time. Mean luminance was reduced 1000-fold to recruit the rod bipolar pathway: rod → rod bipolar cell → AII cell → OFF ganglion cell. The spiking response, measured with loose-patch recording, adapted despite essentially no gain control in synaptic currents. Thus, cone bipolar-driven pathways adapt differently, with kinetic effects confined to the excitatory OFF pathway. The ON bipolar-mediated inhibition reduced gain at high contrast by a mechanism that did not require an iGluR. Under rod bipolar-driven conditions, ganglion cell firing showed gain control that was explained primarily by an intrinsic property.

Contrast adaptation represents a model system for understanding how plasticity in a neural circuit alters the output of a spiking neuron (Kohn, 2007; Wark et al. 2007; Demb, 2008). Contrast represents the variance of light intensities over time, relative to the mean level, and early visual neurons adapt independently to the variance and the mean but not to other statistical properties (e.g. skewness) (Mante et al. 2005; Bonin et al. 2006). Cells adapt to contrast within both laboratory stimuli and more natural stimuli (Lesica et al. 2007; Mante et al. 2008). Depending on stimulus conditions, contrast adaptation can act on fast or slow time scales, from tens of milliseconds to tens of seconds (Baccus & Meister, 2002; Manookin & Demb, 2006); here we focus on adaptation that acts on a fast time scale, also known as ‘contrast gain control.’ At high contrast, retinal ganglion cells adapt by reducing contrast sensitivity, or ‘gain’, and by shortening integration time (Shapley & Victor, 1978; Victor, 1987; Benardete & Kaplan, 1999). The shortened integration time increases response sensitivity to high temporal frequencies in the stimulus. The retina provides an important system to study the cellular basis of contrast adaptation, because adaptation can be studied with physiological stimuli in vitro (Smirnakis et al. 1997; Chander & Chichilnisky, 2001; Kim & Rieke, 2001; Rieke, 2001; Baccus & Meister, 2002; Zaghloul et al. 2005; Beaudoin et al. 2007).

Adaptation in ganglion cell firing arises from at least two mechanisms. First, high contrast causes gain control in the ganglion cell's presynaptic bipolar cells. This was shown by direct recordings in salamander bipolar cells and by recordings of excitatory membrane currents in salamander and mammalian ganglion cells (Kim & Rieke, 2001; Rieke, 2001; Baccus & Meister, 2002; Zaghloul et al. 2005; Beaudoin et al. 2007). The gain control in bipolar cell output does not depend on feedback inhibition from amacrine cells (Rieke, 2001; Beaudoin et al. 2007). However, bipolar and amacrine cells make parallel inputs to ganglion cells, and the relative degree of gain control at these synapses is unknown. Furthermore, gain control in ganglion cell firing exceeds that measured in synaptic responses, suggesting that additional gain control arises in the process of spike generation (Kim & Rieke, 2001; Zaghloul et al. 2005; Beaudoin et al. 2007). Thus, under some lighting conditions, gain control in ganglion cell firing could arise largely or solely through an intrinsic property (Yu & Lee, 2003; Gaudry & Reinagel 2007a,b). For example, it is not known whether synaptic or intrinsic mechanisms explain adaptation of ganglion cell responses driven by the rod bipolar pathway.

Here we tested whether multiple synaptic pathways that converge on a ganglion cell show similar expressions of contrast gain control. We addressed this question by recording contrast gain control in guinea pig OFF α/Y-type ganglion cells in vitro while altering holding potential, using pharmacology or altering mean luminance to emphasize each of three synaptic pathways that converge on the cell (see Fig. 1).

Figure 1. The OFF ganglion cell integrates signals from multiple synaptic pathways.

A, under dim light conditions, rod glutamate release drives ganglion cell responses through two pathways. The first, conventional rod pathway, starts with the rod (r₁) and proceeds along two routes: a direct route, rod → rod bipolar (rb) → AII amacrine cell (AII) → ganglion cell (gc); and an indirect route, rod → rb → AII → OFF cone bipolar (cb) → gc. There is also an unconventional rod pathway, where a rod (r₂) can synapse directly with an OFF cb. B, under bright light conditions, cone glutamate release drives ganglion cell responses through two pathways: an excitatory pathway, cone → OFF cb → OFF gc; and an inhibitory pathway, cone → ON cb → AII → OFF gc. The inhibitory pathway can take also an indirect route, where the AII synapses with the OFF cb. The direct inhibitory pathway does not require an ionotropic glutamate receptor (iGluR). Rod signals contribute to these pathways via electrical synapses (connexin 36, Cx36) with cones. Abbreviations: mGluR6, metabotropic glutamate receptor type 6; glycine-R, glycine receptor.

Methods

Ethical approval

All procedures conformed to University of Michigan and National Institutes of Health guidelines for use and care of animals in research. The animal protocol was reviewed and approved by the University of Michigan Committee on the Use and Care of Animals.

Tissue preparation and electrophysiology

The experimental procedures have been described in detail previously (Demb et al. 1999; Manookin et al. 2008). Hartley guinea pigs (Elms Hill, Chelmsford, MA, USA) were housed in a 12: 12 h light: dark cycle. For some experiments (21 of 74), the animal was dark-adapted for 1 h before further procedures were carried out. The animal was brought to a room illuminated with red light and was anaesthetized with an intramuscular injection of ketamine (100 mg kg⁻¹) and xylazine (10 mg kg⁻¹). Under anaesthesia, the animal was killed by decapitation, and then both eyes were removed. The retina was hemisected under either dim white light (standard conditions) or red light (following dark adaptation) and the vitreous, lens and cornea were removed and discarded. Pieces of the flattened eye cup, including the retina, pigment epithelium, choroid and sclera, were mounted on filter paper and stored at room temperature in oxygenated (95% O₂ and 5% CO₂) bicarbonate-buffered Ames medium (Sigma, St Louis, MO, USA) in a light-tight container until the time of recording (storage time, 0.5–5 h). At the time of recording, the retina was placed in a chamber on a microscope stage and superfused (∼6 ml min⁻¹) with oxygenated Ames medium heated to 33–35°C with an in-line heater (TC-344B, Warner Instruments, Hamden, CT, USA). Dark-adapted retinas were used for about half the experiments at the dimmest mean luminance and for all cells recorded in the presence of l-AP-4 (see below).

The retina and electrode were visualized using a cooled CCD camera (Retiga 1300C, Qcapture software; Qimaging Corporation, Burnaby, British Columbia, Canada) mounted on an Olympus BX51WI microscope (Olympus; Center Valley, PA, USA). We targeted Y-type/α ganglion cells by recording from the largest cell bodies in the ganglion cell layer (diameter: 20–25 μm). Cell type was confirmed by measuring light responses and in some cases by analysing the stratification of the dendritic tree, as previously described (Manookin et al. 2008). A glass electrode (tip resistance, 2–6 MΩ) was filled with either Ames medium, for loose-patch extracellular recording of action potentials, or intracellular solution, for whole-cell recording of membrane currents. In all but one experiment, intracellular solution consisted of the following (in mm): 120 caesium methanesulphonate, 5 TEA-Cl, 10 Hepes, 3 NaCl, 10 BAPTA, 2 QX-314-Cl, 2 ATP-Mg, 0.3 GTP-Na, 0.10% Lucifer Yellow, titrated to pH 7.3. In one experiment (baclofen application), intracellular solution consisted of the following (in mM): 140 potassium methylsulphate, 8 NaCl, 10 Hepes, 0.1 EGTA, 2 ATP-Mg, 0.3 GTP-Na₂, adjusted to pH 7.3. All chemicals were purchased from Sigma-Aldrich (St Louis, MO, USA) except for the following: BAPTA (Invitrogen; Eugene, OR, USA); strychnine (Fisher, Hampton, NH, USA); kainic acid, baclofen, CNQX, d-AP-5, and l-AP-4 (Tocris; Bristol, UK). We used standard concentrations of the receptor agonists and antagonists, following previous studies (Belgum et al. 1984; Zhou & Fain, 1995; Cohen, 1998; Cohen & Miller, 1999; DeVries, 2000).

Membrane current was amplified, sampled at 10 kHz, and stored on a computer using a MultiClamp 700A amplifier, Digidata 1322A analog–digital board and pCLAMP 9 software (Axon Instruments; Union City, CA, USA). Junction potential (−9 mV) was corrected in all cases. Light responses were analysed with custom programs written in Matlab (version 7; The Mathworks; Natick, MA, USA). An error in the holding potential (V_hold) introduced by the series resistance was corrected by the formula:

where V_hold,uncorr is the apparent (uncorrected) holding potential (in mV), I_leak is the leak current (in nA), R_S is the series resistance (17 MΩ; s.d.= 6; n = 96 cells) and R_S,correct is the series resistance compensation. We generally excluded cells from the analysis with R_S > 30 MΩ. R_S,correct was typically 0.4; higher values sometimes resulted in oscillations that destroyed the seal. Thus, the uncompensated series resistance was typically ∼10 MΩ. Most light-evoked responses were < 1 nA deviation from the leak current, and therefore the variation in the holding potential during light-evoked currents was typically < 10 mV.

Visual stimuli

The stimulus was displayed on a miniature monochrome computer monitor (Lucivid MR1-103; Microbrightfield; Colchester, VT, USA) projected through the top port of the microscope through a 4× objective and focused on the photoreceptors (resolution, 640 × 480 pixels; 60 Hz vertical refresh). The relationship between gun voltage and monitor intensity was linearized in software with a lookup table. Stimuli were programmed in Matlab as previously described (Demb et al. 1999). All stimuli were centred on the cell body.

Cells were recorded in the superior retina, where the cone distribution is ∼95% M cones and ∼5% S cones (Rohlich et al. 1994; Yin et al. 2006). During recording, the cell was exposed to stimuli that fluctuated around a constant mean luminance. Light level is described as the photoisomerization rate per photoreceptor (rod, M-cone or S-cone) per second: P_R*, P_M* and P_S*. Photoisomerization rates were calculated based on the spectral output of the monitor, the intensity of the monitor (W mm⁻²) at the plane of the retina, and the photoreceptor properties described in Yin et al. (2006). The typical mean luminance evoked ∼10⁴P_R*, ∼5 × 10³P_M*, and ∼5 × 10²P_S*. Under these conditions, M-cones and rods contribute about equally to the light response (Yin et al. 2006). At this light level, rod contributions presumably arise primarily through their gap junctions with cones but not through the rod bipolar circuit (Bloomfield & Dacheux, 2001; Manookin et al. 2008) (Fig. 1B). In some cases, we inserted neutral density filters (Kodak Wratten Filters, Edmund Scientific, Barrington, NJ, USA) into the light path to reduce mean luminance by 10-, 100-, or 1000-fold. At the two dimmest light levels (∼50 or ∼5 P_M*; ∼100 or ∼10 P_R*), responses are driven by rods (Yin et al. 2006).

The primary stimulus was a spot of 600 μm diameter, presented over the ∼400–700 μm diameter dendritic tree of an OFF α/Y-type cell (Manookin et al. 2008). Spot intensity was modulated by a randomly generated temporal sequence in which intensity values were chosen from a Gaussian distribution at 20 or 60 Hz; this stimulus approximates white noise (Zaghloul et al. 2005). The 60 Hz presentation rate was used in most conditions, at high mean luminance (10⁴P_R*). The 20 Hz presentation rate was used at low mean luminance (10 P_R*); at this light level, the ganglion cell integration time increases, and thus the lower presentation rate was used because it contains relatively more contrast at low temporal frequencies. In one experiment, we compared the gain change at high and low mean luminance and used the 20 Hz rate in both conditions.

In most conditions, the s.d. of the intensity fluctuations was 0.3 times the mean (high contrast) for 10 s followed by 0.1 times the mean (low contrast) for 10 s (i.e. threefold change in contrast); in the low mean luminance condition the low contrast s.d. was 0.15 times the mean (i.e. twofold change in contrast). This 20 s cycle was repeated 10–30 times. Fewer repeats were required for membrane currents recorded at high mean luminance, whereas more repeats were required for membrane currents or spikes recorded at low mean luminance. Adaptation was measured using a model, as described below, which was constructed from data collected 2–7 s after the contrast switch (Beaudoin et al. 2007). The last 3 s in each half-cycle were repeated across cycles, and the data were used to test the model's predictive ability (Beaudoin et al. 2007).

In some experiments, a dark spot (0.6 mm diameter) was presented for 200 ms, followed by 800 ms at a steady, background luminance. Responses were recorded at several levels of background luminance, with or without l-AP-4 in the bath, and responses were averaged over 10–20 repeats of the spot. Each piece of tissue was exposed to l-AP-4 only once.

Analysis: the linear-nonlinear (LN) model

To interpret responses to the flickering spot (membrane current or spikes), we used the linear–nonlinear (LN) cascade analysis (Brenner et al. 2000; Chichilnisky, 2001; Carandini et al. 2005) (Fig. 2). A linear filter represents the cell's impulse response function: the theoretical response to a brief light flash. The linear filter is computed by cross-correlating the stimulus and the response (Chichilnisky, 2001). The same filter, plotted in reverse, represents the cell's ‘weighting function.’ The linear prediction of the response (i.e. the linear model) at any point in time is calculated by multiplying the stimulus by the weighting function, pointwise, and summing the result (Carandini et al. 2005).

Figure 2. The linear–nonlinear (LN) model of the light response.

A, the flickering stimulus is convolved with a linear filter. The resulting product is passed through a static nonlinearity to generate the model output. The model shown (filter and nonlinearity) was constructed from 50 s of data (V_hold=−45 mV). The nonlinearity is relatively straight under this condition but shows more rectification in other figures, where recordings are made at more negative holding potentials or in the presence of CNQX and d-AP-5. B, LN models were built for low and high contrast conditions. The model outputs are plotted with average responses (10 repeats) to 1 s of a 3 s, repeated stimulus. The method for testing the predictive ability of the LN model is described in Methods.

The linear model fails to capture certain features of the response but can be improved significantly by including a time-independent nonlinearity (Chander & Chichilnisky, 2001; Kim & Rieke, 2001; Baccus & Meister, 2002; Zaghloul et al. 2005). The nonlinearity translates the linear model values into output values and accounts for rectification and saturation in the response (Fig. 2). The nonlinearity is computed by plotting the (binned) average output value (in spikes s⁻¹ or nA) for each input value of the linear model (Chander & Chichilnisky, 2001; Kim & Rieke, 2001; Baccus & Meister, 2002; Zaghloul et al. 2005). The shape of the linear filter can be computed accurately despite the presence of the nonlinearity (Chichilnisky, 2001).

The LN model is unique only up to a scale factor. Thus, the y-axis of the linear filter and the x-axis of the nonlinearity can be scaled by the same factor without changing the output of the model (Chander & Chichilnisky, 2001; Kim & Rieke, 2001). We scaled the high contrast nonlinearity (stretched the x-axis) so that it aligned to the low contrast nonlinearity, and then scaled the high contrast filter (stretched the y-axis) by the same factor. The nonparametric procedure for this scaling was performed as previously described (Beaudoin et al. 2007). After aligning the nonlinearities, the gain change between the low and high contrast filters was calculated by taking the ratio of the filter peaks (high: low) (Chander & Chichilnisky, 2001; Kim & Rieke, 2001; Zaghloul et al. 2005). The shape of the nonlinearity for membrane current responses differed depending on the pharmacological and mean luminance conditions. Thus we could compare directly response gain at two contrast levels within a given condition, but we could not compare gain between conditions. The contrast-dependent change in temporal kinetics was measured by comparing the zero-crossing of the filters (high: low) (Chichilnisky, 2001; Zaghloul et al. 2005).

Validating the LN model

The predictive ability of the LN model was tested, in every cell, by constructing the model from one set of data and testing the model on a second set. For this purpose, the nonlinearity (after scaling the two contrast functions into alignment, as described above) was fitted with a cumulative Gaussian, to generate predictions for all values of the input (Chichilnisky, 2001; Kim & Rieke, 2001; Rieke, 2001; Zaghloul et al. 2003). The model-building data were taken from the response 2–7 s after the contrast switch (across 10–30 cycles). The model-testing data were taken from the last 2.5 s of each half-cycle, during the repeated stimulus (see above and Fig. 1 in Beaudoin et al. 2007). Predictive ability was measured by comparing the average correlation (r) between each trial of the repeated stimulus and either the LN model prediction or the maximum likelihood (ML) prediction; the ML prediction, for a given trial, was the average response to the other 9–29 trials. We included cells in the study if the average LN model prediction (r_LN) was at least 85% as good as the average ML prediction (r_ML) for membrane currents, or at least 60% as good for spike recordings. We used a lower criterion for spike responses because the LN model does not account for history-dependent effects on spiking and therefore yields a prediction that is relatively worse for spike rate than membrane current (Pillow et al. 2005). For the membrane currents, the relative predictive ability of the LN model, compared to the ML standard (r_LN/r_ML× 100), was 92 ± 4% (high contrast; mean ±s.d.) or 96 ± 4% (low contrast; n = 96); for spikes, this percentage was 83 ± 7% (high contrast) or 98 ± 10% (low contrast; n = 19). Thus, the LN model provided a good description of the response.

Puffing experiments

To measure empirically the reversal potential for inhibitory and excitatory synapses, we blocked calcium-dependent synaptic transmission with bath-applied CoCl₂ (6 mm) and then puffed neurotransmitter receptor agonists on the cell. Kainate or glycine was applied to open either cation or Cl⁻ channels on the cell membrane. The GABA-B agonist baclofen was applied to open K⁺ channels. The receptor agonists were applied using a Picospritzer III (Parker Hannifin, Cleveland, OH, USA) connected to a patch pipette (resistance of 5–8 MΩ) filled with kainate (10 mm), glycine (100 μm) or baclofen (10 mm) dissolved in Ames medium on the day of the experiment. The pipette tip was advanced into the inner plexiform layer, about 100 μm lateral to the cell body. The pressure and timing of the puff were adjusted for each cell to generate a measurable response.

Unless otherwise indicated, data are reported as means ±s.e.m., and samples were compared with Student's one-tailed t test.

Model of the influence of photon noise on stimulus contrast

We made a simulation, in Matlab, to study the effect of ‘shot noise’, associated with the random arrival of photons, on the stimulus contrast. The simulation was based on 20 Hz Gaussian flicker (i.e. 50 ms frame duration) at low mean luminance (10 R* per rod per second). The Gaussian s.d. (σ) was either 0.30 or 0.15 times the mean (i.e. twofold change in contrast). At cellular stages beyond the photoreceptors, total isomerization rate is integrated over a pool of rods, connected to the cell of interest, and over the frame duration: (R* per rod pool per 50 ms). Consider a Gaussian distribution with k intensity values (i), each with an associated photoisomerization rate (x_i). For each x_i there is an associated probability, p(x_i) determined by the height of the Gaussian distribution at x_i. However, for each x_i, the actual isomerization rate will vary, because of the random arrival of photons, according to a Poisson distribution. For example, across all frames where we intended to present 5 R* per rod per second, there would be a distribution of intensities with a mean and variance both equal to 5 R* per rod per second. Thus, for each value x_i, there is a distribution of isomerization rates where the mean (m_i) and variance (v_i) both equal x_i. The total variance over the k intensity values in the Gaussian distribution is thus the weighted combination of variances of the underlying k Poisson distributions. We can calculate the overall variance by taking the weighted mean of the variances, across the Poisson distributions, plus the weighted variance of the means:

where M is the global mean (i.e. mean of the Gaussian distribution) and summation (∑) is over i = 1 …k. The equation can be derived from the total sum of squares (SOS) for a one-way analysis of variance (i.e. sum of the within-sample SOS and the SOS between samples) (Ott, 1993). Thus, for a given stimulus distribution, we could calculate directly the σ/mean ratio of the isomerization rates as V^0.5/M. We performed this calculation for high and low contrast and for a mean luminance condition (contrast = 0). From this analysis, we could determine, for a range of rod pool sizes (1–5000 rods), whether the σ/mean of the R* distribution resembled the intended contrast of the Gaussian stimulus distribution. Furthermore, we could determine for what pool size there was a ∼2-fold difference between σ at 0.30 contrast (σ_0.30) and at 0.15 contrast (σ_0.15) by comparing the ratio (σ_0.30/σ_0.15) to the 2-fold change in the Gaussian stimulus σ.

In addition to the above calculation, we simulated R* rates in time to visualize the effect of photon shot noise on stimulus contrast. In one case, we simulated the R* rate for each 50 ms frame and show the model response given two pool sizes: 20 or 1000 rods. We made additional simulations with 50 ms frames but with 1 kHz sampling. In these latter simulations, we tested the impact of filtering the model output by taking a running average of 100–400 time points (i.e. convolving the stimulus with a rectangular filter that sums to 1 and integrates over 100–400 ms). The additional filtering has essentially no impact on the σ_0.30/σ_0.15 ratio. Thus, additional temporal integration by cellular processes downstream of the rod outer segments would not substantially affect the main conclusions from the simulations performed with 50 ms time bins.

Results

Responses were measured in OFF α/Y-type ganglion cells by targeting large cell bodies in the ganglion cell layer. Cell type was confirmed by testing for the following properties: a transient OFF-centre response to a dark step; a centre–surround receptive field organization; a frequency-doubled response to a high spatial frequency, contrast-reversing grating; and a low input resistance (∼30–50 MΩ) (Hochstein & Shapley, 1976; Demb et al. 2001; O'Brien et al. 2002; Zaghloul et al. 2005; Manookin et al. 2008). OFF α/Y-type cells stratify their dendrites on the vitreal side of the nearby OFF-layer cholinergic (starburst) amacrine cell band; they can be distinguished from another type of wide-field OFF cell with a relatively large cell body, the OFF δ cell, by their light response and dendrite stratification (Zhang et al. 2005; Manookin et al. 2008). Below, we refer to OFF α/Y-type cells simply as ‘ganglion cells’.

Isolating excitatory and inhibitory currents under voltage clamp

In the experiments below, we recorded light-evoked synaptic responses under voltage clamp. The cells under study are relatively large (dendritic tree diameter of ∼550 μm; Manookin et al. 2008), and thus we tested our ability to clamp cells and measure inhibitory synaptic currents at the cation reversal potential (E_cation, 0 mV). To estimate E_cation, we blocked calcium-dependent synaptic transmission with Co²⁺ and measured the response to kainate applied via a puffer pipette (see Methods; Fig. 3A). The kainate response was blocked by the AMPA-receptor antagonist GYKI (100 μm; Paternain et al. 1995; DeVries, 2000), and thus it was mediated by AMPA receptors (Fig. 3A). Kainate evoked a linear conductance that reversed near 0 mV (Fig. 3B; E_kainate=−0.9 ± 0.3 mV, n = 7 cells). In separate experiments, we measured the reversal potential for Cl⁻ by applying glycine (Fig. 3C). Glycine responses were blocked by strychnine (2 μm), and thus depended on glycine receptors (Fig. 3C). Glycine evoked an outwardly rectifying response that reversed near the calculated E_Cl of −67 mV (Fig. 3C; E_glycine=−69 ± 4 mV, n = 9 cells); the outward rectification can be attributed to Goldman rectification (Zhou & Fain, 1995). We also tested for the presence of GABA-B receptors by applying baclofen (n = 4 cells). We recorded with K⁺-based intracellular solution without Cs⁺ or QX-314 to avoid possible intracellular block of GABA-B responses (Rotolo & Dacheux, 2003). However, there was no response to baclofen (Fig. 3E). Thus, recordings at 0 mV represent inhibitory Cl⁻ currents and recordings at −67 mV represent excitatory cation currents. In recordings below, the reported V_hold was somewhat variable, because we corrected for uncompensated R_s during the recording and adjusted V_hold accordingly (see Methods). Thus, V_hold was typically within 10 mV of E_Cl or E_cation.

Figure 3. Ganglion cells can be voltage-clamped to measure either excitatory or inhibitory ligand-gated conductances.

A, responses to puff application of kainate onto a ganglion cell at two V_hold values (−64 or +5 mV; average of eight puffs). Puff time is indicated by the arrow. Bottom trace shows that the kainate response is blocked by bath application of the AMPA-receptor antagonist GYKI (100 μm). Dashed lines show the leak current before the puff. B, I–V plot for the kainate response. Response is linear and reverses near 0 mV (E_cation). Points indicate the response to the puff, averaged over 200 ms near the peak of the response; error bars indicate s.e.m. across eight puff responses. The dashed line is a linear regression fit through the data. C, same format as A for puff application of glycine (average of seven puffs). The response is blocked by bath application of the glycine-receptor antagonist strychnine (2 μm). D, I–V plot for the glycine response. Response is outwardly rectifying and reverses near −67 mV, the calculated E_Cl. The dashed line is a fit through the data based on the Goldman–Hodgkin–Katz equation (Johnston & Wu, 1994). E, same format as A for puff application of baclofen (average of nine puffs).

In some cases, we recorded at a V_hold between E_Cl and E_cation of around −45 mV. At this V_hold, the driving force on excitation is about twice the driving force on inhibition. The relative contribution of excitation and inhibition at any point in time is impossible to estimate, as the current depends on both the (fixed) driving forces and the (time-varying) conductances. However, recordings near −45 mV served two purposes. First, recording stability was generally better at V_hold of −45 mV than V_hold of 0 mV. Second, the ganglion cell resting potential in situ is approximately 20 mV positive to E_Cl (Murphy & Rieke, 2006). In our recordings, it was necessary that E_Cl be −67 mV, because certain voltage-gated channel blockers (QX-314-Cl, TEA-Cl) in the pipette solution increased Cl⁻ concentration. Thus, V_hold of −45 mV provides an estimate of synaptic currents near rest, where there is a mix of excitation and inhibition.

Excitatory and inhibitory inputs show distinct adaptation of response kinetics

We measured a ganglion cell's response to a flickering spot over the receptive field centre that alternated every 10 s between low and high contrast (see Methods). Responses were analysed using a linear–nonlinear (LN) cascade analysis, which quantifies changes in sensitivity independently of response saturation or rectification (see Methods; Fig. 2). In the excitatory currents (V_hold=−66 ± 3 mV; mean ±s.d.; n = 8), tripling contrast reduced response sensitivity, as quantified by a relative decrease in the height of the linear filter (Fig. 4A). Tripling contrast reduced gain to 0.74 ± 0.02 (mean ±s.e.m.); i.e. a cell was ∼74% as sensitive at high contrast compared to low contrast (Fig. 4C). Tripling contrast also sped up the response kinetics, as measured by a decreased time to the filter zero-crossing (zc; which we used as a proxy measure for integration time). Tripling contrast reduced the integration time (zc_high: zc_low) to 0.92 ± 0.012 (Fig. 4D); i.e. to generate the excitatory response, a cell integrated at high contrast over a time period that was ∼92% as long as the period during low contrast. Thus, excitatory membrane currents showed both reduced gain and reduced integration time at high contrast, as shown previously (Kim & Rieke, 2001; Beaudoin et al. 2007).

Figure 4. Contrast-dependent changes in integration time are larger for excitatory currents than inhibitory currents.

Aa and Ba, linear and nonlinear components of the model at two V_hold values. The initial 200 ms of the linear filter is shown on an expanded scale at right. The zero-crossing of the filter (arrow) was reduced at high contrast with V_hold near E_Cl but not with V_hold near E_cation. There was reduced gain at high contrast at both V_hold values. The nonlinearity changed from outwardly rectifying, at V_hold=−69 mV, to inwardly rectifying, at V_hold=−6 mV. Ab and Bb, traces showing the response to the first second of the repeated stimulus for both contrasts. C, relative gain at high contrast with V_hold near E_Clversus near E_cation (n = 8 cells). The reduced gain at high contrast was similar at the two V_hold values. D, relative zero-crossing time at high: low contrast (zc_high: zc_low) with V_hold near E_Clversus near E_cation. The effect on integration time was more prominent at V_hold near E_Cl. The absolute zc_high was 95 ± 5 ms (n = 8) for V_hold near E_Cl and 89 ± 3 ms for V_hold near E_cation.

In the inhibitory currents (V_hold=−3 ± 2 mV; mean ±s.d.), the gain was reduced at high contrast to 0.77 ± 0.02, similar to the effect size measured in the excitatory currents (Fig. 4B and C). However, there was a smaller reduction of integration time at high contrast (0.97 ± 0.006; difference of 0.05 ± 0.01, P < 0.01; two-tailed t test) (Fig. 4D). Thus, high contrast reduced the gain of both excitatory and inhibitory currents but shortened the integration time most strongly in the excitatory currents.

The ON cone bipolar cell/AII amacrine cell circuit reduces gain at high contrast with no effect on response kinetics

There are two main classes of inhibitory input to OFF ganglion cells. The first class is feed-forward inhibition: a bipolar cell drives both excitation (OFF bipolar cell → OFF ganglion cell) and inhibition (OFF bipolar cell → OFF amacrine cell → OFF ganglion cell) in parallel (Kolb & Nelson, 1993; Zaghloul et al. 2003; Roska et al. 2006). The second class is cross-over inhibition from the ON pathway: an amacrine cell, driven by an ON bipolar cell, inhibits the OFF ganglion cell at light onset (ON bipolar cell → ON amacrine cell → OFF ganglion cell) (Zaghloul et al. 2003; Murphy & Rieke, 2006; Roska et al. 2006; Margolis & Detwiler, 2007). We recently provided evidence that, at the mean luminance of this experiment (∼10⁴P_R*, ∼5 × 10³P_M*; see Methods), the cross-over inhibition arises from the AII amacrine cell, through the following circuit: cone → ON cone bipolar cell → AII amacrine cell → OFF ganglion cell (Manookin et al. 2008); rods could also drive this circuit through their gap junctions with cones (Bloomfield & Dacheux, 2001). A unique feature of this circuit is that photoreceptor signals are transmitted to a ganglion cell without ever crossing a synapse that uses an ionotropic glutamate receptor (iGluR; Fig. 1B). Thus, we performed experiments with bath-applied antagonists to both AMPA/kainate receptors (CNQX, 200 μm) and NMDA receptors (d-AP-5, 200 μm) to test whether the AII circuit adapts its gain without an effect on integration time. Responses were recorded with V_hold of −48 ± 4 mV (mean ±s.d.; n = 9) to provide a driving force on inhibitory currents. Thus, recordings in control conditions reflect a combination of excitation and inhibition (Fig. 5A); whereas recordings in the presence of CNQX and d-AP-5 reflect the inhibitory currents mediated by the AII circuit (Fig. 5B).

Figure 5. Responses driven by the ON cone bipolar cell/AII amacrine cell pathway adapt by reducing gain only.

A and B, linear filters and nonlinearities measured at V_hold=−44 mV under a control condition and in the presence of bath-applied iGluR antagonists (200 μm CNQX and 200 μm d-AP-5). The initial 200 ms of the linear filter is shown on an expanded scale at right. The zero-crossing of the filter (arrow) was reduced at high contrast in the control condition but not in the CNQX/d-AP-5 condition. The reduced gain at high contrast was larger in the CNQX/d-AP-5 condition (0.55) relative to the control condition (0.72). The blockers had two effects on filter kinetics: increased oscillation and removal of the contrast-dependent shortening of integration time. C, relative gain for control and CNQX/d-AP-5 conditions (n = 9 cells). V_hold was −48 ± 4 mV (mean ±s.d.). The gain change was larger in the CNQX/d-AP-5 condition. D, relative zero-crossing time for the control and CNQX/d-AP-5 conditions. The contrast-dependent change in the zero-cross time was removed in the presence of CNQX and d-AP-5. The absolute zc_high was 84 ± 4 ms for the control condition and 90 ± 3 ms for the CNQX/d-AP-5 condition (n = 9).

The response measured in the presence of CNQX and d-AP-5 showed several characteristic features. First, the filter maintained its OFF-centre nature, which for membrane currents reflects an initial upward deflection, but the filter developed oscillations (Fig. 5B). Second, the nonlinearity of the LN model became more outwardly rectifying, presumably because the standard OFF bipolar pathway for excitation, which requires iGluRs (Fig. 1B), is blocked (Fig. 5B). Beyond these features, the CNQX/d-AP-5-resistant response reduced gain at high contrast: the magnitude of the gain reduction actually increased relative to control conditions, from 0.77 ± 0.03 to 0.56 ± 0.02 (difference of 0.21 ± 0.03, P < 0.001; two-tailed t test) (Fig. 5C). Despite this large reduction in gain, the contrast-dependent reduction in integration time was eliminated (control: 0.94 ± 0.006; CNQX/d-AP-5: 1.01 ± 0.006; difference of 0.07 ± 0.008, P < 0.001) (Fig. 5D). Thus, contrast-dependent reductions in gain and integration time can occur independently of one another. Furthermore, the mechanism for the contrast-dependent gain change did not require iGluRs. These results suggest that the ON-bipolar-mediated inhibition of the OFF ganglion cell, driven by the AII circuit, adapts by reducing its gain with no effect on integration time.

The OFF ganglion cell response depends strongly on the rod bipolar cell circuit at ∼10 rhodopsin isomerizations per rod per second (10 P_R*)

The above recordings were made at a high mean luminance, ∼10⁴P_R* (P_M* values here and below were always ∼0.5 ×P_R*), where responses are driven by the two cone bipolar pathways described above (Fig. 1B). Rods contribute to the light response at this level and presumably do so through their gap junctions with cones and possibly through direct synapses with OFF cone bipolar cells (Soucy et al. 1998; Yin et al. 2006) (Fig. 1A, unconventional pathway driven by r₂). At 100-fold dimmer mean luminance (∼10²P_R*), cone signals are lost, and rods support all light responses (DeVries & Baylor, 1995; Soucy et al. 1998; Deans et al. 2002; Yin et al. 2006). At this and dimmer levels of illumination, rods signal through some combination of the cone pathways and the rod bipolar pathway (Fig. 1). As the response depends more heavily on the rod bipolar pathway, two properties should emerge in OFF ganglion cells. First, the synaptic response to a light decrement switches from an excitatory input driven by OFF cone bipolar cells to a ‘disinhibitory’ input driven by AII amacrine cells (Murphy & Rieke, 2006; Manookin et al. 2008); this switch can be monitored by measuring the ratio of excitatory and inhibitory currents at different levels of mean illumination. Furthermore, when the response of an OFF ganglion cell depends on the rod bipolar pathway, the response should be blocked by l-AP-4 (Muller et al. 1988; Soucy et al. 1998; Murphy & Rieke, 2006). l-AP-4 is a group III mGluR agonist and blocks ON bipolar cell responses by continuously activating their mGluR6 receptors, resulting in cation channel closure and hyperpolarization (Slaughter & Miller, 1981; Nakajima et al. 1993). However, the light level at which OFF ganglion cells become sensitive to l-AP-4 differs among species and among cell types (Muller et al. 1988; DeVries & Baylor, 1995; Volgyi et al. 2004; Protti et al. 2005). We therefore recorded excitatory and inhibitory currents and applied l-AP-4 to determine empirically the light level at which the guinea pig OFF ganglion cell response depends on the rod bipolar pathway.

Responses to a dark spot were measured from three levels of steady, mean luminance: 10-, 100- or 1000-fold dimmer than the conditions used above (∼10³, ∼10², or ∼10 P_R*). In one experiment, responses were measured near E_Cl (V_hold=−70 ± 3 mV; mean ±s.d.; n = 6) or near E_cation (V_hold=−4 ± 4 mV) to determine how the balance of excitation and inhibition changed with mean luminance. We made similar measurements previously, at a greater number of holding potentials, in three cells (Manookin et al. 2008). Here, we recorded a larger number of cells (n = 6) and show the effect of applying l-AP-4. As we found previously, there was a shift in the balance of excitation and inhibition with mean luminance: excitation dominated at ∼10³P_R* as indicated by a relatively large excitatory current. At ∼10²P_R*, excitatory and disinhibitory inputs were similar, whereas at ∼10 P_R* the disinhibition dominated (Fig. 6A and B). After applying l-AP-4, the disinhibition at every mean luminance was essentially blocked (Fig. 6); the effects of l-AP-4 could be reversed (n = 2 cells; Fig. 6A). Thus, the disinhibition depended on the AII amacrine cell which itself was apparently driven to varying degrees by ON cone bipolar cells or rod bipolar cells, depending on light level. At each light level, the excitatory current was only partially suppressed by l-AP-4. Thus, excitatory current arises through the OFF cone bipolar pathway even at the dimmest level; at ∼10 P_R*, this current must be mediated through either rod–cone coupling or a direct synapse between the rod and OFF cone bipolar cell.

Figure 6. Evidence that OFF ganglion cell responses depend strongly on the rod bipolar pathway at 10 R* per rod per second.

A, ganglion cell responses to a dark flash (200 ms) over the receptive field centre (spot diameter, 0.6 mm) at three levels of background luminance. Responses were recorded at two V_hold values (−67 mV and −10 mV) under control conditions, after bath application of l-AP-4 (50 μm) and after washing out the drug. The response depended most strongly on excitation (i.e. inward current measured at −67 mV) under the brightest condition and most strongly on disinhibition (i.e. inward current measured at −10 mV) under the dimmest condition. l-AP-4 partially blocked excitatory currents and completely blocked inhibitory currents at all levels of mean luminance. B, average inward currents (periods indicated by grey strips in A) for the control (black) and l-AP-4 conditions (red) at each of three light levels and both V_hold values. Data points are average responses across 6 cells. Vertical error bars indicate s.e.m. across cells; horizontal error bars indicate s.d. of V_hold across cells.

We made additional measurements of the effect of l-AP-4 on the response at ∼10 P_R* at V_hold of −46 ± 3 mV (mean ±s.d.; n = 6). At this V_hold, we measure a mix of the excitatory and inhibitory currents, similar to what occurs in a resting cell in situ (see above). The response to the dark flash was suppressed by 71 ± 7% (P < 0.001; data not shown). Thus, at ∼10 P_R* inhibitory synaptic input depends on the rod bipolar pathway, and current responses recorded at V_hold of ∼−46 mV depend primarily on the rod bipolar pathway.

Degree of gain control depends on mean light level

We compared gain control measured at the brightest mean luminance (10⁴P_R*), used in most experiments above, to that measured at a level driven by rods signalling primarily through the rod bipolar circuit (10 P_R*) (Fig. 7A). In both cases, contrast alternated between 0.30 and 0.15 (two-fold change) and the monitor updated at 20 Hz (see Methods). In these cells (V_hold=−43 ± 3 mV; mean ±s.d.; n = 9), doubling contrast reduced gain to a larger extent at 10⁴P_R* (0.75 ± 0.02; mean ±s.e.m.) compared to 10 P_R* (0.97 ± 0.015; difference of 0.22 ± 0.02, P < 0.005) (Fig. 7B). Reducing the mean luminance lengthened the integration time of the filter, increasing zc_high from 114 ± 2 ms (at 10⁴P_R*) to 170 ± 6 ms (at 10 P_R*). However, the contrast-dependent shortening of integration time at 10⁴P_R* (0.96 ± 0.011) was significantly reduced at 10 P_R* (0.99 ± 0.010; difference of 0.03 ± 0.009, P < 0.05) (Fig. 7C). Thus, synaptic responses driven primarily via the rod bipolar pathway showed essentially no contrast-dependent effects on either gain or integration time.

Figure 7. Contrast adaptation in membrane currents is reduced at dim light levels that depend primarily on the rod bipolar pathway.

A, linear filters and nonlinearities for high (10⁴P_R*) and low (10 P_R*) mean luminance (V_hold=−53 mV). A twofold increase in contrast reduced gain more at 10⁴P_R* (0.74) than at 10 P_R* (0.95). zc_high was longer at ∼10 P_R* (188 ms) than at ∼10⁴P_R* (106 ms). Stimulus was updated at 20 Hz. B, relative gain at high contrast at two levels of mean luminance (n = 9 cells). Gain control was larger at the high mean luminance relative to lower mean luminance. C, relative zero-crossing time at high contrast at two levels of mean luminance. The shortening of zero-cross time was greater at the high mean luminance relative to the lower mean luminance. The absolute zc_high was 114 ± 2 ms for the high mean luminance condition and 170 ± 6 ms for the low mean luminance condition (n = 9).

Adaptation in spiking can arise solely through the ganglion cell's intrinsic mechanism

Responses were recorded at ∼10 P_R* to test whether gain control in ganglion cell firing could arise solely through an intrinsic mechanism. Ganglion cell spiking responses were measured with loose-patch recordings (Fig. 8A). The peak firing rate, measured as the highest level in the nonlinear function for the spiking response (time bin, 20 ms), was 91 ± 26 Hz (n = 9) at 10 P_R*; these rates were about half those measured previously at 10⁴P_R*: 208 ± 55 Hz (n = 37 OFF cells) (Beaudoin et al. 2007). After loose-patch recording, the same cell was recorded with a second electrode to measure synaptic currents either at a V_hold that emphasizes excitatory current (−72 ± 0.4 mV; mean ±s.d.; n = 2) or a mix of excitatory and inhibitory current (−46 ± 4 mV; n = 5) (Fig. 8B). Results at these two V_hold values were similar and are combined below. Additional recordings were made at two V_hold values in the same cells to compare directly gain control in excitatory and inhibitory currents (V_hold=−73 ± 4 mV and −14 ± 7 mV; n = 7).

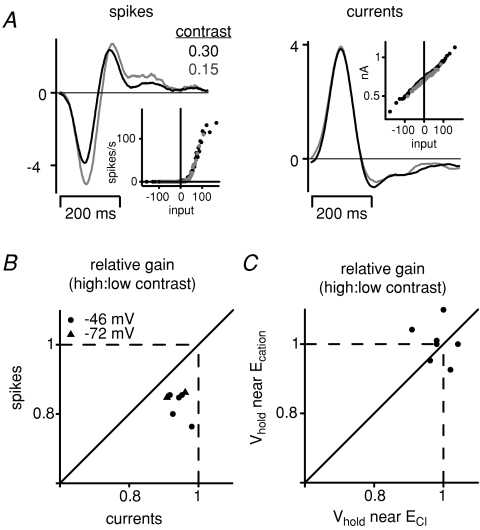
Figure 8. At dim light levels, gain control can arise exclusively in the process of spike generation.

A, linear filters and nonlinearities for the spiking and membrane current responses measured at two contrast levels (0.15 and 0.30) at a mean luminance of 10 P_R*. At high contrast, the spike response reduced gain (0.76) but the current response showed essentially no change (0.98). Stimulus was updated at 20 Hz. B, relative gain at high contrast for spikes versus currents at a mean luminance of 10 P_R*. In all cells, the gain change was larger for the spike response compared to the current response. Cells had V_hold near −46 or −72 mV (see Results). C, relative gain at high contrast for membrane currents recorded at two V_hold values. There was a similar lack of gain control in currents measured at V_hold values close to E_Cl (V_hold=−73 ± 4 mV) or E_cation (V_hold=−14 ± 7 mV; n = 7).

Gain control measured in the spike response exceeded that measured in membrane currents (Fig. 8B). The reduced gain at high contrast was larger for spiking responses (0.83 ± 0.014) compared to membrane current responses (0.94 ± 0.010; difference of 0.11 ± 0.02; P < 0.01). Similarly, the decreased integration time at high contrast was larger for spiking responses (0.91 ± 0.010) compared to membrane current responses (0.98 ± 0.004; difference of 0.07 ± 0.010; P < 0.005). Thus, under conditions where responses depend primarily on the rod bipolar circuit, adaptation in ganglion cell firing arose largely or solely through an intrinsic mechanism. Furthermore, gain control at ∼10 P_R* was similarly absent at V_hold near −73 mV (0.98 ± 0.016; n = 7) and V_hold near −14 mV (1.0 ± 0.02; difference of − 0.02 ± 0.03, NS) (Fig. 8C). Thus, under these dim light conditions, gain control is absent from all synaptic pathways converging on the ganglion cell.

Discussion

Distinct patterns of gain control in parallel cone bipolar cell pathways converging on the same ganglion cell

Our results suggest that two cone bipolar cell pathways converging on the same ganglion cell show distinct patterns of adaptation (Fig. 1B). An excitatory OFF bipolar-mediated pathway adapted at high contrast by reducing gain and shortening integration time (Fig. 4), whereas an ON bipolar-mediated inhibitory pathway adapted by reducing gain with no effect on integration time (Figs 4 and 5).

The lack of an effect on integration time in the OFF ganglion cell's ON-bipolar-mediated inhibitory currents mimicked what we had previously observed in the ON ganglion cell's excitatory currents (Beaudoin et al. 2007). Thus, apparently the ON bipolar pathway adapts with a gain change only and the same pathway both excites the ON ganglion cell (directly) and inhibits the OFF ganglion cell (indirectly; Manookin et al. 2008). At physiological membrane potentials (∼−70 to −40 mV), the OFF ganglion cell's driving force on excitation will be stronger than the driving force on inhibition, given the expected reversal potentials in situ (E_excitation=∼0 mV; E_inhibition=∼−80 mV) (Murphy & Rieke, 2006). This explains why gain control in the OFF ganglion cell's subthreshold membrane potential shows adaptation in response kinetics, resembling the excitatory currents (Zaghloul et al. 2005; Beaudoin et al. 2007).

The ON/OFF asymmetry in the adaptation of response kinetics is consistent with some previous studies. For example, salamander OFF bipolar cells adapt their kinetics at high contrast, whereas ON bipolar cells do not (Rieke, 2001). A similar asymmetry was shown in ganglion cells of salamander and primate (Chander & Chichilnisky, 2001; Kim & Rieke, 2001; Rieke, 2001). However, some studies (primate or cat) report that both ON and OFF cells adapt their kinetics (Shapley & Victor, 1978; Benardete & Kaplan, 1999; Lesica et al. 2007), whereas others suggest that neither ON nor OFF cells adapt their kinetics (Bonin et al. 2006; Gaudry & Reinagel, 2007a). Thus, it is at present unclear under what conditions ON and OFF cone bipolar pathways, and the downstream ganglion and lateral geniculate cells, adapt their response kinetics at high contrast.

Gain control under conditions driven by the rod bipolar cell

Under our conditions, synaptic responses driven by the rod bipolar cell pathway (Fig. 1A) showed little or no adaptation (Figs 7 and 8). Under these dim light conditions, gain control was present in the spiking response and apparently arose through an intrinsic property of the ganglion cell (Fig. 8). These results support modelling studies showing that gain control can arise solely through an intrinsic property of a spiking cell (Yu & Lee, 2003; Gaudry & Reinagel, 2007a,b). A proposed mechanism for this intrinsic property is the reduced availability of sodium channels at high contrast driven by the higher frequency of spike bursts (Kim & Rieke, 2003). This intrinsic mechanism may also explain the persisting adaptation effects in mice with altered OFF bipolar cell circuitry (Kerschensteiner et al. 2008).

Shot noise associated with photon arrival limits the ability to detect contrast when integrating signals over a small rod pool

Our results are consistent with no or very little contrast adaptation at the level of rod bipolar cells. The rod bipolar cell is active at dim light levels, and we therefore asked whether this cell could detect a twofold contrast change under our dim light conditions. The intensity distributions at each contrast are represented in Fig. 9A. However, photon arrival is random, and therefore photoisomerization rates exhibit shot noise described by a Poisson distribution. For example, across all frames where we intended to present an intensity corresponding to 5 R* per rod per second, the actual intensity varied, corresponding to a wide distribution of R* per rod per second values (Fig. 9A, inset). To understand the effect of this shot noise, we made a simple simulation (see Methods).

Figure 9. Detecting a contrast switch under dim light conditions requires integration over hundreds of rods.

A, the intensity distribution in the random flicker stimulus is Gaussian, with a nominal σ/mean value, which defines the contrast. In this example, mean luminance is 10 R* per rod per second and intended σ values are 0.30 or 0.15 times the mean (high and low contrast, respectively). However, the distributions will ultimately be wider than intended because of shot noise associated with photon arrival times (where mean = variance of R*). Inset shows a Poisson distribution with mean = 5 R* per rod per second. B, simulation showing the effect of shot noise on isomerization rate over time. Each point in the simulation shows the R* value summed over a rod pool within each 50 ms frame (i.e. for the 20 Hz flicker stimulus used in the experiment). For a pool of 1000 rods, the two contrasts can be distinguished from one another and from 0% contrast (i.e. mean luminance); the summed isomerization rate resembles the stimulus. For a pool of 20 rods, the three contrast levels yield similar, noisy time courses. C, calculated σ/mean for two contrast levels and the mean luminance given various rod pools. The calculation is based on the experimental condition: mean luminance of 10 R* per rod per second and a frame length of 50 ms. Dashed lines indicate the Gaussian σ values. D, the ratio of σ/mean values for the two contrasts given various rod pool sizes. The mean was constant, so the ratio reduces to σ_0.30/σ_0.15. For a pool size of 20 rods, the twofold change in contrast yields only a 1.23-fold change in the σ_0.30/σ_0.15 ratio. For 1000 rods, the ratio approaches two. Dashed line indicates the two-fold change in the Gaussian σ.

In the simulation, we show the intensity of light, in contrast values, for three stimuli: the mean luminance (contrast = 0) and the Gaussian flicker stimulus at a contrast of 0.15 or 0.30 (Fig. 9B). For each 50 ms frame, we simulated the mean photoisomerization rate over a ‘rod pool.’ In the two cases illustrated, the pool size was 20 rods, similar to that integrated by a rod bipolar cell (Tsukamoto et al. 2001), or 1000 rods. The ganglion cells under study have ∼550 μm diameter dendritic trees (Manookin et al. 2008) and rod density in the dorsal guinea pig retina is ∼120 000–200 000 mm⁻² (Peichl & Gonzalez-Soriano, 1994; Rohlich et al. 1994). Thus, there are ∼36 000–60 000 rods in the full span of the ganglion cell dendritic tree. However, because the ganglion cell shows a dome-like weighting of its synaptic connections, the exact number of rods whose signals are integrated by the ganglion cell is effectively lower (Kier et al. 1995; Jakobs et al. 2008; Xu et al. 2008). For simplicity, we have considered the integration of 1000 rods. Figure 9B shows that for a pool of 1000 rods, low and high contrast stimuli evoke responses that can be distinguished from one another and from the mean luminance; indeed these isomerization rates strongly resemble the stimulus time course. However, for the pool of 20 rods, low and high contrast stimuli evoke similar responses, both of which are difficult to distinguish from the noise at mean luminance. Thus, given a mean luminance of 10 R* per rod per second, the rod bipolar cell would be unable to detect a 2-fold change in contrast.

The relationship between rod pool size and contrast detection could be calculated directly (see Methods). As the rod pool increases from 1 to 5000 rods, there is an increased ability to distinguish the three contrast values from one another, and the shot noise becomes increasingly irrelevant (Fig. 9C). We plot the relationship between the σ of the R* per rod pool per 50 ms distribution for high contrast to low contrast (σ_0.30:σ_0.15) to determine how well a given rod pool could detect a 2-fold contrast change (Fig. 9D). Given the mean of 10 R* per rod per second, a pool size of ∼1000 or more is necessary to detect a ∼2-fold contrast change. We note that three factors trade off: mean luminance, pool size, and stimulus frame duration. For example, if mean luminance were decreased by a factor of 10, to 1 R* per rod per second, the pool size would have to increase 10-fold to maintain a constant level of sensitivity.

Cellular mechanisms for contrast gain control

What is the mechanism for contrast gain control in bipolar cells? Recordings in salamander bipolar cells suggested that a gain control mechanism resides in the bipolar cell dendrites (Rieke, 2001). Consistent with this, we found that the contrast-dependent gain change in ON-bipolar-mediated inhibitory currents in an OFF ganglion cell, measured in the presence of iGluR antagonists (CNQX and d-AP-5), persisted and actually grew larger relative to control conditions (Fig. 5). Thus, the gain change did not rely on a synaptic mechanism involving an iGluR, ruling out a mechanism at a bipolar cell ribbon synapse. This result is consistent with an intrinsic mechanism for a gain change in the ON cone bipolar cell that in turn alters the gain at the synaptic output of an AII cell (Manookin et al. 2008) (Fig. 1B). Compared to control conditions, the contrast-dependent gain change in the ganglion cell increased in the presence of CNQX and d-AP-5 (Fig. 5). This increase, as well as the oscillatory nature of the linear filter, most likely results from the increased activity of ON cone bipolar cells; bipolar cell activity would increase because inhibitory horizontal and amacrine cell feedback is removed in the presence of CNQX (Yang et al. 1998; Sampath & Rieke, 2004; Dumitrescu et al. 2006).

Recently, the rod bipolar cell was shown to express an adaptive mechanism at its synaptic output. Background light that evoked ∼0.5 P_R* depressed the rod bipolar cell's release onto the AII cell (Dunn et al. 2006; Dunn & Rieke, 2008). At a background of ∼10 P_R*, we did not find evidence for contrast gain control in the bipolar cell output (or in the AII cell that conveys the rod bipolar cell signal to the OFF ganglion cell; Figs 7 and 8). Thus, synaptic depression at the rod bipolar cell's ribbon synapse may be involved primarily in mean luminance adaptation but not contrast adaptation. Similarly, ON cone bipolar cells express a synaptic mechanism for adapting their outputs to mean luminance, but the same mechanism apparently does not explain contrast adaptation (Rieke, 2001; Dunn et al. 2007; and see Fig. 4). Thus, depression at ribbon synapses of both rod and ON cone bipolar cells apparently explains adaptation to mean luminance but not contrast. For salamander OFF cone bipolar cells, the mechanism for contrast adaptation was an intrinsic property that depended on calcium (Rieke, 2001). Further studies in mammalian retina are required to characterize a possible intrinsic property for adaptation in cone bipolar cells and to test for a possible mechanism for adaptation at the synaptic output of OFF bipolar cells (Manookin & Demb, 2006).

Conclusion

In conclusion, we have shown that multiple synaptic pathways converging on the same retinal ganglion cell show distinct patterns of contrast adaptation. At high mean luminance, synaptic mechanisms for adaptation combine with an intrinsic property for adaptation in the ganglion cell, whereas at low mean luminance, the intrinsic property for adaptation acts essentially alone. The statistics of photon arrival make it impossible for rod bipolar cells to adapt to contrast under dim light conditions, because these cells integrate signals from only ∼20 rods. With this degree of integration, variance associated with photon shot noise overwhelms the variance of intensities that correspond to the contrast signal. A similar limitation will arise in any case where a neuron adapts its response properties to the variance of a noisy input signal (e.g. synaptic release with low mean probability).