Are Random Forests Better than Support Vector Machines for Microarray-Based Cancer Classification?

Abstract

Cancer diagnosis and clinical outcome prediction are among the most important emerging applications of gene expression microarray technology with several molecular signatures on their way toward clinical deployment. Use of the most accurate decision support algorithms available for microarray gene expression data is a critical ingredient in order to develop the best possible molecular signatures for patient care. As suggested by a large body of literature to-date, support vector machines can be considered “best of class” algorithms for classification of such data. Recent work however found that random forest classifiers outperform support vector machines. In the present paper we point to several biases of this prior work and conduct a new unbiased evaluation of the two algorithms. Our experiments using 18 diagnostic and prognostic datasets show that support vector machines outperform random forests often by a large margin.

Introduction

Gene expression microarrays are becoming increasingly promising for clinical decision support in the form of diagnosis and prediction of clinical outcomes of cancer and other complex diseases. In order to maximize benefits of this technology, researchers are continuously seeking to develop and apply the most accurate decision support algorithms for the creation of gene expression patient profiles. Prior research suggests that among well-established and popular techniques for multicategory classification of micro-array gene expression data, support vector machines (SVMs) achieve the best classification performance, significantly outperforming k-nearest neighbors, backpropagation neural networks, probabilistic neural networks, weighted voting methods, and decision trees ¹.

In the last few years, there is an increased interest within the bioinformatics community in the random forest algorithm ² for classification of microarray and other high-dimensional molecular data ^3–5. Notably, a recent study ⁵ concluded that random forest classifiers have predictive performance comparable to that of the best performing alternatives (including SVMs) for classification of microarray gene expression data. In fact, the data in Table 2 of the study ⁵ suggests that random forests on average across 10 datasets slightly outperform SVMs as well as other methods. The authors also proposed a gene selection method called RFVS intended to preserve classification performance of the random forest. If true, these findings are of great significance to the field, suggesting that random forests are overall the best algorithm for this domain.

Table 2.

Average classification results for SVM and RF classifiers without gene selection. Each cell reports the corresponding average value of classification performance (measured by AUC and RCI).

Classifiers	Average Diagnostic	Average Prognostic	Average Overall
SVM	0.9059	0.6978	0.8249
RF (ntree = 500, mtryFactor = 1)	0.8417	0.6541	0.7688
RF (ntree = 1000, mtryFactor = 1)	0.8500	0.6587	0.7756
RF (ntree = 2000, mtryFactor = 1)	0.8531	0.6648	0.7799
RF (ntree = 500, mtryFactor = 0.5)	0.8293	0.6691	0.7670
RF (ntree = 1000, mtryFactor = 0.5)	0.8267	0.6692	0.7654
RF (ntree = 2000, mtryFactor = 0.5)	0.8334	0.6783	0.7731
RF (ntree = 500, mtryFactor = 2)	0.8620	0.6679	0.7865
RF (ntree = 1000, mtryFactor = 2)	0.8642	0.6754	0.7908
RF (ntree = 2000, mtryFactor = 2)	0.8633	0.6747	0.7900
RF (optimized by cross-val.)	0.8584	0.6590	0.7809

However, the prior work in ⁵ possesses several major data analytic biases that may have distorted its conclusions: First, the performance metric used in ⁵ (proportion of correct classifications) is sensitive to unbalanced distribution of classes and has lower power to discriminate among classification algorithms compared to existing alternatives such as area under the ROC curve and relative classifier information ^6–8. Second, while the random forests were applied to datasets prior to gene selection, SVMs were applied to a subset of only 200 genes. Given that the number of optimal genes varies from a dataset to dataset and that SVMs are known to be fairly insensitive to a very large number of irrelevant genes, such an application of SVMs biases down their performance. Third, a one-versus-one SVM algorithm was applied for the multicategory classification tasks, while it is has been shown that in microarray gene expression domain this method is inferior to other multicategory SVM methods, such as one-versus-rest ^1,9. Fourth, the evaluation of ⁵ was limited only to linear SVMs without optimizing any algorithm parameters.

These biases of the study in ⁵ severely compromise its conclusions and the question whether random forests indeed outperform SVMs for classification of microarray gene expression data is not convincingly answered. In the present work we undertake an unbiased comparison of the two algorithms to determine the best performing technique. We also examine to what extent the gene selection procedure RFVS preserves classification performance of the random forest classifier by using a small subset of genes as claimed in ⁵. To make our evaluation more relevant to practitioners, we focus not only on diagnostic data-sets that are known to have strong predictive signals, but also include several outcome prediction datasets where the signals are weaker.

Methods and Materials

Microarray Datasets and Classification Tasks

Gene expression microarray datasets used in the present work are described in Table 1. All 18 datasets span the domain of cancer; 11 datasets correspond to diagnostic tasks and 7 are concerned with clinical outcome prediction. Out of 18 datasets, 9 are binary classification tasks, while the other 9 are multicategory with 3–26 classes. The datasets contain 50–308 samples and 2,308–24,188 variables (genes) after data preparatory steps described in ¹. All diagnostic data-sets were obtained from http://www.gems-system.org¹ and prognostic datasets were obtained from the links given in ¹⁰. A list of references to the primary study for each dataset is provided in ¹¹.

Table 1.

Gene expression microarray datasets used in this study.

Task	Dataset name	Number of classes	Number of variables (genes)	Number of samples	Diagnostic or outcome prediction task
Diagnosis	Su	11	12533	174	11 various human tumor types
	Ramaswany	26	15009	308	14 various human tumor types and 12 normal tissue types
	Staunton	9	5726	60	9 various human tumor types
	Pomeroy	5	5920	90	5 human brain tumor types
	Nutt	4	10367	50	4 malignant glioma types
	Golub	3	5327	72	Acute myelogenous leukemia (AML), acute lymphoblastic leukemia (ALL) B-cell and ALL T-cell
	Armstrong	3	11225	72	AML, ALL and mixed-lineage leukemia (MLL)
	Bhattacharjee	5	12600	203	4 lung cancer types and normal tissues
	Khan	4	2308	83	Small, round blue cell tumors (SRBCT) of childhood
	Shipp	2	5469	77	Diffuse large B-cell lymphomas (DLBCL) and follicular lymphomas
	Singh	2	10509	102	Prostate tumor and normal tissues
Prognosis	Iizuka	2	7070	60	Hepatocellular carcinoma 1-year recurrence-free survival
	Beer	2	7129	86	Lung adenocarcinoma survival
	Veer	2	24188	97	Breast cancer 5-year metastasis-free survival
	Rosenwald	2	7399	240	Non-Hodgkin lymphoma survival
	Yeoh	2	12240	233	Acute lymphocytic leukaemia relapse-free survival
	Pomeroy	2	7129	60	Medulloblastoma survival
	Bhattacharjee	2	12600	62	Lung adenocarcinoma 4-year survival

Cross-Validation Design

We used 10-fold cross-validation to estimate the performance of the classification algorithms. In order to optimize algorithm parameters, we used another “nested” loop of cross-validation by further splitting each of the 10 original training sets into smaller training sets and validation sets. For each combination of classifier parameters, we obtained cross-validation performance and selected the best performing parameters inside this inner loop of cross-validation. Next, we built a classification model with the best parameters on the original training set and applied this model to the original testing set. Details about the “nested cross-validation” procedure can be found in ^12,13. Notice that the final performance estimate obtained by this procedure will be unbiased because each original testing set is used only once to estimate performance of a single classification model that was built by using training data exclusively.

Support Vector Machine Classifiers

Several theoretical reasons explain the superior empirical performance of SVMs in microarray data: e.g., they are robust to the high variable-to-sample ratio and large number of variables, they can learn efficiently very complex classification functions, and they employ powerful regularization principles to avoid overfitting^1,14,15. Extensive applications literature in text categorization, image recognition and other fields also shows the excellent empirical performance of this classifier in many more domains. The underlying idea of SVM classifiers is to calculate a maximal margin hyperplane separating two classes of the data. To achieve non-linear separation, the data are implicitly mapped to a higher dimensional space by means of a kernel function, where a separating hyperplane is found. New samples are classified according to the side of the hyperplane they belong to ¹⁵. Many extensions of the SVM algorithm can handle multicategory data. The “one-versus-rest” SVM works better for multi-class microarray data ^1,9, so we adopted this method for the analysis of multicategory datasets in the present study. In summary, this approach involves building a separate SVM model to classify each class against the rest, and then predicting the class of a new sample using the SVM model with the strongest vote.

We used the polynomial-kernel SVM implemention in libSVM (http://www.csie.ntu.edu.tw/~cjlin/libsvm) and optimized the kernel degree d and the SVM penalty parameter C by nested cross-validation as described above. Namely, we optimized d over {1, 2, 3} and penalty parameter C over {10^–2, 1, 100}.

Random Forest Classifier

Random forest (RF) is a classification algorithm that uses an ensemble of unpruned decision trees, each of which is built on a bootstrap sample of the training data using a randomly selected subset of variables ². This algorithm is promising for classification of microarray data because it provides theoretical guarantees for optimal classification performance in the sample limit, it employs gene selection embedded in its operation, and it can perform both binary and multicategory classification tasks.

We employed the high-quality implementation of RF available in the R package randomForest ¹⁶. This implementation is based on the original Fortran code authored by Leo Breiman, the inventor of RFs. Following the suggestions of ^16,17 and http://www.stat. berkeley.edu/~breiman/RandomForests/, we applied RFs with different parameter configurations for the values of ntree = {500, 1000, 2000} (number of trees to build), mtryFactor ={0.5, 1, 2} (a multiplicative factor of the default value of mtry parameter denoting the number of genes to be randomly selected for each tree; by default $mtry=\sqrt{number\hspace{0.17em}\cdot of\cdot \hspace{0.17em}genes}$), and nodesize = 1 (minimal size of the terminal nodes of the trees in a random forest). Note that these parameters are also consistent with the recommendations of ⁵. We furthermore applied RFs with ntree and mtry-Factor parameters optimized by nested cross-validation.

Random Forest Gene Selection

In addition to standard RF that employ embedded gene selection, we also used the recently introduced random forest-based backward elimination procedure RFVS ⁵. According to the evaluation of RFVS conducted by its authors, this method “yields very small sets of genes while preserving predictive accuracy” ⁵. The RFVS procedure involves iteratively fitting RFs (on the training data), and at each iteration building a random forest after discarding genes with the smallest importance values. The returned set of genes is the one with the smallest out-of-bag error.

We used the varSelRF implementation of the RFVS method developed by its inventors and applied it with the recommended parameters: ntree = 2000, mtry-Factor = 1, nodesize = 1 and fraction.dropped = 0.2 (a parameter denoting fraction of genes with small importance values to be dropped during backward elimination procedure) ⁵. The meaning of other parameters is explained in the previous subsection.

Classification Performance Evaluation Metrics

We used two classification performance metrics. For binary tasks, we used the area under the ROC curve (AUC) which was computed using continuous outputs of the classifiers (distances from separating hyperplane for SVMs and outcome probabilities for RFs) ⁷. For multicategory tasks, where classical AUC is inapplicable, we employed the relative classifier information (RCI) ⁶. RCI is an entropy-based measure that quantifies how much the uncertainty of a decision problem is reduced by a classifier relative to classifying using only the prior probabilities of each class. We note that both AUC and RCI are more discriminative than the accuracy metric (also known as proportion of correct classifications) and are not sensitive to unbalanced distributions ^6–8. Both AUC and RCI take values on [0, 1], where 0 denotes worst possible classification and 1 denotes perfect classification.

Statistical Comparison among Classifiers

To test that differences in AUC of two classification methods are not due to chance, we employed a non-parametric procedure by DeLong et al ¹⁸. The significance of differences in RCI were assessed by a permutation test ¹⁹. All statistical significance testing in this work was performed at the 0.05 level.

Results

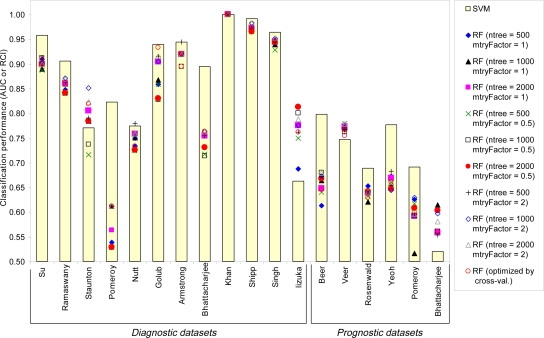
The performance results of classification without gene selection are shown in Figure 1, and the detailed results are provided in the online appendix ¹¹. In 13 datasets SVMs outperform the RF classifier optimized by cross-validation, and in 7 out of these 13 datasets (names shown with bold in Figure 1) the differences in performances are statistically significant. In 1 dataset (Khan) SVMs and optimized RF perform exactly the same, and in the remaining 4 datasets optimized RF performs better than SVMs, however the differences in performances are statistically significant only in 1 dataset (Iizuka). Similarly, in 11 datasets SVMs outperform the best of 9 RF classifiers with fixed parameters, and in 6 out of these 11 datasets (names shown in bold in the Figure 1 excluding Rosenwald) the differences in performances are statistically significant. In 1 dataset (Khan) SVMs and the best RF perform exactly the same, and in the remaining 6 datasets the best RF performs better than SVMs, however the differences in performances are statistically significant only for 1 dataset (Iizuka). The average results are provided in Table 2. For diagnostic tasks, SVMs outperform RFs by >0.04 AUC and RCI, while for prognostic tasks SVMs are better than RFs by >0.02 AUC. On average over all 18 datasets, SVMs demonstrate superior classification performance to RFs by >0.03 AUC and RCI.

Figure 1.

Classification performance results without gene selection. The horizontal axis shows datasets. The vertical axis corresponds to classification performance: AUC for binary tasks and RCI for multicategory tasks. For clarity, the vertical axis is shown for the range [0.5, 1]. Please see text for details.

The results for random forest gene selection method RFVS are provided in Table 3. It does not follow from our evaluation that RFVS preserves classification performance of the RF model without gene selection as its inventors claim ⁵. Specifically, for prognostic tasks the average performance drops by 0.0447 AUC, and only in diagnostic tasks the performance is preserved. It is not surprising that ⁵ did not observe this finding their original evaluation consisted primarily of diagnostic datasets.

Table 3.

Results for random forest variable selection method RFVS. The column “number of genes selected by RFVS” reports the average number of selected genes over 10 training sets during cross-validation. The improvement of performance by RFVS is computed by subtracting performance of RF w/o gene selection (with parameters ntree = 2000 and mtryFactor = 1) from performance of RF & RFVS.

Task	Dataset	Number of genes selected by RFVS	Perfor- mance of RF & RFVS	Improve- ment of performance by RFVS
Diagnosis	Su	844.6	0.9185	0.0183
	Ramaswany	966.2	0.8736	0.0122
	Staunton	151.5	0.8144	0.0091
	Pomeroy	34	0.6885	0.1255
	Nutt	126.2	0.6747	–0.0833
	Golub	455.9	0.9326	0.0277
	Armstrong	709	0.8273	–0.0924
	Bhattacharjee	26.8	0.8019	0.0476
	Khan	16.8	0.9702	–0.0298
	Shipp	14.5	0.9567	–0.0166
	Singh	57.9	0.9560	0.0120
Prognosis	Iizuka	37.8	0.6625	–0.1125
	Beer	15.4	0.5591	–0.0885
	Veer	123.6	0.7412	–0.0321
	Rosenwald	123.9	0.6310	–0.0081
	Yeoh	21.4	0.7054	0.0366
	Pomeroy	29.1	0.5583	–0.0334
	Bhattacharjee	45.5	0.4833	–0.0750

Discussion

The results presented in this paper illustrate that on average SVMs offer classification performance advantages compared to RFs. We emphasize that when it comes to clinical applications of such models because the size of the patient populations is huge, even very modest differences in performance (e.g., at the order of <0.01 AUC and RCI) can result in very substantial differences in total clinical outcomes (e.g., life-years saved) ²⁰.

It is worth emphasizing that SVMs in current experiments were applied without gene selection due to the significant computational requirements of the large-scale comparison. We plan to extend this comparison to include gene selection algorithms for SVMs such as RFE ²¹ and/or Markov blanket methods ²² that provide optimality guarantees for selected genes under fairly broad distributional assumptions.

Data analysts have to be aware of a limitation of RFs imposed by random gene selection. In order for a RF classification model to overcome the trap of large variance, one has to use a large number of trees and build trees based on a large number of genes. The exact values of these parameters depend on both the complexity of the classification function and the number of genes in a microarray dataset. Therefore, in general, it is advisable to optimize these parameters by cross-validation taking into account the variability of the random forest model.

Conclusion

The primary contribution of the present work is that we conducted the largest evaluation of RFs and SVMs performed so far, using 18 diagnostic and outcome prediction datasets. Contrary to a smaller-scale prior comparison that was compromised by several data analytic biases ⁵, we found that on average and in the majority of datasets, RFs are outperformed by SVMs even when SVMs are not employed with the benefit of optimized gene selection.