Template-Driven Spatial-Temporal Outbreak Simulation for Outbreak Detection Evaluation

Abstract

We developed a non-disease specific template-driven spatial-temporal outbreak simulator for evaluating outbreak detection algorithms. With only a few outbreak parameter settings, our simulator can generate different patterns of outbreak cases either temporally or spatial-temporally using three different generation algorithms: deterministic, independent, Poisson process. Our simulator is flexible, easy to implement and provides case event times rather than aggregated counts. We provide examples of outbreak simulations using linear template functions. Our Template-Driven Simulator is a useful tool for evaluating of outbreak detection algorithms.

Introduction

Biosurveillance systems collect and automatically analyze various types of data, searching for possible disease outbreaks. For example, a system may obtain, from a subset of emergency departments (EDs) in a region, the daily counts of the number of respiratory ED visits. The automatic analysis of biosurveillance data is conducted by outbreak detection algorithms. Researchers have developed numerous algorithms for detecting outbreaks, ranging from temporal algorithms that detect changes in time series for a single geographic region¹, to spatial-temporal algorithms that utilize both spatial and temporal data².

Evaluation of detection algorithms requires surveillance data from outbreak and non-outbreak periods. Data are often available for non-outbreak periods. However, due to the rarity of real outbreaks, many evaluations cannot use data from real outbreaks. In such situations, researchers construct semi-synthetic data by simulating captured outbreak cases (those captured by the surveillance system) and adding those cases to real non-outbreak data.

One type of outbreak simulator consists of disease-specific simulators. For example, Hogan et al.³ used a model of an aerosol anthrax release to evaluate detectability of anthrax outbreaks. Watkins et al.⁴ have developed software for a geographic information system (GIS) environment for simulating spatial-temporal disease outbreaks. Such simulators can offer good face validity and permit investigation in to the role of meaningful outbreak parameters.

Another type consists of simulators that are not disease-specific. These simulators are typically defined by a template function that describes the temporal shape of the outbreak in surveillance data. For example, Reis et al.⁵ created outbreaks in temporal data consisting of 20 cases per day for 7 days. Researchers can tailor the shape, magnitude and duration to match those of a hypothetical outbreak of interest, and add noise to improve realism. Researchers have also used simple extensions of this approach to create outbreaks in spatial-temporal data⁶. Cassa et al.⁷ developed the open-source AEGIS Cluster Creation Tool for simulating spatial-temporal outbreaks that are not disease-specific.

One limitation of all of the above non-disease specific simulators is that they create temporally-aggregated counts, for example, daily counts of ED visits. Such data can create difficulties when comparing algorithms that run on data that are aggregated differently, or algorithms that run at different frequencies. Clearly these difficulties are surmountable by using the least common denominator for temporal aggregation, or by simulating visit times in a second simulation step. An alternative solution would be to simply simulate visit times directly instead of simulating aggregated counts. This would also have the added advantage of forcing the logical separation between the simulation method and the aggregation routines used by surveillance systems.

In this paper, we develop a non-disease specific simulator that creates outbreak patterns in temporal and spatial-temporal event-time data in accordance with user-defined template functions. Our objective is to create an intuitive simulator of event times that can be easily controlled through the use of template functions. We describe our Template-Driven Simulator in the context of ED visit data and illustrate the ease and flexibility of our simulator by generating temporal and spatial-temporal outbreaks datasets.

Methods

The Template-Driven Simulator can generate purely temporal and spatial-temporal disease patterns. We begin by describing creation of temporal outbreaks.

Temporal Outbreak Simulation

Three components are required to create temporal outbreaks. The first component is the outbreak magnitude, given as the number or expected number of captured outbreak cases. The second component is the temporal template that describes how the rate of new cases changes across time. For example, a temporal template may indicate that cases will appear at a linearly-increasing rate over three days. The third component is the generation algorithm that describes how visit times are generated in accordance with the temporal template.

Outbreak Magnitude

The outbreak magnitude C is the number or expected number of captured outbreak cases over the duration of the outbreak. Whether C denotes the number or expected number of captured cases depends on the generation algorithm.

Temporal Template

The temporal template is a function f that describes how the rate of new cases changes over time. Specifically, we define f to be a bounded probability density function that is zero outside of an outbreak interval [0,T), that is, f satisfies the following constraints.

$$\begin{array}{l}0\le f(t)\le f*,\hspace{1em}t\in [0,T)\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}f(t)=0,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}t\notin [0,T)\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\underset{0}{\overset{T}{\int }}f(t)dt=1.\end{array}$$ (1)

Generation Algorithm

We have three approaches for generating visit times in accordance with the temporal template function f : deterministic, independent, and Poisson process. As the names suggest, deterministic generation creates visit times in a non-random pattern while independent and Poisson process generation create visit times stochastically. The primary difference between independent and Poisson process generation is that the number of visits is fixed for independent generation, but only the expected number of visits is set for Poisson process generation while the actual number of visits remains random.

Deterministic Generation

Deterministic generation creates visit times in a regular, non-random pattern that is moderated by the template function f. The goal is to construct visit times t₁,..., t_C for C total captured cases in a time interval[0,T). Let u₁,..., u_c be a grid on [0, 1):

$$u_i=\frac{i}{C}-\frac{1}{2C},i=1,\mathrm{...},C$$ (2)

We calculate the visit times:

$$t_i=F^{-}(u_i),i=1,\mathrm{...},C$$ (3)

where, F is the cumulative density function defined by $F(t)={\int }_0^{t}f(x)dx$ for 0 ≤ t < T, and F^– is the generalized inverse of F, defined as:

$$F^{-}(u)=\text{inf}\hspace{0.17em}\{t:F(t)\ge u\}.$$

The above approach is based upon the general technique of inversion for simulating random numbers⁸ but uses a regular grid instead of a random sample from a uniform distribution.

Independent Generation

Independent generation creates the visit times for C total captured cases by drawing C random samples according to the probability density function f. Inversion is a simple technique for simulating these visit times. Let u₁,..., u_c be independent draws from a uniform distribution on [0,1). The visit times are then calculated by (3).

Poisson Process Generation

Poisson process generation creates the visit times as a heterogeneous Poisson arrival process in a fixed time interval [0,T). In contrast to the simulators above, Poisson process generation interprets C as the expected number of captured cases and simulates visit times according to the heterogeneous rate function:

$$\lambda (t)=C\cdot f(t)\hspace{0.17em},0\le t<T$$ (4)

One of the methods to generate a heterogeneous Poisson process is thinning a homogeneous Poisson process with a Poisson rate λ* = C · f* ⁹. Specifically, inter-arrival times (the times between successive visits) are simulated independently from an exponential distribution with mean 1/λ*. Candidate visit times are then constructed from the inter-arrival times. Each candidate visit time t is accepted with probability λ(t) /λ* ; otherwise the visit time is excluded.

Example 1

We illustrate temporal outbreak simulation using a linearly increasing template function:

$$f(t)=\{\begin{array}{cc}2t/T^2& 0\le t<T\\ 0& otherwise\end{array}$$

We simulate three outbreaks, one using each of the three generation approaches. For each simulation we set T = 3 days and C = 300 cases. We use inversion for deterministic and independent generation, which requires the calculation of F^– :

$$F^{-}(u)=\{\begin{array}{l}\begin{array}{cc}0& u\le 0\end{array}\\ \begin{array}{cc}T\sqrt{u}& 0<u<1\end{array}\\ \begin{array}{cc}T& u\ge 1\end{array}\end{array}$$

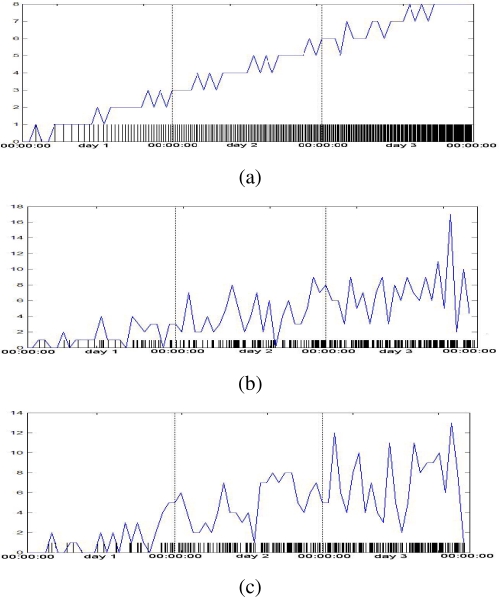
The simulated visit times are aggregated into hourly counts and graphed in Figure 1 (a – c).

Figure 1.

Simulated visit times using a linear template function. Hourly-aggregated visit times are created using deterministic (a), independent (b), and Poisson process (c) generation.

Spatial-Temporal Outbreak Simulator

We now turn to spatial-temporal simulation, in which we simulate visit times for cases in multiple geographic regions such as zip codes or counties. Consistent with common terminology, we call the geographic regions tracts. We assume that there is a finite set of N tracts S in the study region. Our spatial-temporal simulator is defined by replacing the temporal template with a spatial-temporal template and modifying visit time generation. We examine some special forms for spatial-temporal templates that decompose a template meaningfully into a temporal template, a spatial template, and a lag function.

Outbreak Magnitude

The outbreak magnitude C is the total number or expected number of captured outbreak cases across all tracts in S over the duration of the outbreak.

Spatial-Temporal Template

The spatial-temporal template is a function f that describes how the rate of new cases changes across time and space. Specifically, we define f to be a bounded function that satisfies the following constraints.

$$\begin{array}{l}0\le f(s,t)\le f*,\hspace{1em}s\in S,t\in [0,T)\\ f(s,t)=0,\hspace{1em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}s\notin S\hspace{0.17em}\text{or}\hspace{0.17em}t\notin [0,T)\\ \sum _{s\in S}\underset{0}{\overset{T}{\int }}f(s,t)dt=1\end{array}$$

For convenience, we define $p_s={\int }_0^{T}f(s,t)dt$.

Generation Algorithm

As with temporal simulation, we have three approaches for generating spatial-temporal case times in accordance with the template function f : deterministic, independent, and Poisson process.

Deterministic Generation

Deterministic generation distributes the cases in a regular spatial and temporal pattern that is moderated by the template function f. Ideally, the spatial distribution of cases would amount to having exactly C · p_s cases in each tract s. However, these quantities are generally not integers. Instead, we adopt the following algorithm to determine the number of cases in each tract. Let S = [s₁,..., s_N], define h₀ = 0 and h_i = round(CΣ_j=1,...,i p_sj) for i = 1,..., N. We then set the number of cases in tract s_i to be C_i = h_i – h_i–1. This algorithm ensures that each C_i is a non-negative integer and that the total number of cases equals C.

After determining the number of cases in each tract, we calculate their visit times using purely temporal deterministic generation.

Independent Generation

With independent generation, we determine the number of cases in each tract by simulating one draw from a multinomial distribution:

$$(C_1,\mathrm{...},C_N)\sim Multinomial(C,(p_S,\mathrm{...},p_{S_N}))$$

We then generate visit times for each tract using purely temporal independent generation.

Poisson Process Generation

Poisson process generation simulates visit times for each tract independently according to a Poisson process. Specifically, visit times for tract s are generated using a heterogeneous Poisson process with rate function

$${\lambda }_s(t)=Cf(s,t)\hspace{1em}0\le t<T$$

Special Forms for the Spatial-Temporal Template

The spatial-temporal template is defined by equation (1). We now define two special forms of the spatial-temporal template that decompose the template into simple and intuitive components: the independence form and the lagged form.

Independence Form

The independence form for the template specifies that the time and location of each case are statistically independent. That is, the independence form expresses the spatial-temporal template as a product of a spatial template and a temporal template:

$$f(s,t)=f_S(s)f_T(t)$$

The temporal template is defined as above. The spatial template only needs to satisfy:

$$\begin{array}{l}(f_s(s)\ge 0,\hspace{1em}s\in S\\ \sum _{s\in S}{f}_s(s)=1\end{array}$$

We interpret f_s (s) as the probability that each captured case is assigned to tract s. However, this probability is not only a function of the elevated risk in tract s of having, for example a respiratory ailment and visiting an emergency department, but also of the coverage of the surveillance system, that is, of the probability that a respiratory case will be captured by the system. Specifically, for tract s, let v_s denote the coverage, r_s denote the elevated disease risk, and n_s denote the population. Then,

$$f_s(s)=\frac{v_s{n}_s{r}_s}{\sum _{s^{\prime }\in S}{v}_s,n_s,r_s,}$$

While the population of each tract is often known, the coverage is not. However, if historical data are available for a non-outbreak period in which the baseline disease risk is approximately constant across tracts, then the expected number of captured historical cases in tract s is proportional to v_s n_s.

Therefore, if there are H_s captured historical cases in tract s, then

$$f_s(s)\approx \frac{H_s{r}_s}{\sum _{s^{\prime }\in S}{H}_s,r_s,}$$

Therefore, we can approximate the spatial template function by specifying the elevated disease risk for each tract, and by either estimating the coverage and population for each tract or using historical data.

The elevated disease risk r_s may be set in a variety of ways. One simple approach is to make the elevated disease risk constant across a subset of the tracts in S and zero outside of the subset. Another approach is to specify an outbreak center, say tract s₀, and define r_s to be a function of the distance from s to s₀. For example, r_s could be a decreasing linear function of distance from s to s₀.

Lagged Form

One intuitive approach for incorporating some dependence between the spatial and temporal distributions of cases is to define a non-negative lag function on S. We then define the spatial-temporal template as:

$$f(s,t)=f_s(s)f_T(t-lag(s))$$

We next present an example of our spatial-temporal simulator using the lagged form.

Example 2

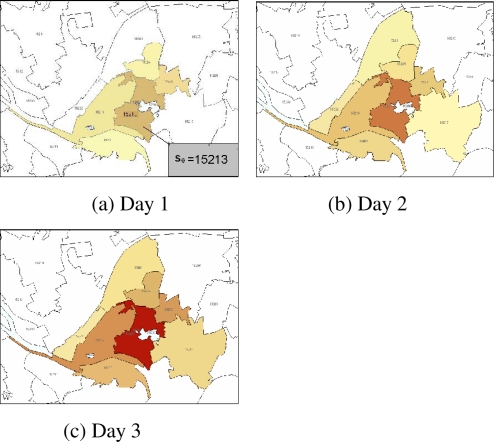
In this example, we use Poisson process generation with a lag form of the spatial-temporal template. We define r_s to be a decreasing function of distance from the zip code s₀ = 15213 in the Pittsburgh area, with r_s = 0 for zip codes at least 7.4 kilometers from s₀. We then use historical data to compute f_s (s). The lag function is defined in days as a function of the distance d (in km) from s₀ = 15213.

$$lag(s)=\{\begin{array}{cc}d(s)-2& 2\le d(s)<7.4\\ 0& otherwise\end{array}$$

We set C = 900 cases and T = 3 days. To account for non-uniform coverage of historical data, we define the outbreak intensity in an area as the number of simulated cases over the mean number of historical cases during the past year. Figure 2 (a – c) shows outbreak intensity by day in each affected zip code:

Figure 2.

A lighter color indicates a smaller outbreak intensity in that area, while a darker color indicates a heavier outbreak intensity.

Discussion

We presented a simulator that researchers can use to generate visit times across spatial tracts. These visit times can be injected into baseline data to create semi-synthetic outbreaks that can be used to assess the sensitivity and timeliness of outbreak detection. We presented several forms that use simple and intuitive parameters but are quite flexible for simulating outbreaks for evaluation purposes.

The simulation uses common techniques such as inversion and thinning to generate visit times. We presented simple steps for generating visit times using these techniques. While the methods presented are general and fairly robust, there are other methods available for simulating from these processes that may be more efficient in certain circumstances. For example with independent generation, if F^– is not available in closed form, it may be more efficient to use an acceptance-rejection method, which is analogous to thinning, instead of inversion. See Robert and Casella⁸ and L’Ecuyer⁹ for more information on random number generation.

The simulation methods presented herein are easy to implement in a variety of software environments. An implementation will also be available in a forthcoming release of HiFIDE¹⁰, which is a software tool for evaluating detection algorithms.

The extent to which these simulation models can mimic sophisticated disease-specific models of outbreaks or explain real outbreak data remains to be determined and is a subject for future work. Another interesting open problem is estimation of the simulation model from real outbreak data. Solutions to this inverse problem would enable simulation of outbreaks based upon one or more real outbreaks, similar to the initial simulation method in HiFIDE¹⁰