An Agent Based Simulation Tool for Scheduling Emergency Department Physicians

Abstract

Emergency department overcrowding is a problem that threatens the public health of communities and compromises the quality of care given to individual patients. The Institute of Medicine recommends that hospitals employ information technology and operations research methods to reduce overcrowding. This paper describes the development of an agent based simulation tool that has been designed to evaluate the impact of various physician staffing configurations on patient waiting times in the emergency department. We evaluate the feasibility of this tool at a single hospital emergency department.

Introduction

In their recent report, Hospital Based Emergency Care: At the Breaking Point, the Institute of Medicine (IOM) reported that from 1993 to 2003 annual patient visits to the emergency department (ED) increased by 26% while the number of EDs decreased by 9 %. These national trends have created an environment in which many overburdened EDs regularly operate beyond their designed capacity. [1,2] Overcrowding in the ED leads to dissatisfaction of both patients and providers, as well as to reductions in the timeliness and quality of care delivered. [3] These shifts in supply and demand make the efficient allocation of ED resources increasingly important. A key recommendation from the IOM report is that hospitals and EDs explore the use of operations research (OR) methods and information technologies to improve patient flow and the timeliness of care. [1] One way in which these OR methods can improve the timeliness of care is by serving as the core logic for decision support tools that help ED clinicians and administrators to optimize their physician resources. Timely access to a physician is critical component of patients’ perceptions of ED service quality and to their overall length of stay. [4,5] ED physicians represent a critical path through which patients must pass and they are often the primary bottlenecks constricting patient flow. Therefore, reductions in “Door-to Doc” times are frequently at the forefront of ED quality improvement initiatives.[4,5] Choosing the optimal staffing configuration for an ED is complicated by the fact that the patient arrivals are inherently unpredictable. However, consistent intra-day and intra-week patterns emerge and significant reductions in patient waiting times can be made if physician staffing appropriately accounts for these patterns. [4]

Background

The IOM has encouraged hospitals to use informatics and OR methods to facilitate patient flow. [1] The OR literature is replete with case studies that describe various modeling and analytical approaches to the physician scheduling problem in a variety of healthcare settings. [6–9] However, we could find little in the informatics literature describing the use of these methods to improve the allocation of human and physical resources in clinical settings. A 2002 special topics issue of the Journal of the American Medical informatics Association focused on the applicability of simulation in medical informatics; however, none of these articles described the utility of simulation models in providing decision support for resource allocation or staffing tasks. [10]

Our review of the OR literature determined that common approaches to solving the physician scheduling problem include queueing theory, linear programming, and simulation. [6–9] Each approach is valid, however in this paper we explore the use of agent based modeling. Agent based simulation is a technique that models a given system as collection of autonomous entities called agents. Each agent is capable of acting independently and is guided by a set of programmed rules. The agent based framework for simulation is advantageous because it facilitates the identification of emergent phenomena and as the individual agents interact the encompassing system’s dynamics can be studied. [11]

Objective

Our objective was to develop an agent based modeling tool based on general ED processes and inputs that could be used to evaluate different ED physician staffing schedules. The modeling tool is particularly useful for evaluating the impact of different ED physician schedules on the time patients wait for their initial physician evaluation. In this paper we present the details relating to the construction of our modeling tool and evaluate whether or not our modeling tool is able to accurately model waiting times at a single ED.

Methods

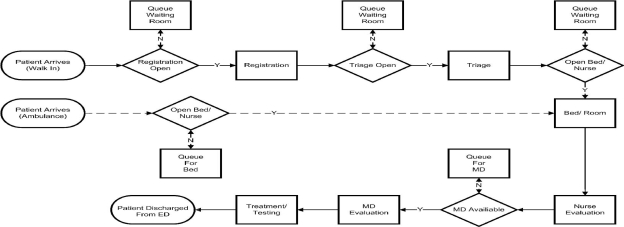
Simulation modeling can be extremely labor intensive and can require a high level of detail in order to accurately represent the system being modeled. However, as a given model becomes more detailed it loses generality and its utility in other similar settings will decrease. [6,7] We desired to develop a tool that would be useful for more than one ED, therefore we chose to use a set of simple process to describe the operations of an ED. Additionally, our model included five classes of agents: patients, physicians, registration units, triage units, and beds. An example of the processes upon which the modeling tool was developed is presented in Figure 1. Our model focus primarily on delays that ensue during the early stages of the patient’s visit and does not account for delays associated with diagnosis and treatment. This is a limitation, but it is also reflective of the scope of the model’s use, i.e., as a tool to evaluate the impact of physician staffing configurations on door-to-doc times.

Figure 1.

Process model for patient agents.

The modeling tool was developed using NetLogo (version 4.0.2), a free for use computer simulation and modeling tool that is well suited for modeling a wide variety of agent based systems. [12] The model is composed of five classes of autonomously functioning agents. In the following paragraphs we will describe how the user interacts with the agents and the encompassing system, as well as describe the rules that guide the behavior of each agent class.

The modeling tool was designed to be useful for EDs of various sizes. To facilitate flexibility the model requires a great deal of input from the user. User input is collected from a set of prerequisite input files and through a graphical user interface (GUI). First, the modeling tool requires six input files that the user must generate prior to the modeling process. The first input is the weekly distribution of patient arrivals. This distribution was approximated by calculating the average count of patient arrivals for each of the 168 hours of the week, and then dividing those averages by the average weekly count of patient arrivals. Patient arrivals follow a heterogeneous Poisson process, where the user supplied arrival distribution represents the expected arrival rate, λ, for each hour of the week. Therefore, interarrival times during a given hour of the week will be exponentially distributed with mean 1/ λ. The second user input file is the number of physicians scheduled to work during each of the 168 hours of the week. The primary intent of the modeling tool is to allow the user to experiment with different physician schedules. The third prerequisite user input file is the weekly registration clerk schedule. The fourth user input file is the weekly schedule for staffing the triage unit(s), and the fifth input file is the acuity distribution for each discharge disposition. This requires the user to supply a file that lists the estimated proportion of patients that are assigned a given triage category for a given discharge disposition. The modeling tool assumes that triage categories are based on the Emergency Severity Index and that a patient’s discharge disposition falls into one of the following categories: discharged, admitted, transferred, left against medical advice, left without treatment, or expired. Since acquiring specific acuity/disposition data may be difficult, default values are provided and the user can proceed without the final input file.

Most of the user’s interaction with the modeling tool will be with the GUI. In its current form, the modeling tool allows the user to alter 18 variables over a range of values. Each variable along with its corresponding definition is listed in Table 1. The GUI allows the user to specify the physical resources available at their ED in the form of the number of beds (the number of triage and registration units is determined from the user’s input files). The user can also specify the average weekly volume at their ED. This can be used to both model current conditions as well as model the effects of increases in patient volume that might be expected in the future. The user can specify the percentage of patients that arrive at the ED via ambulance, the rate of each discharge disposition, and the average service time (defined as the time from placement in an ED bed until the patient leaves the ED) for each discharge disposition type. Along with the average service time for each disposition, the user is asked to provide the average service time for the registration and triage processes. All service times are assumed to be exponentially distributed. The user can also specify the average capacity of physicians at their ED to take on and treat new patients. This is done by specifying the patients per hour variable. Each physician agent is assigned a patients per hour capacity at the beginning of their shift, the value assigned is a random variable from a Poisson distribution with mean equal to the user specified patients per hour. Finally, the user can specify a service standard at which they are interested in determining what portion of patients have had their initial visit with a physician, for instance an ED administrator can determine what percentage of patients have door-to-doc times less than or equal to 30 minutes.

Table 1.

Variables that are configurable using the simulation modeling tool’s graphical user interface

Variable	Site Specific Setting
Number of beds	32
Average weekly patient arrivals	769
% of patients arriving via ambulance	18%
% of patients admitted	21%
% of patients of patients leave without treatment	1%
% of patients transferred	2%
% of patients leave against medical advice	4%
% of patients expired	0.07%
Average registration time	5
Average triage time	6.5
Average service time:
Discharged patients	153
Average service time:
Admitted patients	211
Average service time:
Transferred patients	218
Average service time:
Against Medical Advice patients	139
Average service time:
Expired patients	160
Average Bed Cleaning Time	10.6
Average MD patients per hour	2.1
Service Standard	30

Patients

Each patient agent is assigned three characteristics based on the user’s inputs. The three characteristics are acuity, discharge disposition, and length of service time. Figure 1 presents the process map for patient agents. Patients arrive in one of two ways (walk in or ambulance). Patients who arrive via ambulance skip the registration and triage processes and are placed directly in a bed. If a bed is not available, the patient jumps directly to the front of the ED bed queue. The first point of contact for walk in patients is the registration desk where patients are seen on a first come first serve basis. After the registration process is completed the patients queue for triage on a first come first serve basis. At triage the patient is assigned to a triage category. The patient is assigned to one of five bed queues based on their triage level. The patient queues until they are at the head of their respective queue and all other queues of higher priority are empty. Once in a bed the patient queues for a physician. The queue for a physician is priority based on patient acuity. After the patient is evaluated by a physician their treatment and testing begins, the duration of which is determined by the value assigned to the patient agent at their creation. Once the patient’s service time is complete they are discharged and leave the system.

Physicians

Each physician agent is created at the beginning of their shift and assigned their patients per hour capacity from a Poisson distribution. The patients per hour variable determines how often a physician agent will take on a new patient with the times between patients being randomly assigned from an exponential distribution with a mean value equal to 60 / patient per hour capacity. The programmed rules for the physician agents are simple. If patients are waiting to be evaluated and a physician is available the physician will provide an initial evaluation. Following the initial evaluation the physician is “busy” for a period of time based on their capacity. In real life this time is likely to be spent providing treatment, placing orders, consulting with other clinical staff, reviewing test results, or following up with other patients. This process is repeated until the physician shift is over and they leave the system.

Beds, Registration and Triage Units

Beds can be in one of four states: open, occupied, closed, or being cleaned. Beds rotate through these four states as patient demand and nurse staffing change over the simulation period. Similar to beds, the registration and triage units rotate through a cycle of being either open, occupied, or closed.

Output

In its current form the modeling tool presents the user with several simple outputs via the GUI, additionally several output files are saved to the local directory that can be used to conduct further analysis. The GUI outputs include the mean waiting time for the registration and triage units, the mean door-to-bed and door-to-doc times, as well as the percentage of patients that are seen by the user specified service standard. The output files consist of the raw waiting times. These data files can be used to validate whether or not the modeling tool provides an accurate representation of reality and to estimate how changes to the system are likely to affect patient waiting times.

Evaluation

In order to determine whether our modeling tool is capable of providing accurate estimates of door-to- doc times we chose to evaluate our tool at a single hospital ED. The ED chosen is 32-bed ED located in a 520-bed urban Level 1 Trauma Center. The ED treats approximately 40,000 patients each year and is staffed by a 16 member physician practice group as well as a group of emergency medicine resident physicians. The ED is staffed for 56 hours of attending physician coverage Tuesday trough Thursday and for 60 hours of coverage Friday through Monday. Nurse staffing was closely aligned with historical demand patterns, and ranged from eight nurses in the afternoon and evening hours to three nurses during the early morning hours. Existing staffing configurations provided by the ED administrators as well as estimates of service times obtained from the ED information system were used to provide the required user inputs for the modeling tool, the estimates used are listed in Table 1. We used the modeling tool in conjunction with our site specific parameters and scheduling practices to simulate 10 months, and for comparison purposes we collected patient door to doc times for the first 10 months of 2007. We compared the distribution of our simulated data to the distribution of our observed data via the calculation of descriptive statistics (mean, median, and interquartile range), visual analysis, and by the Wilcoxon rank-sum test, which is a non-parametric test for determining whether two samples of data come from the same underlying distribution.

Results

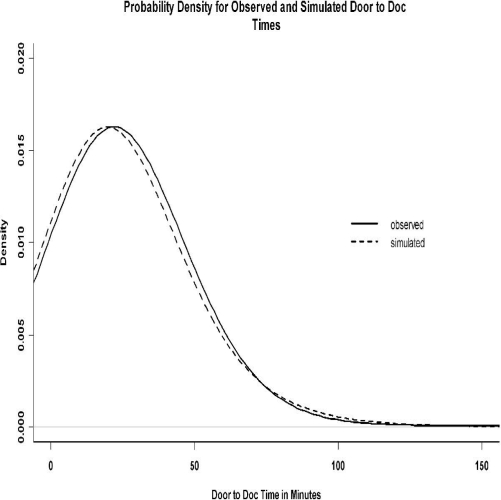
The results of our formal hypothesis indicate that the distributions are slightly different (Wilcoxon rank-sum test, p <0.01). However, Figure 2 indicates that the simulated data closely match the observed data, and the summary statistics confirm a reasonably close match. The interquartile range of the observed door to doc times was 14.05 minutes to 32.38 minutes with mean and median door to doc times of 25.83 minutes and 21.93 minutes, while the same range for the simulated data was 13 minutes to 30 minutes with mean and median times of 24.28 and 20 minutes.

Figure 2.

Distribution for observed and simulated door to doc times

Limitations

Our evaluation is limited in that we used our modeling tool at a single facility. The model also relies on some fairly rigid queuing rules that might not be wholly representative of reality. The evaluation site does not have a “fast-track” or an observation unit, which are two areas that can significantly impact patient flow. It would be important for the modeling tool to be able to account for these types of ED configurations; however in its current form our modeling tool does not. Nor does the modeling tool incorporate nurse and clinical support staffing This is a major limitation of the tool’s usefulness, as nurse and technician staffing account for a large portion of the typical EDs operating budget and have important effects on the quality and efficiency of ED operations. Future iterations of the modeling tool must incorporate the ability to model alternate ED configurations and nurse and technician staffing. Additionally this iteration of the model does not fully take advantage of the agent based framework, i.e., the agent based framework allows for the observation of emergent phenomena that stem from the behavior of the individual agents. Future iterations of the model could also benefit from more fully utilizing the capabilities of the agent based framework. For instance using the agent based framework it would be possible to model physicians decreasing capacity to take on new patients over the duration of their shift.

Conclusion

In this paper we provide a description of an agent based simulation model for evaluating physician staffing configurations in the ED. The tool used simple processes and general inputs that are likely to be accessible at most EDs. We evaluated our modeling tool at a single ED and found that the modeling tool was capable of providing a reasonably accurate representation of patient waiting times. The evaluation of our general tool at specific site offered some interesting insights. The most important being that even though our model did not account for some important site specific characteristics, such as the fact that the ED is located in a Level I trauma center or that it is a teaching facility, we were still able to provide a sufficiently accurate representation of patient waiting times. Suggesting that despite its generality, the tool proposed here can serve as a reliable means for evaluating ED physician staffing configurations. This result is encouraging because the effort and expertise necessary to develop simulation models of individual departments is significant, and if a simple tool can provide a sufficiently accurate representation of reality then much of the duplication of effort and the development of highly specific models that are only suited for an individual site can be replaced by more general and flexible tools that can benefit multiple facilities interested in improving their allocation of staffing resources.