Models for Predicting and Explaining Citation Count of Biomedical Articles

Abstract

The single most important bibliometric criterion for judging the impact of biomedical papers and their authors’ work is the number of citations received which is commonly referred to as “citation count”. This metric however is unavailable until several years after publication time. In the present work, we build computer models that accurately predict citation counts of biomedical publications within a deep horizon of ten years using only predictive information available at publication time. Our experiments show that it is indeed feasible to accurately predict future citation counts with a mixture of content-based and bibliometric features using machine learning methods. The models pave the way for practical prediction of the long-term impact of publication, and their statistical analysis provides greater insight into citation behavior.

Introduction

A commonly accepted metric for evaluating the impact and quality of an article is the citation count which is the number of citations received by this article within a pre-specified time horizon [1]. The main limitation of citation count is its unavailability before this horizon expires (typically several years after publication). This delay renders citation counts primarily useful for historical assessment of the scientific contribution and impact of papers. Another limitation of citation count is that it is a subjective measure [1].

Automatic prediction of citation counts would provide a powerful new method for evaluating articles while alleviating many difficulties associated with the explosive growth of the biomedical literature. Faster identification of promising articles could accelerate research and dissemination of new knowledge. Accurate models for citation count prediction would also improve our understanding of the factors that influence citations.

Predicting and understanding article citation counts is however a very hard problem both on theoretical grounds and on the basis of several decades of related empirical work. In fact, the bulk of the literature concerning citation counts relates to understanding the motivating factors for article citations rather than predicting them. For an excellent survey, see [1].

From a theoretical point of view, it has been found that citation prediction is difficult because of the nature and dynamics of citations [2, 3]. Citations are a noisy, indirect quality measure, and accumulation rates vary unpredictably between articles. Breakthrough papers can stop receiving citations after review articles replace them or the subject matter becomes common knowledge [2]. Predictions based on current data assume that citation behavior will not change in the future, and this assumption may be violated in fast-paced research fields such as biomedicine. Another difficulty in making accurate predictions is the sparseness of a citation network [3]. Fitting a reliable statistical model is difficult since the number of links is small compared to the number of nodes, and negative cases (i.e., non-connected nodes) grow much more rapidly than positive cases (i.e., connected nodes) [4].

From an empirical perspective, previous research has predicted long-term citation counts based on citations accumulated shortly after publication. In the Knowledge Discovery and Data Mining Cup competition of 2003 [5], research groups predicted the evolution of the number of citations received by a set of 441 well-cited articles in high-energy physics during successive three month periods. In other work, Castillo et al. [6] used linear regression and citation count after 6 months to predict citation count after 30 months. They incorporated author-related information (i.e., the number of previous citations, publications, and coauthors for an author) to improve predictions. The resulting model had a correlation coefficient of 0.81 between the true number of citations received and predicted values for 1500 articles from Citeseer, a database of computer science articles.

A recent report by Lokker [7] is closest to the aims of our work. It presents a regression model to predict citation counts in a time horizon of two years based on information available within three weeks of publication. It uses characteristics of an article that are either structural (e.g., whether it contains a structured abstract) or a result of manual systematic review criteria. This model has modest predictivity and explanatory power (0.76 area under the receiver operating characteristic curve and 60% explained variation).

In our work, we hypothesize that we can achieve much greater predictivity and a deeper prediction horizon (ten years instead of two) compared to prior efforts by including in the model the full content terms of the MEDLINE abstract and MeSH keywords as well as bibliometric information about the authors, journals, and institutions. Furthermore, we only use information available at publication time. As a corollary to the above model-building effort, we also study factors that correlate strongly and potentially determine the chances of an article being cited by many subsequent articles.

Methods

Predictive Features and Response Variables

Table 1 lists the input features used to construct a learning corpus for predictive modeling. The number of articles or citations for first and last authors was counted for 10 years prior to publication. Publication type indicates if a paper was identified as an article or review by the bibliometric database which was the Web of Science (WOS) of the Institute of Scientific Information (ISI) [8]. The Academic Ranking of World Universities (ARWU) [9] was used as the measure of quality for first author’s institution. Number of institutions refers to unique home institutions for all authors. All other variables are self-explanatory.

Table 1.

List of features included in each learning model

Feature	Complete model	Content model	Biblio. model	I.F. model
Article title	x	x
Article abstract	x	x
MeSH terms	x	x
Number of articles for first author	x		x
Number of citations for first author	x		x
Number of articles for last author	x		x
Number of citations for last author	x		x
Publication type	x		x
Number of authors	x		x
Number of institutions	x		x
Journal impact factor	x		x	x
Quality of first author’s institution	x		x

The response variable is defined by a set of citation thresholds to determine if an article is labeled positive or negative. For a given threshold, a positive label means that an article received at least that number of citations within 10 years of publication. Thresholds were chosen (before analysis) to be 20, 50, 100, and 500 citations. In the space of topics covered by the corpus (see next subsection), papers with at least 20, 50, 100, and 500 citations within 10 years can be interpreted to be at least: mildly influential, relatively influential, influential, and extremely influential respectively.

Predictions were made for a binary response variable rather than a continuous one in the present analysis primarily because error metrics for discrete values are easier to interpret than continuous ones. Continuous loss functions such as mean square error or percent variation explained are more difficult to interpret in terms of practical significance.

Corpus Construction

We built a corpus for model training and evaluation by specifying a set of topics, journals, and dates. Eight topics were chosen from internal medicine as defined by the MeSH vocabulary: Cardiology, Endocrinology, Gastroenterology, Hematology, Medical Oncology, Nephrology, Pulmonary Disease, and Rheumatology. An article was operationally considered relevant to a topic if its MEDLINE record contained one of the eight MeSH terms, a related topic from the “See Also” field of the MeSH record, or a term from a sub-tree of one of these terms (http://www.nlm.nih.gov/mesh/). For example, an article was Cardiology-related if it contained the MeSH heading “Cardiology”, a related term like “Cardiovascular Diseases”, or a term from a sub-tree.

Articles were included from six journals: American Journal of Medicine, Annals of Internal Medicine, British Medical Journal, Journal of the American Medical Association, Lancet, and New England Journal of Medicine. The journals were selected to include popular journals with a broad range of impact factors. The corpus contained articles published between 1991 and 1994 to allow collection of citation data for a 10 year period after publication of the most recent articles. The window length was chosen so that citation rates would have sufficient time to become relatively stable.

PubMed was queried for all desired articles, and additional information was downloaded from the bibliometric database, the ISI Web of Science (WOS) [8]. Documents were excluded if bibliometric data was unavailable, and the final corpus contained 3788 documents. The complete model consisted of 20005 total features, and information was downloaded in May 2007. Positive-to-negative class ratios for each threshold were as follows: 2705/1083 for threshold 20, 1858/1930 for threshold 50, 1136/2652 for threshold 100, and 100/3688 for threshold 500 citations.

Document Representation

Articles were formatted for learning by text preprocessing and term weighting. The title, abstract, and MeSH terms were extracted from MEDLINE records. PubMed stop words (http://www.ncbi.nlm.nih.gov/books/bv.fcgi?rid=helppubmed.table.pubmedhelp.T43) were removed from the title and abstract. Multiple forms of the same word were eliminated with the Porter stemming algorithm [10] to reduce the dimensionality of the input space. Terms were weighted using log frequency with redundancy which considers term frequency in a document and the corpus [11, 12]. Each weight was a value between 0 and 1. In the end, the corpus was represented as a matrix where rows corresponded to documents and columns represented terms. Bibliometric features were also scaled linearly between 0 and 1.

Learning Method

Support vector machine (SVM) models were used as the learning algorithm. They are a supervised learning method where a kernel function maps the input space to a higher-dimensional feature space, and a hyperplane is calculated to separate the classes of data. The optimal hyperplane is the solution to a constrained quadratic optimization problem. SVM models are usually sparse since the solution depends on the support vectors or points closest to the hyperplane [13]. SVMs are well suited for representing text which typically involves high-dimensional data. Prior research has demonstrated that they perform well in categorizing text and identifying high-quality articles [11, 12].

Model Selection and Error Estimation

We performed 5-fold nested cross validation and optimized parameters for cost and degree in the inner loop while the outer loop produced an unbiased estimate of model predictivity. The set of costs was [.1, .2, .4, .7, .9, 1, 5, 10, 20], and the set of degrees was [1, 2, 3, 4, 5, 8]. Performance was measured by area under the receiver operating characteristic curve (AUC). AUC was chosen instead of accuracy since AUC is not dependent on the ratio of positive and negative cases. Recall that an AUC of 0.5 describes a random classifier, AUC of ~.75 a mediocre classifier, AUC of ~0.85 a very good classifier, and AUC > 0.9 an excellent classifier (while an AUC of 1 denotes perfect classification).

Analysis of Influential Features

After fitting the complete models (i.e., with all features) and estimating their performance, we identified the most influential features using two types of analysis. First, we trained three reduced-feature models for each threshold based only on the content, bibliometric data, or impact factor. Table 1 shows the features included in each model. Performance of these models revealed whether one type of feature was more important than the others.

A second feature-specific analysis was performed as follows: we reduced the total number of features by selecting only features in the Markov Blanket of the response variable (i.e., number of citations received). The Markov Blanket is the smallest set of features conditioned on which all remaining features are independent of the response variable. Thus it excludes both irrelevant and redundant variables without compromising predictivity, and it provably results in maximum variable compression under broad distributional assumptions [14]. The specific algorithm used was semi-interleaved HITON-PC without symmetry correction which is an instance of the Generalized Local Learning class of algorithms [14]. Before proceeding, we verified that the reduced feature set indeed predicts citation counts as well as the original model. After this variable selection and verification step, logistic regression analysis was employed to estimate for each feature the magnitude of its effect and statistical significance on predicting citation counts while controlling for all other features in the LR model. Notice that the raw SVM weights, or Recursive Feature Elimination (RFE) weights in the polynomial SVM case, cannot be used for the same purpose. SVMs do not control for the effect of all other variables on the weight of each feature in the SVM model contrary to logistic regression. Instead SVMs “spread” weights to otherwise conditionally independent features in order to implicitly model a smoother decision function.

Implementation Details

Corpus construction and feature weighting were implemented in custom Python scripts. For text-based features, the scripts constructed PubMed queries, retrieved desired articles, downloaded MEDLINE records, and preprocessed text. For bibliometric features, the WOS database was queried with the title, author, and journal of each article. If a match was found, a user session was simulated by navigating through the website and extracting desired information about the document and authors.

The remainder of the code was written in MATLAB. LIBSVM was used to train SVM models, and it included a MATLAB interface [15]. Scripts were written to perform cross-validation and estimate performance. A custom MATLAB implementation for HITON was used as well as the logistic regression implementation of the MATLAB statistics toolbox.

Results

Overall Predictivity

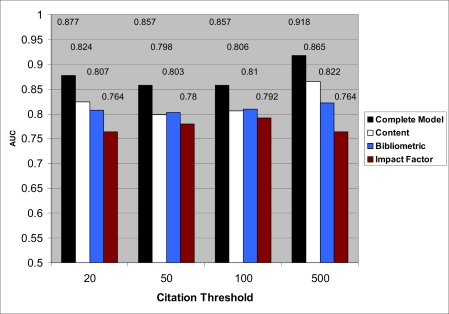
Figure 1 shows the performance of four different types of models: the complete model with all features, models with only content features, models with only bibliometric features, and models with only the impact factor. The complete model accurately predicted whether a publication received a given number of citations for each citation threshold. AUC values range from 0.857 to 0.918 depending on threshold.

Figure 1.

Performance for models based on all features, content, bibliometric features, and impact factor

Testing for Overfitting

In response to the unexpectedly high level of achieved predictivity, we performed an additional analysis to verify that the results were generalizable (i.e., not overfitted). The analysis borrowed from state-of-the-art analysis of high-throughput data by randomly reshuffling citation counts followed and rebuilding all models on the reshuffled data [16] exactly as was done for non-shuffled data. This procedure yielded AUC estimates of 0.5 since reshuffling eliminated the predictive association of the features to the outcome. This result verified that our original analysis was not overfitted.

Predictivity by Feature Type

After establishing that model performance was not due to overfitted analysis, we focused our attention on estimating predictivity when learning was performed on subsets of the features. As shown in Figure 1, the consistent trend in all thresholds was: AUC(complete model) ≥ AUC(content only features) ≥ AUC(bibliometric only features) ≥ AUC(impact factor only). The impact factor model had the lowest predictivity for all thresholds. This predictivity was much lower than that of the complete model (differences in AUCs range from 0.065 to 0.154). The results in Figure 1 also show that both content and bibliometric features had individually high predictivity. AUC was maximized only when combining all types of predictive features.

Analysis of Individual Features

As explained in the methods section, Markov Blanket induction was used to select only non-redundant and relevant features, and logistic regression was used to estimate feature importance and statistical significance of the selected features. The original set of 20,005 features was reduced to 169, 125, 132, and 138 features for thresholds 20, 50, 100, and 500 respectively. Table 2 shows the top 10 ranked features according to absolute values of regression coefficients for citation thresholds 50 and 100. A full-length journal version of the present work will provide the full results.

Table 2.

Top 10 features sorted by absolute value of regression coefficients for thresholds of 50 (left) and 100 (right) citations.

Feature	Reg. Coeff	P-value	Std. Error
splenectomi	−3.406	0.006	1.243
Journal Impact Factor [WOS]	3.342	0.000	0.164
Last Author Citations [WOS]	3.147	0.001	0.914
ciprofloxacin	−2.858	0.019	1.223
Anemia, Sickle Cell [MeSH]	−2.760	0.000	0.681
Rural Health [MeSH]	−2.668	0.015	1.097
brain	2.574	0.000	0.635
history [MeSH]	−2.442	0.046	1.227
Zidovudine:therap. use[MeSH]	2.424	0.030	1.114
Death, Sudden [MeSH]	−2.329	0.014	0.948
First Author Citations [WOS]	5.753	0.000	1.469
Smoking:mortality [MeSH]	4.224	0.018	1.785
offset	3.347	0.007	1.232
Journal Impact Factor [WOS]	3.320	0.000	0.180
Last Author Citations [WOS]	3.023	0.001	0.872
Birth Weight [MeSH]	2.954	0.000	0.770
Pilot Projects [MeSH]	−2.912	0.013	1.173
Autoantibodies:blood [MeSH]	2.783	0.001	0.810
Family Practice [MeSH]	−2.746	0.016	1.140
person [Title]	2.576	0.002	0.828

Recall that a positive unit change in a regression coefficient β for a feature corresponds to e^β increase in the odds of exceeding the citation count threshold for which the model is built. For example, “First Author Citations” had the largest coefficient of 5.753 for citation threshold 100. This value indicates that an article with the greatest number of first author citations was about 315 times (e ^5.753 ≈ 315) more likely to receive 100 citations than an article with no first author citations (notice that a one-unit change for interval-based features corresponds to a difference between the largest and smallest values since interval variables were scaled in the [0,1] range).

The feature-specific analysis points to several important conclusions: (a) certain “hot” topics were associated with high citation rates (e.g., smoking:mortality [MeSH] was 68 times more likely to exceed 100 citations when controlling for other factors); (b) other topics or types of practice indicated smaller citation probability (e.g., splenectomi* and family practice were about 33 and 17 times less likely to receive 50 and 100 citations); (c) citation history of first and last author played a significant role in citation rates by increasing the chances of exceeding 100 and 50 citations by 315 and 23 times when comparing the best and worst citation histories; (d) For each threshold, different sets of content features were selected (and ranked differently in the top positions) which indicates that the importance of content changed for different levels of citation impact. On the other hand, bibliometric features and impact factor were predictive and always had large positive effects for all thresholds studied.

Discussion

Our experiments show that article citations can be predicted accurately for several distinct levels of citation performance even in a deep time horizon and with information strictly available at publication time.

In constructing the corpus, we hypothesized that information about the publication history of first and last author as well as the home institution of the first author would be highly predictive for citation counts. Furthermore, another reason why these analyses were successful compared to previous approaches is that newer developments in classifier technology allowed the routine use of all content terms in article titles, abstracts, and MeSH terms without adversely affecting predictivity with this high dimensionality. It is important to note that the use of content terms limits our method to journals indexed by PubMed.

Our modeling is very different from that of Lokker [7] both in design and results. Specifically, we attempted and achieved a prediction that spans a longer time horizon. We started with a very large predictive feature space and utilized machine learning and feature selection algorithms to identify predictive patterns while narrowing down the required features. Our starting features differed substantially since we relied on content and bibliometric information whereas [7] used article-specific structural and systematic review criteria. The models produced in this work achieved predictivity that exceeded the predictivity of [7] by about 0.10 to 0.16 AUC depending on the model. Notably, the reported predictivity of the model in [7] of AUC 0.76 should be no better (as evidenced in our experiments with different feature sets) than a single relatively weak variable: the impact factor, which was not used in their models. Note that one cannot conclusively compare results for the two studies because of the differences in chosen journals and time horizons. Because the two studies were independently conducted during roughly the same period,¹ we did not have access to the set of features chosen or the corpus used in the study of [7] in order to perform a head-to-head comparison with the methods herein. This is clearly an area of interesting future research.

In conclusion, the results of the present work pave the way for practical models to predict future citations without requiring citations to slowly build over time. Such models have the potential to render citation counts a more practical tool for evaluating long-term impact of recent work and their authors instead of waiting for years as is current practice. Avoiding excessive reliance on less accurate heuristics such as impact factor is another advantage. Finally, analysis of the relative importance of various input variables for citation counts suggests that several factors may causatively influence or even bias citation practices, and this is an important direction for our future work.