Effect of cholesterol on the structure of a phospholipid bilayer

Abstract

Cholesterol plays an important role in regulating the properties of phospholipid membranes. To obtain a detailed understanding of the lipid–cholesterol interactions, we have developed a mesoscopic water–lipid–cholesterol model. In this model, we take into account the hydrophobic–hydrophilic interactions and the structure of the molecules. We compute the phase diagram of dimyristoylphosphatidylcholine–cholesterol by using dissipative particle dynamics and show that our model predicts many of the different phases that have been observed experimentally. In quantitative agreement with experimental data our model also shows the condensation effect; upon the addition of cholesterol, the area per lipid decreases more than one would expect from ideal mixing. Our calculations show that this effect is maximal close to the main-phase transition temperature, the lowest temperature for which the membrane is in the liquid phase, and is directly related to the increase of this main-phase transition temperature upon addition of cholesterol. We demonstrate that no condensation is observed if we slightly change the structure of the cholesterol molecule by adding an extra hydrophilic head group or if we decrease the size of the hydrophobic part of cholesterol.

In this article we address a seemingly simple thermodynamic question: how does the area per molecule of a phospholipid membrane change if we add cholesterol? This question was first posed by Leathes (1) in 1925 and is still being discussed today. The significance of this question relates directly to the importance of cholesterol for the functioning of membranes of higher eukaryotes. For example, cholesterol regulates the fluidity of the membrane and modulates the function of membrane proteins (2). Understanding these mechanisms has motivated many researchers to investigate the lipid–cholesterol interactions in detail. Because a membrane can be seen as a 2D liquid, a first estimate of how the area per molecule would change upon the addition of cholesterol would be to assume ideal mixing, where the area per molecule is simply a weighted average of the pure-components areas. In 1925 Leathes showed that, instead of ideal mixing, one observes a striking nonideal behavior (1). This nonideal behavior is called the condensing effect (3) because the area per molecule is much lower compared with ideal mixing. Because a membrane behaves as an incompressible fluid, a decrease of the area per molecule will result in a corresponding significant increase of the total thickness of the bilayer. Such an increase of the thickness signals a reorganization of the structure of the membrane. Because changes in the structure of the membrane may have important consequences for the functioning of proteins (2), it is important to have a better molecular understanding of the cholesterol-induced changes.

Different conceptual models have been proposed to explain the nonideal cholesterol–lipid interactions. Examples include the condensed-complexes model (4, 5), the superlattice model (6), and the umbrella model (7). The condensed-complexes model explains the condensation effect by assuming that cholesterol induces the reversible formation of a stoichiometric cholesterol–lipid complex. In such a complex the membrane is condensed as the lipid acyl chains are more ordered. At a given cholesterol concentration, an equilibrium composition exists between these condensed cholesterol–lipid complexes and ordinary lipids. The superlattice model assumes that at critical concentrations the cholesterol molecules exhibit a specific long-ranged order. The umbrella model takes the point of view that the hydrophilic part of cholesterol is too small and therefore the lipids need to contribute to the screening of the cholesterol molecules from hydrophobic interactions with water. The phospholipids can only create this umbrella if these molecules straighten to make space for cholesterol. In these models the underlying mechanisms leading to condensing are very different. Interestingly, a recent experimental study concluded that their data supported the condensed-complexes model (8), whereas another set of experiments did not find any indication of the condensed complexes and supported the umbrella model (9). These differences in insights motivated us to develop a mesoscopic model of a lipid–cholesterol–water system. We used molecular simulations to shed some light on the lateral organization of cholesterol in lipid membranes and the underlying lipid–cholesterol interactions that induce the condensation effect.

Several molecular simulations of all-atom and coarse-grained models of cholesterol in lipid bilayers have been reported in the literature (for some recent examples, see refs. 10–13 and references therein). Ideally, one would like to use all-atom simulations to study the condensing effect over a large range of temperatures and compositions. At present, however, these simulations are too time-consuming. Therefore, we use a coarse-grained model, in which efficiency is gained by integrating out some of the details of an all-atom model. Our model is based on the model of Kranenburg and coworkers (14, 15). The model uses explicit water molecules. Lipids and cholesterol consist of hydrophilic and hydrophobic particles (see Fig. 1). This model lumps groups of atoms into one mesoscopic pseudoatom. The intramolecular interactions include bond vibrations and bond bending of which the parameters have been optimized to mimic the structure of a single all-atom phosphatidylcholine molecule in water. The hydrophilic and hydrophobic interactions are described with soft-repulsive interactions, and the parameters of these interactions are related to the solubility parameters by using the method described by Groot and Rabone (16). The idea of this model is that the main driving forces of cholesterol–phospholipid mixing are the hydrophobic and the hydrophilic interactions, which is the conclusion of many experimental studies (7, 9, 17). In our model, the unit of length is directly related to the effective size of a pseudoatom, i.e., one pseudoatom occupies a volume of 90 ų. The unit of energy follows from the matching of the soft-repulsion parameters of the mesoscopic water particles to the compressibility of water at ambient conditions. The simplicity of the models requires a reparameterization of these soft repulsions if the temperature is changed. However, in this work, we assume the parameters to be independent of temperature. The temperature scale is set by fitting to the experimental-phase transition temperatures. Further details and applications of this model can be found in ref. 18.

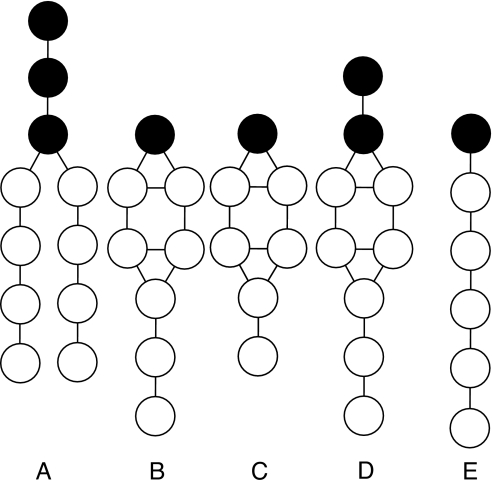
Fig. 1.

Schematic drawing of the mesoscopic models that are studied in this work. (A and B) Figure represents DMPC (A) and cholesterol (B). The model contains hydrophobic (white) and hydrophilic (black) beads that are connected with springs and bond-bending potentials. The model contains explicit water molecules that are modeled as hydrophilic beads. To study the effect of change in the chemical structure of cholesterol we introduce three “new” molecules in which we change the hydrophobic–hydrophilic balance of cholesterol. (C) Cholesterol with a shorter tail length. (D) Cholesterol that is more hydrophilic. (E) Cholesterol that is less hydrophobic.

Our model of cholesterol, shown in Fig. 1B, is based on the same assumptions about the effective size and interactions as the lipid model. Following McMullen et al. (19), we made the hydrophobic part of the cholesterol model slightly longer than the hydrophobic part of the lipid model, which aims to represent dimyristoylphosphatidylcholine (DMPC). For simplicity, we have assumed that the hydrophobic and hydrophilic interactions of a cholesterol molecule are similar to those in a lipid. To gain insight into the molecular mechanism of the condensing effect of cholesterol, we have introduced three cholesterol-like molecules in which we perturb the hydrophobic–hydrophilic balance of the molecule: one in which we decrease the hydrophobic tail length (see Fig. 1C), one in which we add an additional hydrophobic group (Fig. 1D), and one in which we replace the ring by a simple chain (Fig. 1E).

Fig. 2 shows the computed temperature composition phase diagram of the water–phospholipid–cholesterol system. The phase boundaries were obtained from a visual inspection of the snapshots and, more quantitatively, from the inflection points of the curves that give the area per lipid, the average hydrophobic thickness of the membrane, and the tail order and tilt parameters. These properties were computed as a function of temperature and cholesterol content.

Fig. 2.

Phase diagram and the structure of the various phases. (Left) Computed-phase diagram as a function of temperature (in degrees centigrade) and cholesterol concentration. The black lines give the phase boundaries. The color coding gives the condensation effect at a given state point, where blue indicates very little condensation and orange a large condensation effect. (Right) Schematic drawing of the various phases. L_α, lipids in the liquid phase; P′_β, ripple phase; L′_β, gel phase with tilted lipid chains; L′_c, gel phase with lipid chains not tilted; L_II, gel phase, similar to L′_c, containing small cholesterol clusters; L_o, liquid-ordered phase. The condensation effect is defined as the difference, in Ų, between A_{M, sim} and A_{M, ideal}.

Let us first focus on the pure-lipid phases, and the effect of cholesterol will be discussed next. For the pure-lipid bilayer, the phase diagram has been calculated by Kranenburg and Smit (14) for a system that is four times smaller. We used the same methodology to locate the phase boundaries as Kranenburg and Smit did (14). Our results are in excellent agreement with this study, which indicates that the finite-size effects are small. For the pure phospholipid, we observe at high temperatures a liquid phase (L_α) in which the tails are disordered. At low temperatures, the tails are ordered and tilted, which defines the gel phase (L′_c). These two phases are separated by the rippled phase (P′_β), in which we observe a microphase separation of domains in which the bilayer is thick and the lipids are ordered and domains in which the bilayer is thin and the lipids disordered. The presence of these three phases indicates that the resulting phase diagram is in very good agreement with the experimental diagram of the pure lipid (20). The temperature scale is set by matching the temperatures of the phase transitions of the gel phase to the ripple phase (T_p) and the ripple phase to the liquid phase (T_m) with the corresponding experimental-phase transition temperatures of pure DMPC. A further comparison with the experimental data is made for the average area per molecule of the bilayer (Fig. 3A), for the bilayer thickness (Fig. 4A), and for the lipid tail order (Fig. 4B). For the area per lipid we obtain 56 Ų per molecule compared with the experimental (21) 60 Ų per molecule. For the bilayer thickness we computed a value of 38.7 Å, which compares well with the experimental value of 36 Å (21), and a similar agreement is obtained for the tail order (see Fig. 4B). To compute the area per molecule for pure cholesterol, we simulated a bilayer of pure cholesterol. We obtained a value of 40.3 Å, which compares very well with the most recent experimental value of 41 Å (22) for a monolayer of cholesterol. Considering the approximations made in our model, the agreement between the experimental and the simulated values is surprisingly good.

Fig. 3.

Area per molecule as a function of the cholesterol concentration for the molecules shown in Fig. 1. Data for cholesterol (A) and for the modified cholesterol (B) molecules shown in Fig. 1 C–E. (A) We compare experimental data of Hung et al. (21) with our simulation results and the ideal mixing estimates. This estimate is given by A_M,mix = (1 − x_c)A_L + x_cA_C, with x_c as the mole fraction of cholesterol. A_L and A_C are the pure-component area per lipid and the area per cholesterol, respectively. The experimental data and simulations were both at T = 30 °C. (B) Effect of changes of the cholesterol hydrophobic–hydrophilic balance; the circles are for cholesterol in which the hydrophilic part is increased, the squares are for cholesterol with a decreased hydrophobic part, and the triangles are for cholesterol with a shorter tail length (see Fig. 1).

Fig. 4.

The relative bilayer thickness (A) and order parameter (B) of the DMPC–cholesterol system as a function of cholesterol concentration. (A) We compare the experimental data of Pan et al. (30) and Hung et al. (21) with the results of our simulation. The relative bilayer thickness swelling is defined as d/d₀, with d the phosphorus-to-phosphorus distance in the electron density profile and d₀ the thickness of the pure bilayer. (B) Experimental data are from Pan et al. (30) and Mills et al. (31). The orientational lipid tail order parameter, S_NMR, is defined as S_NMR = 0.5 〈3 cos θ² − 1〉, where θ is defined as the angle between the orientation of the vector along two beads in the chain and the normal to the bilayer plane, and the average is taken of the ensemble average over all beads. S_X-ray quantifies the average tilt of the chain of the lipids by using the same formula where the angle θ is between the orientation of the vector along the first and the last tail beads and the normal to the bilayer plane. The experimental data and simulations were both at T = 30 °C.

Let us now turn to the effect of cholesterol on the properties of the bilayer. The first question we will address is whether our model can reproduce the condensation effect. Fig. 3A shows the effect of cholesterol on the area per molecule as a function of the cholesterol concentration. Comparison with the experimental data once again shows very good agreement. In this figure we also show the area per molecule assuming ideal mixing. This figure convincingly illustrates the condensation effect; the area per molecule decreases much more than one would expect on the basis of ideal mixing. Other experimental data include the effect of cholesterol on the bilayer swelling (Fig. 4A) and the tail order parameter (Fig. 4B). Both the experimental data and the simulation show that cholesterol increases the thickness of the bilayer and its order. Also for these two properties, our simulation results are in very good agreement with the experimental data. The simulation and experimental data (Figs. 3A and 4 A and B) show that the addition of cholesterol strongly modifies the properties of the lipid bilayer up to ±30 mol% cholesterol. After this, a region is reached where further addition of cholesterol has only a slight effect. At 30 mol% cholesterol, both the area per molecule and the lipid tail order and tilt parameters have values that are typical for the gel phase.

The color coding in Fig. 2 shows the difference between the simulated area per lipid and the value estimated by assuming ideal mixing. We observe that at high and low temperatures, the condensation effect is relatively small. The condensation effect is maximal in a well-defined region in phase space that is located just above the main-phase transition of the pure phospholipid. To understand better the nature of the condensation effect, it is important to understand the effect of adding cholesterol on the phase behavior of the membrane.

Fig. 2 shows the most important features of the phase diagram. The different phases we observed in our simulations have also been observed experimentally, although not always for the specific mixture of DMPC and cholesterol (20, 23, 24). However, the different experimental studies show qualitatively very different phase diagrams, which limits our possibilities to make a detailed comparison. Snapshots of the various phases can be found in Fig. 5.

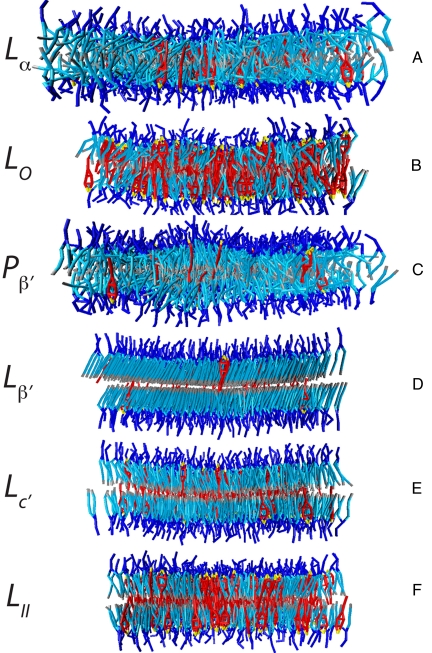
Fig. 5.

Snapshots of a side view of the bilayer. (A) L_α phase for 10% cholesterol at T = 37 °C. (B) L₀ phase for 40% cholesterol at T = 37 °C. (C) Ripple (P′_β) phase for 5% cholesterol at T = 20 °C. (D) L′_β phase for 5% cholesterol at T = 5 °C. (E) L′_c phase for 15% cholesterol at T = 5 °C. (F) L_II phase for 40% cholesterol at T = 5 °C. The hydrophilic and the hydrophobic beads of the phospholipids are depicted in dark blue and in light blue, respectively. The end beads of the lipid tails are depicted in gray. The cholesterol headgroup is depicted in yellow, the cholesterol tetrameric ring and tail beads are depicted in red. For clarity, water beads are not shown. The difference in the width of the bilayers illustrates the condensation effect nicely.

At very high temperatures, the addition of up to 50 mol% cholesterol has little effect on the structure of the membrane, and we observe the L_α phase for all concentrations (24). At temperatures below T_p, we observe that cholesterol changes the structure of the gel phase by inhibiting the tilt of the lipid tails, causing the formation of the L′_c phase (20) (compare Fig. 5 D with E). At higher cholesterol concentrations (>20%), we observe the formation of small, cholesterol-rich clusters. We denote this phase by L_II, and this phase is shown in Fig. 5E. At temperatures between T_p and T_m, the pure bilayer is in the ripple phase, and cholesterol transforms this ripple phase (see Fig. 5C) into a liquid-ordered phase (23) (Fig. 5B). The term liquid-ordered phase was introduced by Ipsen et al. (25). The thickness of the bilayer is intermediate between the thickness of the liquid and the gel phase. The lipid tail-order parameters have values that are close to the gel phase; however, contrary to the gel phase, the lipids are more disordered and do not tilt. Cholesterol gradually increases the temperature at which the L_α to L_o phase transition occurs. At very high cholesterol concentrations, the liquid-ordered phase transforms into a gel phase (L_II) when the temperature is decreased below T_m. This phase has been observed experimentally for dipalmitoylphosphatidylcholine (26), but we have not found experimental data for DMPC at these conditions. Let us now return to the condensation effect. Fig. 2 shows that the condensation effect is maximal at a temperature just above the main transition T_m. The reason is that at these conditions the pure bilayer is in a liquid-disordered state, whereas the addition of cholesterol to the bilayer transforms it into a liquid-ordered phase, which has an area per lipid that is much smaller compared with the liquid-disordered state. This large difference causes a large condensation effect. At higher temperatures, the liquid phase remains stable for all cholesterol concentrations, giving a much smaller condensation effect. At lower temperatures, the pure lipid bilayer has an area per lipid that is much closer to the area per lipid of the liquid-ordered phase, and as a result the condensation effect is far less.

The above results indicate that the condensation effect is a direct consequence of particular changes in the phase behavior that cholesterol is inducing. In the literature there are various speculations about those aspects of the cholesterol structure that are specifically responsible for its condensing effect. For example, the umbrella model is based on the notion that compared with phospholipids, the hydrophilic part of cholesterol is much smaller and needs the phospholipid, as an umbrella, for additional screening from interactions with water. This suggests that an additional hydrophilic group would change the properties completely. Another important factor is the bulky ring structure; if we replace the ring by a tail we obtain a molecule that resembles more an alcohol molecule (27). However, shortening the hydrophobic tail would have little effect. Fig. 1 shows the modified cholesterol molecules that mimic these changes. Indeed, the results in Fig. 3B show that shortening the tail of cholesterol shows the same condensation effect. However, Fig. 3B shows that for both other modifications of the cholesterol molecule, adding an additional hydrophilic group and replacing the ring by a linear chain, no condensing effect is observed. We observe the opposite effect: adding these molecules causes the bilayer to become more expanded compared with ideal mixing. The effect of (smaller) alcohols on the area per molecule has been measured experimentally, and the experimental data also show an increase (28). Closely connected to this, we observed that for both cases in the phase diagram the liquid phase was stable over the entire concentration range. In fact, we observe that adding these molecules decreases the main transition temperature, and hence there is no region in the phase diagram where there is a large condensation effect.

Simulations with these structural variations of cholesterol indicate how surprisingly subtle the mechanism is. The main transition in a pure bilayer is very sensitive to the hydrophobic interactions. The headgroups of the lipids screen the hydrophobic tails from the water. At high temperatures, the area per lipid is high, and this screening is far from optimal; but at these conditions the chain entropy dominates. Decreasing the temperature makes it increasingly important to screen the hydrophobic interactions and at the main transition eventually induces an ordering of the chains. A key aspect is to understand how cholesterol destabilizes the liquid phase. Cholesterol has a smaller hydrophilic head and is therefore less efficient in shielding the hydrophobic interactions. At high temperatures, the lipid bilayer can accommodate this, but at lower temperatures the lipids can only contribute to the screening of the cholesterol by decreasing its area per lipid. This causes the observed ordering and explains why the main transition increases. The two changes we introduced to the cholesterol structure influence its hydrophobic screening; in both variants the intrinsic undershielding of cholesterol disappears. If these molecules are added to the bilayer, there is no need for additional screening of the hydrophobic interactions, and these molecules prevent the formation of an ordered phase.

Let us compare our observations with the previous models that have been introduced to explain the condensation effect. First, our model does not give any indication of long-range ordering as is assumed in the superlattice model. Implicit in both the umbrella model and the condensed complexes is the assumption of some kind of local organization. For example, in the umbrella model it is assumed that one lipid molecule could screen one or two neighboring cholesterol molecules (see e.g., ref. 2). Our simulations show a much more disordered structure in which we cannot identify these ordered structures. At this point it is important to recall that our model contains many assumptions, and this raises the question of whether the conclusions we draw from our simulations are relevant for the experimental systems. We were very surprised to see that we were able to obtain such a rich phase behavior by using a coarse-grained model that uses purely repulsive forces. Our model gives a very reasonable quantitative description of recent experimental data on the structure of the bilayer. The other interesting aspect is that our calculations predict that the condensation effect is maximal in a narrow temperature range above the main transition. It might be possible to verify this experimentally. A very stringent test of our model would have been a detailed comparison with the experimental-phase diagram. In this context, it is encouraging that the phases we have found have been observed experimentally, although not always for exactly the system simulated. By carefully selecting those experimental data that agree with our simulations we could even claim very good agreement. A possible reason for the disagreement between the various experiments is that different techniques are used, and not all techniques are equally sensitive to the differences in the structure of the various phases. We hope that the combination of a phase diagram and detailed information on the structure of the various phases gives some guidelines as to whether a particular experimental technique can identify a particular phase transition.

Materials and Methods

Our mesoscopic model was studied by using dissipative particle dynamics (DPD) (29). The equations of motion were integrated by using a modified version of the velocity Verlet algorithm with a reduced time step 0.03. The main modification of the standard DPD algorithm is a method we have implemented to ensure that the membrane is simulated in a tensionless state. After on average 15 time steps, a Monte Carlo step was made that involved an attempt to change the area of the lipid in such a way that the total volume remained constant. The acceptance rule for this move involves the imposed interfacial tension (15), which was set to zero for our simulations. Further details on the simulation techniques can be found in ref. 15. To ensure sufficient hydration, we used a system of 100,000 water molecules for a total of 4,000 cholesterol and lipid molecules. Cholesterol molecules were added to the system by randomly replacing a lipid molecule by a cholesterol molecule in such a way that the concentration of cholesterol molecules remained the same on the two sides of the membrane.