Breakdown of the Debye approximation for the acoustic modes with nanometric wavelengths in glasses

Abstract

On the macroscopic scale, the wavelengths of sound waves in glasses are large enough that the details of the disordered microscopic structure are usually irrelevant, and the medium can be considered as a continuum. On decreasing the wavelength this approximation must of course fail at one point. We show here that this takes place unexpectedly on the mesoscopic scale characteristic of the medium range order of glasses, where it still works well for the corresponding crystalline phases. Specifically, we find that the acoustic excitations with nanometric wavelengths show the clear signature of being strongly scattered, indicating the existence of a cross-over between well-defined acoustic modes for larger wavelengths and ill-defined ones for smaller wavelengths. This cross-over region is accompanied by a softening of the sound velocity that quantitatively accounts for the excess observed in the vibrational density of states of glasses over the Debye level at energies of a few milli-electronvolts. These findings thus highlight the acoustic contribution to the well-known universal low-temperature anomalies found in the specific heat of glasses.

Glasses display a set of universal low-temperature properties (1). In particular, at a temperature of ∼10 K the specific heat is characterized by an excess over the level predicted by the continuum Debye model. This excess, absent in the corresponding crystalline phases, is related to the so-called boson peak, an excess over the Debye level that appears at energies of a few milli-electronvolts in the vibrational density of states. The physical origin of this universal property has been livelily discussed in the literature for many decades; however, an agreed on solution is still lacking. For example, one interpretation supports the idea that the boson peak is produced by soft vibrations that would be present in glasses in addition to the acoustic ones (2–4). Another interpretation is mainly based on models for the vibrational dynamics of glasses in terms of harmonic oscillators with disorder in the force constants: it supports the idea that the boson peak marks the transition between acoustic-like excitations and a disorder-dominated regime for the vibrational spectrum (5–7). Qualitatively similar results appear as well in recently developed theories for the vibrational spectrum of model systems with random spatial variations in the elastic moduli (8). In another interpretation, the boson peak is related to the characteristic vibrations of nanometric clusters (9, 10) that would exist in the glass as a consequence, for example, of a spatially inhomogeneous cohesion and that would hybridize with the acoustic modes (11). The idea of an inhomogeneous elastic response has been recently reconsidered by using a different approach: numerical studies show that the classical elasticity description breaks down in glasses on the mesoscopic length scale (12–14), and the boson peak would appear at the frequency corresponding to this length scale.

One of the main reasons for the proliferation of so many models lies in the experimental difficulties of studying the acoustic excitations of disordered systems in the milli-electronvolts (meV) and sub-meV energy range. A tunnel junction technique allowed measuring the transverse acoustic modes in a thin film of silica glass showing that the acoustic dispersion curve is still perfectly linear up to ∼2 meV (15), an energy, however, that is still lower than the boson peak position in that glass. The more recent development of the inelastic X-ray scattering (IXS) technique has opened access to the wavenumber (q) and energy (E) dependence of the longitudinal acoustic-like modes at higher energy (16). However, the IXS experiments are currently limited to q ≥ 1 nm ⁻¹ with an energy resolution of ∼1 meV: the (q,E) region crucial for studying the boson peak then remains close to the edge of the capabilities of the technique. Early IXS results (16) were suggesting that the longitudinal sound waves in glasses are unaffected across the energy range where the boson peak appears. More recent results (17) have clarified that the acoustic-like excitations actually experience below the boson peak energy position a regime of strong scattering where their broadening increases with energy at least as E⁴. Following the continuous development of the IXS technique (18), we present here data of unprecedented quality that shed light on the high-frequency dynamics of glasses. We show below that a characteristic, unexpected softening appears in the sound velocity corresponding to longitudinal acoustic-like modes with nanometric wavelengths, and that this signature is at the origin of the universal anomalies observed in the specific heat of glasses at low temperatures (1). This softening, which marks the breakdown of the Debye approximation, appears together with the previously mentioned strong scattering regime and corresponds to a cross-over between well-defined acoustic modes at wavelengths larger than a few nanometers and ill-defined ones at wavelengths smaller than that.

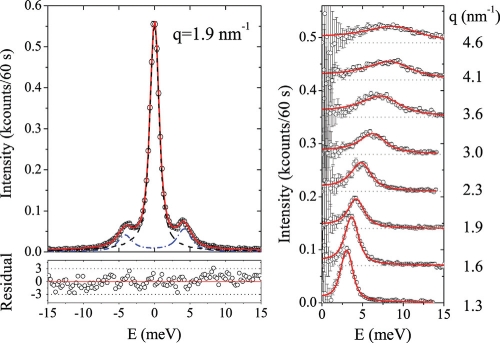
Specifically, we report IXS measurements on a glycerol glass at the temperature of T = 150.1 K, the glass transition temperature being T_g = 189 K (19). In Fig. 1 Upper Left a representative spectrum is reported. It is composed of an elastic peak and a Brillouin doublet. The IXS spectra can be formally expressed as:

where S_L(q,E) is the longitudinal dynamic structure factor; n(E) is the Bose factor, n(E) = (exp(E/(k_BT)) − 1)⁻¹, with k_B the Boltzmann constant; and A(q) is a normalization factor mainly reflecting the q dependence of the atomic form factors. The data have been analyzed using a model for S_L(q,E) that is the sum of a delta function for the elastic component and a damped harmonic oscillator function for the inelastic component (20):

where S(q) is the static structure factor; Ω and 2Γ represent the characteristic energy and broadening (FWHM) of the longitudinal acoustic-like modes, respectively; and f_q is the spectral fraction of elastic scattering. This model describes the measured spectra very well, as shown in Fig. 1 Lower Left. In Fig. 1 Right the Stokes component (energy-loss side) of the Brillouin doublet is reported at selected q values.

Fig. 1.

Brillouin X-ray scattering spectra of a glycerol glass. (Upper Left) Representative IXS spectrum of glycerol at T = 150.1 K and q = 1.9 nm ⁻¹ (open circles) together with the best fitting lineshape of model Eq. 1 and 2 (full red line). The elastic (dashed black line) and inelastic (dash-dotted blue line) components of the fitting model are also reported after convolution to the instrumental function. (Lower Left) Residual of the fit, in standard deviation units. (Right) The energy loss part of the Brillouin doublet at selected q values (open circles) together with the best fitting lineshape (full red line). These spectra have been obtained by subtracting the best fitting elastic component from the measured spectra. The error bars reported on the experimental points take into account the additional contribution due to the subtraction procedure. The spectra are vertically shifted by multiples of 70 counts per 60 s.

The q dependence of the characteristic energy of the Brillouin peaks is shown in Inset Fig. 2A. An inspection of these data confirms some results already reported (16). (i) The Brillouin peaks shift toward higher energy on increasing q. (ii) The acoustic dispersion curve at low q tends to the macroscopic limit set by the longitudinal speed of sound measured by using low-frequency techniques, whereas on increasing q it bends as usually found in crystals. A closer inspection of the dispersion data can be obtained looking at the apparent longitudinal phase velocity, v_L(q) = Ω(q)/(ℏq), as reported in Fig. 2A. There, the data derived from the present experiment are compared with those obtained by using lower-frequency techniques (21–23). We observe that the sound velocity measured in the present experiment does not reach the corresponding macroscopic value, not even at the lowest probed q value of ∼1 nm ⁻¹. Moreover, it shows a rapid decrease with q (softening) down to ∼2.2 nm ⁻¹, and then a plateau up to ∼4.5 nm ⁻¹. Only above this q value we start to observe the expected crystal-like decrease of the sound velocity caused by the bending of the dispersion curve on approaching the first sharp diffraction peak. In other words, the macroscopic Debye limit breaks down not continuously, on approaching the microscopic scale, as it takes place in crystals and as it was considered to be the case in glasses as well (16); it is signaled by a sudden decrease of the sound velocity on the mesoscopic scale of a few nanometers, and it is then related to the medium range order of the glass.

Fig. 2.

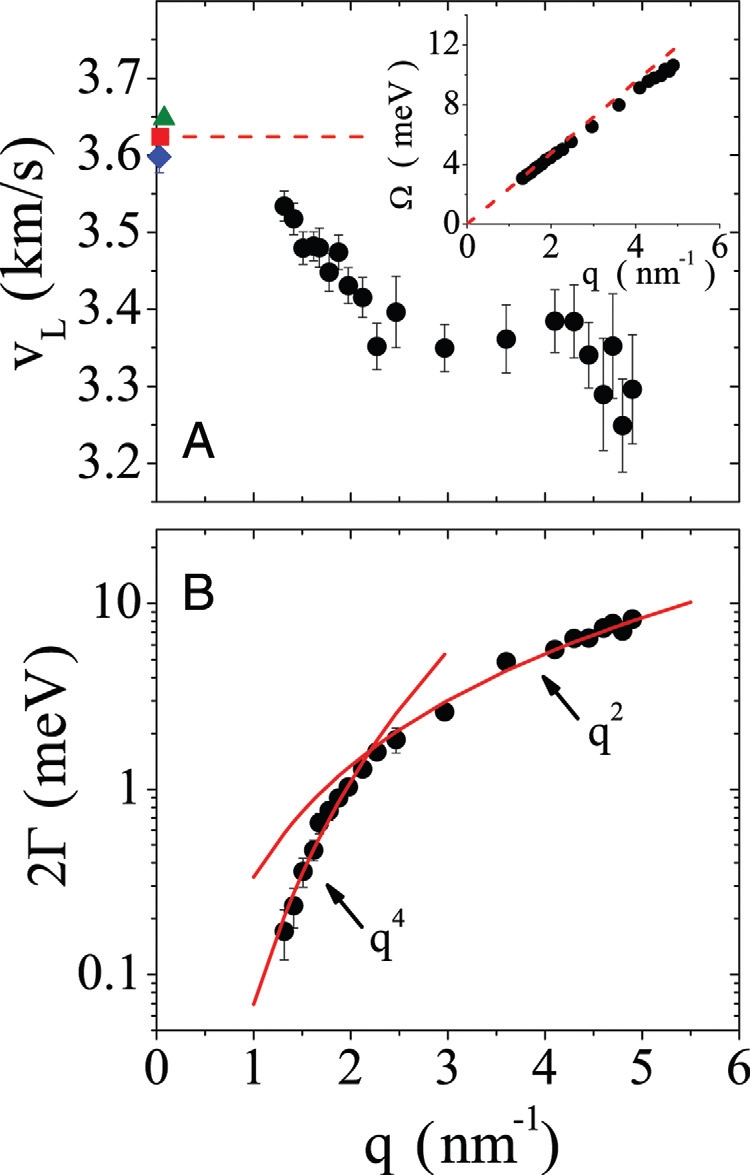
Breakdown of the Debye approximation for the acoustic modes with nanometric wavelengths. (A) q dependence of the apparent longitudinal phase velocity of a glycerol glass at 150.1 K derived from the present IXS experiment (black circles) and from lower-frequency techniques: stimulated Brillouin gain spectroscopy (blue rhomb, from ref. 22), Brillouin light scattering (red square, from ref. 21), and inelastic ultraviolet scattering (green triangle, from ref. 23). The dashed line indicates the macroscopic sound limit from Brillouin light scattering results (21). (Inset) The low q portion of the acoustic-like dispersion curve (black circles). The dashed line corresponds to that in the main image. (B) q dependence of the broadening (FWHM) of the Brillouin peaks derived from the present IXS experiment (black circles). The red lines correspond to the best q⁴ and q² functions fitting the low and the high q portion of the IXS data, respectively.

Additional information on the nature of the acoustic excitations can be gained looking at the q dependence of the broadening of the Brillouin peaks, as reported in Fig. 2B. We can observe a remarkably steep increase of the broadening with q. In particular, for q ≤ 2.2 nm ⁻¹ this increase can be well described by a q⁴ power law that then turns into a q² behavior for higher q values (red lines in Fig. 2B). These results confirm the phenomenology previously observed in network glasses (17) and extend it to the case of molecular glasses as glycerol. However, the important information to be underlined here is that the q⁴ regime for 2Γ is found in the same energy range where the softening of the acoustic branch appears in Fig. 2A. This implies that this softening comes together with a regime (q⁴) where the acoustic modes are strongly scattered and which marks a cross-over between well-defined plane-wave-like acoustic excitations at larger wavelengths and ill-defined excitations at smaller wavelengths.

The relevance of our findings is immediately clear: the softening of the apparent sound velocity directly implies the existence of acoustic-like excitations in excess with respect to the Debye level on the mesoscopic scale or at energies of a few meVs. This is the energy range where the boson peak appears in glasses. In glycerol, in particular, the boson peak is at ∼4 meV (24) that, using the value for the longitudinal sound velocity (21), corresponds to a q of ∼1.7 nm ⁻¹; this is exactly the range where we observe the softening of the longitudinal sound velocity. Alternatively stated, the softening of the sound velocity adds to the glass soft acoustic-like modes that will certainly contribute to the boson peak. It becomes clear as well that it is then inappropriate to refer to the boson peak as to an excess of states with respect to the Debye level; the reference Debye frame does no longer hold at energies corresponding to the boson peak.

A quantitative comparison between the softening reported here and the boson peak is established in what follows. If we would deal with a harmonic crystal, the density of normal modes could be formally expressed in terms of phonon dispersion curves. In the present case of a glass, things are less simple: q is no longer a good quantum number. At high q, the meaning of dispersion curve in a glass becomes questionable, and the limiting q value up to which it is still possible to talk of acoustic modes remains controversial (25, 26). It is, however, reasonable to use q to count the low-energy modes as far as they are still plane-wave-like, or as far as the Brillouin peaks are still well defined. As a first step, we will use a crystal-like approach in the whole q range covered in Fig. 2, and we will later go beyond this approximation. The acoustic density of states can then be directly related to the acoustic dispersion E(q) ≡ Ω(q) through the relation:

where q_D is the Debye wavevector, and L and T stand for the longitudinal and transverse branch. To obtain the quantities entering Eq. 3, it is preferable to model our data and compute the derivative of this model function instead of using the experimental data directly. Specifically, we use here the following empirical function:

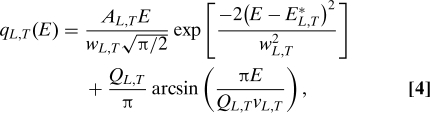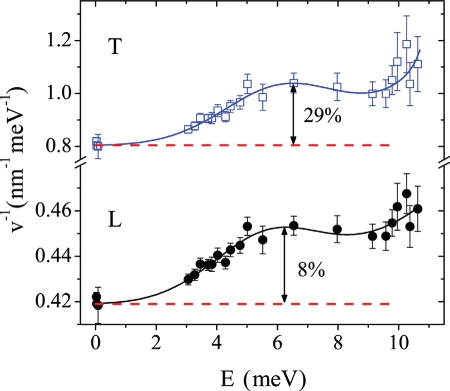
where—for both longitudinal and transverse branches—A, w, E*, and Q have to be considered simply as fitting parameters, and v ≡ v(E = 0) is the macroscopic sound velocity (21, 27). This empirical model is found to describe well our data, as shown in Fig. 3; in particular, the gaussian term of Eq. 4 well accounts for the maximum appearing in the 1/v_L(E) data at ∼6 meV, where the softening of the longitudinal sound velocity is 8% of the corresponding mascroscopic value. Although we have only experimental access to the longitudinal sound excitations, it is clear that the most important contribution to the vibrational density of states comes from the transverse acoustic branch. To estimate that, and based on the results of recent simulation studies (14), we can assume that the softening that we observe on the longitudinal branch is simply the signature of an effect that takes place on the transverse branch. This choice sets the strength of the softening on the transverse branch, and, in particular, attributing completely the effect to the transverse modes, sets it to the maximum possible value compatible with our longitudinal sound data. Moreover, we can assume that the softening on the transverse branch appears at the same energy as on the longitudinal branch, as justified by recent simulation results (28). The preceding assumptions are equivalent to saying that the bulk modulus, B, can be considered as being essentially constant over the considered energy range, so that the transverse sound velocity v_T(E) can be simply calculated as:

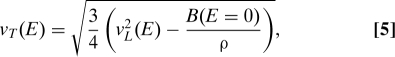where ρ is the mass density from ref. 29 and the bulk modulus B at zero energy is calculated from the known macroscopic longitudinal and transverse velocity values (21, 27). The transverse velocity data obtained in such a way are reported in Fig. 3 together with the best fitting lineshape of model Eq. 4. The calculated data look quite similar to the measured longitudinal ones, and it is then not surprising that the model of Eq. 4 describes them well. The softening that we derive for the transverse excitations at ∼6 meV is 28% of the corresponding macroscopic value, thus—as expected—much larger than that directly measured on the longitudinal branch.

Fig. 3.

Dispersion of the longitudinal and transverse sound velocities. The inverse of the phase velocity, 1/v, is reported for both the longitudinal (L, black circles) and transverse (T, blue squares) acoustic-like branches. The former results are experimental data and correspond to those reported in Fig. 2; the latter results have been derived from the former ones assuming a constant bulk modulus. The dashed lines indicate the corresponding macroscopic values (21, 27). The full lines through the data are the best fitting lineshapes of model Eq. 4.

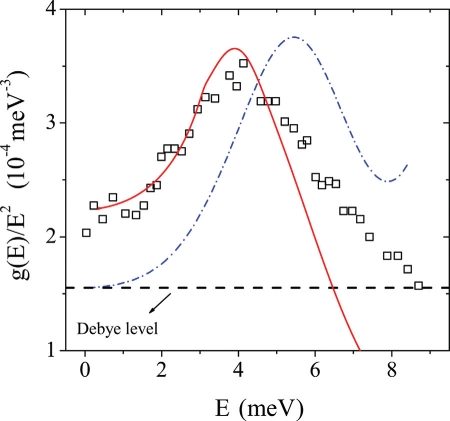
The acoustic contribution to the reduced vibrational density of states through Eq. 3 is reported in Fig. 4 (dash-dotted line) together with inelastic neutron-scattering measurements (squares) on glycerol at T = 170 K (24). It is remarkable to observe that our simple calculation not only predicts the presence of a peak in the reduced density of states, but also does reproduce quantitatively the boson peak intensity. It is clear as well that the boson peak position is overestimated. We now improve on the crystal-like approximation underlying Eq. 3 by explicitly taking into account the fact that the acoustic-like modes that we measured are actually not plane waves but are instead characterized by a finite and strongly varying width. To do that, we make use of the relation (8):

where S_L^I(q,E) is the inelastic part of the longitudinal dynamic structure factor, S_T^I(q,E) is the corresponding transverse function, and M is the molecular mass. To calculate the dynamic structure factors, and consistently with the analysis reported above, we use here the damped harmonic oscillator model of Eq. 2. We parametrize this model using, for the longitudinal polarization, our fit results and, for the transverse one, Brillouin peak position values from Fig. 3 and FWHM values assuming that the transverse and longitudinal excitations broadening are the same at the same energy (6). Moreover, the higher integration limit in Eq. 6 has been fixed here to 7.5 nm ⁻¹, that is, to the highest q value where we could count on reliable fit parameters. The corresponding calculation is reported in Fig. 4 (full red line) and shows a convincing agreement with both the position and the intensity of the boson peak. Only the high-frequency tail is clearly too weak, which might derive from the reduced integration range used to calculate Eq. 6. However, although the assumptions used to perform this calculation (shape of the spectra, integration limit, choice for the transverse broadening) may influence the details of the obtained curve, the main information of Fig. 4 is very robust: the fact of taking into account the broadening of the acoustic-like excitations modifies the result of Eq. 3 by essentially shifting it down toward lower frequencies and leads to a quantitative description of the boson peak. It is clear, but still may be important to underline, that, because the measured vibrational density of states is consistent with the specific heat data (24), the acoustic softening and broadening reported here can then as well account for the well-known anomaly found in the specific heat of glasses in the ∼10 K temperature range.

Fig. 4.

Reduced density of vibrational states of a glass of glycerol. The black squares are experimental data from an inelastic neutron-scattering experiment performed at 170 K (24). The blue dash-dotted line is the prediction of Eq. 3 for the density of acoustic states assuming that the softening observed on the longitudinal branch in Fig. 2 is the result of a phenomenology that directly appears on the transverse branch; it not only shows the presence of an excess over the Debye level (dashed horizontal line) in the reduced density of states, but it accounts as well for the experimental boson peak intensity. However, it overestimates the energy position of this excess with respect to the experimental data. This discrepancy disappears if the broadening of the acoustic-like excitations is taken into account via Eq. 6; in this case, the calculation well reproduces the boson peak both in position and in intensity (full red line).

In conclusion, the data presented here clarify some relevant aspects of the vibrational dynamics of glasses. In particular, our results highlight the central role of the acoustic excitations in any theory or model attempting to describe the low-temperature-specific heat anomalies of glasses. In fact, the acoustic waves are not at all simple spectators here, because the macroscopic Debye continuum model fails at energies roughly corresponding to the boson peak. This failure adds naturally to the system soft states in excess over the Debye level in the meV energy range, i.e., the acoustic modes pile up at low energy to build an excess in the reduced vibrational density of states. In the case of glycerol, we have shown that the softening of the acoustic modes reported here does account quantitatively for the intensity of the boson peak. It is possible as well that additional modes, e.g., optic-like ones, pile up in the same energy range; for example, this seems to be the case of vitreous silica (30). However, the mechanism proposed here is likely to be universal, and, in particular, explains the ubiquitous presence of the boson peak in glasses. The present findings are also probably at the basis of the observation that the boson peak intensity scales with the continuum elastic properties under different experimental conditions (31). Thus, our results on one side give an explanation for the universality of the low-temperature thermal behavior of glasses, and on the other side clarify the reference frame for any further modeling of their high-frequency dynamics. This is clearly relevant because almost all analyses of thermal properties of glasses assume that the Debye approximation is valid, and discuss any unusual behavior simply in terms of the scattering of sound waves.

Materials and Methods

The high-frequency dynamics of glycerol has been investigated by analyzing the scattering vector, q, and energy, E, dependence of the longitudinal dynamic structure factor, S_L(q,E), measured in a high-resolution inlastic X-ray scattering (IXS) experiment carried out at the beamline ID16 of the European Synchrotron Radiation Facility. The monochromatic X-ray beam at the sample position had an energy of 23,725 eV, a spot of 250 × 150 μm² horizontal × vertical sizes, and an intensity of ∼1.2 · 10⁹ photons per second at the 70 mA average current in the storage ring (16-bunch operation). In our IXS experiment energy spectra were measured at several q values between 1 and 11 nm ⁻¹, with special emphasis on q values lower than 5 nm⁻¹. The energy spectra were collected in the −30 to 30 meV energy range with a total integration time of ∼500 s per energy point. The energy resolution was q -independent with a FWHM of 1.4 meV, whereas the q resolution was fixed to 0.37 nm ⁻¹ FWHM. The sample cell was a borosilicate glass tube with two opposite 0.5-mm-thick diamond windows for the incoming and scattered (forward direction) X-ray beam. The length of the cell along the beam path was 20 mm to match the absorption length of glycerol at the working X-ray energy. The glycerol sample (purity 99.5%, purchased from Aldrich) was loaded in the sample cell in an Ar-filled glove box without further purification. A cryostat was then used to cool down the sample through its glass transition temperature T_g = 189 K to the temperature chosen for the experiment T = 150.1 K with a cooling rate of ∼4 K/min. The temperature stability has been ±0.5 K during the whole experiment. The empty cell has been carefully checked to give a negligible contribution to the measured spectra.