Power of deep, all-exon resequencing for discovery of human trait genes

Abstract

The ability to sequence cost-effectively all of the coding regions of a given individual genome is rapidly approaching, with the potential for whole-genome resequencing not far behind. Initiatives are currently underway to phenotype hundreds of thousands of individuals for major human traits. Here, we determine the power for de novo discovery of genes related to human traits by resequencing all human exons in a clinical population. We analyze the potential of the gene discovery strategy that combines multiple rare variants from the same gene and treats genes, rather than individual alleles, as the units for the association test. By using computer simulations based on deep resequencing data for the European population, we show that genes meaningfully affecting a human trait can be identified in an unbiased fashion, although large sample sizes would be required to achieve substantial power.

Whole-genome association studies based on genotyping have recently demonstrated potential for identifying SNPs and haplotypes associated with a range of common clinical phenotypes (1–3). However, only a small fraction of observed phenotypic variation is currently attributable to identified allelic variants. Association studies are fundamentally limited by previously known genetic variation, featuring predominantly high-frequency SNPs. By contrast, deep resequencing has the potential to reveal a vast trove of low-frequency alleles. Low-cost–high-throughput sequencing technologies hold the potential to propel discovery of gene–phenotype associations incorporating low-frequency allelic variation on a large scale.

Although knowledge of all variants segregating in the population would seem to increase the power of genetic analysis, this prospect faces daunting statistical challenges, because an expanding pool of variants requires more stringent multiple testing correction, whereas the power to detect association with low-frequency variants is reduced. This problem may be surmounted by pooling allelic variants in a single candidate gene (4–6) or pathway (7–9). However, if most variation in a gene or pathway is neutral, this pooling strategy will not provide a sufficient signal-to-noise ratio (10). To enrich variation in functionally significant alleles, the analysis should be limited to nonsynonymous coding variation as one obvious functional class. Site-directed mutagenesis and comparative genomics have shown that the large fraction of de novo missense mutations are of functional significance (11–14). Consequently, many mildly deleterious coding variants are expected to be segregating in the human population at low allele frequencies, as was originally proposed by Tomoko Ohta in the “nearly neutral theory” of molecular evolution (15). Indeed, the statistically significant excess of combined rare missense variation in individuals at phenotypic extremes was detected in candidate gene studies for several phenotypes (4–6).

Results

Simulation of Resequencing Studies.

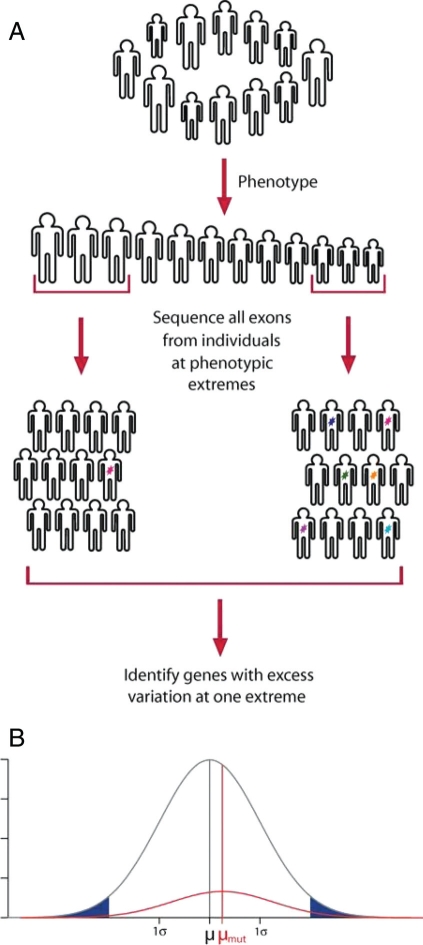
Although success with highly targeted candidate gene resequencing has been reported (4–6), the potential for unbiased discovery of new gene–phenotype associations by resequencing large numbers of genes in large numbers of individuals has not been considered. It is therefore unclear whether clinical populations of realistic size would provide sufficient statistical power for new gene discovery by using this approach. We address these questions through simulation of resequencing studies (Fig. 1A). We focus on quantitative rather than qualitative phenotypes (Fig. 1B). However, our strategy involves comparison of two groups of individuals at phenotypic extremes and, therefore, can be extended to dichotomous traits with specified penetrance. Quantitative traits allow for additional flexibility in selecting most informative individuals. Our simulations make no assumptions about the existence of specific causal variants with specified allele frequencies. Instead, they rely on the influx of new mutations and resulting collective effect of low-frequency hypomorphic alleles.

Fig. 1.

Simulated resequencing study. (A) Design of simulated resequencing study. Color marks represent various new mutations discovered in sequenced individuals. (B) Modeling the effect of mutations effect on phenotype. Distribution of quantitative trait for noncarriers is shown in gray. Distribution of the same quantitative trait for individuals that carry at least one moderately deleterious mutation is shown in red. Observed distribution of QT in the whole population is the sum of these distributions. Individuals from the phenotypic extremes marked by blue are subjects for resequencing.

Assessing the feasibility of identifying human trait genes from “all-exon” sequence data is tantamount to determining the potential for detecting the impact of cumulative variation within an individual gene on a phenotype at a high level of statistical significance (2.5 · 10⁻⁶, equivalent to a level of P < 0.05 following Bonferroni correction for 20,000 genes). We combine multiple rare variants from the same gene and treat genes rather than individual alleles as the units for the association test.

We based our computational model of coding human genetic variation on existing population sequencing data and extrapolated this model to even larger population samples. We analyzed the deepest systematic resequencing dataset currently available, comprising 58 genes (exons plus flanking intronic and intergenic regions) that were resequenced in 757 individuals of European ancestry (8). The present analysis is focused exclusively on individuals of European ancestry because of the lack of deep resequencing data from other populations.

The feasibility of gene mapping by resequencing coding regions depends on mutation rate, population demographic history, selection coefficients, and phenotypic effects associated with new missense mutations. We assumed a mutation rate of 1.8 · 10⁻⁸ per generation (16), and used the conventional four-parametric model of the history of the European population with long-term constant size followed by a bottleneck and then by an exponential expansion (17).

Demographic Model.

To estimate parameters of the demographic model, we computed a likelihood function for the observed site-frequency spectrum of synonymous and noncoding SNPs by using diffusion approximation of the Wright–Fisher model. We used the infinite-number-of-sites model and obtained a time-dependent solution for the population with the variable effective size (18, 19) (see Materials and Methods). We verified this analytical approach using forward simulations [supporting information (SI) Appendix, Fig. S1].

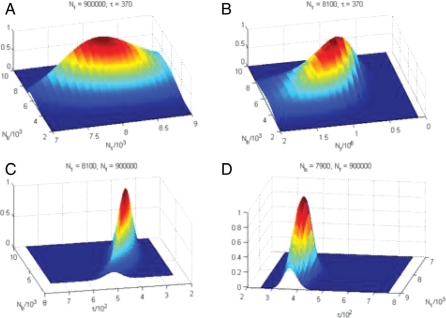
The likelihood has a single well-defined maximum in the space of the four parameters of the model (Fig. 2, SI Appendix, Fig. S3). The largest uncertainty was observed in the bottleneck population size due to sparse data on high-frequency SNPs in the resequencing dataset that we used.

Fig. 2.

Two-dimensional sections of the likelihood surface for the demographic model that was fitted to the systematic resequencing data. Population history model, long-term constant population size is followed by a bottleneck and subsequent exponential population growth. The model has four parameters and limited to the European population: N₁, ancestral population size; Nb, bottleneck population size; N_f, final population size; π, time of the population expansion since the bottleneck.

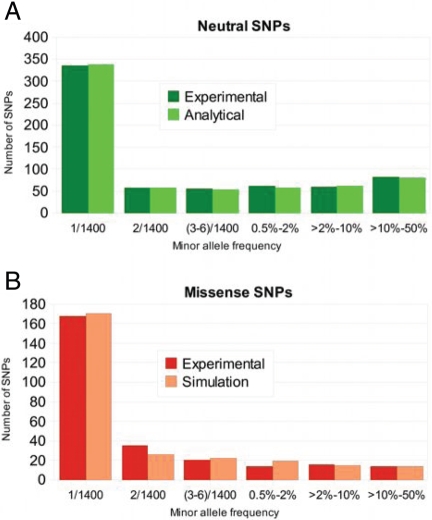
Our demographic model reproduces observed site-frequency spectrum well (Fig. 3A). Under this model, the spectrum of neutral genetic variation in European populations is explained best by population growth that started approximately 7,500–9,000 years ago (average, 20–25 years per generation), coinciding with the spread of agriculture in Europe (20). As expected, our analysis of deep resequencing data resulted in a larger estimate of current effective population size (900,000) compared with demographic models constructed by using smaller population samples (17, 21–25). Explicit modeling of exponential population growth enabled us to extrapolate more accurately and thus simulate outcomes of resequencing projects involving significantly larger numbers of individuals.

Fig. 3.

Agreement of experimental allele frequency spectra with the modeled spectra (A) neutral SNPs and (B) missense SNPs.

The deep resequencing dataset used in our study is not informative about the ancient population bottleneck, a well-known feature of the demographic history of Europeans. This is not surprising because almost all variants in this dataset have low population frequency. According to the demographic model, essentially all rare variants originated by mutations in the recent population growth phase, whereas most frequent SNPs originated by mutations prior to the growth phase (SI Appendix, Fig. S4A).

To ensure that this is not an artifact of our method, we applied it to SeattleSNPs sequencing dataset, which covers as many as 320 genes in as few as 23 individuals of European origin. The inferred population history is in general agreement with previous coalescence-based analyses and reproduces a deep ancient bottleneck (21–25). However, SeattleSNPs dataset is not informative about the recent population growth, i.e., different growth rates have comparable likelihoods. Combined analysis of the two datasets (maximizing the product of the two likelihoods) results in a demographic history, which includes both deep ancient bottleneck and recent growth. This demographic history model generates numbers of rare SNPs highly similar to the model based solely on the deep sequencing dataset (SI Appendix, Fig. S4B). This model also predicts that the overwhelming majority of rare variants originated in the recent population growth phase.

It is likely that modeling the demographic history of Europeans by using datasets rich in both rare and frequent variants would require more complex demographic models. However, because almost all rare variants originated in the population growth phase, the recent history mostly determines results of our study. The parameters of our model corresponding to the recent history were estimated with a high degree of confidence by using the deep resequencing dataset. Therefore, we present here results obtained by using this demographic model.

Distribution of Selection Coefficients.

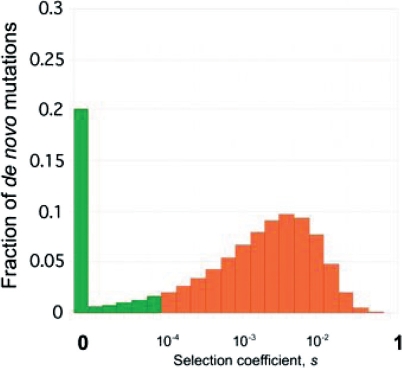
As a next step we added a distribution of selection coefficients for new missense mutations to the model and estimated this distribution from the site-frequency spectrum of nonsynonymous SNPs by using forward simulations. We modeled a distribution of selection coefficients by a gamma distribution with parameters estimated by maximum likelihood. Simulated site-frequency spectrum agrees well with the observed spectrum for nonsynonymous SNPs (Fig. 3B). All suboptimal distributions consistent with the data have the maximum probability mass in the range of selection coefficients between 0.0006 and 0.004 (Fig. 4), which is in good agreement with multiple recent studies (11–14). There is a consensus that the majority of new missense mutations are moderately deleterious both in humans (11–14) and flies (26).

Fig. 4.

Distribution of selection coefficients for de novo missense mutations. Distribution was modeled by gamma distribution and fitted to deep resequencing data by the maximum likelihood method. Mutations with selection coefficient < 10⁻⁴ were assumed to have no effect on quantitative phenotype in our model and are shown in green. Mutations assumed to be functional are shown in orange.

We note that this analysis assumed complete neutrality of synonymous sites. Incorporating weak negative selection acting on synonymous sites would result in slightly higher estimates of selection coefficients for nonsynonymous mutations and in lower estimates of the recent population growth rate.

Simulation of Phenotypic Variation.

To simulate population phenotypic variation, we first simulated nonsynonymous genetic variation in the average human protein coding gene (∼500 aa) by using the estimated demographic history and distribution of selection coefficients. To simulate corresponding quantitative trait (QT) variation, we used a simple model of genotype–phenotype relationship. We assumed that QT is distributed normally and individuals carrying at least one functional nonsynonymous allele have QT values distributed with a shifted mean, but with the same variance (Fig. 1B). In our simulation we subdivided new nonsynonymous mutations into functional (i.e., affecting QT) and nonfunctional classes by using two different approaches. First, we assumed all missense mutations with selection coefficient >10⁻⁴ to be functional. This assumption implies neither that a given mutation is under selection due to its effect on QT of interest, nor that QT of interest is under selection at all. The simple reasoning behind this assumption is that if amino acid change is visible to purifying selection through its effect on at least some traits, it affects protein molecular function.

In addition, to analyze a possibility that the effect of mutations on QT of interest is independent of the integrated strength of natural selection (either direct or pleiotropic), we randomly assigned mutations to functional and nonfunctional classes irrespective of the selection coefficients associated with them.

We further assumed that all functional missense mutations in a given gene bias QT in one direction. This assumption is based on the fact that the vast majority of de novo amino acid mutations with a measurable effect reduce protein activity. Gain-of-function mutations are much less frequent and are restricted to specific residues or domains. Although very important in a number of rare, Mendelian syndromes, gain-of-function mutations do not represent a sizable fraction of human deleterious variation, and thus can be disregarded in our analysis. Loss-of-function mutations in different genes can bias QT in different directions (depending on the molecular function and position in biological networks), but loss-of-function mutations in the same gene should bias QT in the same direction.

The exact distribution of effects of new missense mutations on QTs is unknown, but on average, de novo missense mutation in a gene highly relevant to a given phenotype should have phenotypic effect smaller than new complete loss-of-function mutations but larger than segregating nonsynonymous SNPs.

De novo mutations associated with dominant syndromes caused by haploinsufficiency are known to cause shifts in QT means exceeding one standard deviation (σ). For example, loss-of-function mutations in NSD1 causing Sotos syndrome increase mean occipitofrontal head circumference by >2σ (27); mutations in JAG1 causing Alagille syndrome decrease mean height by 2σ (28); dominant-negative mutations in FBN1 producing Marfan syndrome reduce mean bone mineral density by 1.5σ (29); and LDL receptor mutations causing hypercholesterolemia increase mean LDL-bound cholesterol level by >4σ (30). However, a segregating nonsynonymous SNP A390P in CETP is associated with 0.4σ decrease in plasma HDL-C levels (31). We therefore concentrated on values of 0.25σ and 0.5σ for new missense mutations but also considered a wide range of QT means shifts (SI Appendix, Fig. S5A). In the context of a trait such as human height, 0.25σ would correspond to a change in mean height of 0.5 inch.

Simulation of Resequencing of Individuals from Phenotypic Extremes.

Next, we simulated results of resequencing of individuals with extreme QT values. Simulated individuals were sorted according to their QT values and gene sequence information was extracted for individuals from lower and upper percentiles. Although it is easy to incorporate sequencing errors in the model, in this work we assumed ideal quality of sequence data.

Simulation of Detection of QT Affecting Genes.

Finally, we tested whether lower and upper tails of the trait distribution were significantly (at the genome-wide level) different in the total amount of rare nonsynonymous variants. Current candidate gene-based studies focus on variants observed exclusively in one of the tails. With increasing sample size, this approach will have decreased power because at would ignore variants observed predominantly, albeit not exclusively in one of the extremes (Fig. 5). We used two alternative approaches: one in which only rare variants were analyzed and the other in which information on common variants was also included to further improve power (32).

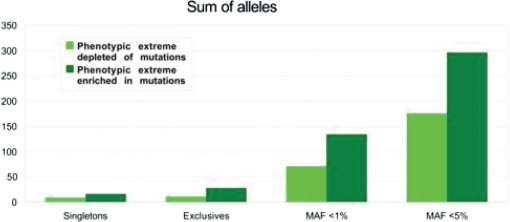
Fig. 5.

Excess of missense variants at one of the phenotypic extremes. Data are shown for simulation of 5,000 individuals sequenced at each of two 5% phenotypic extremes. Sums of the alleles (cumulative frequencies of pooled variants) were averaged over 10,000 simulations. Shift of quantitative trait median in mutation carriers is assumed to be equal to 0.5σ.

In the “rare variants only” approach SNPs with the observed frequency above >5% in either of the two tails were considered to be common and were excluded from further analysis. We then calculated the cumulative frequency of rare variants separately at each phenotypic extreme, by summing counts of rare SNPs. We calculated statistical significance of departure of rare variants distribution between two phenotypic tails from 50%/50% ratio using the χ² test. If the obtained P -value was < 0.05 after Bonferroni correction to 20,000 genes, the association between the gene and the phenotype was counted as identified.

To incorporate information about common alleles we compared contingency table of allele counts between two phenotypic extremes considering all SNPs with minimal observed frequency above >5% independently and the remaining rare SNPs grouped into one category with all allele counts summed. Dissimilarity between distributions of allele counts in the two phenotypic extremes was detected by using χ² test.

Estimation of Number of Required Individuals and Power of Resequencing Studies.

For each set of parameters the simulation described above was run 10,000 times. Power of the test was calculated as the fraction of simulations in which enrichment of rare variants in the proper phenotypic tail was detected. As shown in Table 1, achieving substantial power for individual gene discovery by using this study design would require large population samples. Sequencing of 10,000 individuals (with 5,000 from the upper and 5,000 from the lower fifth percentiles) would require 100,000 phenotyped individuals and would provide 77% and 40% power for genes with the effect of new missense mutations of 0.5σ and 0.25σ, respectively. The power estimates were 78% and 49% for the above parameters, under the model that assumed disassociation between a mutation's effect on phenotype and the strength of purifying selection acting on the mutation.

Table 1.

Estimated power of gene mapping by complete resequencing

Effect of functional mutations (in fractions of standard deviation)	No. of sequenced individuals	No. of phenotyped individuals
		12,500	25,000	50,000	100,000	200,000
0.25σ	5,000	0.11	0.18	0.24
	10,000		0.24	0.31	0.40
	20,000			0.38	0.51	0.59
0.5σ	5,000	0.36	0.47	0.57
	10,000		0.56	0.69	0.77
	20,000			0.76	0.84	0.88

Incorporating frequent variants in addition to rare variants increases the power by 3%. It should be noted, however, that our analysis was focused on the utility of rare, deleterious SNPs in identification of genes affecting human traits. Our simulations do not incorporate balancing selection, selection reversal, antagonistic pleiotropy, or any other evolutionary forces that might lead to high-frequency functional variants. Correspondingly, the real gain of power from analysis of common variants in addition to pooled rare variants might be significantly higher that these estimates.

Sampling of suboptimal demographic histories and distributions of selection coefficients (SI Appendix, Fig. S6 and Table S1) suggests that our power estimates are within the range of 20% to 70%. Dependencies of the power estimates on other model parameters are shown in SI Appendix, Fig. S5.

A much smaller sample size of 1,000 individuals would have >75% power to detect effect sizes of 2σ. If pathways rather than individual genes would be considered as units of the association test, a sample of 1,000 would be sufficient to achieve over >60% power (assuming 20 genes per pathway and effect size of 0.5σ).

Although 100,000 individuals is substantially larger than any currently existing well-phenotyped clinical population, efforts to aggregate populations on this scale are underway and will be greatly facilitated by electronic medical records. Notably, the total number of unique individuals in published systematic retrospective clinical studies currently available for genetic analysis substantially exceeds 100,000. Genome-wide association studies have already been conducted on >15,000 individuals (2). Also, numerous trait genes may in fact be uncovered with far shallower levels of resequencing.

Meta-Analysis of MC4R Gene Resequencing Studies.

To illustrate the feasibility of this approach we performed a meta-analysis of four resequencing datasets of the MC4R gene, mutations that are known to be strongly overrepresented among severely obese individuals (8, 33–35) (SI Appendix, Table S2). Forty-three individuals with rare missense variants were found among 2,940 obese individuals (99th BMI percentile), while only 3 individuals with rare missense variants were detected in 1,925 lean individuals (<15th BMI percentile). With the described approach, MC4R would be readily detected with P -value < 5 · 10⁻⁷, achieving genome-wide statistical significance. As such, this gene could have been discovered by resequencing a sample of < 5,000 individuals.

Discussion

Importantly, our simulations do not assume that protein-coding variation is solely responsible for phenotypic variation. In contrast to previous studies (36–38) the goal of these simulations was not to predict the allelic spectrum of human disease, but rather to probe the utility of rare missense SNPs in discovery of genes influencing human traits. The considered study design is similar in concept to a genetic screen utilizing naturally occurring mutations. Even if a large fraction of trait variance were explained by noncoding cis-regulatory variation (e.g., causing changes in expression levels of genes associated with phenotypes), hypomorphic coding mutations arising in the same genes would lead to some level of functional polymorphism detectable by resequencing of these genes in a sufficiently large population. Accordingly, resequencing of only coding regions should be sufficient to identify genes affecting traits of interest, but to explain population variation in phenotype, resequencing of noncoding region might be necessary. We note, however, that extending the very same type of analysis to highly conserved non-coding regions is unlikely to be successful because the effect of mutations in these regions is probably much weaker than the effect of coding mutations. Deletions of ultraconserved regions were not shown to lead to any detectable phenotypes (39) and population genetics studies suggest that conservation of many of the conserved regions is maintained by weak selective pressure (40–42).

We conclude that a simple study design combining the pending availability of both low-cost–high-volume sequencing technology and large well-phenotyped population samples has the potential to facilitate discovery of genes relevant to human phenotypes.

Materials and Methods

Demographic Model.

Overall, the demographic model included four parameters: (i) long-term ancestral effective population size; (ii) bottleneck population size; (iii) duration of exponential growth in generations; and (iv) recent effective population size. In the analysis, experimental site frequency spectrum was represented by synonymous and noncoding variants combined. Allelic spectra of these categories of SNPs were similar, and pooling them together resulted in an increase of the amount of data. Although we used data on 757 individuals sequenced (1,514 chromosomes), due to failed base calls in some cases, we approximated number of sequenced chromosomes as 1,400. The combined number of sequenced neutral nucleotide sites was approximated as 63,000 (see SI Appendix, Methods).

Neutral Wright–Fisher Model for Variable Population Size.

Let ϕ(q,t|p) be the probability density that the allele frequency in the t th generation is between x and x + dx, (0 < x < 1) given its starting frequency p. It has been shown (43–47) that ϕ(q,t|p) satisfies the forward Kolmogorov equation:

For a constant population size, N_t = N₀, the transient solution:

where C_i^3/2 is the Gegenbauer polynomial with λ = 3/2. For general time-dependent population size N_t, we can obtain ϕ(q,t|p) by defining effective time t′, such that dt′ = (N₀/N_t)dt. Written in terms of the effective time t′, forward Kolmogorov equation becomes

Consequently, the solution at time π is

For N_t = N₀ · e^γt,

Site-Frequency Spectrum at Present.

The expected site frequency spectrum f(q), produced by the above demographic model in today's population, is given by a sum of the contribution of ancestral mutations originated at the stationary phase prior to the bottleneck and the contribution of recent mutations occurring in the population with the cumulative rate 2N_tμ per generation t.

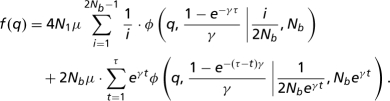Likelihood.

In a sample of N_s chromosomes the number of segregating sites observed with polymorphic multiplicity i is given by

In absence of additional information about which allele is the ancestor, what is actually recorded is the minority multiplicity, i.e., F_j^(b) = 63,000(F_j + F_Ns−j), for j = 1,…,N_s/2 − 1. The number of monomorphic sites is given by F₀ = 63,000 − ∑_{j = 1}^N/2F_j^(b). The probability that SNP will be found i times of N_s is then P_j = F_j^(b)/63,000.

Assuming independence between SNPs, the likelihood is given by

Note that because the likelihood includes monomorphic sites, maximizing it maximizes match in the observed units and not merely the distribution form. The 4D likelihood surface was studied extensively and shown to possess a single maximum. Its 2D projections are shown in Fig. 2.

Estimation of Selection Coefficient Distributions.

Distribution of selection coefficients was modeled as a gamma distribution with addition of completely neutral sites (selection coefficient, s = 0) and sites under “lethally” strong selection (s = 1). Intermediate categories of sites with selection coefficients in the range of 10⁻⁵ − 10⁻¹ were modeled by a gamma distribution:

where Γ(k) is a gamma function. Continuous gamma distribution was transformed to a 20-bin histogram by numerical integration within corresponding bin boundaries uniformly spaced in the logarithmic scale between 10⁻⁵ and 10⁻¹. We determined parameters of the distribution by using an exhaustive grid search. Fraction of neutral and invariable sites were allocated in 5% minimal “blocks,” while remaining 20 bins described by gamma distribution were normalized so the sum of all bins was equal 1. All possible values from 0% to 100% were tested for values of extreme bins. Values of θ and k parameters were taken from the logarithmic grid: θ from 10⁻⁵ to 10⁻¹ with $\sqrt{10}$ step; k from 10⁻² to 10 with $\sqrt{10}$ step.

Allele frequency spectra were computed by using forward simulations with a predefined demographic history and a chosen distribution of selection coefficients. Log-likelihood LL, for each model was computed as:

where n_i^exp is a number of nonsynonymous SNPs in which minor allele was observed i times in the experimental resequencing dataset, n_i^simul is a number of SNPs with simulated minor allele count equal to i, n^total is the total number of simulated “missense” sites (20,000), and M is the number of sequenced chromosomes.