Hierarchical control of static prehension: II. Multi-digit synergies

Abstract

The purpose of this study was to explore the ability of the central nervous system (CNS) to organize synergies at two levels of a hypothetical control hierarchy involved in two-hand multi-finger prehension tasks with one or more persons participating in the task together. At the higher level of the hierarchy, the total force and moment of force produced on an object are distributed between the thumb and the virtual finger (an imagined finger with mechanical output equal to the involved fingers of the hand), while at the lower level the virtual finger action is distributed among the four fingers. We tested a hypothesis that the CNS is able to organize synergies at only one level of the hierarchy. The subjects held vertically one of the two handles, a narrow one and a wide one. They used the four fingers of the right hand opposed by either the right hand thumb, the left hand thumb, the left hand index finger, the thumb of an experimenter, the index finger of an experimenter, or an inanimate object. Forces and moments of force produced by each digit were recorded. Indices of synergies stabilizing the mechanical output variables at each of the two levels were computed. Contrary to the expectations, force and moment of force stabilizing synergies were found at one or both levels of the hierarchy across all tasks. Unimanual tasks exhibited higher synergy indices compared to all tasks, while intrapersonal synergy indices were higher than those of interpersonal synergies. The results suggest that both feed-forward and feedback mechanisms may be used to create force and moment of force stabilizing synergies. We invoke the notion of chain effects and generalize it for relations among variance components related to stabilization of different mechanical variables. The reference configuration hypothesis offers a fruitful framework for analysis of prehension synergies.

Introduction

When a person grasps an object and statically maintains its position, an infinite number of finger-tip force combinations can be used to perform such a task; this is an example of the so-called Bernstein problem (Bernstein 1967; Turvey 1990; Latash 1996). The abundance of such solutions allows the central nervous system (CNS) to select different force patterns that may vary from trial to trial while the total output of the digits remains relatively unchanged. According to the principle of abundance (Gelfand and Latash 1998), commands to the fingers do not vary independently across trials; they are organized by the CNS into synergies that reduce deviations in resultant force and moment of force to maintain static equilibrium of the object. Here, we consider synergies as neural organizations that produce stable output by coordinating the outputs of elements of the hand(s).

In previous studies, the hand has been viewed as being controlled by a two-level hierarchy (Arbib et al. 1985; MacKenzie and Iberall 1994). The total force and moment of force produced on an object are distributed at the higher level of the hierarchy between the thumb and the virtual finger (VF, an imagined finger with mechanical output equal to the involved fingers of the hand). At the lower level of the hierarchy, the VF action is distributed among the fingers that form the VF.

A recent development of the equilibrium-point hypothesis (Feldman 1966, 1986) has addressed the issue of grasp force production as a particular example of neural control using reference body configurations (Ostry and Feldman 2003; Pilon et al. 2007). Within this framework, peripheral motor patterns, such as finger tip forces, emerge as results of a discrepancy between a centrally specified reference position and an actual position that may be constrained by external forces. In particular, grip force may be viewed as resulting from a discrepancy between the centrally specified reference aperture and actual aperture. The reference aperture may be viewed as resulting from a set of reference positions for all the digit tips –potentially a redundant problem. This problem does not have to be solved explicitly but may be associated with synergies among digit tip reference positions stabilizing the reference aperture. We assume that in static tasks with an unchanged aperture, digit forces are adequate peripheral reflections of the centrally specified reference positions. We perform analysis in the space of finger forces since accurate recording of the reference configuration of all the involved digits in a sufficient number of trials (to perform variance analysis) is beyond our current technical means.

There have been several recent studies exploring force and moment of force stabilizing synergies at the two levels of the hypothetical hierarchy in unimanual prehensile tasks (Baud-Bovy and Soechting 2001; Gao et al 2005; Shim et al. 2005a, b; Zatsiorsky et al. 2003a). At the higher hierarchical level (the VF-TH level), force and moment of force produced by the VF and thumb co-vary to stabilize the total force and moment of force applied to the hand-held object (Budgeon et al. 2008; Shim et al. 2005a; Zatsiorsky et al. 2003a). At the lower hierarchical level (the individual finger level, the IF level) the forces produced by the individual fingers co-vary to stabilize the overall VF force direction (Gao et al. 2005) and magnitude (Shim et al. 2005a).

In contrast, several studies of multi-finger pressing tasks have reported the absence of covariation of finger forces (or hypothetical commands to fingers, finger modes, Danion et al. 2003) at the lower level of the hierarchy in two-hand tasks (fingers of each hand were viewed as a VF) despite strong force stabilizing synergies at the upper level of the hierarchy (across the hands; Gorniak et al. 2007a, b; Kang et al. 2004). Such observations have promoted the hypothesis that the CNS is able to create new synergies at only the highest level of the hierarchy. Note that these studies used rather artificial multi-finger pressing tasks by the two hands while the earlier mentioned studies that produced evidence for synergies at both levels of the hypothetical control hierarchy used well practiced unimanual prehensile tasks.

Thus, we have decided to explore whether the CNS is limited in creating synergies at both levels of the hierarchy simultaneously during tasks that involved unimanual prehension and during similar but less usual tasks involving two hands of the same person, two hands of different persons and one hand helped by an inanimate object. Based on the mentioned studies, we expected to observe force and moment of force stabilizing synergies at both levels of the control hierarchy, the VF-TH and IF levels, during unimanual tasks. When the four fingers are opposed by a digit from the other hand, we expected the task to become sufficiently novel such that the synergies would be observed only at the VF-TH level, but not at the IF level (similar to Gorniak et al. 2007a, b). However, when the opposing force is provided by another person or by an inanimate object, the IF level becomes the highest level for the subject’s CNS, and hence we expected synergies at this level to re-emerge. As in the companion paper, we manipulated object width in this experiment with an underlying assumption that two-hand actions are more natural for larger objects. This assumption is based on studies that explored preferred grasping patterns for objects of different size and weight (Cesari and Newell 1999, 2000). We did not know a priori whether or not object width would affect the presence and/or strength of synergies at either hierarchical level; hence, this was an exploratory manipulation.

In this paper, we present only the results of synergy analyses. In the companion paper (Gorniak et al. 2009), details describing the mechanical behavior of the digits are presented and discussed.

Methods

Detailed information regarding subjects, experimental setup, experimental procedure, and basic data analysis can be found in the Methods of the companion paper (Gorniak et al. 2009). Here we only describe methodological details pertinent to the variance analyses presented in this paper.

Briefly, five male and six female students served as subjects in this study. The subjects sat in a chair and grasped the handle instrumented with six-component force/torque sensors using one of six different finger combinations (six for the narrow handle and five for the wide handle). Finger combinations were: T_R + IMRL_R, T_L + IMRL_R, T_E + IMRL_R, I_L + IMRL_R, I_E + IMRL_R, Object + IMRL_R; where T = thumb, I = index, M = middle, R = ring, L = little fingers, and the subscripts denote the hand to which the fingers belong (R = right, L = left, E = experimenter). In the Object + IMRL_R condition, the handle (in the upright position) was pressed against a large flat inanimate object, which had a level surface parallel to the contact surface of the thumb sensor. Throughout the Results and in the figures, IMRL_R will be referred to as VF_R for brevity. Data were collected over 10 s during steady-state holding of the vertically oriented handle.

Variance Analysis

The purpose of this analysis was to compute indices of co-variation of elemental variables (forces and moments of force) produced by sets of effectors that reflect the stabilization of combined effector outputs. This analysis has been performed at two levels: the individual finger (IF) level and the virtual finger – thumb (VF-TH) level. At the IF level, co-variation of elemental variables produced by individual fingers was studied; while at the VF-TH level, covariation of elemental variables produced by the VF and the opposing effector was studied. The index of co-variation was computed as the difference between the sum of the variances of elemental variables [ΣVar(EV)] and the variance of the total output of these elemental variables [Var(ΣEV)]. According to the Bienaymé theorem (Loeve, 1955), for independently varying variables, the two values should be equal to each other. Hence positive values of the index corresponded to predominantly negative co-variation among the elemental variables, which we interpret as stabilization of their combined output. The index of co-variation was computed across trials using values measured within the interval 5–6 s of each trial. It was further normalized by ΣVar(EV) to allow comparisons across conditions and subjects.

For an object to be in static equilibrium, the sum of all forces and moments of force acting on the object should be equal to zero. For this study, we focused on the constraints that satisfy these conditions in the grasp (Y–Z) plane. Thus, the three following requirements should be satisfied to achieve static equilibrium:

1. The sum of the normal forces of the four digits consisting the virtual finger should be equal and opposite to the normal force of the thumb;

2. The sum of vertical tangential forces of produced by all of the digits should be equal to the weight of the object; and

3. The total moment of force produced by the digits should be equal to zero.

For more detailed description of these constraints, please see the companion paper (Gorniak et al. 2009).

At the IF level, we were interested in examining the co-variation of the following elemental variables produced by the individual fingers within the VF: normal forces of individual digits ( $F_j^n$, j = i, m, r, and l), tangential forces of individual digits ( $F_j^t$), and the moments produced by these forces ( $M_j^n$ and $M_j^t$). Similarly, at the VF-TH level, we were interested in examining the co-variation of the following quantities produced by the VF and the opposing effector: Fⁿ, F^t, Mⁿ, M^t, and the total moment of force, M^TOT (see equations 1–9). The following time-varying variables were computed for each subject over the fifteen trials within each condition:

1. The total normal (grip) and vertical tangential (load bearing) forces: $F_{\mathit{TOT}}^n(t)$ and $F_{\mathit{TOT}}^t(t)$ of all the digits involved in the given task, and their respective variances, $\mathit{Var}{F}_{\mathit{TOT}}^n(t)$ and $\mathit{Var}{F}_{\mathit{TOT}}^t(t)$;

2. The sum of variances of individual finger forces produced by the fingers of the VF: $\sum \mathit{Var}{F}_j^n(t)$ and $\sum \mathit{Var}{F}_j^t(t)$;

3. Variance of the VF and opposing effector forces: $\mathit{Var}{F}_{VF}^n(t),\mathit{Var}{F}_{VF}^t(t),\mathit{Var}{F}_{OE}^n(t),\mathit{Var}{F}_{OE}^t(t)$. Forces generated by the VF were computed as the sum of the forces produced by the index, middle, ring and little fingers of the right hand;

4. The moments of force: Mⁿ (t) and M^t (t) and their respective variances Var Mⁿ (t) and Var M^t (t);

5. The sum of variances of individual finger moments of force produced by the fingers of the VF: $\sum \mathit{Var}{M}_j^n(t)$ and $\sum \mathit{Var}{M}_j^t(t)$; and

6. The variance of the VF and opposing effector moments of force: $\mathit{Var}{M}_{VF}^n(t),\mathit{Var}{M}_{VF}^t(t),\mathit{Var}{M}_{OE}^n(t)$, and $\mathit{Var}{M}_{OE}^t(t)$. $M_{VF}^n$ and $M_{VF}^t$ were computed as the moments produced by the resultant normal and tangential forces generated by the index, middle, ring, and little fingers, respectively.

Further, an index of force co-variation (for both normal and tangential forces) at the IF level was computed as:

$$\mathrm{\Delta }{V}_{F,IF}(t)=\left[\sum \mathit{Var}{F}_j(t)-\mathit{Var}{F}_{VF}(t)\right]/\sum \mathit{Var}{F}_j(t).$$ (10)

A similar index of force co-variation at the VF-TH level (for both normal and tangential forces) was computed as:

$$\mathrm{\Delta }{V}_{F,VF-TH}(t)=[(\mathit{Var}{F}_{VF}(t)+\mathit{Var}{F}_{OE}(t))-\mathit{Var}{F}_{\mathit{TOT}}(t)]/(\mathit{Var}{F}_{VF}(t)+\mathit{Var}{F}_{OE}(t))$$ (11)

Likewise, indices for moment co-variation (for the moments produced by the grip and load forces; as well as their sum, total moment, M^TOT) at the IF and VF-TH levels were computed as:

$$\mathrm{\Delta }{V}_{M,IF}(t)=\left[\sum \mathit{Var}{M}_j(t)-\mathit{Var}{M}_{VF}(t)\right]/\sum \mathit{Var}{M}_j(t)$$ (12)

$$\mathrm{\Delta }{V}_{M,VF-TH}(t)=[(\mathit{Var}{M}_{VF}(t)+\mathit{Var}{M}_{OE}(t))-\mathit{Var}M(t)]/(\mathit{Var}{M}_{VF}(t)+\mathit{Var}{M}_{OE}(t))$$ (13)

where OE stands for opposing effector.

Here, we have defined ΔV indices in such a way that their positive values imply predominantly negative co-variation among forces (or moments of force) produced by the individual digits. We interpret such values as signs of a force (or moment of force) stabilizing synergy (Gorniak et al. 2007a, b; Kang et al. 2004; Shim et al. 2005b). Large positive ΔV values correspond to larger amounts of negative co-variation, thus a stronger synergy. A result of ΔV = 0 implies independent variation of digit forces (or moments of force), and correspondingly the absence of a synergy, while ΔV < 0 may be interpreted as co-variation of elemental variables destabilizing their combined output. Here, the normalization limits the value of ΔV indices by +1 for perfect force (or moment) stabilizing synergies (the individual elemental variables change their value in time but variance of the performance variable equals zero).

Statistics

The data are presented in the text and figures as means and standard errors. Mixed model analyses of variance (ANOVAs) were performed on the ΔV data with the factors: Finger Configuration (six levels for the narrow handle width and five levels for the wide handle width; T_R + VF_R, T_L + VF_R, T_E + VF_R, I_L + VF_R, I_E + VF_R, Object + VF_R), Width (two levels; narrow and wide), and Finger (four levels; one for each of the single digits of VF_R involved in the task). A random factor of Subject (10 levels; one for each subject) was also used in the statistical analyses, however significant effects of this factor are not necessarily interpretable and thus not presented in this paper. Post-hoc pair-wise comparisons were performed using Tukey’s tests and Bonferroni statistics to further analyze significant effects of ANOVAs. The ΔV data were subjected to Fisher transformation during ANOVA testing to mitigate the ceiling effects; however, untransformed data are shown in the figures to avoid confusion. Individual t-tests with Bonferroni corrections were performed to compare ΔV indices with zero.

Results

This section is organized in the following way. The results of the ΔV analysis are presented for normal forces, ΔV(Fⁿ); tangential forces, ΔV(F^t); moments due to the normal forces, ΔV(Mⁿ); moments due to the tangential forces, ΔV(M^t); and total moment of force, ΔV(M^TOT). The analyses were performed at two levels: the VF-TH level and the IF level. At the VF-TH level, the VF and the opposing effector were considered as elements; while at the IF level, the four fingers of the right hand were considered as elements. A summary of force and moment of force sharing between the VF and opposing effector are presented in the Appendix.

A summary of the main statistical results on the ΔV indices can be found in Table 1 (ΔV > 0 implies a synergy stabilizing that particular performance variable, while ΔV ≤ 0 implies a lack of such a synergy, see Methods). Note that Table 1 does not include subdivisions for the ΔV indices for each of the tested digit configurations. In brief, this is due to our finding that these indices did not show the patterns of co-variation suggested by the hypotheses presented in the Introduction but rather showed common patterns across digit configurations that differed for different performance variables. Synergies were found at one or more levels of the proposed hierarchy for all tested variables, independently of finger configuration. In the following subsections, a detailed description of the data and statistical analyses used to determine these effects are presented.

Table 1.

Summary of ΔV indices at the two hierarchical levels

Variable	ΔVVF-TH	ΔVIF
F n	> 0	~ 0
F t	> 0	> 0
M n	> 0	< 0
M t	< 0	> 0
MTOT	> 0	> 0

Synergy indices (ΔV) at the two hierarchical levels of analysis (VF-TH and IF) are shown. Variables Fⁿ, F^t, Mⁿ, M^t, and M^TOT refer to: normal force, tangential force, moment of normal forces, moment of tangential forces, and total moment, respectively. ΔV > 0 (shown in bold) indicates the existence of a synergy at a given hierarchical level.

Since the T_R + VF_R condition was not possible for the wide configuration, two sets of mixed effect ANOVAs were performed in order to analyze the effects of this finger configuration. ANOVA-1 refers to analysis of all finger configurations except T_R + VF_R (for both the narrow and wide handle widths) with the factors: Subject, Width, Finger Configuration, and any interaction terms. ANOVA-2 refers to analysis of all finger configurations (including T_R + VF_R) possible for the narrow handle width only; hence, ANOVA-2 involves the Subject and Finger Configuration factors, but not the Width factor.

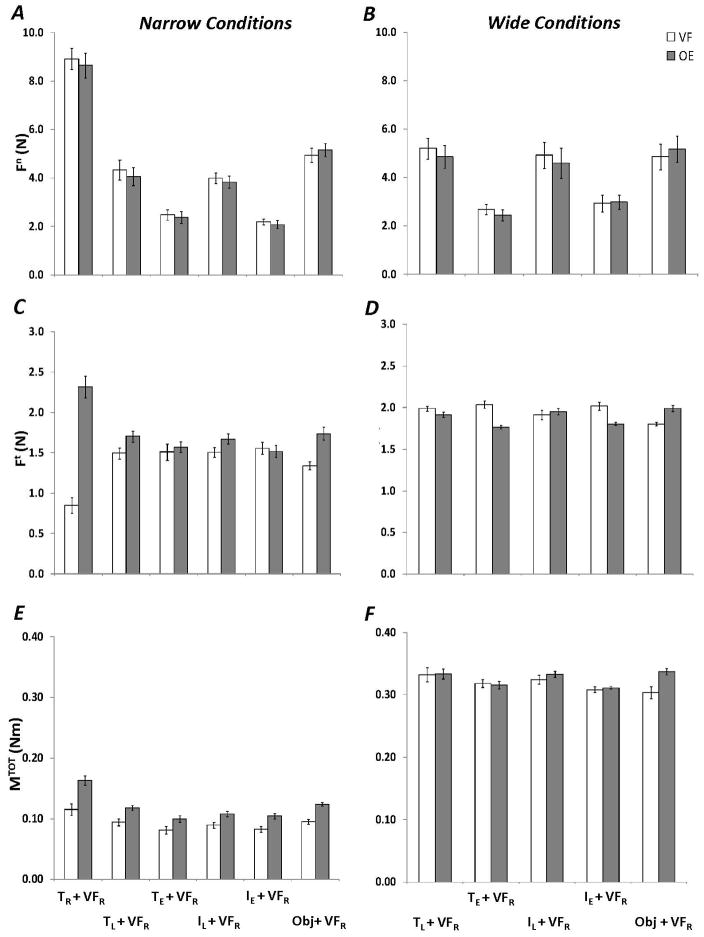
Normal force co-variation, ΔV(Fⁿ)

To quantify normal force stabilizing synergies we used indices of normal force covariation, ΔV(Fⁿ), at both hierarchical levels. The analysis has shown normal force stabilizing synergies at only the VF-TH level across all finger configurations and handle widths (gray columns in panels A and B of Figure 1). Note that ΔV(Fⁿ)_VF-TH indices were significantly larger than zero across all conditions, while ΔV(Fⁿ)_IF indices (the white columns) were not significantly different from zero, with the exception of the T_R+VF_R and I_E + VF_R conditions. This was confirmed with individual t-tests with Bonferroni corrections (μ_A > 0; grand average ΔV(Fⁿ)_VF-TH = 0.836 ± 0.017, t > 49.0, p < 0.001; grand average ΔV(Fⁿ)_IF = 0.0136 ± 0.0543, t = 0.25, p > 0.1). Additional analysis indicated that ΔV(Fⁿ)_IF for the T_R+VF_R finger configuration was significantly less than zero (t = −4.23, p < 0.001) while the same index for the I_E + VF_R finger configuration was larger than zero (for both the narrow and wide conditions; t = 4.11, p < 0.001 and t = 3.32, p < 0.01, respectively).

Figure 1.

Mean and standard error of indices of co-variation of normal [ΔV(Fⁿ)_IF and ΔV(Fⁿ)_VF-TH] and tangential forces [ΔV(F^t)_IF and ΔV(F^t)_VF-TH] for both levels of the proposed synergy hierarchy [denoted by the subscripts, individual finger level (IF) and virtual finger – thumb level (VF-TH)] are shown across finger configurations and handle widths. A: ΔV(Fⁿ)_IF and ΔV(Fⁿ)_VF-TH for the narrow handle. B: ΔV(Fⁿ)_IF and ΔV(Fⁿ)_VF-TH for the wide handle. C: ΔV(F^t)_IF and ΔV(F^t)_VF-TH for the narrow handle. D: ΔV(F^t)_IF and ΔV(F^t)_VF-TH for the wide handle. Abbreviations are the same as in Figure 1.

Further analysis revealed that ΔV(Fⁿ)_VF-TH was largest when one hand from one person performed the task (T_R+VF_R and Object + VF_R) and lowest when two people held the object (T_E+VF_R and I_E+VF_R). This was confirmed using ANOVA-1 and ANOVA-2; main effects of Finger Configuration [F_4,81 = 14.87, p < 0.001 and F_5,45 = 12.19, p < 0.001] were found, respectively. Pair-wise comparisons have shown that finger configurations T_E + VF_R and I_E + VF_R yielded the smallest ΔV(Fⁿ)_VF-TH overall.

Tangential force co-variation, ΔV(F^t)

In contrast to the normal force results, tangential force stabilizing synergies were found at both the VF-TH and IF levels across all finger configurations; as indicated by positive ΔV(F^t)_VF-TH and ΔV(F^t)_IF values shown in panels C and D of Figure 1. Panel C shows ΔV(F^t)_IF as white bars and ΔV(F^t)_VF-TH as gray bars for the narrow conditions while panel D shows the same indices for the wide conditions. These findings were confirmed with individual t-tests with Bonferroni corrections (μ_A > 0; grand average ΔV(F^t)_VF-TH = 0.5639 ± 0.0278, t = 20.30, p < 0.001; grand average ΔV(F^t)_IF = 0.773 ± 0.0173, t = 45.77, p < 0.001).

The ΔV(F^t)_VF-TH index was consistently smaller for the wide handle as compared to the narrow handle. This was confirmed using ANOVA-1; a main effect of Width [F_1,81 = 80.32, p < 0.001] was found with no interactions. Analysis of ΔV(F^t)_VF-TH for the narrow width revealed no significant effects in regard to finger configuration.

Statistical analysis of ΔV(F^t)_IF indicated that this co-variation index was consistently larger for the wide handle as compared to the narrow handle. Comparison of finger configurations indicated that the unimanual condition (T_R+VF_R) yielded the lowest ΔV(F^t)_IF index. This was confirmed using ANOVA-1 and ANOVA-2; main effects of Width [F_1,81 = 96.47, p < 0.001] and Finger Configuration [F_5,45 = 4.78, p < 0.005] were found, respectively. Pair-wise comparisons have confirmed that the condition T_R+VF_R showed the lowest ΔV(F^t)_IF values across all finger configurations.

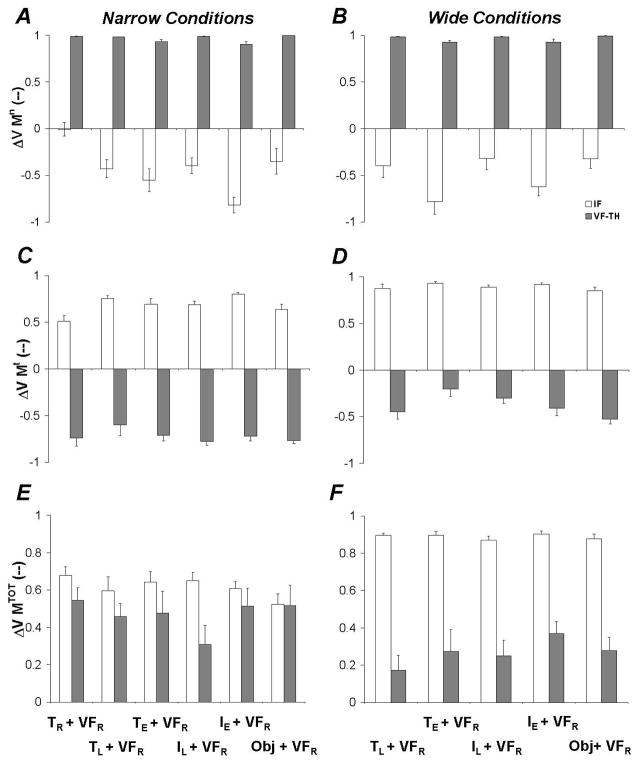
Moment of normal force co-variation, ΔV(Mⁿ)

Moment of normal force stabilizing synergies were found at only the VF-TH level across all finger configurations and handle widths, as shown in panels A and B of Figure 2. Figure 2 shows ΔV(Mⁿ), ΔV(M^t), and ΔV(M^TOT) indices across all finger configurations tested for both handle widths. Panel A shows ΔV(Mⁿ)_IF as white bars and ΔV(Mⁿ)_VF-TH as gray bars for the narrow conditions while panel B shows the same indices for the wide conditions. Panels A and B of Figure 2 illustrate that ΔV(Mⁿ)_VF-TH was significantly larger than zero while ΔV(Mⁿ)_IF was less than zero for all finger configurations except T_R+VF_R. This was confirmed with individual t-tests with Bonferroni corrections (μ_A > 0; grand average ΔV(Mⁿ)_VF-TH = 0.9645 ± 0.0058, t = 166.24, p < 0.001; grand average ΔV_Mⁿ_{, IF} = −0.4543 ± 0.0378, t = −12.01, p > 0.05). Additional investigation of ΔV(Mⁿ)_IF indicated that the index was significantly negative across all finger configurations (tested μ₀ = 0 and μ_A < 0; ΔV(Mⁿ)_IF = −0.4543 ± 0.0378, t = −12.01, p < 0.001).

Figure 2.

Mean and standard error of indices of co-variation of the moments of normal forces [ΔV(Mⁿ)_IF and ΔV(Mⁿ)_VF-TH], moments of tangential forces [ΔV(M^t)_IF and ΔV(M^t)_VF-TH], and total moment of force [ΔV(M^TOT)_IF and ΔV(M^TOT)_VF-TH] for both levels of the proposed synergy hierarchy are shown across finger configurations and handle widths. A: ΔV(Mⁿ)_IF and ΔV(Mⁿ)_VF-TH for the narrow handle. B: ΔV(Mⁿ)_IF and ΔV(Mⁿ)_VF-TH for the wide handle. C: ΔV(M^t)_IF and ΔV(M^t)_VF-TH for the narrow handle. D: ΔV(M^t)_IF and ΔV(M^t)_VF-TH for the wide handle. E: ΔV(M^TOT)_IF and ΔV(M^TOT)_VF-TH for the narrow handle. F: ΔV(M^TOT)_IF and ΔV(M^TOT)_VF-TH for the wide handle. Abbreviations are the same as in Figure 1.

The ΔV(Mⁿ)_IF index was the most negative for finger configurations involving two persons (T_E+VF_R and I_E+VF_R). This was confirmed using ANOVA-1 and ANOVA-2; main effects of Finger Configuration [F_5,40 = 6.38, p < 0.001] were found only for ANOVA-2. Pairwise Tukey tests revealed that ΔV(Mⁿ)_IF was lowest for the T_E + VF_R and I_E + VF_R configurations compared to the other finger configurations.

Further analysis has indicated that ΔV(Mⁿ)_VF-TH was lowest for finger configurations involving the digits of another person but was not affected by handle width. This was confirmed using ANOVA-1 and ANOVA-2; main effects of Finger Configuration [F_4,81 = 22.98, p < 0.001 and F_5,45 = 11.43, p < 0.001] were found. Pair-wise Tukey tests also revealed that ΔV(Mⁿ)_VF-TH was lowest for the T_E + VF_R and I_E + VF_R configurations compared to the other finger configurations.

Moment of tangential force co-variation, ΔV(M^t)

In this section, we examined whether moment of tangential force stabilizing synergies were present by analyzing ΔV(M^t) at both hierarchical levels. Statistical analysis showed that moment of tangential force stabilizing synergies were found at only the IF level across all finger configurations and both handle widths. Values for these indices can be found in panels C (narrow conditions) and D (wide conditions) of Figure 2. It can be seen that ΔV(M^t)_VF-TH was less than zero while ΔV(M^t)_IF was significantly greater than zero. This was confirmed with individual t-tests with Bonferroni corrections (μ_A > 0; grand average ΔV(M^t)_VF-TH = −0.5634 ± 0.0276, t = −20.38, p > 0.05; grand average ΔV(M^t)_IF = 0.7772 ± 0.0170, t = 45.77, p < 0.001).

Additional investigation of ΔV(M^t)_VF-TH indicated that the index was significantly negative across all finger configurations (tested μ₀ = 0 and μ_A < 0; ΔV(M^t)_VF-TH = −0.5634 ± 0.0276, t = −20.38, p < 0.001). ANOVA testing also showed that ΔV(M^t)_VF-TH was larger for the wide handle. This was confirmed using ANOVA-1 and ANOVA-2; a main effect of Width [F_1,81 = 76.52, p < 0.001] was found.

Further analysis has shown that ΔV(M^t)_IF was larger for the wide handle width; it was smallest for the one-hand condition (panel C of Figure 2). This was confirmed using ANOVA-1 and ANOVA-2; main effects of Width [F_1,81 = 96.43, p < 0.001] and Finger Configuration [F_5,45 = 4.78, p < 0.005] were found with no interactions. Pair-wise analysis confirmed that the T_R+VF_R condition yielded the lowest ΔV(M^t)_IF values across all tested conditions.

Total moment of force co-variation, ΔV(M^TOT)

In this final subsection of the Results, we investigate whether total moment of force stabilizing synergies were present at both hierarchical levels. Here, we defined total moment of force for the virtual finger as the sum of moments of both normal and tangential forces produced by the fingers of the right hand. Similarly, we defined total moment of force produced by the opposing effector as the sum of moments of normal and tangential forces produced by that effector. Overall, it was found that total moment of force stabilizing synergies were found at both the VF-TH and IF levels across all finger configurations; as indicated by positive ΔV_M^TOT_,VF-TH and ΔV_M^TOT_,IF, shown in panels E and F of Figure 2. Panel E shows ΔV_M^TOT_,IF as white bars and ΔV_M^TOT_,VF-TH as gray bars for the narrow conditions while panel F shows the same indices for the wide conditions. These findings were confirmed with individual t-tests (μ_A > 0; grand average ΔV_M^TOT_,VF-TH = 0.3781 ± 0.0288, t = 13.13, p < 0.001; grand average ΔV_M^TOT_,IF = 0.7405 ± 0.0182, t = 40.79, p < 0.001).

It was found that ΔV_M^TOT_,VF-TH was consistently larger for the narrow handle as compared to the wide handle but no differences were found across finger configurations. This was confirmed using ANOVA-1; a main effect of Width [F_1,81 = 17.08, p < 0.001] was found.

Statistical analysis of ΔV_M^TOT_,IF indicated that this co-variation index was consistently larger for the wide handle as compared to the narrow handle with no differences across finger configurations. This was confirmed using ANOVA-1; a main effect of Width [F_1,81 = 208.54, p < 0.001] was found.

Discussion

The main purpose of the current experiment was to establish whether or not the CNS is able to organize both force- and moment of force stabilizing synergies simultaneously at two levels of a control hierarchy during unimanual and bimanual prehension. Within our proposed hierarchy, at the higher level the task is distributed between the two digits, the virtual finger (VF) and an opposing digit; at the lower level, VF output is distributed among the individual digits that form the VF. We quantified both force- and moment of force stabilizing synergies during prehension tasks involving one hand (by itself as well as against an inanimate object) and two hands (of one or two persons). The main finding is that both force- and moment of force stabilizing synergies were not consistently present at both levels of the control hierarchy. In fact, such synergies might exist at the lower level of the hierarchy but not at the higher level and vice versa. However, across all conditions tested, synergies were observed for each of the finger combinations at one or both hierarchical levels.

In the following paragraphs, we address the presence and absence of synergies within a hierarchy for tasks involving one or two hands. The results of this study are compared to static unimanual prehensile tasks as well as bimanual force production tasks. While our hypotheses on the presence or absence of synergies depending on the number of hands (and persons) has been falsified, we found consistent patterns of force and moment of force stabilizing synergies with respect to normal and tangential forces (and their respective moments of force) across all tasks examined. Accordingly, we will focus the discussion on such issues as chain effects, tasks involving one and two persons, and possible central mechanisms involved in the prehension synergies.

Hierarchies of synergies

The concepts of control hierarchies and synergies were developed by Nikolai Bernstein in describing the coordinated action of muscle groups (1947, 1967, 1996). Later work by Gelfand and Tsetlin (1966) refined the definition of synergies (“structural units”) as neural organizations of many elements organized in a hierarchical way: Each synergy receives an input from a hierarchically higher synergy and produces an output, which serves as an input to a hierarchically lower synergy. Here, we assume that the highest level of the hierarchy receives an input from the task and its lowest level acts on the environment. In fact, the idea of a two-level hierarchy controlling the hand (the VF-TH level and the IF level) is a simplification of a much more complex control structure. This simplification bypasses such important steps as the generation of neural control variables and their projection on the many muscles and motor units involved in any hand action.

Several recent studies have addressed hierarchies of synergies during tasks involving digit coordination. It has been shown that the VF and the thumb are coordinated to stabilize the hand gripping and rotational action (Baud-Bovy and Soechting 2001; Shim et al. 2005a; Zatsiorsky et al. 2003a) while fingers within the VF are coordinated to stabilize the direction and magnitude of VF force (Gao et al. 2005; Shim et al. 2005a; Zatsiorsky et al. 2003a). In contrast, recent studies of multi-finger pressing tasks have reported a lack of force stabilizing synergies within the VF during both unimanual and bimanual tasks (Gorniak et al. 2007a,b; Kang et al. 2004).

In the current study, force-stabilizing synergies could be simultaneously present at both levels of the synergy hierarchy during bimanual tasks, similar to results from the cited studies of unimanual actions. However, this was true only for the load-resisting tangential force and for the total moment of force. For other components of the prehensile action, force- and moment of force-stabilizing synergies were only seen at one level of the hierarchy; not necessarily at the higher level of the hierarchy, in contrast with previous research (Gorniak et al. 2007a,b; Kang et al. 2004). Force- and moment of force-stabilizing synergies were exhibited at the higher VF-TH level for normal forces applied to the object (and the resulting moment of normal force). Synergies were present only at the lower hierarchical level for the moment produced by the tangential forces. A summary of the main findings can be found in Table 1.

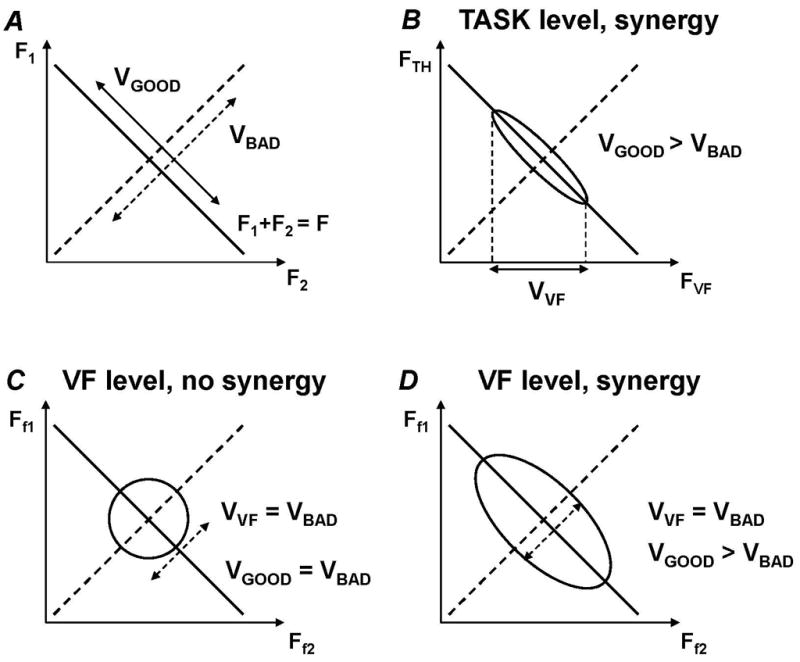
In previous papers (Gorniak et al. 2007a,b), we associated the lack of synergies at the lower hierarchical level with a limitation of the CNS to form synergies at the two levels simultaneously. It is possible that the CNS is faced with a trade-off during such force and moment of force production tasks. Consider Figure 3, which illustrates a simple case when two effectors (fingers) contribute to the VF force (the lower level), while the VF and the thumb act together to produce a constant total force (the higher level) required by the task. This example may be viewed as an illustration of the load-resisting (tangential) action of the digits in static prehension. At the higher level of the hierarchy, variance in the space of elemental variables may be viewed as consisting of two components. One of them, labeled ‘good variance’ (V_GOOD) does not affect the combined output of the two variables (F); while the other one labeled ‘bad variance’ (V_BAD) does (panel A in Fig. 3). By definition (reviewed in Latash et al. 2007), a total force stabilizing synergy has to be associated with an inequality ΔV > 0 where ΔV = [V_GOOD − V_BAD]/V_TOTAL (panel B in Fig. 3). Thus, an increase in V_GOOD would contribute to a stronger synergy at the higher hierarchical level. However, V_GOOD contributes to the total variance of the output of each of the two effectors, for example variance in the VF force (V_VF in panel B of Fig. 3). At the lower level of the hierarchy, two elemental variables are expected to co-vary to stabilize VF force; hence, V_VF corresponds to ‘bad variance’ in that space (V_BAD in panel C of Fig. 3). Thus an increase in V_GOOD at the higher hierarchical level would cause an increase in V_BAD at the lower hierarchical level. Hence, a two-level hierarchical control scheme has an inherent trade-off between synergies at the two levels.

Figure 3.

A: An illustration of variability in a two effector force production task. In the space of elemental variables (forces produced by the two effectors) the “good” and “bad” variance components are shown, denoted as V_GOOD and V_BAD. B: An illustration of a VF-TH force production task, in which V_GOOD > V_BAD. VF force variability is by definition V_BAD at the lower hierarchical level. C: An illustration of force production by the VF consisting of two fingers. In this example, V_GOOD = V_BAD, i.e. there is no force stabilizing synergy. D: In this example, V_GOOD > V_BAD at the lower hierarchical level, i.e. there is a VF force stabilizing synergy.

For synergies to exist at both levels, the inequality V_GOOD > V_BAD must be satisfied for both levels of analysis. This is possible but requires that V_GOOD,IF > V_BAD,IF and V_GOOD,VF-TH > V_BAD,VF-TH (compare panels B and D of Fig. 3). In our experiments, we observed examples of all possible situations: V_GOOD,IF > V_BAD,IF and V_GOOD,VF-TH > V_BAD,VF-TH (for the tangential force and for the total moment of force), V_GOOD,IF < V_BAD,IF and V_GOOD,VF-TH > V_BAD,VF-TH (for the normal force and for the moment of normal force), and V_GOOD,IF > V_BAD,IF and V_GOOD,VF-TH < V_BAD,VF-TH (for the moment of tangential force). These differences may in part be due to phenomena termed ‘chain effects’ which are discussed and developed in the next section.

Chain Effects

Chain effects have been previously suggested for planar prehension tasks (Zatsiorsky and Latash 2004; Zatsiorsky et al. 2003b) and have also been documented in three-dimensional unimanual prehension tasks (Shim et al. 2005a). Those studies implied under chain effects sequences of cause-effect pairs that may lead to non-trivial co-variation patterns between pairs of elemental variables. In the current experiment, we observed chain effects of this type (see the companion paper, Gorniak et al. 2009) as well as a different type of chain effects that we would like to term synergic chain effects. Consider the following example of the former chain effects: The normal force produced by the index and middle fingers (primarily the index finger) was larger than the normal force output of the ring and little fingers. This imbalance led to a pronation moment of force about the X-axis. In order to maintain static equilibrium of the handle, the moment of load-resisting forces produced by the thumb and the VF was in the direction of supination about the X-axis. Since the lever arms of these forces were constant, this was achieved by increasing the upwards thumb force and decreasing the upward force of the VF (to make sure that the weight of the handle was balanced by the sum of the two load-resisting forces). Similar modulation of load-resisting forces in response to changes in grip forces has also been noted in other prehensile studies (Freitas et al. 2007; Jaric et al. 2006; Pataky et al. 2004b).

The synergic chain effects relate to chain relations in the amounts of good and bad variance (illustrated in Figure 3) for related variables at different levels of analysis. To satisfy the equilibrium constraints, the three variables that describe the hand action on the handle (F^t, Fⁿ, and M^TOT) are expected to show low variability and synergies at the VF-TH level stabilizing those variables. This was true for Fⁿ; its ΔV index showed very high positive values at the VF-TH level; these values were also positive but significantly smaller for F^t and M^TOT. At the IF level, the relation inverted with higher ΔV index values for F^t and M^TOT. On the other hand, contributors to M^TOT, M^t and Mⁿ, could show negative values of the index of synergy. Why is it so? Consider the following logical chain.

At the VF-TH level, one of the main constraints of statics required the total tangential force to be equal to the weight of the handle. A strong F^t stabilizing synergy might be expected. However, such a synergy would lead to destabilization of the moment of tangential forces (see ΔV<0 for M^t in Figure 2), which could potentially complicate the task of keeping rotational equilibrium. Indeed, since the tangential forces of the VF and the opposing effector have to add up to the weight of the handle (cf. ΔV > 0 for F^t), a change in one has to be associated with a change in the other in opposite direction. This leads to negative co-variation of forces but positive co-variation of the moments these forces produce in pronation-supination, M^t about a horizontal axis passing through the center of the handle. Our results suggest that the controller solved the problem by organizing a F^t stabilizing synergy but keeping its “good variability”, V_GOOD relatively low to keep down negative effects on the moment these forces produce.

In contrast, at the IF level, stabilization of the VF tangential force directly leads to stabilization of the moment this force produces because the lever arms of all the finger forces are constant and their rotational effects sum up exactly like the forces do. Hence, there is no tradeoff between force and moment of force stabilizing synergies, and the controller facilitated strong synergies stabilizing F^t at the IF level.

Given the mentioned inherent lack of M^t stabilizing synergy at the VF-TH level, to avoid large variations in the total moment of force applied to the handle, the controller organized a synergy stabilizing the other contributor to M^TOT, namely Mⁿ (cf. Figure 2A,B). This resulted in relatively high V_GOOD for Mⁿ produced by the opposing effector and VF, which translated into large variance of VF Mⁿ. As illustrated in Figure 3, this makes it hard for the controller to have a Mⁿ stabilizing synergy at the IF level reflected in ΔV<0.

Despite the different signs of ΔV for M^t and Mⁿ at the VF-TH level, the ΔV index for M^TOT was positive at the VF-TH level, compatible with the task of maintaining rotational equilibrium of the handle.

Unimanual vs. Bimanual Tasks

The results of the current study show that, generally, synergy indices are higher for unimanual tasks as compared to bimanual tasks. In particular, indices of synergies at the VF-TH level for Fⁿ and Mⁿ were higher for the unimanual task as compared to tasks involving both hands of one person as well as two hands from different persons. Similarly, indices of synergies at the IF level for F^t and M^t were higher for the unimanual tasks as compared to tasks involving two hands from different persons. It is possible that these results are due to the over-practiced nature of unimanual prehension. In day to day activities, unimanual prehension is used quite commonly –in contrast to situations in which unusual combinations of fingers from both hands (or from the hand of another person) are used. Such habits may encourage use of variable solutions in force and moment of force production. It is possible that the synergies in the bimanual tasks would strengthen with training, similarly to the previously published results (Kang et al. 2004; Sharp and Newell 2000).

Our observations have implications with respect to upper limb rehabilitation. Several recent studies have proposed the use of bimanual training as treatment for stroke and cerebral palsy patients (Charles and Gordon 2006; Rose and Winstein 2004; Steenbergen et al. 2008). Specifically, Steenbergen and colleagues (2008) recommend bimanual activities during rehabilitation to facilitate the redevelopment of fine force control of an affected hand. Our finding of synergies at both hierarchical levels for load force supports this approach to rehabilitation. The results with respect to other mechanical variables such as grip force and moment of force ask for more caution: In the presence of trade-offs between hierarchical levels, using bi-manual tasks may slow down restoration of within-a-hand synergies.

Synergies in One- and Two-Person Actions

The existence of interpersonal synergies has been documented in rhythmic coordination tasks (Black et al. 2007; Schmidt et al. 1990). Here, we confirm the existence of both intrapersonal and interpersonal synergies during static prehension tasks. Note that interpersonal synergies were generally weaker as compared to intrapersonal synergies, supporting the observations by Black and colleagues (2007). This was found to be true at the higher hierarchical level for Mⁿ as well as at the lower hierarchical level for F^t and M^t.

At the VF-TH level, the stronger intrapersonal synergies are likely due to the direct neural coupling of the two hands. Several hypotheses have been formulated on the neural origin of synergies. According to one of them, synergies emerge as the result of feed-forward control involving superposition of two neural signals, only one of which is related to the explicit task (Goodman and Latash 2006). According to this scheme, only effectors that are controlled by shared neural structures are expected to show synergies. An optimal feedback control scheme implies an important role of peripheral feedback in synergy formation (Todorov and Jordan 2001). According to this scheme, both intrapersonal and interpersonal synergies are possible as long as appropriate feedback is available for the CNS. Our results are partly compatible with each of these schemes. On the one hand, interpersonal synergies (ΔV > 0) were observed, in line with the feedback-based scheme. On the other hand, they were significantly weaker, more in line with predictions of the feed-forward control scheme. It is possible, therefore, that synergies can be based on either principle or even on a combination of both.

When the four fingers of a subject were opposed by an inanimate object, some of the covariation patterns at the VF-TH level could be expected from the Third Newton’s Law. In particular, variations in the VF normal force were expected to be accompanied by equal variations of the reactive force thus stabilizing the resultant normal force. Similarly, stabilization of the total load force (F^t) could be expected. When the opposing force was provided by another person, the situation was more complex because of two factors. First, the opposing digit could be expected to provide non-rigid, elastic resistance to VF force variations (cf. Flash 1987). Second, there could be active changes in the opposing digit’s force. This might be the reason for generally smaller ΔV values for the two-person tasks as compared to the task involving action against an inanimate object.

Effects of Object Width

In this experiment, we manipulated object width with an underlying assumption that two-hand actions are more natural for larger objects. This assumption is based on studies that explored preferred grasping patterns for objects of different size and weight (Cesari and Newell 1999, 2000). The experiments have shown larger synergy indices for grip configurations using the wide object at the lower hierarchical level (the IF level). In contrast, at the higher hierarchical level (VF-TH level), synergy indices were either unchanged or smaller for the digit configurations with the wide object. These observations may be seen as reflections of the mentioned trade-off between synergies at the two hierarchical levels (see Figure 3). It is indeed possible that holding a wider object favors more independent control of the two opposing effectors. This results in stronger within-an-effector synergies (the IF level), which naturally limit the “good variability” at the higher (VF-TH) level and makes it harder for the neural controller to organize synergies at the higher level.

Possible physiological mechanisms

Several views have been expressed on possible neurophysiological mechanisms involved in multi-element synergies stabilizing a particular performance variable. Two models are based on explicit corrections of the outputs of the elements based either on sensory signals from peripheral receptors (Todorov and Jordan 2002) or using central back-coupling loops similar to the system of recurrent inhibition (Latash et al. 2005). As mentioned in the earlier subsection, sensory feedback, likely from pressure-sensitive receptors (reviewed in Johansson 1996, 1998), may lead to the formation of synergies more in line with the optimal feedback control model by Todorov and Jordan (2002). The stronger, intrapersonal synergies may also be based on a similar mechanism. However, a number of recent experimental studies (Gorniak et al. 2008; Shapkova et al. 2008) have provided evidence that favors a feed-forward control scheme more in line with a model by Goodman and Latash (2007). Likely, synergies may be based on a variety of neural mechanisms, possibly even on schemes combining feed-forward and feedback loops.

The reference configuration hypothesis (an extension of the equilibrium-point hypothesis, Feldman and Levin 1995; Feldman et al. 2007) suggests that the CNS defines a time profile of a reference configuration defined as a configuration of the body at which all the muscles would be at the threshold for activation. Such configurations are typically unattainable because of external force fields and anatomical constraints. For example, the production of task-specific Fⁿ, F^t and M^TOT in unimanual tasks may be associated with specification of a reference aperture between the thumb and VF (cf. Pilon et al. 2007), a reference hand position in the vertical direction, and a reference pronation-supination hand orientation (in our experiments, the external torque was close to zero; hence, the reference hand orientation was neutral). Consider, for example, what could be expected from setting the reference aperture with a certain trial-to-trial variability. Varying the reference aperture may be expected to lead to corresponding variability of the normal forces of both effectors while keeping the resultant force close to zero because the principle of control forces the system to reach an equilibrium. This means, in our terms, very low V_BAD for the resultant Fⁿ while V_GOOD for this variable may be high or low. The same can be said about the other two variables: Setting their reference positions makes the system reach an equilibrium where the total action (F^t or M^TOT) is exactly balanced by the external force and moment of force. For example, setting a somewhat different reference vertical position in a particular trial will not lead to an error in the total tangential force but rather to a perfect balance between the force of gravity and the total tangential force applied to the handle at a somewhat different vertical location. Hence, this mode of control is expected to lead to required values of the three performance variables with low trial-to-trial variability (low V_BAD), while being compatible with both high and low V_GOOD. Hence, control with reference configurations is compatible with synergies stabilizing the three performance variables, although it does not dictate their presence.

When the neural structures controlling the two opposing effectors are not shared (as in two-person trials) or shared via the transcortical loops (as in one-person, two-hand trials), the mode of control may change: Reference configurations are expected to be specified for the opposing effectors separately and adjusted to fit the task requirements based on sensory feedback from visual, cutaneous, and proproiceptive receptors (Johansson 1996, 1998; Boudreau and Smith 2001). This type of control resembles the scheme developed by Smeets and Brenner (1999, 2001) who analyzed reach-to-grasp action as a superposition of two pointing movements by the two opposing effectors. Co-varied changes in the reference configurations for the two effectors leading to synergies at the VF-TH level are expected to be based on feedback loops. The presence of synergies at the VF-TH level across all conditions suggests that this is possible; however, the higher indices of synergies for the one-hand tasks suggest that the feedback-based mode of static prehension control may be viewed as less efficient (see also the companion paper, Gorniak et al. 2009). This conclusion is in line with an intuitive consideration that specifying three variables at a control level is preferred to specifying six variables (three per effector).

Appendix

Force and moment of force sharing at the VF-TH level

The equations of statics impose constraints on the forces and moments of force produced by the elements at both VF-TH and IF levels. However, the system is redundant at both levels (reviewed in Zatsiorsky and Latash 2008); hence, different magnitudes of the outputs of individual elements can be used at both levels. Only data for the virtual finger – opposing effector level are presented here; the data for the individual fingers within the VF can be found in the companion paper (Gorniak et al. 2009).

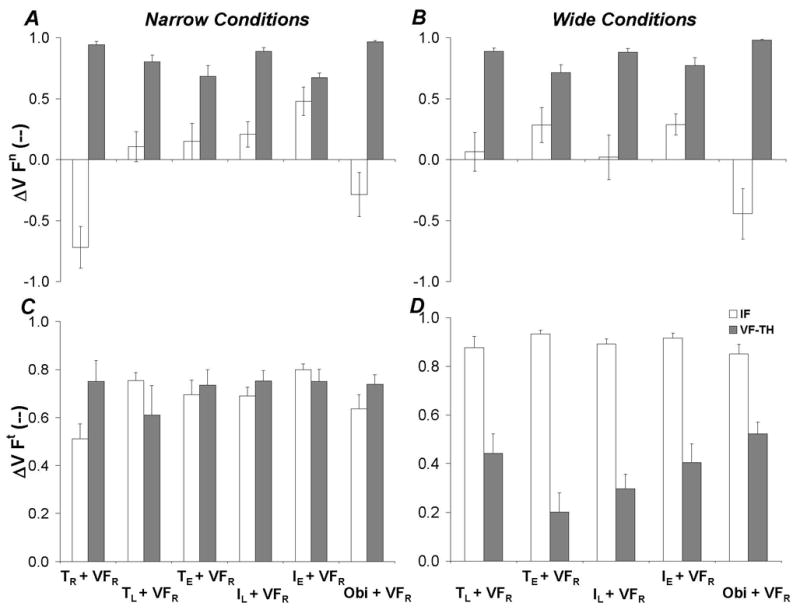
Figure 4 presents average data across subjects normal force, tangential force, and moment of total force data for the virtual finger and opposing effector across all tested conditions. Force and moment of force produced by the virtual finger are represented by white bars while opposing effector forces and moments of force are represented by gray bars. Data are presented in local frames of reference (sensor based frames of reference); note that moments produced by the virtual finger would pronate the object while moments exerted by the opposing effector would supinate the object.

Figure 4.

The normal force (Fⁿ, panels A and B), tangential force (F^t, panels C and D), and total moment of force (M^TOT, panels E and F) exerted on the handle for the narrow (panels A, C, and E) and wide (panels B, D, and F) handle widths. The data averaged across all subjects with standard error bars are shown. White bars indicate forces and moments of force produced by the virtual finger (VF) while grey bars indicate forces and moments of force produced by the opposing effector (OE). The data averaged across all subjects with standard error bars are shown. The abscissa shows finger configurations; T – thumb, I – index finger, Obj – inanimate object, subscripts R and L refer to the right and left hands, subscript E refers to the experimenter.

Panels A and B of Figure 4 show the magnitudes of normal forces for both the narrow and wide handle widths, respectively. Note that each of the two opposing effectors produced normal forces that varied broadly across the conditions while, within each condition, the forces were nearly equal to each other in magnitude. The tangential forces produced by the two effectors (panels C and D of Figure 4) were similar to each other in all conditions except the one-hand grasp, T_R + VF_R, for which VF produced significantly lower force as compared to the opposing effector. The total moment of force was not exactly zero, corresponding to a net supination moment of force as shown in panels E and F. Statistical analysis revealed that total moment of force was smallest for the narrow handle and finger configurations involving two persons. This was confirmed with ANOVA-1 and ANOVA-2; main effects of Width [F_1,81 = 20.72, p < 0.001] and Finger Configuration [F_4,81 = 14.32, p < 0.001 and F_5,45 = 16.2, p < 0.001] were found, respectively. Pair-wise comparisons have shown that finger configurations T_E + VF_R and I_E + VF_R yielded the smallest overall total moment of force.