Latent volumetric structure of the human brain: Exploratory factor analysis and structural equation modeling of gray matter volumes in healthy children and adults

Abstract

Previous studies have investigated patterns of volumetric covariance (i.e. intercorrelation) among brain regions. Methodological issues, however, have limited the validity and generalizability of findings from these prior studies. Additionally, patterns of volumetric covariance have often been assumed to reflect the presence of structural networks, but this assumption has never been tested formally. We identified patterns of volumetric covariance, correlated these patterns with behavioral measures, and tested the hypothesis that the observed patterns of covariance reflect the presence of underlying networks. Specifically, we performed factor analysis on regional brain volumes of 99 healthy children and adults, and we correlated factor scores with scores on the Stroop Word‐Color Interference Test. We identified four latent volumetric systems in each hemisphere: dorsal cortical, limbic, posterior, and basal ganglia. The positive correlation of the right posterior system with Stroop scores suggested that larger latent volumes are detrimental to inhibitory control. We also applied Structural Equation Modeling (SEM) to our dataset (n = 107) to test whether a model based on the anatomical pathways within cortico‐striatal‐thalamic‐cortical (CSTC) circuits accounts for the covariances observed in our sample. The degree to which SEM predicted volumetric covariance in the CSTC circuit depended on whether we controlled for age and whole brain volume in the analyses. Removing the effects of age worsened the fit of the model, pointing to a possible developmental component in establishing connections within CSTC circuits. These modeling techniques may prove useful in the future for the study of structural networks in disease populations. Hum Brain Mapp 2008. © 2007 Wiley‐Liss, Inc.

INTRODUCTION

The study of volumetric covariance among brain regions can provide information that complements other techniques aimed at investigating anatomical and functional connectivity in health and illness. Although total cerebral volume contributes to covariance of volumes across brain subregions, volumes of different structures still covary even after adjusting for overall brain size (i.e. after accounting for scaling effects) [Allen et al.,2002; Kennedy et al.,1998; Mechelli et al.,2005]. Those patterns of volumetric covariance correspond closely, at least for some brain regions, with known patterns of anatomical connectivity and with patterns of connectivity demonstrated using diffusion tensor imaging [Lerch et al.,2006]. Normal patterns of volumetric covariance have been shown to be altered in studies of disease populations, including schizophrenia [Mitelman et al.,2005], and similar alterations of covariance patterns have been hypothesized to occur in Alzheimer's disease [Braak and Braak,1991; Lerch et al.,2006].

Extant studies of volumetric covariance among brain regions [Herbert et al., 2003; Kennedy et al.,1998; Lerch et al.,2006; Mechelli et al.,2005; Tien et al., 1996; Wright et al.,1999] have been beset with various methodological limitations, including: (1) failure to control for age or total cerebral volume, both of which can drive volumetric correlations among brain regions that are independent of any systems‐level connectivity; (2) inadequate sample sizes, particularly relative to the number of brain regions examined, thereby compromising the statistical stability of factor analyses or other, similar techniques for analyzing covariance; (3) use of measures derived from voxel‐based morphometry (VBM), which may be vulnerable to artifacts related to coregistration and which are therefore difficult to interpret biologically; (4) failure to analyze cortical and subcortical volumes concurrently, or investigating only a small set of regions based on a priori hypotheses, thus limiting the inferences that can be made about the brain as a whole; (5) restriction of the analytic approach to a principal component analysis, which is predominantly a technique for data reduction that does not allow for the exploration of the underlying latent causes of volumetric covariance.

In this study, we use factor analysis to identify the latent causes for the patterns of volumetric covariance observed across the brain, including both cortical and subcortical regions, measured in high‐resolution magnetic resonance images (MRIs). We show that our results compare favorably with those obtained in postmortem data from humans and from other species that have been analyzed using similar statistical techniques. We also assess how these latent structures of volumetric covariance correlate with behavioral and neuropsychological variables. Finally, we use Structural Equation Modeling (SEM) to test the assumption that volumetric covariance reflects the presence of anatomical or functional connections within circuits whose components and connections are highly specified, such as cortico‐striatal‐thalamic‐cortical (CSTC) circuits [Albin et al.,1995; Alexander et al.,1990; Haber et al.,1995; Middleton and Strick,2002; Voorn and Louk,2004]. We attempt to address the methodological limitations of prior studies by controlling for the effects of age and whole brain volume (WBV) in analyses of a large sample of healthy individuals, so as to provide a ratio of subjects per brain regions examined that would enhance statistical stability. We also include a large number of children in our analyses to allow assessment of developmental effects on patterns of volumetric covariance. We have elected to study comparatively larger cortical subdivisions to reduce measurement error and inter‐individual variability in regional volumes [Kennedy et al.,1998].

METHODS

Sample Recruitment and Characterization

Our sample consisted of 107 healthy subjects who ranged in age from 7 to 57 years (mean 22.8 years, SD: 13.5 years). Subjects were recruited from a list of 10,000 names purchased from a telemarketing company [Peterson et al.,2001]. The sample was similarly distributed across gender (males: 54.2%) and was predominantly right‐handed (91.6%). We oversampled children (36.4% of the cases were <12 years old) so as to capture developmental effects, which tend to occur more rapidly in children than in adults. The socioeconomic status (SES), estimated with the Hollingshead Index of Social Status, indicated that our sample was primarily middle to upper middle class (mean: 46.5, SD: 10.8) [Hollingshead,1975].

Exclusion criteria included: (1) age 60 years or older; (2) any current Axis I disorder or lifetime history of psychotic disturbance, substance dependence, tic disorder, OCD, ADHD, seizure, head trauma with loss of consciousness, or other neurologic disorder; (3) IQ < 80. Psychiatric diagnoses were established using the Kiddie‐Schedule for Affective Disorders and Schizophrenia Epidemiologic version for children [Kaufman et al.,1997] or the Schedule for Affective Disorders and Schizophrenia for adults [Endincott and Spitzer,1978]. From our total sample of 107 subjects, eight had one or more brain regions defined, either because of technical limitations associated with partial volume effects, or because tissue contrast was inadequate to delineate them accurately; therefore, we elected not to risk adding this measurement noise to the covariance structure of our data. Thus for factor analysis, which requires that data for all regions be analyzed, we used data from the remaining 99 subjects (mean age 21.3 years, SD 13.4 years, males 53%, right‐handed subjects 90.9%). For SEM, not all regions are necessary for the analysis, and therefore we used data from all 107 subjects.

Neuropsychological Assessment

IQ estimates based on standard assessments [Naugle et al.,1993; Peterson et al.,2001; Weschler,1981] for 88 members of the total sample included Full‐Scale IQ (FSIQ) (mean: 119.69, SD: 17.46), Verbal IQ (VIQ) (mean: 118.39, SD: 18.73), and Performance IQ (PIQ) (mean: 116.76, SD: 17.35). In addition, we employed the Stroop task to assess mental flexibility and response inhibition [Stroop,1935] in 66 members of the total sample. The Stroop is composed of three tasks (A, B, and C). In Task A, subjects were asked to name as quickly as possible the color (red, green, or blue) of 126 dots, 5.6 mm in diameter, arrayed randomly in nine columns and 14 rows on an 8.5 × 11 inch sheet of white paper, scanned left to right and then top to bottom. In Task B, participants were asked to read as quickly as possible an equal number of similarly arrayed words (“red,” “green,” or “blue”) which were printed in black ink. In Task C, participants were asked to name as quickly as possible a similar array of words written in incongruent colors. To perform task C, subjects had to suppress a prepotent response (word reading) and instead name the color of the ink in which the word was printed. The increase in time required to complete this task compared with the time required to complete tasks A or B represented the effects of interference between word‐naming and color‐naming. An index that gauges these interference effects was derived based on time to complete each of the three tasks. Stroop interference scores were calculated using the following formula: C – [(A × B)/(A + C)] [Golden,1978].

MRI Acquisition

Structural images were acquired for each subject using a 1.5 Tesla scanner (GE Signa; General Electric, Milwaukee, WI). Head positioning in the scanner was standardized using canthomeatal landmarks. A three‐dimensional spoiled gradient‐echo sequence was obtained using the following parameters: time to repeat (TR), 24 ms; time to echo (TE), 5 ms; flip angle, 45°; matrix size, 256 × 192; no wrap; number of excitations: 2; field of view (FOV): 30 cm; 124 contiguous sagittal slices, each 1.2‐mm thick.

Image Analysis

Morphometric analyses were performed on Sun Ultra 10 workstations using ANALYZE 7.5 software (Rochester, MN). Images were flipped randomly in the left‐right direction prior to region definition to eliminate the effects of perceptual bias on lateralized measures. Flips were corrected during the calculation of regional volumes. Inter‐rater reliability of the measurements was assessed on 20 scans each measured by four raters. Intraclass correlation coefficients were calculated using a two‐way random‐effects model [Shrout and Fliess, 1979].

Regional cerebral volumes

An isointensity contour function was used along with manual editing to isolate the cerebrum exclusive of the cerebellum. Cerebral hemispheres were divided using a curved hermite spline surface that was interpolated from standard midline landmarks. Our parcellation scheme subdivided the cerebrum into eight regions (frontal, premotor, sensorimotor, parietal, occipital, orbitofrontal, subgenual, midtemporal, and inferior occipital). This scheme utilizes one horizontal plane passing through the anterior commisure (AC)–posterior commisure (PC) line (tangent to the top of the AC and bottom of the PC) and three coronal planes–one tangent to the genu of the corpus callosum, one tangent to the anterior border of the AC, and one through the PC at midline [Peterson et al.,2001; Tailarach and Tournoux,1988] (Fig. 1). We measured the volumes of each of these eight regions, including both gray and white matter.

Figure 1.

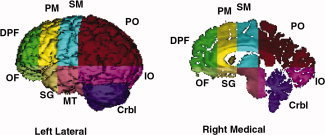
Parcellation units defined using standard anatomical landmarks. The medial view is a parasagittal slice, allowing visualization of structures within the hemisphere. Crbl, cerebellum; DPF, dorsal prefrontal; IO, inferior occipital; MT, mid‐temporal; OF, orbitofrontal; PM, premotor; PO, parieto‐occipital; SG, subgenual; SM, sensorimotor. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]

Volumes of pure cortical gray matter for each parcellation were obtained using a gray‐scale threshold that was calculated as the mean of samples of pure gray matter and pure white matter made bilaterally at four standard locations throughout the cerebrum (frontal, temporal, parietal, and occipital regions). The automated classification of tissues was then edited manually in each of the three views to yield pure cortical gray matter. Intraclass correlation coefficients were >0.98 for volumes of gray matter in each cortical subregion.

Amygdala and hippocampus

Amygdala and hippocampus volumes were defined by manual tracing in the coronal plane using previously described techniques [Kates et al.,1997; Watson et al.,1992]. The anterior limit of the amygdala was the most anterior slice in which the AC crossed the midline. When the boundary between amygdala and hippocampus was not clear, it was defined as the line connecting the inferior horn of the lateral ventricle with the amygdaloid sulcus. If the sulcus was not clearly identifiable, the boundary was defined as a straight horizontal line connecting the inferior horn of the lateral ventricle with the surface of the uncus. The posterior limit of the hippocampus was the last slice in which the crus of the fornix and the fimbria could be identified. Intraclass correlation coefficients were >0.85 for the amygdala and >0.90 for the hippocampus.

Whole brain volume

Whole brain volume (WBV) was used to control for the generalized effects of scaling. The measure included gray and white matter as well as ventricular CSF (cerebrospinal fluid) and CSF spaces within the brain.

Statistical Analyses

These were performed using SAS® v 9.1 (SAS Institute, Cary, NC) and SPSS 13.0 (SPSS, 2004) software packages. Distributions and outliers for each variable were assessed by calculating mean, variance, skew, and kurtosis and by visually inspecting Q/Q plots and box plots.

Exploratory factor analysis

Regional brain volumes were regressed individually with either age or WBV or both. Residuals were then calculated for each individual regression and used to construct the covariance matrices. Residual plots and residual Q/Q plots were also produced for each regression. We analyzed a total of four covariance matrices: (1) one generated using raw volumes, (2) one generated using residuals obtained after controlling for WBV (and therefore after controlling for scaling effects), (3) one generated using residuals after controlling for age, and (4) one obtained using residuals generated after controlling for both WBV and age. Two independent factor analyses based on each covariance matrix were performed separately, using volumes from the right and left hemispheres. This strategy was chosen to decrease the number of variables to be entered in the factor analysis (i.e. to increase the subject‐to‐variable ratio). Squared multiple correlations were used as prior communality estimates. A maximum likelihood method was employed to extract factors, and then a varimax rotation was applied. The number of eigenvectors to be extracted was based on inspection of the scree‐plot. A variable was considered clearly to load on one factor if the loading on the factor was 0.40 or greater. Finally, a promax rotation was applied to the factor structure to assess whether an oblique rotation (which allows factors to be correlated) yielded a substantially different factor structure. Because the oblique rotation yielded the same factor pattern, however, only the varimax rotation is reported.

Regression analyses using factor scores

Estimated factor scores were calculated for each subject and regressed separately on psychometric and behavioral measures. PIQ and VIQ were not entered in the same regression model because of their high inter‐correlation.

SEM of volumes within CSTC circuits

Whereas exploratory factor analysis (EFA) does not make any assumption about the underlying structure of the data and is most commonly used as a theory‐building tool [Kline,2005], SEM is a form of covariance analysis that allows testing of a priori propositions about causality among variables. Thus, SEM requires specification of a causal model that is subsequently tested on observed data. The causality that is tested is a statistical one that represents the linear influence of an independent variable on a dependent one. The model is called “structural” because it assesses causal statistical relationships among latent variables, which represent theoretical constructs that underlie specific manifestations of those constructs in measured observations (manifest variables). Explicit theories or models of the causal relationships among the latent variables are specified a priori, and their fit to observed data is assessed. To fit the observed data well, these explicit models should constructed to be as parsimonious as possible, and they should be based on previous empirical evidence for the existence of the proposed causal pathways. SEM and related techniques have been used in previous imaging studies to assess models of functional connectivity across brain regions [Glabus et al., 2003].

We chose to study CSTC circuits using SEM because these circuits have been investigated extensively and are anatomically well described in multiple animal models [Albin et al.,1995; Alexander et al.,1990; Haber et al.,1995; McHaffie et al.,2005; Middleton and Strick,2002; Voorn and Louk,2004]. Therefore, a causal model for this human imaging study rests on a solid empirical foundation from extensive prior animal studies. The specific model tested here is shown in Figure 2. Arrows indicate statistical pathways of linear influence from one (independent) variable upon another (dependent) variable. We elected to enter overall cortical volume, instead of individual subregions within cortical gray matter, as the only exogenous latent variable influencing volumes of the basal ganglia nuclei because virtually the entire cortical mantle projects to the basal ganglia [Heimer,2003], and because use of overall volume limited the numbers of paths tested in the model, thereby enhancing its overall statistical stability. Based on prior animal studies, cortical volume was postulated to determine volumes of both the putamen and caudate nuclei; in turn, caudate and putamen volumes were postulated to determine volumes of the globus pallidus, which then influenced thalamic volumes further downstream. We entered putamen, caudate, and globus pallidus as latent variables representing shared variance between homologous structures in the left and right hemispheres [Raz et al.,2005]. We included feedback projections from the thalamus to the putamen and caudate nuclei, because the globus pallidus is known in animals to project to the centromedian and parafascicular nuclei of the thalamus, which in turn project back to the striatum [Smith et al.,2004]. The known feedback paths from the thalamus to the cortex in animals could not be modeled here, because introducing paths that pointed to the exogenous latent variable rendered our model statistically unstable.

Figure 2.

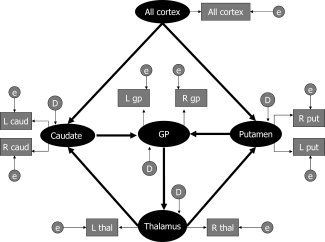
SEM of the CSTC circuit latent variables is denoted by ovals and manifest variables by rectangles. Disturbance factors and errors (both latent variables) are also represented by ovals as they are not measured and are respectively indicated with the letter D and E. In standard SEM language, estimated residuals for the manifest variables are called “errors” and estimated residuals for the latent variables are called “disturbance factors.” Thick arrows represent the structural paths. Thin arrows represent the manifest paths. All cortex, sum of all cortical regional volumes; L cau, left caudate volume; R cau, right caudate volume; L put, left putamen volume; R put, right putamen volume; L gp, left globus pallidus volume; R gp, right globus pallidus volume; L thal, left thalamus volume; R thal, right thalamus volume; e, measurement error.

Data were analyzed in SAS® using the PROC CALIS procedure [Hatcher,1994]. The analysis of covariance structure was conducted using maximum likelihood estimation. The model χ ²/χ ² df ratio was used as a preliminary measure of overall fit, with conventional values for an acceptable fit being <2. Because the null hypothesis was that the specified model would fit the data (i.e., the predicted and observed covariance matrices would not differ significantly), non‐significant χ ² P‐values were required as evidence to support the specified model. Comparative indices of fit reflected the improvement in fit obtained when using the hypothesized model instead of the null or baseline model. Therefore, a Non‐Normed Fit Index (NNFI) > 0.9 and a Comparative Fit Index (CFI) > 0.9 were interpreted as indicating a reasonable fit for the combined model. We also used the Root Mean Square Error of Approximation (RMSEA), an index of the error between the model and the observed data, with values <0.05 or <0.08 indicating excellent and modest approximations, respectively [Stevens,2002]. Convergence of the estimated covariance matrix with the sample covariance matrix was assessed by inspection of the matrix of normalized residuals. Parameter estimates for both manifest and latent variable equations were calculated and construed as indicating the strength of each individual path within the model. In post hoc assessments of the strength of each path within the model, we considered as significant those nonstandardized parameter estimates in which the absolute t‐values were >1.96. Finally, R ² values for latent variables were evaluated because they provided a measure of the variance that was explained by each structural path.

RESULTS

Exploratory Factor Analysis in the Left Hemisphere

We performed an EFA on data from 99 subjects for volumes in the left side of the brain (Table I) with a subject‐to‐variable (STV) ratio of 6.6. We carried out EFA without controlling for age and WBV and controlling for either covariate, one at a time. When covariate effects were not removed, we could not discern a clear factor structure because of the effects of scaling on the analyses, which produced one factor that accounted for most of the overall variance, as well as three other factors that could not be interpreted. When the effects of only one covariate at a time were removed, a factorial structure could then be discerned (less so in the right hemisphere), although its interpretation was difficult for cortical areas because they are more sensitive to the effects of age and WBV. Thus, we report results for analyses in which we removed the effects of both covariates first because those results were most readily interpretable.

Table I.

Exploratory factor analyses of left and right gray matter volumes

	Left hemisphere				Right hemisphere
	Limbic factor (factor 1)	Dorso‐cortical factor (factor 2)	Posterior factor (factor 3)	Basal ganglia factor (factor 4)	Posterior factor (factor1)	Limbic factor (factor 2)	Dorso‐cortical factor (factor 3)	Basal ganglia factor (factor 4)
Frontal cortex	8	52	8	3	−9	6	47	17
Premotor cortex	49	26	−33	−27	30	26	34	−44
Sensorimotor cortex	13	69	6	−2	7	18	67	0
Parietal‐occipital cortex	13	71	−30	−10	26	−2	60	0
Orbitofrontal cortex	64	4	−20	20	44	59	−7	−4
Subgenual cortex	83	13	13	−25	5	73	10	−42
Midtemporal cortex	58	39	23	8	−7	56	37	−2
Inferior occipital cortex	−5	11	75	−4	−73	35	8	12
Caudate	0	−1	−8	22	10	−11	12	21
Putamen	−8	1	−5	55	9	7	−6	70
Globus pallidus	7	3	−14	62	3	3	13	38
Amygdala	53	7	−32	22	71	36	−1	21
Hippocampus	3	−1	3	10	−5	15	2	6
Brainstem	−22	−4	25	−10	−32	−5	−6	−4
Thalamus	3	28	−51	15	52	−13	13	5

From the covariance matrix obtained after removing the effects of age and WBV, we extracted four eigenvectors that accounted for 55, 22, 18, and 13%, respectively, of the total shared variance. Regions in the left hemisphere that loaded on the first factor included, in order, the subgenual, orbitofrontal, and midtemporal cortices, the amygdala, and the premotor cortex. We interpreted this first factor as a “limbic system.” Brain areas that loaded on the second factor included the sensorimotor, parieto‐occipital, and prefrontal cortex. We interpreted this second factor as a “dorsal cortical system.” The third factor was associated with loadings of opposite signs for the inferior occipital cortex and left thalamus. We construed this third factor as a “posterior system”. The globus pallidus and putamen loaded on the fourth factor, which we interpreted as a “basal ganglia system.”

Exploratory Factor Analysis in the Right Hemisphere

We also performed EFA on data from the same 99 subjects for volumes in the right side of the brain (Table I). From the covariance matrix obtained after removing the effects of age and WBV, we extracted four eigenvectors which accounted for 45, 18, 17, and 14%, respectively (and 94% overall), of the total shared variance. Right‐hemisphere brain regions that loaded on the first factor included, in order, the inferior occipital cortex, thalamus, orbitofrontal cortex, and amygdala from negative to positive loadings, which we interpreted as a “ventral‐posterior system.” Brain areas that loaded on the second factor included the subgenual, orbitofrontal, and midtemporal cortices, which we interpreted as a “limbic system.” The third factor was associated with loadings of sensorimotor, parieto‐occipital, and frontal cortices, thus representing a “dorsal cortical system.” Finally, the putamen loaded on the fourth factor, which also showed negative loadings for premotor and subgenual cortices. We interpreted this fourth factor as a “basal ganglia system.” The orbitofrontal and subgenual regions both loaded onto more than one factor. Thus across the analyses of the left and right hemispheres, the results from EFA reveal that the brain is organized into four volumetric systems in both hemispheres, with some minor variation as to the identity of the loading regions.

Regressions of Factor Scores

Regressions of factor scores with Stroop interference scores in subjects for whom these scores were available (N = 63) were significant in the right hemisphere for the ventral‐posterior system (PE = 0.00341, P = 0.02, adjusted R ² = 0.069) (Fig. 3). Factor scores did not correlate significantly with gender, SES scores, or IQ scores. Because some of these measures were not available for the entire sample, these correlation analyses may have suffered from reduced statistical power to detect real effects.

Figure 3.

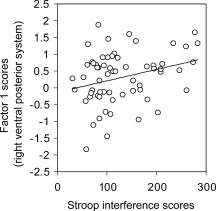
Correlation of factor scores with behavioral measures (Stroop scores) Right hemisphere. Scatterplot representing the relationship between scores for the ventral‐posterior system (factor 1) on the y‐axis and Stroop scores on the x‐axis. The scatterplot indicates that larger latent volumes for the ventral posterior system are correlated with worse performance on the Stroop task (i.e. inability to suppress automatic responses). Factors scores are conventionally reported as standardized and centered scores and they range between −1.83 and +1.86 with raw volumes that load on this factor ranging from 1,054 mm³ (Right Amygdala) to 54,401.25 mm³ (Parieto‐Occipital Cortex).

SEM

Modeling CSTC circuits using volumetric measures without controlling for age or WBV showed an acceptable overall fit with the data (Model χ ² P value = 0.08, Model χ ²/χ ² df ratio = 0.91, NNFI = 0.98, CFI = 0.98, RMSEA estimate = 0.06, N = 107). Normalized residuals yielded a distribution centered on zero, with no residual >2. Small normalized residuals (<2) with symmetric distribution centered on zero are preferable, as they indicate that the model predicts the observed covariances well. All paths were statistically significant (t‐values > 1.96), with the exception of the feedback paths from thalamus to the putamen and caudate. Standardized parameter estimates for significant paths are provided in Figure 4 (Panel A). Three latent variables had R ² values >0.25 (R ² _putamen = 0.56, R ² _caudate = 0.43, R ² _{globuspallidus} = 0.55).

Figure 4.

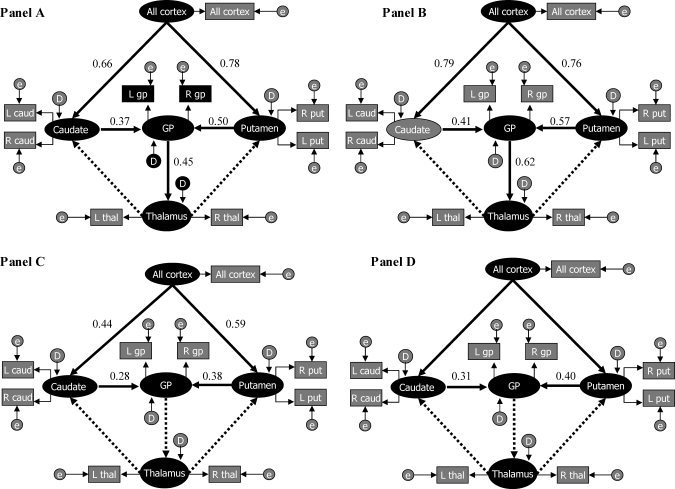
SEM of CSTC circuits. Panel A: Without covariates. Panel B: Controlling for age effects. Panel C: Controlling for scaling effects. Panel D: Controlling for age and scaling effects latent variables are denoted by ovals and manifest variables by rectangles. Disturbance factors and errors are also represented by ovals as they are not measured and are respectively indicated with the letter D and E. In standard SEM language, estimated residuals for the manifest variables are called “errors” and estimated residuals for the latent variables are called “disturbance factors.” Thick arrows represent the hypothesized structural paths. Thin arrows represent the manifest paths. Structural paths for which the parameter estimates are significant are indicated by thick arrows. Non‐significant paths are indicated by thick broken arrows. Standardized parameter estimates are reported.

When controlling only for age, the fit of the model to the observed data was more limited than when not controlling for those effects (Model χ ² P value = 0.0021, Model χ ²/χ ² df ratio = 2.05, NNFI = 0.95, CFI = 0.96, RMSEA estimate = 0.09, N = 107). None of the values of normalized residuals was >2. All paths continued to show t‐values >1.96, with the exception of the feedback paths from thalamus to the putamen and caudate. Standardized parameter estimates for significant paths are provided in Figure 4 (Panel B). Three latent variables had R ² values >0.25 (R ² _putamen = 0.37, R ² _caudate = 0.48, R ² _{globuspallidus} = 0.60).

When controlling for the effects of scaling across brain regions by covarying for WBV, the model fit the data well (Model χ ² P value = 0.15, Model χ ²/χ ² df ratio = 1.28, NNFI = 0.98, CFI = 0.98, RMSEA estimate = 0.05, N = 107). None of the values of normalized residuals was >1.5. Only cortical–striatal paths and striatal–pallidal paths continued to show t‐values >1.96. Standardized parameter estimates for significant paths are provided in Figure 4 (Panel C). Two latent variables showed R ² values >0.25 (R ² _putamen = 0.35, R ² _{globuspallidus} = 0.28).

Finally, the fully adjusted model constructed from volumetric measures obtained after controlling for age and WBV showed an acceptable overall fit, with the exception of a non‐optimal model χ ² P‐value (Model χ ² P value = 0.03, Model χ ²/χ ² df ratio = 1.57, NNFI = 0.96, CFI = 0.97, RMSEA estimate = 0.07, N = 107). Normalized residuals yielded a distribution centered on zero, with only one residual >2 (residual referring to the covariance between volumes of the right caudate and right putamen). Only paths leading from the putamen or caudate to the globus pallidus yielded parameter estimates having significant t‐values (>1.96). Standardized parameter estimates for significant paths are provided in Figure 4 (Panel D). Only one latent variable had R ² values >0.25 (R ² _{globuspallidus} = 0.26).

DISCUSSION

To our knowledge, this is the first study to apply both Exploratory Factor Analysis and SEM to anatomical brain measures from a large sample of children, adolescents, and adults. Factor analyses of volumetric covariances demonstrated that the latent structure of regional brain volumes in each hemisphere is organized into dorsal cortical, limbic, posterior, and basal ganglia systems. These systems can be interpreted as latent standardized volumes (they are standardized because we controlled for scaling effects). The latent volumes of one system in the right hemisphere (the posterior system) correlated with behavioral measures of response inhibition, and we interpreted these findings as signifying that larger latent volumes in this system are associated with poorer behavioral performance. Finally, we used SEM to test and confirm hypotheses concerning structural connectivity within CSTC circuits. Our findings indicated that the CSTC model is sensitive to the effects of age, thus suggesting the presence of strong developmental determinants of anatomical volumes in cortical‐subcortical pathways. Furthermore, we demonstrated that the causal paths of volumetric covariance in the CSTC circuit follow the paths of known anatomical and functional circuitry described previously in animal studies.

Factor Analyses

Our in vivo evidence for the existence of discrete dorsal cortical and limbic volumetric systems within the human brain is similar to findings from prior morphological studies in humans and animals. One human imaging study, for example, identified a fronto‐parietal and a limbic‐paralimbic system based on estimates of the degree of heritability of each regional volume in the brain [Wright et al.,2002]. Furthermore, a multivariate analysis of volumetric measures from brains in 131 species across three orders (insectivores, bats, and primates) demonstrated that the isocortex and the olfactory bulb (along with other classically limbic areas) load onto two separate factors [Finlay and Darlington,1995].

We also identified a discrete basal ganglia system, comprising slightly differing structures in each hemisphere. In the left hemisphere, this system included the putamen and globus pallidus, whereas in the right hemisphere, it included the putamen together with the subgenual and premotor cortices. These findings in the right hemisphere are consistent with extensive neuroanatomical evidence suggesting that the ventral striatum is closely linked anatomically to subgenual cortices [Haber et al.,1995; Heimer,2003] and that the dorsal striatum is linked anatomically with the premotor cortex [Herrero et al.,2002; Middleton and Strick, 2000]. We have no clear explanation, however, for the differences in factor loadings between hemispheres identified within this system.

We identified a posterior volumetric system that included the inferior occipital cortex and thalamus in both hemispheres, as well as the orbitofrontal cortex and amygdala in the right hemisphere. Our finding of right‐left asymmetry in the constituent components of this posterior system (i.e. inclusion of the amygdala and orbito‐frontal cortex on the right side but not on the left) is supported by the prior observation that volumetric correlations of the right and left amygdala with other brain regions differ across hemispheres [Mechelli et al.,2005]. Moreover, these anatomical asymmetries in the amygdala may have functional correlates. The right amygdala and right visual areas exhibit enhanced functional coupling, with the right amygdala likely providing top‐down modulation of sensory input to visual areas, possibly biasing right‐sided visual systems toward emotionally salient stimuli [Noesselt et al.,2005]. This functional distinction of the right and left amygdala agrees with our findings. We believe that the left posterior system may represent a simple visual network, whereas the right posterior system represents a ventral posterior emotional–attentional network that includes not only the occipital cortex and thalamus, but also the amygdala and the orbitofrontal cortex. This hypothesized function of the right posterior system is consistent with the preferential role of the right hemisphere in mediating attentional processes [Corballis,2003; Pardo et al.,1991; Posner and Petersen,1990] and with the inclusion of the orbitofrontal cortex (OFC) in an emotional attentional system that detects affectively salient stimuli [Corbetta and Shulman,2002; Schoenbaum et al.,2006].

Regressions of Factor Scores With Measures of Cognitive Functioning

We observed a positive association between scores on the Stroop task and factor scores for the posterior cortical system in the right hemisphere (Fig. 3), perhaps reflecting the preferential role of this system for mediating inhibitory control and attentional processes [Marsh et al.,2006; Peterson et al.,1999]. Indeed, this volumetric system includes the visual cortices, amygdala, and thalamus, which we have postulated constitute an emotional–attentional system, and all of which participate in the attentional networks that subserve performance of the Stroop task [Compton et al.,2003; Peterson et al.,2002]. Higher factor scores accompanied worse performance on the Stroop, suggesting that larger latent volumes of this system are associated with worse Stroop performance and, by extension, with poorer emotional‐attentional control. This finding is consistent with prior evidence that better intellectual performance accompanies decreasing thickness of the cortical mantle [Sowell et al.,2001,2003,2004].

SEM of CSTC Circuits

Volumetric covariance is often presumed, though it has not thus far been proved, to represent the presence of underlying structural or functional circuits across brain regions that covary in volume. We therefore used SEM to test the assumption that volumetric covariance represents underlying anatomical or functional connectivity among these regions. Our results showed that paths of causal statistical influence among volumes follow known anatomical paths within CSTC circuits. Furthermore, SEM demonstrated that known anatomical connections accounted for volumetric covariances only under certain conditions. In the model containing no covariates, all paths were significant, except for feedback paths from the thalamus to the striatum. When controlling only for age, the same paths as in the unadjusted model remained significant, but the overall fit for the model was relatively poor. One possible interpretation for the poorer fit when controlling for age is that age drives underlying patterns of morphological causation in the brain.

In contrast, when controlling for scaling effects by covarying for WBV only, the overall fit of the model improved significantly, which we interpreted as indicating that WBV obfuscates the underlying patterns of covariance in these circuits. The effects of WBV may obscure these volumetric relationships because scaling creates a generalized form of covariance among brain regions that is not specific to a given pathway or circuit. Thus, by removing the effects of WBV on the covariance among volumes, we removed “noise” from the structural model. Although the strength of individual paths in the model covarying for WBV appeared smaller than in the prior two models, we emphasize that the magnitude of the individual parameter estimates cannot be interpreted reliably across different models.

Finally, when covarying for both age and WBV, cortico‐striatal and pallido‐thalamic paths were no longer significant, leaving statistically significant only the paths within the basal ganglia nuclei themselves. These findings suggest that the strengths of the cortico‐striatal and pallido‐thalamic paths are driven primarily by the combined effects of age and scaling, consistent with findings when covarying for those effects individually. Paths within the basal ganglia, in contrast, seem to be invariant to age and scaling effects. Thus by hierarchically covarying for differing covariates, we were able to establish that structural models should account for the confounding effects of scaling. The over‐sampling of children ensured that we would not disregard the contribution of developmental processes in establishing cortico‐subcortical connections.

We conclude that the effects of age appear to be more selective and circuit‐specific than are those of scaling, and that these effects likely drive volumetric covariances between the basal ganglia and other brain regions. Indeed, white matter tracts that originate or terminate in the basal ganglia and thalamus are known to mature through childhood and adolescence [Barnea‐Goraly et al.,2005]. Maturational processes involving both the striatum and cortex [Marsh et al.,2006; Sowell et al.,1999] could also plausibly produce volumetric covariation within CSTC circuits. Similar developmental phenomena have been noted among cortical areas, with a strengthening of structural correlations between Broca's area and the temporal lobe likely reflecting the maturation of language‐related circuits and their underlying white matter tracts [Lerch et al.,2006].

Limitations

Although our sample size was relatively large, some investigators believe that the number of subjects included in a factor analyses should exceed 100 or 200. Neuroimaging samples, however, rarely exceed 200 subjects. We therefore chose to address the limitation of sample size in part by ensuring that the ratio of subjects to variables was greater than 5, a standard criterion for the lower limit on the numbers of subjects required for an exploratory factor analysis. We did not apply factor analysis to the left and the right hemispheres concurrently, because we reasoned that the high correlation between identical regions across hemispheres [Mechelli et al.,2005] would produce factors composed only of homologous regions in the right and left hemispheres, leaving little variance to be explained by volumetric covariances among non‐homologous structures. Our scheme for parcellating the cerebrum did not provide regional volumes that followed precise cytoarchitectonic boundaries, although this is true to varying degrees for all parcellation schemes of MRI data [Peterson,2003]. We note that our use of larger parcellation units offers advantages over finer‐grained parcellation schemes, in that smaller subdivisions contain more measurement error and greater inter‐individual variability [Kennedy et al.,1998], which would be detrimental to factor analyses involving those data. Our sample consisted of individuals ranging in age from 7 to 57 years, allowing us to assess the effects of age on our measures of volumetric covariation. Clearly, however, simply controlling statistically for age across the sample does not necessarily eliminate all effects of development on regional volumes. Regression procedures account only for a linear effect of age on regional volumes and the effects of covariates are not identical across all brain regions. Because we performed individual regressions for each region separately prior to entry of the volumes into factor analyses or SEM, however, we allowed the effects of age and WBV to vary independently across regions. Finally, we add that as in all factor analytic techniques, the factor structure that we report should be replicated in an independent sample of subjects using confirmatory factor analysis (CFA). The absence of a sufficiently large replication dataset precluded that analysis.

The Potential Scientific Utility of Latent Volumetric Variables

Latent volumes may prove useful in the identification of disease processes that would not be detectable if only individual volumes were measured and compared across diagnostic groups. Volumetric covariance provides qualitatively different information than does the use of individual regional volumes, and such multivariate techniques are statistically more powerful than more traditional univariate approaches for the analysis of regional volumes. This advantage may be especially useful in the study of the early stages of psychiatric illness, when changes are likely to be small and distributed. Multivariate analyses similar to ours have already been successfully employed to study complex medical datasets [Dempsey et al.,1995; Henessy et al.,2005]. In general, these techniques provide a useful framework for the more efficient and statistically more powerful integration of multidisciplinary and multidimensional datasets, including variables from genetic and developmental studies [Wright et al.,1999]. Arguably, latent volumes and the modeling of entire circuits may be more suitable for correlation with behavioral variables, because behaviors are likely subserved by distributed networks rather than by individual regions. More importantly, confirmatory models such as ours allow one to minimize multiple comparisons by dispensing with the need to select a single brain region to correlate with every other region [Lerch et al.,2006; Mechelli et al.,2005].

Confirmatory models that explore various anatomical or functional circuits should be tested to determine whether pathways within those circuits behave differently in psychiatric patients than in healthy subjects. If volumetric covariation in the normal brain does indeed follow functional and anatomical pathways, as it appeared to do in our model, then alterations of connections within the circuit in disease populations should in principle be detectable using these models. Structural models of a‐priori defined circuits may disclose specific patterns of abnormalities within different patient populations, ultimately revealing the disordered brain architecture that underlies specific neuropsychiatric disorders.