Abstract
Background
The study of how the quality of pediatric end-of-life care varies across systems of health care delivery and financing is hampered by lack of methods to adjust for the probability of death in populations of ill children.
Objective
To develop a prognostication models using administratively available data to predict the probability of in-hospital and 1-year postdischarge death.
Methods
Retrospective cohort study of 0–21 year old patients admitted to Pennsylvania hospitals from 1994–2001 and followed for 1-year postdischarge mortality, assessing logistic regression models ability to predict in-hospital and 1-year postdischarge deaths.
Results
Among 678,365 subjects there were 2,202 deaths that occurred during the hospitalization (0.32% of cohort) and 860 deaths that occurred 365 days or less after hospital discharge (0.13% of cohort). The model predicting hospitalization deaths exhibited a C statistic of 0.91, with sensitivity of 65.9% and specificity of 92.9% at the 99th percentile cutpoint; while the model predicting 1-year postdischarge deaths exhibited a C statistic of 0.92, with sensitivity of 56.1% and specificity of 98.4% at the 99th percentile cutpoint.
Conclusions
Population-level mortality prognostication of hospitalized children using administratively available data is feasible, assisting the comparison of health care services delivered to children with the highest probability of dying during and after a hospital admission.
Introduction
The provision of pediatric palliative care in the United States occurs in a context in which the death of children due to a medical condition is an infrequent event.1 Because of this rarity, the study of pediatric palliative and end-of-life care benefits when conducted from the perspective of large populations, both providing an adequate sample size and also enabling the comparison, among hospitals and across health care systems, of processes of care and of outcomes. In order for studies of this regional or national scale to be feasible, economically and logistically, pediatric researchers use preexisting data, often involving hospital administrative data.2–6
An analytic linchpin in the conduct of such population-level health services research studies is the ability to adjust for individual patient characteristics so that comparisons of hospitals and health care systems in fact compare differences in processes of care, and not merely detect confounded associations arising from differences in the clinical characteristics of patients cared for by these hospitals or systems.7,8 In the particular case of pediatric palliative care health services research, a key concern is the ability to predict the probability that a given type patient will die based on the available demographic and clinical information. Sufficiently accurate calculation of the probability of mortality would enable comparison of the processes of care, such as receipt of palliative or hospice services, or of specific medical interventions, or location of death at home or in a hospital, among patients with similar likelihood of dying.
Importantly, for this form of analytic comparison, emphasis is placed on the phrase “sufficiently accurate,” which implies some degree of tolerance of individual-level predictive error, requiring instead that the group-level predictions of mortality are well-calibrated.9 This tolerance contrasts with the need for virtually perfect accuracy for any scheme of mortality prediction used to guide the care of individual patients, a goal that has eluded various mortality risk scoring systems in the setting of hospital intensive care units.10–15
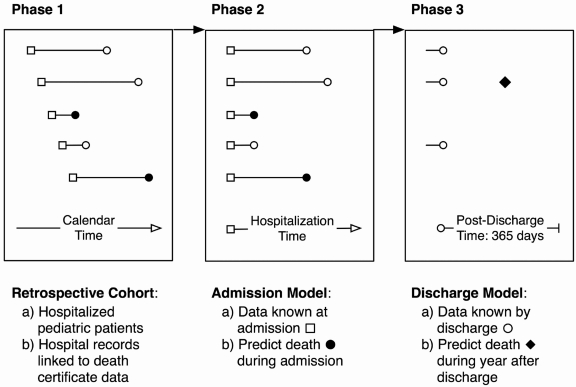
Guided by this line of motivation, we sought to develop, evaluate, and validate a practical pediatric mortality prediction model, based on administrative hospitalization data drawn from a retrospective cohort of children admitted to all Pennsylvania hospitals during a 6-year period and who were assessed for morality during the year after discharge from the hospital. We used two models, one to predict in-hospital deaths and another to predict 1-year postdischarge deaths (Fig. 1). We also aimed to compare the parsimonious model, the components of which were based on our prior population-level research regarding pediatric mortality and end-of-life care, with similar models that also contained severity of illness and risk of mortality scores that were based on more detailed laboratory and physiologic data about patients at the time of admission to the hospital and on the full complement of diagnoses at the time of discharge.
FIG. 1.
Retrospective cohort study design for both models.
Methods
Study design
We conducted a retrospective cohort study of persons less than 21 years of age who were hospitalized in the Commonwealth of Pennsylvania between 1995 and 2000, with 1 year of prehospitalization observation (or less, for subjects under a year of age) to assess for previous hospitalizations, and 1-year of posthospitalization discharge observation to assess 1-year postdischarge mortality. This study was approved by The Children's Hospital of Philadelphia Committee for the Protection of Human Subjects.
Data source
We used data specially prepared by the Pennsylvania Healthcare Cost Containment Council (PHC4). PHC4 matched the administrative hospital record data to death certificate data. We excluded records of normal newborns, patients discharged from psychiatric facilities, and patients who died due to trauma, homicides, suicides, and sudden infant death syndrome.
Selection of index hospitalization and study time
If a patient had more than one hospitalization between 1995 and 2000, we randomly selected a single hospitalization as the index hospitalization. The study time frame for each subject extended from the 365 days prior to the day of admission to the index hospitalization, to 365 days after the index hospitalization discharge.
Outcome of interest
Patients who were observed to have died 365 days ore less after the index hospitalization discharge had the outcome of interest, which were subclassified as having either occurred during the index hospitalization (“hospitalization death”) or during the ensuing 365 days (“1-year postdischarge death”).
Predictor variables
Predictor variables from the index hospitalization were conceptualized as either known at the time of admission to the hospital or at the time of discharge from the hospitalization. Data known at the time of admission included demographic information, certain historical clinical information (including any diagnoses during a prior admission of a Complex Chronic Condition [CCC] based on the International Classification of Disease-9 Clinical Modification codes16–19), and the facilty type for the index hospitalization (classified as pediatric hospital or other). Data known by the end of the index hospitalization included that hospitalization's length of stay, CCC diagnoses, the All Patient Refined-Diagnosis Related Group (APR-DRG), and the APR-DRG-specific risk of mortality (ROM) index rating. The APR-DRG major diagnostic codes were included as 24 indicator variables, and interacted with the APR-DRG specific risk of mortality score, which were ranked ordinally from 0 to 4.
Primary statistical analysis
Two “base” logistic regression models were built to estimate the likelihood of having the outcome of in-hospital and 1-year postdischarge deaths 365 days or less after the index hospitalization discharge. Covariates in both models included information that could be known at the time of hospital admission, as well as indicator variables for 10 of the largest Pennsylvania hospitals as fixed effects. The “admission model” did not contain length of stay or the APR-DRG and APR-ROM measures, since the information upon which these are based is known only at the time of discharge. The “discharge model” did include these variables. These models were then compared to models that included the physiologic MediQual Severity Index.
To evaluate and compare the fit for each of the models, we evaluated each model's C statistic, Brier score20 and Hosmer-Lemeshow test statistic.21 To demonstrate the performance of the chosen model, we also provide a classification of the observed and predicted readmission rates and the sensitivity and specificity at the 95th and 99th percentile probability of death cutpoints.
The models were developed using a random selection of cases comprising half of the original sample, with subsequent assessment of the models on the other “validation” half of the sample. Since the model-fit assessments from the validation subsample were almost identical to the development subsample (for the hospitalization model, C statistics of 0.907 for the development subsample and 0.908 for the validation sub-sample; for the 1-year postdischarge model, 0.928 for development subsample, and 0.940 for the validation subsample), we report the results using the entire sample.
Additional statistical analyses
To assess for potential bias arising from missing data, we performed multiple imputation (using the Stata “ice” command) to compare C statistic results of the models in datasets with imputed missing data. To assess whether the performance of the final prediction model depended upon the particular composition of our dataset, we performed internal validation using the regular bootstrap with 1,000 replications using resampling with replacement.22
All analyses were performed using SAS version 9.1 (SAS Institute Inc, Cary, NC) and Stata SE version 10.0 (Stata Corp, College Station, TX). Due to large sample size, p values less than 0.001 were considered statistically significant.
Results
Characteristics of subjects in the cohort
Among the 678,861 hospitalization records of patients between the ages of 0 and 21 years who were hospitalized in Pennsylvania between 1995 and 2000, there were 2,202 patients (0.32%) who died during the index hospitalization, and 860 (0.13%) patients who died 1 year or less postdischarge from their index hospitalization discharge (Table 1).
Table 1.
Demographic Characteristics of Pennsylvania Pediatric Subjects Who Died Three Hundred Sixty-Five Days or Less after Hospital Discharge
| |
|
|
Death in hospital |
Death after discharge |
||
|---|---|---|---|---|---|---|
| n = | Total 678,635 (100%) | 2202 (0.32%) | p-valueb | 860 (0.13%) | p-valueb | |
| Age | <1 month | 59,351 (8.8%) | 1,496 (2.5%) | < 0.0001 | 12 (0.02%) | < 0.0001 |
| 1–11 months | 99,983 (14.7%) | 330 (0.3%) | 131 (0.13%) | |||
| 1–9 y | 199,734 (29.4%) | 177 (0.1%) | 333 (0.17%) | |||
| 10–18 y | 218,912 (32.3%) | 137 (0.1%) | 272 (0.12%) | |||
| 19–20 y | 100,655 (14.8%) | 62 (0.1%) | 112 (0.11%) | |||
| Gender | Female | 354,945 (52.3%) | 962 (0.3%) | < 0.0001 | 403 (0.11%) | 0.001 |
| Male | 323,613 (47.7%) | 1,240 (0.4%) | 457 (0.14%) | |||
| Missing | 77 (0.01%) | |||||
| Race | White | 449,250 (66.2%) | 1,365 (0.3%) | < 0.0001 | 639 (0.14%) | 0.007 |
| Black | 122,010 (18.0%) | 356 (0.3%) | 135 (0.11%) | |||
| Other | 33,587 (5.0%) | 145 (0.4%) | 34 (0.10%) | |||
| Missing | 73,788 (10.9%) | |||||
| Year admitteda | 1995 | 127,756 (18.8%) | 430 (0.3%) | 0.279 | 149 (0.12%) | 0.586 |
| 1996 | 116,297 (17.1%) | 336 (0.3%) | 160 (0.14%) | |||
| 1997 | 111,050 (16.7%) | 368 (0.3%) | 132 (0.12%) | |||
| 1998 | 103,806 (15.3%) | 337 (0.3%) | 129 (0.12%) | |||
| 1999 | 110,718 (16.3%) | 336 (0.3%) | 158 (0.14%) | |||
| 2000 | 109,008 (16.1%) | 395 (0.4%) | 132 (0.12%) | |||
| Payer | None | 22,600 (3.3%) | 97 (0.4%) | 11 (0.05%) | ||
| Medicaid | 178,092 (26.2%) | 512 (0.3%) | 247 (0.14%) | |||
| Blue Cross | 226,415 (33.4%) | 760 (0.3%) | 279 (0.12%) | |||
| HMO | 138,102 (20.4%) | 435 (0.3%) | 155 (0.11%) | |||
| Othera | 110,663 (16.3%) | 397 (0.4%) | 166 (0.15%) | |||
| Missing | 2,763 (0.41%) | |||||
| Median Income for zip code | ≤$24,000 | 57,761 (8.5%) | 167 (0.3%) | 38 (0.07%) | < 0.0001 | |
| $24,001–$29,000 | 102,243 (15.1%) | 310 (0.3%) | 112 (0.11%) | |||
| $29,001–$35,000 | 131,076 (19.3%) | 415 (0.3%) | 177 (0.14%) | |||
| $35,001–$46,000 | 156,071 (23.0%) | 540 (0.4%) | 214 (0.14%) | |||
| $46,001–$60,000 | 83,692 (12.3%) | 327 (0.4%) | 119 (0.14%) | |||
| >$60,001 | 60,578 (8.9%) | 225 (0.4%) | 58 (0.10%) | |||
| Missing | 87,214 (12.9%) | |||||
| Complex chronic conditions | None | 642,563 (94.7%) | 1,688 (0.3%) | 637 (0.10%) | < 0.0001c | |
| Neuromuscular | 5,545 (0.8%) | 45 (0.8%) | 35 (0.64%) | |||
| Cardiovascular | 10,154 (1.5%) | 254 (2.5%) | 39 (0.39%) | |||
| Respiratory | 2,117 (0.31%) | 31 (1.5%) | 8 (0.38%) | |||
| Metabolic | 749 (0.1%) | 17 (2.3%) | 3 (0.41%) | |||
| Congenital or Genetic | 1,808 (0.3%) | 76 (4.2%) | 6 (0.35%) | |||
| Malignancy | 6,611 (1.0%) | 68 (1.0%) | 116 (1.77%) | |||
| Other | 7,100 (1.1%) | 14 (0.2%) | 11 (0.16%) | |||
| Missing | 1,988 (0.3%) | |||||
| Number of prior hospital admissions | 0 | 609,788 (89.9%) | 2,032 (0.3%) | 303 (0.05%) | < 0.0001 | |
| 1 | 46,205 (6.8%) | 68 (0.2%) | 158 (0.34%) | |||
| 2 | 12,037 (1.8%) | 23 (0.2%) | 107 (0.89%) | |||
| 3+ | 10,605 (1.6%) | 79 (0.7%) | 292 (2.78%) | |||
| Previous complex chronic condition | No | 672,894 (99.2%) | 2,136 (0.3%) | 599 (0.09%) | < 0.0001 | |
| Yes | 5,741 (0.9%) | 66 (1.2%) | 261 (4.60%) | |||
| Length of stay (days) | <2 days | 206,256 (30.4%) | 894 (0.4%) | 156 (0.08%) | ||
| 2–7 days | 407,152 (60.0%) | 560 (0.1%) | 452 (0.11%) | |||
| 8–14 days | 37,346 (5.5%) | 234 (0.6%) | 132 (0.36%) | |||
| 15+ days | 27,974 (4.1%) | 514 (1.8%) | 120 (0.44%) | |||
| Facility type | Pediatric | 175,673 (25.9%) | 945 (0.5%) | 387 (0.22%) | < 0.0001 | |
| General | 502,962 (74.1%) | 1,257 (0.3%) | 473 (0.09%) | |||
| Severity score | 0 | 303,259 (44.7%) | 139 (0.05%) | 139 (0.05%) | < 0.0001 | |
| 1 | 162,785 (24.0%) | 263 (0.2%) | 309 (0.19%) | |||
| 2 | 23,284 (3.4%) | 311 (1.3%) | 154 (0.67%) | |||
| 3 | 6,736 (1.0%) | 389 (5.8%) | 81 (1.28%) | |||
| 4 | 1,030 (0.2%) | 203 (19.7%) | 9 (1.09%) | |||
| Missing | 181,541 (26.8%) | |||||
The category “other insurance” included self-insured individuals.
Univariable logistic regression.
Metabolic and congenital were grouped together for the χ2 test.
Predictive performance of the hospitalization death models
The C statistic for the hospitalization death model without the severity index was 0.912, and with the severity index was 0.937 (Table 2), both high values that suggest “outstanding” discriminative predictive performance.21 Brier scores (with the lowest possible score of 0 connoting perfect prediction) were identical (0.0031) for both models (Table 2). At the 95th and 99th percentiles of the probabilities of death predicted by both models, the specificity of these cutoff values exceeded 92.9%, with sensitivity ranging from 21.6% to 30.7% at the 99th percentile cutoff and from 65.9% to 71.6% at the 95th percentile, for the models without and with the severity score, respectively (Table 2).
Table 2.
Performance Statistics for Models
| |
|
|
Occurrence of death at 95th and 99th percentiles of predicted probability |
||
|---|---|---|---|---|---|
| Model | C statistic | Brier score | 95% | 99% | |
| Hospitalization death | |||||
| A. Without severity score | 0.9122 | 0.0031 | Sensitivity | 65.9% | 21.6% |
| Specificity | 92.9% | 99.2% | |||
| B. With severity score | 0.9364 | 0.0031 | Sensitivity | 71.6% | 30.7% |
| Specificity | 94.5% | 99.2% | |||
| 1-year postdischarge death | |||||
| A. Without severity score | 0.9204 | 0.0012 | Sensitivity | 56.1% | 32.2% |
| Specificity | 98.4% | 99.7% | |||
| B. With severity score | 0.9238 | 0.0013 | Sensitivity | 57.8% | 33.4% |
| Specificity | 98.3% | 99.7% | |||
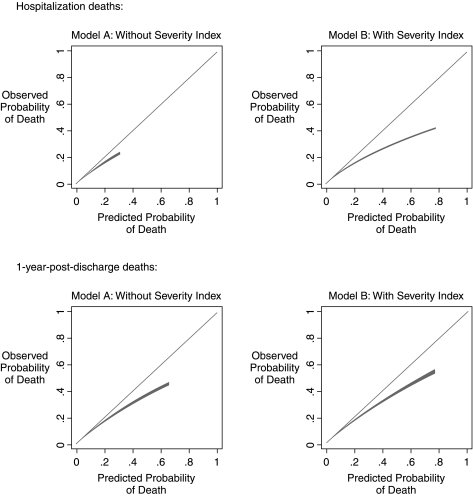
To assess the calibration of the hospitalization deaths models, we plotted the degree of correspondence between the observed proportions of patients who actually died across the range of the predicted probabilities of death (Fig. 2, upper panel), demonstrating a high degree of accuracy of the predictions for both models across the range of predicted probabilities; the model without the severity index generated a small range of predicted mortality values, 0.00006 to 0.3060, whereas the model with the severity index generated values of predicted mortality extending to 0.7888. We also divided the sample into 10 equally sized groups, based on the predicted probability, tabulated the observed number of deaths and the predicted number of deaths in each group (Table 3). This analysis revealed that the model without the severity index was more accurately calibrated than the model with the severity index. The Hosmer-Lemeshow test detected a statistically significant degree of miscalibration in both models, due to the extremely large sample size of the models, as the differences between the observed and expected values within each group are relatively small.
FIG. 2.
Calibration of the mortality prediction models with 95% confidence intervals, which appear as very narrow light gray bands surrounding the linear estimate.
Table 3.
Calibration of Models
| Group | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Hospitalization deaths | ||||||||||
| A: Without Severity Index | ||||||||||
| Probability | 0.0002 | 0.0003 | 0.0003 | 0.0003 | 0.0006 | 0.0009 | 0.0012 | 0.0019 | 0.0076 | 0.3060 |
| Observed | 8 | 11 | 11 | 16 | 15 | 52 | 67 | 70 | 293 | 1659 |
| Expected | 14.4 | 16.6 | 18.4 | 20.8 | 26.7 | 50.6 | 68.2 | 94.4 | 261.3 | 1630.5 |
| Hosmer-Lemeshow χ2 = 24.69, p value = 0.0018 | ||||||||||
| B: With Severity Index | ||||||||||
| Probability | 0.0002 | 0.0002 | 0.0003 | 0.0003 | 0.0005 | 0.0007 | 0.0010 | 0.0019 | 0.0058 | 0.7788 |
| Observed | 9 | 3 | 6 | 3 | 11 | 27 | 37 | 51 | 241 | 1814 |
| Expected | 11.8 | 14.8 | 16.8 | 20.0 | 26.8 | 41.3 | 56.9 | 87.2 | 222.9 | 1703.4 |
| Hosmer-Lemeshow χ2 = 76.67, p value < 0.0001 | ||||||||||
| One-year postdischarge deaths | ||||||||||
| A: Without Severity Index | ||||||||||
| Probability | 0.0000 | 0.0001 | 0.0001 | 0.0002 | 0.0003 | 0.0004 | 0.0005 | 0.0007 | 0.0015 | 0.6555 |
| Observed | 5 | 5 | 4 | 5 | 11 | 13 | 17 | 28 | 50 | 573 |
| Expected | 1.1 | 2.4 | 5.0 | 8.6 | 13.1 | 17.6 | 23.4 | 32.9 | 55.0 | 551.9 |
| Hosmer-Lemeshow χ2 = 24.41, p value = 0.0020 | ||||||||||
| B: With Severity Index | ||||||||||
| Probability | 0.0000 | 0.0001 | 0.0001 | 0.0002 | 0.0003 | 0.0003 | 0.0005 | 0.0007 | 0.0015 | 0.7632 |
| Observed | 5 | 5 | 3 | 3 | 14 | 16 | 10 | 25 | 52 | 578 |
| Expected | 1.1 | 2.3 | 4.7 | 8.3 | 12.6 | 16.6 | 21.8 | 30.9 | 52.4 | 560.3 |
| Hosmer-Lemeshow χ2 = 30.18, p value = 0.0020 | ||||||||||
Predictive performance of the one-year postdischarge models
The C statistic for the 1-year postdischarge death model without the severity index was 0.920, and the C statistic for the model with the severity index was 0.924. Brier scores for both models were very similar, 0.0012 without the severity index and 0.0013 with the severity index. At the 95th and 99th percentile and of 56.1% of the predicted probability for both models, the specificity at these cutoff values exceeded 98.3%, with sensitivity of 32.2% to 33.4% at the 99th percentile and of 56.1% to 57.8% at the 95th percentile cutoff, for the models without and with the severity score, respectively (Table 2).
To assess the calibration of the 1-year postdischarge death models, we again plotted the degree of correspondence between the observed proportions of patients who died across the range of the predicted probabilities of death (Fig. 2, lower panel), demonstrating a high-degree of accuracy of the predictions for both models across the range of predicted probabilities extending from 0 to 0.6552 for the model without the severity index, and extending to 0.7630 for the model with the severity index. We divided the sample into 10 equally sized groups (Table 3); this analysis again revealed that the model without the severity index was more accurately calibrated than the model with the severity index (and again detected a statistically significant degree of miscalibration due to the exceedingly large sample size, with relatively small observed-versus-expected differences).
Sensitivity analyses of the hospitalization and postdischarge models
We conducted two sensitivity analyses to assess the whether the discriminative accuracy of the models (as measured by the C statistic) was influenced by either the small amount of missing data in the original sample, or by the precise configuration of the original sample. Multiple imputation techniques were used to address the potential bias of missing data, and bootstrap re-sampling to address the possibility of model over-fitting (Table 4), we observed essentially identical C statistics and thus no evidence to suggest either type of bias in any of the models.
Table 4.
Sensitivity Analyses of Discriminative Accuracy of Models Comparing Results from Original Sample with Imputed Samples and Bootstrap Samples
| C statistic | ||
|---|---|---|
| Multiple Imputation Samples | Original | Imputed |
| 1. Hospitalization death model with no severity score | 0.9122 | 0.9104 |
| 2. Hospitalization death model with severity score | 0.9364 | 0.9512 |
| 3. 1-year postdischarge death model with no severity score | 0.9204 | 0.9208 |
| 4. 1-year postdischarge death model with severity score | 0.9238 | 0.9246 |
| Bootstrap Samples | Original | Imputed |
| 1. Hospitalization death model with no severity score | 0.9122 | 0.9100 |
| 2. Hospitalization death model with severity score | 0.9364 | 0.9364 |
| 3. 1-year postdischarge death model with no severity score | 0.9204 | 0.9206 |
| 4. 1-year postdischarge death model with severity score | 0.9238 | 0.9241 |
Adjusted associations between patient characteristics and odds of death during index hospitalization
The adjusted odds of death during the index hospitalization (Table 5)was most strongly associated with patient age, with infants less than 1 month of age at the time of hospital admission having 30 times the likelihood of mortality than patients older than 1 year of age at the time of hospital admission (infants 1–11 months of age have a 5-fold increase in the odds of mortality). The size of the age association was comparable to the size of the association with the five levels of the severity score, which demonstrated a 36-fold increase in the odds of death for those patients who had the highest score, compared to those with the lowest score. Examining the association with specific types of complex chronic conditions, patients with malignancies had the highest adjusted odds ratio for the model that did not include the severity score (odds ratio [OR] 5.3, 95% confidence interval [CI]: 4.1–6.9), but a considerably lower score for the model that did include the severity score (OR 1.6, 95%CI: 1.2–2.1), suggesting that the risk of mortality for pediatric oncology patients was strongly associated with the components of the physiologic severity score that were gathered at the time of hospital admission. This contrasts with patients with metabolic disorders, who had the second highest adjusted OR in the model that did not include the severity score (OR 4.4, 95% CI: 2.7–7.3) and the highest and essentially unchanged adjust OR in the model that included the severity score (OR 4.0, 95% CI: 2.4–6.6), suggesting that for these patients, the severity score did not denote a higher risk of mortality. Similarly, the association between the history of 3 or more prior admission and the odds of mortality was essentially the same for the models without (OR 6.7, 95% CI: 4.9–9.2) and with (OR 6.3, 95% CI: 4.6–8.6) the severity index.
Table 5.
Adjusted Associations of Patient Characteristics and Odds of Death in the Hospitalization Deaths Models
| |
|
Base model n = 678558 |
With severity index n = 678558 |
||
|---|---|---|---|---|---|
| OR (95% CI) | p-value | OR (95% CI) | p-value | ||
| Age | <1 month | 38.0 (29.0–49.9) | < 0.0001 | 31.2 (23.7–41.0) | < 0.0001 |
| 1–11 months | 4.7 (3.5–6.2) | 4.8 (3.6–6.4) | |||
| 1–9 y | 1.1 (0.8–1.5) | 1.2 (0.9–1.6) | |||
| 10–18 y | 0.9 (0.7–1.2) | 0.9 (0.7–1.3) | |||
| 19–20 y | Ref | Ref | |||
| Gender | Male | 1.1 (1.0–1.2) | 0.057 | 1.1 (1.0–1.2) | 0.163 |
| Female | Ref | Ref | |||
| Race | White | Ref | 0.3547 | Ref | 0.5227 |
| Black | 1.0 (0.8–1.1) | 0.9 (0.8–1.1) | |||
| Other | 1.1 (0.9–1.3) | 1.1 (0.9–1.3) | |||
| Year admitted | 1995 | 1.1 (0.9–1.2) | 0.0013 | 0.7 (0.6–0.8) | < 0.0001 |
| 1996 | 0.8 (0.7–1.0) | 0.6 (0.5–0.7) | |||
| 1997 | 0.9 (0.8–1.1) | 0.6 (0.5–0.8) | |||
| 1998 | 0.8 (0.7–1.0) | 0.6 (0.5–0.7) | |||
| 1999 | 0.8 (0.7–1.0) | 0.6 (0.5–0.7) | |||
| 2000 | Ref | Ref | |||
| Payer | None | 1.6 (1.3–2.0) | 0.0002 | 1.6 (1.3–2.1) | 0.0003 |
| Medicaid | 1.0 (0.9–1.2) | 1.0 (0.9–1.2) | |||
| HMO | 1.0 (0.8–1.1) | 1.0 (0.9–1.2) | |||
| Other | 0.9 (0.8–1.1) | 1.0 (0.8–1.1) | |||
| Commercial | Ref | Ref | |||
| Median income for subject's zip code | ≤$24,000 | Ref | 0.2540 | Ref | 0.3570 |
| $24,001–$29,000 | 0.9 (0.8–1.1) | 0.9 (0.8–1.1) | |||
| $29,001–$35,000 | 0.9 (0.7–1.0) | 0.9 (0.8–1.0) | |||
| $35,001–$46,000 | 0.9 (0.8–1.1) | 1.0 (0.9–1.1) | |||
| $46,001–$60,000 | 1.0 (0.9–1.2) | 1.1 (0.9–1.2) | |||
| >$60,001 | 1.0 (0.8–1.1) | 1.0 (0.9–1.2) | |||
| Complex chronic condition | None | Ref | < 0.0001 | Ref | < 0.0001 |
| Neuromuscular | 1.8 (1.3–2.4) | 1.3 (0.9–1.7) | |||
| Cardiovascular | 2.8 (2.4–3.2) | 1.1 (0.9–1.3) | |||
| Respiratory | 2.0 (1.4–2.9) | 1.8 (1.2–2.6) | |||
| Metabolic | 4.4 (2.7–7.3) | 4.0 (2.4–6.6) | |||
| Congenital | 4.2 (3.2–5.3) | 2.3 (1.7–3.0) | |||
| Malignancy | 5.3 (4.1–6.9) | 1.6 (1.2–2.1) | |||
| Other | 0.3 (0.2–0.6) | 0.3 (0.2–0.4) | |||
| Previous chronic complex condition | No | Ref | < 0.0001 | Ref | < 0.0001 |
| Yes | 2.1 (1.5–3.0) | 2.4 (1.7–3.5) | |||
| Prior Admission | 0 | Ref | < 0.0001 | Ref | < 0.0001 |
| 1 | 1.5 (1.1–1.9) | 1.6 (1.2–2.0) | |||
| 2 | 2.0 (1.3–3.2) | 2.1 (1.3–3.2) | |||
| +3 | 6.7 (4.9–9.2) | 6.3 (4.6–8.6) | |||
| Facility | Pediatric hospital | 0.3 (0.2–0.4) | < 0.0001 | 0.3 (0.2–0.4) | < 0.0001 |
| Other | Ref | Ref | |||
| Severity score | 0 | Ref | < 0.0001 | ||
| 1 | 0.7 (0.6–0.8) | ||||
| 2 | 3.4 (3.0–3.9) | ||||
| 3 | 10.0 (8.7–11.5) | ||||
| 4 | 36.1 (29.7–44.0) | ||||
The p values for each variable represent the significance test for the entire block of values of that variable.
OR, odds ratio; CI, confidence interval.
The adjusted odds of mortality during the 1-year postdischarge from the index hospitalization (Table 6)was most strongly associated with the number of prior admissions that had occurring during the year before the index hospitalization, with a 20-fold increase (95% CI: 15.9–25.7) in the odds of death among those subjects who had been previously admitted 3 or more times compared to patients who had not been previously admitted. The admission physiologic severity index continued to be significantly associated with post-discharge mortality, but to an attenuated degree compared to the association observed during the index hospitalization, with only a 4-fold (95% CI: 1.6–7.9) increase in the likelihood of death among subjects in the higher index risk levels compared to the lowest level. The types of medical condition most associated with postdischarge death were malignancies (4-fold increase, 95% CI: 1.5–10.1) and neuromuscular conditions (2-fold increase, 95% CI: 1.2–3.0), and having had a diagnosis of any complex chronic condition during a prior hospital admission (1.5-fold increase, 95% CI: 1.2–1.9); none of these associations was substantially different in the models without or with the severity index. Subjects who had been admitted to a pediatric hospital for the index admission had a 2.5-fold increase (95% CI: 0.6–10.5) in the odds of death during the year after discharge, and the likelihood of mortality after discharge was not associated with subjects' age.
Table 6.
Adjusted Associations of Patient Characteristics and Odds of Death in the One-Year Postdischarge Deaths Models
| |
|
Base model n = 549,035 |
With severity index n = 549,035 |
||
|---|---|---|---|---|---|
| OR (95% CI) | p-value | OR (95% CI) | p-value | ||
| Age | <1 month | ||||
| 1–11 months | 0.9 (0.6–1.2) | 0.52 | 0.9 (0.6–1.2) | 0.48 | |
| 1–9 y | 0.8 (0.6–1.0) | 0.8 (0.6–1.0) | |||
| 10–18 y | 0.8 (0.6–1.0) | 0.8 (0.6–1.0) | |||
| 19–20 y | Ref | Ref | |||
| Gender | Male | 0.9 (0.8–1.1) | 0.207 | 0.9 (0.8–1.1) | 0.187 |
| Female | Ref | Ref | |||
| Race | White | Ref | 0.08 | Ref | 0.1308 |
| Black | 0.8 (0.6–1.0) | 0.8 (0.6–1.0) | |||
| Other | 0.8 (0.5–1.2) | 0.8 (0.5–1.2) | |||
| Year | 1995 | ||||
| 1996 | 1.5 (1.2–2.0) | 0.0153 | 1.7 (1.3–2.2) | 0.0025 | |
| 1997 | 1.3 (1.0–1.7) | 1.3 (1.0–1.7) | |||
| 1998 | 1.3 (1.0–1.7) | 1.3 (1.0–1.7) | |||
| 1999 | 1.4 (1.1–1.8) | 1.4 (1.1–1.8) | |||
| 2000 | Ref | Ref | |||
| Payer | None | 0.7 (0.4–1.4) | 0.2134 | 0.7 (0.4–1.4) | 0.2258 |
| Medicaid | 0.8 (0.7–1.0) | 0.8 (0.7–1.0) | |||
| HMO | 0.9 (0.7–1.2) | 1.0 (0.8–1.3) | |||
| Other | 1.1 (0.8–1.4) | 1.1 (0.8–1.4) | |||
| Commercial | Ref | Ref | |||
| Median income for subject's zip code | ≤$24,000 | Ref | 0.0542 | Ref | 0.0644 |
| $24,001–$29,000 | 1.3 (1.0–1.7) | 1.3 (1.0–1.7) | |||
| $29,001–$35,000 | 1.3 (1.0–1.7) | 1.3 (1.0–1.7) | |||
| $35,001–$46,000 | 1.2 (0.9–1.5) | 1.2 (0.9–1.6) | |||
| $46,001–$60,000 | 1.4 (1.1–1.9) | 1.4 (1.1–1.9) | |||
| >$60,001 | 1.0 (0.7–1.4) | 0.9 (0.6–1.4) | |||
| Chronic complex condition | None | Ref | 0.0023 | Ref | 0.0003 |
| Neuromuscular | 1.9 (1.2–3.0) | 2.2 (1.4–3.4) | |||
| Cardiovascular | 1.0 (0.6–1.7) | 1.1 (0.6–1.9) | |||
| Respiratory | 0.7 (0.3–1.8) | 0.9 (0.4–2.3) | |||
| Metabolic and congenital | 0.5 (0.1–2.5) | 0.5 (0.1–2.4) | |||
| Malignancy | 3.9 (1.5–10.1) | 4.0 (1.6–10.4) | |||
| Other | 0.6 (0.3–1.2) | 0.6 (0.3–1.2) | |||
| Previous complex chronic condition | No | Ref | < 0.0001 | Ref | < 0.0001 |
| Yes | 1.5 (1.2–1.9) | ||||
| Prior Admission | 0 | Ref | < 0.0001 | Ref | |
| 1 | 6.9 (5.5–8.7) | 7.3 (5.7–9.2) | |||
| 2 | 14.6 (11.2–19.1) | 15.3 (11.7–20.0) | |||
| +3 | 20.2 (15.9–25.7) | 21.9 (17.3–27.9) | |||
| Facility | Pediatric Hospital | 2.5 (0.6–10.5) | 0.196 | 2.6 (0.6–11.1) | 0.182 |
| Other | Ref | Ref | |||
| Length of stay | <2 days | Ref | < 0.0001 | Ref | 0.001 |
| 2–7 days | 1.2 (1.0–1.5) | 1.2 (0.9–1.4) | |||
| 8–14 days | 1.9 (1.5–2.6) | 1.7 (1.3–2.2) | |||
| 15+ days | 1.9 (1.4–2.6) | 1.6 (1.2–2.2) | |||
| Severity score | 0 | Ref | |||
| 1 | 1.3 (1.1–1.6) | ||||
| 2 | 2.9 (2.2–3.7) | ||||
| 3 | 4.1 (2.9–5.7) | ||||
| 4 | 3.6 (1.6–7.9) | ||||
The p values for each variable represent the significance test for the entire block of values of that variable.
OR, odds ratio; CI, confidence interval.
Association of predicted probability of death after discharge and location of death
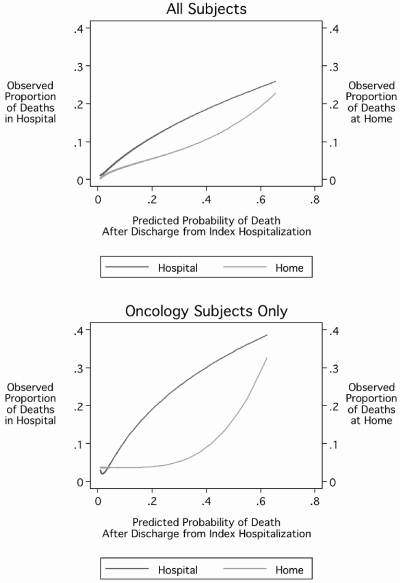
To assess the possible utility of the predicted probability of death, we examined the association between the 1-year post-discharge mortality probability prediction and the proportion of deaths that occurred in either the hospital or the home setting. Among all subjects (Fig. 3, upper panel), as the predicted probability of death increased, the proportion of subjects who died either in the hospital or at home increased, with a slight acceleration in the proportion who died at home as the predicted probability of death increased beyond 0.4. Among only those subjects who had oncologic diagnoses (Fig. 3, lower panel), the same pattern, but more accentuated, was evident. These patterns would be consistent with a pattern of care whereby the planning and provision of home-based end-of-life care services occurs to a greater degree once a certain threshold of 1-year postdischarge mortality risk is exceeded.
FIG. 3.
One-year postdischarge probability of death and location of death.
Discussion
Using readily available administrative data from hospital discharge records, we were able in this large cohort of hospitalized children in Pennsylvania to predict both in-hospital mortality and mortality during the year after discharge with an extremely high level of accuracy. The addition of a “physiologic severity index” that was based upon specially collected clinical and laboratory data for the subjects improved the accuracy of the in-hospital mortality model to a modest degree, but had essentially no impact on the 1-year postdischarge model. Furthermore, these predictions of mortality were associated with demonstrable differences in outcome, specifically regarding location of death among those patients who survived the initial hospitalization, attesting both to the validity of the construct and highlighting how these predictions could be used to assess differences in systems of health care.
This study has several strengths that should be kept in mind. First, applying predictive modeling of mortality probability to populations of patients as an analytic aid in the assessment of end-of-life care and outcomes is innovative, opening new avenues and approaches to palliative care health services research. Second, the population-basis of the cohort minimizes the risk of sampling bias. Third, careful selection of variables contained in the hospitalization model excluded information that was likely unknown on the initial day of the index hospitalization, such as the ensuing length of stay or the final diagnoses as conveyed by the APR-DRG classification. Fourth, the stability of the accuracy of the predictive models was affirmed both by the initial split-sample assessment and by further bootstrap resampling validation, as well as assessing that potential bias due to missing data was minimal through the multiple imputation of missing values sensitivity analysis.
Turning to consider weaknesses of the study, first, we cannot evaluate the completeness or accuracy of the match of hospital records to any corresponding death certificate information. We do note, however, that the occurrence of either failed matches (whereby subjects who died after discharge from the hospital were not identified as having died) or incorrect matches (whereby subjects were classified as having died when in fact they did not) would most likely have resulted in nondifferential misclassification biasing our results toward the null. Second, our results cannot be assuredly extrapolated outside of the cohort, to either other locations or other time periods. Finally, reemphasize a crucial point, these models do not demonstrate sufficient accuracy to be used for individual-level predictions.
We conclude by underscoring three important implications of this study. First, the methodology developed in this study enables population-level comparisons across different systems of health care, adjusting for differences between these systems in terms of patient “case mix” and the associated differences mortality risks, thereby enabling better comparisons of how differences in the processes of care between the systems affect outcomes. For example, with appropriate adjustment for subjects' risk of mortality after discharge, one could analyze how different methods of managing the process of introducing hospice services to patients or families affected the likelihood of deaths occurring back in the hospital or at home. Second, the ability to predict with substantial accuracy the likelihood of death during and then after hospitalization, using only routine administrative hospitalization data, suggests that such comparative studies can be performed widely at relatively low cost. Finally, the strong association between the history of prior hospitalizations and the likelihood of death highlights the value of datasets that enable the longitudinal linkage of hospitalization records for subjects.
Acknowledgments
This study was funded by grant number R21-NR008614 (PI, Chris Feudtner) from the National Institute of Nursing Research of the National Institutes of Health. This funder had no role in the design and conduct of the study, in the collection, analysis, and interpretation of the data, and in the preparation, review, or approval of the manuscript.
Author Disclosure Statement
No competing financial interests exist.
References
- 1.Hamilton BE. Minino AM. Martin JA. Kochanek KD. Strobino DM. Guyer B. Annual summary of vital statistics: 2005. Pediatrics. 2007;119:345–360. doi: 10.1542/peds.2006-3226. [DOI] [PubMed] [Google Scholar]
- 2.Lewis CW. Carron JD. Perkins JA. Sie KC. Feudtner C. Tracheotomy in pediatric patients: A national perspective. Arch Otolaryngol Head Neck Surg. 2003;129:523–529. doi: 10.1001/archotol.129.5.523. [DOI] [PubMed] [Google Scholar]
- 3.Levine LJ. Schwarz DF. Argon J. Mandell DS. Feudtner C. Discharge disposition of adolescents admitted to medical hospitals after attempting suicide. Arch Pediatr Adolesc Med. 2005;159:860–866. doi: 10.1001/archpedi.159.9.860. [DOI] [PubMed] [Google Scholar]
- 4.Zaoutis TE. Argon J. Chu J. Berlin JA. Walsh TJ. Feudtner C. The epidemiology and attributable outcomes of candidemia in adults and children hospitalized in the United States: A propensity analysis. Clin Infect Dis. 2005;41:1232–1239. doi: 10.1086/496922. [DOI] [PubMed] [Google Scholar]
- 5.Brandon D. Docherty SL. Thorpe J. Infant and child deaths in acute care settings: Implications for palliative care. J Palliat Med. 2007;10:910–918. doi: 10.1089/jpm.2006.0236. [DOI] [PubMed] [Google Scholar]
- 6.Feudtner C. Levin JE. Srivastava R. Goodman DM. Slonim AD. Sharma V. Shah SS. Pati S. Fargason C., Jr Hall M. How well can hospital readmission be predicted in a cohort of hospitalized children? A retrospective multi-center study. Pediatrics. 2009;123:286–293. doi: 10.1542/peds.2007-3395. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Rosenbaum PR. Observational Studies. 2nd. New York: Springer; 2002. [Google Scholar]
- 8.Iezzoni LI. Risk Adjustment for Measuring Health Care Outcomes. 3rd. Chicago, IL: Health Administration Press; 2003. [Google Scholar]
- 9.Slater A. Shann F. The suitability of the Pediatric Index of Mortality (PIM), PIM2, the Pediatric Risk of Mortality (PRISM), and PRISM III for monitoring the quality of pediatric intensive care in Australia and New Zealand. Pediatr Crit Care Med. 2004;5:447–454. doi: 10.1097/01.PCC.0000138557.31831.65. [DOI] [PubMed] [Google Scholar]
- 10.Gemke RJ. van Vught J. Scoring systems in pediatric intensive care: PRISM III versus PIM. Intensive Care Med. 2002;28:204–207. doi: 10.1007/s00134-001-1185-2. [DOI] [PubMed] [Google Scholar]
- 11.Grisoni E. Stallion A. Nance ML. Lelli JLJ. Garcia VF. Marsh E. The New Injury Severity Score and the evaluation of pediatric trauma. J Trauma. 2001;50:1106–1110. doi: 10.1097/00005373-200106000-00021. [DOI] [PubMed] [Google Scholar]
- 12.Pollack MM. Patel KM. Ruttimann UE. PRISM III: An updated Pediatric Risk of Mortality score. Crit Care Med. 1996;24:743–752. doi: 10.1097/00003246-199605000-00004. [DOI] [PubMed] [Google Scholar]
- 13.Richardson DK. Gray JE. McCormick MC. Workman K. Goldmann DA. Score for neonatal acute physiology: A physiologic severity index for neonatal intensive care. Pediatrics. 1993;91:617–623. [PubMed] [Google Scholar]
- 14.Slater A. Shann F. Pearson G. PIM2: A revised version of the Paediatric Index of Mortality. Intensive Care Med. 2003;29:278–285. doi: 10.1007/s00134-002-1601-2. [DOI] [PubMed] [Google Scholar]
- 15.Gagliardi L. Cavazza A. Brunelli A. Battaglioli M. Merazzi D. Tandoi F. Cella D. Perotti GF. Pelti M. Stucchi I. Frisone F. Avanzini A. Belló R. Assessing mortality risk in very low birth-weight infants: A comparison of CRIB, CRIB-II, and SNAPPE-II. Arch Dis Child Fetal Neonatal Ed. 2004;89:F419–422. doi: 10.1136/adc.2003.031286. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Feudtner C. Christakis DA. Zimmerman FJ. Muldoon JH. Neff JM. Koepsell TD. Characteristics of deaths occurring in children's hospitals: Implications for supportive care services. Pediatrics. 2002;109:887–893. doi: 10.1542/peds.109.5.887. [DOI] [PubMed] [Google Scholar]
- 17.Feudtner C. Christakis DA. Connell FA. Pediatric deaths attributable to complex chronic conditions: A population-based study of Washington State, 1980–1997. Pediatrics. 2000;106(1 Pt 2):205–209. [PubMed] [Google Scholar]
- 18.Feudtner C. DiGiuseppe DL. Neff JM. Hospital care for children and young adults in the last year of life: A population-based study. BMC Med. 2003;1:3. doi: 10.1186/1741-7015-1-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Feudtner C. Hays RM. Haynes G. Geyer JR. Neff JM. Koepsell TD. Deaths attributed to pediatric complex chronic conditions: National trends and implications for supportive care services. Pediatrics. 2001;107:E99. doi: 10.1542/peds.107.6.e99. [DOI] [PubMed] [Google Scholar]
- 20.Brier GW. Verification of forecasts expressed in terms of probability. Monthly Weather Rev. 1950;78:1–3. [Google Scholar]
- 21.Hosmer DW. Lemeshow S. Applied Logistic Regression. 2nd. New York: Wiley; 2000. [Google Scholar]
- 22.Steyerberg EW. Harrell FE., Jr. Borsboom GJ. Eijkemans MJ. Vergouwe Y. Habbema JD. Internal validation of predictive models: Efficiency of some procedures for logistic regression analysis. J Clin Epidemiol. 2001;54:774–781. doi: 10.1016/s0895-4356(01)00341-9. [DOI] [PubMed] [Google Scholar]