Lower-limb growth: how predictable are predictions?

Abstract

Purpose

The purpose of this review is to clarify the different methods of predictions for growth of the lower limb and to propose a simplified method to calculate the final limb deficit and the correct timing of epiphysiodesis.

Background

Lower-limb growth is characterized by four different periods: antenatal growth (exponential); birth to 5 years (rapid growth); 5 years to puberty (stable growth); and puberty, which is the final growth spurt characterized by a rapid acceleration phase lasting 1 year followed by a more gradual deceleration phase lasting 1.5 years. The younger the child, the less precise is the prediction. Repeating measurements can increase the accuracy of predictions and those calculated at the beginning of puberty are the most accurate. The challenge is to reduce the margin of uncertainty. Confrontation of the different parameters—bone age, Tanner signs, annual growth velocity of the standing height, sub-ischial length and sitting height—is the most accurate method. Charts and diagrams are only models and templates. There are many mathematical equations in the literature; we must be able to step back from these rigid calculations because they are a false guarantee. The dynamic of growth needs a flexible approach. There are, however, some rules of thumb that may be helpful for different clinical scenarios.

Calculation of limb length discrepancy

For congenital malformations, at birth the limb length discrepancy must be multiplied by 5 to give the final limb length discrepancy. Multiple by 3 at 1 year of age; by 2 at 3 years in girls and 4 years in boys; by 1.5 at 7 years in girls and boys, by 1.2 at 9 years in girls and 11 years in boys and by 1.1 at the onset of puberty (11 years bone age for girls and 13 years bone age for boys).

Timing of epiphysiodesis

For the timing of epiphysiodesis, several simple principles must be observed to reduce the margin of error; strict and repeated measurements, rigorous analysis of the data obtained, perfect evaluation of bone age with elbow plus hand radiographs and confirmation with Tanner signs. The decision should always be taken at the beginning of puberty. A simple rule is that, at the beginning of puberty, there is an average of 5 cm growth remaining at the knee. There are four common different scenarios: (1) A 5-cm discrepancy—epiphysiodesis of both femur and tibia at the beginning of puberty (11 years bone age girls and 13 years in boys). (2) A 4-cm discrepancy—epiphysiodesis of femur and tibia 6 months after the onset of puberty (11 years 6 months bone age girls, 13 years 6 months bone age boys, tri-radiate cartilage open). (3) A 3-cm discrepancy—epiphysiodesis of femur only at the start of puberty, (skeletal age of 11 years in girls and 13 years in boys). (4) A 2-cm discrepancy—epiphysiodesis of femur only, 1 year after the start of puberty (12 years bone age girls and 14 years in boys).

Growth is a change in proportion

At birth, the standing height is 50 cm: 70% (35 cm) for sitting height and 30% (15 cm) for sub-ischial length. In contrast, at skeletal maturity, the sitting height accounts for 52% of the standing height and the sub-ischial length is 48%. Sitting height will increase by 53 cm in girls and by 57 cm in boys. Sub-ischial length increases from 15 cm at birth to 81 cm in boys and 74.5 cm in girls at skeletal maturity.

Thus, from birth to skeletal maturity, lower-limb length increases by a factor of 5.25 compared with only 2.67 times for spinal growth. This is the first important factor in the management of lower-limb growth discrepancies.

Repeated serial measurements of standing height, sitting height and sub-ischial lengths are the only way to best capture the complexity of growth. These measurements provide a real-time image of growth and, when carefully recorded in a continually updated “growth notebook”, they provide charts that assist in decision-making processes [1, 2].

Periods of growth

Growth is a complex and well-synchronized phenomenon that dictates the final stature and proportions in adult life. It is difficult to capture such complexity with two-dimensional graphs and mathematical equations. However, in order to facilitate our comprehension of this remarkable process, we may conveniently separate growth into four time periods:

1. Antenatal growth

2. Birth to 5 years of age

3. 5 years of age to puberty

4. Puberty

Antenatal growth–exponential growth

At 3 months of intra-uterine life, the cartilaginous anlage is complete and ossification has begun. By 14 weeks, primary ossification is sufficient to allow ultrasonographic measurement of femoral length, and the length of the femur is 14 mm and the tibia is 11 mm. Longitudinal growth continues, as shown in Fig. 1, so that by full term the femoral diaphyseal length is 75 mm and the tibia diaphyseal length is 62 mm. At birth, the lower limbs reach 20% of their final length.

Fig. 1.

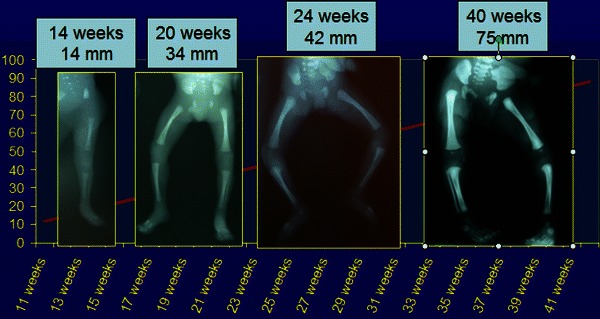
Foetal femoral diaphyseal growth with radiographic images at 14, 20, 24 and 40 weeks

Modern ultrasonography can give an idea of foetal lower-limb growth during antenatal life, and there are many established databases for estimating foetal femoral length [3–6]. The growth curve gives the impression that growth is linear but, by closer analysis of antenatal growth velocity, we can see that there is a definite peak of growth velocity at 4 months (Fig. 2). Ultrasound evaluation, however, can only measure the ossified portion of the long bones, i.e. the diaphysis, and thus all subsequent calculations must take this into account.

Fig. 2.

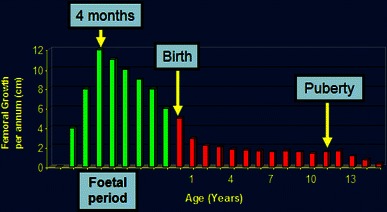
Femoral growth velocity from the foetal period to skeletal maturity (girls) demonstrating a peak growth velocity at 4 months of antenatal life

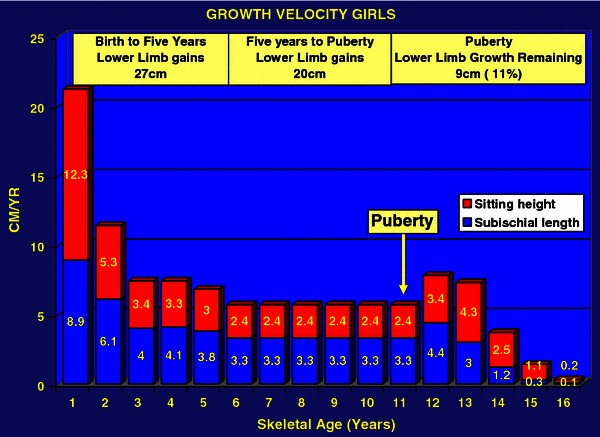
Birth to 5 years

From birth to 5 years, the standing height increases from 50 to 105 cm. The sub-ischial length gains about 27 cm from birth to 5 years of age: 10 cm in the first year; 5 cm in the second year; and 4 cm in each of the third, fourth and fifth years (Figs. 3, 4).

Fig. 3.

Growth velocity in boys from birth to skeletal maturity

Fig. 4.

Growth velocity in girls from birth to skeletal maturity

At birth, the difference between the femur and tibia length is 1.2 cm, compared with 10 cm at skeletal maturity. Importantly, the tibia remains at a constant length of 80% of femoral length throughout growth. This is very useful information because the relative lengths remain the same regardless of the position of the child on the growth curve.

Five years to puberty

From 5 years to the onset of puberty, growth velocity stabilizes. The standing height increases from 108 to 153 cm in boys and from 107 to 143 cm in girls. The annual growth velocity of the standing height reduces to 5.5 cm/year, of which 3.2 cm/year is the sub-ischial length, i.e. 65% of height gain is from the lower limbs versus only 35% from the sitting height during this period. The knee (distal femur plus proximal tibia) grows at an average of 2 cm/year until puberty. This is a relative catch-up time in terms of growth for the lower limbs in comparison with spinal growth.

Puberty

The final growth spurt before skeletal maturity commences at the onset of puberty. This starts at 13 years of bone age for boys and 11 years of bone age for girls. Growth velocity increases from 5.5 to 7.8 cm/year. Standing height increases from 153 cm (±1 cm) to 175 cm (±1 cm) in boys and from 142 cm (±1 cm) to 162 cm (±1 cm) in girls. Therefore, the average growth remaining at the onset of puberty in terms of standing height is 22 cm (±1 cm) for boys and 20 cm (±1 cm) for girls [2]. The growth remaining in the lower limbs is ~10 cm in boys and 9 cm in girls (Figs. 5, 6). Lower-limb growth velocity increases from 3.2 to 5 cm/year at the peak of puberty. Peak growth velocity in the lower limbs occurs 6 months earlier than spinal growth peak velocity, i.e. at 14 years skeletal age in boys and 12 years skeletal age in girls. Lower-limb growth during puberty is characterized by rapid growth acceleration for 1 year only followed by a more gradual deceleration phase. Growth in the lower limbs will cease 2 years and 6 months after the onset of puberty, after elbow closure, when the distal phalangeal physes have fused and at Risser 1 [2].

Fig. 5.

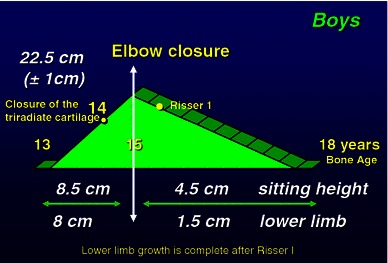
Pubertal growth in boys [24, p 44]

Fig. 6.

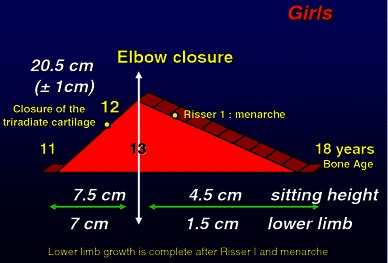
Pubertal growth in girls [24, p 43]

Therefore, it can be seen that lower-limb growth relative to spinal growth decreases, with only 45% of height achieved during puberty coming from the lower limbs. This is because lower-limb growth ceases before spinal growth.

Once puberty has started the time remaining for lower-limb growth is very short. Decisions in relation to the timing of epiphysiodesis must be taken at the very start of puberty, otherwise it will be too late.

Predicting limb length inequality

When considering limb discrepancy we must answer three fundamental questions;

• What will be the final deficit?

• What will be the final stature?

• What is the correct timing for epiphysiodesis?

Final deficit estimation

To consider the final deficit, it is important to make the distinction between congenital limb deficiencies and post-traumatic growth disturbances. In congenital limb discrepancies, the relative discrepancy remains static throughout growth. There is usually a constant growth inhibition such that the percentage shortening remains constant during skeletal growth [7]. Post-traumatic discrepancies, however, should be calculated by estimating the amount of growth remaining at the injured growth plate along with the skeletal age. For example, a boy with a post-traumatic growth arrest at the distal femur at a skeletal age of 9 years will have a final discrepancy of 1.1 cm multiplied by 7 (years of growth remaining): equals 7.7 cm.

Growth of the lower limb was been very well documented by Anderson and Green [8]. From their work, we know that, after 5 years, the lower limbs grow 3.5 cm/year; 2 cm/year in the femur and 1.5 cm/year in the tibia. There are many methods to predict final leg length inequality; the methods of Lefort, Moseley, Carlioz, Menelaus and Paley [9–13] are all based on the data of Green and Anderson. They merely reflect different mathematical formulas of the same data. There is an easy rule of thumb to predict the final deficit at skeletal maturity when managing lower-limb discrepancies.

At birth, the lower limb has reached 20% of its final length, the multiplier factor is therefore 100/20 = 5. Therefore, for a discrepancy of 3 cm at birth, you multiply by 5 to give a final predicted discrepancy of 15 cm. At 1 year, the acquired length is 33%, therefore the multiplier is 100/33 = 3; at 4 years in boys and 3 years in girls the acquired length is 50% and the multiplier is 100/50 = 2; at 7 years the acquired growth is 65% and the multiplier is 100/65 = 1.5; at the onset of puberty the acquired growth is 90% and the multiplier is 100/90 = 1.1 (Figs. 7 and 8). The younger the child, the less precise are the predictions; however, repeating measurements can increase the accuracy of predictions.

Fig. 7.

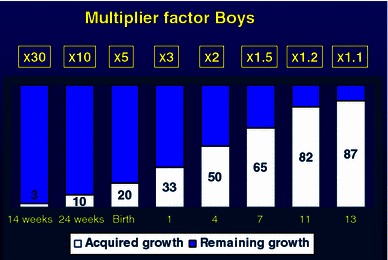
Multiplier factor for boys from fetal life to skeletal maturity. At birth the acquired length is 20% therefore multiplier by 5 to calculate the estimated limb length discrepancy; multiply by 2 at 4 years of age and by 1.1 at the onset of puberty

Fig. 8.

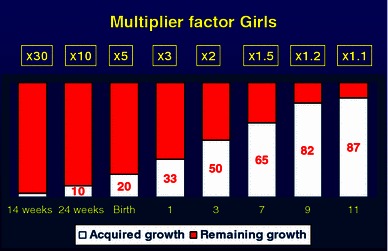
Multiplier factor for girls from fetal life to skeletal maturity. At birth the acquired length is 20% therefore multiplier by 5 to calculate the estimated limb length discrepancy; multiply by 2 at 3 years of age and by 1.1 at the onset of puberty

Predictions before 5 years of age are approximate at best, but, after the age of 5 years, measurements give a more reliable estimation. Predictions calculated at the beginning of puberty are the most accurate; during this time it is easy to predict the final deficit in congenital deficiencies as the remaining growth is 10% in the lower limbs.

One measurement may be an error, two measurements give a trend and three measurements allow a curve to be drawn.

Antenatal multiplier

Predictions are now also possible during antenatal life. Paley has developed the concept of the multiplying factor and has recently applied this to the antenatal period [14]. At 14 weeks of intra-uterine life, the femur has acquired 3% of its final length and, therefore, the multiplier is 30; at 24 weeks the acquired length is 10% and the multiplier is 10.

In our opinion, this method gives a rough idea of final discrepancy but is less accurate than post-natal predictions. It gives a broad idea of the severity of the discrepancy (i.e. <5 cm, 5–10 cm or >10 cm) rather than an accurate measurement which may give some guidance during antenatal counselling.

Final stature estimation

It is important to know the final stature when managing children with limb length discrepancies. There are many methods to predict this. Growth charts are available but the final stature is ultimately dependent on the timing of the onset of puberty [15]. All children will follow their growth curve until the onset of puberty. If puberty commences early, the final height will be shorter than predicted; if puberty is delayed, the final height will be taller than predicted. Once puberty has begun there are no more uncertainties in relation to growth. Therefore, the best method to reduce errors is to follow the child on their growth curve and detect the beginning of puberty. If this final stature is tall, an epiphysiodesis may be favoured over a more complicated limb lengthening procedure.

Regardless of the methods used, bone age must always be taken into account. We consider it to be important to base our calculations on skeletal age rather than chronological age, because only 50% of the population have a chronological age that is in harmony with bone age [2]. Figure 17 demonstrates the growth curve of two sisters. Sister 1 commenced puberty at a chronological age of 10 years, whereas sister 2 did not commence until age 12 years. The final height difference, despite having the same original growth curve, was 10 cm. Skeletal age is therefore important when decisions are taken regarding final height estimation.

Fig. 17.

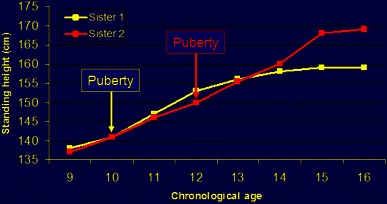
Growth chart of standing height for two sisters demonstrating the unpredictability of chronological age. Sister 1 commenced puberty at 10 years of age, sister 2 commenced at 12 years of age, with a resultant 10-cm difference in final height

However, the younger the child the less predictable is the bone age [16]. At puberty, elbow maturation is more precise than Greulich and Pyle charts for the estimation of the timing of epiphysiodesis [17, 18].

The onset of puberty is heralded by acceleration of the annual growth velocity of more than 6 cm/year, and the onset of Tanner signs [19], double ossification of the olecranon and ossification of the sesamoid of the thumb [17] (Figs. 9, 10).

Fig. 9.

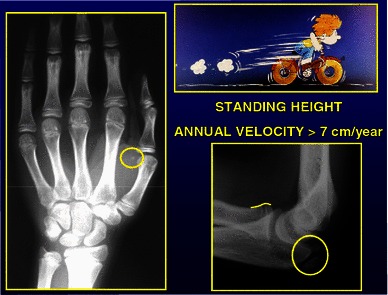
Radiological changes at the onset of puberty, sesamoid ossification left hand, double ossification left olecranon apophysis

Fig. 10.

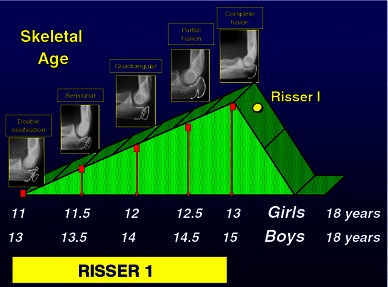
Pubertal diagram showing characteristic morphology of the left olecranon apophysis during puberty. Double ossification at onset of puberty, semilunar apophysis at puberty plus 6 months, quadrangular apophysis at puberty plus 1 year and complete fusion at peak pubertal growth velocity (puberty plus 2 years). (with permission Dimeglio et al., Accuracy of the sauvegrain method in determining skeletal age during puberty. JBJS (Am). 2005;87:1689–96.)

Timing of epiphysiodesis

The right choice at the right moment. How to increase the accuracy of predictions

The biggest difficulty with epiphysiodesis is the uncertainty of timing, and the challenge is to reduce the margin of error. There are many methods available to calculate the appropriate timing of epiphysiodesis. All calculations are invariably based on the fundamental measurements of Green and Anderson [20–22].

Menelaus’s original paper [9] used chronological age to calculate the growth remaining and assumed that growth ceases at a chronological age of 16 years in boys and 14 years in girls, thus calculating 3 years of growth from the onset of puberty. He used the original suggestion of White and Stubbins [23] that the distal femur grows at 0.9 cm/year and the proximal tibia 0.6 cm/year. Thus, according to the Menelaus technique, the growth remaining at the knee from the onset of puberty is 0.9 cm + 0.6 cm = 1.5 cm multiplied by 3 years to equal 4.5 cm.

The Diméglio method [1] calculates growth at the knee as 2 cm/year, 1.1 cm from the femur and 0.9 cm from the tibia. However, in contrast to Menelaus, we calculate the time for growth remaining as 2.5 years because the pubertal diagram for the lower limb is characterized by a short and rapid acceleration, followed by a more gradual deceleration with lower-limb growth ceasing by bone age of 15 years and 6 months for boys and 13 years 6 months for girls (Risser 1). The final results are approximately the same (Menelaus 1.6 cm × 3 years = 4.8 cm versus Diméglio 2 cm × 2.5 years = 5 cm). It is merely to emphasize that the lower-limb growth spurt at puberty is short and, as such, decisions must be taken early relative to the timing of epiphysiodesis. It must be emphasized that, of the 5-cm growth remaining at the knee at the onset of puberty, 2.6 cm (i.e. >50%) occurs during the first year.

Several simple principles must be observed to reduce the margin of error: (1) strict and meticulous repeated measurements; (2) rigorous analysis of the data obtained (simple miscalculations have been shown to occur in 18% of cases [20]); (3) perfect evaluation of bone age using elbow plus hand radiographs [17]; (4) the decision always taken at the beginning of puberty.

When considering the Anderson and Green curve, the average remaining growth of the knee at the beginning of puberty is about 5 cm (3 cm femoral and 2 cm tibial). When puberty starts, the remaining growth of the knee is about 5 cm (girls and boys average, Figs. 15 and 16).

Fig. 15.

Knee growth (distal femur and proximal tibia) remaining in girls 10–14 years of age [24, p 59]

Fig. 16.

Knee growth (distal femur and proximal tibia) remaining in boys 10–16 years of age [24, p 59]

There are four common different scenarios (Fig. 13):

Fig. 13.

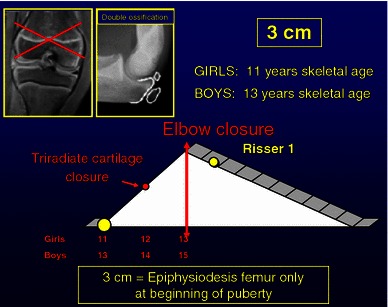
A 3-cm discrepancy can be corrected by performing an epiphysiodesis of distal femur only at the beginning of puberty (11 years skeletal age girls, 13 years skeletal age boys)

5-cm discrepancy: epiphysiodesis of both femur and tibia at the beginning of puberty (11 years bone age in girls and 13 years in boys) (Fig. 11).

Fig. 11.

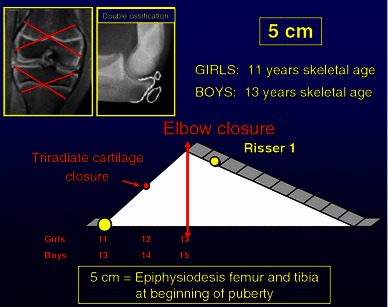
A 5-cm discrepancy can be corrected by performing an epiphysiodesis of both distal femur and proximal tibia at the beginning of puberty (11 years skeletal age girls, 13 years skeletal age boys).

4-cm discrepancy: epiphysiodesis femur and tibia 6 months after the start of puberty (i.e. 11 years 6 months bone age in girls, tri-radiate cartilage open; 13 years 6 months bone age in boys) (Fig. 12).

Fig. 12.

A 4-cm discrepancy can be corrected by performing an epiphysiodesis of both distal femur and proximal tibia at puberty plus 6 months (11 years 6 months skeletal age girls, 13 years 6 months skeletal age boys)

3-cm discrepancy: epiphysiodesis femur only at the start of puberty (11 years bone age in girls and 13 years in boys) (Fig. 13).

2-cm discrepancy: epiphysiodesis femur only, 1 year after the start of puberty or tibia only at the beginning of puberty (12 years bone age in girls and 14 years in boys) (Fig. 14).

Fig. 14.

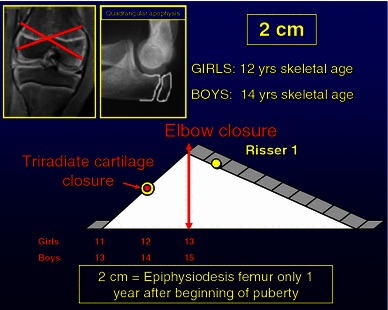
A 2-cm discrepancy can be corrected by performing an epiphysiodesis of distal femur only at puberty plus 1 year (12 years skeletal age girls, 14 years skeletal age boys)

Obviously this can be adapted to individual cases. For instance, if there is only 2 cm of tibial shortening, epiphysiodesis can be done on the tibia only at the onset of puberty.

Moseley has emphasized that skeletal age is important when considering limb length discrepancies [16]. In the example of the two sisters in Fig. 17, we can see that skeletal age is essential for accurately predicting the correct timing of epiphysiodesis. If an epiphysiodesis of the distal femur and proximal tibia is performed in sister 1 at a chronological age of 11 years, she would have 2.9 cm of growth remaining. If an epiphysiodesis of the distal femur and proximal tibia is performed in sister 2 at a chronological age of 11 years, she would have 7.3 cm of growth remaining, a difference of 4.4 cm.

Lessons learned from growth

Predictions may be predictable

The challenge of understanding growth is the essence of paediatric orthopaedic surgery. There are many mathematical equations and rigid formulas in the literature that have been honestly created in order to try and capture the complexity of growth. However, we must be able to step back from these. It is a false guarantee to be guided by mathematical equations. The dynamic of growth needs a flexible approach. Measurement of the standing height without annual growth velocity is meaningless, as is bone age without Tanner signs. Reliance on chronological age for estimation of timing of epiphysiodesis may lead to serious errors—50% of children have an advanced or retarded skeletal age. Decisions in relation to the timing of epiphysiodesis must be taken at the beginning of puberty, the onset of which can be more accurately determined by annual growth velocity, Tanner signs and radiographs of left wrist and elbow.

Serial measurements of several parameters must be made for each child; a measurement in isolation is meaningless. Percentages provide an extremely objective tool for evaluating residual growth. Under these conditions, predictions may be more accurate.