Tomographic subvolume alignment and subvolume classification applied to myosinV and SIV envelope spikes

Abstract

Electron tomography is a technique for three-dimensional reconstruction, that is widely used for imaging macromolecules, macromolecular assemblies or whole cells. Combined with cryo-electron microscopy, it is capable of visualizing structural detail in a state close to in vivo conditions in the cell. In electron tomography, micrographs are taken while tilting the specimen to different angles about a fixed axis. Due to mechanical constraints, the angular tilt range is limited. As a consequence, the reconstruction of a 3D image is missing data, which for a single axis tilt series is called the “missing wedge”, a region in reciprocal space where Fourier coefficients cannot be obtained experimentally. Tomographic data is analyzed by extracting subvolumes from the raw tomograms, by alignment of the extracted subvolumes, multivariate data analysis, classification, and class-averaging, which results in an increased signal-to-noise ratio and substantial data reduction. Subvolume analysis is a valuable tool to discriminate heterogeneous populations of macromolecules, or conformations of a macromolecule or macromolecular assembly as well as to characterize interactions between macromolecules. However, this analysis is hampered by the lack of data in the original tomograms caused by the missing wedge. Here, we report enhancements of our subvolume processing protocols in which the problem of the missing data in reciprocal space is addressed by using constrained correlation and weighted averaging in reciprocal space. These procedures are applied to the analysis of myosin V and simian immunodeficiency virus (SIV) envelope spikes. We also investigate the effect of the missing wedge on image classification and establish limits of reliability by model calculations with generated phantoms.

Introduction

The widespread use of electron tomography has increased the need for analyzing and visualizing three-dimensional data. Methods that have been applied in cryo-electron microscopy in the field of single particle analysis have proven to be useful for the analysis of volumetric data as well, such as averaging to improve the signal-to-noise ratio (SNR), multivariate data analysis as a tool for data reduction, and classification for the separation of different species or conformations of macromolecules. In single particle analysis, which starts with two-dimensional projection images of the molecules, the goal is to reconstruct the 3D density based on the 2D projections. Usually, the assumption is made that there is only a single species and conformation of a macromolecule, and the requirement is that the molecules must be imaged in as many orientations in space as possible in order to reconstruct the original density distribution faithfully. This is achieved by separating the collection of molecular images computationally into classes which represent projections of similarly oriented molecules. Orientation parameters are then assigned to each class average representing a particular projection in order to compute a volume with 3D-reconstruction algorithms such as weighted backprojection (van Heel et al., 2000; Frank, 2002).

Similar averaging strategies can be applied to tomographic data. However, in this case the volume already exists. The purpose of alignment, classification, and averaging is to separate a population of molecules or macromolecular assemblies extracted from the tomograms, based on structural or conformational variability, to improve the SNR, and minimize the effect of the missing wedge. This differs from the classic single particle approach, where distinct projection images arise due to orientational differences of otherwise identical molecules. While the orientation of the objects contained in the extracted subvolumes from tomograms may still be arbitrary, it can be determined by alignment. Subvolumes brought into register by this alignment step can then be analyzed and classified with the methods well established in single particle analysis.

A further distinction between subvolume analysis of tomographic data and single particle analysis can be made by characterizing the type of specimens that can be investigated, and the final result of the analysis, the 3D density maps. In subvolume analysis, macromolecules and assemblies can be imaged in situ, and produce a 3D image that shows a biological system close to in vivo conditions, if cryo-techniques are applied. Conversely, single particle methods are essentially restricted to in vitro studies, since data are usually collected from a purified preparation of a molecule or molecular complex. In addition, the reconstruction is necessarily computed from a multitude of copies of a molecule, so that the final result is an average picture of the underlying structure, and the quality of the reconstruction depends on the particle homogeneity. In contrast, a tomographic reconstruction contains 3D images of individual molecules or macromolecular assemblies. Even though they are averaged in the course of the subvolume processing, members of the averages can always be traced back to the location in the original tomogram. This enables us to characterize individual molecules in the context of the whole system. Unfortunately, the tomographic approach suffers from artifacts that are not present in single particle reconstructions. Due to the way tilt series are collected with the electron microscope, the tomograms lack data in a substantial region in reciprocal space, because the specimen cannot be rotated in a full circle. The limited tilt angle range of the goniometer for a single axis tilt series produces a wedge shaped region, called the “missing wedge” where no data is present. Consequently, resolution is anisotropic in a tomogram reconstructed from such data and features within the tomogram are elongated in a direction corresponding to the wedge orientation.

In our studies of insect flight muscle we have adapted methods commonly used in single particle analysis for use with tomographic data (Winkler and Taylor, 1999). These methods include a variant of principal component analysis, modulation analysis (Borland and van Heel, 1990), and hierarchical ascendant classification (van Heel, 1989). We have used the tomographic subvolume analysis for the characterization of crossbridge conformations (Liu et al., 2004), and later, the same methods were also applied successfully to other specimens (Liu et al., 2006a; Zhu et al., 2006). Insect flight muscle is particularly well suited for subvolume processing because of its para-crystalline structure. In insect flight muscle, actin and myosin filaments form a lattice, so that the tilt axis in a tomogram has the same approximate direction relative to the filament lattice. Under these circumstances, any effect of the missing wedge on the processing of individual subvolumes is the same for each subvolume. Consequently, no special treatment of the missing wedge was necessary. With the application of the subvolume analysis to other specimens with more variable orientation, the need for an explicit treatment of missing wedge effects arose. The improved computational methodology (Winkler, 2007) is based on techniques summarized below.

In the alignment of subvolumes extracted from tomographic data, the relative orientation of the missing wedge with respect to the tomogram could potentially introduce a bias in favor of the wedge orientation and the alignment of arbitrarily oriented objects within the subvolumes may fail. This bias can arise in a cross-correlation alignment, when the overlap of the sampled volumes (in reciprocal space) is maximal, meaning that the missing wedges are in register. The effect of the missing wedge can be alleviated by taking the overlap into account in the normalization of the cross-correlation function (constrained correlation) (Frangakis et al., 2002). The assumption is that although the overlapping sampled volume (in reciprocal space) contributing to the cross-correlation calculation is smaller and incomplete, the normalization over the smaller volume approximates the true cross-correlation better. This technique of alignment by constrained cross-correlation was applied in a study of envelope glycoproteins of leukemia viruses from cryo-electron tomograms (Förster et al., 2005). A similar method for dealing with missing data was published by Schmid et al. (Schmid and Booth, 2008). It differs from constrained cross-correlation in that the normalization scheme is based on the size of the volume of the overlapping sampled regions in reciprocal space and is thus computationally simpler.

Additionally, eigenvector analysis and classification are further processing steps where the effects of missing data in tomographic reconstructions have been observed (Walz et al., 1997). In this study, particles occurring in random orientations, that were first aligned to a common orientation, tended to be grouped according to the missing wedge orientation rather than the particle structure. Recently, Förster et al. described a procedure to separate a mixed population of simple GroEL and GroEL/ES complexes by classification using pairwise cross-correlation of subvolumes (Förster et al., 2008). In this study, the use of the constrained cross-correlation coefficient proved to be a better metric than the standard cross-correlation coefficient. The choice of a single number as a difference measure may, however, be a limiting factor for the detection of more subtle spatial density variations than the mere presence or absence of a whole subunit (GroES in this case). With classification techniques used in single particle analysis, which are based on image densities directly, Liu et al. could differentiate variably distorted rigor crossbridges in insect flight muscle (Liu et al., 2004). Instead of image densities, functions derived from the image densities may be advantageous for alignment and classification. The autocorrelation function, for instance, is invariant to translation, so that a rotational alignment can be carried out without prior knowledge of the exact rotation axes. Schatz et al. proposed a method to classify a data set without prior alignment by calculating a modified autocorrelation function, the “double self-correlation function” which is translationally and rotationally invariant (Schatz and van Heel, 1990). We used a similar function to align and classify subvolumes of insect flight muscle, where the thin filaments can assume orientations that differ by a rotation of 180° about the filament axis (Winkler and Taylor, 1999). In a similar application of invariant functions to volume data, Fourier transform magnitudes were computed which were projected onto the unit sphere and analyzed by decomposition into spherical harmonics (Bartesaghi et al., 2008). This procedure also included a computational treatment of the missing wedge which is equivalent to the constrained cross-correlation method.

We describe herein our enhanced subvolume analysis procedures that take into account the missing data in tomographic reconstructions explicitly. The techniques are based on constrained cross-correlation functions and have been implemented in an updated version of our software (Winkler, 2007). Furthermore, we have also implemented and tested alignment strategies for data with a low SNR that are more robust and less prone to reference bias. These include the multi-reference alignment that we have been using extensively in our insect flight muscle studies, and a method termed “alignment by classification” (Dube et al., 1993) that we first applied in the analysis of cryo-data of membrane-bound integrin molecules (Ye et al., 2008). In this report, we apply the methodology to two data sets, to myosin V in the inhibited state (Liu et al., 2006a), and to simian immunodeficiency virus (SIV) envelope spikes (Zhu et al., 2006; Roux and Taylor, 2007). Myosin V was adsorbed on lipid monolayers and forms two-dimensional arrays of flower-like motifs. The SIV envelope spikes represent viral surface features that are not symmetrically arranged and each spike is composed of three gp120 head and three gp41 stalk components. Both specimens were investigated by cryo-electron tomography and missing wedge compensated subvolume analysis.

Materials and Methods

Tomographic data

The tomographic data sets used in this study and the results from subvolume averaging were published previously: the structure of myosin V in the inhibited state (Liu et al., 2006a), and SIV virus envelope spikes (Zhu et al., 2006). In these previous studies, the processing methodology did not include any missing wedge compensation. In the following, we summarize the data collection and image processing techniques used in the previous studies that produced the tomograms which are the basis of this work. The SIV image data of the virus cryo-samples was collected on a Philips CM300 FEG electron microscope equipped with a goniometer and a Tietz TemCam F224 CCD camera (2048×2048 pixels), at 300 kV and a magnification of 43,200 under low-dose conditions. Defocus values were in the range of 4 – 6 μm. Three tilt series with 70 – 80 images were collected that covered an angular tilt range up to 70°. Variable increments were chosen according to the Saxton rule (Saxton et al., 1984), starting with a 2° step at 0° tilt for two series, and a 3° step for the other series. The pixel size at the specimen level was 0.56 nm. The tilt series were processed with the “protomo” software package (Winkler and Taylor, 2006) using marker-free alignment and the final maps were computed with weighted backprojection. A total of 2,004 subvolumes were selected by visual inspection from the original 6,175 subvolumes of the earlier study. Selection criteria were the overall appearance of the subvolumes and the location within the tomogram, i. e. subvolumes originating from regions of the tomograms with apparent lower resolution or poorer structural preservation were rejected, as well as subvolumes near the edges of the tomograms.

Cryo-electron microscopy and tomography of the second specimen, myosin V in the inhibited state adsorbed on lipid monolayers (Liu et al., 2006a), were carried out under the same conditions as described above for the SIV envelope spikes. Eight tilt series were collected with a starting angle increment of 2°, and the tilt range covered angles up to 70°. The pixel size at the specimen level was 0.56 nm. The defocus range of the eight collected tilt series was between 5 and 12 μm. For the last tilt series alignment cycle and the computation of the final maps, defocus corrected micrographs were used. Images taken at tilt angles greater than 30° were defocus gradient corrected (Winkler and Taylor, 2003), while the other images were simply corrected with a Wiener filter. The subvolume positions were derived from the location of the “flower motifs” in the myosin V arrays, whereby the parameters for each of the six “petal motifs” (consisting of two lever arms and a cargo-binding domain of the myosin V molecule) were calculated by applying a shift and a rotation, resulting in a total of 11,112 subvolumes containing the petal motifs.

Subvolumes from each data set were reanalyzed with the volumetric data processing package described in (Winkler, 2007). Unlike the previously published results, the alignment of the subvolumes now included a compensation for the missing wedge, which is based on the principle of constrained correlation (Frangakis et al., 2002). Multivariate data analysis and hierarchical ascendant classification were applied to analyze the structural heterogeneity. Class averages were computed by averaging Fourier coefficients, so that missing regions are taken into account explicitly. The processed 2,004 SIV subvolumes had a size of 48×48×48 pixels, whereas subvolumes of 72×60×36 pixels were used for the 11,112 petal motifs of myosin V.

Subvolume processing

Two strategies of aligning and classifying subvolumes have been applied. The first one follows established procedures used in single particle analysis. An alignment step brings the raw subvolumes into register and is followed by a classification and averaging step. This process is iterative: class averages obtained in one cycle are used as alignment references in the subsequent cycle. For cross-correlation alignment, one or more references were created to which the raw subvolumes were aligned. Except for the initial alignment, multiple references were always used, since the investigated structures are expected to be variable to a certain extent. The second strategy is called “alignment by classification” (Dube et al., 1993). With this variant, differences in orientation are separated by classification. Subsequently, class averages are aligned with respect to each other, rather than raw images. The resulting alignment transformations are then applied to the raw subvolumes, at which point a new cycle of the iterative procedure can be started.

For the SIV envelope spikes, the orientation was initially determined by fitting an ellipsoidal surface to the picked spike positions and the spike axes were approximated by the calculated surface normals at the picked positions (Winkler, 2007). This procedure cannot determine the spike rotation about the spike axis, so that only two of the three Euler angles are obtained at this stage. The initial orientation parameters (3 spike origin coordinates and 2 Euler angles) were refined by a cross-correlation alignment to a global spike average that had been rotationally averaged about the spike axis. The choice of a rotationally averaged reference reduces the rotational grid search to two parameters, thus speeding up the otherwise time-consuming procedure in the initial stages, when the spike orientations are still inaccurate and larger grid search ranges are required. The third Euler angle was included in the refinement of the orientation parameters in later processing cycles, after a classification produced appropriate references that discriminated the varying orientations.

For the more or less planar arrangement of the myosin V petal motifs, positions (2 origin coordinates) and in-plane rotations (1 rotation angle) were derived from the flower motifs, each of which consists of six petals. The flower motifs are arranged in an imperfect hexagonal lattice, which simplified locating the motifs automatically by cross-correlation methods and determining the in-plane rotations. This was all carried out with projections of the myosin V maps to speed up the initial processing, and the first cycle of processing used projections rather than volumes also. In subsequent cycles, the alignment was switched to the volume data and the search range was limited to a few degrees in order to take into account the wrinkling of the monolayers.

At the beginning of each cycle of the first processing variant (alignment of raw subvolumes), multiple references were selected from class averages produced by the preceding cycle. Care has been taken in the selection process that the references represented the whole spectrum of variance obtained by the classification. For the SIV specimen, 10 – 25 references were selected, and, for myosin V, where the larger number of subvolumes allowed us to produce more classes with a similar number of class members, up to 60 classes were selected. The references were first windowed to exclude regions outside a volume slightly larger than the observed molecular density. In addition, the membrane of the SIV virion was also partially windowed in order to focus the alignment on the spike structure rather than the membrane density, which appeared to be relatively strong in some classes. Finally, the references were band-pass filtered, the low-pass limit was chosen to be equal or less than the spatial frequency of the first zero of the CTF, and the high-pass limit chosen to remove low-frequency density variations.

Each raw subvolume was extracted from the maps given the geometric parameters (position and orientation) from the previous cycle and the subvolume was cross-correlated with each reference. The constrained cross-correlation coefficient served as a similarity measure. The new parameters were obtained with a grid search over the rotation parameters from the reference which produced the highest co-efficient, and the geometric parameters were updated accordingly. Aligned subvolumes were not stored, since it is sufficient to record the updated parameters. Instead, the aligned subvolumes were re-interpolated on the fly with the updated alignment parameters, when needed. This approach saved large amounts of storage space for intermediate results during the processing cycles, and avoided multiple re-interpolations of the image data. The rotational alignment was carried out with a grid search by modifying the orientation with which the subvolumes were extracted. An exhaustive search over all possible orientations in space was not needed, since an approximate orientation of the motifs was known. Thus, for the SIV spikes the polar angle was only searched in 2° steps on cones with half-widths of 2° and 4°, the half-width subsequently being reduced to 1° for the final cycle. Rotation about the spike axis was initially tested in 7.5° steps and gradually reduced to 2° steps for later cycles. The myosin V orientation was refined after the initial projection alignment to correct for deviations caused by wrinkling and to account for lattice distortions of the para-crystalline array. In the final cycles, the orientation was searched on cones with half-widths of 1°, the in-plane rotational search was restricted to ±0.5°.

Principal component analysis using the modulation metric (Borland and van Heel, 1990) was applied after the subvolume alignment. Relevant voxels of the re-extracted aligned subvolumes were selected by specifying a binary mask. The mask was generated in such a way that it contained mostly voxels of the molecular volume, and excluded the surrounding vitrified ice. At some stages of the SIV analysis, cylindrical masks containing a spike were also used that necessarily included a slightly larger volume in the stalk region, but were easier to generate. In any case, the masks always excluded the virion membrane from the analysis. Hierarchical ascendant classification (van Heel, 1989) was carried out to find groups of similar subvolumes. For the SIV specimen, 50 classes were normally generated so that the number of averaged subvolumes per class was around 30 – 60. Whereas in the iterative processing stages, a large number of classes was generated to obtain as many potential variations of the spike conformations, this number was reduced to 8 in the final cycle for visualization. In the case of myosin V, where five times as many subvolumes were available as compared to SIV, 20 – 80 classes were generated resulting in averages with an accordingly higher number of subvolumes. Since most averages did not differ substantially from each other, only 5 classes were chosen in the final classification. Averaging was carried out in Fourier space, so that Fourier coefficients falling in the region of the missing wedge could be excluded from the summation.

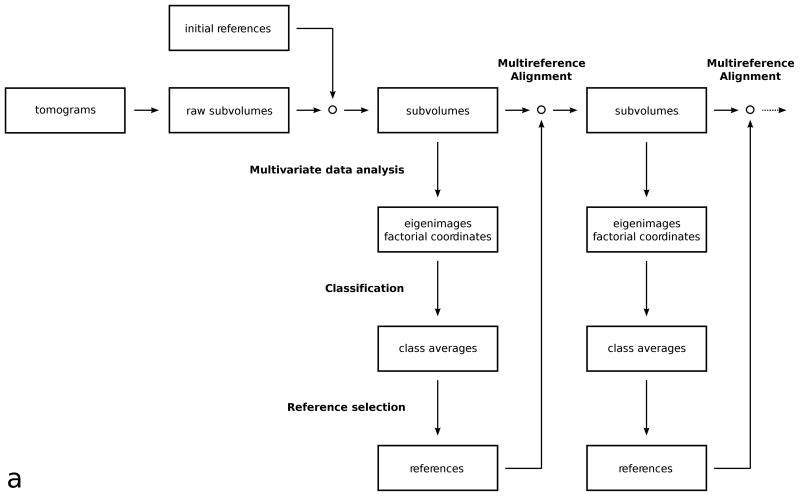
One cycle of the first variant of subvolume processing can be summarized as follows (Fig. 1a):

Figure 1.

(a) Flowchart of the multi-reference alignment and classification protocol.

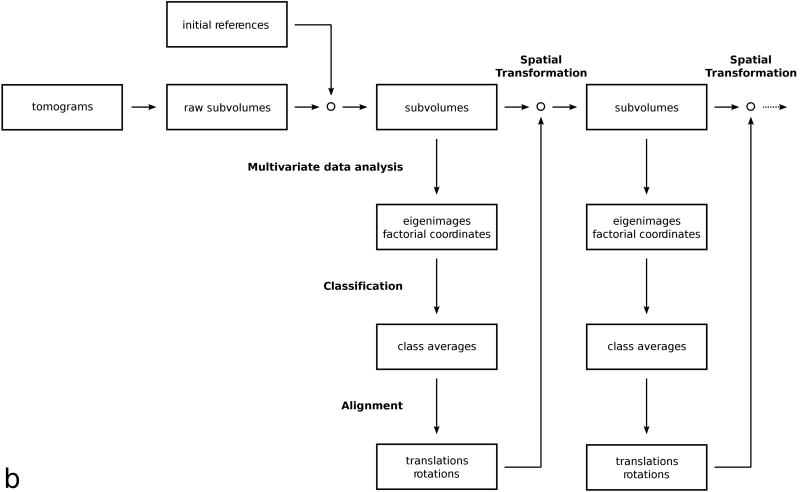
(b) Flowchart of the classification by alignment protocol.

1. Multivariate data analysis: The subvolumes were re-interpolated based on the stored alignment parameters, then masked so that only voxels representing the molecular volume were active in the analysis. An eigenvector/eigenvalue decomposition was performed and factorial coordinates of each subvolume were computed.

2. Classification: Factorial coordinates of the subvolumes, corresponding to the most significant eigenvectors were clustered with a hierarchical ascendant algorithm. Subvolumes of the desired size were extracted from the tomograms and were averaged separately for each cluster.

3. Reference selection: Multiple references were selected from the class averages. The references were band-pass filtered and an apodized real space mask was applied.

4. Multi-reference alignment: Subvolumes were re-extracted and cross-correlated with each reference. Rotational alignment was achieved by an orientation grid search, translational alignment by locating the position of the correlation peak. The new alignment parameters of the subvolumes were selected from the cross-correlation with the reference that produced the highest correlation peak, and stored for the next cycle.

The second variant of subvolume processing was applied to the SIV data sets only. This variant is based on a reference-free alignment method dubbed “alignment by classification” (Dube et al., 1993). In the cited study, the method was applied to two-dimensional images of a portal protein of a bacteriophage, and in order not to introduce any symmetry bias, the authors first aligned the noisy images translation-ally to a rotationally averaged reference, then utilized classification procedures to find similar images in similar rotational orientations. In our three-dimensional case, we aligned the raw subvolumes to a single, rotationally averaged reference only at the very beginning. To avoid any reference bias in subsequent alignment cycles, class averages were aligned, which have a higher SNR than raw subvolumes. The alignment transformations obtained from mutual alignment of class averages were then applied to the constituent members of each class. At this point, we continued processing with classification to split the subvolumes into as many classes of different structure and orientation as possible. When the distribution of orientations is continuous, a wider spectrum of the structural variance can be captured by generating a large number of classes. Considering the trade-off between number of classes generated and SNR improvement by averaging subvolumes, we usually chose 50 classes as a reasonable compromise. One cycle of this processing scheme can be summarized as follows (Fig. 1b):

1. Multivariate data analysis: The subvolumes were re-interpolated based on the stored alignment parameters, then masked so that only voxels representing the molecular volume were active in the analysis. An eigenvector/eigenvalue decomposition was performed and factorial coordinates of each subvolume were computed.

2. Classification: Factorial coordinates of the subvolumes, corresponding to the most significant eigenvectors were clustered with a hierarchical ascendant algorithm. Subvolumes of the desired size were extracted from the tomograms and were averaged separately for each cluster.

3. Alignment: The class averages were band-pass filtered and aligned with respect to each other. Rotational alignment was achieved by an orientation grid search, translational alignment by locating the position of the correlation peak.

4. Spatial transformation: The resulting incremental changes in alignment obtained for each class average were applied to the stored alignment parameters of the constituent members of each class, and the resulting new set of parameters was stored for the next cycle. No re-interpolation of subvolumes was carried out at this point.

Model calculations

Density maps were computed with the program “pdb2mrc” from the EMAN package (Ludtke et al., 1999). Five maps were generated from atomic coordinates which included copies of a gp120 glycoprotein simulating artificial envelope spikes: a monomer, a dimer, and three trimers. The trimers differed in the way the density was distributed in the head part and the leg part of the spikes. From these density maps, phantoms were assembled by inserting the spike maps into the surface of a spherical vesicle-like structure and filling the remaining space with a Poisson-distributed density as a model for amorphous ice. The density profile of the vesicle-like membrane structure was designed to mimic a lipid bilayer and was also generated based on atomic coordinates of a patch of lipid (Feller et al., 1997). The sampling distance for the phantoms was 0.5 nm.

Fifty phantoms were used for the model calculations. Each contained about 75 spikes that were randomly distributed on the spherical surface and also randomly rotated about the spike axis or surface normal. Spike positions were generated with a statistically uniform distribution on the unit sphere (Marsaglia, 1972), so that each surface point was equally likely to be selected. At each computed spike position, one of the five maps was randomly selected with equal probability. With this arrangement, preferential orientations of the spikes are unlikely to occur. The phantoms were band-pass filtered in Fourier space with an apodized filter that approximated roughly the contrast transfer function of the experimental data (defocus of 4 μm at 300 kV). The location of the first zero at this defocus value corresponds to a low-pass cutoff at 1/(2.85 nm). Additional wedge filters were applied to simulate tomographic data with tilt angle ranges of ±48°, ±60°, or ±75°. Thus, the missing data amounts to a wedge with angles 84°, 60°, and 30°, respectively. For each of these three cases, subvolumes were extracted and classified. Subsequently the class memberships of the subvolumes were compared with the original input to assess the accuracy of the classification.

Results

Myosin V adsorbed on lipid monolayers

In this specimen, the flower motifs and hence the petal motifs have a preferential orientation, because the adsorption process binds myosin V to the lipid monolayer in a para-crystalline array. The only degree of freedom in addition to translation is an in-plane rotation. Since six petals make up one flower motif, the in-plane orientation of these six petals is correlated and was used to determine the positions of each petal. Each flower motif is part of a larger, imperfect hexagonal array (Fig. 2a), so that the motif orientation is also correlated at this level. Even though the motifs were picked from multiple tomograms and patches of arrays, and the direction of the tilt axis varies by a few degrees from tomogram to tomogram, there is still a pronounced preference observed in the distribution of orientations of the tilt axes with respect to the myosin V petal coordinate frame (Fig. 2b).

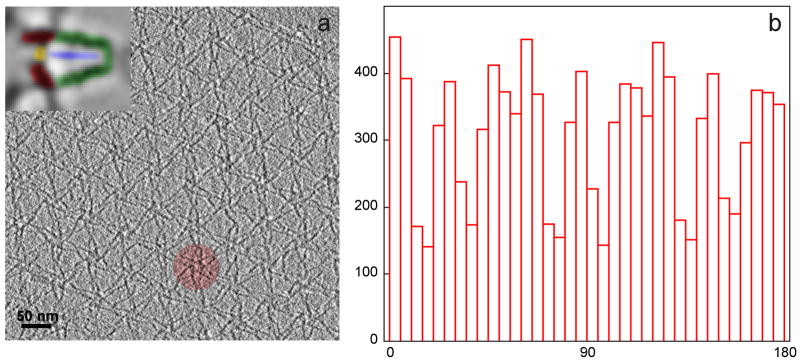
Figure 2.

(a) Section through a tomogram of myosin V in the inhibited state, adsorbed on a lipid monolayer, showing the para-crystalline, hexagonal arrangement of the “flower motifs” with one of the flower motifs highlighted. Inset: a petal of the flower motif with the molecular domains of myosin V highlighted. Red: motor domains, yellow: cargo-binding domain, blue: S2 domain, green: lever arms. (b) Histogram of the tilt axis directions (0° to 180°) in all aligned subvolumes with respect to the myosin V structure (“petals” within a flower motif). Note that not all orientations are equally represented, due to the para-crystalline arrangement.

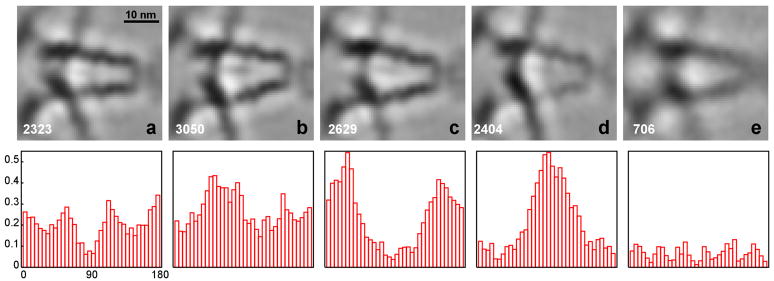
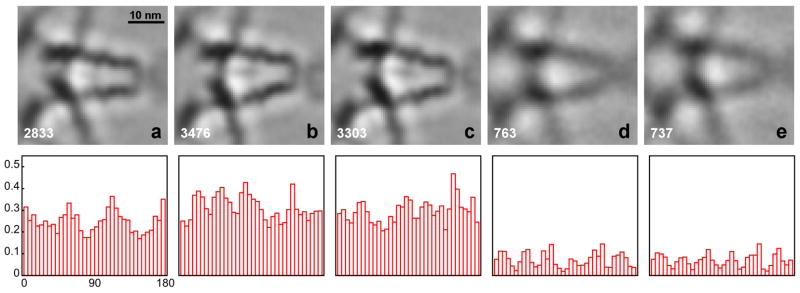
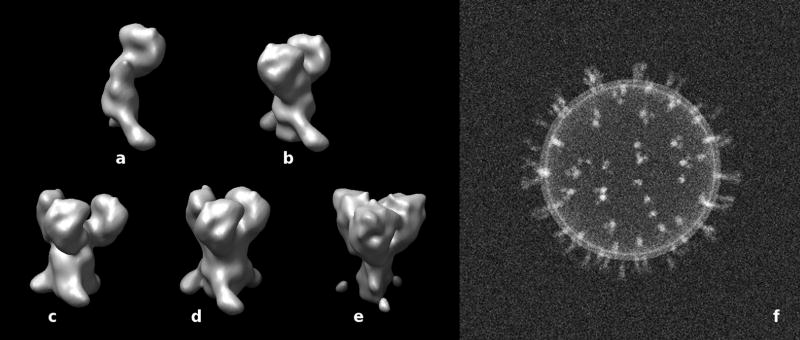
During alignment, a larger number of classes were usually generated for reference construction than for the final classifications shown here (Fig. 3 and Fig. 4). A visual comparison of the former classes, typically 40 or 60 classes, revealed only slight differences in the arrangements of the major components (inset Fig. 2a), the motor domain (red), the cargo-binding domain (yellow), the lever arms (green) and the S2-domain (blue), indicating that the assembly is flexible to a certain extent. The five classes shown in the figures illustrate the range of the observed most significant structural variation. The images represent sections through 3D averages in the x–y plane, slicing through the middle of the lever arms of myosin V in the z-direction. For each class, a histogram of the tilt axis orientation relative to the myosin V molecules in the range of 0° to 180° is shown below the image. Each histogram bin represents the fraction of subvolumes with respect to the whole data set (Fig. 2b), in order to take into account the orientation preference due to the para-crystalline arrangement.

Figure 3. Classification of myosin V petal motifs.

The classification was carried out with the aligned subvolumes. The top row shows five classes (a–e), the number of subvolumes that contributed to the class averages is indicated at the bottom left of each average. The bottom row shows histograms of the tilt axis directions calculated with respect to the petal motif of the aligned subvolumes. Each histogram bin represents a fraction of the subvolumes in a particular angle range relative to the total number of subvolumes (Fig. 2b).

Figure 4. Classification of myosin V petal motifs.

The classification was carried out with projections of the subvolumes instead of the subvolumes themselves. Refer to Fig. 3 for further details.

The results in Fig. 3 and 4 show two different applications of classification to the myosin V data. In Fig. 3 the appropriately masked volume data was used, whereas in Fig. 4 the computation was carried out with the projections of the subvolumes. In both cases, however, the alignment and class averaging was performed with volume data. As the histograms of the tilt axis directions indicate, the analysis of subvolumes is prone to bias caused by the missing wedge: subvolumes cluster preferentially with respect to tilt axis direction. The effect is most pronounced for the class averages in Fig. 3c and Fig. 3d and the two classes are surprisingly similar in that the lever arms, motor domains and cargo-binding domains are identically placed. They differ primarily in that the lever arms and S2 domains are less dense in Fig. 3d than in Fig. 3c and the cargo-binding domain is less dense in Fig. 3c than in Fig. 3d. Thus, low density in the lever arm is correlated with class members whose tilt axis directions are largely oriented perpendicular to the lever arm direction, and high density in the lever arm is correlated with class members whose tilt axis directions are oriented parallel to the lever arm direction. The cargo-binding domain, which is oriented at 90° to the lever arms, have high density when the lever arms are weak and low density when the lever arms are strong. The small amount of missing wedge bias shown by the class in Fig. 3a is similar to that of Fig. 3c, and predictably, the lever arms and S2 density is high in class (3a).

The missing wedge bias is alleviated to a great extent by using the projections (Fig. 4) for classification, because the central section in reciprocal space corresponding to the projection in real space is not affected by the missing wedge. In this case, we see no correlation between class averages and the direction of the tilt axis. It should be noted that class (3e) does not seem to be affected by the missing wedge, and that this class, and also classes (4d) and (4e) have a significantly lower number of class members. The appearance of these lower quality classes can be attributed to the fact that all available subvolumes were retained in our analysis in order to obtain the statistical information about the orientation of the tilt axes. Normally, a certain percentage of subvolumes would be eliminated computationally in the classification or class averaging algorithms to improve the overall quality of the classes. Visual inspection of the other class images (a, b, c) does not reveal significant differences between the volume analysis (Fig. 3) and the projection analysis (Fig. 4). Among these three classes, the two lever arms in class (a) appear closer spaced than in (b) and (c). The difference between (b) and (c) is more subtle. The S2 domain, a weaker, central density between the two lever arms, is slightly angled upwards in class (c) compared to (b), for instance.

SIV envelope spikes

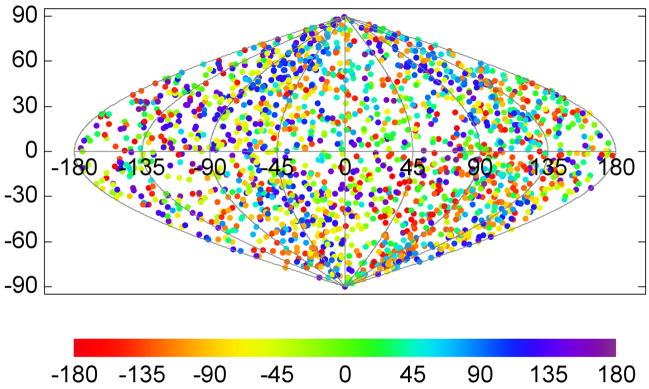
Envelope spike motifs were picked from the top, bottom and the side of the more or less ball-shaped virions by visual inspection. Care has been taken that no particular location was over- or underrepresented, and consequently, no preferential orientation of the spikes would be expected. When comparing the individual tomograms, the direction of the tilt axes with respect to the full tomographic volumes all lie within a few degrees of each other, since the tilt series were collected in the same way under similar conditions. The direction of the tilt axes with respect to the aligned subvolumes and thus the spike structure which are variable, are plotted in Fig. 5. Tilt axis directions were first mapped onto the unit sphere and then projected onto the plane with a sinusoidal projection (also known as Sanson-Flamsteed projection). In the plot, horizontal lines indicate constant latitude, sinusoidal curves constant longitude. The direction towards the spike head would be mapped to the “north pole”, the direction towards the spike leg to the “south pole”. A point plotted at the north pole indicates a subvolume where the tilt axis coincides with the spike axis, and thus corresponds to a spike extracted from the side of a virion. The points were color-coded to indicate the rotational orientation of the wedge with respect to the tilt axis. It should be noted, that a property of the sinusoidal projection is the preservation of area, so that denser clusters of plotted points would indicate an orientation preference.

Figure 5. Spatial distribution of the tilt axis direction for the SIV specimen.

The tilt axis direction is calculated with respect to the spike coordinate frame and mapped onto the surface of a unit sphere, which is then converted to a two-dimensional representation with a sinusoidal projection. Latitude 90° (vertical coordinate axis in the plot), for instance, corresponds to a tilt axis direction along the spike axis pointing to the spike head, −90° to the spike leg. Each plotted point indicates the tilt axis direction for a particular spike in the data set and the rotational orientation of the missing wedge relative to the tilt axis is color-coded. A property of the sinusoidal projection is that it preserves the area, so that the density of the plotted points is the same as on the spherical surface. The relatively uniform distribution indicates that the spikes were picked without favoring a particular orientation on the virion surface.

In previous studies of insect flight muscle (Liu et al., 2006b), we have developed a technique for selective classification of substructures of a molecular assembly which we have now applied to the SIV data. In the present case we independently classified the head region (gp120) and the leg region (gp41) in a spike. The general analysis procedure was identical with the exception of creating classification masks that retained only voxels in the head region, leg region, or the whole spike, respectively. A visual comparison of a whole spike versus head region classification is shown in Fig. 6. The larger head part (H) and the shorter leg part (L) used in the construction of the masks are indicated in panel (1d). In row (a) where the mask encompassed the whole spike, the trimeric appearance is less pronounced than in row (b) where the analysis focused on the head part. In the latter variant, spikes (5b) and (7b) exhibit the trimeric arrangement most clearly. The trimers of the different classes are not in register with respect to each other, since unlike in the classification, a volume encompassing the entire spike was used in the multi-reference alignment. Consequently, the most dominating features determine the result of the alignment, which in this case seems to be the deviation of the spikes from an upright position. This is best seen in the side views, row (c), which correspond to the top views, row (b). A good example of a spike that is not upright with respect to the membrane is (7c). It should also be noted that at no point was any symmetry imposed during processing. Although the head region appears to be trimeric, it is not necessarily three-fold symmetric and even if the head region were symmetric, this may not apply to the leg region at the same time. We also observe a density in the leg region that is broadening towards the base of a spike which is compatible with the suggested tripod-like model (Zhu et al., 2006). Sections perpendicular to the spike axis at the lower end in the leg region, close to the membrane, reveal that the density has a trimeric appearance in most classes, as shown in row (e), which is based on a classification focused on the leg part. The surface views cannot clearly reveal this trimeric appearance however, due to the proximity of the dense membrane.

Figure 6. Classification of SIV spikes.

Eight classes were generated (columns 1 – 8). Row (a): The mask used for the multivariate data analysis included the head and leg region of the spike, but not the slightly curved membrane. For rows (b, c, d), the mask included only the head region, for (e) only the leg region. Head (H) and leg (L) regions are marked with black lines in panel (1d). Rows (a, b) are surface rendered top views, (c) are the side views of (b) and the viewing direction with respect to the top view is indicated in panel (8b). In row (d), slices through the volumes of rows (b, c) are shown as gray-scale representations. The orientation of the slicing plane is indicated in panel (1b). Row (e) represent slices through the leg region perpendicular to the spike axis, i. e. slices are parallel to a tangential plane of the curved membrane.

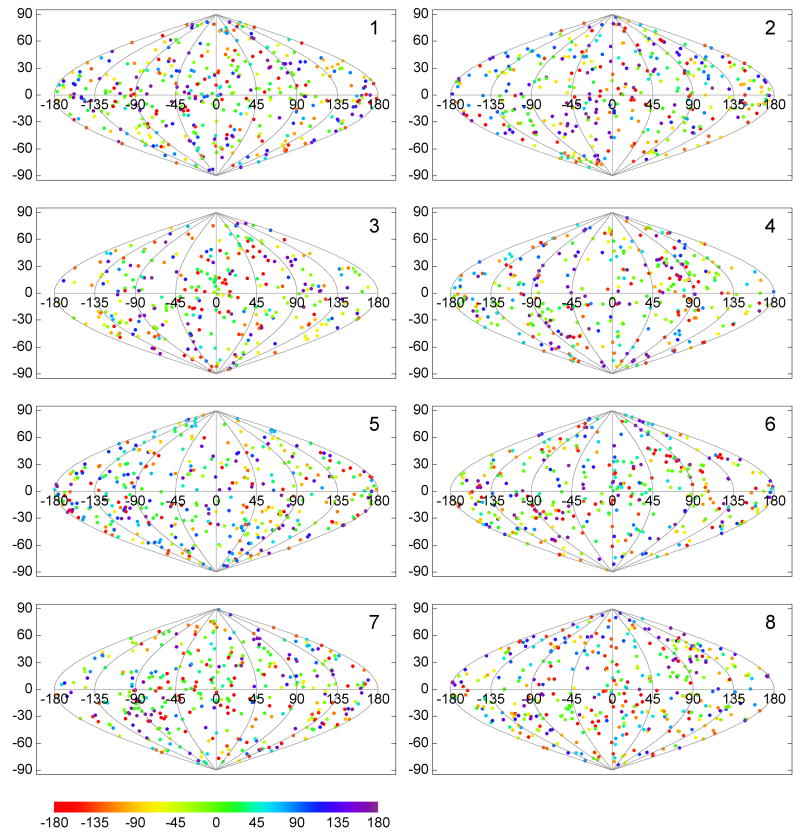
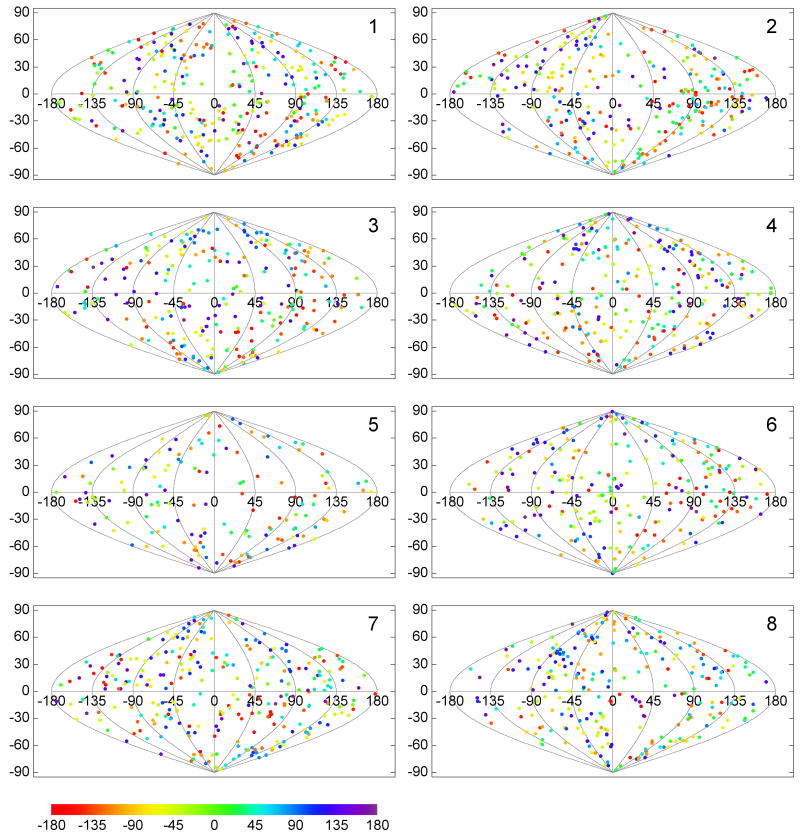
In order to assess the potential effect of the missing wedge in the data analysis, the orientations of the tilt axis were calculated and plotted as described above, but now for the subvolumes of each class separately (Fig. 7 and Fig. 8). The analysis was carried out in two variations, with multi-reference alignment of raw subvol-umes against references selected from class averages (Fig. 7) and with alignment by classification (Fig. 8). In both cases we find that the plotted tilt axis directions are distributed over the whole unit sphere surface, indicating that the missing wedge orientations of the subvolumes within each class cover the whole range of possible orientations. If preferential, relative orientations of the missing wedge were present, denser clusters of plotted points would be evident, which is not the case for either of our processing schemes.

Figure 7. Distribution of the tilt axis directions per class.

The classes were produced by the multi-reference alignment scheme. Directions of the tilt axis for the same spikes as in Fig. 5 are plotted here separately for each of eight classes. The relatively uniform distribution in all directions of space for each of the classes indicates that the orientation of the missing wedge had no major effect on the classification, i. e. the subvolumes were not grouped according to the relative orientation of the tilt axis with respect to the spike.

Figure 8. Distribution of the tilt axis direction per class.

The classes were produced by the alignment by classification scheme. For other details refer to Fig. 7.

Model calculations

Artificially generated density maps of the spikes and an example of an assembled phantom are shown in Fig. 9. The five spike forms used in the model are monomers (a), dimers (b), and trimers (c, d, e). The three trimers have a different density distributions in the head and leg region. In (c), the subunits in the head region are more widely spaced than in (d, e), i. e. an offset of 1 nm between the subunits has been applied. (e) was generated with a narrower and less dense leg region and a more dense head region. It should be emphasized that the position of the gp120 and gp41 elements is not intended to faithfully mimic the data obtained by cryo-electron tomography and features such as the gap between the gp120 subunits has been arbitrarily chosen. All applicable processing steps in the model calculations were carried out in the same way as with the real data. Table 1 shows the distribution of assignments of the five provided artificial spike maps (a – e) among the ten resulting classes for three different tilt angle ranges and the ideal case with no missing data. Each column of the table lists the contributions from the five spike forms to a particular class. Only columns with a single, non-zero entry represent classes with assignments that are all correct, i. e. if more than one entry in a column is non-zero, part of the assignments must be false. Thus, the condition for a completely correct classification of a particular species (a – e) is a row in which all non-zero entries also correspond to a column where all other entries are zero. This condition was only fulfilled for the classification with no missing wedge.

Figure 9. Model calculations.

(a–e) Surface renderings of density maps of artificially created spike structures. It should be noted that these spike structures are not intended to mimic actual spikes faithfully. (a) monomer, (b) dimer, (c, d, e) trimers with different density distributions in the head and leg region. In (c), the subunits in the head region are more widely spaced than in (d), i. e. an offset of 1 nm between the subunits has been applied. (e) was generated with a narrower and less dense leg region. (f) Projection of an assembled phantom using randomly selected maps (a–e) and a spherical vesicle-like structure generated with a lipid bilayer density profile.

Table 1.

Classification accuracy in the presence of a missing wedge. (Number of subvolumes, in percent, assigned to 10 classes)

Tilt angle range: ±48°
class number	1	2	3	4	5	6	7	8	9	10
(a) monomer	37	23	40	0	0	0	0	0	0	0
(b) dimer	0	35	0	2	16	11	11	14	10	1
(c) trimer, wide spacing	0	0	0	18	17	12	14	13	11	15
(d) trimer, narrow spacing	0	0	0	17	19	10	14	15	10	15
(e) trimer, thin stalk	0	0	0	18	14	10	17	12	10	19
Tilt angle range: ±60°
class number	1	2	3	4	5	6	7	8	9	10
(a) monomer	57	43	0	0	0	0	0	0	0	0
(b) dimer	0	0	57	0	3	35	5	0	0	0
(c) trimer, wide spacing	0	0	0	19	17	0	17	18	13	16
(d) trimer, narrow spacing	0	0	0	19	18	0	16	19	12	16
(e) trimer, thin stalk	0	0	0	23	17	0	13	18	15	14
Tilt angle range: ±75°
class number	1	2	3	4	5	6	7	8	9	10
(a) monomer	100	0	0	0	0	0	0	0	0	0
(b) dimer	0	68	32	0	0	0	0	0	0	0
(c) trimer, wide spacing	0	0	0	22	27	26	25	0	0	0
(d) trimer, narrow spacing	0	0	0	26	28	24	22	0	0	0
(e) trimer, thin stalk	0	0	0	0	0	0	0	35	36	29
No missing wedge
class number	1	2	3	4	5	6	7	8	9	10
(a) monomer	51	49	0	0	0	0	0	0	0	0
(b) dimer	0	0	51	49	0	0	0	0	0	0
(c) trimer, wide spacing	0	0	0	0	48	52	0	0	0	0
(d) trimer, narrow spacing	0	0	0	0	0	0	51	49	0	0
(e) trimer, thin stalk	0	0	0	0	0	0	0	0	49	51

Correct assignment was dependent on the size of the missing wedge. In most cases, the monomer was identified correctly. Only in one of two classes for the largest missing wedge (±48° tilt angle range), were the monomer subvolumes mixed up with dimers. A ±48° tilt angle range is clearly insufficient to produce maps for which the other species, dimers and trimers, could be clustered correctly. At ±60°, pure classes of monomers and dimers were produced, but a small percentage of the dimers (a total of 8%) were still falsely assigned to the trimer classes. Not counting these false assignments, the three trimer forms could only be distinguished together as a group from the dimer and monomer forms, i. e. the subtle differences among the trimers were not detected. While the classification accuracy improves with the larger tilt angle range of ±75° and smaller missing wedge, the clustering algorithm still cannot distinguish between the trimers with different subunit spacings in the head region (c and d). Although the difference in subunit spacing is apparently too small to be detected, the difference in density distribution in the head and leg parts of the spike is sufficient for detection, i. e. in Table 1, classes 4 – 7 contain a mixed population of members (c) and (d), whereas species (e) is uniquely assigned to classes 8 – 10 and thus discernible from the other trimer species.

Discussion

We analyzed two experimental data sets and carried out model calculations to test and validate our methodology for subvolume alignment and classification. The first data set (myosin V) is an example of an object having a preferred orientation, i. e. adsorbed molecules are restricted in orientation with respect to the plane of the monolayer surface. The second (SIV spikes) represents a case with an overall arbitrary orientation. While individual spikes are still restricted with respect to the virion surface, the spike distribution over the whole virion surface results in a coverage of all orientations in space. In addition to the experimental data sets, we used model calculations as a tool to explore both the feasibility and the limitations of our approach of characterizing structural heterogeneity by classification. Whereas our alignment and averaging procedures did take into account the missing wedge, it should be noted that we did not apply any computational compensation in our classification procedure. The multivariate data analysis methods are essentially the same as those applied in single particle analysis, and are based on the analysis of image densities of the aligned subvolumes. Since quantities in real space are involved, missing data in reciprocal space cannot be directly taken into account with this method. Effects of the missing wedge orientation in the absence of any compensation have been observed in a previous study (Walz et al., 1997).

Attempts have been made elsewhere to include an explicit treatment of the missing wedge in the classification (Förster et al., 2008; Bartesaghi et al., 2008). This approach only works insofar as overlapping regions of sampled data in reciprocal space are considered in the analysis. The fundamental problem is that the missing information may be needed to determine similarity or dissimilarity. If all distinguishing features fall in the missing region, it will be impossible to tell whether the underlying structures are different. For arbitrarily oriented structures, this effect could be alleviated though, if similarity is inferred from overlapping neighboring regions. Furthermore, classification based on a similarity measure such as the constrained cross-correlation coefficient may succeed to distinguish a few well defined and distinct conformational variants of a structure that give rise to a significant difference in correlation, but a correct partitioning is expected to fail if the extent of structural differences is small, or is of the same order of magnitude as image deformations caused by the missing data. If image densities are analyzed, then not only differences in signal magnitude but also the spatial distribution matters, and we expect a more robust partitioning.

In our approach, we partitioned the data sets in as many classes as possible that still produced averages with an acceptable SNR. This is a crucial step for the alignment by classification in order to separate the various orientations. For a multi-reference alignment it also ensured that references could be generated from conformations with a low occurrence rate. If too few classes are computed, members in low-occurrence classes may be mingled within classes containing the more abundant conformations. After classification, we verified the results by examining each class for a potential bias that the missing wedge orientation could have introduced. Such a bias would give rise to preferential grouping of the subvolumes according to the orientation, and would be recognizable in the plots of Figures 7 and 8. If a bias were present, areas on the unit sphere that were more densely populated would indicate preferential orientations in a particular class which would be counterbalanced by less dense areas in other classes in order to maintain the overall distribution of subvolume orientations as observed in Fig. 5.

We have also validated the procedures using model data. Since for these calculations, no atomic model of a SIV envelope spike exists at this time, we studied the effect of the missing wedge on classification with a plausible, artificial model. The generated phantoms were noise-free, and since experimental uncertainties such as alignment errors were not built into the modeling process, the results represent a best case scenario in which all conditions are ideal at the chosen resolution. We found that under these conditions, the classification procedure was able to group according to the most prominent differences among the five spike variants in the generated phantoms. More subtle differences such as a small relative distance between the subunits in the trimeric spike head, however, could not be distinguished, even for the smallest missing wedge. Considering the fact that the subunit displacements were only 1 nm and the resolution cutoff was slightly less than 3 nm, the failure to separate these two very similar species could be explained by the lack of sufficient resolution. The outcome also suggests that a ±60° tilt range is not quite satisfactory in this context, and higher tilt angles are desirable to render smaller structural detail faithfully.

The insight gained with the model calculations provides us with guidelines on how to interpret the results of the SIV envelope spike classifications. If monomeric or dimeric forms were present in the real data, we would expect that they show up in distinct classes. The experimental class averages do not show such evidence, however. The spikes seem to be of similar size and volume. The head region of the spikes seems to be variable to a certain extent, not all spike heads exhibit a clear trimeric shape. We can assume, though, that they still contain three subunits (gp120) due to the size of the spike volumes. Possible explanations for the variability could be structural flexibility, or a varying degree of structural preservation of the spikes. In the leg region, we should also be able to distinguish forms with differing morphology according to the model calculation, if such differences are present in the experimental data. Some variation can be observed, though the most striking feature is the deviation of the spike axis from an upright position. Furthermore, in comparison with an earlier report (Zhu et al., 2006), the previously observed tripod-like leg region, the gp41 ectodomain, is also not as obvious, especially in the surface rendered models (Fig. 6c). Rather, at the very base of the legs, close to the membrane, a broadening leg density was found that splits up into three components which were most evident in density cross-sections (Fig. 6e). This morphology is incompatible with another spike model obtained by cryo-electron tomography, which reported a thin, compact vertical stalk with little indication of basal broadening at the membrane (Zanetti et al., 2006). In the absence of CTF-correction, an electron-dense membrane can obscure parts of an adjacent protein structure due to the pronounced Fresnel fringe it produces at higher defocus. The fringe is uncorrelated with the protein structure and may thus distort its intrinsic shape, so that a stalk emerging from the membrane may not be rendered faithfully.

It was suggested that the differences in morphology of the two published models of the SIV envelope spikes, (Zhu et al., 2006) and (Zanetti et al., 2006), could have been due to artifacts caused by neglecting missing wedge effects in the data analysis in the Zhu et al. study (Subramaniam, 2006). We have now presented evidence that these effects may not be as significant as might have been anticipated in those studies. Our data indicates, that specific properties or attributes of a particular specimen structure can accentuate or mitigate the effects of the missing wedge. For example, our myosin V data showed a tendency of preferential grouping with respect to the missing wedge orientation despite the restricted rotational degrees of freedom, whereas the unrestricted orientations of the SIV spikes, surprisingly, did not show a sensitivity towards the missing wedge orientation. We believe that this can be explained in the following manner. In the case of myosin V, the structure consists of several “rod-like” components, namely the lever arm and the S2 domain. It is well known that the visibility of filaments in tomograms obtained from single axis tilt series show a strong effect of the missing wedge (Mastronarde, 1997). Filaments are most visible when the tilt axis is roughly parallel with the filament axis, and are least visible when the tilt axis and filament axis are perpendicular to each other. The two classes most affected (Fig. 3c and 3d), which were otherwise very similar, probably differed mostly in this particular characteristic. The other classes, which show less of an effect of the missing wedge, were probably more heterogeneous, so that the structural heterogeneity rather than the missing wedge effects were the distinguishing factor. We expect a 2D array to have less conformational variability than isolated molecules, consequently, making the missing wedge effect more apparent for the conformationally homogeneous motifs.

In the SIV subvolume classification, the strongest effect of the missing wedge is on membrane visibility; spikes extending out the top and bottom of a virion show no accompanying membrane while those on the sides do. In this case, however, a judicious choice of mask could minimize the effect. There is no such option in the case of filaments. Thus, in the one case where we might have expected there to be no missing wedge effect, due to the preferred orientation, it was unavoidable, whereas in the other case, where we expected to see the greatest effect of the missing wedge, it could be avoided by judicious choice of mask. Experimentally, there may still be a visible missing wedge effect on the subvolume classification for specimens like the SIV spikes, but it may require higher resolution and perhaps a less flexible structure to bring them out.

A general conclusion might be that missing wedge effects are highly dependent on the particular specimen, in particular its size, shape, context, and the particular density distribution within the molecular volumes, as well as the resolution of the original tomograms. The shape of a molecular assembly affects the classification, because a directional sensitivity would be more pronounced for a thin and elongated structure than for a more ball-shaped structure. An option to reduce detrimental effects for very thin, slab-like specimens with preferred orientations, such as myosin V, is to use the projection of the subvolumes as the basis for classification. The amount of missing data would be minimal in that case, because the tilt axis would lie nearly in the same plane as the central section in reciprocal space corresponding to the real space projection for a sufficiently flat specimen. Tomogram resolution may also increase the sensitivity to the missing wedge orientation, because a relatively larger volume in reciprocal space is affected at higher resolution. For the two specimens, the previous studies reported resolutions of 2.4 nm for the myosin V data and 3.2 nm for SIV, which could be another possible explanation of the more pronounced effect in the myosin V data.

In the subvolume classification of the SIV spikes, we would have expected a greater influence of the missing wedge based on earlier experience. In the previous work on SIV (Zhu et al., 2006), the dependence on the missing wedge orientation was alleviated by processing spikes originating from the top and bottom parts of the virions separately from those originating from the sides. We attribute the lack of a similar orientation dependence in the current study to the fact that we excluded the membrane density from the analysis in the classification step, whereas in the previous study it was included. Inclusion of the membrane will introduce a bias, because it is a strong feature that virtually disappears for a particular orientation of the missing wedge relative to the membrane surface (spikes from top and bottom of the viruses, relative to the tomogram). Another study has corroborated these findings (Ye et al., 2008). Methodologically, the averaging of membrane bound integrin molecules, incorporated into lipid vesicles, is comparable to the SIV case, and it also shows a classification bias in the presence of the membrane.

Our analysis has shown, that the compensation of missing wedge effects is not a major factor which would adversely affect the processing of the SIV data. In fact, we applied the same methodology in the investigation of a very similar specimen (HIV-1 envelope spikes) (Zhu et al., 2008) and found the results to be in good agreement in this respect. However, when compared to earlier studies, we observe differences in spike morphology and spike heterogeneity (Roux and Taylor, 2007). We attribute these differences primarily to the image processing involved. One major difference in the processing protocols is the use of a single reference in the former studies versus multiple references and reference-free alignment in the present work. Additionally, the single reference in one of the former studies had been symmetrized early in the iterative alignment and classification scheme. Reliance on a single reference, however, may introduce a significant reference bias. A demonstration of such a reference bias with a simple computational experiment is included in Fig. 10: the SIV data set, which had been aligned as described in the methods section, served as the input for an additional alignment cycle with symmetrized references. After the alignment with a single reference, the eigenimages of the data set were computed. The resulting eigenimages, especially the first one and to a lesser extent the second one, clearly exhibit the symmetry of the alignment reference. Since this occurs for three-, four-, and five-fold symmetric references alike, it must be attributed to reference bias rather than intrinsic symmetry of the aligned structure.

Figure 10. Reference bias in a single reference alignment.

Row (a) shows the first five eigenimages taken from a processing cycle of the SIV data set. An additional single reference alignment is carried out with the artificially created references in column (R) which have 3, 4, and 5-fold symmetry. The aligned subvolumes were then subjected to eigenvalue/eigenvector decomposition. The eigenimages of the data set after the single reference alignment are shown in rows (b – d). The first eigenimage (column 1) and to a lesser extent the second one (column 2) show clearly the symmetry of the reference, indicating an alignment bias towards the chosen reference. All panels represent sections through volumes perpendicular to the spike axis at a level in the head region of the spike.

Considering these facts, we avoided single references for the alignment (with the exception of the initial alignment), and used multiple references representing the actual structural variance found within the data set by classification, and avoided any imposition of symmetry. These measures should have greatly reduced the risk of introducing a bias in our first processing scheme. Even though we usually selected a subset of references from the class averages of a preceding processing cycle, the selection criteria were geared towards keeping as many different conformations as possible. The reason for selecting fewer references was primarily to reduce the computational effort. Corroborating evidence that reference bias can still be minimized with the multi-reference alignment protocol is provided by the results of the reference-free processing protocol which avoided altogether a subjective selection process and the alignment of raw subvolumes with a very low SNR to references with a higher SNR. The reference-free alignment scheme, or alignment by classification, improves the reliability of the alignment, because only class averages with increased SNR are aligned with respect to each other. Additionally, it reduces the computational effort, because only a relatively small number of references need to be aligned with respect to each other, whereas the multi-reference alignment requires a very large number of subvolumes to be aligned to each reference. To summarize, alignment by classification has several advantages: no reference bias, no selection process, more robust alignment, and increased computational efficiency. A disadvantage is that the alignment transformations are applied to the subvolumes in batches and not individually as with multi-reference alignment.

In conclusion, our results show that the subvolume processing methods were able to discriminate between various forms of SIV spikes, where previous methods only yielded a single structure, thus making the method particularly useful for investigating heterogeneous structures. Missing wedge effects on the classification were minimized by creating specifically adapted masks, by using constrained cross-correlation in the alignment and by forming class averages in reciprocal space to exclude missing regions in the averaging process. Furthermore, we note that reference bias is a significant factor of concern, perhaps more so than missing wedge effects, especially when only single references are used in the alignment.