An Imaging Workflow for Characterizing Phenotypical Change in Large Histological Mouse Model Datasets

Abstract

Motivation

This paper presents a workflow designed to quantitatively characterize the 3-D structural attributes of macroscopic tissue specimens acquired at a micron level resolution using light microscopy. The specific application is a study of the morphological change in a mouse placenta induced by knocking out the retinoblastoma gene.

Result

This workflow includes four major components: (i) Serial-section image acquisition, (ii) image preprocessing, (iii) image analysis involving 2-D pair-wise registration, 2-D segmentation and 3-D reconstruction, and (iv) visualization and quantification of phenotyping parameters. Several new algorithms have been developed within each workflow component. The results confirm the hypotheses that (i) the volume of labyrinth tissue decreases in mutant mice with the retinoblastoma (Rb) gene knockout and (ii) there is more interdigitation at the surface between the labyrinth and spongiotrophoblast tissues in mutant placenta. Additional confidence stem from agreement in the 3-D visualization and the quantitative results generated.

Availability

The source code is available upon request.

1 INTRODUCTION

This paper presents an imaging workflow designed to quantitatively characterize 3-D structural attributes of microscopic tissue specimens at micron level resolution using light microscopy. The quantification and visualization of structural phenotypes in tissue plays a crucial role in understanding how genetic and epigenetic differences ultimately affect the structure and function of multi-cellular organisms [1–5].

The motivation for developing this imaging workflow is derived from an experimental study of a mouse placenta model system wherein the morphological effects of inactivating the retinoblastoma (Rb) tumor suppressor gene are studied. The Rb tumor suppressor gene was identified over two decades ago as the gene responsible for causing retinal cancer (retinoblastoma) but has also been found to be mutated in numerous other human cancers. Homozygous deletion of Rb in mice results in severe fetal and placental abnormalities that lead to lethality by prenatal day 15.5 [6–8]. Recent studies suggest that Rb plays a critical role in regulating development of the placenta and Rb^−/− placental lineages have many fetal abnormalities [8–10].

Our previous work suggested that deletion of Rb leads to extensive morphological changes in the mouse placenta including possible reduction of total volume and vasculature of the placental labyrinth, increased infiltration from the spongiotrophoblast layer to the labyrinth layer, and clustering of labyrinthic trophoblasts [8]. However, these observations are based solely on the qualitative inspection of a small number of histological slices from each specimen alone. In order to fully and objectively evaluate the role of Rb deletion, a detailed characterization of the mouse placenta morphology at cellular and tissue scales is required. This permits the correlation of cellular and tissue phenotype with Rb^−/− genotype. Hence, we develop a microscopy image processing workflow to acquire, reconstruct and quantitatively analyze large serial-sections obtained from a mouse placenta. In addition, this workflow has a strong visualization component that enables exploration of complicated 3-D structures at cellular/tissue levels.

Using the proposed workflow, we analyzed six placentae samples which included three normal controls and three mutant (Rb^−/−) samples. A mouse placenta contains a maternally derived decidual layer and two major extra-embryonic cell derivatives namely, labyrinth trophoblasts and spongiotrophoblasts. Placental vasculature that lays embedded within the labyrinth layer is the main site of nutrient-waste exchange between mother and fetus and consists of a network of maternal sinusoids interwoven with fetal blood vessels. The quantitative analysis of placentae samples validates observations published in [10] that Rb-deficient placentae suffer from a global disruption of architecture marked by increased trophoblast proliferation, a decrease in labyrinth and vascular volumes, and disorganization of the labyrinth-spongiotrophoblast interface.

To summarize, in this paper we report the architecture and implementation of a complete microscopic image processing workflow as a novel universal 3-D phenotyping system. The resulting 3-D structure and quantitative measurements on the specimen enable further modeling in systems biology study. While some of the algorithms presented here are optimized for characterizing phenotypical changes in the mouse placenta in gene knockout experiments, the architecture of the workflow enables the system to be easily adapted to countless biomedical applications including our exploration of the organization of tumor microenvironment [16].

1.1 Related Work

The quantitative assessment of morphological features in biomedical samples is an important topic in microscopic imaging. Techniques such as stereology have been used to assess 3-D attributes by sampling a small number of images [17]. Using statistical sample theory, stereological methods allow the researcher to gain insights on important morphological parameters such as cell density and size [18, 19]. However, an important limitation of stereology is that it is not useful for large scale 3-D visualization and tissue segmentation, both of which are potentially critical for biological discovery. Therefore, we need new algorithms to enable objective large-scale image analysis. Since our work involves multiple areas of image analysis research, we delegate algorithmic literature review to the corresponding subsections in Section 2.

There has been some work focusing on acquiring the capability for analyzing large microscopic image sets. Most of these efforts involve developing 3-D anatomical atlases for modeling animal systems. For instance, in [20], the authors developed a 3-D atlas for the brain of honeybees using stacks of confocal microscopic images. They focus on developing a consensus 3-D model for all key functional modules of the brain of the bees. In the Edinburgh Mouse Atlas Project (EMAP), 2-D and 3-D image registration algorithms have been developed to map the histological images with 3-D optical tomography images of the mouse embryo [21]. Apart from atlas related work, 3-D reconstruction has also been used in clinical settings. In [1], the authors build 3-D models for human cervical cancer samples using stacks of histological images. The goal was to develop an effective non-rigid registration technique and identify the key morphological parameter for characterizing the surface of the tumor mass. In this paper, instead of focusing on a single technique, we present the entire workflow with a comprehensive description of its components.

2 COMPONENTS AND ALGORITHMS OF THE WORKFLOW

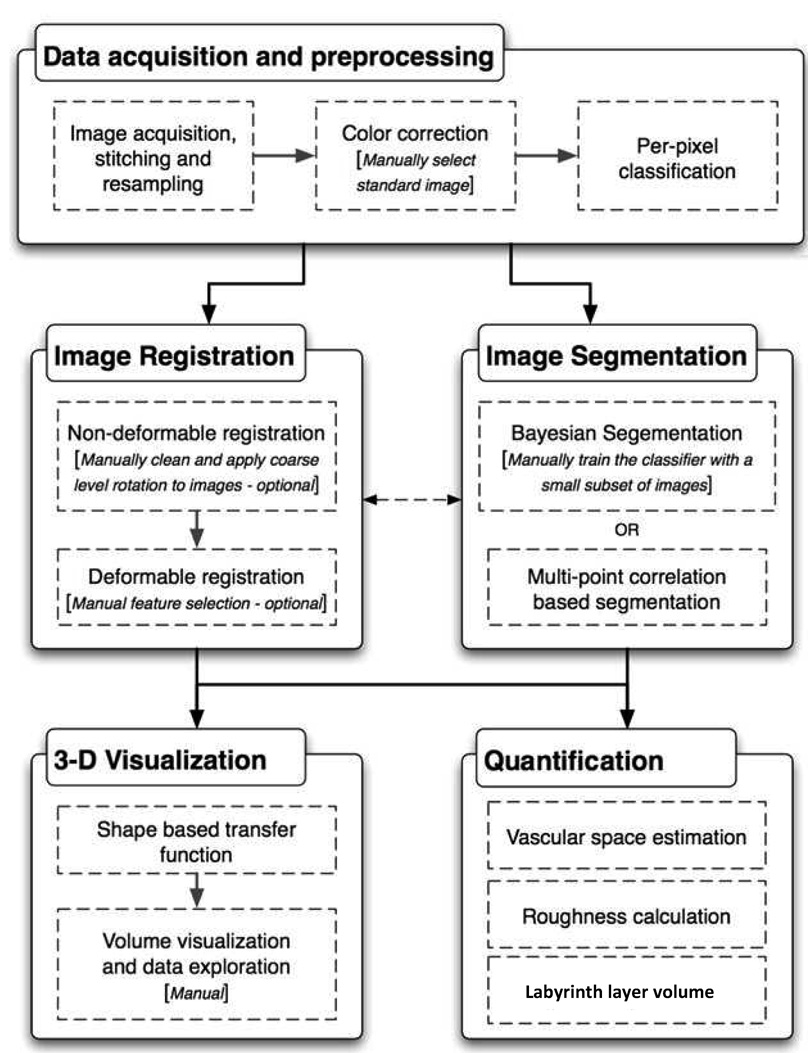
In this section, we describe the components of the workflow and the related image processing algorithms. Please refer to Figure 2 for a schematic representation of the three stages.

Figure 2.

The imaging workflow for characterizing phenotypical changes in microscopy data. Components that involve manual intervention are identified.

1. In the first stage, large sets of histological slides are produced and digitized. The preprocessing of the images includes color correction to compensate for intensity inconsistency across slides due to staining variations and pixel-based color classification for segmenting the image components such as cell nuclei, white spaces (including purported vasculature spaces), cytoplasm and red blood cells. These standard pre-processing steps build the foundation for the next two stages of investigation.

2. The second (middle) stage consists of image registration and segmentation. The registration process aligns 2-D images in a pair-wise manner across the stack. Pair-wise alignments provide 3-D coordinate transforms to assemble a 3-D volume of the mouse placenta. The segmentation process identifies regions corresponding to different tissue structures such as the labyrinth and spongiotrophoblast layers. In our current realization, the image registration and segmentation process do not directly interact with each other. However, in other applications, results from image segmentation provide the landmarks that may used in image registration [16].

3. The final stage (bottom) of the workflow supports user-interaction, exploration via visualization and quantification. For this project, the quantification is focused on testing three hypotheses about the effects of Rb deletion in placental morphology. We provide the hypotheses specifics later in Section 2.6. The quantification step in our workflow provides measurements of morphological attributes relevant to the hypothesis. The visualization step allows the researcher to further study the 3-D structures in detail. Volumetric rendering techniques are developed because we are interested in visualization of multiple interleaving types of tissue that will further confirm the quantifications.

The details in the three levels of the workflow are given in Section 2.1 – 2.6. Please note that in stage 2, we adopt a multiresolution strategy. For example, image registration/segmentation is carried out at lower resolutions in order to reduce computational costs. Furthermore, we note that the performance of a segmentation algorithm is dependent on the resolution scale. Later stages often process segmented images at different resolutions. Hence, multiple algorithms have been developed for the same technical component.

2.1 Data acquisition

2.1.1 Image Acquisition and Stitching

Six mouse placenta samples, three wild-type and three Rb^−/−, were collected at embryonic day 13.5. The samples were fixed in formalin, paraffin-embedded, sectioned at 5-µm intervals and stained using standard haematoxylin and eosin (H&E) protocols. We obtained 500–1200 slides approximately for each placenta specimen that were digitized using a Aperio ScanScope slide scanner with 20× objective length and image resolution of 0.46 µm/pixel. Digitized whole slides were acquired as uncompressed stripes due to the constrained field-of-view of the sensor. The digitization process also produces a metadata file that contains global coordinates of the stripes and describes the extent of any overlap with adjacent stripes. This file is used to reconstruct the digital file of the whole slide from the stripes using a custom Java application that we developed for this purpose.

2.1.2 Image Re-sampling

Each serial-section produces a digitized RGB format image with dimensions approximately 16K × 16K pixel units. A entire set of the placenta image stacks (each containing approximately 500–1200 images) occupies more than 3 Terabytes (Tb) of data storage. The processing of such large datasets is beyond the computational capability of most workstations, especially since most imaging algorithms require the full image to be loaded into memory. For certain tasks, it is convenient to down-sample images by a factor of 2 to 10 depending on the algorithm and performance. The down-sampling process employs linear interpolation to maintain continuity of the features.

2.2 Image preprocessing

2.2.1 Color Correction

Digitized images of sectioned specimens usually exhibit large staining variations across the stack. This occurs due to idiosyncracies in the slide preparation process, including section thickness, staining reagents and reagent application time. The process of color correction seeks to provide similar color distributions (histograms) in images from the same specimen. This process greatly facilitates later processing steps, because consistent color profiles narrow the range of parameter settings in algorithms. Color correction is accomplished by normalizing all images in a specimen to a standard color histogram profile. The standard histogram is computed from a manually pre-selected image with a color profile that is representative of the whole image stack.

The color profiles are normalized using MATLAB’s Image Toolbox histogram equalization function [22]. We ensure that pixels representing foreground tissue alone participate in the color normalization process. We developed an algorithm to identify foreground tissue pixels from background by thresholding the image in HSL (hue, saturation, and luminance) color space. The HSL color space is less sensitive to intensity gradients within a single image that result from light leakage near edges of glass slides.

2.2.2 Pixel-based color segmentation

Pixels in an H&E-stained image correspond to biologically salient structures, such as placental trophoblast, cytoplasm, nuclei and red blood cells. These different cellular components can be differentiated based on color in each specimen, and the per-pixel classification result is used in image registration and segmentation.

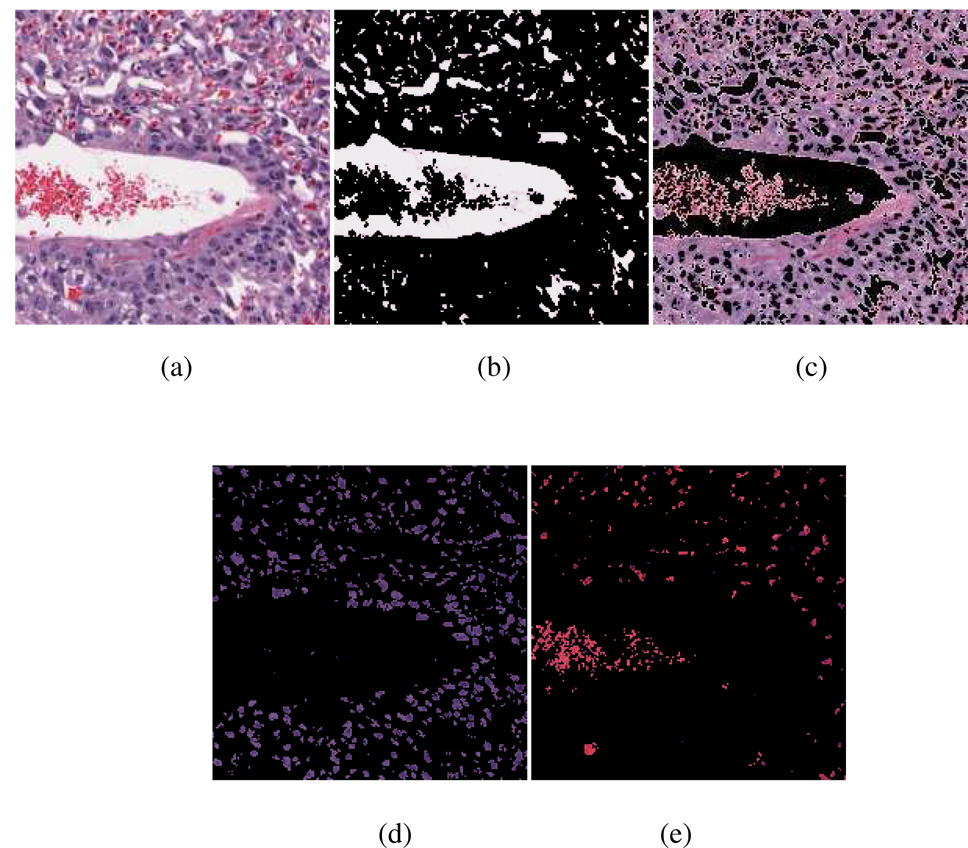
A maximum likelihood estimation (MLE) algorithm is implemented to classify the pixels into four classes in the RGB color space: red blood cells, cytoplasm, nuclei, and background. For simplicity, we assume that the histograms of the bands of data have normal distributions. The a priori information related to the four classes is learnt via the following training process. For the image dataset of each placenta specimen (usually contains 500 to 1200 images), one representative image is selected as training image (the same one used to normalize the color profile). A custom-built application randomly selects pixels from the images, displays patches of the training image centering at the selected pixel and highlights the center pixels. The user then chooses among the four classes and a pass option. This procedure provides the training samples and their classifications from manual input. The spatial locations and RGB triplet values are used as attributes for these randomly selected pixels. The covariance matrices, mean values and prior probability weights are then calculated for each individual class. The maximum logarithmic probability rule is invoked to determine the final class membership. Here the pixels classified as background are from three possible sources. One source is the white background of the images. In each image, the foreground (the region corresponding to the specimen) is surrounded by a large region of white background space. Therefore pixels in the largest region of background can be easily removed. Another source of background pixels is the white space in the blood vessels. Since most red blood cells are removed from the blood vessel during the preparation of the slides, the regions corresponding to cross sections of blood vessels usually appear in the form of small white areas with a small number of red pixel clusters (red blood cells). The pixels corresponding to the blood vessels are important in determining the area of vasculature space in the images. The third source of white pixels is the cytoplasm areas for large cells such as giant cells in the spongiotrophoblast layer and the glycogen cell clusters. An example of the pixel classification result is shown in Figure 3. The classification results are used in the subsequent stages based on requirements in classification granularity.

Figure 3.

An example of the color segmentation. (a): A 200-by-200 pixel patch of the original image (downsampled by four times for visualization purposes). (b): Segmented background region. Most of the white background regions correspond to blood vessels. A small fraction of them (in the bottom left corner of the image) correspond to cytoplasm regions for the large cells in the spongiotrophoblast layer. (c): Segmented cytoplasm region. (d): Segmented cell nuclei region. (e): Segmented red pixels corresponding to the remaining red blood cells in the blood vessels.

2.3 Image Registration

During the slide preparation process, a tissue section is mounted with a random orientation on the glass slide. The section remains displaced in orientation and offset from the previous sliced section. The nature of physical slicing causes deformation and non-linear shearing in the soft tissue. Image registration seeks to compensate for the misalignment and deformation by aligning pair-wise images optimally under pre-specified criteria. Hence, image registration allows us to assemble a 3-D volume from a stack of images. In our study, we employ rigid and non-rigid registration algorithms successively. While rigid registration provides the rotation and translation needed to align adjacent images in a global context, it also provides an excellent initialization for the deformable registration algorithm [1]. Non-rigid registration compensates for local distortions in an image caused by tissue stretching, bending and shearing [22, 26–28].

2.3.1 Rigid registration algorithms

Rigid registration methods involve the selection of three components: the image similarity metric (cost function), the transformation space (domain), and the search strategy (optimization) for an optimal transform. We present two algorithms for rigid registration. The first algorithm is used for reconstructing low-resolution mouse placenta images. The second algorithm is optimized for higher resolution images.

1. Rigid registration via maximization of mutual information

This algorithm exploits the fact that the placenta tissue has an elongated oval shape. We carry out a principal component analysis of the foreground region to estimate the orientation of the placenta tissue. This orientation information is used to initialize an estimate of the rotation angle and centroid translation. After the images are transformed into a common coordinate reference frame, a maximum mutual information based registration algorithm is carried out to refine the matching [12, 23]. The algorithm searches through the space of all possible rotation and translations to maximize the mutual information between the two images.

MI based methods are effective in registering multi-modal images where pixel intensities between images are not linearly correlated. While the placenta images are acquired using the same protocol, they have multimodal characteristics due to staining variations and the occasional luminance gradients. Rigid body registration techniques requiring intrinsic point or surface-based landmarks [41] and intramodal registration methods [42] that relying on linear correlation of pixel values are inadequate under these conditions.

It has been shown [43] that MI registration with multiresolution strategies can achieve similar robustness compared to direct registration. Studholme [44] reported no loss in registration precision and significant computational speed-up when comparing different multiresolution strategies. We adopt the multiresolution approach, using 3-level image pyramids. The image magnifications used were 10×, 20×, and 50×. Optimal transforms obtained from a lower magnification are scaled and used as initialization for registration of the next higher magnification. Registration is then performed on the images, potentially with different optimizer parameters, to refine the transforms. The process is repeated for each magnification level to obtain the final transforms. We note that at magnifications higher than 50×, the computation cost for registration outweighs the improvements in accuracy. The details of the implementation can be found in [12].

2. Fast rigid registration using high-level features

This algorithm segments out simple high-level features that correspond to anatomical structures such as blood vessels using the colorbased segmentation results in both images. Next, it matches the segmented features across the two images based on similarity in areas and shapes. Any two pairs of matched features can potentially be used to compute rigid transformation between the two images. The mismatched features are removed with a voting process, which selects the most commonly derived rigid transformation (rotational and translational) from the pairs of matched features. This algorithm was implemented to register large images with high speed [11].

2.3.2 Non-rigid registration

In our workflow, the rigidly-registered image stack serves as input for further refinement using non-rigid methods. In order to visualize a small localized tissue microenvironment, non-rigid registration was conducted by manually selecting point features in each slice of the microenvironment. While we obtained good quality visualizations, repeating this procedure is cumbersome and forced us to consider automated techniques.

(The literature review part has been consolidated and shrunk.)

There are many previous studies on automatic non-rigid registration. Johnson and Christensen present a hybrid landmark/intensity-based technique [45]. Arganda-Carreras et al present a method for automatic registration of histology sections using Sobel transforms and segmentation contours [47]. Leung and Malik et al use the powerful cue of contour continuity to provide curvilinear groupings into region-based image segmentation [48]. Our data does not however have well defined contours on a slice by slice basis. Thus, contour based registration techniques fail on our dataset.

In our approach, automated pair-wise non-rigid registration is conducted by first identifying a series of matching points between images. These points are used to derive a transformation by fitting a nonlinear function such as a thin-plate spline [26] or polynomial functions [25, 28]. We have developed an automatic procedure for selecting matching points by searching for those with the maximum cross correlation of pixel neighborhoods around the feature points [11].

Normally, feature points in an image are selected based on their prominence. Our approach differs with the previous ones in that we select points uniformly. For instance, we choose points that are 200 pixels apart both vertically and horizontally. The variation in a 31 × 31 pixel neighborhood centered at each sampled point is analyzed. The selection of the neighborhood window size depends on the resolution of the image so that a reasonable number of cells/biological features are captured. Please note that we only retain feature points belonging to the foreground tissue region. The neighborhood window is transformed into the grayscale color space and its variance is computed. We retain the selected point as a feature point only when the variance of the neighboring window pixel intensity value is large enough (which implies a complex neighborhood). The unique correspondence of a complex neighborhood with a novel region in the next image is easy to determine. On the other hand, regions with small intensity variance tend to generate many matches and prone to false-positives. For example, consider an extreme example in which a block of white space can be matched to many other blocks of white spaces without knowing the correct match. This step usually yields about 200 features points that are uniformly distributed across the foreground of each image.

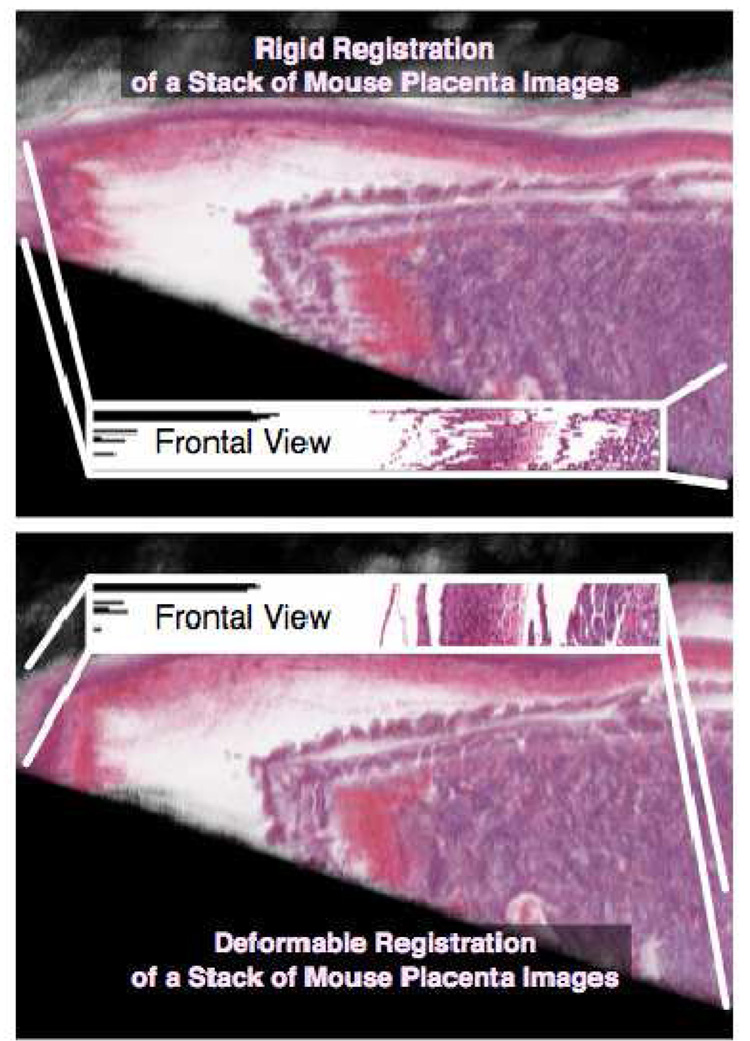
In the second step, we rotate the window around the feature point by the angle that is already computed in the rigid registration procedure. This gives a template patch for initialization in the next image. In the next image, a much larger neighborhood (e.g., 100 × 100 pixels) is considered at the same location. A patch in this larger neighborhood with the largest cross correlation with the template patch from the first image is selected. The center of this patch is designated as the matching feature point. The two steps together usually generate more than 100 matched feature points between the two images. These points are then used as control points to compute the nonlinear transformation using the thin-plate splines or polynomial transformations [25, 28]. In this project, we tested both six-degree polynomial transformations and piecewise affine transformations. The 3-D reconstructions are similar in both schemes while the piecewise affine transformation is easier to compute and propagate across a stack of images. Figure 4 shows renderings of the placenta that were reconstructed using the rigid and deformable registration algorithms. This approach is used to generate high resolution 3D reconstructions of the samples.

Figure 4.

Comparison of rigid and deformable registration algorithms. A stack of twenty five images were registered using rigid registration algorithm (top) and nonrigid registration algorithm (bottom) and the 3-D reconstruction results are rendered. The frontal views show the crosssections of the reconstructed model. The benefits of using deformable registration algorithms are clearly visible in the frontal view of the image stack cross-section. In the top frontal view which is the cross section of the rigid registered images, the structures are jaggy and discontinuous. In the bottom frontal view, the results from the nonrigid (deformable) registration algorithm display smooth and continuous structures.

2.4 Image Segmentation

In processing biological images, a common task is to segment the images into regions corresponding to different tissue types. For analysis of the mouse placenta, we segmented images into three tissue types, labyrinth trophoblast, spongiotrophoblast, and glycogen cells (a specialized derivative of the spongiotrophoblast lineage). Each H&E-stained tissue type can be classified by distinctive texture and color characteristics of cell nuclei and cytoplasm and by presence of vacuoles and red blood cells. The segmentation algorithm, therefore, is based on object texture, color, and shape.

The automatic segmentation of natural images based on texture and color has been widely studied in computer vision [30–32]. Most segmentation algorithms contain two major components: the image features and the classifier (or clustering method). Image features include pixel intensity, color, shape, and spatial statistical features for textures such as Haralick features and Gabor filters [33, 34]. A good set of image features can substantially ease the design of the classifier. Supervised classifiers are used when training samples are available. Examples of such classifiers include Bayesian classifier, K-nearest neighbor (KNN), and support vector machine (SVM). If no training example is available, unsupervised clustering algorithms are needed. Examples of such algorithms are K-means, generalized principal component analysis (GPCA)[32], hierarchical clustering, and self-organizing maps (SOM). Active contour algorithms, such as the level set based ones [35], can also be considered as an unsupervised method.

In our project, both manual and automatic segmentation procedures have been conducted on the image sets. For each placenta, manual segmentation of the labyrinth layer was carried out on ten images that are evenly spaced throughout the image stack. These manually segmented images are used as the ground truth for training and testing the automatic segmentation algorithms. In addition, manual segmentation allows for higher level of accuracy in the estimation of area of the labyrinth layer, which also translates to more accurate volume estimates. However, manual segmentations are not feasible for the purpose of visualizing the boundary between the labyrinth and the spongiotrophoblast layers since it is impractical to manually segment all the images. Instead, we adopted automatic segmentation for this purpose.

New features for histological images

In histology-based microscopy images, there has been little work on the automatic segmentation of different types of tissues or cell clusters in histological images. Due to the complicated tissue structure and large variance in biological samples, none of the commonly used image segmentation algorithms that we have tested can successfully distinguish the biological patterns in microstructure and organization [13]. To solve this problem, we designed new segmentation algorithms. The idea was to treat each tissue type as one type of heterogeneous biomaterial composed of homogeneous microstructural components such as the red blood cells, nuclei, white background and cytoplasm. The distribution and organization of these components determine the tissue type. For such biomaterials, quantities such as multiple-point correlation functions (especially the two-point correlation function) can effectively characterize their statistical properties [36] and thus serve as effective image features.

The two-point correlation function (TPCF) for a heterogeneous material composed of two components is defined as the probability that the end points of a random line with length l belong to the same component. TPCF has been used in analyzing microstructures of materials and large images in astrophysics. However, our study marks the first time that TPCF is introduced in characterizing tissue structures in histological images. For materials with more than two components, a feature vector replaces the probability with each entry being the correlation function for that component. In our work, the four components are cell nuclei, cytoplasm, background and red blood cells, which are obtained through pixel classification in the preprocessing stage. In addition to the two-point correlation function, three-point correlation function and lineal-path function can also be similarly defined. These functions form an excellent set of statistical features for the images, as demonstrated in Section 3.

Supervised classification

In addition to feature selection, another aspect of the segmentation problem is to select the classification procedure. In our project, we selected the K-nearest neighbor (KNN) due to both its effectiveness and easy implementation [14]. For each placenta specimen, about 500 to 1200 serial images are generated. Due to the large variation in morphology, intensity and cell distributions across the different placenta datasets, the KNN classifier is trained on a per placenta dataset basis prior to segmenting all the images.

Within each placenta dataset, ten evenly spaced images were selected from the stack. These ten images were then manually segmented by the pathologist. A representative image of the 2-D morphology for this placenta specimen was selected by the pathologist as the training sample from the set of 10 images. Image patches of size 20-by-20 pixels were randomly generated and labeled as labyrinth, spongiotrophoblast, glycogen cells or background. A patch lying on the boundaries remained ambiguous and was not chosen into the training dataset. A total of 2200 regions were selected from the image slide (800 for labyrinth, 800 for spongiotrophoblast, and 600 for the background) for training. Please note that the color-correction of the serial-section stacks (Section 2.1.2) allowed the tissue components to share similar color distributions across the images and hence training based on a representative slide was applicable throughout. The remaining nine images were used for validation purposes as ground-truth.

Evaluation of the automatic segmentation algorithm

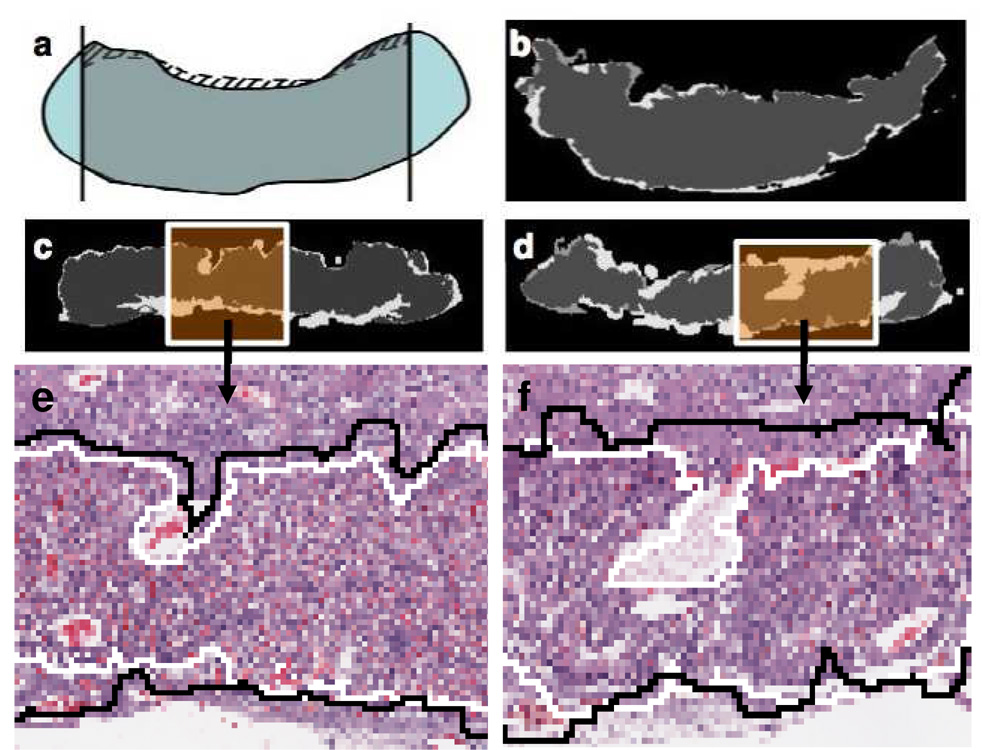
In our study, we found that automatic segmentation tends to generate relatively large error in images obtained from the end regions of the placenta slice sequence, which can bias the volume estimation. However, for the mid-section of the sequence, automated segmentation provided a visually satisfactory boundary between the two layers of tissues. These tests were carried out in three placentae with one control and two mutants. The observation is further confirmed by a quantitative evaluation process as shown in Figure 6. In the figure, the automatically segmented labyrinth is overlaid on the manually segmented labyrinth tissue. For all the manually segmented images, the error is measured as the ratio between the area encircled by the two tissue boundaries (manually and automatically generated boundaries) and the manually segmented labyrinth area. For the three samples, the mean errors are 6.6±1.6%, 5.3±3.3%, and 16.7±7.4%. The two samples (one control and one mutant) with mean error less than 8% are then used for visualization. As shown in Figure 6e and 6f, the discrepancy between the two segmentation methods can be attributed to two major factors: the use of a large sliding window in automatic segmentation which leads to the “dilation effect”, and the discrepancy in assigning the large white areas on the boundary. This white region is actually the cross-section of a blood vessel at the boundary of the labyrinth tissue layer and the spongio-trophoblast tissue layer. The designation of such regions usually requires post-processing based on explicit anatomical knowledge which is not incorporated in the current version of the automatic segmentation algorithm.

Figure 6.

Evaluation of the automatic segmentation algorithm. (a): The solid line is the manually marked boundary and the dashed line is the automatic segmentation result. The boundary estimation error is defined as the ratio between the shaded area and the grey area. (b), (c) and (d): examples of images with boundary estimation errors being 2.5%, 8.4% and 16.5%. The boundary is in the top portion of the image. The dark gray area is the manual segmentation result, and the light gray area is the automatic segmentation result. (e) and (f): a larger view of the difference between manual segmentation (black) and automatic segmentation (white).

2.5 Visualization in the 3-D space

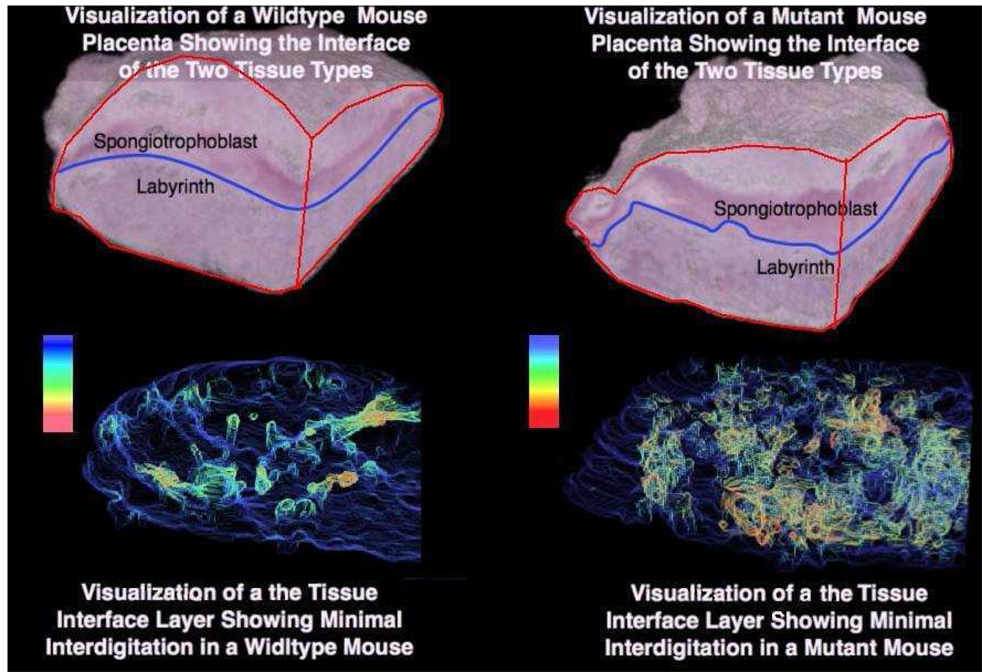
We are interested in quantifying the 3D finger-like infiltration (referred as pockets) that occurs on the labyrinth-spongiotrophoblast tissue interface of the mouse placenta (Figure 5). The presence of pockets has a direct correlation with surface morphological parameters such as interface surface-area, convolutedness and the extent of tissue infiltration.

Figure 5.

Visualizing the interdigitation at the interface of the labyrinth and the spongiotro-phoblast tissue layers in control (left) and mutant (right) mouse placenta. The detected pockets are colored using a heat map. Red regions indicate large pockets and yellow regions indicate shallow pockets.

The registered stack of images is treated as volume data and visualized using volumetric rendering techniques. In volumetric rendering, a transfer function maps the feature value (e.g. pixel intensity) to the rendered color and opacity values. It allows the user to highlight or suppress certain values by adjusting the transfer function. In our approach we evolve a front in the close vicinity of the target surface. The front initially represents a global shape of the surface without pockets. As the front progresses towards the target surface, it acquires the features on the surface and finally converges to it. This leads to a natural definition of feature size at a point on the contour as the distance traveled by it from the initial front to the target surface. Surface pockets have larger feature sizes compared to the flat regions owing to the larger distances traversed. Hence they are suitably extracted. Figure 5 shows the resultant visualizations from a transfer function that highlights high feature values. The details of the implementation can be found in [49].

2.6 Quantification

Our application requires the quantitative testing of three hypotheses regarding the morphological changes in mouse placenta induced by the deletion of Rb. These hypothesized changes include the increased surface complexity between the labyrinth layer and the spongiotrophoblast layer, the reduced volume of the labyrinth layer, and reduced vasculature space in the labyrinth layer. Here we describe the quantification processes for measuring the three morphological parameters.

2.6.1 Characterizing the complexity of the tissue layer interface

Rb mutation increases the number of shallow interdigitations at the interface of the spongiotrophoblast and the labyrinth tissue layers. In order to quantify the increased interdigitation, we calculate the number of pixels at the interface and the roughness of the interfacial area between the two layers, based on the assumption that increased interdigitation is manifested as increased area of the interface and greater roughness. The number of pixels at the interface is computed based on the image segmentation results. In addition, given the fractal nature of the surface area between the two tissue layers, the boundary roughness is quantified by calculating the Hausdorff dimension, a technique that is well-known and commonly used in geological and material sciences for describing the fractal complexity of the boundary [40]. Typically, the higher the Hausdorff dimension, the more rough the boundary. In order to calculate the Hausdorff dimension, we take the 2-D segmented image and overlay a series of uniform grids with cell size ranging from 64 pixels to 2 pixels. Next we count the number of grid cells that lie at the interface of the two tissue layers. If we denote the cell size of the grids as ε and the number of grid cells used to cover the boundary as N(ε) Then the Hausdorff dimension d can be computed as

$$\mathit{d}=-{\mathit{\text{lim}}}_{\epsilon ⤍0}\mathit{(}\mathit{\text{ln}}\mathit{(}N\mathit{(}\epsilon \mathit{)}\mathit{)}/\mathit{\text{ln}}\mathit{(}\epsilon \mathit{)}\mathit{)}.$$

In practice, d is estimated as the negated slope of the log-log curve for N(ε) versus ε.

2.6.2 Estimating the volumes of the labyrinth tissue layer in mouse placentae

The volume of the labyrinth is estimated using an approach analogous to the Riemann Sum approximation for integration in calculus. The labyrinth volume for a slice is computed from the pixel count of the labyrinth mask obtained from the 2D segmentation, the 2D pixel dimensions, and section thickness. The labyrinth volume is accumulated across all serial sections in a dataset to obtain an approximation of the total labyrinth volume.

2.6.3 Estimating the vascularity in the labyrinth tissue layer

The vascularity of the labyrinth is estimated by the ratio of total blood space volume to total labyrinth volume, which is referred to as intravascular space fraction. The estimation of total labyrinth volume is described in the above section. The total blood space is calculated by counting all pixels previously classified as red blood cell pixels or as background pixels within the labyrinth tissue. The labyrinth mask generated by the segmentation step is used to identify the background pixel in the second case. The intravascular space fraction is then computed.

3 RESULTS: A CASE STUDY ON THE EFFECTS OF RB DELETION IN PLACENTAL MORPHOLOGY

3.1 Manual and automated stages

Whole slide imaging for histology and cytology usually involves a large amount of data and is typically not suitable for manual annotation. Three-dimensional processing of serial sections further motivates the need for automation of different stages in the workflow. However, biological systems are characterized by a high incidence of exceptions, and these are especially evident in systems with high-level of detail such as microscopic imaging. Human intervention and semiautomated approaches are often essential components in image analysis workflows. The manual components are identified in the schematic representation shown in Figure 2.

3.2 Results

The last stage of the workflow discussed in Section 2 generates results for the application – namely quantified parameters and visualizations. For this project, the quantification is focused on testing the three hypotheses about the effects of Rb deletion in placental morphology, namely reduced volumes of the placental labyrinth layer (Section 3.2.3), decreased vasculature space in the labyrinth layer (Section 3.2.4), and increased roughness of the boundary between the labyrinth and spongiotrophoblast layers (Sections 3.2.1 and 3.2.2).

3.2.1 Reconstruction and Visualization in 3-D

Figure 5 shows the final reconstructed mouse placenta using rigid registration results. Different tissues are highlighted by incorporating the segmentation results in the transfer function adjustment during volumetric rendering. Earlier, in Section 2.5, we mentioned about the 3D fingerlike infiltration that occurs on the labyrinth-spongiotrophoblast tissue interface of the mouse placenta. The presence of pockets has a direct correlation with surface morphological parameters such as interface surface-area, convolutedness and the extent of tissue infiltration. We automatically detect pockets using a level-set based pocket detection approach to determine a pocket size feature measure along the interface (16). The bottom section of the figure shows the infiltration structure in detail by using these feature measurements in the transfer function. The resulting visualization reveals extensive shallow interdigitation in mutant placenta in contrast with fewer but larger interdigitations in the control specimen. These observations are quantitatively verified by calculating the fractal dimension.

3.2.2. Quantifying complexity of the tissue interface

We first computed the number of pixels at the interface between the two tissue layers in littermates. The number of interface pixels for the controls are 1738 and 2374 (in the images downsampled by 20 times to save computational cost for the image segmentation algorithm) while the interface pixels for the corresponding mutants are 3413 and 4210 respectively. Therefore in both cases, the numbers of interface pixels are almost doubled in mutants than in controls. However, the result for computing the Hausdorff dimension is not as significant. Among the three pairs of littermates, the increase in the Hausdorff dimensions in mutants comparing to the controls are only 3%, 2.5% and 0.5% when the grid cell sizes between 2 pixels and 64 pixels are used. However, in the mutant placenta, the number of grid cells of size no more than 8 pixels that lie on the interface layer is significantly increased. This suggests that most of the disruption at the interface is due to small shallow interdigitations which are difficult to be characterized using fractal dimensions. This observation supports our result determined in Section 3.2.1 above on surface pockets. Available work in literature have also reported difficulty in computing fractal dimensions [1].

3.2.3 Volume of labyrinth tissue layer estimation

The volume of the labyrinth tissue layer for each specimen was estimated by summing the areas of the labyrinth layer in each of the ten manually segmented images then multiplying by the distance between consecutive images. This method gives a first order approximation of the labyrinth layer volume. The estimated volumes of the labyrinth layer for the three control mice are 11.0mm³, 9.0 mm³, and 12.8 mm³. While the measurements for their corresponding littermates are 7.9 mm³, 8.2 mm³, and 9.3 mm³. A consistent reduction of labyrinth layer volume in the range of 9% to 28% is therefore observed for the three pairs of littermates.

3.2.4 Intravascular space fraction estimation

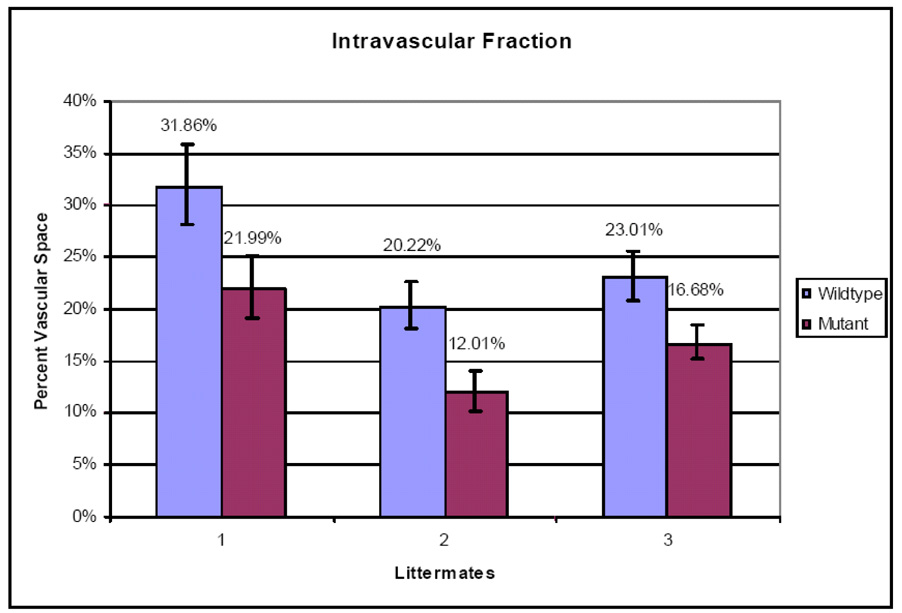
The intravascular space fraction is estimated by combining the color segmentation and image segmentation results. We compute the percentage of white and red pixels in the segmented labyrinth layers. As shown in Figure 7, for all three pairs of mutant and control samples, significant decrease in intravascular space fraction is observed.

Figure 7.

Intravascular space fraction estimation. The intravascular space fraction is measured for each sample in ten manually segmented images. The mean and standard deviation of the measurement are presented here.

The reduction in the volume and the intravascular space of the labyrinth layer in the mouse placenta is consistent with our hypothesis that Rb deletion causes significant morphological disruption in mouse placenta which negatively affects fetal development.

4 CONCLUSION AND DISCUSSION

In this paper, we presented an imaging workflow for reconstructing and analyzing large sets of microscopy images in the 3-D space. The goal of this work is to develop a new phenotyping tool for quantitatively studying sample morphology at tissue and cell level. We developed a set of algorithms that include the major components of the workflow using a mouse placenta morphology study as a driving application. This workflow is designed to acquire, reconstruct, analyze, and visualize high-resolution light microscopy data obtained from a whole mouse placenta. It allows the researchers to quantitatively assess important morphological parameters such as tissue volume and surface complexity on a microscopic scale. In addition, it has a strong visualization component that allows the researcher to explore complicated 3-D structures at cellular and tissue levels. Using the workflow, we analyzed six placenta including three controls and three Rb^−/− mutant with gene knockout and quantitatively validated the hypotheses relating to Rb in placenta development [10]. Analysis of placenta indicated that Rb mutant placenta exhibit global disruption of architecture, marked by an increase in trophoblast proliferation, a decrease in labyrinth and vascular volumes, and disorganization of the labyrinth-spongiotrophoblast interface. The analytical results are consistent with previously observed impairment in placental transport function [8, 10]. These observations include an increase in shallow finger-like interdigitations of spongiotrophoblast that fail to properly invade the labyrinth and clustering of labyrinth trophoblasts that was confirmed with the 3-D visualization. Due to the intricacy of carrying out experiments with transgenetic animals, we had only a small number of placenta samples which just satisfied the basic statistical requirement. However, the consistent changes in placental morphology we have obtained from large scale image analysis and visualization provide strong evidence to support our hypothesis.

One of the major challenges we faced in the process of workflow development was to strike a good balance between automation and manual work. On one hand, large data size forced us to develop automatic methods to batch process the images. On the other hand, large variations in the images required us to take several manual steps to circumvent the technical difficulties and achieve more flexibility. While this work was largely driven by the mouse placenta study, it is subsequently applied to process other data sets including our ongoing work in phenotyping the mouse breast tumor microenvironment. Other directions include developing a parallel processing framework for handling images in their original high resolution and a middleware system to support the execution of the workflow on multiple platforms, improving the accuracy of the image segmentation algorithm to obtain higher accuracy and better time performance, and extending the image registration algorithm to deal with images from slides stained with different staining techniques (e.g., H&E versus immunohistochemical staining) so that we can map molecular expression to different types of cells.

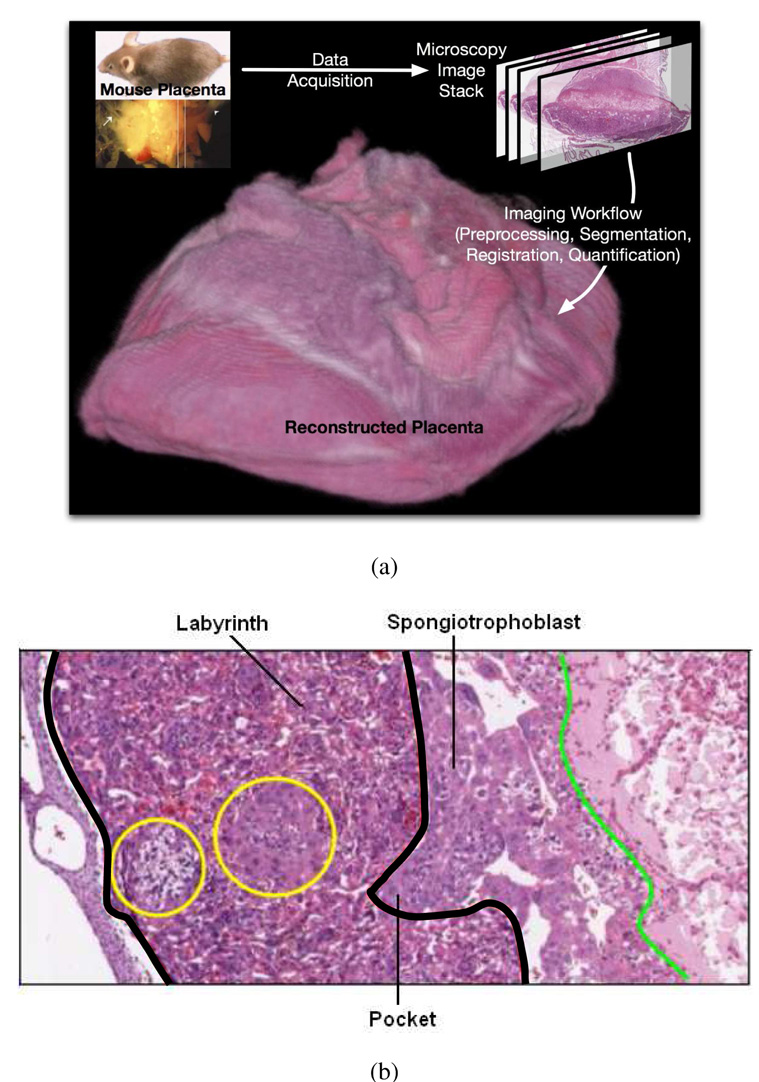
Figure 1.

(a) A mouse placenta reconstructed in 3D with the described imaging workflow. (b) Zoomed placenta image showing the different tissue layers. The tissue between the two thick black boundaries is the labyrinth tissue. The pocket area is an example of the infiltration (interdigitation) from the spongiotrophoblast layer to the labyrinth layer. The cells in the left circle are glycogen cells.