Assessing Sexual Attitudes and Behaviors of Young Women: A Joint Model with Nonlinear Time Effects, Time Varying Covariates, and Dropouts

Abstract

Understanding human sexual behaviors is essential for the effective prevention of sexually transmitted infections. Analysis of longitudinally measured sexual behavioral data, however, is often complicated by zero-inflation of event counts, nonlinear time trend, time-varying covariates, and informative dropouts. Ignoring these complicating factors could undermine the validity of the study findings. In this paper, we put forth a unified joint modeling structure that accommodates these features of the data. Specifically, we propose a pair of simultaneous models for the zero-inflated event counts: Each of these models contains an auto-regressive structure for the accommodation of the effect of recent event history, and a nonparametric component for the modeling of nonlinear time effect. Informative dropout and time varying covariates are modeled explicitly in the process. Model fitting and parameter estimation are carried out in a Bayesian paradigm by the use of a Markov Chain Monte Carlo (MCMC) method. Analytical results showed that adolescent sexual behaviors tended to evolve nonlinearly over time and they were strongly influenced by the day-to-day variations in mood and sexual interests. These findings suggest that adolescent sex is to a large extent driven by intrinsic factors rather than being compelled by circumstances, thus highlighting the need of education on self protective measures against infection risks.

1 Introduction

Human sexual contacts are the primary pathway for sexually transmitted pathogens such as Chlamydia trachomatis (CT), Neisseria gonorrhoeae (NG), and Trichomonas vaginalis (TV). Despite the existence of efficacious antimicrobial agents against the organisms, these diseases remain prevalent in the US population. The burden of the diseases is disproportional on adolescents and young adults. For example, although young people aged 15 to 24 account for only a quarter of the sexually active population, they represent nearly half of new infections (Weinstock, Berman, and Cates 2004). Since the diseases are transmitted through behavior, the development of effective prevention strategies requires an improved understanding of human sexual behaviors, particular those of the young. Because adolescent sexual behaviors tend to change with time and experience, and are likely influenced by proximal phenomena such as mood and sexual interest, it is essential to model behavioral events longitudinally with full consideration of the contextual information. But the analysis of longitudinal behavioral data collected from observational studies is often complicated by potentially nonlinear time effects, large between-subject variability, time-varying covariates, and informative dropouts. This paper presents a unified analytical framework for the modeling of longitudinally collected counts of human sexual events, with explicit accommodation of these various complications.

1.1 An Epidemiological Study of Sexual Behaviors of Young Women

Young women were recruited for participation in a behavioral epidemiological study from three urban primary care clinics. The overall objective of the study is to examine the behavioral factors related to the sexually transmitted infections (STI). Eligibility criteria included that the young woman be between the ages 14 and 17 years, be able to understand English, not have any serious psychiatric disturbances or mental handicaps, and attend one of the three recruiting clinics. These clinics serve a predominantly urban and lower income population. Individuals who did not plan to continue residence in the area for the next three months or who were pregnant were excluded from the study. At the participating sites, all women who met the enrollment criteria, regardless of prior sexual experience, were identified by clinical schedule and those who agreed to participate were enrolled at the current or subsequent clinical visit. Informed consent and parental permission were obtained at the time of enrollment.

All subjects had quarterly clinic visits for the duration of the study period. In addition to the quarterly clinic visits, the study subjects also completed daily behavioral diaries, which provided detailed records of the subject's sexual behaviors in their original time sequence. Specifically, the diary was a structured mini-survey in which the subject reported sexual intercourse, condom protection, STI symptoms, and daily mood and sexual interest. Since coitus is relatively infrequent in adolescents and may exhibit certain day-of-the-week patterns, we summarized the daily events into weekly event counts and focused on the description of weekly rate of sexual intercourse.

The original study is designed to have a total length of followup of 27 months, and it is currently ongoing. In this analysis we used a subset of 282 subjects who had been enrolled into the study for at least six months (24 weeks), including those who had dropped out of the study before the completion of the six-month interview; recent enrollees who had entered the study in the last five weeks were not considered in the current analysis. The subject characteristics that we considered in this analysis included age, lifetime number of partners, and history of STI, all measured at enrollment. STI history is thought to be a marker of the more risky sexual behaviors in young women, and the lifetime number of partners to be markers of subject's sexual experience and partner availability.

The focus of this analysis was to examine whether positive mood and sexual interest were associated with the level of sexual activity in adolescent women. In this study, positive mood was assessed via diary by asking the subject to indicate percent of time in the day that she felt “happy”, “cheerful”, and “friendly”. The responses were on a Likert scale ranging from “not at all” (1 point), “some of it” (2 points), “about half” (3 points), “most of it” (4 points), or “all day” (5 points). The responses to these three items produced a mood score between 3 and 15 points. The purpose of having these correlated items in the scale is to achieve a better representation of the unobserved underlying construct of positive mood. Similarly, daily “sexual interest” was measured by one item in the diary on the same five-point Likert scale. In the present research, we calculated and used the average weekly mood and sexual interest scores in the analysis.

1.2 Analytical Issues of Longitudinally Measured Behavioral Data

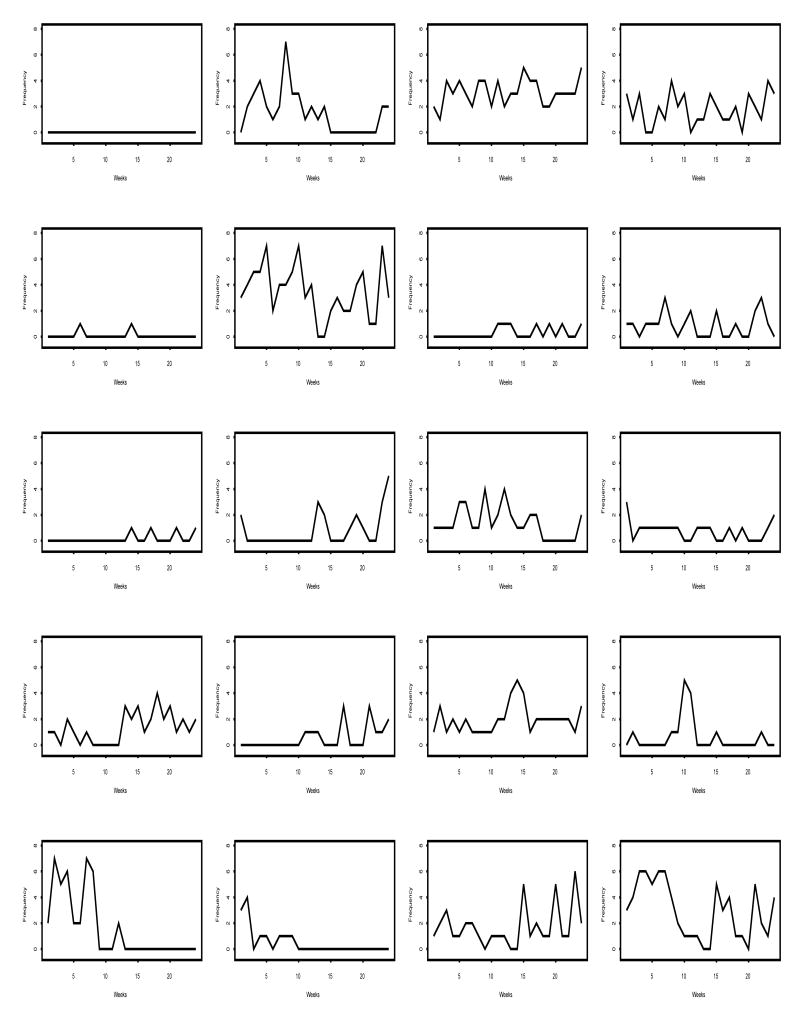
The primary response variable of interest of this analysis was the weekly number of coital events. The weekly coital frequency counts of the study cohort are depicted in Figure 1. These counts ranged from 0 to 8 with more than half of the observations being zero. When the number of zeros in the data set exceeds the probability mass that the Poisson distribution allocates to the point of zero, the data are said to be zero-inflated. In the presence of zero inflation, modeling the event count via Poisson regression is no longer appropriate; instead, zero-inflated Poisson (ZIP) regression models are often used in place of the classical Poisson regression models (Lambert 1992). Since Lambert's seminal work on ZIP regression models, a variety of applied ZIP regression models have been successfully used in several important clinical applications (Böhning, Dietz, Schlattmann, Mendonca, and Kirchner, 1999; Yau and Lee, 2001; Cheung, 2002; Lu, Lin, and Shih, 2004, Ghosh, Mukhopadhyay, and Liu, 2006). However, a number of methodological issues have complicated the analysis of the study data.

Figure 1.

Weekly coital frequency counts of 282 young women over a 24 week period.

1. Repeatedly measured event counts contributed by the same subject tend to be correlated, and current event count is likely to be associated with past event counts. Hall and Zhang (2004) discussed model-fitting procedures for marginal ZIP regression models for clustered count data. Min and Agresti (2005) and Hall and Wang (2005) considered mixed-effects ZIP regression models for repeatedly measured or cluster correlated data. But in this application, since the levels of sexual activities vary significantly from person to person, and the event count of the current week is likely to depend on those of the previous weeks, a more natural approach is to develop an autoregressive model where the outcome at current time point depends on its value at previous time points (Diggle et al, 2002, Chapter 10). Previous investigation has indicated the validity of this structure in the context of sexual behavioral research (Fortenberry et al, 2005).

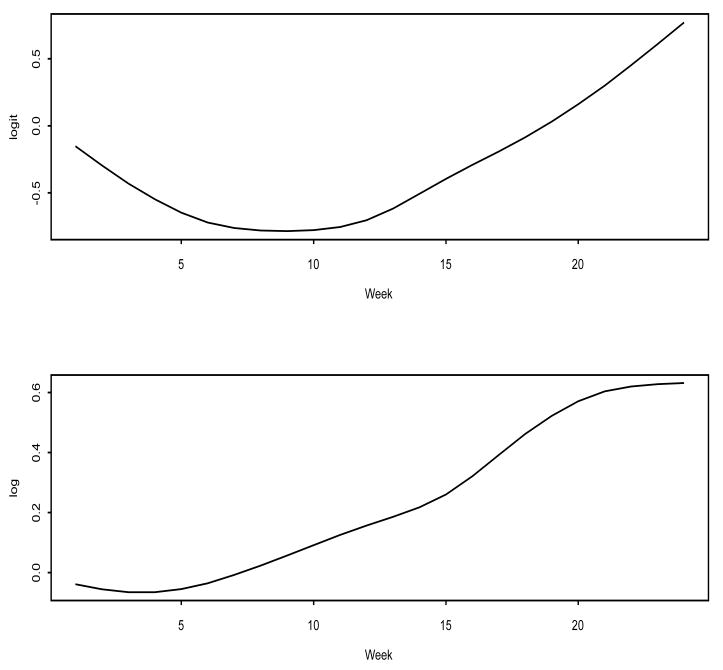
2. Human behaviors often change gradually over time. Such time effects are typically unobservable but ignoring them could have serious consequences. Additionally, repeated behavioral assessments themselves could have a subtle but non-ignorable impact on the behavior being studied. One of the concerns here is that repeated questioning about sexual activities could “activate” the subject, thus gradually influence her behavior. Methodologically, it is often impossible to independently verify the existence of such activation effects because of the lack of appropriate control subjects who are not subjected to these assessments. The dilemma is that, had there been such a control group, it would produce no behavioral data for the comparison due to the lack of assessments! But, if the data collection instruments have an activating effect, the effect is likely to express itself over time. For this reason, it becomes critically important for us to account for the time effect explicitly in the model to ensure the validity of inference on the important independent variables. This said, we note two difficulties with the modeling of the time effect: First, there is no guarantee that the time effect is linear; indeed, since the true functional form of time covariate is unknown, the assumption of linear time effect may not be always justifiable. Second, the time effect could differ by individual subjects. Examining the event profiles of 20 randomly chosen subjects (Figure 2), it becomes clear that they do not correspond to a particular parametric form, and between-subject variation is quite evident. These considerations have led us to consider a semiparametric approach for the cohort time effect using spline models. We use this approach to explore the features of the population and individual curves within the mixed model framework.

3. The observation of longitudinal cohorts are often accompanied by dropouts. The probability of a subject's dropping out of a study may be related to the subject's self-reported event rate. In the context of adolescent sexual behaviors, some have suspected that dropout is often a marker of higher risk behavior. A missing data mechanism where a subject's probability of dropping out depends on the rate of the Poisson process was referred to as “informative censoring” by Wu and Carroll (1988) and “informative missingness” by Follman and Wu (1995). We use the term “informative dropout” to describe this situation. In this application, we use a logistic model to depict the drop-out probability as a function of the subject's baseline characteristics, her observed event counts before the dropout time, and a random subject effect. In this example, we had about 20% of subjects that had dropped out of the study during the course of follow-up.

4. Because mood and sexual interest are collected over time together with coital counts, they can be viewed not only as time varying covariates, but also as realizations of some underlying psychological processes (Fortenberry et al., 2006). Therefore, directly modeling them may enhance our understanding of these effects. For example, an explicit covariate model will allow us to assess the strength of correlations of the mood and sexual interest measures within the subject over time. In addition, these time-varying covariates are not observed at the time of dropout leading to missingness in the covariates. Roy and Lin (2005) has shown that ignoring this missingness in the covariates will yield inconsistent estimates of the model parameters. Thus we directly model the time-varying covariates using a mixed model framework.

Figure 2.

Sample Longitudinal Profiles of Weekly Coital Frequency for 20 Subjects.

It should also be noted that in behavioral data, these complications rarely appear in isolation. Therefore in the present paper, we propose a joint modeling approach for the sexual activity data. Specifically, the behavioral events are modeled by an autoregressive ZIP regression structure with a semiparametric component for the accommodation of a potentially nonlinear time effect. The ZIP regression models share the subject-specific random effect with the logistic model for dropout. Time varying covariates such as mood and sexual interest are modeled via linear mixed model with autoregressive structures. The model is thus semiparametric in nature as the time effect is modeled nonlinearly. Within this unified modeling framework, a Bayesian approach was developed for parameter estimation. As an applied statistical method, this work is in contrast to the previous approaches by providing a joint modeling structure for the depiction of behavioral events in a longitudinal study. This research has incorporated some of the more recent modeling techniques in a ZIP regression set up: (1) it simultaneously models the probability weights of the mixture distributions; (2) it incorporates semiparametric functions for the time effects; (3) it explicitly accounts for informative dropouts; and (4) it accommodates the missing covariates. Since these characteristics are not uncommon in longitudinal studies of behavioral outcomes, the method is potentially useful for a wider class of applications.

2 Model Specification

2.1 Zero-inflated Poisson Model

Let Y_ij be the count of behavioral events reported by the ith subject in the jth time unit, i = 1, 2, …, m; j = 1, 2,…, n, where m represents the number of subjects in the study, and n is the designed number of time units in the follow-up period. In the context of this research, Y_ij is the number of sexual episodes reported by the ith subject in the jth week. Depending on the subject's current state of sexual activeness, a large number of zeros may be observed in Y. Following Lambert (1992), Hall (2000), Dagne (2004) and Ghosh, Mukhopadhyay, and Liu (2006), we further assume that for each observed event count, Y_ij, there is an unobserved random variable for the state of sexual activeness, U_ij, where P(U_ij = 0) = p_ij if Y_ij comes from the degenerate distribution, and P(U_ij = 1) = 1 − p_ij if Y_ij ∼Poisson λ_ij:

$$Y_{ij}=\{\begin{array}{ll}0\hfill & \text{with probability}{p}_{ij}\hfill \\ \text{Poisson}({\lambda }_{ij}),\hfill & \text{with probability}(1-p_{ij}),\hfill \end{array}$$ (1)

where Poisson(λ_ij) is defined by density function $P(Y_{ij}=y_{ij})=\text{exp}(-\lambda ij){\lambda }_{ij}^{y_{ij}}/y_{ij}!$.

It should be noted that both the degenerate distribution and the Poisson process can produce zero observations. Such a formulation is often referred to as the zero-inflated Poisson (ZIP) distribution. It then follows that

$$\text{Pr}(Y_{ij}=0)=p_{ij}+(1-p_{ij})\text{exp}(-{\lambda }_{ij})$$ (2)

$$\text{Pr}(Y_{ij}=y_{ij})=(1-p_{ij})\frac{\text{exp}(-{\lambda }_{ij}){\lambda }_{ij}^{y_{ij}}}{y_{ij}!},y_{ij}=1,2,\dots .$$ (3)

In this research, one could conceptualize the degenerate distribution as representing a “sexually inactive” state with probability p_ij, while the Poisson process represents a “sexually active” state with λ_ij being the mean weekly number of sexual episodes.

Because the weekly event counts are simultaneously influenced by the state that the subject is in during the week and the weekly event rate given she is in an active state, we consider simultaneous modeling of both λ_ij and p_ij.

2.2 Simultaneous Models of Behavioral Event Counts

We assume the following logistic and log-linear regression models for p_ij and λ_ij:

$$\begin{array}{ll}\text{logit}(1-p_{ij})=\hfill & {\text{S}}_i^T{\beta }_1^p+{\text{T}}_{ij}^T{\beta }_2^p+\text{∑}_{q=1}^Q{\beta }_{3q}^p{Y}_{i,j-q}+{\text{Z}}_{ij2}^T{b}_{i1}\hfill \\ \hfill & +f^p(t_{ij})+h_i^p(t_{ij});\hfill \end{array}$$ (4)

$$\begin{array}{ll}\text{log}({\lambda }_{ij})=\hfill & {\text{S}}_i^T{\beta }_1^{\lambda }+{\text{T}}_{ij}^T{\beta }_2^{\lambda }+\text{∑}_{q=1}^Q{\beta }_{3q}^{\lambda }{Y}_{i,j-q}+{\text{Z}}_{ij1}^T{b}_{i2}\hfill \\ \hfill & +f^{\lambda }(t_{ij})+h_i^{\lambda }(t_{ij}).\hfill \end{array}$$ (5)

The logistic model in (4) explicitly depicts the probability that the observation is from the degenerate distribution; and the loglinear model in (5) quantifies the “intensity” of the Poisson process. Herein, S_i denotes the baseline characteristics and T_ij is the time-varying covariate vector for the ith subject at time j. Although we assumed the same set of covariates for the p_ij and λ_ij in the above formulation, the models can easily be modified to accommodate different covariates in the two processes. The parameters, ${\beta }_1^p$, ${\beta }_2^p$, ${\beta }_1^{\lambda }$, ${\beta }_2^{\lambda }$ are vectors of regression coefficients for the fixed effects. Note that in (4) and (5), the subject's response at time j, Y_ij, depends on the subject's past events through embedded qth order autoregressive structures. Parameters ${\beta }_3^p=({\beta }_{31}^p,\dots ,{\beta }_{3Q}^p)$ and ${\beta }_3^{\lambda }=({\beta }_{31}^{\lambda },\dots ,{\beta }_{3Q}^{\lambda })$ are associated with the autoregressive process. In this application, the reported number of sexual episodes may vary from week to week in an unknown fashion. Thus, the time effects on p_ij and λ_ij are modeled by unspecified nonparametric functions f^p(t) and f^λ(t), respectively. These unspecified smooth functions reflect the nonlinear effect of the time. However, these functions represent only the population averages; individual trajectories may still vary from subject to subject and the individual pattern may not follow the pattern of the population curve. These subject effects may also contribute to the correlation of the longitudinal measurements within subjects. Therefore we add a subject specific nonparametric function h_i(·), which represents the subject's deviation from the group curves. The population curves f(t) is important as it describes the overall cohort time effect on the parameter of interest. At the same time, individual curves h_i(t) are introduced to represent subject-specific variations around the population time effect. Together, the population average and individual specific curves serve to improve the fitness of the model to inform the investigators about the nature of the cohort time effect. To accommodate any extra within-subject correlation due to the large within-subject variability in the cohort, we introduce additional random effects (b_i1, b_i2) into the models.

He, Fung and Zhu (2005), and Zhao, Staudenmayer, Coull, and Wand (2006) discussed the incorporation of semiparametric population curves in generalized linear models. This research further extends those methods by embedding both population average and subject-specific splines in a ZIP regression model. In doing so, the proposed semiparametric ZIP model offers a greater flexibility in the modeling of zero-inflated event counts. The model reduces to a parametric ZIP model when f^p (t), f^λ (t), $h_i^p(t)$, and $h_i^p(t)$ are constants. Following (Ruppert et al. 2003), we assume that the spline functions take the following general forms of a piecewise polynomial of degree τ:

$$\begin{array}{c}{f}^p(t)=v_1^{p}t+v_2^p{t}^2+\cdots +v_{\tau }^p{t}^{\tau }+\sum _{d=1}^{D_1}{u}_{d1}^p{(t-{\kappa }_{d1}^p)}_{+}^{\tau };\\ f^{\lambda }(t)=v_1^{\lambda }t+v_2^{\lambda }{t}^2+\cdots +v_{\tau }^{\lambda }{t}^{\tau }+\sum _{d=1}^{D_1}{u}_{d1}^{\lambda }{(t-{\kappa }_{d1}^{\lambda })}_{+}^{\tau };\\ h_i^p(t)={\rho }_{1i}^{P}t+{\rho }_{2i}^P{t}^2+\cdots +{\rho }_{\tau i}^P{t}^{\tau }+\sum _{d=1}^{D_2}{u}_{id2}^p{(t-{\kappa }_{d2}^p)}_{+}^{\tau };\\ h_i^{\lambda }(t)={\rho }_{1i}^{\lambda }t+{\rho }_{2i}^{\lambda }{t}^2+\cdots +{\rho }_{\tau i}^{\lambda }{t}^{\tau }+\sum _{d=1}^{D_2}{u}_{id2}^{\lambda }{(t-{\kappa }_{d2}^{\lambda })}_{+}^{\tau };\end{array}$$

where, X₊ = x if x > 0; and 0 otherwise, and $k_{d1}^p$, $k_{d1}^{\lambda }$, $k_{d2}^p$, $k_{d2}^{\lambda }$s are the known knot points. The choice of the knots will be described in the data analysis section. Note that in the population spline we do not have any intercept to avoid unidentifiability. We assume $u_{d1}^p\sim N(0,{\sigma }_{up}^2),u_{d1}^{\lambda }\sim N(0,{\sigma }_{u\lambda }^2),u_{id2}^p\sim N(0,{\sigma }_{1p}^2),u_{id2}^{\lambda }\sim N(0,{\sigma }_{1\lambda }^2)$. The above spline model of order τ represents adequate fits for most situations. But the number of parameters may not be practical for smaller data sets. In those situations, simpler spline models such as linear splines may be used, or subject specific splines may be dropped. Typically, linear (τ = 1), quadratic (τ = 2) or cubic (τ = 3) splines are common choices in practice as they ensure a certain degree of smoothness in the fitted curve. The above spline models can be embedded in the mixed model framework for a general structure as follows:

Let X_1ij = (t, …, t^τ) ^T, ${\text{W}}_{ij1}^p=[{(t-k_{11}^P)}_{+}^{\tau },\dots ,{(t-k_{D_{1}1}^P)}_{+}^{\tau }{]}^T$, ${\beta }_4^p={({\nu }_1^p,\dots ,{\nu }_{\tau }^p)}^T$, ${\text{u}}_1^p={(u_{11}^p,\dots ,u_{D_{1}1}^p)}^T$, ${\rho }_i^p={({\rho }_{1i}^p,\dots ,{\rho }_{\tau i}^p)}^T$, ${\text{u}}_{i2}^p={(u_{i12}^p,\dots ,u_{i{D}_{2}2}^p)}^T$. In a similar way, we define ${\text{W}}_{ij2}^{\lambda }$, ${\beta }_4^{\lambda }$, ${\text{u}}_1^{\lambda }$, ${\rho }_i^{\lambda }$, ${\text{u}}_{i2}^{\lambda }$. Then,

$$\begin{array}{ll}{f}^p(t)+h_i^p(t)\hfill & =X_{1ij}^T{\beta }_4^p+W_{ij1}^{p^T}{u}_1^p+X_{1ij}^T{\rho }_i^p+Z_{ij2}^{p^T}{u}_{i2}^p\hfill \\ \hfill & =X_{1ij}^T{\beta }_4^p+W_{ij1}^{p^T}{u}_1^p+V_{ij}^{p^T}{w}_i^p,\hfill \end{array}$$ (6)

$$\begin{array}{ll}{f}^{\lambda }(t)+h_i^{\lambda }(t)\hfill & =X_{1ij}^T{\beta }_4^{\lambda }+W_{ij2}^{{\lambda }^T}{u}_1^{\lambda }+X_{1ij}^T{\rho }_i^{\lambda }+V_{ij2}^{{\lambda }^T}{u}_{i2}^{\lambda }\hfill \\ \hfill & =X_{1ij}^{{\lambda }^T}{\beta }_4^{\lambda }+W_{ij2}^{{\lambda }^T}{u}_1^{\lambda }+V_{ij}^{{\lambda }^T}{w}_i^{\lambda },\hfill \end{array}$$ (7)

where $V_{ij}^p=(X_{1ij}^T,Z_{ij2}^{p^T})$, $w_i^p={({\rho }_i^p,u_{i2}^p)}^T$. Similarly, $V_{ij}^{\lambda }$, $w_i^{\lambda }$ is defined. Also, $E(u_1^p)=0$, $\text{cov}(u_1^p)={\sigma }_{up}^2{I}_{D_1}$, $E(w_i^p)=0$, $\text{cov}(w_i^p)=\text{diag}({\sum }_{\rho }^p,{\sigma }_{1p}^2{I}_{D_1})$, $E(u_1^{\lambda })=0$, $\text{cov}(u_1^{\lambda })={\sigma }_{u\lambda }^2{I}_{D_1}$, $E(w_i^{\lambda })=0$, and $\text{cov}(w_i^{\lambda })=\text{diag}({\sum }_{\rho }^{\lambda },{\sigma }_{1\lambda }^2{I}_{D_1})$.

The splines above are partitioned into fixed linear component plus a random component, with zero expectation, representing smooth deviations about the linear trend.

Letting $X_{ij}={(S_i^T,T_{ij}^T,Y_{i,j-1},\dots ,Y_{i,j-Q},X_{1ij}^T)}^T$, ${\beta }^p={({\beta }_1^p,{\beta }_2^p,{\beta }_3^p,{\beta }_4^p)}^T$, (β^λ defined similarly), and plugging expressions (6-7) into equations (4-5), we get:

$$\begin{array}{cc}\text{logit}(1-p_{ij})\hfill & ={\text{S}}_i^{\text{T}}{\beta }_1^p+{\text{T}}_{ij}^T{\beta }_2^p+\sum _{q=1}^Q{\beta }_{3q}^p{Y}_{i,j-q}+X_{1ij}^{p^T}{\beta }_4^p+W_{ij1}^{p^T}{u}_1^p+V_{ij}^{p^T}{w}_i^p+{\text{Z}}_{ij1}^T{b}_{i1};\hfill \\ \hfill & =X_{ij}^T{\beta }^p+W_{ij1}^{p^T}{u}_1^p+V_{ij}^{p^T}{w}_i^p+{\text{Z}}_{ij1}^T{b}_{i1},\hfill \end{array}$$ (8)

$$\begin{array}{cc}\text{log}({\lambda }_{ij})\hfill & ={\text{S}}_i^{\text{T}}{\beta }_1^{\lambda }+{\text{T}}_{ij}^T{\beta }_2^{\lambda }+\text{∑}_{q=1}^Q{\beta }_{3q}^{\lambda }{Y}_{i,j-q}+X_{1ij}^{{\lambda }^T}{\beta }_4^{\lambda }+W_{ij2}^{{\lambda }^T}{u}_1^{\lambda }+V_{ij}^{{\lambda }^T}{w}_i^{\lambda }+{\text{Z}}_{ij2}^T{b}_{i2}\hfill \\ \hfill & =X_{ij}^T{\beta }^{\lambda }+W_{ij2}^{{\lambda }^T}{u}_1^{\lambda }+V_{ij}^{{\lambda }^T}{w}_i^{\lambda }+{\text{Z}}_{ij2}^T{b}_{i2}.\hfill \end{array}$$ (9)

2.3 Informative dropout in Cohort Studies

Dropouts are not uncommon in observational studies of large cohorts. Here we define the dropout as someone who did not come to a scheduled visit and had not come back by the end of the study. Since the measurements are missing after the last kept visit, analysis of the incomplete data poses additional challenges. If the dropouts are due to a mechanism that is unrelated to the investigation, i.e., the unobserved behaviors are missing completely at random, these dropouts can be ignored. However, this is unlikely to be the case for most of the longitudinal studies of human behavior. In adolescent health studies, there are suspicions that the dropouts may be associated with certain traits that can be characterized as lack of discipline. These traits not only influence the dropout process, but also correlate with the sexual behaviors themselves, thus giving us an incentive for a joint modeling of the outcomes and dropout process.

Specifically, for each Y_ij we define a missing indicator variable R_ij, such that R_ij = 1 if Y_ij was missing, and 0 otherwise. Thus, R_i = (R_i1, …, R_in)^T is a vector of missing response indicators for individual i. Then a simple model could be constructed to describe the nonignorable missing response:

$$R_{ij}\sim \text{Bernoulli}({\eta }_{ij})\text{where}{\eta }_{ij}=\text{Pr}(R_{ij}=1|{\text{Y}}_{ij},{\text{Y}}_{i(j-1)})$$ (10)

$$g({\eta }_{ij})={\text{L}}_{ij}^T\xi +{\psi }_1{Y}_{ij}+\sum _{s=2}^{Q_1}{\psi }_s{Y}_{i,j+1-s}+\sum _{k=1}^K{\zeta }_k{T}_{ijk}+Z_{ij3}^T{\text{b}}_{i3}$$ (11)

where Y_{i, (j−1)} denotes a subset of the history of the data, e.g., it can be the previous responses (y_i,j−1) and/or previous time-varying covariates T_i,j−1,k. Note that ψ₁ ≠ 0 gives nonignorable missingness. Here g(·) is a link function; we let g(x) = logit(x). In the above model, L_ij is the vector of baseline covariates and b_i3 is the vector of random subject effects corresponding to the dropout model. The T_ijk is the kth time-varying covariate. The unknown parameters are (ξ, ψ₁, …, ψ_Q1, ζ₁, …, ζ_K).The baseline covariates and the time-varying covariates may be same as in the response model. The non-ignorable dropout mechanism is modeled by the dependence of the dropout probability on the unobserved outcome y_ij at the time of dropout and on the outcome before dropping out. As for the random subject effects vector b_i = (b_i1, b_i2, b_i3)^T we assume b_i ∼ N(0, Δ_b). Thus, the correlated random effect allows for the association between dropout and the outcome.

2.4 Modeling Time-varying Covariates

In the above model we have covariates which are also measured over time along with the response variable. It is usual that some of the covariates will be unobserved because of dropout in the data. Due to the presence of this missingness in the time-varying covariates, we need to model the covariate process (Roy and Lin, 2006). We develop a multivariate linear mixed model (Shah et al., 1997) to describe the covariate process.

Let T_ijk be the kth covariate for the ith subject measured at time j. We assume the following linear mixed model for the different time-varying covariates:

$$T_{ijk}={\text{A}}_{ijk}^T{\gamma }_{0k}+{\gamma }_{1k}{T}_{i,j-1,k}+{\text{B}}_{ijk}^T{\delta }_{ik}+e_{ijk},$$ (12)

where A_ijk is the design matrix for the fixed effects. The model assumes that the kth time-varying covariate at the current time depends on its value at the previous time point, δ_ik is the random subject effect for the ith subject in the kth marker, and e_ijk is the measurement error.

Let T_ij = (T_ijk, …, T_ijK)^T, e_ij = (e_ij1, …, e_ijk), γ₀ = (γ₀₁, …, γ_0K), γ₁ = (γ₁₁, …, γ_1K), δ_i = (δ_i1, δ_i2, …, δ_iK)^T. Then in matrix notation we have,

$${\text{T}}_{ij}={\text{A}}_{ij}^T{\gamma }_0+{\gamma }_1{\text{T}}_{i,j-1}+{\text{B}}_{ij}^T{\delta }_i+{\text{e}}_{ij}$$ (13)

where e_ij ∼ N(0, Σ = diag $\left\{{\sigma }_k^2\right\}$), δ_i ∼ N(0, Σ_δ), Σ_δ being the variance-covariance matrix for the random effects δ_i. We assume independence between the random effects and error distribution.

The Markovian structure of the model allows for a longitudinal correlation structure for the same covariates over time.

3 Bayesian Inference: Likelihood, Priors and Posterior

3.1 The Likelihood Function

Let Y_obs,i = (Y_i1, …, Y_ini)^T, and T_obs,i = (T_i1, …, T_ini)^T denote the observed values of Y_i and T_i, respectively. We also assume that for subjects who dropped out from the study, Y_drop,i = (Y_i,ni+1, …, Y_in)^T and T_drop,i = (T_i,ni+1, …, T_in)^T represent the missing response and covariates respectively. Then ${\text{Y}}_i={({\text{Y}}_{\text{obs},i}^T,{\text{Y}}_{\text{drop},i}^T)}^T$, and ${\text{T}}_i={({\text{T}}_{\text{obs},i}^T,{\text{T}}_{\text{drop},i}^T)}^T$. We define S_i and Z_ij similarly. Further, we write $\beta ={({\beta }_1^{\lambda },{\beta }_2^{\lambda },{\beta }_3^{\lambda },{\beta }_1^p,{\beta }_2^p,{\beta }_3^p)}^T$, (ψ₁, …, ψ_Q1)^T, and ζ = (ζ₁, …, ζ_K)^T.

Let Ω = (Ω₁, Ω₂, Ω₃, Ω₄, Ω₅) be the parameter space. Here ${\Omega }_1=(\beta ,{\sigma }_{up}^2,{\sigma }_{u\lambda }^2,{\sigma }_{1p}^2,{\sigma }_{1\lambda }^2)$ is the parameter vector for the joint model, Ω₂ = (ξ, ψ, ζ)^T) is the parameter vector for the dropout model, ${\Omega }_3=(\gamma ={({\gamma }_0,{\gamma }_1)}^{\text{T}},{\sigma }_1^2,\dots ,{\sigma }_K^2)$ is the parameter vector for the time-varying covariate model, Ω₄(= Δ_b) is the parameter of the random effect b_i, and Ω₅(= Σ_δ) is the parameter of the random subject effects W_i.

Then under the assumption of nonignorable dropout (ψ₁ ≠ 0), the joint likelihood can be written as

$$\begin{array}{l}L({\text{Y}}_{\text{obs},i},{\text{T}}_{\text{obs},i},{\text{R}}_i|{\text{S}}_i,{\text{T}}_{i1},{\text{b}}_i,{\delta }_i;\Omega )\propto \\ L({\text{Y}}_i|{\text{Y}}_{i1},{\text{S}}_i,{\text{T}}_i,{\text{b}}_i;{\Omega }_1)L({\text{T}}_i|T_{i1},{\text{S}}_i,{\delta }_i;{\Omega }_2)\\ \times L(R_i|Y_i,T_{\text{obs},i},S_{\text{obs},i},{\text{b}}_i;{\Omega }_3)L({\text{b}}_i;{\Omega }_4)L({\delta }_i;{\Omega }_5),\end{array}$$ (14)

where

$$\begin{array}{cc}L({\text{Y}}_i|Y_{i1},{\text{S}}_i,{\text{T}}_i,{\text{b}}_i;{\Omega }_1)=\hfill & {\prod _{j=2}^{n_i}\left[p_{ij}+(1-p_{ij})e^{-{\lambda }_{ij}}\right]}^{I_{[Y_{ij}=0]}}\hfill \\ \hfill & \times {\left[\frac{(1-p_{ij})e^{-{\lambda }_{ij}}{\lambda }_{ij}^{Y_{ij}}}{Y_{ij}}\right]}^{1-I_{[Y_{ij}=0]}}\hfill \end{array},$$ (15)

with P_ij and λ_ij given in equation (4-5), and

$$L({\text{T}}_i|T_{i1},{\text{S}}_i,{\delta }_i;{\Omega }_2)\propto \frac{1}{{|\sum |}^{n_i/2}}\text{exp}\left\{-\frac{1}{2}\sum _{j=2}^{n_i}{({\text{T}}_{ij}-{\mu }_{{\text{T}}_{ij}})}^T{\sum }^{-1}({\text{T}}_{ij}-{\mu }_{{\text{T}}_{ij}})\right\},$$ (16)

where ${\mu }_{{\text{T}}_{ij}}={\text{A}}_{ij}^T{\gamma }_0+{\gamma }_1{\text{T}}_{i,j-1}+B_{ij}^T{\delta }_i$; and

$$\begin{array}{cc}L({\text{R}}_i|{\text{Y}}_i,{\text{T}}_{\text{obs},i},{\text{S}}_{\text{obs},i};{\Omega }_3,{\text{b}}_i)=\hfill & \prod _{j=2}^{n_i}{\{\text{Pr}(r_{ij}=1|{\text{Y}}_i,{\text{T}}_{\text{obs},i},{\text{S}}_{\text{obs},i};{\Omega }_3,{\text{b}}_i)\}}^{r_{ij}}\hfill \\ \hfill & \times {\{1-\text{Pr}(r_{ij}=1|{\text{Y}}_i,{\text{T}}_{\text{obs},i},{\text{S}}_{\text{obs},i};{\Omega }_3,{\text{b}}_i)\}}^{1-r_{ij},}\hfill \end{array}$$ (17)

and L(b_i; Ω₄) and L(δ_i; Ω₅) denote the multivariate normal distributions with zero mean vector and variance-covariance matrices Δ_b and Σ_δ, respectively.

3.2 Prior Distribution

To complete Bayesian specification of the model, we must assign priors to the unknown parameters. Since we have no prior information from historical data or from experiment, we take the usual route and assign conjugate priors to the parameters. We assume elements of the $\Omega =(\beta ,\xi ,\psi ,\zeta ,\gamma ,{\Delta }_b,{\sum }_{\delta },{\sigma }_{up}^2,{\sigma }_{u\lambda }^2,{\sigma }_{1p}^2,{\sigma }_{2p}^2,{\sigma }_{1\lambda }^2,{\sigma }_{2\lambda }^2,{\sigma }_1^2,\dots ,{\sigma }_K^2)$ are independently distributed. For each fixed effect we assume a normal density prior and for the variance parameter we assume an inverse-Gamma (IG) prior, while for the variance-covariance matrix we assume an inverse Wishart prior. An inverse-Gamma prior with shape parameter a and scale parameter b is denoted by x ∼ IG(a, b) and is given by $f(x)\propto x^{-a}\text{exp}(\frac{-b}{2x^2})$. Additionally, we assume a Wishart distribution for the inverse of a variance-covariance matrix, where a W_q(ϱ, S) is a q dimensional Wishart distribution with ϱ degrees of freedom and mean ϱS⁻¹. For our analysis, diffuse priors can be chosen so that the analysis is dominated by the data likelihood. Specifically, to represent the vague prior knowledge, we propose to set the degrees of freedom for the Wishart distribution to be the minimum possible, viz., the rank of the variance-covariance matrix.

We specify the following priors on the model parameters for the fixed effects, π(β) ∼ N(μ_β, Σ_β), π(ξ) ∼ N(μ_ξ, Σ_ξ), π(ψ) ∼ N(μ_ψ, Σ_ψ), π(ζ) ∼ N(μ_ζ, Σ_ζ), π(γ) ∼ N(μ_γ, Σ_γ).

For the variance parameter we assume an inverse-gamma prior as follows: $\pi ({\sigma }_{up}^2)$∼ IG(a_up, b_up), $\pi ({\sigma }_{u\lambda }^2)$∼ IG(a_uλ, b_uλ), $\pi ({\sigma }_{1p}^2)$ ∼ IG(a_1p, b_1p), $\pi ({\sigma }_{1\lambda }^2)$ ∼ IG(a_1λ, b_1λ), and $\pi ({\sigma }_k^2)$ ∼ IG(c_k, d_k); k = 1,2, …, K.

Finally, the variance-covariance parameters of the random subject effect take the following forms: $\pi ({\Delta }_b^{-1})\sim \text{Wishart}({\varrho }_b,S_{\varrho })$, $\pi ({\sum }_{\delta }^{-1})\sim \text{Wishart}({\varrho }_{\delta },S_{\delta })$.

3.3 Posterior Distribution and Inference

The joint posterior distribution of the parameters of the models conditional on the data is obtained by combining the likelihood in (14) and the prior densities using Bayes' theorem:

$$\begin{array}{cc}f(\Omega ,b,\delta ,u|y)\hfill & \propto \prod _{i=1}^m\{L({\text{y}}_{\text{obs},i},{\text{T}}_{\text{obs},i},{\text{R}}_i|S_i,T_{i1},b_i,{\delta }_i;\Omega )\}\pi (\beta )f({\sigma }_{up}^2)\pi ({\sigma }_{u\lambda }^2)\pi ({\sigma }_{1p}^2)\hfill \\ \hfill & \times \pi ({\sigma }_{1\lambda }^2)\pi (\xi )\pi (\psi )\pi (\zeta )\pi (\gamma )\pi ({\Delta }_b^{-1})\pi ({\sum }_{\delta }^{-1})\prod _{k=1}^{K}f({\sigma }_k^2).\hfill \end{array}$$

The posterior distributions are analytically intractable. However, models described above can be fitted using the Markov Chain Monte Carlo (MCMC) methods such as the Gibbs sampler (Gelfand and Smith, 1990). Since the full conditional distributions are not standard, a straightforward implementation of the Gibbs sampler using standard sampling techniques may not be possible. However, sampling methods can be performed using adaptive rejection sampling (ARS; Gilks and Wild, 1992). Recently, Ghosh, Mukhopadhyay, and Liu (2006) have advocated the use of ARS for a ZIP model. In this research, we follow their procedure, which first uses a data augmentation step to sample the values of the latent variables (sexual activities) based on the current value of the parameters, and then samples the parameters using the ARS method given the latent variables. Samples were directly obtained from the joint posterior distribution of the parameters as well as the latent variables. Implementation of this method is relatively easy in publicly available software WinBUGS (2005). The samples from the posterior obtained from the MCMC will allow us to achieve summary measures of the parameter estimates, and to obtain credible intervals of the parameters of interest. See Section 4.2 for more computational details of the data analysis.

4 Data Analysis

4.1 Model Specification

Using the proposed model, we analyzed the data collected from the behavioral epidemiological study. The data set contained weekly coital frequency counts (Y_ij) of 282 young women measured over a period of 24 weeks, i = 1, 2, …, 282; j = 1, 2, …, 24. The vector of baseline characteristics, S_i = (AGE_i, STD_i, PTR_i)^T, where AGE_i, STD_i, and PTR_i were respectively the ith subject's age, STD history, and lifetime number of sexual partners, is measured at the time of enrollment. The vector of time-varying covariates had two elements, T_ij = (MOOD_ij, SI_ij)^T, where MOOD_ij and SI_ij were respectively the weekly average mood and sexual interest scores reported by the ith subject in the jth week. Under a first order auto-regressive structure (Q = 1), we had the following semiparametric autoregressive ZIP models:

$$\begin{array}{ll}\hfill \text{logit}(1-p_{ij})=& {\beta }_{11}^p+{\beta }_{12}^p{\text{AGE}}_i+{\beta }_{13}^p{\text{STD}}_i+{\beta }_{14}^p{\text{PTR}}_i\hfill \\ \hfill & +{\beta }_{21}^p{\text{MOOD}}_{ij}+{\beta }_{22}^p{\text{SI}}_{ij}+{\beta }_{31}^p{Y}_{i,j-1}\hfill \\ \hfill & +b_{i1}+f^p(t_{ij})+h_i^p(t_{ij}),\hfill \\ \hfill \text{log}({\lambda }_{ij})=& {\beta }_{11}^{\lambda }+{\beta }_{12}^{\lambda }{\text{AGE}}_i+{\beta }_{13}^{\lambda }{\text{STD}}_i+{\beta }_{14}^{\lambda }{\text{PTR}}_i\hfill \\ \hfill & +{\beta }_{21}^{\lambda }{\text{MOOD}}_{ij}+{\beta }_{22}^{\lambda }{\text{SI}}_{ij}+{\beta }_{31}^{\lambda }{Y}_{i,j-1}\hfill \\ \hfill & +b_{i2}+f^{\lambda }(t_{ij})+h_i^{\lambda }(t_{ij}).\hfill \end{array}$$

Please note that for the convenience of model interpretation, we chose to model the probability that the ith subject was in a sexually active state (1 − p_ij) at jth visit in the logistic model.

For the fitting of the models, there is no clear rule on how many knot points to include or where to locate them in the spline functions. More knots are needed in regions where the function is changing rapidly (Ruppert et al. 2003). Sometimes knowledge of subject matter may be relevant in placing knots where a change in the shape of the curve is expected. Using too few knots or poorly sited knots means the approximation to the curve will be degraded. By contrast, a spline using too many knots will be imprecise. Since the subjects were assessed regularly with equally spaced intervals in this study, we selected the knots from the existing values that were equally spaced within the range [min(x), max(x)]. Thus the six knots were placed at weeks 5, 8, 11, 14, 17, 20.

A model for dropout was assumed in case the dropouts were informative. Preliminary data analysis suggested that the dropout might depend on the current or previous coital frequency counts, as well as on some of the baseline covariates. So we considered the following simple model:

$$\text{Logit}({\eta }_{ij})={\xi }_1+{\xi }_2{\text{AGE}}_i+{\xi }_3{\text{STD}}_i+{\psi }_1{Y}_{ij}+{\psi }_2{Y}_{i,j-1}+b_{i3},$$ (18)

where b_i3 was the random subject effect. As detailed in Section 4.3, although the dropout probability was modeled as a function of subject's enrollment age, STD history, and the weekly coital frequency counts prior to the dropout time, we chose the above model for dropout based on a set of model selection criteria described in section 4.4.

Similarly, the time-varying covariates mood and sexual interest were modeled as follows:

$$\begin{array}{cc}{\text{MOOD}}_{ij}=& {\gamma }_{01}+{\gamma }_{11}{\text{MOOD}}_{i,j-1}+W_{i1}+W_{i2}{t}_{ij}+e_{ij1},\hfill \\ \hfill {\text{SI}}_{ij}=& {\gamma }_{02}+{\gamma }_{12}{\text{SI}}_{i,j-1}+W_{i3}+W_{i4}{t}_{ij}+e_{ij2}.\hfill \end{array}$$

Again, the autoregressive structures embedded in the time-varying covariate models allowed us to examine the strength of the autocorrelation within the covariates. This was not only of scientific interest to the investigation, but also helpful for the exploration of the modeling structure. For example, a very strong autocorrelation in mood would not only counter the speculation of mood swing in adolescents, but also render it unnecessary to collect mood measure so frequently, or to treat it as a time-varying variable.

Since the study was still ongoing and data were still being collected at the time of this report, the currently available data set was not large enough to be divided for the purpose of prior elicitation. Prior information based on expert opinion, even if available, is nonetheless user specific. Hence, in this analysis we chose our priors to be proper but weakly informative. Specifically, we take a N (0, 50) prior for each of the regression parameters and for each variance parameter (=1/precision) we use an IG(2.01, 1.01) prior, giving rise to a prior mean of 1 and prior variance of 1,00. For the variance-covariance matrix ${\Delta }_b^{-1}$ we assumed Wishart $\left(3,\left(\begin{array}{cc}0.1& 0\\ 0& 0.1\end{array}\right)\right)$, and for ${\Delta }_w^{-1}$ we assumed Wishart $\left(2,\left(\begin{array}{cc}0.1& 0\\ 0& 0.1\end{array}\right)\right)$.

4.2 Computational Details

We ran two chains of the Gibbs sampler with widely dispersed initial values. The initial values for the fixed parameters were selected by starting with the prior mean and covering ±3 standard deviations. The initial values for the precision were arbitrarily selected. Initially, some evidence of poor mixing was found regarding the standard deviation of the random effect slope in the spline model. Following Zhao, Staudenmayer, Coull, and Wand (2006), we then used several other choices of the inverse gamma and the folded-t prior distributions for the standard deviations. The folded-t class of prior densities have been recommended by Gelman (2005) in a hierarchical model over the commonly used inverse-gamma distribution. The folded-t prior has the advantage of improving computational efficiency by reducing dependence among parameters (Liu, rubin, and Wu, 1998; Liu and Wu, 1999) and yields a Gibbs sampler that is less prone to slow mixing when the standard deviations are near zero. We found that use of a moderate to highly dispersed inverse gamma prior behaved erratically. However, the use of folded-t prior on standard deviations dramatically improved the mixing and fits were stable. Thus, we resort to the folded-t class of prior for our results. See Zhao, Staudenmayer, Coull, and Wand (2006) and Gelman (2005) for details of this prior. We also centered the covariates about mean to have better convergence. In our simulation, 25,000 samples were discarded as burn-in, and of the next 75,000 samples, we used every third value to construct the posterior estimate. Convergence was assessed visually by monitoring the dynamic traces of Gibbs iterations and by computing the Gelman-Rubin convergence statistic (Gelman and Rubin, 1992). In order to check for the sensitivity we ran the proposed model with different sets of priors and found little evidence of any prior sensitivity, although slow mixing was evident in analysis using a highly diffuse prior.

4.3 Analytical Results

Of the 282 subjects enrolled into the study 91% were African American. Enrollment age ranged from 14 to 17 with a mean of 15 years and a standard deviation of 1.1 years. Lifetime number of partners reported at the time of enrollment ranged from zero to 28 with a mean of 2.85 (median 2) and a standard deviation of 3.8. Forty four of the study subjects (15.6%) had a history of STD infection.

Table 1 reports the posterior mean, median, standard deviation (SD), and 95% credible interval (CI) for the parameters in the ZIP regression model. Similarly, the parameter estimates for the dropout and time-varying covariate models are reported in Table 2.

Table 1.

Parameter Estimates of the ZIP Regression Models

Parameter	Mean	Median	SD	95% C.I.
Zero-inflated
Logit
${\beta }_{11}^p$ (Intercept)	0.4463	0.4402	0.102	(0.046, 1.69)
${\beta }_{12}^p$ (AGE)	0.6874	0.7155	0.249	(0.0864, 1.18)
${\beta }_{13}^p$ (STD)	0.2583	0.2445	0.2892	(0.0949, 1.923)
${\beta }_{14}^p$ (PTR)	0.375	0.337	0.118	(0.1902, 0.462)
${\beta }_{21}^p$ (MOOD)	-0.2318	-0.2305	0.077	(-0.3904, -0.0908)
${\beta }_{22}^p$ (SI)	0.5769	0.5758	0.4489	(-0.295, 1.55)
${\beta }_{31}^p$ (AR(1))	1.306	1.288	0.173	(1.029, 1.713)
Log-linear
${\beta }_{11}^{\lambda }$ (Intercept)	0.0296	0.0302	0.0035	(-0.0722, 0.1259)
${\beta }_{12}^{\lambda }$ (AGE)	-0.0251	-0.027	0.14	(-0.031, 0.0306)
${\beta }_{13}^{\lambda }$ (STD)	0.2307	0.2383	0.258	(-0.3383, 0.6504)
${\beta }_{14}^{\lambda }$ (PTR)	0.0325	0.0293	0.024	(-0.0101, 0.0802)
${\beta }_{21}^{\lambda }$ (MOOD)	0.1034	0.105	0.026	(0.0572, 0.1493)
${\beta }_{22}^{\lambda }$ (SI)	0.4193	0.3945	0.2482	(0.1181, 0.906)
${\beta }_{31}^{\lambda }$ (AR(1))	0.0355	0.03257	0.00882	(0.0239, 0.0567)

Table 2.

Parameter Estimates for the Dropout Model and Time-varying Covariates

Parameter	Mean	Median	SD	95% C.I.
Dropout parameter
ζ1 (Intercept)	0.2651	0.2809	0.8061	(-0.414, 1.79)
ζ2 (AGE)	0.7953	0.7694	0.1051	(0.6348, 1.032)
ζ3 (STD)	0.0392	0.0296	0.16	(0.013, 1.319)
ψ1 (Current obs)	1.977	1.97	0.2052	(1.571, 2.391)
ψ2 (Prev. Obs)	-0.4828	-0.4806	0.1444	(-0.7759, -0.2086)
MOOD (Covariate)
α01 (Intercept)	3.556	3.65	0.182	(2.692, 4.95)
α11 (AR(1))	0.0955	0.0954	0.084	(0.0788, 0.1116)
SI (Covariate)
α02 (Intercept)	1.138	1.137	0.04707	(1.047, 1.232)
α12 (AR(1))	0.2908	0.291	0.0103	(0.2698, 0.3117)

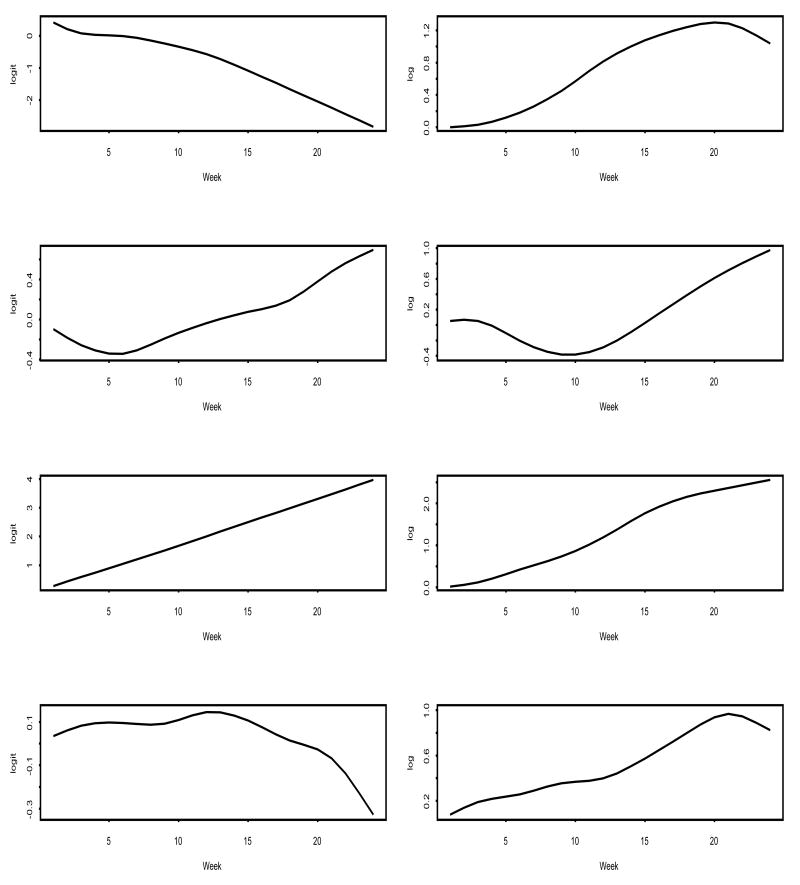
The ZIP regression analysis yielded a number of observations: (1) Older age was associated with increased probability of the subject being in the sexually active state (Odds ratio(OR)=exp $({\widehat{\beta }}_{12}^p)$= 1.99, 95% CI= [exp(0.0864), exp(1.180)]= [1.09, 3.25]), although an increase in age did not necessarily increase the weekly rate of coital frequency given the subject was in a sexually active state. (2) Baseline STD history was a strong indicator for the subject's state of sexual activity (OR=exp $({\widehat{\beta }}_{13}^p)$= exp(0.2583)=1.29, 95% CI=[1.10, 6.84]). A young woman that had a positive STD history at enrollment was more likely to be in the sexually active state during the study period. However, STD history did not appear to affect the rate of coital events. (3) Lifetime number of partners that the subject reported at baseline was also positively associated with the probability of being in a sexually active state (OR=exp $({\widehat{\beta }}_{14}^p)$=1.45, 95% CI=[1.21, 1.59]). Again, no similar effect was observed for the rate of coital frequency. (4) Lower positive mood was associated with an increased probability of being in a sexually active state (OR=exp $({\widehat{\beta }}_{21}^p)$=0.79, 95% CI=[0.68, 0.91]); but for a subject that was in the sexually active state, higher positive mood was associated with increased coital frequency (incident rate ratio or IRR=exp $({\widehat{\beta }}_{21}^{\lambda })$=1.11, 95% CI=[1.06, 1.16]). (5) Higher sexual interest was associated with increased coital frequency (IRR=exp $({\widehat{\beta }}_{22}^{\lambda })$=1.52, 95% CI=[1.13, 2.47]). (6) Coital frequency in the prior week was associated with both increased probability of being in a sexually active state (OR=exp $({\widehat{\beta }}_{31}^p)$=3.69, 95% CI=[2.80, 5.55]) and increased coital frequency in the current week (IRR=exp $({\widehat{\beta }}_{31}^{\lambda })$=1.04, 95% CI=[1.02, 1.06]). (7) From Figures 3 and 4, it is evident that both the probability of being in a sexually active state and the rate of coital frequency given the subject was in an active state exhibit nonlinear time effects, and the effects vary from subject to subject. In particular, the rate parameter was monotonically increasing over time, suggesting either a developmental effect of sexuality in adolescents or a possible activation effect of repeated questionnaires. For example, Figure 3 shows that in the study cohort, the probability of a subject being in a sexually active state is not entirely monotone, but the intensity of sexual activities is steadily increasing over time. (8) Finally, we noted that the correlation was modest between random subject effects in the logistic and loglinear models (0.29), suggesting a relatively weak positive link between the subject's current state of sexual activity and her intensity or the level of activity of sexual behaviors given she was in an active state. This last observation demonstrates the usefulness of the proposed joint modeling structure in assessing the interrelationship among latent states, which may be particularly useful in the analysis of behavioral data from a variety of fields.

Figure 3.

Spline Estimates of the Average Time Effects on logitp and logλ.

Figure 4.

Spline Estimates of Individual Time Effects on logitp and logλ of Four Individual Subjects.

Similarly, from the estimates of parameters in the dropout and time-varying covariate models (Table 2), we had the following observations: (1) The dropout probability appeared to be related to the baseline covariates AGE, STD, and current and previous coital frequency values. (2) The estimates of the parameters ψ₁, ψ₂ of the dropout models were 1.977 and -0.4828 respectively, suggesting that dropout might be informative and the missing probability of y_ij might depend more on the current values of the coital frequency and less on the previous value. Thus, any statistical analysis that ignores the dropout may be biased. (3) Older subjects and those with an STD history were more likely to drop out, perhaps due to competing demands for time in older teens. (4) Both mood and sexual interest measures of the current week were correlated with their corresponding values of the previous week, suggesting continuity in the adolescent mood and sexual interest.

4.4 Model Comparison

To compare candidate models, we computed p(Y_obs,i, T_obs,i, R_i|Y_obs,−i, T_obs,−i, R_−i) (Geisser and Eddy 1979), which is the posterior predictive density of (Y_obs,i, T_obs,i, R_i) for subject i conditional on the observed data with a single data point deleted. This value is known as the conditional predictive ordinate (CPO; Gelfand, Dey and Chang (1992); Chen et al, (2000)) and has been widely used for model diagnostic and assessment.

For the ith subject, the CPO statistic under model M_l; 1 ≤ l ≤ L is defined as:

$$\begin{array}{ll}{\text{CPO}}_i\hfill & =p(Y_{\text{obs},i},T_{\text{obs},i},R_i|Y_{\text{obs},-i},T_{\text{obs},-i},R_{-i})\hfill \\ \hfill & =E_{{\theta }_l}[p(Y_{\text{obs},i},T_{\text{obs},i},R_i|{\theta }_l\text{)}|Y_{\text{obs},-i},T_{\text{obs},-i},R_{-i}]\hfill \end{array}$$

where −i denotes the exclusion of the data from subject i. The θ_l is the set of parameters of model M_l and p(Y_obs,i, T_obs,i, R_i|θ_l) is the sampling density of the model evaluated at the ith observation. The expectation above is taken with respect to the posterior distribution of the model parameters θ_l given the cross-validated data (Y_obs,−i, T_obs,−i, R_−i). For subject i, the CPO_i can be obtained from the MCMC samples by computing the following weighted average:

$${\widehat{\text{CPO}}}_i={\left(\frac{1}{M}\sum _{m=1}^M\frac{1}{f(Y_{\text{obs},i},T_{\text{obs},i},R_i|{\theta }_l^{(m)})}\right)}^{-1}$$

where M is the number of simulations. The ${\theta }_l^m$ denotes the parameter samples at the mth iteration. A large CPO value indicates a better fit. A useful summary statistic of the CPO_i is the logarithm of the pseudomarginal likelihood (LPML), defined as $\text{LPML}={\sum }_{i=1}^n\text{log}({\widehat{\text{CPO}}}_i)$. Models with greater LPML values represent a better fit. LPML is well defined under the posterior predictive density and it is computationally stable. LPML has been used extensively in Bayesian analysis for model selection in situations of simpler and more complicated models and has a long history in the statistics literature (see Chen et al, (2000), Chapter 10; Brown and Ibrahim, (2003); Brown, Ibrahim, and DeGruttola (2005)).

We compared the following models using LPML:

• Model 1: This is the model that we used in the analysis.

• Model 2: Model 1 without the spline components in ZIP model, i.e., the splines are replaced by a linear time effect (t_ij).

• Model 3: Independent model, i.e., the ZIP model is independent of the dropout process.

We then considered several dropout models, keeping other parts of the model unchanged:

• Model 4: Logit(η_ij) = ξ₁ + ξ₂Age_i + ξ₃STD_i + ψ₁y_ij

• Model 5: Logit(η_ij) = ξ₁ + ψ₁y_ij + ψ₂y_i,j−1

• Model6: Logit(η_ij) = ξ₁ + ψ₁y_ij

The LPML values for Models 1-6 were −10405.7, −12198.4, −11201.8, −11086.1, −11066.9, and −11132.5, respectively. The proposed model had the highest LPML values, suggesting that it had the best fit among the six candidate models. The large difference between the LPML values of Models 1 and 2 indicated the presence of a nonlinear time effect, and justified the use of the spline-based model for time effects in the analysis.

4.5 Simulation

In this section, we present a small simulation study to justify the relative complexity of the proposed model and to verify the performance of the model fitting procedure. We first note that the complexity of the model arises primarily from four aspects: (1) explicit modeling of autoregressive effect of the main outcome variable; (2) explicit inclusion of time-varying covariates; (3) spline-based modeling of non-linear time effects; and (4) accommodation of nonignorable dropout. While it is well known that failure to accommodate informative dropouts may lead to questionable inference (Wu and Carroll, 1988; Schluchter, 1992; Little, 1995; Roy and Lin, 2005; Wu, 2007), the impact of inattention to the first three complicating factors has not been well studied. We therefore focus on these three issues in the simulation study. Additionally, the simulation study has also given us a chance to verify the performance of our model fitting procedure.

Specifically, we consider the following model:

$$\begin{array}{rr}\hfill \text{logit}(1-p_{ij})& ={\beta }_{11}^p+{\beta }_{13}^p{\text{X}}_i+{\beta }_{21}^p{\text{Z}}_{ij}+{\beta }_{31}^p{Y}_{i,j-1}+b_{i1}+f^p(t_{ij})\hfill \\ \hfill \text{log}({\lambda }_{ij})& ={\beta }_{11}^{\lambda }+{\beta }_{13}^{\lambda }{\text{X}}_i+{\beta }_{21}^{\lambda }{\text{Z}}_{ij}+{\beta }_{31}^{\lambda }{Y}_{i,j-1}+b_{i2}+f^{\lambda }(t_{ij}),\hfill \end{array}$$ (19)

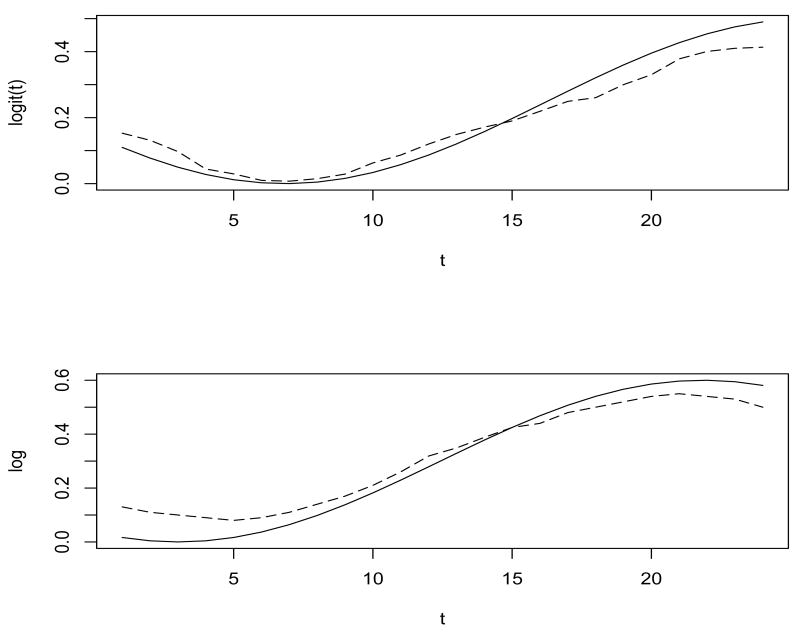
where we use $f^p(t)=\frac{1}{2}{\text{cos}}^2(\frac{t+12}{12})$ and $f^{\lambda }(t)=0.6{\text{sin}}^2(\frac{t-3}{12})$, for t = 1, 2, …, 24 to depict the nonlinear time effects (see Figure 5). Also in this model we consider a subject-specific covariate X_i, random intercepts b_i = (b_i1, b_i2)^t, as well as a time-varying covariate Z_ij, where i = 1, 2, …, 50, j = 1, 2, …, 24.

Figure 5.

The True and Estimated Average Time Effects on logitp and logλ from the Simulation Study.

Note: Solid line represents the true curves and dashed line represents the estimated curves.

Data were generated from (19) to mimic the real data presented in the paper. Specifically, for the ith subject, we first generated X_i from a Bernoulli distribution with probability $p_0^{(x)}$. For the same subject, we then generated a 24-dimensional vector Z_i = (Z_i1, …, Z_i24)^t ∼MVN(μ_Z, Σ_Z) to represent the values of the time-varying covariate Z_ij for the 24 time points. We gave Σ_z, an AR(1) variance-covariance structure to maintain a correlation between the Z values in adjacent weeks within the subject. Similarly, random intercepts b_i = (b_i1, b_i2)^t were generated from a bivariate normal distribution. We then calculated the values of $f^p(t_{ij})=\frac{1}{2}{\text{cos}}^2(\frac{t_{ij}+12}{12})$, and $f^{\lambda }(t_{ij})=0.6{\text{sin}}^2(\frac{t_{ij}-3}{12})$ at each time points. Finally, we generate the baseline value for the Y_i1 from ZIP (p₁, λ₁). Models in (19) were then used to calculate p_i2 and λ_i2. From p_i2 and λ_i2, we generated Y_i2 ∼ZIP (p_i2, λ_i2). We then repeated this last step to generate the rest of the Y values. Parameter values used in the simulation were chosen to produce data that are similar to the real data. In particular, we take ${\beta }_{11}^p=0.45$, ${\beta }_{13}^p=0.25$, ${\beta }_{21}^p=-0.21$, ${\beta }_{31}^p=1.3$ and ${\beta }_{11}^{\lambda }=0.1$, ${\beta }_{13}^{\lambda }=0.25$, ${\beta }_{21}^{\lambda }=0.2$, ${\beta }_{31}^{\lambda }=0.04$. One hundred simulated data sets were used in the simulation study.

Using generated data, we fitted our proposed semiparametric ZIP regression model as well as the ZIP regression model with a linear time effect (i.e., without splines for time effect). Results are presented in Table 3. We computed the “relative bias” (RB) which is defined as the ratio of bias and the absolute value of the true parameter, mean square error (MSE) and coverage probability (CP). The numbers in parenthesis in Table 4 are the true value of the parameters.

Table 3.

Simulation Results

	Model with Spline				Linear Model
Parameter	Mean	RB	MSE	CP	Mean	RB	MSE	CP
${\beta }_{11}^p$ (0.45)	0.47	-0.02	0.042	.94	0.43	0.03	0.048	.93
${\beta }_{12}^p$ (0.23)	0.25	0.02	0.023	.92	0.21	0.02	0.037	.91
${\beta }_{13}^p$ (-0.21)	-0.2	-0.03	0.029	.96	-0.13	0.063	1.89	.89
${\beta }_{14}^p$ (1.3)	1.37	-0.02	0.047	.95	1.1	0.05	0.1	.92
${\beta }_{11}^{\lambda }$ (0.1)	0.1	0.01	0.041	.94	0.12	0.01	0.052	.94
${\beta }_{12}^{\lambda }$ (0.25)	0.23	0.02	0.08	.92	0.2	0.04	0.11	.90
${\beta }_{13}^{\lambda }$ (0.2)	0.22	0.02	0.06	.97	0.08	0.07	1.46	.88
${\beta }_{14}^{\lambda }$ (0.004)	0.004	0.01	0.032	.97	0.004	0.03	0.04	.98

A number of observations can be made from the simulation results: (1) that the proposed method is able to produce accurate estimates of the model parameters with minimal bias, MSE, and which have good coverage probabilities. (2) In the presence of nonlinear time effects, traditional ZIP regression models with linear time effect often produce biased estimates, larger MSEs, and substantially lower coverage probability in the time-varying covariates, although other covariates appear to be spared from such effects of the model mis-specification. Figure 5 clearly shows that proposed model is able to recover the unobserved nonlinear time effects reasonably well. (3) Finally we observed from the simulation that the proposed semiparametric regression model had larger LPML values then their parametric counterparts, suggesting improved fit of the new model. Based these observations, we contend that the models used in the analysis have good performance in the modeling of zero-inflated behavioral counts. Despite the increased complexity, the new analysis provides a safe-guard against potential effects of mis-specification of the time effects, thus preventing the occurrence of large biases in the estimation of time-varying effects.

5 Discussion

Sexually transmitted infections (STI) are spread primarily through sexual intercourse. A young woman is at risk of STI once she becomes sexually active. Yet little is known about the contextual factors that are associated with the occurrence of coitus, and the temporal patterns in which adolescent sexual behaviors evolve. This study is perhaps the first longitudinal examination of these issues based on a sizable cohort. A major strength of this investigation is the inclusion of young teens that were still in their early years of sexual experience. Other strengths of the study include the longitudinal follow-up and the extensive behavioral information that were collected in the process.

Contrary to the alarming anecdotes reported by the lay press in recent years, the findings of this paper reveal a more complicated picture: Sexual behaviors in adolescents are influenced strongly by intrinsic factors such as mood and sexual interest, rather than being driven completely by circumstances over which the teens have little control. This gives us reason to believe that more effective education and promotion of self-protective behaviors might help to reduce the risk of disease transmission. It also suggests that future prevention strategies should take into account of the emotional needs of the teens. The increasing levels of sexual activity over time are not surprising, but their individual-specific patterns seem to suggest that there are no uniformally followed patterns in terms of sexual behavioral development. Considering the age range of our study participants (14 to 17 years), we believe that intervention measures must start early to be effective.

Methodologically, the most challenging aspect in the modeling of human behavior is perhaps the incorporation of relevant contextual information. In studies of STD epidemiology and human sexuality, this contextual information often includes the concurrent mood, sexual interest, prior behavior, and subtle time effects that cannot be dismissed. Along the same line, issues such as dropout and autocorrelations existing among the time-varying covariates also complicate the analysis. These various factors form an interactive system in which the behaviors of interest are influenced by the other factors, which in turn are influenced by the observed behaviors. Therefore, a unidimensional modeling approach with a narrower focus often fails to capture the full complexity of the situation, and may produce an overly simplistic depiction of the behavior.

To address these shortcomings, we propose a new analytical framework that takes into account most of the major components in the modeling of human behaviors. Our joint model is a complicated system, but it is also necessary in order to place the behavioral event in its original context. Such an approach is likely to help investigators achieve a more comprehensive understanding of the studied behavior. As an applied statistical tool, this method is motivated by a real epidemiological investigation. Although the data analysis that we presented in this paper is preliminary in nature due to the fact that the full data are still being collected, the initial results are promising and they have revealed some previously under-appreciated characteristics of adolescent behavior. As a result, we feel that the basic construction of the model might be appropriate for other longitudinal studies as well. Although we recognize that this is an initial step in seeking a more comprehensive solution, our effort has demonstrated the feasibility of this general strategy. Preliminary results from the simulation study have provided assurance of the modeling procedure. Additionally, it has also highlighted the potential pitfalls of using mis-specified parametric ZIP regression models.

Technically, the model employs some of the more recent developments in statistical methodology. The proposed joint model is flexible and new in several aspects: (1) it represents a semiparametric development of the ZIP model. The semiparametric approach is useful, particularly when the linearity of time effect is in question. (2) it incorporates the dropout process in the ZIP model. Without the accommodation of dropout, models may produce biased results. (3) It take into account of time-varying covariates. (4) the autocorrelation structure among behaviors and time-varying covariates. Our joint modeling approach deals with both missing response and missing covariate simultaneously and is built to borrow strength from each of the modeling components. Through a real application, we have demonstrated that the joint modeling increased the LPML values and resulted in a better fit of the data.

A few limitations of our methods must be underlined. One of the major issues is the robustness of the distributional assumption. In our application, we use a parametric normal distribution for the random effects. A broader class of distributions such as Dirichlet processes, may be a viable alternative. Another issue is the fixed knot points. Random knot points would be more flexible; however, such models will be numerically challenging in this set up. Third, the parametric dropout model may be overly simplistic. Given a sufficient number of dropouts, one can build a more complex parametric or semiparametric structure as suggested by Chen and Ibrahim (2006). It will be worthwhile to see if the complex modeling of the dropout and the use of robust random effects would improve the goodness-of-fit and change the results of the analysis. We are currently exploring these aspects of the modeling. Notwithstanding these limitations, this research has pointed to a new road map for the analysis of longitudinally measured behavioral data.