Model Membrane Thermodynamics and Lateral Distribution of Cholesterol: From Experimental Data To Monte Carlo Simulation

Abstract

Thermodynamic analysis and Monte Carlo simulation techniques were used to study cholesterol-lipid interactions in lipid membranes. Experimental data, including the maximum solubility of cholesterol in lipid bilayers, the 1-to-1 displacement of cholesterol by ceramide, and the cholesterol chemical activity with cholesterol oxidase (COD), were systematically analyzed using thermodynamic principles. A conceptual model, the umbrella model, is presented to describe the key cholesterol-lipid interaction in lipid membranes. In a lipid membrane, nonpolar cholesterol relies on polar phospholipid headgroup coverage to avoid the unfavorable free energy of cholesterol contact with water. This coverage requirement leads to cholesterol's strong tendency not to clustering in a bilayer, its preferential association with large headgroup lipids with saturated acyl chains, and its competition with ceramide for large headgroup lipids. The umbrella model was parameterized into a form of multibody (i.e., nonpairwise) interaction for Monte Carlo simulation, and the measured chemical potentials of cholesterol agreed favorably with the predictions from the simulation. Under the right conditions, the multibody interactions can also lead to the formation of cholesterol superlattices. Also, an intrinsic thermodynamic connection between a jump in chemical potential and a regular distribution (RD) of membrane molecules was uncovered. This study shows that combining thermodynamics with computer simulation can be a productive approach for analyzing and interpreting complex experimental data, and thermodynamics can yield a predicting power in bioscience research.

1. Introduction

Synthetic liposomes provide a valuable platform for studying the behaviors of membrane molecules in a controlled environment with a well-defined membrane composition and heterogeneity. Under normal experimental conditions, multicomponent liposomes are sufficiently large and are in thermodynamic equilibrium. Therefore, thermodynamics can be a powerful tool to analyze and interpret the complex experimental results.

Cholesterol is a major constituent of the mammalian plasma membranes. It has been shown that cholesterol has a remarkable ability to alter the physicochemical properties of membranes and to induce membrane heterogeneity. The presence of cholesterol in a lipid membrane can drastically increase lipid acyl chain order, induce regular distributions (RD) of lipids or lipid raft domains, and modulate the activities of surface acting enzymes (Ahn and Sampson, 2004; Brown and London, 2000; Chong, 1994; Vist and Davis, 1990). In general, the interactions between cholesterol and other membrane molecules are not ideal. Mean-field regular solution theories are often inadequate to describe the complicity of the systems, because lipid mixtures are often heterogeneous, and distributional as well as conformational entropies play important roles. To overcome the shortcoming, computer simulation has become a valuable tool to explore the molecular interactions between membrane molecules and to simulate membrane domain distributions as well as phase separations.

In this article, we show that thermodynamics played an important role in understanding the complex experimental data, including the maximum solubility of cholesterol in lipid membranes, the competition between ceramide and cholesterol, the driving forces of cholesterol regular distributions (superlattices), and cholesterol's chemical activity with cholesterol oxidase (COD). Combining thermodynamic principles with Monte Carlo simulation, it allowed us to quantitatively describe the key cholesterol-lipid interactions and to predict the behavior of cholesterol in lipid membranes.

2. Materials and Methods

2.1. Materials

Phosphatidylcholines (PC), phosphatidylethanolamine (PE), and brain ceramide were purchased from Avanti Polar Lipids (Alabaster, AL). Cholesterol was purchased from Nu Chek Prep (Elysian, MN). Lipid purity (>99%) was confirmed by thin layer chromatography (TLC) on washed, activated silica-gel plates (Alltech Associates, Deerfield, IL) and developed with a 65/25/4 chloroform/methanol/water mixture for phospholipid analysis or with a 7/3/3 petroleum ether/ethyl ether/ chloroform mixture for cholesterol analysis. Concentrations of phospholipid stock solutions were determined with a phosphate assay (Kingsley and Feigenson, 1979). Aqueous buffer [5 mM PIPES, 200 mM KCl, and 1 mM NaN₃ (pH 7.0)] was prepared from deionized water (≈18 MΩ) and filtered through a 0.1 μm filter before use. Recombinant cholesterol oxidase (COD) expressed in Escherichia coli (C-1235), peroxidase (P-8250) from horseradish, and other chemicals for the cholesterol oxidation measurements were obtained from Sigma (St. Louis, MO).

2.2. Liposome preparation for COD activity measurement

The cholesterol content in all samples was kept at 60 μg, and the cholesterol mole fractions of samples were adjusted by adding appropriate amounts of PC or ceramide. Liposomes were prepared by the rapid solvent exchange (RSE) method (Ali et al., 2006; Buboltz and Feigenson, 1999). First, lipids were dissolved in 70 μL of chloroform. The lipid solution was then heated to 55 °C briefly in a glass tube, and 1.3 mL of aqueous buffer was added. While the mixture was kept vigorously vortexed in the glass tube, the bulk solvent was removed by gradually reducing the pressure to 3 cm of Hg using a home-built vacuum attachment. The remaining trace chloroform was removed by vortexing for an additional 1 min at the same pressure. The liposomes prepared by these procedures were all sealed under argon. Sample tubes were placed in a programmable water bath (VWR, model 1187P), preheated to 50 °C for the subsequent heating and cooling cycle. The samples were first cooled to 24 °C at a rate of 10 °C/h and again heated to 50 °C at the same rate. The samples were then kept at 50 °C for an additional 1 h before finally being cooled to room temperature at a rate of 1.5 °C/h. Finally, the liposomes were stored at room temperature on a mechanical shaker for 10 days in the dark before the cholesterol oxidation measurements. The majority of liposomes made by the RSE method are large unilamellar vesicles and can settle down in a test tube under gravity in a few hours (Buboltz and Feigenson, 1999). Compared with the ethanol injection and the extrusion method, RSE is a convenient method with no lipid-binding, solvent-contamination, or lipid-demixing concerns.

2.3. Liposome preparation for X-ray diffraction measurement

The liposome samples for X-ray diffraction measurement were either made by the original Rapid solvent exchange (RSE) method or by the low temperature trapping (LTT) method. The original RSE method is described in detail in Buboltz and Feigenson (1999). Briefly, lipids were codissolved in 10–100 μl of dichloromethane (0.1% MeOH, 0.05% H₂O) and then sprayed into vortexing buffer at reduced pressure, rapidly vaporizing the solvent and precipitating the lipid mixture in an aqueous environment. For sample preparation of mixtures containing DPPC, the buffer was maintained at 50 °C throughout the RSE procedure, before cooling to room temperature. All samples were sealed under argon immediately following RSE. In the LTT method, lipids were dissolved in CHCl₃ and the solvent removed under vacuum at ≈30 millitorr for ≈10 h. Lipids were redissolved in dry chloroform containing 1% methanol, then frozen in liquid nitrogen. Samples were lyophilized at low temperature, carefully controlling the temperature so that the chloroform remains solid. After bulk solvent had been removed, the lipid powders were kept cool (−20 °C) during continued vacuum incubation (≈12 h) to remove residual solvent. Just before hydration, the sample was warmed to room temperature in a stirring water bath for 1 min, then buffer added to the dry powder. The suspension was immediately vortexed for 1 min. Samples containing DPPC were hydrated and vortexed at 50 °C. All samples were sealed under argon following hydration. Hydrated liposome dispersions made by LTT were first pelleted at 1,000g for 10–25 min; dispersions made by RSE were pelleted at 20,000g for 15 min. The lipid sediment was loaded into thin-walled 1.0-mm glass X-ray capillaries and further centrifuged in a buoyant support apparatus (Buboltz and Feigenson, 1999) at 20,000g for 15 min to produce a uniformly dense pellet. Capillaries were sealed by paraffin wax under argon gas. A typical sample contained about 1.5 mg of lipid.

2.4. X-ray diffraction

X-ray diffraction experiments were carried out at the A-1 and F-1 beam-lines at the Macromolecular Diffraction Facility at the Cornell High Energy Synchrotron Source (MacCHESS). Samples were illuminated by an intense synchrotron x-ray beam, with a wavelength of 0.908 Å, passing through a 0.2-mm collimator. Diffraction images were collected with a Princeton 2K CCD detector containing 2048 × 2048 41-micron pixels. Both the low-angle and wide-angle diffraction patterns (from 3.8 Å to 110 Å) were captured simultaneously on the same image. Depending on beam intensity and sample density, the exposure time for hydrated samples varied from 10–80 s. Samples were scanned 2–3 mm along the capillary axis during exposure, using a stepping motor. This procedure reduces radiation damage to the lipid and achieves more representative sampling. Image files were corrected for geometric distortions introduced by the CCD camera. To transform the powder patterns into radial profiles of diffraction intensity, each image was circularly integrated (using the IMP program provided by CHESS). The center of the beam and the tilt angle of the detector surface were precisely determined to prevent line broadening.

2.5. Cholesterol oxidase activity assay

Cholesterol oxidase (COD) is a water-soluble monomeric enzyme that catalyzes the conversion of cholesterol to cholest-4-en-3-one. The initial rate of oxidation of cholesterol by the oxidase enzyme was determined through a coupled enzyme assay scheme:

$$\begin{array}{l}\text{Cholesterol}+{\text{O}}_2\stackrel{\text{COD}}{\to }{\text{H}}_2{\text{O}}_2+\text{Cholest–4–en–3–one}\\ 2{\text{H}}_2{\text{O}}_2+4–\text{Aminoantipyrine}+\text{Phenol}\stackrel{\text{POD}}{\to }\text{Red Quinoneimine}+{\text{H}}_2\text{O}\end{array}$$

The total reaction involves two steps. In the first step, the COD-mediated oxidation of membrane cholesterol produces two products, hydrogen peroxide and cholest-4-en-3-one (Ahn and Sampson, 2004). Catalyzed by peroxidase (POD), the production of hydrogen peroxide in the first step subsequently leads to reaction with 4-aminoantipyrine and phenol and produces red-colored quinoneimine, which has a distinctive absorption peak at 500 nm. For each cholesterol oxidation measurement, 1.3 mL of liposomes was first mixed with 0.2 mL of a 140 mM phenol solution. After mixing had been carried out, 1 mL of reaction buffer [1.64 mM aminoantipyrene and 10 units/mL peroxidase in PBS buffer (pH 7.40)] was added. The preceding mixture was then incubated at 37 °C for at least 10 min and finally transferred to a cuvette preheated to 37 °C in a heating block. The sample in the cuvette was maintained at 37 °C and stirred with a home-built magnetic mini-stirrer during the measurement. An HP-8453 (UV-vis) linear diode array spectrophotometer (Agilent Technologies, Wilmington, DE) was used to measure the absorption spectra of the samples. The reaction was started by injecting 20 μL of a COD solution (5 units/mL) into the cuvette. The spectra were collected at a rate of two spectra per second, and the total data collection time per sample was 120 s. Background-corrected time dependent absorption of quinoneimine was determined by calculating the difference in the absorption at 500 nm and the background average over the range of 700–800 nm as a function of time. The initial oxidation rate (i.e., the rate of change in the quinoneimine absorption at time zero) was determined using a second-order polynomial fit to the first 40 s of the absorption data. All data acquisition and data analysis were performed using the UV-visible ChemStation Software provided by Agilent Technologies.

2.6. Monte Carlo simulation of lipid membranes using a lattice model

The cholesterol/phospholipid bilayer is modeled as a 2-dimensional hexagonal lattice. Each lattice site can be occupied by either a phospholipid acyl chain or a cholesterol molecule. Because the sizes and packing details are surely not identical for cholesterol and phospholipid acyl chains, a distorted hexagonal lattice seems likely. Such a distorted hexagonal lattice will serve our purpose well, as long as each site has 6 nearest neighbors. The effects of water and conformation entropies are taken into account via the energy parameters. The main advantages this Monte Carlo simulation are that it can handle large simulation size, and true equilibrium distribution of the molecules can be reached, thereby making possible the connection to equilibrium thermodynamic data, such as chemical potentials. All the simulations were performed on a 120 × 120 hexagonal lattice with a standard periodical boundary condition. As demonstrated earlier (Huang and Feigenson, 1993), such a large-scale simulation makes the simulation size effect negligible. Neighboring cholesterols and acyl chains can exchange their position with a probability given by the Metropolis method. All simulations started from a random mixture of given composition. Equilibrium conditions were established after an initial 25,000–70,000 Monte Carlo steps. The ensemble average of the data was obtained in 10,000 Monte Carlo steps after equilibrium. Data were averaged from three independent runs.

2.7. Pairwise interactions and multibody interactions

The Hamiltonian has two major components: one describing pairwise interactions and another for cholesterol multibody interactions with its nearest neighbors (Huang and Feigenson, 1999).

$$H_{\mathit{\text{total}}}=H_{\mathit{\text{pair}}}+H_{\mathit{\text{multi}}}.$$ (12.1)

The pairwise part of the Hamiltonian includes the interactions of acyl chain-acyl chain, cholesterol-cholesterol, and acyl chain-cholesterol contact pairs:

$$H_{\mathit{\text{pair}}}=\frac{1}{2}\sum _{i,j}{E}_{\mathit{\text{aa}}}{L}_{\mathit{\text{ai}}}{L}_{\mathit{\text{aj}}}+\frac{1}{2}\sum _{i,j}{E}_{cc}{L}_{\mathit{\text{ci}}}{L}_{cj}+\frac{1}{2}\sum _{i,j}{E}_{ac}(L_{ai}{L}_{\mathit{\text{cj}}}+L_{ci}{L}_{aj}),$$ (12.2)

where E_aa, E_cc, and E_ac are the interaction energies between acyl chains, between cholesterols, and between acyl chain-cholesterol, respectively; L_ai and L_ci are the occupation variables (= 0 or 1) of acyl chains and cholesterols, respectively. The summation i is over all lattice sites, and j is over the nearest-neighbor sites of i only. The factor 1/2 is necessary to avoid counting each contact pair twice.

For this lattice system, the three interaction energies in Eq. (12.2) can be further reduced to just one independent variable. Eq. (12.2) is rewritten as:

$$H_{\mathit{\text{pair}}}=\frac{Z}{2}\sum _i{E}_{\mathit{\text{aa}}}{L}_{\mathit{\text{ai}}}+\frac{Z}{2}\sum _i{E}_{\mathit{\text{cc}}}{L}_{\mathit{\text{ci}}}+\frac{1}{2}\sum _{i,j}\mathrm{\Delta }{E}_m(L_{\mathit{\text{ai}}}{L}_{\mathit{\text{cj}}}+L_{\mathit{\text{ci}}}{L}_{\mathit{\text{aj}}}),$$ (12.3)

where Z is the number of nearest-neighbors to a lattice site, which is 6 for a hexagonal lattice. ΔE_m is the pairwise-additive excess mixing energy of acyl chains and cholesterols, defined as

$$\mathrm{\Delta }{E}_m=E_{\mathit{\text{ac}}}-(E_{\mathit{\text{aa}}}+E_{\mathit{\text{cc}}})/2.$$ (12.4)

In a canonical Monte Carlo simulation, the total number of lattice sites (N), the number of acyl chains $(N_a={\sum }_i{L}_{\mathit{\text{ai}}})$, the number of cholesterols $(N_c={\sum }_i{L}_{\mathit{\text{ci}}})$, and the temperature (T) are all fixed for each simulation. Therefore, the first two terms in Eq. (12.3) are independent of lipid lateral distribution, and the entire contribution of pairwise-additive interactions to the lipid mixing behavior is determined by the value of ΔE_m in the third term.

The cholesterol multibody interaction with its 6 nearest neighbors is given by:

$$H_{\mathit{\text{multi}}}=\sum _i\sum _{s=0}^6\mathrm{\Delta }{E}_c{c}_s{L}_{\mathit{\text{si}}}{L}_{\mathit{\text{ci}}},$$ (12.5)

where ΔE_c is the strength of the cholesterol multibody interaction, c_s are the energy scaling factors, and L_si is the environment variable of a lattice site, which is defined as

$$\begin{array}{l}{L}_{si}=\{\begin{array}{ll}1,& \text{if site}i\text{has}s\text{cholesterol as it nearest neighbor}\\ 0,& \text{otherwise.}\end{array}\end{array}$$

In Eq. (12.5) the summation s is over seven possible environments for lattice site i: a site can have zero to six cholesterols as nearest neighbors. Thus, if a cholesterol molecule is surrounded by s other cholesterols, then the multibody interaction energy for this cholesterol would be ΔE_c c_s. No energy difference is assumed for the different arrangements of these s cholesterols among the nearest-neighbor sites. Seven energy scaling factors (c₀,c₁,…,c₆) define the relative magnitude of the multibody interaction in the seven possible situations, and ΔE_c determines the overall strength of the cholesterol multibody interaction.

2.8. Calculation of chemical potential of cholesterol from simulation

To relate our microscopic interaction model to experimental data, it is crucial to be able to calculate the chemical potential of cholesterol from computer simulations. We applied the Kirkwood coupling parameter method (Chialvo, 1990; Haile, 1986) to calculate the excess Gibbs free energy of the cholesterol/phospholipid mixtures. Although this approach is computationally intensive, it provides complete information: mixing free energy, enthalpy, entropy, and chemical potentials of cholesterol and acyl chains.

Following similar steps described in our earlier paper (see Huang et al., 1993, appendix), the excess Gibbs free energy of a cholesterol/phospholipid mixture is given by

$$\begin{array}{l}\mathrm{\Delta }{G}^E(\mathrm{\Delta }{E}_m,\mathrm{\Delta }{E}_c)=N_0{\int }_0^{\mathrm{\Delta }{E}_m}\frac{<\frac{1}{2}\text{∑}_{i,j}(L_{ai}{L}_{cj}+L_{ci}{L}_{aj})>{\lambda }_c=0}{N}d{\lambda }_E\\ +N_0{\int }_0^{\mathrm{\Delta }{E}_c}\frac{<\text{∑}_i\text{∑}_{s=0}^6{C}_s{L}_{si}{L}_{ci}>{\lambda }_E=\mathrm{\Delta }{E}_m}{N}d{\lambda }_C-N_0\mathrm{\Delta }{E}_c{C}_6\frac{N_c}{N},\end{array}$$ (12.6)

where N₀ is Avogadro's number; λ_E and λ_C are coupling parameters; and angle brackets denote an ensemble average from Monte Carlo simulations. By performing numerical integration, ΔG^E can be calculated. The excess enthalpy ΔH^E and entropy ΔS^E are given by:

$$\begin{array}{l}\mathrm{\Delta }{H}^E=N_0<\frac{1}{2}\sum _{i,j}(L_{ai}{L}_{cj}+L_{ci}{L}_{aj})>\mathrm{\Delta }{E}_m/N\\ +N_0<\sum _i\sum _{s=0}^6{C}_s{L}_{si}{L}_{ci}>\mathrm{\Delta }{E}_c/N-N_0\mathrm{\Delta }{E}_c{C}_6{N}_c/N,\end{array}$$ (12.7)

and

$$\mathrm{\Delta }{S}^E=(\mathrm{\Delta }{H}^E-\mathrm{\Delta }{G}^E)/T.$$ (12.8)

The excess chemical potentials of cholesterol and phospholipid ( ${\mu }_{\mathit{\text{chol}}}^E$ and ${\mu }_{\mathit{\text{lipid}}}^E$) can be obtained by differentiating ΔG^E,

$$\mathrm{\Delta }{G}^E={\mu }_{\mathit{\text{chol}}}^E{N}_c/N+{\mu }_{\mathit{\text{lipid}}}^E{N}_a/N.$$ (12.9)

For convenience, we choose the standard state of ${\mu }_{\mathit{\text{chol}}}^E$ as that in which cholesterols are infinitely dilute in a phospholipid bilayer, and the standard state of ${\mu }_{\mathit{\text{lipid}}}^E$ as that in a pure phospholipid bilayer. Because each phospholipid has two acyl chains, the mole fraction of cholesterol in a bilayer is given by

$${\chi }_{\mathit{\text{chol}}}=2N_c/(2N_c+N_a).$$ (12.10)

3. Result and Discussion

3.1. Maximum solubility of cholesterol in PC bilayers

The maximum solubility of cholesterol in a lipid bilayer ( ${\chi }_{\mathit{\text{chol}}}^{\ast }$) is the upper limit of the mole fraction of cholesterol that can be incorporated into a lipid bilayer. When the cholesterol mole fraction of a sample exceeds this limit, excess cholesterol precipitates from the bilayer to form cholesterol monohydrate crystals. In terms of thermodynamics, this limit defines the phase boundary that separates a 1-phase region containing lipid bilayers in the liquid-ordered phase from a 2-phase region containing lipid bilayers saturated with cholesterol and cholesterol monohydrate crystals.

Making a truly equilibrium phospholipid and cholesterol suspension at high cholesterol mole fraction is a challenging task and the key to making an accurate measurement of ${\chi }_{\mathit{\text{chol}}}^{\ast }$ is good sample preparation. It has been shown that artifactual demixing of cholesterol can occur during conventional sample preparation (either by a dry film method or by lyophilization) and that this demixed cholesterol may produce artifactual cholesterol crystals in a sample at a χ_chol far below the true cholesterol solubility limit. Therefore, a falsely low ${\chi }_{\mathit{\text{chol}}}^{\ast }$ value could result from conventional sample preparation. Two novel preparative methods, LTT (Huang et al., 1999) and RSE (Buboltz and Feigenson, 1999), have been developed to prevent the demixing. Both methods can produce truly equilibrium phospholipid and cholesterol suspensions.

We found that X-ray diffraction can quantitatively and sensitively detect the formation of cholesterol monohydrate crystals. Experiments based on LTT or RSE sample preparation methods yield reproducible and precise cholesterol solubility limits. Fig. 12.1 shows a typical result of the X-ray diffraction experiment: The diffraction intensity of cholesterol monohydrate crystal remains zero until χ_chol in POPC bilayers is greater than 0.66, which is determined to be the maximum solubility of cholesterol in POPC bilayers. Table 12.1 summarizes the measured values of ${\chi }_{\mathit{\text{chol}}}^{\ast }$ in various lipid bilayers. Here, a clear pattern merges: ${\chi }_{\mathit{\text{chol}}}^{\ast }$ for many phosphatidylcholine bilayers is 0.66, and for a phosphatidylethanolamine bilayer is 0.51 (Huang et al., 1999).

Figure 12.1.

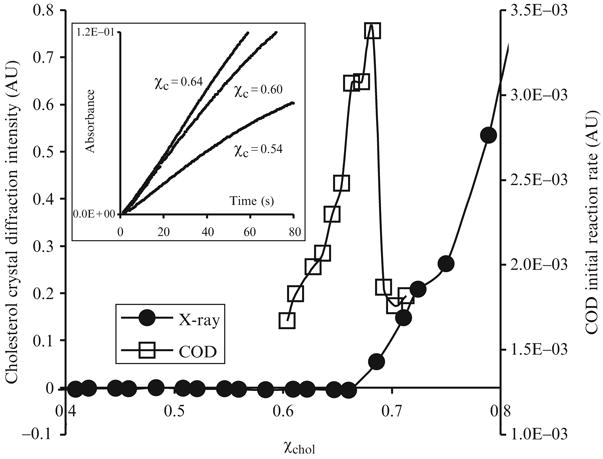
Experimental determination of the maximum solubility of cholesterol, ${\chi }_{\mathit{\text{chol}}}^{\ast }$, in POPC bilayers. Circles: Cholesterol crystal diffraction intensity versus cholesterol mole fraction. The intensity increases steadily as χ_chol > 0.66. Squares: The initial reaction rate of COD as a function of χ_chol. The rate has a sharp peak at χ_chol = 0.67. Inset: COD reaction progress curves at χ_chol = 0.54, 0.60, and 0.64.

Table 12.1.

Maximum solubility of cholesterol in PC and PE bilayers measured by X-ray diffraction or COD activity assay

Bilayer type	Maximum solubility by X-ray diffraction	Maximum solubility by COD activity assay
16:0, 18:1-PE (POPE)	0.51 (±0.01)a
16:0, 18:1-PC (POPC)	0.66 (±0.01)a	0.67 (±0.015)b
di22:1-PC	0.66 (±0.01)a
di16:0-PC (DPPC)	0.66 (±0.01)a	0.68 (±0.015)b
di12:0-PC (DLPC)	0.66 (±0.01)a	0.67 (±0.015)c
di14:0-PC (DMPC)		0.67 (±0.015)c
di18:1-PC (DOPC)		0.66 (±0.015)b

^aFrom Huang et al., 1999.

^bFrom Ali et al., 2007.

^cUnpublished data.

Recently, we developed a cholesterol oxidase (COD) activity assay, which can also be used to measure ${\chi }_{\mathit{\text{chol}}}^{\ast }$ in various lipid mixtures. After the injection of the COD enzyme, the height of the absorption peak of the COD assay product, red quinoneimine at 500 nm was found to increase steadily with time, indicating the progress of the COD-mediated cholesterol oxidation reaction. The insert of Fig. 12.1 shows the absorption at 500 nm versus time for three POPC/cholesterol mixtures: χ_chol = 0.54, 0.60, and 0.64. Because of the concern that the accumulation of the oxidized cholesterol product (i.e., cholest-4-en-3-one) in the lipid bilayer may alter the membrane properties, only the first 40 s of data was used to fit a second-order polynomial and to calculate the initial rate (i.e., initial slope) of the reaction. Fig. 12.1 also shows the initial rate of COD reaction as a function of χ_chol in POPC bilayers. The initial reaction rate has a sharp peak at χ_chol of 0.67, which coincides with ${\chi }_{\mathit{\text{chol}}}^{\ast }$ in POPC bilayers measured by X-ray diffraction within experimental uncertainty.

Why does the initial reaction rate of COD reaction peak at the composition corresponding to the maximum solubility of cholesterol? Below ${\chi }_{\mathit{\text{chol}}}^{\ast }$, the initial rate increases with χ_chol. Ahn and Sampson have pointed out that the initial rate of COD reaction is related to the chemical potential of cholesterol (μ_chol) in a lipid bilayer (Ahn and Sampson, 2004). As discussed in later sections, μ_chol should increase sharply near ${\chi }_{\mathit{\text{chol}}}^{\ast }$, to approach that in cholesterol monohydrate crystals. When the overall cholesterol mole fraction is above ${\chi }_{\mathit{\text{chol}}}^{\ast }$, COD initial reaction rate no longer reflects the behavior of μ_chol and drops sharply due to following reasons: (1) Because every sample has an identical amount of cholesterol (60 μg), when the overall cholesterol mole fraction of a sample is above ${\chi }_{\mathit{\text{chol}}}^{\ast }$, some cholesterol is in the cholesterol crystal form, and less cholesterol remains in the bilayer phase available to react with COD; (2) cholesterol microcrystals could physically change the packing order of lipids and the curvature of lipid bilayers and affect COD activity. In previous X-ray diffraction experiments, it has been found that as soon as the cholesterol mole fraction passes the solubility limit and cholesterol monohydrate crystals begin to form, the broad wide-angle diffraction peak at 4.9 Å, corresponding to the acyl chain packing in the bilayers, quickly disappears (Huang et al., 1999). Because the location of the sharp peak in the COD initial reaction rate coincides with the cholesterol solubility limit, it allows us to conveniently and sensitively measure ${\chi }_{\mathit{\text{chol}}}^{\ast }$ using this COD activity assay. Table 12.1 also lists some ${\chi }_{\mathit{\text{chol}}}^{\ast }$ values measured by COD activity assay, and the numbers agree quite well with those obtained by X-ray diffraction within experimental uncertainty.

The values of ${\chi }_{\mathit{\text{chol}}}^{\ast }$ in binary mixtures of cholesterol and phospholipid show a very interesting pattern: for many PCs studied, regardless of acyl chain type (di12:0 or di14:0 or di16:0 or 16:0,18:1 or di22:1) the value of is ≈0.67. In contrast, we found the distinctly different result that for POPE is ≈0.5. These results naturally lead us to the following interesting questions: Why are the values of ${\chi }_{\mathit{\text{chol}}}^{\ast }$ insensitive to the type of phospholipid acyl chains? Why ${\chi }_{\mathit{\text{chol}}}^{\ast }$ occur close to cholesterol:phospholipid mole ratios of 1:1 and 2:1? What is the lateral packing of cholesterol and phospholipids at the cholesterol solubility limit? What kind of microscopic interactions in cholesterol/phospholipid mixtures could give rise to the observed values of 0.67 and 0.5? It turns out that thermodynamics is a key tool to answer these questions.

3.1.1. General picture of the chemical potential of cholesterol near ${\chi }_{\mathit{\text{chol}}}^{\ast }$

Chemical potential of cholesterol (μ_chol), an important thermodynamic quantity, is a function of χ_chol. μ_chol can be interpreted as the molar free energy cost of adding one more cholesterol molecule to a lipid bilayer, thus its value reflects the interactions of cholesterol molecules with their surrounding molecules. Given the experimental data of ${\chi }_{\mathit{\text{chol}}}^{\ast }$ in Table 12.1, what is the general picture of the way in which cholesterol chemical potential changes as its mole fraction increases in a bilayer? First, the chemical potential of cholesterol in monohydrate crystal, ${\mu }_{\mathit{\text{chol}}}^{\mathit{\text{crystal}}}$, is a constant, as cholesterol monohydrate crystal is a pure substance. On the other hand, the chemical potential of cholesterol in a lipid bilayer, μ_chol, is a function of the bilayer composition. When ${\chi }_{\mathit{\text{chol}}}<{\chi }_{\mathit{\text{chol}}}^{\ast },{\mu }_{\mathit{\text{chol}}}$ must be less than ${\mu }_{\mathit{\text{chol}}}^{\mathit{\text{crystal}}}$ for the bilayer to be the only stable phase. When ${\chi }_{\mathit{\text{chol}}}\ge {\chi }_{\mathit{\text{chol}}}^{\ast }$, the lipid bilayer phase and the cholesterol monohydrate crystal phase coexist. In this 2-phase region, the chemical potential of cholesterol in the bilayer must be equal to the chemical potential of cholesterol in the monohydrate crystal, ${\mu }_{\mathit{\text{chol}}}={\mu }_{\mathit{\text{chol}}}^{\mathit{\text{crystal}}}$. Thus, as χ_chol increases to the value of ${\chi }_{\mathit{\text{chol}}}^{\ast }$, the chemical potential of cholesterol in the bilayer must increase to equal ${\mu }_{\mathit{\text{chol}}}^{\mathit{\text{crystal}}}$. Because the ${\chi }_{\mathit{\text{chol}}}^{\ast }$ for PCs with very different acyl chains are almost identical, whatever is the nature of the microscopic interaction that induces the cholesterol precipitation, it must cause the chemical potential of cholesterol in the bilayer to increase so sharply at ${\chi }_{\mathit{\text{chol}}}^{\ast }$ that other contributions can be neglected. The experimental measurement of μ_chol (see section 3.3) showed that this general picture of μ_chol is correct.

3.1.2. Multibody interactions and jumps in cholesterol chemical potential

What kind of molecular interaction between cholesterol and PC can produce a steep increase of chemical potential of cholesterol at χ_chol = 0.50 and 0.67 (or at cholesterol:PC ratio of 1:1 and 2:1)? We explored various molecular interactions using Monte Carlo simulation, and reached a very interesting conclusion. A relatively simple form of the cholesterol multibody interaction can produce a sharp increase of μ_chol either at χ_chol = 0.50, or 0.571, or 0.667 (i.e., at cholesterol:PC ratio of 1:1, or 4:3, or 2:1). Accompanying each steep increase, the lateral distribution of cholesterol in the bilayer adopts a well-defined regular distribution (RD) pattern: a hexagonal monomer pattern at χ_chol = 0.5, an aligned dimer pattern at 0.571, and a maze pattern at 0.667 (Fig. 12.4). In general, pairwise interactions cannot produce these steep increases. Thus, the data of maximum solubility of cholesterol is only consistent with the assumption that the key interaction between cholesterol and phospholipid is a multibody interaction.

Figure 12.4.

Six regular distributions of cholesterol that have been successfully simulated using MC simulation based on the umbrella model. Black circles: cholesterol. Open circles: acyl chains of PC. (A) χ_chol = 0.154; (B) χ_chol = 0.25; (C) χ_chol = 0.40; (D) The “monomer” pattern at χ_chol = 0.50; (E) The dimer pattern at χ_chol = 0.571; (F) The “maze” pattern at χ_chol = 0.667, which is the maximum solubility limit of cholesterol in PC.

For a pairwise interaction, the number of interaction pairs is counted, and the total interaction energy increases linearly with the number of interaction pairs. For example in Eq. (12.2), E_cc is the interaction energy for a cholesterol-cholesterol pair. If there are n cholesterol-cholesterol contacts, then the total energy is simply nE_cc. Thus, the total pairwise energy is the sum of the energies of each individual pair. In contrast, the multibody interaction energy is a description of the interactions of all nearest neighbors considered as a group. The multibody interaction Hamiltonian in Eq. (12.5) allows the total interaction energy to increase nonlinearly with the number of cholesterol-cholesterol contacts. For example, if a cholesterol has two cholesterol-cholesterol contacts, the interaction energy would be c₂ΔE_c instead of 2ΔE_c. Here c₂ is a chosen parameter. Thus, six parameters, c₁…c₆(c₀ is always 0) need to be specified for the cholesterol multibody interaction in a hexagonal lattice. Table 12.2 lists four sets of multibody interaction energy parameters (MIEP), which can produce jumps in ${\mu }_{\mathit{\text{chol}}}^E$ at certain cholesterol mole fractions. It is interesting to notice that a pairwise interaction is actually a special case of multibody interaction. For example, in the first parameter set, MIEP I, the energy scaling factors of cholesterol multibody interaction are assigned as (c₀, c₁, …, c₆) = (0, 1, 2, 3, 4, 5, 6) (i.e., the total energy increases linearly with the number of cholesterol-cholesterol contacts), and the multibody interaction Hamiltonian is reduced to a pairwise Hamiltonian. Thus, the term, “cholesterol multibody interaction”, precisely means the nonlinear increase of the total interaction energy with the number of cholesterol-cholesterol contacts.

Table 12.2.

Examples of cholesterol multibody interaction energy parameter set for MC simulation.

Multibody interaction energy parameter set	Energy cost for each additional cholesterol-cholesterol contact	Eq. (12.5) coefficients c0 c1 c2 c3 c4 c5 c6
MIEP I	0 1 1 1 1 1 1	0 1 2 3 4 5 6
MIEP II	0 1 8 3 3 3 3	0 1 9 12 15 18 21
MIEP III	0 1 1 10 3 3 3	0 1 2 12 15 18 21
MIEP IV	0 1 2 3 4 5 6	0 1 3 6 10 15 21

The second set, MIEP II, is constructed to create a relatively small energy cost for each pair of cholesterols that are in contact but completely surrounded by phospholipids (i.e., a dimer), with a much greater energy cost for three cholesterols in contact. The first cholesterol-cholesterol contact costs 1 unit of energy, whereas the next one costs 8 energy units, much higher than the first. Contacts that are even higher order are not so critical, so all are assigned to 3 units. Thus, c₁ = 1, c₂ = 1 + 8 = 9, c₃ = 1 + 8 + 3 =12, and so on. Fig. 12.2 shows snapshots of cholesterol and acyl chain lateral distributions simulated with MIEP II. With a low magnitude of ΔE_c (0.2 kT), as shown in Fig. 12.2D, at χ_chol = 0.57 the distribution shows no particular pattern. However, at the same composition, with ΔE_c = 0.5 kT, cholesterol molecules form a regular distribution (RD): an aligned dimer pattern, in which each cholesterol has exactly one cholesterol-cholesterol contact (Fig. 12.2B). Fig. 12.3B shows the excess chemical potential of cholesterol versus ${\chi }_{\mathit{\text{chol}}}\cdot {\mu }_{\mathit{\text{chol}}}^E$ has a sharp jump at 0.57 for ΔE_c ≥ 0.5 kT. Because ${\mu }_{\mathit{\text{chol}}}=kT\text{ln}{\chi }_{\mathit{\text{chol}}}+{\mu }_{\mathit{\text{chol}}}^E$, and the first term (i.e., the ideal mixing chemical potential) is a smooth function of χ_chol, a jump in ${\mu }_{\mathit{\text{chol}}}^E$ is equivalent to a jump in μ_chol. Understanding the mechanism of the dimer pattern formation can help one to understand how other multibody interaction sets work. The formation of the dimer pattern and abrupt increase of ${\mu }_{\mathit{\text{chol}}}^E$ at χ_chol = 0.57 are direct results of this particular choice of the multibody interaction parameters. In Table 12.2, MIEP II is deliberately formulated to make the second cholesterol-cholesterol contact cost much more energy than the first. The mixture responds to MIEP II with a distribution that minimizes the second cholesterol-cholesterol contact, as shown in Fig. 12.2B. At χ_chol = 0.57, the cholesterol:PC ratio is 4:3. The dimer pattern is the only pattern at this composition such that no cholesterol has the second cholesterol-cholesterol contact (i.e., the minimum energy distribution at this composition).

Figure 12.2.

Snapshots of phospholipid and cholesterol lateral distribution simulated using MIEP II. (A) χ_chol = 0.51 and ΔE_C = 0.5 kT; (B) χ_chol = 0.57 and ΔE_C = 0.5 kT. Cholesterols form an aligned dimer pattern; (C) χ_chol = 0.62 and ΔE_C = 0.5 kT; (D) χ_chol = 0.57 and ΔE_C = 0.2 kT. Filled circles: cholesterol. Open circles: Acyl chains of PC.

Figure 12.3.

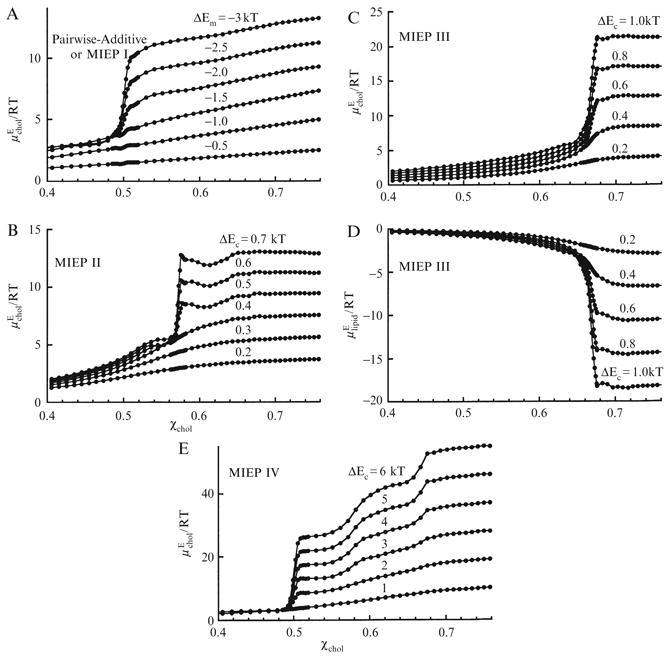
Excess chemical potential of cholesterol, ${\mu }_{\mathit{\text{chol}}}^E$, or of phospholipid, ${\mu }_{\mathit{\text{lipid}}}^E$, as a function of χ_chol. (A) ${\mu }_{\mathit{\text{chol}}}^E$, simulated using MIEP I (equivalent to pairwise); (B) ${\mu }_{\mathit{\text{chol}}}^E$, simulated using MIEP II; (C) ${\mu }_{\mathit{\text{chol}}}^E$ and (D) ${\mu }_{\mathit{\text{lipid}}}^E$, simulated using MIEP III; (E) ${\mu }_{\mathit{\text{chol}}}^E$, simulated using MIEP IV. From Huang and Feigenson (1999), with permission.

MIEP III can produce a steep increase of ${\mu }_{\mathit{\text{chol}}}^E$ and the maze regular distribution pattern at χ_chol = 0.67. As shown in Fig. 12.4F, at ΔE_c = 0.6 kT, cholesterol molecules form the maze pattern: the majority of cholesterols have two cholesterol-cholesterol contacts. MIEP III is formulated so that the first two cholesterol-cholesterol contacts only cost 1 energy unit each, but the third one costs 10 units, much higher than the first two. The mixture responds to MIEP III with another RD, which minimizes the third cholesterol-cholesterol contact, as shown in Fig. 12.4F. The excess chemical potential of the mixture components is shown in Fig. 12.3C,D. With Δ_Ec ε 0.3kT, ${\mu }_{\mathit{\text{chol}}}^E$ has a steep increase at χ_chol = 0.67. The excess chemical potential of the acyl chains is plotted in Fig. 12.3D. It shows the decrease at χ_chol = 0.67 expected from the Gibbs-Duhem equation.

Similarly, MIEP I can produce a steep increase of ${\mu }_{\mathit{\text{chol}}}^E$ at χ_chol = 0.50. Fig. 12.4D is a snapshot of lipid distribution simulated with MIEP I. When ΔE_c ≥ 4 kT (i.e., ΔE_m < −2 kT, using Eq. (12.4)), cholesterol molecules form a hexagonal monomer pattern: the majority of cholesterols have no cholesterol-cholesterol contact. In this case, the energy cost for the first cholesterol-cholesterol contact becomes so high that cholesterol is avoiding any clustering. The excess chemical potential of cholesterol is shown in Fig. 12.3A. As ΔE_m < −2 kT, ${\mu }_{\mathit{\text{chol}}}^E$ has a steep increase at χ_chol = 0.50.

MIEP I, MIEP II, or MIEP III were designed to produce a single regular distribution pattern and a cholesterol chemical potential jump at χ_chol = 0.50, 0.57, or 0.67, respectively. It is actually possible to have a MIEP set that produces all three regular distribution patterns and jumps: The basic requirement is that there must be an accelerating increase of interaction energy as a function of the number of cholesterol-cholesterol contacts (i.e., (c_i+1 − c_i) > (c_i − c_i-1). MIEP IV in Table 12.2 satisfies such a requirement. In MIEP IV, the energy cost for each additional cholesterol-cholesterol contact was chosen to be 1 unit higher than the preceding one. Thus, c_i increases nonlinearly from 0 to 21. Fig. 12.3E shows the excess chemical potential of cholesterol versus χ_chol. This curve has 3 steep increases for ΔE_c ≥ 3 kT: a steep jump at χ_chol = 0.5, and more gradual rises at 0.57 and 0.67. The steepness of each increase can be adjusted by fine-tuning MIEP parameters.

Fig. 12.5 shows a plot of ΔG^E and ΔH^E, together with −TΔS^E for ΔE_c = 0.6 kT, simulated with MIEP II. ΔG^E and ΔH^E are both at global minima at χ_chol = 0.57. On the other hand, −TΔS^E has a peak at χ_chol = 0.57. This indicates that by forming the aligned dimer pattern at χ_chol = 0.57, as in Fig. 12.2B, the excess entropy ΔS^E is drastically reduced. The entropy part of the Gibbs free energy −TΔ^SE actually increases to a peak at χ_chol = 0.57. In general, whenever a regular distribution is formed, the excess entropy, ΔS^E, reaches a minimum, and therefore −TΔ^SE is always at a peak. In contrast, ΔH^E is always at a local (sometimes global) minimum. On the other hand, ΔG_E is not always at a minimum, but usually has a sudden change of slope at a regular distribution composition.

Figure 12.5.

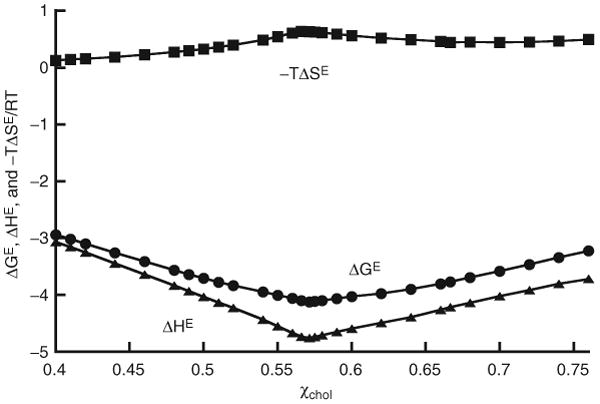
ΔG^E and ΔH^E, and −TΔS^E as functions of cholesterol mole fraction, for ΔE_C = 0.6 kT, simulated with MIEP II. From Huang and Feigenson (1999), with permission.

3.1.3. Physical origin of the cholesterol multibody interaction: The umbrella model

The key characteristic of the multibody interaction is that the energy cost for some higher-order cholesterol-cholesterol contacts must become higher than that for lower-order contacts, which produces steep increases in cholesterol chemical potential at χ_chol = 0.50 and 0.67. The umbrella model was proposed to explain the physical origin of the multibody interactions (Huang and Feigenson, 1999).

Cholesterol has a large nonpolar steroid ring body and a relatively small polar hydroxyl headgroup. In water, cholesterol forms monohydrate crystals instead of bilayers, because the small hydroxyl group is unable to protect its large nonpolar body from water. When cholesterols are incorporated into a phospholipid bilayer, neighboring phospholipid headgroups provide cover to shield the nonpolar part of cholesterol from exposure to water to avoid the unfavorable free energy. Cholesterol hydroxyl groups also interact at the aqueous interface to provide partial coverage, but these hydroxyls cannot completely cover the nonpolar part of cholesterol without help from phospholipid headgroups. This is illustrated schematically in Fig. 12.6A. Phospholipid headgroups act like umbrellas. The space under the headgroups is shared by acyl chains and cholesterols.

Figure 12.6.

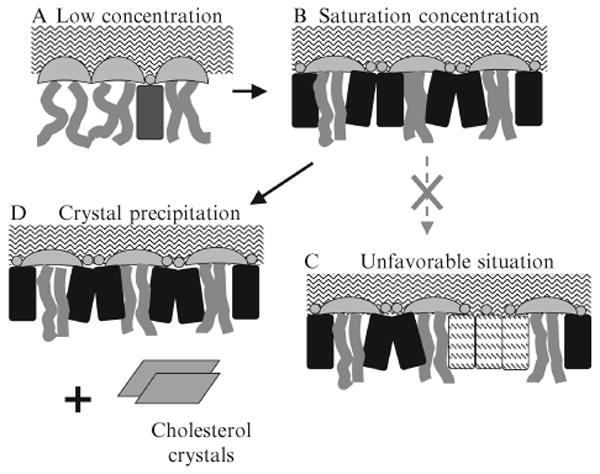
The umbrella model and the physical interpretation of cholesterol maximum solubility limit. (A) At low cholesterol concentration, headgroups of neighboring PCs easily cover the hydrophobic bodies of cholesterol. Motion of acyl chains next to cholesterol is restricted by the rigid body of cholesterol. (B) At the saturation concentration, headgroups of PCs work together to cover the maximum amount of cholesterol. The acyl chains of PCs become highly ordered. (C) If more cholesterol were added and stays in the bilayer, patches of pure cholesterol would form, and some cholesterol would be exposed to water, which is highly unfavorable. (D) To avoid forming cholesterol patches, excess cholesterol precipitate and form cholesterol crystals, and the lipid bilayer retains the maximum amount of cholesterol that can be covered.

As the cholesterol content in a bilayer increases, phospholipids laterally redistribute and their polar headgroups reorient to provide more coverage per headgroup for the increasing fraction of cholesterol molecules, as drawn in Fig. 12.6B. The headgroup umbrellas are stretched to provide more coverage area. Under the umbrella, acyl chains and cholesterol molecules become tightly packed. No cholesterol is exposed to water at this point. Obviously, it would be much easier for neighboring phospholipids to cover a cholesterol monomer than to cover a cholesterol cluster, and the free energy cost of the coverage must increase rapidly with the size of the cholesterol cluster. This is likely to be the physical origin of the large increase of multibody interaction energy for some higher-order cholesterol-cholesterol contacts. As cholesterol concentration increases, fewer and fewer lateral distributions of lipid can satisfy the coverage requirement. This forces cholesterol to form regular distributions (e.g., hexagonal or maze patterns) in the bilayer. As illustrated in Fig. 12.6C, if the phospholipid headgroups are stretched to their limits, they can no longer provide shielding for additional cholesterols. Exposure of cholesterol to water is very unfavorable. This may well be the big increase in energy cost for acquiring an additional cholesterol-cholesterol contact needed to produce the regular distribution of cholesterol and the steep jump of μ_chol at critical mole fractions. To lower the overall free energy, instead of allowing the hydrophobic regions of bilayers to be exposed to water, excess cholesterol molecules precipitate, forming cholesterol monohydrate crystals, as shown in Fig. 12.6D. Therefore, in the umbrella model, ${\chi }_{\mathit{\text{chol}}}^{\ast }$ has a clear physical meaning: ${\chi }_{\mathit{\text{chol}}}^{\ast }$ is a cholesterol mole fraction at which the capability of phospholipid headgroups to cover cholesterol molecules from water has reached its maximum. Any additional cholesterol in the bilayer would be exposed to water.

The difference in ${\chi }_{\mathit{\text{chol}}}^{\ast }$ values of PE and PC may originate from the size of their headgroups. Here, we mean the effective size of the headgroup, including bound water. The smaller headgroup of PE would be less effective than that of PC in providing shielding, so PE/cholesterol mixtures would have a high energy cost even for covering a cholesterol dimer cluster. This is equivalent to a relatively high energy cost for the first cholesterol-cholesterol contact in our simulation, which results in μ_chol rising sharply at 0.50, and thus ${\chi }_{\mathit{\text{chol}}}^{\ast }$ = 0.50. At its maximum solubility limit in a PE bilayer, cholesterol forms the hexagonal lateral distribution pattern, in which all cholesterols stay as monomers. In contrast, the larger headgroup of PC might well accommodate the first two cholesterol-cholesterol contacts, but be overwhelmed by the third one. The energy cost profile could then be modeled by MIEP III (i.e., very high energy cost for the third cholesterol-cholesterol contact). This would result in ${\chi }_{\mathit{\text{chol}}}^{\ast }$ = 0.67;. At its maximum solubility limit in a PC bilayer, cholesterol forms the maze lateral distribution pattern. So if the size of the phospholipid headgroup is the dominating factor, then the lack of acyl chain dependence of ${\chi }_{\mathit{\text{chol}}}^{\ast }$ for PCs is explained. Thus, the cholesterol multibody interaction described here is the parameterization of the free energy cost for the bilayer to cover a cholesterol cluster, and this cost indeed should increase nonlinearly with the size of cholesterol cluster.

3.1.4. The intrinsic connection between a regular distribution and a jump in chemical potential

Is there an intrinsic connection between a regular distribution and a jump in chemical potential in general? The answer is yes. This intrinsic connection is best explained by Ben Widom's (1963) test particle insertion method. As pointed out by Widom, the excess chemical potential of a particle can be estimated by an ensemble average

$${\mu }^E=-kT\mathrm{\text{ln}}\langle \mathrm{\text{exp}}\left(-V_{\mathit{\text{test}}}/kT\right)\rangle ,$$ (12.11)

where V_test is the potential energy change that would result from the addition of a ghost particle to the system. We will use the regular distribution at χ_c = 0.57 (Fig. 12.2B) as an example. This regular distribution is characterized by each cholesterol having exactly one cholesterol as its nearest neighbor. Because MIEP II is deliberately formulated to make the second contact cost much more energy than the first, to lower the energy of the whole system, cholesterol molecules avoid two or more cholesterol-cholesterol contacts. At χ_chol less than 0.57, for example, at χ_c = 0.51 (Fig. 12.2A), the concentration of cholesterol is relatively low and there are many sites into which a ghost cholesterol can be inserted without creating multiple cholesterol-cholesterol contacts. These low-energy insertions make the majority contribution to the ensemble average in Eq. (12.11). Therefore the cholesterol chemical potential would be low. However, at χ_c = 0.57 or greater (Fig. 12.2B or 12.2C), any insertion of a ghost cholesterol into the distribution would create multiple cholesterol-cholesterol contacts. Thus, the energy cost of insertion must suddenly becomes higher, and the chemical potential evaluated by Eq. (12.11) must have a jump at χ_c = 0.57. The magnitude of the jump is largely determined by the energy difference between the first and the second cholesterol-cholesterol contacts (i.e. (c₂ − c₁)E_c).

To take the preceding argument a step further, a general statement can be made that any stable regular distribution must result in a jump in chemical potential, without regard to the details of the distribution and molecular interactions. We can justify the above statement by the following arguments: Comparing a highly ordered RD with other disordered distributions at the same composition, the difference in free energy, ΔG = G(RD) − G(other) = ΔH − TΔS, must be negative, for the given molecular interactions. The entropy of the RD state must be lower. Thus, −TΔS must be positive, as demonstrated in Fig. 12.5. Thus, ΔH must be negative (i.e., the energy of a regular distribution must be lower than any other disordered distributions). At a cholesterol mole fraction slightly below the RD composition, there will be some areas not covered by RD pattern. Thus, the energy cost of insertion of a cholesterol in these areas will be low. Again, these low-energy insertions make the majority contribution to the ensemble average in Eq. (12.11). However, at a RD composition, the entire membrane is in regular distribution. Adding a cholesterol to a regular distribution must bring a higher energy cost now, as it creates a more disordered state, which would result in a jump in chemical potential.

3.2. The competition between cholesterol and ceramide in POPC bilayers

More insight into the physical packing of lipid bilayers at the cholesterol solubility limit was provided by the effect of ceramide on the value of ${\chi }_{\mathit{\text{chol}}}^{\ast }$ in a lipid bilayer (Ali et al., 2006). Although the molecular structure of ceramide is quite different from that of cholesterol, both molecules have a small polar headgroup and a large nonpolar body. Like cholesterol, ceramide cannot form a bilayer by itself and is present as crystals in water. Also like cholesterol, a substantial amount of ceramide can be incorporated into a phospholipid bilayer. Using optical microscopy, the maximum solubility of brain ceramide in a POPC bilayer was determined to be 0.68 ± 0.02 (Ali et al., 2006). This number by itself is very interesting, because it is similar to the maximum solubility of cholesterol in POPC bilayers. On the basis of the umbrella model, it is likely that ceramide in a lipid bilayer also seeks the coverage of the neighboring PC headgroups to shield its large nonpolar body from water exposure, like cholesterol does. If there is a competition between cholesterol and ceramide for the coverage of neighboring PC headgroups, the more ceramide is present in a PC bilayer, the less the bilayers can accommodate cholesterol. Thus, one expects a consistent decline of the value of ${\chi }_{\mathit{\text{chol}}}^{\ast }$ in response to an increasing ceramide content in the lipid bilayer. Using the COD activity assay, the maximum solubility of cholesterol in POPC bilayers with various amounts of brain ceramides has been investigated. Fig. 12.7 shows the maximum solubility of cholesterol in ternary mixtures of POPC/cholesterol/ceramide as a function of the molar ratio R, defined as ceramide/(ceramide + POPC). As shown in Fig. 12.7, at R = 0, there is no ceramide, and the mixtures are actually POPC/cholesterol binary mixtures, and the ${\chi }_{\mathit{\text{chol}}}^{\ast }$ value is 0.67. As the ratio R increases (i.e. more ceramide is present in the lipid bilayers), the maximum solubility of cholesterol continuously decreases, and eventually reaches zero at R = 0.68 (i.e., at the maximum solubility of ceramide in POPC bilayer). It is more revealing to plot the ratio (chol+cer)/(chol+cer+POPC) at the cholesterol solubility limit, which is given by $R(1-{\chi }_{\mathit{\text{chol}}}^{\ast })+{\chi }_{\mathit{\text{chol}}}^{\ast }$, as a function of R. As shown in Fig. 12.7, this ratio essentially stays constant at 0.67. Therefore, at the cholesterol solubility limit, the ratio (chol+cer):POPC is simply 2:1, regardless of the amount of ceramide in the mixtures.

Figure 12.7.

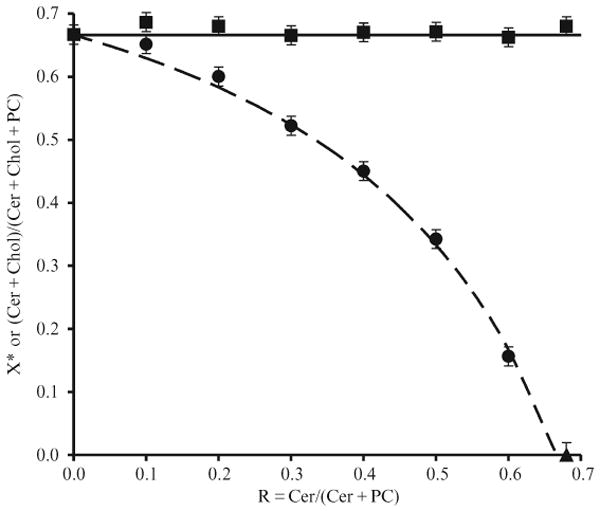
The maximum solubility of cholesterol, ${\chi }_{\mathit{\text{chol}}}^{\ast }$, or the ratio (ceramide+choleserol)/(ceramide+cholesterol+PC) as a function of ceramide/(ceramide+POPC) ratio. Circles: ${\chi }_{\mathit{\text{chol}}}^{\ast }$, measured by COD activity assay. Triangle: The maximum solubility of ceramide in POPC bilayers determined by optical microscopy measurement. The dashed line is the theoretical ${\chi }_{\mathit{\text{chol}}}^{\ast }$ curve with the assumption that one ceramide molecule displaces one cholesterol from the bilayer phase into the cholesterol crystal phase. Squares: the ratio (ceramide+choleserol)/(ceramide+cholesterol+PC) at the cholesterol solubility limits.

The results showed that cholesterol is displaced by ceramide from the bilayer phase into the crystal phase at its solubility limit. Most significantly, the data also demonstrated that each ceramide molecule displaces exactly one cholesterol molecule from the bilayer phase. This 1-to-1 displacement relationship keeps the ratio of (chol+cer):POPC at the constant 2:1. According to the umbrella model, at the solubility limit, the coverage capability of PCs has been stretched to the limit and lipids form a highly ordered maze pattern lateral distribution in the bilayer, so covering one additional ceramide is at the cost of covering one fewer cholesterol. A POPC bilayer could accommodate either up to 67 mol % cholesterol, 67 mol % ceramide, or a combined 67 mol % cholesterol and ceramide. The 1-to-1 displacement validates the umbrella model's physical interpretation of ${\chi }_{\mathit{\text{chol}}}^{\ast }$.

The data also suggested that ceramide has a much higher affinity for the ordered bilayer phase than does cholesterol, and cholesterol cannot displace brain ceramide from the lipid bilayer phase. One possible reason is that the long saturated chains of ceramide allow a tight packing of the acyl chains of PC around ceramide, which is more difficult with the sterol rings of cholesterol. Megha and London (2004) have shown that the tight lipid packing is important for the displacement of cholesterol. Another possible contribution to ceramide's high affinity is the fact that ceramide has a higher headgroup/body ratio than cholesterol (Ali et al., 2006). It should be easier for the neighboring PCs to cover ceramide than cholesterol, or equivalently, the free energy cost for covering ceramide should be lower than that for covering cholesterol.

3.3. Measurement and simulation of the chemical potential of cholesterol in PC bilayers

The focus of the preceding sections is the thermodynamics of cholesterol-phospholipid interaction at the cholesterol solubility limit. In this section, cholesterol-phospholipid interaction over the entire range of χ_chol will be discussed. Despite significant technical advances in lipid membrane research in recent years, the detailed nature of cholesterol-lipid interactions is still a subject of ongoing debate. Existing conceptual models, including the condensed complex model, the superlattice model, and the umbrella model, identify different molecular mechanisms as the key to cholesterol–lipid interactions in biomembranes. Here, an important thermodynamic parameter, i.e., the chemical potential of cholesterol over a wide range of cholesterol mole fraction, will be analyzed and its implication to cholesterol-lipid interaction will be discussed.

3.3.1. Current conceptual models of cholesterol-lipid interactions

(i) The condensed complex model

The model was initially proposed based on a study of lipid monolayers at the air–water interface (Radhakrishnan and McConnell, 1999). The model hypothesizes the existence of low free-energy stoichiometric cholesterol–lipid chemical complexes that occupy smaller molecular lateral areas (Radhakrishnan et al., 2000; Radhakrishnan and McConnell, 1999). At a stoichiometric composition, such as at cholesterol:lipid = 1:1 or 1:2, a sharp jump in cholesterol chemical potential has been predicted from a mean-field calculation as shown in Fig. 12.8A. Because the proposed condensed complex has a compact low-energy structure, the model explicitly predicted that cholesterol is more likely to form condensed complexes with lipids with which it can mix favorably, such as phosphatidylcholine (PC) with long saturated chains, or sphingomyelins. It has also been suggested that cholesterol superlattices as well as lipid rafts are examples of the proposed condensed complexes (Radhakrishnan et al., 2000; Radhakrishnan and McConnell, 2005). In this model, the strong tendency to form cholesterol–lipid condensed complexes represents an essential feature of cholesterol–lipid interactions.

Figure 12.8.

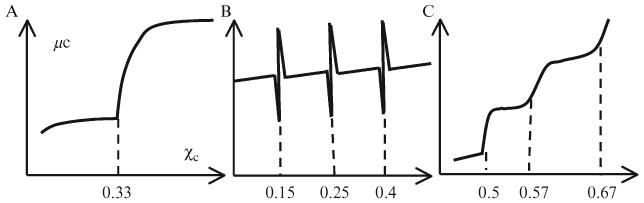
Schematic of the chemical potential of cholesterol as a function of χ_chol predicted by various models. (A) The condensed complex model predicted a jump in μ_chol at a stoichiometric composition. (B) The superlattice model predicted dips in free energy at superlattice compositions, which also implied sharp spikes in μ_chol. (C) The umbrella model predicted a cascade of jump in μ_chol, and each jump corresponds to a stable cholesterol regular distribution.

(ii) The superlattice model

This model suggests that the difference in the cross-sectional area between cholesterol and other lipid molecules can result in a long-range repulsive force among cholesterols and thereby produce superlattice distributions (Chong, 1994; Somerharju et al., 1985). Many superlattice patterns, either hexagonal or centered rectangular, have been predicted from a set of algebraic equations based on a geometric-symmetry argument. At the cholesterol mole fractions where superlattices occur, dips in free energy have also been suggested (Somerharju et al., 1999). Because μ_chol can be calculated by taking the derivative of the free-energy profile (Huang and Feigenson, 1999), this prediction also implies that μ_chol should have sharp spikes at those predicted mole fractions (Fig. 12.8B). The superlattice model emphasizes that the long-range repulsive force among cholesterols plays the dominant role in cholesterol–lipid interactions.

(iii) The umbrella model

As described in the previous section, the umbrella model suggests that the mismatch between the small cholesterol polar headgroup with its large nonpolar body determines its preferential association with large-headgroup lipids, such as PCs or sphingomyelins. Because it costs much more free energy to cover a cholesterol cluster than a single cholesterol, cholesterol molecules have a strong tendency not to cluster or at least not to form large clusters. In the high-cholesterol region (χ_chol > 0.45), to reduce the free-energy cost, cholesterol in a bilayer distributes in a manner so as to minimize cholesterol cluster size. This mechanism can be formulated as a cholesterol multibody interaction. Monte Carlo simulations based on this interaction showed that cholesterol can form a hexagonal monomer pattern at μ_chol = 0.50, or a dimer pattern at 0.571, or a maze pattern at 0.667 (Fig. 12.4). In addition, any stable regular distribution is always accompanied by a jump in μ_chol. In addition, with the assumption that there is an accelerating increase of the coverage cost with the size of cholesterol clusters, a cascade of jumps in μ_chol is possible (Fig. 12.8C). In the low-cholesterol region (χ_chol < 0.45), three more regular distributions (superlattices) have been successfully simulated. They occur at cholesterol mole fraction of 0.154, 0.25, and 0.4, corresponding to cholesterol:phospholipid ratio of 2:11, 1:3, and 2:3, respectively. Conclusively, the study showed that any pairwise repulsive forces between cholesterol cannot produce these regular distributions. Two requirements are needed to generate these cholesterol superlattices: (i) a large interaction against any cholesterol clustering; and (ii) a smaller unfavorable acyl chain multibody interaction, which increases nonlinearly with the number of chain-cholesterol contacts and tends to minimize the acyl chain contact with cholesterol (Huang, 2002). A delicate balance must be maintained among the magnitudes of the two interactions and the combined effect of both interactions must still favor the cholesterol-phospholipid mixing. The first interaction likely originates from the requirement for PC to cover cholesterol, and the second unfavorable interaction is likely from the sharp decrease of acyl chain conformation entropy due to chain-cholesterol contact. Although mixing cholesterol with phospholipids must have an overall favorable free energy, from the point of view of acyl chains, cholesterol molecules are aggressive invaders. Cholesterol molecules have to partially hide under the headgroups of phospholipids, and occupy the lateral spaces that would otherwise be available to acyl chains. The rigid, bulky sterol rings of cholesterol can significantly reduce the number of possible conformations of neighboring acyl chains, which is evidenced by increasing chain order parameter when cholesterol is added to a bilayer (Vist and Davis, 1990). Similar to the regular distributions in the high cholesterol region, each formation of regular distributions in the low-cholesterol region is also accompanied by a jump in chemical potential of cholesterol (unpublished data). This finding is consistent with our earlier argument that any stable regular distribution must result in a jump in chemical potential, based on the Widom's test particle insertion interpretation of chemical potential. Thus, experimentally, a jump in μ_chol can be considered as a thermodynamic indicator for a regular distribution.

Interestingly, there are some common features in all three models: (i) The overall interaction between cholesterol and phospholipid is attractive, or equivalently, the interaction between cholesterols is repulsive; (ii) There could be some special lateral distributions of molecules (i.e., SL or RD or condensed complex) at some well-defined bilayer compositions, at which the ratio cholesterol:phospholipid = m:n; here, m and n are both integers. Therefore, there is some confusion about the validity of each model as well as the differences between models. However, different models have different predictions for the chemical potential profile. Therefore, an experimental measurement of μ_chol can provide a strong test of the models.

3.3.2. Chemical potential of cholesterol in DOPC, POPC, and DPPC bilayers explored by COD activity assay

The COD activity assay has been used to measure the chemical potential profile of cholesterol (Ali et al., 2007). It has been shown that a COD enzyme first physically associates with lipid bilayers without perturbing the membrane structure (Ahn and Sampson, 2004). The enzyme then goes through conformation changes and provides a hydrophobic binding cavity that allows a favorable partitioning of the cholesterol from the membrane into the COD cavity. The cavity can be viewed as a standard state, and the rate of cholesterol partition into the cavity depends on its chemical activity in the bilayer. The initial-reaction rate of the oxidation should depend on COD concentration, cholesterol concentration (i.e., substrate concentration), the binding affinity of COD for lipid vesicles, and the cholesterol chemical activity in a lipid bilayer. Because the COD concentration and cholesterol content in our samples were kept constant, they should not contribute to the change of the initial rate. Ahn and Sampson (2004) have shown that the binding affinity of COD for vesicles is only a weak function of χ_chol. Thus, the changing of the initial rate essentially reflects the behavior of the chemical activity of cholesterol, which relates to the chemical potential of cholesterol μ_chol in lipid bilayers by exp(μ_chol/kT). μ_chol is directly related to the cholesterol interaction with surrounding lipids and the lateral organization within the bilayer.

Fig. 12.9 shows the COD initial reaction rate as a function of cholesterol mole fraction in the high-cholesterol region (χ_chol > 0.45) (Ali et al., 2007). The initial rate has a global peak around χ_chol = 0.67 in all three PC bilayers, indicating the maximum solubility of cholesterol in these bilayers. The values are in good agreement with the previous measurements by X-ray diffraction, light scattering, and fluorescence spectroscopy (Huang et al., 1999; Parker et al., 2004). As χ_chol approaches the maximum solubility limit, μ_chol in lipid bilayers increases sharply until it equals μ_chol in cholesterol monohydrate crystals and results in a sharp increase of the COD initial reaction rate. At greater than the maximum solubility limit, the bilayer phase and the cholesterol crystal phase coexist, and μ_chol should remain constant. However, once the crystal phase appears, the COD initial reaction rate no longer follows the behavior of μ_chol, and displays a sharp decline as discussed earlier. An obvious feature in Fig. 12.9 is that the COD initial rate is highest in DOPC bilayers and lowest in DPPC bilayers at the same χ_chol. Because the initial rate largely reflects μ_chol, it indicates that μ_chol is lowest in a PC bilayer with all saturated chains (DPPC), higher in a PC bilayer with mixed chains (POPC), and highest in a PC bilayer with all unsaturated chains (DOPC). A higher μ_chol reflects a stronger tendency for cholesterol to escape from the bilayer. This result indicates that cholesterol interacts more favorably with saturated chains than unsaturated chains.

Figure 12.9.

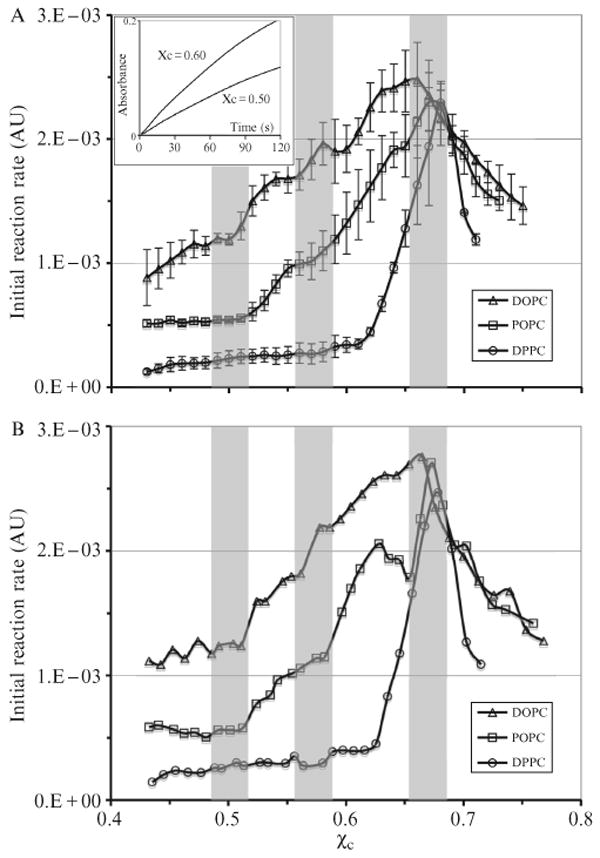
COD initial reaction rate as a function of cholesterol mole fraction in the high-cholesterol region. The shaded bars indicate the locations of expected jumps at 0.50 and 0.571 and the cholesterol maximum solubility limit at 0.667 predicted from the MC simulations based on the umbrella model. The width of the bars reflects the experimental uncertainty in χ_chol in our samples (±0.015) (A) Average curves, each obtained from three independent sample sets. (B) Individual curves. The jumps at 0.5 and 0.57 appear sharper. Inset: COD reaction progress curves of DOPC/cholesterol mixtures. The reaction rate is higher at χ_chol = 0.60 than that at 0.50. From Ali et al. (2007), with permission.

Fig. 12.9A shows the average curves of COD initial rates in DOPC, POPC, and DPPC bilayers, each obtained from three independent sample sets. The COD initial rate shows several interesting jumps. In POPC bilayers, the initial rate has clear jumps at χ_chol = 0.52 and 0.58. In DOPC bilayers, the initial rate shows jumps at χ_chol = 0.51, 0.57, and 0.62. In contrast, the initial rate in DPPC bilayers only has a large jump at χ_chol 0.63 and a tiny jump at 0.58. It should be pointed out that these jumps are usually steeper in individual sample sets, as shown in Fig. 12.9B. Because of the experimental uncertainty in cholesterol mole fraction in our samples (±0.015), the sharpness of the jumps in the average curves (Fig. 12.9A) is smoothed out considerably. The vertical shaded bars in Fig. 12.9 indicate the positions of expected chemical potential jumps at χ_chol = 0.50 and 0.571 and cholesterol maximum solubility limit at 0.667 predicted from the MC simulations based on the umbrella model. The width of the bars represents the experimental uncertainty in χ_chol in our samples (±0.015). Therefore, the locations of jumps agree favorably with the predicted values within the standard deviations of the data.

According to the MC simulations, the molecular driving force for the regular distribution at χ_chol = 0.50 is that the free energy cost of covering a cholesterol dimer is significantly higher than that of covering a cholesterol monomer (Huang and Feigenson, 1999). If the difference is sufficiently large, cholesterol would stay as monomer as long as the composition allows. This can result in a monomer regular distribution pattern at 0.50 (Fig. 12.4D). The height of the jump in μ_chol is related to that energy difference. Because an unsaturated chain containing a cis double bond is bulkier or less compressible than a saturated chain, DPPC with both saturated chains should have the largest headgroup/body ratio (or excess headgroup capacity to cover neighboring cholesterol clusters) among the three PCs. Therefore it is reasonable to assume that DPPC can cover a cholesterol dimer more easily (i.e., at a lower free-energy cost) than POPC or DOPC does. Thus, the driving force to form regular distribution at χ_chol = 0.50 is weakest in DPPC, but strongest in DOPC. This is indeed the case, as shown in Fig. 12.9. No jump is seen at χ_chol = 0.50 in DPPC bilayers, and the jump was larger in DOPC than in POPC (Fig. 12.9B). Similarly, the driving force to form the dimer regular distribution pattern at χ_chol = 0.571 (Fig. 12.4E) is that the free-energy cost of covering a larger cholesterol cluster is much higher than that of covering a cholesterol dimer. As shown in Fig. 12.9, a small jump was observed at = 0.58 in DPPC, and bigger jumps were present in POPC and DOPC bilayers. The data show that all three PC are capable of covering cholesterol clusters up to the solubility limit (≈0.67), but the free-energy cost of the coverage in DOPC increases much more rapidly with the number of cholesterol-cholesterol contacts than for the other PCs because of the chain unsaturation. The measured chemical potential profile in DOPC is similar to that simulated with MIEP IV in Fig. 12.3E. On the other hand, the measured chemical potential profile in DPPC is more similar to that simulated with MIEP III in Fig. 12.3C, indicating the free-energy cost of covering cholesterol monomer or dimers are low in DPPC bilayers, due to its large headgroup/body ratio.

It is interesting that the COD initial rate in DPPC bilayers jumps at χ_chol = 0.63. In several measurements with DPPC and DOPC, jumps around 0.63 have also been observed. Previously, small dips in fluorescence energy transfer efficiency and DPH-PC fluorescence anisotropy have been found at 0.63 in DOPC bilayers (Parker et al., 2004). Whether this previously unassigned critical composition of 0.63 represents a regular distribution made of a trimer or tetramer pattern remains elusive. More study is needed to verify this interesting possibility.

Fig. 12.10 shows the COD initial reaction rate in the low-cholesterol region (χ_chol < 0.45) (Ali et al., 2007). To resolve small jumps at very low cholesterol concentrations, three times more COD (0.3 unit per sample) was used for the low-cholesterol samples. Similar to the high-cholesterol region, the dominant feature of the figure is that the initial rate is highest in DOPC bilayers and lowest in DPPC bilayers. The differences in rate are quite spectacular. For example, at χ_chol = 0.35, the rates in POPC and DOPC bilayers are about 11 and 44 times higher than that in DPPC bilayers, respectively. The data indicate that cholesterol interaction with unsaturated acyl chains is very unfavorable compared with saturated chains in this region. Although the COD initial rate generally increases with χ_chol in all three PC bilayers, the rate behaves quite differently in different bilayers. Clear jumps can be seen at χ_chol = 0.25 and 0.40 in DOPC and POPC bilayers, whereas the rate in DPPC bilayers is featureless and flat. A close look at low χ_chol showed that the rate also has a small but distinct jump at χ_chol = 0.15 in DOPC but not in others (Fig. 12.10, inset).

Figure 12.10.

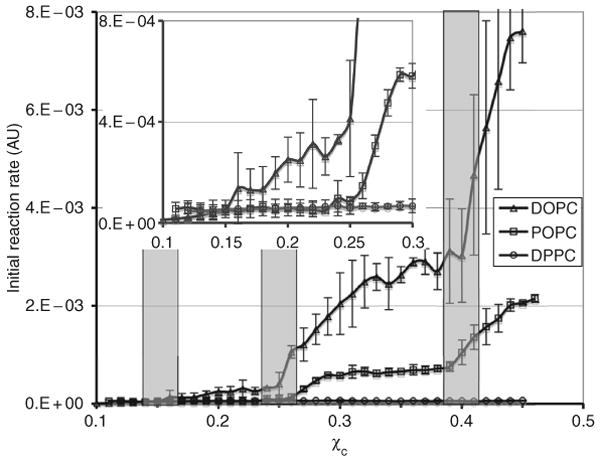
COD initial reaction rate as a function of χ_chol in the low-cholesterol region. The shaded bars indicate the locations of expected jumps at 0.154, 0.25, and 0.40 predicted from the MC simulations. The width of the bars reflects the experimental uncertainty in χ_chol. From Ali et al. (2007), with permission.

In the low-cholesterol region, according to MC simulation, two opposing types of interactions are required to produce a regular distribution: A large unfavorable interaction for any cholesterol clustering, and a smaller unfavorable acyl chain multibody interaction, which increases nonlinearly with the number of chain-cholesterol contacts. To satisfy the first requirement, the headgroup/body ratio of a PC must be in some optimal range to create a strong tendency for cholesterol to avoid clustering in that particular bilayer. This strong tendency can be experimentally verified by examining whether cholesterol forms the monomer (i.e., hexagonal) regular distribution at χ_chol = 0.50. Thus, forming a stable regular distribution at χ_chol = 0.50 would meet the first necessary condition for forming regular distributions in the low cholesterol region, because it indicates that cholesterol tries to avoid forming dimer clusters in the bilayer due to the high free energy cost of covering a cholesterol dimer cluster. The second necessary interaction is likely from the reduction of acyl chain conformation entropy due to cholesterol contact. Because cholesterol does not form stable regular distributions at χ_chol = 0.50 in DPPC bilayers, the first necessary condition is not met. This explains why there is no stable regular distribution in the low-cholesterol region in DPPC. On the other hand, cholesterol does form regular distributions at χ_chol = 0.50 in POPC and DOPC bilayers. COD initial reaction rate curves show that cholesterol forms regular distributions at 0.25 and 0.4 in both bilayers. The data clearly demonstrate the direct correlation between the regular distribution at χ_chol = 0.50 and the regular distributions in the low-cholesterol region (0.40, 0.25, and 0.154).

Composition dependence of the chemical activity of cholesterol can provide valuable information about cholesterol-lipid interaction. As shown previously, it can be used to compare relative affinity of cholesterol for various bilayers, and to detect possible superlattices or condensed complexes. In addition, μ_chol increases with χ_chol in all three PC bilayers, which indicates that mixing of cholesterol with PC is favorable, and the overall interaction between cholesterol and PC is attractive, not repulsive.

3.3.3. Comparison of models of cholesterol-lipid interaction

The condensed complex model

In Figs. 12.9 and 12.10, the COD initial reaction rate shows a series of jumps in POPC and DOPC bilayers. Could the corresponding cholesterol regular distributions (i.e., superlattices) at these compositions be the condensed complexes, as suggested previously (Radhakrishnan et al., 2000; Radhakrishnan and McConnell, 2005)? A careful analysis of data will show that regular distributions cannot be condensed complexes: (1) Cholesterol regular distributions are neither condensed nor low-free-energy aggregates. In Figs. 12.9 and 12.10, there is no jump in the initial rate in DPPC bilayers for χ_chol < 0.57, but four jumps appear in DOPC bilayers in the same region. Obviously, the tendency to form cholesterol regular distributions is much stronger in DOPC bilayers, which are bilayers with which cholesterol has a less favorable interaction, indicated by the high chemical potential. The condensed complexes are supposed to be low free-energy aggregates of cholesterol and lipids, which occupy a smaller membrane lateral area. According to the condensed complex model (Radhakrishnan and McConnell, 2005), the condensed complexes should be formed in a PC bilayer with which cholesterol can mix very favorably, such as with DPPC or sphingomyelins, but not with DOPC or POPC. The data obtained directly contradict the model. It is well known that PC with unsaturated chains occupies more lateral area. Therefore, the regular distributions in DOPC or POPC bilayers are not structurally condensed. In addition, the μ_chol is higher in DOPC or POPC than that in DPPC. Thus, the observed regular distributions in DOPC and POPC actually have higher free energies than the cholesterol/DPPC mixtures with the same lipid compositions. (2) Regular distributions lack lipid specificity. The same regular distribution can exist in DOPC, POPC, and other bilayers. In fact, not only are the phospholipids in regular distributions exchangeable, even cholesterol can be partially or completely replaced by ceramide in the regular distributions occurring at the cholesterol solubility limit. The lack of molecular specificity is inconsistent with the idea of a stoichiometric chemical complex. (3) Cholesterol is a relatively simple molecule. It is conceptually difficult to justify that cholesterol can form six different low free-energy stoichiometric complexes with one type of lipid (e.g., DOPC), and also μ_chol in these complexes monotonically increases with χ_chol.

The superlattice model

The superlattice model correctly describes a general picture of cholesterol and PC mixing: Cholesterols tends to keep a distance from each other in a PC bilayer. The model suggests that superlattices are resulted from the physical shape of lipid molecules, not from specific chemical complexes, which is consistent with experiment data. The model also predicts many highly symmetrical regular distribution patterns (superlattices) at some well-defined lipid compositions, and a number of those distributions have been verified experimentally through various techniques (Chong and Olsher, 2004; Somerharju et al., 1999). However, the model does have a few deficiencies: (1) It incorrectly requires a long-range repulsive force among cholesterols to produce superlattices. While this mechanism does favor the mixing of cholesterol with phospholipids, it is not necessarily able to produce a regular distribution. MC simulations have demonstrated that multibody interactions are required for superlattice formation; (2) the superlattice model predicts superlattices based on geometric symmetry, not based on a quantitative free-energy calculation. The model does correctly predict the superlattices at χ_chol = 0.154, 0.25, 0.4, and 0.50, but it fails to predict the regular distribution at χ_chol = 0.571 (dimer pattern) and 0.667 (maze pattern) because these two patterns are neither hexagonal nor centered rectangular. In addition, it predicts many other superlattices that are unlikely to exist, particularly at low-cholesterol mole fractions; (3) it has been hypothesized that a superlattice distribution produces a dip in free energy. The corresponding chemical potential profile (Fig. 12.8B) has been proved incorrect. In fact, free energy has a sudden change of slope at each regular distribution composition, not necessary a local minimum, as shown in Huang and Feigenson (1999). However, this free-energy minimum prediction was not a fundamental assumption of the model, which is largely a geometrical model without any explicit assumptions of specific molecular interactions among the lipid molecules.

The umbrella model

The umbrella model and the consequent MC simulations have proved quite successful in predicting and explaining cholesterol's mixing behavior with PCs: (1) the measured chemical potential profiles have excellent agreement with the calculated profiles from the MC simulation based on the model. This shows that the umbrella model captures the key cholesterol-lipid interaction. (2) The jumps in μ_chol at χ_chol = 0.154, 0.25, 0.40, 0.50, 0.571, and 0.667 predicted from MC simulation based on the umbrella model have all been observed experimentally, which indicates that stable regular distributions can exist at these compositions. (3) The umbrella model naturally explains the detailed molecular interactions required for each regular distribution. The experimental result strongly supports the explanation of the driving forces for regular distributions. It shows that both the headgroup/body ratio of PC and the acyl-chain conformational entropy play the key roles in cholesterol superlattice formation. (4) Unlike the condensed complex model, which assumes specific chemical complex formation between cholesterol and other lipids, the umbrella model suggests that the key cholesterol-lipid interaction is a hydrophobic interaction, which arises from the shape of a cholesterol molecule: a small polar headgroup and a large nonpolar body. The model can be generalized and applied to the interactions between other small headgroup molecules (e.g., diacylglycerol or ceramide) and large headgroup lipids (e.g., PC or sphingomyelins). In addition, the umbrella model also provided a possible driving force for the formation of lipid rafts (Parker et al., 2004).

3.3.4. Quantitative indication of cholesterol affinity to lipid bilayers

The umbrella model together with the MC simulations showed that the change in the ${\chi }_{\mathit{\text{chol}}}^{\ast }$ value is likely to be discontinuous in response to the change of headgroup/body ratio of host lipids. Some small changes in the headgroup/body ratio would not alter the ${\chi }_{\mathit{\text{chol}}}^{\ast }$ value (e.g., from DPPC to DOPC), but a sufficiently large change can cause membrane lipids to adopt a new regular distribution packing pattern and result in an abrupt change in ${\chi }_{\mathit{\text{chol}}}^{\ast }$ (e.g., from POPE to POPC). ${\chi }_{\mathit{\text{chol}}}^{\ast }$ could jump discretely from one regular distribution to another (e.g. from 0.50 hexagonal pattern to 0.57 dimer pattern and then to 0.67 maze pattern”), as the headgroup/body ratio increases continuously. The 1-to-1 replacement indicates that the lateral packing of ceramide with POPC is likely to be the same maze pattern, which suggests that the difference in the headgroup/body ratio of ceramide and cholesterol does not cause the bilayers to adopt a different lateral packing pattern to accommodate ceramide. Therefore, the value of ${\chi }_{\mathit{\text{chol}}}^{\ast }$ in a particular lipid bilayer is just a rough measure of the affinity of cholesterol for that bilayer: a higher ${\chi }_{\mathit{\text{chol}}}^{\ast }$ value does indicate that the mixing of cholesterol with that particular lipid is more favorable. However, if the value of ${\chi }_{\mathit{\text{chol}}}^{\ast }$ is the same in several lipid bilayers, such as in POPC, POPD and DPPC bilayers, it does not indicate the mixings are equally favorable, because the value of ${\chi }_{\mathit{\text{chol}}}^{\ast }$ cannot reflect relatively small differences in affinity. On the other hand, a lower cholesterol chemical potential indicates a more favorable mixing of cholesterol with that particular bilayer. Thus, measuring chemical potential of cholesterol in lipid bilayers is the more precise thermodynamical method to find out the relative affinity. In addition, it also can reveal the formation of regular distribution of lipids.

4. Concluding Remarks

Cholesterol is the most fascinating and the most studied membrane molecule. Despite decades of research, our understanding of lipid-cholesterol-protein interactions at the molecular level in three or more component systems is still quite primitive. In this article, we showed that in the process of uncovering the key cholesterol-lipid interaction in binary mixture systems, a thermodynamic quantity (i.e., the chemical potential of cholesterol), served as an essential link between various experimental data and the microscopic molecular interactions. We are optimistic that the combination of experimental data, thermodynamics, and computer simulation can be a powerful approach to uncover the key molecular interactions and to predict the behaviors of biomolecules in more complex systems.