Implementation of Card: Curve-Fitting Allelochemical Response Data

Abstract

Bioassay techniques are essential methods used to study the effects of allelochemicals on plant processes. It is often observed that the biological processes are stimulated at low allelochemical concentrations and inhibited as the concentrations increase. Liu et al., (2003) developed a simple model to fit this type of allelochemical response data. Based on the model, CARD (curve-fitting allelochemical response data) was developed as a Windows based program that can be used to fit a stimulation-inhibition response data. An example of using CARD is given.

INTRODUCTION

Bioassay techniques are widely used for quantitative determination of biological responses to allelochemicals. Leather and Einhellig (1986, 1988) have comprehensively reviewed the nature and types of bioassay techniques used in studies of allelopathy. In many cases, it is found that responses to allelochemicals feature stimulation at low concentrations and inhibition at high concentrations (Lovett et al., 1989). In the field of plant allelopathy, the dose-response relationship has, usually, an inverted U-shape with stimulation occurring in a very narrow range of the lower concentrations. Other kinds of response, such as absence of stimulation, are also often found.

Several models have been proposed to describe allelochemical dose-response relationships. A log-logistic equation (Finney 1979) was used in studying the allelopathic potential of wheat (Triticum aestivum L.) and curve-fitting the root length of annual ryegrass (Lolium rigidum) to wheat sowing density (Wu et al., 2000). The log-logistic equation is widely used in herbicide dose response, but it does not include stimulations at low doses. Brain and Cousens (1989) modified the log-logistic equation and proposed a model that can account for the stimulative responses. This attempt was further pursued by Schabenberger et al., (1999) who developed statistical test for the modified log-logistic model. An et al., (1993) presented a model, based on enzyme kinetics, which was theoretically able to describe the feature of stimulation, but it could not fit the observed data statistically. Recently Dias (2001) used a Weibull function to fit allelochemical effects to a germination process, but the Weibull function, like many other equations, can not demonstrate the nature of stimulation. Liu et al., (2003) developed a flexible but simple equation for describing the general pattern of stimulation-inhibition in dose-responses of allelochemicals. Even though the equation is simple, the calculation is quite time-consuming as it involves the determination of the number of ln-transformation that gives the best fit of the model to observed data. This paper introduces a windows based program CARD that facilitates a solution. Progress toward determination of the best ln-transformation is shown using a set of allelochemical-dose response data.

MATERIALS AND METHODS

The Software

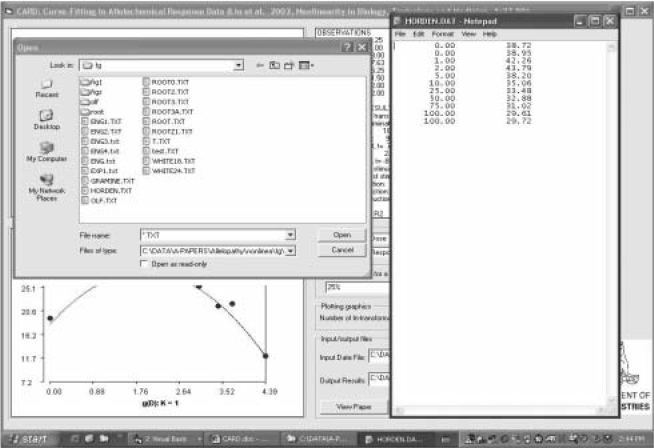
CARD, written in Visual Basic 6, contains data input and output compounds and a user-friendly interface. The input data file is a two-column text-format file. The first column is dose and the second column is the corresponding response to the dose. The data files are named with an extension of *.txt which can be entered from Excel and saved as Text (MS-DOS) (*.txt) format, or from a text editor. The data (as shown in Figure 1) can be selected from the interface by press button “Get Data File”, shown in Figure 2.

FIGURE 1.

CARD interface displaying the input data that is in a two-column text formatted file (top right) with files named as *.txt (top left).

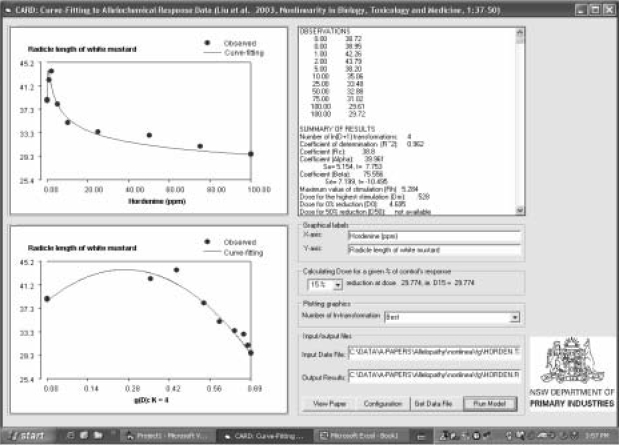
FIGURE 2.

CARD interface displaying the curve-fitting results in graphics and in text for the data from Liu (1991).

The statistical results are shown in a list box (Figure 2) and also as an output file named as “*.rlt”. The labels for axes can be changed from text boxes, Graphical labels. CARD runs and determines the best number of ln-transformation. The fitted coefficients, α and β are reported with standard errors (s.e.) and value of t-test (t). Coefficient of determination (r²), F-test, root mean square error (RMSE, Equation 1) (Janssen and Heuberger 1995) and model efficiency (ME, Equation 2) (Nash and Sutcliffe 1970) are calculated. r² and F-test are based on a multiple linear regression with the transformed data. RMSE and ME are, respectively, defined as:

$$RMSE=\sqrt{\frac{\underset{i=1}{\overset{n}{\Sigma }}{(O_i-P_i)}^2}{n}}$$ (1)

and

$$ME=1-\sqrt{\frac{\underset{i=1}{\overset{n}{\Sigma }}{(O_i-P_i)}^2}{\underset{i=1}{\overset{n}{\Sigma }}{(O_i-\overline{O})}^2},}$$ (2)

where O is the observed response value, P is the predicted response value. is the mean of observed response values. It should be noted that the ME and r² have identical values.

The maximum value of stimulation (R_h) and the dose for the maximum stimulation (D_m) are reported (Figure 2). The doses for p% reduction are also calculated. While p = 0, 50 and 100 are reported, the user can select a p% from a dropdown menu for calculating the corresponding dose. The dose for 25% reduction is suggested as a measure of the inhibition potency of an allelochemical or the sensitivity of the testing organism to the allelochemical.

The presentation of the graphics that show the observed and predicted values against actual doses and the transformed doses (g(D), see Liu et al., 2003) can help provide insight to curve-fitting. While at default, predictions at the best fitted ln-transformation are plotted, and the predicted and observed values with a given number of ln-transformations can be viewed.

Application

The effects of hordenine, released from barley (Hordeum vulgare cv. Triumph), on the radicle length of white mustard (Sinapis alba) (Liu 1991) was used as an illustration and application of the CARD model.

RESULTS AND DISCUSSIONS

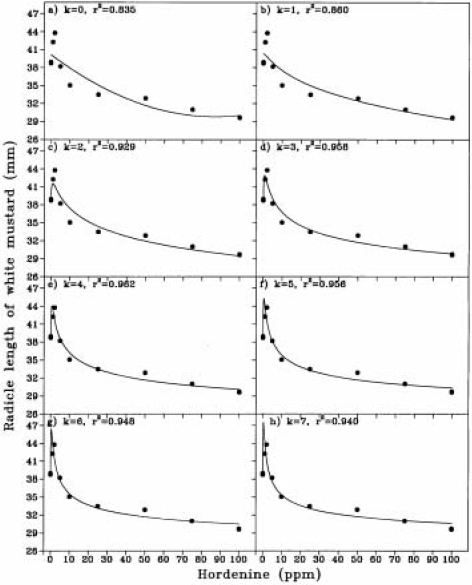
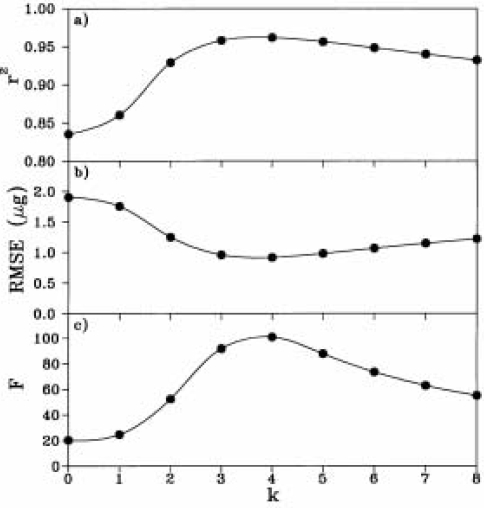
CARD is a simple, but useful program. It is very handy if one wants to fit dose-response data to the model described by Liu et al., (2003). Figure 2 shows the interface displaying the curve-fitting results of response of radicle length of white mustard to hordenine. Figure 3 shows the details of the fitting by various ln-transformations. r² and ME reached the highest value of 0.962 at the 4^th ln-transformation (Figure 4). CARD calculates an additional four ln-transformations after the best number of ln-transformations is determined. At the best number of ln-transformations the RMSE is the smallest (0.92 mm), while the value of r², ME and F-test are the highest. Further increase in ln-transformation will increase RMSE and decrease r², ME and F-test. The criteria for determination of the best number of ln-transformations (see Liu et al., 2003) can be customised from Configuration. For this example, 0.001 was used for this study. In the configuration interface (Figure 5) the number of data points calculated for plotting graphics needs to be a variable for covering the wide range of stimulation-inhibition curve types.

FIGURE 3.

Details of k = 0 (a), 1 (b), 2 (c), 3(d), 4(e), 5 ( f ), 6 (g), 7 (h) in the procedures of curve-fitting (the solid lines) to observations (soil dots) in responses of the radicle length of white mustard to hordenine (Data from Liu 1991).

FIGURE 4.

Statistics for number of ln-transformation (k) calculated by CARD.

FIGURE 5.

Configuration of the critical value used in the criterion for determination of k and number of data points for plotting graph in CARD.

The response of radicle length of white mustard to hordenine can be described by

$$R=38.8+39.96g(D)-75.56{[g(D)]}^2$$ (3)

where g(D) = ln(ln(ln(ln(D+1)+1)+1)+1), and in accordance with the notations defined in Liu et al., (2003), R_c = 38.8, α = 39.96 (s.e. = 5.15, t = 7.75), β = 75.56 (s.e. = 7.20, t = 10.50). r² =0.962, R is radicle length in mm, D is concentration of hordenine in ppm.

The highest stimulation value (R_h) was

$$R_h=\frac{{\alpha }^2}{4\beta }=5.28 \text{mm}$$ (4)

and the dose giving the highest stimulation was

$$D_m=\text{exp}\hspace{0.17em}\text{(exp (exp}\hspace{0.17em}\text{(exp}\left(\sqrt{\frac{\alpha }{2\beta }}\right)=0.528\hspace{0.17em}\text{ ppm hordenine}\text{.}$$ (5)

In order to interpret the model in more biological terms, Equation (4) can be re-expressed as

$$R=[38.80+5.28]-75.56\left[\text{ln(ln(ln(ln(}D\hspace{0.17em}+1)+\mathrm{1)}+\mathrm{1)}+\mathrm{1)}-\sqrt{\frac{5.28}{75.56}}\right]$$ (6)

Further, the dose (D_p) that resulted in a p% reduction in the process, due to the effect of allelochemicals, was calculated by

$$D_p=Exp\left(\cdots \left(Exp\left(exp\left(\frac{\alpha +\sqrt{{\alpha }^2+0.04p\beta R_c}}{2\beta }\right)-1\right)\cdots \right)-1\right)$$ (7)

After entering a p value into CARD through the interface, the doses that resulted in a reduction of 0, 10, 15, 22.5% were calculated as D₀ =4.70 ppm, D₁₀ = 15.07 ppm, D₁₅ = 29.77 ppm and D_22.5 =100 ppm hordenine, respectively.

In the studies of biologically active secondary metabolites of barley alkaloids, Liu and Lovett (1993) found that a concentration of hordenine at 48 ppm can cause a substantial response in the form of increases in number and size of vacuoles and seriously damaged cell walls in the root tips of white mustard. Using CARD, it attains that this concentration (48 ppm hordenine) used to treat the root tips of white mustard causes 18% of reduction in radicle length. Cells treated with a concentration of 100 ppm hordenine showed autophagic phenomena (Liu 1991), but the radicle length was reduced moderately by 22.5%. Secondary indicators, such as reduction in radicle length of roots, are symptoms of the allelochemical effects, while the primary effects such as the disorganization within cells are primary cause of allelochemical effect (Lovett and Potts 1987). As the reduction in relative small scale, such as 10 to 20% in the secondary effects of allelochemicals, can be due to a phytotoxicity that is strong enough to cause dysfunction of enzyme systems or disorganization within cells (Rice 1984), the accurate estimation of the secondary effect through the curve-fitting technique can be used to help in interpreting the effects of allelochemicals.

While testing organisms, such as plants or animals, respond to allelochemicals both stimulated and inhibited, depending upon allelochemical concentrations, the shape of curves for stimulation-inhibition behaviour varies, depending on the sensitivity of testing species to allelochemicals. The most important features of the model described by Liu et al., (2003) are that the ln(D+1) cumulative transformations give various shapes and at any number of cumulative ln-transformations the dose of the control remains at zero. In addition, after each ln-transformation, the model remains a simple quadratic equation, which can be fitted by a standard multiple linear regression. Because of this feature, CARD can be used to fit a nonlinear relationship by a linear least squares regression.

Availability of CARD

CARD on a CD ROM is available from “CARD Request, NSW DPI, Wagga Wagga Agricultural Institute, PMB, Wagga Wagga, NSW 2650, Australia” at the cost of AU$20 for material, postage and handing, or email to the corresponding author for a free electronic copy.

CONCLUSIONS AND REMARKS

CARD is a user-friendly computer software. It is easy to use for curve-fitting allelochemical response data. The model developed by Liu et al., (2003) is simple and quite flexible for describing the typical stimulation-inhibition responses. Owing to the variable nature of allelochemicals and to the shapes of the biological response curves, the number of ln-transformation varies and thereby introduces an uncertain parameter into the model. While such a parameter complicates the model, CARD greatly facilitates a solution. While CARD can accommodate a wide range of stimulation-inhibition dose-responses, some responses, such as the absence of stimulation, may not be effectively fitted.