Dose-Response—A Challenge for Allelopathy?

Abstract

The response of an organism to a chemical depends, among other things, on the dose. Nonlinear dose-response relationships occur across a broad range of research fields, and are a well established tool to describe the basic mechanisms of phytotoxicity. The responses of plants to allelochemicals as biosynthesized phytotoxins, relate as well to nonlinearity and, thus, allelopathic effects can be adequately quantified by nonlinear mathematical modeling. The current paper applies the concept of nonlinearity to assorted aspects of allelopathy within several bioassays and reveals their analysis by nonlinear regression models. Procedures for a valid comparison of effective doses between different allelopathic interactions are presented for both, inhibitory and stimulatory effects. The dose-response applications measure and compare the responses produced by pure allelochemicals [scopoletin (7-hydroxy-6-methoxy-2H-1-benzopyran-2-one); DIBOA (2,4-dihydroxy-2H-1,4-benzoxaxin-3(4H)-one); BOA (benzoxazolin-2(3H)-one); MBOA (6-methoxy-benzoxazolin-2(3H)-one)], involved in allelopathy of grain crops, to demonstrate how some general principles of dose responses also relate to allelopathy. Hereupon, dose-response applications with living donor plants demonstrate the validity of these principles for density-dependent phytotoxicity of allelochemicals produced and released by living plants (Avena sativa L., Secale cereale L., Triticum L. spp.), and reveal the use of such experiments for initial considerations about basic principles of allelopathy. Results confirm that nonlinearity applies to allelopathy, and the study of allelopathic effects in dose-response experiments allows for new and challenging insights into allelopathic interactions.

1 INTRODUCTION

“All things are poison and not without poison; only the dose makes a thing not a poison”

—Philippus Aureolus Theophrastus Bombastus von Hohenheim, also known as Paracelsus (1493–1541).

Almost no other single statement in the history of science has been repeated or paraphrased (“the poison is in the dose”) as often as this observation of the early 16^th century. For this, Paracelsus is perhaps justly considered as the ‘herald’ of modern toxicology. Almost 500 years later, the fundamental concept of the interdependence between the dose of a chemical and the nature of the response of an organism applies to a broad range of research fields. In weed science, dose-response studies have become prevalent in understanding the efficacy and mechanisms of action of commercial herbicides along with the description of responses of target-species by nonlinear mathematical modeling. Although dose-response modeling in weed science has focused on commercial herbicides, the past decade has seen that the fundamental concept of Paracelsus relates to natural phytotoxins in the same way as to commercial herbicides. Hence, studies modeling dose-dependent phytotoxicity of natural herbicidal agents, also referred to as allelochemicals, have become an increasing area of focus (e.g. An et al. 1993; Rimando et al. 1998; Streibig et al. 1999; Petersen et al. 2001; Duke et al. 2003; Liu et al. 2003).

Meanwhile, such classical dose-response studies that measure dose-dependent phytotoxicity of applied, pure natural compounds have become prevalent in understanding the efficacy of allelochemicals and investigating their mechanisms of action influenced by such factors as chemistry, plant species, or environmental parameters. Nevertheless, mathematical modeling of dose-response data by nonlinear regression techniques is still rare. In order to advance dose-response modeling in allelopathy, classical allelochemical-based bioassays at hand exemplify the aptness of a log-logistic response model for allelopathy research and demonstrate some general dose-response principles used for bioassay in other biological sciences. However, allelopathy can go beyond these sole classical applications. Research in allelopathy investigates responses of organisms to biosynthesized allelochemicals which are released by the producing plant to interfere with surrounding plants. Allelopathic plants are provided with an in situ herbicidal system to produce and release phytotoxic metabolites in numerous ways, including root exudation. Thus, why not let the plant dose the poison on its own? As demonstrated by Wu et al. (2000a) for a Triticum aestivum L. cultivar, the capacity to exude allelochemicals is sufficient to be exploited in dose-response studies by exposing test plants to different densities of allelopathic plants. This approach is unique to allelopathy, as it measures density-dependent phytotoxicity of allelochemicals continuously supplemented by the donor via root exudation. Nevertheless, the case studies presented here demonstrate that the responses of plant growth and development to allelochemicals produced and release by living plants can be described with equivalent mathematical modeling as in classical dose-response applications if the response is curve-fitted to donor plant density.

Many investigations in science use dose-response experiments, and the use of such studies should also become an integral part of the science of allelopathy. The objective of this paper is therefore to apply selected dose-response principles to assorted aspects of allelopathy within several bioassays and to demonstrate their analysis by nonlinear dose-response modeling whether pure compounds or intact, growing plants are used to deliver the dose of allelochemicals. The dose-response applications presented here allow new and challenging insights into allelopathy and might therefore be suitable for a variety of approaches and more complex studies.

2 MATERIALS AND METHODS

2.1 The Dose-Response Model

Plant responses to allelochemicals were evaluated as a function of dose by a nonlinear regression model. In herbicide-based studies, the most extensively used mathematical expression relating the average response y to the dose x is the following four parameter log-logistic response function [Streibig (1988) based on Finney (1978)]:

$$y=\text{C}+\frac{\text{D}-\text{C}}{1+e^{[\text{B}•{\text{ln(x}/\text{ED}}_{50}\text{)}]}}$$ (Eq.1)

with C = lower asymptote or response at indefinitely large doses, D = upper asymptote or mean response of the untreated control, B = slope or rate of change around ED₅₀, and ED₅₀ = dose causing 50 % of the total response or the point of inflection. The model expresses the response as strictly decreasing or increasing as a function of dose and describes a sigmoid curve, symmetrical to its point of inflection, the ED₅₀. The log-logistic model has been successfully used to express various herbicide dose responses for many compounds and plant species (e.g., Streibig 1988; Jensen and Kudsk 1988; Kudsk and Streibig 1993; Seefeldt et al. 1995; Streibig et al. 1995, 1998; Michel et al. 1999). Allelochemical-based studies (e.g., Streibig et al. 1999; Petersen et al. 2001; Belz and Hurle 2004) already revealed that the model is not limited to herbicides and if the response is curve-fitted to donor plant-density, the log-logistic model can even be extended to yield estimates of responses to changes in allelochemical concentration in the case of density-dependent phytotoxicity (Wu et al. 2000a; Belz and Hurle 2004).

2.1.1 The Experimental Design

A range of requirements have been described, which must be fulfilled to allow adequate analysis with the log-logistic model (e.g., Streibig 1988; Streibig et al. 1995; Seefeldt et al. 1995; Michel et al. 1999). A major consideration in dose-response studies is to include a wide dose range, covering responses between no effects to total response. Therefore, in each of the presented experiments a range of seven to ten doses or densities was tested in three to six replications in either a completely randomized design or as randomized complete blocks.

2.1.2 The Log-Logistic Analysis

The log-logistic model (Equation 1) is nonlinear in its four parameters (C, D, B, and ED₅₀) and, thus, it was fitted to data by nonlinear regression analysis using SPSS^® Regression Models [method of Levenberg-Marquardt (Marquardt 1963), 1/e⁸ convergence of error sum of squares]. Variance of responses was stabilized at each dose by the inverse standard deviation of replicates as weight. The quality of the description of responses by the log-logistic model was assessed by F test for lack-of-fit based on an analysis of variances at a probability level of P = 0.05 (Seefeldt et al. 1995; Michel et al. 1999; Schabenberger et al. 1999). In such cases, where the log-logistic model was essentially invalid, polynomial models were fitted to data.

2.1.3 Model Comparisons

Comparisons of two or more dose-response curves for similarity in regression parameters (C, D, B, and ED₅₀) were done by horizontal assessment using the lack-of-fit F test (P = 0.05) (Streibig 1988; Seefeldt et al. 1995; Michel et al. 1999). The comparison starts with an F test considering similarity in lower and upper asymptotes (C and D), which is a necessary condition to further test for similarity in slope B and ED₅₀. For the majority of our experiments C was zero and could be omitted, e.g., petri dish assays or evaluation of the rate of change in response. With an identical D-value (and C), curves are tested for similarity in slopes B. If the hypothesis of parallelism is rejected, curves are considered as significantly different, if not, curves are considered parallel. In the latter case, the ED₅₀-value represents a measure for the horizontal displacement of the curves along the x-axis and the hypothesis of identical curves, i.e., same ED₅₀, is finally tested. In the case of similarity in ED₅₀, the dose-response curves are identical in all parameters and potential differences are not significant. Thus, the compared curves expose identical phytotoxicity. If the hypothesis of identity is rejected, the parallel displacement is significant and, therefore, the doses of each of the treatments producing a similar response differ significantly. The quotient between dose levels of two treatments giving similar responses is called the relative potency R (Streibig 1988). R was currently studied based on ED₅₀-values of parallel curves and consequently expresses the quotient between doses giving a 50% response:

$${\text{R}=\text{ED}}_{50;\text{curve I}}/{\text{ED}}_{50;\text{curve II}}.$$ (Eq.2)

In case in which curves significantly differed in asymptotes, response measurements were normalized by the lower and upper asymptote, according to [(y – C) / (D – C)] (Streibig et al. 1995) before testing for similarity in slope B and ED₅₀. This method scales the responses between zero and one, whereby B- and ED₅₀-values of resulting relative dose-response curves remain since scale-independent (Streibig et al. 1999).

2.1.4 The Parallel-Line Concept in Classical Applications

The shape of a dose-response curve is only dependent on the mode of action ( Jensen and Kudsk 1988). This theory is the fundamental basis of the parallel-line concept. Accordingly, if the same active compound is tested, i.e., consistent mode of action, the response curve only depends on the effective dose, being the amount of the applied dose reaching the site of action. Thus, all factors influencing penetration, translocation, or speed of biochemical processes change only the effective dose, and, hence, the horizontal position of a curve, but not the shape (Streibig 1988; Jensen and Kudsk 1988; Kudsk and Streibig 1993; Streibig et al. 1998). This seems to be the case for a variety of factors, e.g., environmental factors ( Jensen and Kudsk 1988; Michel et al. 1999), test species, biotypes (Seefeldt et al. 1995; Michel et al. 1999), growth stages ( Jensen and Kudsk 1988; Michel et al. 1999), or application techniques (formulations, adjuvants) (Kudsk and Streibig 1993). Dealing with a compound-specific assay, parallel dose-response curves are therefore generally a priori expected.

If different active compounds are compared, the situation is more challenging. A general assumption is that response curves of compounds having an identical mode of action have identical slopes (Streibig 1988; Seefeldt et al. 1995; Streibig et al. 1998). In this case, a parallel displacement is supposed to be caused by structural differences merely leading to variations in the effective dose reaching the site of action (Petersen et al. 2001). For example, essentially similar slopes were observed for effects of isothiocyanate analogs from cruciferous species (Petersen et al. 2001) and analogs of the PS II inhibitor sorgoleone, an allelochemical from Sorghum bicolor (L.) Moench. (Streibig et al. 1999). However, by comparing the sorgoleone analogs with synthetic PS II inhibitors, having the same mode of action, but putatively a different binding site, Streibig et al. (1999) found evidence that in vitro not only an identical mode of action may be necessary for parallelism, but also a similar mechanism of binding to the target site. Thus, it seems that in site-specific bioassays, parallel slopes can only be expected if compounds completely correspond in the molecular mechanism of action. On the other hand, a nonparallel displacement in site-specific assays may assist the understanding of molecular mechanisms at the same target site. If compounds with different site(s) of action are compared, nonparallel response curves are not obligatory, but this was the case for PS II inhibitors in comparative dose-response experiments with sulfonylureas (amino acid inhibitors) (Streibig 1983), germination inhibitors (Nyffeler et al. 1982), and the auxin-like herbicide fluroxypyr (Greiner 2001). In each case, the response curves of the PS II inhibitors had a steeper slope.

Nevertheless, the reverse of this basic principle, i.e., observing parallelism and assuming similar active compounds or identical site(s) of action, is not valid. Significant parallel or nonparallel relations may, however, provide a valuable first indication about mode(s) of action or may assist causative explanations for observed effects. While the parallel-line concept is often adopted for classical applications, the question of whether it is suitable for density-dependent phytotoxicity and what conclusions can be drawn from such comparisons is the subject of the unique applications.

2.2 Examples for Classical Applications—Dose-Response with Allelochemicals

2.2.1 The Parallel-Line Concept—ED₅₀ in Comparison

The hypothesis of a parallel displacement was investigated for changes in phytotoxicity of the allelochemical benzoxazolin-2(3H)-one (BOA obtained from Fluka) subjected to different target species and environmental conditions. Bioassays were conducted as germination assays in glass petri dishes (4.5 cm in diam.). In each case, 15 seeds were placed on one layer of filter paper (Rundfilter 595, Schleicher and Schuell) and exposed in quintuplicates to 2 ml of distilled water containing 8 to 12 different concentrations of BOA ranging from 0 to 600 μg/ml. Methanol in a concentration of 0.4 % (vol.) served as a solvent for BOA. Controls were performed with methanol only. Petri dishes were sealed with parafilm and incubated in a growth chamber [24/18 °C, 50/0 μE/m²/s light (12/12 hr)] as randomized blocks. After 6 d, the root length was measured (radicle length ≥1 mm) and dose-response curves were compared after scaling by the upper asymptotes D (C = 0).

Species-Specific Phytotoxicity

In a comparative bioassay the phytotoxicity of BOA was studied in regard to a possible displacing influence of the following ten plant species: Agrostemma githago L., Bromus sterilis L., Galinsoga ciliata (Raf.) Blake, Lactuca sativa L. var. capitata L., Lepidium sativum L., Matricaria chamomilla L., M. inodora L., Medicago sativa L., Poa annua L., and Sonchus asper (L.) Hill. Due to a slow germination, sampling time was extended to 10 d for M. chamomilla.

Environmental Factors—Substrate

In a comparative bioassay a possible substrate-specific displacement of the phytotoxicity of BOA was studied with L. sativa. For this, the filter paper was replaced either by 0.4 g vermiculite (2/3 mm, BayWa, Germany), by 3.7 g silica (SiO₂, crystalline, 0.1–0.6 mm, Roth) with 5% (wt.) vermiculite, or by 4.4 g silty loam (1.8% organic matter). Substrates were heat sterilized prior to bioassay (20 min. at 120 °C). The quantity of substrate per petri dish was based upon the substrate-specific water-holding capacity and was calculated to give 140% saturation with the applied 2 ml of test solution (Table 1).

TABLE 1.

Gravimetric water-holding capacity of tested substrates and quantity applied in the bioassay to accomplish 140% water potential with 2 ml test solution.

Substrate	Gravimetric Water-Holding Capacitya [%]	Net Weight [g/Petri Dish]
Loam	32.2 ±1.5	4.4
Silica/Vermiculite	38.4 ±2.5	3.7
Vermiculite	383.6 ±37.2	0.4

^a Determined according to Parent and Caron (1993).

2.2.2 Non-Parallel Displacement—Slope B in Comparison

A comparative whole-plant dose-response bioassay was conducted with Lemna paucicostata Hegelm. to contrast the effects of the wheat- (Triticum L. spp.) and rye- (Secale cereale L.) specific allelochemicals 2,4-dihydroxy-2H-1,4-benzoxazin-3(4H)-one (DIBOA obtained from BASF Corporation), BOA, and 6-methoxy-benzoxazolin-2(3H)-one (MBOA obtained from Sigma-Aldrich), with 7-hydroxy-6-methoxy-2H-1-benzopyran-2-one (scopoletin obtained from Sigma-Aldrich) as an oat- (Avena sativa L.) specific allelochemical. Lemna stocks were precultivated in a growth chamber (25 °C, 79 μE/m²/s) starting from one three-frond plant in filter sterilized (0.2 μm) nutrient solution containing (in g/l): 1.52 KNO₃, 0.68 KH₂PO₄, 0.49 MnSO₄·7 H₂O, 0.02 Na₂CO₃, 1.18 Ca(NO₃)₂·4 H₂O, 5·10^–4 H₃BO₃, 0.5middot;10^–4 ZnSO₄, 1.2·10^–4 Na₂MoO₄, 4.7·10^–4 MnCl₂, 0.25·10^–4 CoCl₂, 0.25·10^–4 CuSO₄, and 183.6·10^–4 Fe-EDTA. Dose-response experiments were conducted in sterile nonpyrogenic polystyrene 6-well plates (CoStar 3506, Corning Incorporated) containing 5 ml of nutrient solution per well. Dimethyl sulfoxide at 1% (vol.) served as a solvent for the tested compounds. Controls were performed with solvent only. The pH was adjusted to 5.5 with 1 N sodium hydroxide if necessary. Each well was inoculated with two three-frond plants, which were exposed to seven to nine different concentrations of the tested compounds. Plates were sealed with parafilm and incubated in the growth chamber in triplicates as randomized blocks. Bioassays were conducted simultaneously for all four compounds and repeated once. The frond area of the colonies was measured with a scanalyzer (LemnaTec GmbH, Würselen, Germany) at day zero and day seven. Results of both experiments were pooled, and relative dose-response curves were calculated and compared for the increase in frond area after scaling by the upper asymptotes D (C = 0). In the case of scopoletin, the frond area of the colonies was measured daily in order to investigate chronological changes in the dose-response relation.

2.3 Examples of Unique Applications—Dose-Response with Allelopathic Crops

The allelopathy unique applications with allelopathic crops were conducted in hydroponic culture according to Belz and Hurle (2004) to study the impact of allelochemicals in root exudates of grain crop cultivars (A. sativa, Triticum aestivum L., T. durum Desf., T. spelta L., S. cereale) on Sinapis alba L. cv. Albatros. Briefly, donor and receiver plants were pregerminated apart for 4–5 d, subsequently transferred to aluminum-coated glass beakers containing 290 ml aerated distilled water, and cultivated as mixed culture for 6 d under greenhouse conditions [24/16 °C, 16 hr light (300 μE/ m²/s)]. At each time, four S. alba plants were cocultured with seven different donor densities (0–45 plants/pot) in triplicates in a complete randomized design. Evaporation losses were replenished daily with distilled water. Response parameters, mainly root length, were evaluated at day zero and day six and dose-response relations calculated and compared for the increase in response (C = 0).

2.3.1 The Dose is in the Density

The assumption of increasing amounts of allelochemicals in the test medium with increasing donor density was evaluated by spectroscopic analysis of root exudates of A. sativa cv. Jumbo and chemical analysis of two benzoxazinoids (Bx) [DIBOA, DIMBOA (2,4-dihydroxy-7-methoxy-2H-1,4-benzoxazin-3(4H)-one)] in root exudates of S. cereale cv. Amilo. Exudates were collected at the end of the dose-response bioassay at each donor density. In the case of A. sativa, a pooled aliquot of the aqueous test solution was directly transferred to a test tube and blue fluorescence imaged at 254 nm using an electronic multiwave transilluminator (Ultra Lum). In the case of S. cereale, root exudates were collected in triplicates over a period of 2 hr in aerated distilled water (x plants/100 ml). At each density, a pooled aliquot of 150 ml was concentrated 300-fold by solid phase extraction (ISOLUTE^® ENV+, 200 mg, IST) and analyzed by high performance liquid chromatography (HPLC-DAD) according to Belz and Hurle (2005). Bx were identified and quantified at 220 nm using internal standards.

2.3.2 Measuring the Response

The importance of the measurement of effects was investigated by the response of S. alba to the interference from S. cereale cv. Amilo as a function of the parameter and the plant tissue measured. Dose-response relationships were generated for the increase in fresh weight of shoots and roots of S. alba, as well as for the extractable enzyme activity of phenylalanine ammonia-lyase in leaves and roots [according to Konstantinidou-Doltsini et al. (1988)]. Response data was fitted to the log-logistic model or optionally to second order polynomial models.

2.3.3 The Parallel-Line Concept—ED₅₀ in Comparison

Environmental Factors—Light

The hypothesis of a horizontal displacement subjected to environmental factors was studied for changes in light. Dose-response curves were generated for two cultivars of T. aestivum (cv. Moldau, cv. Petrus) for the inhibition of the root growth of S. alba. Two light intensities were considered: normal greenhouse conditions (16 hr light, 300 μE/m²/s) and 50% shading (shadowing grid, BayWa, Germany). Changes in dose of allelochemicals were verified for Bx (DIBOA, DIMBOA) by chemical analysis of root exudates, collected at the end of the bioassay by transferring the highest density (30 plants/pot) over a period of 2 hr in 100 ml aerated distilled water. An aliquot of 12 ml of each of the three replicates was concentrated 60-fold at 40 °C under vacuum for 24 hr (RVC 2–25, Christ, Germany, with cooling trap) and analyzed by HPLC-DAD according to Belz and Hurle (2005). Bx were identified at 220 nm using internal standards and data subjected to an analysis of variance with multiple comparison (Tukey-test, P = 0.05) using SPSS^®. Finally, the light-specific allelopathic activity was correlated to the respective exudation of total Bx.

Dilution of Allelochemicals

The hypothesis of a horizontal displacement subjected to a dilution of root exudates, i.e., decrease in dose, was evaluated for T. aestivum cv. Moldau interfering with S. alba. A hydroponic bioassay was conducted comparing a ‘mixed cultivation’ of receiver and donor plants in 290 ml distilled water with a ‘monoculture’ of both species in 290 ml respectively, but with daily reciprocal exchange of pots. Accordingly, the volume of test solution doubles in monoculture (two pots) and, thus, the actual dose of allelochemicals should be 2-fold diluted. The dilution was verified for Bx by chemical analysis of the root exudates, collected at the end of the bioassay. At each replicate, a 12 ml aliquot of the test solution (30 plants/x ml/6 d) was analyzed, as well as a 12 ml aliquot taken from a 2-hr collection (30 plants/100 ml/2 hr). Aliquots were concentrated 60-fold at 40 °C under vacuum for 24 hr and Bx content (DIBOA, DIMBOA) determined by HPLC-DAD analysis (Belz and Hurle 2005). Data was subjected to an analysis of variances with a multiple comparison test (Tukey-test, P = 0.05) using SPSS^®.

2.3.4 Dose-Response Curves on the Move—Slope B in Comparison

Time Courses

Chronological changes in dose-response relations with increasing time of exposure were investigated for the interference of T. aestivum cv. Pegassos on S. alba. Dose-response curves were evaluated for the increase in root length of S. alba after 3, 4, 5, and 6 d. To allow for a complete description of the dose-response relationship, effects on the growth curve were included in terms of a generalized dose-response growth surface (Streibig et al. 1993). Growth curves were analyzed by second order polynomial regression and combined with the corresponding dose-response curves to model the three-dimensional response surface.

Dose-Response to Distinguish between Allelopathic Species and Cultivars?

The hypothesis of a species- or cultivar-specific pattern of response curves was investigated by comparing the effects of root exudates of cultivars of A. sativa, Triticum spp., and S. cereale on root growth of S. alba. Root exudates were collected at the end of the bioassays and analyzed by HPLC-DAD for the content of Bx (DIBOA, DIMBOA) and scopoletin.

3 RESULTS AND DISCUSSION

3.1 Classical Applications

3.1.1 The Parallel-Line Concept—ED₅₀ in Comparison

Species-Specific Phytotoxicity

A comparative germination assay was conducted with ten mono- and dicotyledonous species to generate and compare dose-response curves for BOA. Dealing with the same active compound, parallel dose-response curves merely differing in ED₅₀-values were expected for all species. Results showed that species varied considerably in their sensitivity to BOA (Table 2). The two Matricaria species were most sensitive, whereas the largest-seeded A. githago and M. sativa were least sensitive. Dose-response curves were parallel (average B = 2.3) with the exception of M. chamomilla, with a significantly shallower slope (B = 1.5). Thus, with one exception, the hypothesis of a horizontal displacement attributed to different test species was confirmed. The shallow slope for M. chamomilla was confirmed twice and the variation from the parallel-line concept might result from its slow germination and seedling development, requiring a prolonged sampling time and causing a different developmental stage in comparison to the other species. For the other species, the horizontal displacement was likely to be caused by differences in effective dose. Among other things, the seed size is a crucial factor for sensitivity in germination assays and the sequence of species-specific sensitivity to BOA showed a distinct positive correlation to the seed size, indicated by the 1,000 kernel weight (Table 2). A general lower sensitivity of large-seeded weed species in germination assays, whether mono- or dicotyledonous, was previously observed for BOA as well as DIBOA by Burgos and Talbert (2000) and also for isothiocyanates (Petersen et al. 2001). Besides seed size, the species-specific ability to metabolize BOA might also contribute to observed differences. Plants detoxify BOA by glucosylation and detoxification efficiency varies between species (Schulz and Wieland 1999). M. chamomilla for example is able to detoxify BOA by N- and O-glycosylation, while G. ciliata is unable to perform the more efficient N-glycosylation (Schulz and Wieland 1999). Consequently, because of the higher metabolization capacity of M. chamomilla, it should be less sensitive to BOA than G. ciliata, which was not the case. Furthermore, the metabolization capacity of the comparable insensitive species A. githago is considered as moderate to low (Sicker et al. 2000, 2003) in contrast to the moderate capacity of the most sensitive species M. chamomilla. Thus, species-specific metabolization capacity seems to have no importance under the conditions of the present bioassay. This lack of correlation may be due to the fact that the in vitro activity of the degrading enzymes (Schulz and Wieland 1999) may not reflect in vivo activity. Besides metabolization by the plant, the degradation of BOA by root colonizing microorganisms could be a displacing factor too. Degradation of BOA to 2-amino-(3H)-phenoxazin-3-one changes its phytotoxicity and is species-dependent as well (Friebe et al. 1996). Microbial degradation of BOA occurs in nonsterile petri dish assays, but a quantification of the metabolite is difficult since it precipitates on root surfaces (Friebe et al. 1996; Schulz and Wieland 1999). A contribution of microbial degradation to the parallel displacement is probable, but because of the marked correlation between sensitivity and seed size, one must assume that the seed size is a major factor influencing the dose reaching the molecular target(s) and, thus, sensitivity in germination assays.

TABLE 2.

Effect of benzoxazolin-2(3H)-one on the root growth of ten different plant species and the interdependence with seed size

Species	ED50 [μ g/ml]	B	R	Correlation
Agrostemma githago	194.4 (171.6–217.3)	3.5 (2.4–4.5)	3.7
Medicago sativa	135.9 (91.1–180.7)	2.1 (1.8–2.4)	2.8
Bromus sterilis	128.3 (98.8–157.9)	2.8 (1.7–4.1)	2.3
Lepidium sativum	126.9 (113.2–140.6)	2.6 (2.2–3.0)	2.4
Poa annua	109.2 (89.8–128.5)	2.5 (1.5–3.5)	2.1
Galinsoga ciliata	104.3 (82.4–126.1)	2.8 (1.5–4.0)	2.0
Sonchus asper	95.4 (87.4–103.4)	2.2 (1.8–2.5)	1.9
Lactuca sativa	85.3 (73.7–96.8)	2.4 (1.9–3.0)	1.6
Matricaria inodora	49.7 (45.9–53.4)	2.0 (1.8–2.4)	1.0
M. chamomilla	41.1 (37.5–44.8)	1.5 (1.4–1.6)	–

Response curves normalized by the D parameter with C = 0; ED₅₀ = effective dose causing 50% inhibition in root length; B = slope; asymptotic 95% confidence interval in parentheses; R = relative potency for ED₅₀ of parallel curves; R² = coefficient of determination; r = Pearson correlation coefficient (significant at P = 0.01).

In the case of M. sativa, low doses of BOA stimulated root growth, which could not be adequately captured by the sigmoid log-logistic model since it ignores the stimulatory effect. Such a stimulatory or beneficial effect of toxic compounds at subinhibitory doses is termed hormesis (Southman and Ehrlich 1943). Plant responses to various allelochemicals can change from stimulatory to inhibitory as their dose increases (Sikkonen 2001). In the case of BOA, it is supposed to be partly caused by a stimulation of plasma membrane H⁺-ATPase (Friebe et al. 1997). If the study of subinhibitory doses is not the main objective of an assay, the log-logistic model can still be used either by omission of data in the stimulatory dose range or the control (Streibig 1980). However, in doing so for M. sativa , the ED₅₀ for the omission of the peak (y ≤ mean response of untreated control; ED₅₀ = 174.8 μg/ml) differed considerably from the ED₅₀ for the omission of control (x > 0; ED₅₀ = 110.2 μg/ml). Thus, ignoring the hormetic effect in the present case would substantially bias estimates of effective doses and, therefore, a log-logistic modeling seemed critical (Streibig 1988; Brain and Cousens 1989; Schabenberger et al. 1999). An adequate description of the hormetic trend is obtained by incorporating a parameter f ≥0 into the log-logistic model (Eq. 1), which measures the initial rate of increase in response at subinhibitory doses [Schabenberger et al. (1999) based on Brain and Cousens (1989)]:

$$\text{y}\hspace{0.17em}=\hspace{0.17em}\text{C}\hspace{0.17em}+\frac{\text{D}-\text{C}\hspace{0.17em}+\hspace{0.17em}f•\hspace{0.17em}\text{x}}{1+\left(\begin{array}{c}1+\frac{2•f•{\text{ED}}_{50}}{\text{D}-\text{C}}\end{array}\right)•e^{[\text{B}•ln({\text{x}/\text{ED}}_{50})]}}.$$ (Eq.3)

All parameters retain their meanings and, thus, the model reduces to a log-logistic function for f = 0. The hormetic effect is significant at P = 0.05, if the 95% confidence interval for the estimate of f does not include zero (Schabenberger et al. 1999), which was the case for M. sativa [f = 0.4 (0.1 – 0.7)]. The dose level giving a similar response as the untreated control (x = 0), i.e., the dose at which the hormetic effect has disappeared or the limited dose for stimulation (LDS), can be estimated according to Schabenberger et al. (1999) by:

$$\text{y}\hspace{0.17em}=\hspace{0.17em}\text{C}\hspace{0.17em}+\frac{\text{D}-\text{C}\hspace{0.17em}+\hspace{0.17em}f•\hspace{0.17em}\text{x}}{1+\left(\begin{array}{c}1+\frac{f•\text{LDS}}{\text{D}-\text{C}}\end{array}\right)•e^{[\text{B}•ln(\text{x}/\text{LDS})]}}.$$ (Eq.4)

In the presence of hormesis, besides the LDS, the dose giving maximum response (M) can be estimated (Schabenberger et al. 1999):

$$\text{y}\hspace{0.17em}=\hspace{0.17em}\text{C}\hspace{0.17em}+\frac{\text{D}-\text{C}\hspace{0.17em}+\hspace{0.17em}f•\hspace{0.17em}\text{x}}{1+\left(\begin{array}{c}\frac{f•\text{M}}{\text{(D}-\text{C)}•\text{B}-f•\text{M}•\text{(1}-\text{B)}}\end{array}\right)•e^{[\text{B}•ln(\text{x}/\text{M})]}}$$ (Eq.5)

Applying the peaked model for M. sativa revealed that the highest response (13.2 mm; 169% of control) appeared at M = 25.8 μg/ml, the hormetic effects disappeared at doses x > 81.2 μg/ml, and 50% inhibition occurred at 160.4 μg/ml (Figure 1). Thus, the log-logistic model led to a 1.1-fold underestimation of the ED₅₀ if the peak was omitted, an overestimation by 1.5 if control was omitted, and 1.2 if no data was omitted. An analogous 1.4-fold underestimation of the ED₅₀ resulted for glyphosate-treated Echinochloa crus-galli (L.) P. Beauv. by ignoring the observed growth stimulation at subinhibitory doses (Schabenberger et al. 1999). An under- or overestimation by 1.1–1.2 may appear negligible in this assay, particularly since neither the original sequence of species-specific sensitivity to BOA nor the correlation between seed size and ED₅₀ is altered (Table 2). Thus, fitting the log-logistic model and ignoring the hormetic effect in the present case does not change the conclusions drawn from the experiment. However, applying the peaked model changed the relative potency for M. sativa from R = 2.8 to 3.1 and improved the overall quality of fit from R² = 0.71–0.77 to 0.81 (R² = 1 – residual SS / corrected SS). This strengthens the aptness of the peaked model in the case of pronounced hormesis and recommends favoring this model if a more precise determination of the ED₅₀ or R is required. Furthermore, the lack-of-fit F test still proved parallelism, i.e., same B as for the log-logistic curves of the other species, if the peaked model was applied for M. sativa. Thus, the peaked log-logistic model is directly valid for comparisons with treatments showing log-logistic behavior ( f = 0) without affecting the parallel-line concept. In presence of significant hormetic effects, it is therefore advisable to accommodate hormesis by a simple modification of the log-logistic model.

FIGURE 1.

Stimulation of root growth of Medicago sativa at low doses of benzoxazolin-2(3H)-one and its description by the peaked logistic model [Schabenberger et al. (1999)]. ED₅₀ = effective dose causing 50% inhibition in root growth; LDS = limited dose for stimulation; M = dose giving maximum response; R² = 1 – residual SS / corrected SS.

Environmental Factors—Substrate

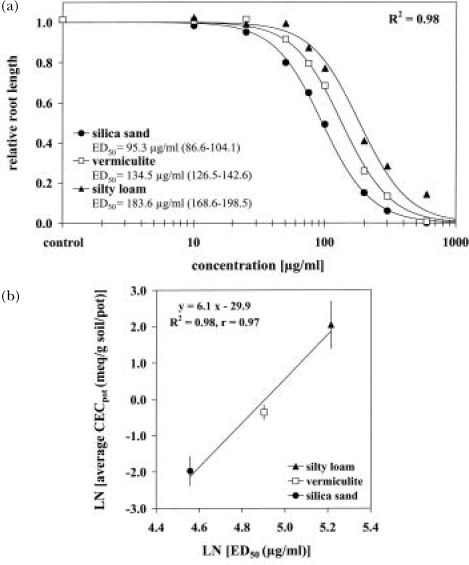
The effective concentration of an active compound in soil solution is a function of several biotic and abiotic factors. Compounds can be immobilized by reversible or irreversible sorption to soil particles, colloids or organic matter. Consequently, the dose of a soil-applied compound will vary as a function of soil substrate, which should result in a horizontal displacement of the response curves. This hypothesis was evaluated for the sensitivity of L. sativa to BOA applied to three different substrates (silica sand, vermiculite, loam). The dose-response curves for the different substrates were parallel (average B = 2.3), thus confirming the parallel-line concept, but differed significantly in ED₅₀-values (Figure 2a). BOA was most active in silica sand with an ED₅₀ of 95.3 μg/ml, followed by application on vermiculite and finally on silty loam. BOA should act as weak base in aqueous solution and be adsorbed on a soil matrix according to the specific cation exchange capacity. This assumption was confirmed since the sequence of substrate-specific efficacy of BOA was significantly associated with the average potential cation exchange capacity of the appropriate substrates (Figure 2b). Consequently, it seemed most likely that the observed horizontal displacement was dose-dependent and resulted from variations in effective dose according to the substrate-specific adsorption of BOA.

FIGURE 2.

Influence of test medium (silica sand, vermiculite, loam) on the effect of benzoxazolin-2(3H)-one on the root growth of Lactuca sativa (a) and the interdependence with mean potential cation exchange capacity [CEC_pot according to Scheffer and Schachtschabel (2002), Kuntze et al. (1994), LfU (2002)] (b). Response-curves normalized by the D parameter with C = 0; ED₅₀ = effective dose causing 50% inhibition in root length; asymptotic 95 % confidence interval in parentheses; nonlinear R² = 1 – residual SS / corrected SS; linear R² = coefficient of determination; r = Pearson correlation coefficient (significant at P = 0.01).

3.1.2 Non-Parallel Displacement—Slope B in Comparison

Previous bioassays were conducted with only one active compound and, thus, identical slopes of the response curves were expected. In the following bioassay the effect of BOA on the growth of L. paucicostata should be contrasted to those of its analog MBOA, its precursor DIBOA, and scopoletin. This time, parallel curves were only expected for BOA and MBOA, since methoxylation may not influence the mechanism of action. L. paucicostata was most sensitive to DIBOA with an ED₅₀ of 70.8 μM, followed by MBOA and BOA, with an average 4.4-fold higher ED₅₀ (Figure 3). A general higher activity of DIBOA compared to BOA is consistent with previously observed in vitroand in vivoactivities (Barnes and Putnam 1987; Friebe et al. 1997; Burgos and Talbert 2000). MBOA (ED₅₀ = 311.2 μM), was slightly more reactive than BOA (ED₅₀ = 330.5 μM), which is supposed to be caused by the electron-donating 6-methoxy group. However, observed differences in activity between analogs were not significant. Scopoletin was significantly less phytotoxic with a 6.5-fold higher ED₅₀ than DIBOA. The horizontal assessment revealed a significant shallower slope for DIBOA (B = 1.1) and parallelism for BOA, MBOA, and scopoletin (average B = 3.2) (Figure 3). On the basis of the parallel-line concept, it could be hypothesized that DIBOA may have a different site of action than its metabolite BOA, MBOA, and scopoletin. Furthermore, BOA and MBOA may have a similar site of action, and maybe scopoletin as well. An unambiguous evaluation of this hypothesis against the background of the compounds-specific modes of action is hampered by the fact that the primary mode(s) of action of these allelochemicals are yet unknown, although some physiological processes are known. On the molecular level, Bx (DIBOA, DIMBOA) are believed to act as inhibitors of various enzymes involved in metabolic processes (Pérez and Niemeyer 1989). They inhibit the chloroplast ATPase coupling factor (Queirolo et al. 1981, 1983) and the plasma membrane H⁺-ATPase (Friebe et al. 1997). On the physiological level, a reduction of the energy transfer in chloroplasts and mitochondria has been described (Queirolo et al. 1981, 1983; Massardo et al. 1994), as well as a stimulation of NADH-oxidation by cell wall peroxidases, leading to enhanced H₂O₂-formation and phenol coupling at cell walls (Rojas et al. 1997; González and Rojas 1999). Although in vitro benzoxazolinones (BOA, MBOA) also slightly inhibited the plasma membrane H⁺-ATPase (Friebe et al. 1997), observed inhibition of cell elongation by benzoxazolinones suggested that the allelopathic action is mainly due to interference with auxin-induced growth (Venis and Watson 1978; Hasegawa et al. 1992; Hoshi-Sakoda et al. 1994). Scopoletin may interfere with auxin-induced growth by inhibition of indole-3-acetic acid oxidation (Andreae 1952). Thus, if the described activities are the first-line mechanisms of action for the tested compounds, observed differences in slopes would reflect compound-specific modes of action and confirm the parallel-line concept. However, at present the primary site(s) of action of these compounds are speculative, and conclusions drawn from the experiment should be restricted to a putative similar action of benzoxazolinone analogs.

FIGURE 3.

Effect of DIBOA (2,4-dihydroxy-2H-1,4-benzoxazin-3(4H)-one), BOA (benzoxazolin-2(3H)-one), MBOA (6-methoxy-benzoxazolin-2(3H)-one), and scopoletin (7-hydroxy-6-methoxy-2H-1-benzopyran-2-one) on the relative increase in leaf area of Lemna paucicostata. Response curves normalized by the D parameter with C = 0; B = slope; ED₅₀ = plant density causing 50% inhibition; asymptotic 95% confidence interval in parentheses; R² = 1 – residual SS / corrected SS.

3.1.3 Dose-Response Curves on the Move—Time Courses

The dose is a function of both the concentration of an active compound and the length of exposure. The latter is critical in dose-response studies, since the development of symptoms takes time, but on the other hand, plants damaged by sublethal doses can sometimes recover and reverse the initial phytotoxicity. Poisoning as well as a possible decrease in phytotoxicity with time of exposure is reflected in the regression parameters of the log-logistic model and knowledge of the dynamics of a dose-response relation is crucial for the choice of the right end point and the conclusions drawn from such an experiment.

In order to demonstrate the dynamics of parameters, a bioassay was conducted with L. paucicostata affected by scopoletin over a period of 7 d. Figure 4a displays the appropriate dose-response relations as a function of the sampling time. Data could be fitted to the log-logistic model from day two on. However, the quality of fit was insufficient for day two and three resulting in broad confidence intervals for estimates, allowing a fit for almost every curve. The remaining dose-response curves displayed a positive dependence between sampling time, upper asymptote D, and slope B, and the opposite for the ED₅₀ (Figure 4b). Thus, a prolongation of the length of exposure steepened the curve, lowered the ED₅₀ values, and enhanced the measurable phytotoxicity.

FIGURE 4.

Effect of scopoletin (7-hydroxy-6-methoxy-2H-1-benzopyran-2-one) on the leaf area of Lemna paucicostata depending on the time after exposure (a) and the chronology of the interdependence between ED₅₀, slope B, and upper asymptote D for scopoletin (b). ED₅₀ = effective dose causing 50% inhibition.

Steepening of the dose-response curve with increasing time of exposure is considered a basic principle in whole-plant studies (Seefeldt et al. 1995). The parallel-line concept is therefore not applicable for time courses, since time affects the performance of a compound and the shape of the dose-response curve. Consequently, the study of the parallel-line concept as the main objective of an experiment requires consistent test conditions, including the length of exposure. In the present case observed time courses were not significant with an average B-value of 2.6 and an ED₅₀ of 481.3 μ M, in contrast to the significant increase of D. If an ED₅₀, as the most robust dose-response level to study phytotoxicity in general (Streibig et al. 1995, 1999), does not significantly change with time, and the study of the shape is not the main objective of an experiment, why not evaluate it as soon as possible? Early estimations of ED₅₀ doses tend to have a relatively high variability, arguing against premature determinations of the ED₅₀. The variability is related to the slope of the curve, such that the steeper the slope the less variable the ED₅₀ (Streibig et al. 1999). This is reflected by the asymptotic standard errors for the estimated ED₅₀-values. At day three for example, the standard error for the ED₅₀ was > 10,000, at day four still > 100, whereas at day seven <50, allowing a much more exact estimation and enhancing the significance of comparative assessments, as well as reproducibility. As modeling seeks the best fit, the most complete description of a dose-response relationship is certainly obtained by evaluation of time courses. In regard to the rather large experimental design needed, especially for destructive measurements in whole-plant studies, usually only one end point is considered. The choice of it should be deliberate and avoid recovery of plants at low dose levels and secure maximum response at high doses (Michel et al. 1999).

3.2 Unique Applications

3.2.1 The Dose is in the Density

The amount of an allelochemical released by living plants is among other things a function of the density of the allelopathic plant; thus, in unique applications the dose relies on the donor plant density. The validity of this principle was spectroscopical visualized for a cultivar of A. sativa by relative fluorescence of its root exudates (Figure 5a). Chemical analysis of collected exudates revealed that the apparent increase in blue fluorescence with plant density was mainly due to scopoletin, a major constituent of A. sativa root exudates (Fay and Duke 1977). In exudates of S. cereale, besides other compounds, Bx (DIBOA, DIMBOA) are claimed as allelopathic metabolites (Pérez and Ormeño-Nuñez 1991, 1993; Pethö 1992). Focusing on the non-fluorescent Bx, an equivalent imaging as for A. sativa was not feasible, but chemical analysis of root exudates of S. cereale confirmed a similar density-dependence for Bx-exudation (Figure 5b). Observed density-dependence clearly demonstrates that the amount of exuded allelochemicals can be dosed by varying the density of the producing plant. Furthermore, density-dependence is a necessary condition for any exudate compound that might contribute to the overall allelopathic effect in dose-response studies with living plants. Hence, scopoletin and Bx are good candidate allelochemicals in root exudates of A. sativa and S. cereale, although this is not sufficient to assume that they account for all or part of the observed density-dependent phytotoxicity of the root exudates.

FIGURE 5.

Increase in amount of allelochemicals in hydroponic culture with plant density. (a) Density-dependent fluorescence (254 nm) mainly due to scopoletin (7-hydroxy-6-methoxy-2H-1-benzopyran-2-one) in aliquots from root exudates of Avena sativa cv. Jumbo (x plants/290 ml/6 d). (b) Density-dependent increase in amount of benzoxazinoids [DIBOA (2,4-dihydroxy-2H-1,4-benzoxazin-3(4H)-one), DIMBOA (2,4-dihydroxy-7-methoxy-2H-1,4-benzoxazin-3(4H)-one)] in root exudates of Secale cereale cv. Amilo (x plants/100 ml/2 hr; 13-d-old plants).

3.2.2 Measuring the Response

A great variety of parameters can be measured in dose-response experiments, whereby the choice of measurement plays a decisive role for the demonstration and nature of effects. The response of an organism to a chemical is often very complex and has an impact at different biological levels. Depending on the compound-specific molecular site(s) of action, the response can be measured on every affected biological level and on each level with various parameters. Which is the best way to demonstrate an effect?

Inhibition versus Stimulation

The impact of root exudates of S. cereale cv. Amilo on S. alba plants was measured at the cellular level on the basis of the extractable enzyme activity of phenylalanine ammonia-lyase (PAL), in comparison with effects on fresh weight on whole-plant level. The different trends in dose responses of S. alba could not be reduced to a single pattern or described by a unique theoretical response function (Figure 6). The most sensitive impact was on the extractable PAL activity of the roots, which was stimulated with an ED₁₀ < 2 plants/pot. Maximum stimulation occurred for a plant density of 9 plants/pot, with a subsequent decrease to the response level of the control at approximately 45 plants/pot. A similar, but delayed and more pronounced stimulation was observed for extractable PAL activity of the leaves. In comparison to the control, inhibitory effects on PAL activity were not observed, but might be detectable in a broader range of applied densities. For both response patterns, the log-logistic model was not the proper analysis technique and also the peaked model was invalid because of the limited dose-range. Polynomial models as well could not adequately describe the response observed for PAL activity. Increased PAL activity, the key enzyme of the phenylpropanoid pathway, leads to accumulation of phenylpropanoids, low-molecular-weight defense compounds that are believed to play a role in chemical-induced resistance (Sauerborn et al. 2002). Theoretically, the observed enhancement of PAL activity could be a specific defense response of the receiver to an allelochemical. On the other hand, an increase in the activity of PAL, along with certain other enzymes is considered as an early, inspecific indicator for various stress factors (Renneberg and Brunold 1994). A comparable weak, but nonsignificant stimulation at low donor densities was observed for the root fresh weight. The log-logistic model resulted in an ED₅₀ of 10.6 plants/pot. Despite the significant inhibition of the root fresh weight, no effect on shoot fresh weight was apparent after 6 d. These findings evidently show that the demonstration of an allelopathic effect depends on the measurement: the extractable PAL activity proves stimulatory allelopathy, the root fresh weight demonstrates inhibitory allelopathy, and the shoot fresh weight suggests absence of allelopathy. The parameter measured can determine conclusions regarding inhibitory or stimulatory allelopathy and consequently not “. . . only the dose makes a thing not a poison”—the measurement does as well.

FIGURE 6.

Effect of root exudates of Secale cereale cv. Amilo on fresh weight and phenylalanine ammonia-lyase activity (PAL) of leaves and roots of Sinapis alba.

Hormesis

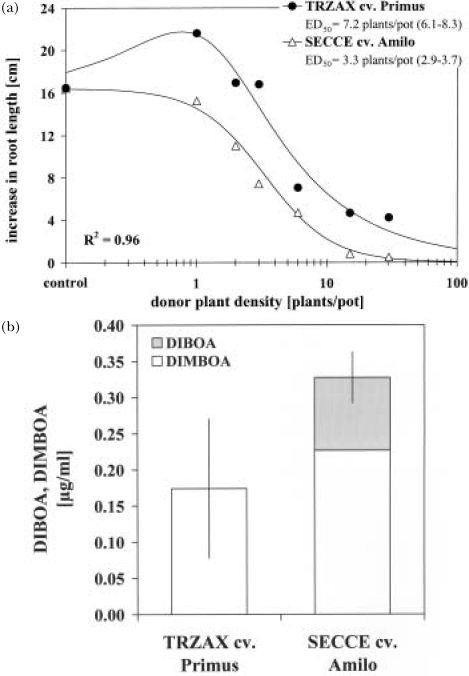
Allelopathy is a chemical-mediated process which may be stimulatory or inhibitory. If hormesis occurs, either type of allelopathy can be found with the same allelochemical, depending on its concentration. Inhibitory responses to allelochemicals are widely observed, while stimulation at low concentrations of allelochemicals is rarely described in allelopathy research. In dose-response studies with living plants, effects of allelopathic root exudates may be beneficial at low donor densities and may become harmful as plant density increases. In order to investigate potential hormetic effects, density-dependent phytotoxicity of the weaker allelopathic T. aestivum cv. Primus was compared with phytotoxic effects of the more allelopathic S. cereale cv. Amilo. In the case of cv. Primus, significant hormesis was observed at the lowest applied donor density of 1 plant/pot [f = 17.0 (0.9–33.1); M = 0.8 plants/pot; LDS = 2.5 plants/pot], while applying the same density of cv. Amilo had no significant effect on root length of S. alba (Figure 7a). Increasing donor plant density inhibited the root growth of S. alba in both cultivars. The dose-response curves were parallel (average B = 1.7), but differed significantly in ED₅₀ (R = 2.1). By assuming the reversed parallel-line concept, parallelism may indicate similarity in allelopathic effects of both cultivars and, thus, effects could rely upon the same active compound(s). If so, the differences in effects between the two cultivars may be only dose-dependent and the weaker allelopathic cv. Primus should exude lower amounts of particular allelochemicals than cv. Amilo. The chemical analysis of root exudates at the end of the bioassay revealed a differential Bx-exudation by the tested cultivars. T. aestivum cv. Primus exuded 1.9 times less Bx, comprised of only DIMBOA, compared to the total Bx-exudation by cv. Amilo, comprised of both DIBOA and DIMBOA (Figure 7b). Observed differences in Bx were almost equivalent to the relative potency of the ED₅₀ values, which supports Bx as good candidate allelochemicals in both cases, although this is not sufficient to prove that they account for all or part of the observed effects. Nevertheless, results suggest that the observed differences in density-dependent phytotoxicity may be just dose-dependent and could partly result from cultivar-specific differences in the capacity to exude Bx. Whatever the primary allelochemicals might have been, the stronger allelopathic cv. Amilo at a density of 1 plant/pot was exuding these in amounts greater than the limited dose for stimulation and, thus, hormesis was masked.

FIGURE 7.

Stimulatory allelopathy at low densities of Triticum aestivum (TRZAX) cv. Primus compared to Secale cereale (SECCE) cv. Amilo on Sinapis alba (a) and the amount of DIBOA (2,4-dihydroxy-2H-1,4-benzoxazin-3(4H)-one) and DIMBOA (2,4-dihydroxy-7-methoxy-2H-1,4-benzoxazin-3(4H)-one) in root exudates of both cultivars (30 plants/100 ml/2 hr; 12-d-old plants) (b). ED₅₀ = plant density causing 50% inhibition in root growth; asymptotic 95% confidence interval in parentheses; R² = 1 – residual SS / corrected SS.

These results demonstrate that the observability of beneficial effects in dose-response application with allelopathic plants depends on the density of the producing plants, but also on their capacity to exude active allelochemicals. Studying hormetic effects in unique applications needs to consider genotypic differences in concentrations of exuded allelochemicals by adjusting the range of densities or applying dilution series corresponding to the particular allelopathic potential.

3.2.3 The Parallel-Line Concept—ED₅₀ in Comparison

Environmental Factors—Light

Allelopathic effects are dependent on numerous abiotic factors, each having a definite and specific influence on the overall allelopathic phenomenon. Abiotic factors can impact biosynthesis, translocation, and exudation of active compounds by donor plants, their fate (half-life and location) in the environment, and their efficacy on receiver plants. All three processes inevitable alter the effective dose and should move the curve along the x-axis without affecting its shape. This hypothesis was investigated for two different cultivars of T. aestivum interfering with S. alba under two different light intensities. The response curves for both cultivars were parallel displaced (average B = 1.8) to higher doses for the lower light intensity with an average R of 1.3 ± 0.1 (Table 3). The parallel-line concept was herewith confirmed, but the question of causality remained. Since the aqueous test medium was protected from lighting, effects of light on the donor and/or on the receiver plants must be considered.

TABLE 3.

Effect of root exudates of two cultivars of Triticum aestivum (TRZAX) on the root length of Sinapis alba under different light intensities

Light Intensity [μE/m2/s]	ED50 [Plants/Pot]
	TRZAX cv. Moldau	TRZAX cv. Petrus
300 (100%)	5.8 (5.0–6.7)	8.3 (6.5–10.3)
150 (50%)	8.0 (6.3–9.6)	10.6 (9.1–12.1)
R	1.4	1.3

ED₅₀ = plant density causing 50% reduction in root growth; asymptotic 95% confidence interval in parentheses; R = relative potency for ED₅₀.

Light effects on photosynthesis should influence the production and release of allelochemicals via root exudation. Thus, the exudation of any allelochemical potentially involved in observed effects, should be affected by light. The chemical analysis of root exudates confirmed a photosensitive exudation of Bx, whereby only DIMBOA appeared in root exudates of both T. aestivum cultivars. Low light intensity reduced the exudation of DIMBOA for both cultivars with a factor of 1.3 ± 0.1, which is identical with the relative potency of the dose-response curves. Although, the observed differences in DIMBOA-exudation were not significant (Tukey-test, P = 0.05), there appeared to be a strong inverse relationship between the allelopathic activity (ED₅₀) and DIMBOA-exudation at different light intensities with a coefficient of correlation of -0.95 (Figure 8). These findings indicate that the cultivar-specific exudation of DIMBOA and its photosensitivity may have contributed to the observed parallel displacement. DIMBOA is the most abundant Bx in T. aestivum exudates and the exudation of this bioactive compound has been demonstrated to be highly cultivar-dependent (Pethö 1992; Wu et al. 2000a, 2001a, 2002; Belz and Hurle 2005) and susceptible to stress or environmental factors (e.g., Pethö 1992; Collantes et al. 1999). Thus, a causative involvement of DIMBOA in observed differential allelopathic effects of T. aestivum cultivars seems likely, but besides DIMBOA, further aspects, such as other allelochemicals, in particular phenolic acids or Bx-metabolites (Wu et al. 2002; Huang et al. 2003), or the influence of light on the sensitivity of the receiver species may also be involved. Light has been demonstrated to influence the sensitivity of target species to synthetic herbicides. The efficacy of some herbicides is enhanced at lower light intensities (Coupland 1986, 1987; Merrit 1984; Dogan and Hurle 1998), while for others activity is increased by light (Devine et al. 1993; Petersen and Hurle 2001). A similar increase in efficacy of exuded allelochemicals by light may also caused observed differential allelopathic effects. Although a contribution of other factors presently cannot be judged, the observed correlation strongly suggests a dose-dependent parallel displacement and supports the relevancy of DIMBOA for the allelopathy of T. aestivum root exudates.

FIGURE 8.

DIMBOA (2,4-dihydroxy-7-methoxy-2H-1,4-benzoxazin-3(4H)-one) content in root exudates (30 plants/100 ml/2 hr; 12-d-old plants) of two cultivars of Triticum aestivum, cultivated under two different light intensities [100% (300 μE/m²/s), 50% (150 μE/m²/s)] and the interdependence with their allelopathic activity on Sinapis alba 2. ED₅₀ = plant density causing 50% inhibition of root growth; R² = 1 – residual SS / corrected SS; r = Pearson correlation coefficient (significant at P = 0.05).

Dilution of Allelochemicals

While in the previous experiment the dose of root exudates was indirectly affected by different light intensities or cultivars, now the applied dose was directly modified by dilution. T. aestivum cv. Moldau was either co-grown with S. alba in 290 ml water (mixed cultivation), or donor and receiver were grown separately in 290 ml each with daily reciprocal exchange of test solution (monoculture). Thus, the test volume in monoculture doubled, theoretically diluting the root exudates to half that in mixed culture. This should result in a parallel displacement by R = 2. In fact, the dose-response curves were horizontally displaced (average B = 1.7), indicating dose-dependent differences, but R was 2.6 for parallel curves and 3.2 for the individual curve fitting (Figure 9a). Obviously, the pure mathematical dilution of the dose proved to be erroneous and the change in test volume must have had an indirect effect on root exudation by the donor plants and/or degradation of allelochemicals in the aqueous test medium. Thus, in this experiment, any allelochemical potentially involved in the observed effects, must be sensitive to variations in test volume. The chemical analysis of the test solution confirmed this to be true for Bx, whereby DIMBOA was the only Bx detected for T. aestivum cv. Moldau. At the end of the bioassay at day six, a 5.9-fold higher concentration of DIMBOA was found in the test medium in mixed cultivation than in monoculture. This difference probably enhanced the expected R-value and, despite a delayed degradation of DIMBOA at higher concentrations, it may be due to the fact that plants raised in mixed cultivation tended to exude higher amounts of DIMBOA. At the end of the bioassay plants grown in mixed cultivation exuded 1.6-times more DIMBOA within a 2-hr collection in trap solution (Figure 9b). Relating these exudation rates to the conditions of the bioassay with a 2-fold dilution of exudates in monoculture (580 ml), a 3.2-times higher dose of DIMBOA would results for the mixed cultivation (290 ml). This proportion is identical with the relative potency for the individual curve fitting.

FIGURE 9.

Growth inhibition of Sinapis alba by Triticum aestivum cv. Moldau in mixed cultivation versus monoculture (a) and the concentration of DIMBOA (2,4-dihydroxy-7-methoxy-2H-1,4-benzoxazin-3(4H)-one) in the test solution (30 plants/x ml/6 d) and directly exuded (30 plants/100 ml/2 hr; 12-d-old plants) (b). ED₅₀ = plant density causing 50% inhibition in root growth; asymptotic 95% confidence interval in parentheses; R² = 1 – residual SS / corrected SS; small letters indicate significant differences (Tukey-test, P = 0.05).

An et al. (2003) found evidence for the existence of a periodic production and release of allelochemicals in living plants as a response to plant stress, which should ultimately influence the allelopathic potential. This phenomenon is documented for Bx-biosynthesis and exudation by different species, and occurs upon induction by various biotic and abiotic factors, e.g., insect attack, defoliation, Fe-deficiency (e.g., Niemeyer et al. 1989; Pethö 1992; Collantes et al. 1999). Thus, the plasticity of DIMBOA biosynthesis and exudation as part of the plants chemical defense system is known, but the reasons for observed differences here are presently unexplained. Two aspects could have contributed: chemical stress by the more concentrated exudate compounds of donor plants itself or of receiver plants in mixed culture. Anyhow, the observed sensitivity of DIMBOA-exudation to variations in test volume and its correspondence with the relative potency of dose-response curves suggests a contribution of DIMBOA-exudation to observed effects and would confirm the hypothesis of a dose-dependent parallel displacement.

Results demonstrated that the parallel-line concept is also valid with the unique approach, since allelopathic interactions between living plants are affected by environmental factors. In contrast to classical applications, where the amount of the applied dose reaching the site(s) of action only depends on uptake, translocation and/or metabolic processes of the receiver plant, effects on biosynthesis, translocation, and exudation on the part of the donor have to be considered as well. This renders density-dependent applications more complex; however, the log-logistic model simulates well such interactions and simplifies their complexity. Knowledge of the behavior of a relationship under a wide variety of environmental conditions is essential for practical applications and dose-response modeling provides a mean for analyzing and predicting the impact of numerous environmental factors on a plant’s allelopathic potential.

3.2.4 Dose-Response Curves on the Move—Slope B in Comparison

Time Courses

The dose-response studies with pure scopoletin revealed that the characteristic features of the log-logistic model change with the length of exposure. The same interdependence was observed for T. aestivum cv. Pegassos interfering with S. alba. The estimated parameters displayed a positive association between sampling time and upper asymptote D, a steepening of the curve with time, and an increase in phytotoxicity, i.e., decrease in ED₅₀. Response curves differed significantly in D-values, while changes in B (1.3 ± 0.2) and ED50 (6.6 ± 1.4 plants/pot) were not significant. However, as observed with scopoletin, time influenced the quality of modeling. The decrease in asymptotic standard errors for the estimates, as well as the closer limits of the asymptotic 95% confidence intervals with increase in sampling time, confirms a more exact estimation of effective doses and a better reproducibility for prolonged sampling times.

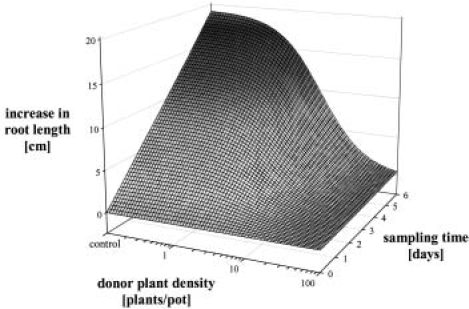
In contrast to the continuous increase in the mean root length of unaffected S. alba plants with time, root development of plants exposed to higher doses was more and more retarded until growth ceased at the highest donor density. Thus, generating time courses allows further insight in a dose-response relationship, since effects on the growth curves complete the description of the particular relationship. In the present case, effects on the growth curves at given densities were combined with the response curves at given times to form a generalized response surface for the interference of cv. Pegassos on S. alba (Figure 10). Dose-response curves run parallel to the density axis and perpendicular to the time axis, and second order polynomial growth curves run parallel to the time axis and perpendicular to the density axis. As mentioned before, a dose-response relationship needs time to develop, and response surfaces provide a valuable and complete description of the chronological development of phytotoxicity. In contrast to a single time assessment, this gives the opportunity to record differences in the speed of response processes subjected to various factors, e.g., mode of action or chemistry of allelochemicals, environmental factors, and receiver or donor species. Similar studies have not been published in connection with allelopathy, but the value of such experiments seems to justify additional experimental efforts.

FIGURE 10.

Chronological development of the dose-response relationship for the interference of Triticum aestivum cv. Pegassos with Sinapis alba, displayed as generalized dose-response growth surface.

Dose-Response to distinguish between Allelopathic Species and Cultivars?

Allelopathic root exudates vary in their quantitative and/or qualitative composition depending in the producing plant. In dose-response studies with living donor plants, quantitative differences should merely result in a dose-dependent horizontal displacement of response curves, while qualitative differences may also change the shape, provided the different allelochemicals have different modes of action. If this assumption is true, differences in allelopathic effects between species or cultivars may be parameterized by the slope of dose-response curves. The relevancy of this hypothesis was investigated comparing the dose-response patterns of cultivars of A. sativa, S. cereale, and Triticum spp.

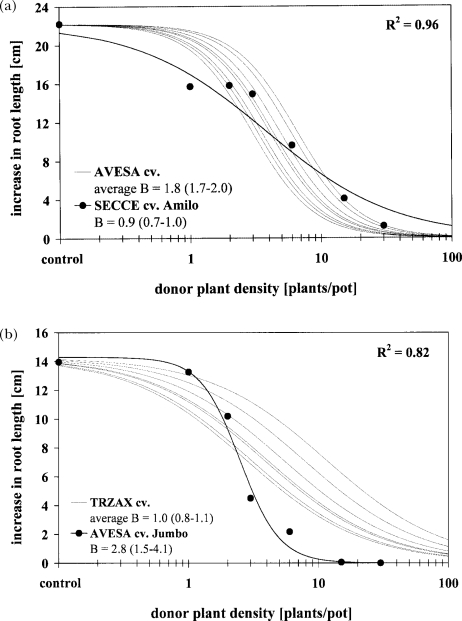
Cultivars differed in their ability to suppress the root growth of S. alba, whereby intra-specific model comparisons revealed parallel curves (Figure 11a and b). Inter-specific model comparisons proved parallelism for various combinations of Triticum spp. and S. cereale (Figure 11c), while for a combination of cultivars of A. sativa with S. cereale cv. Amilo significant differences in slope occurred (Figure 11a). The same phenomenon was observed comparing T. aestivum cultivars with A. sativa cv. Jumbo (Figure 11b). Although, individual dose-response curves of two T. aestivum cultivars did not significantly differ in slope from A. sativa, the hypothesis of an identical slope proved true with one exception—A. sativa cv. Jumbo, having a significantly steeper slope than the average of the wheat cultivars. This may indicate similar allelochemicals or site(s) of action within species, as well as between Triticum spp. and S. cereale, while the primary active compounds in root exudates of A. sativa may differ from wheat and rye. However, to draw definite conclusions, these indications must be substantiated by chemical analysis of root exudates along with a bioassay-guided isolation of the active compound(s) as well as the determination of the mode(s) of action. At present, an association between allelochemicals in root exudates and observed dose-response relationships was investigated by HPLC-DAD analysis of exudates.

FIGURE 11.

Comparison between the effects of root exudates of different plant species and cultivars on the root growth of Sinapis alba. (a) Secale cereale (SECCE) cv. Amilo versus cultivars of Avena sativa (AVESA; N = 8). (b) Triticum aestivum (TRZAX; N = 7) versus A. sativa cv. Jumbo. (c) S. cereale cv. Amilo, T. aestivum cv. Rimpaus Bastard II, T. durum cv. Extradur, and T. spelta cv. Ostar. (d) Correlation between allelopathic ability of cultivars of A. sativa (N = 9) and the exudation of scopoletin (7-hydroxy-6-methoxy-2H-1-benzopyran-2-one; 30 plants/100 ml/2 hr; 12-d-old plants). ED₅₀ = plant density causing 50% inhibition in root growth; B = slope; asymptotic 95% confidence interval in parentheses; nonlinear R² = 1 – residual SS / corrected SS; linear R² = coefficient of determination; r = Pearson correlation coefficient (significant at P = 0.01).

Intra-Specific Assessment. The chemical analysis of the root exudates of cultivars of A. sativa revealed that scopoletin was the most plentiful component. Furthermore, there appeared to be a significant inverse correlation between the amount of scopoletin in root exudates and the cultivar-specific ED₅₀ in bioassay with a coefficient of correlation of – 0.77. Thus, the variation of scopoletin in root exudates of A. sativa cultivars would explain 77% of the cultivar-specific allelopathic activity on S. alba (Figure 11d). A stronger growth inhibiting effect with increased exudation of scopoletin by A. sativa cultivars was also observed by Fay and Duke (1977) for Sinapis arvensis L., but the detected amounts were insufficient to have sole causality for the observed growth inhibition. Therefore, they concluded that activity resulted from a joint action of several allelochemicals, especially scopoletin and blue-fluorescing phenolic acids.

Preceding dose-response bioassays revealed an association between Bx-exudation and observed responses of S. alba to root exudates of Triticum spp. and S. cereale. In the case of a T. durum cultivar, Huang et al. (2003) quantified the capacity of DIBOA and its methoxylated analog DIMBOA to account for observed phytotoxicity of root exudates at 68%. Since both Bx were also the leading compounds presently found in root exudates of Triticum spp. and S. cereale, a corresponding crucial role of Bx in the observed allelopathic effects of these species seemed likely. A similar statistical linkage analysis as for oat showed that the allelopathic activity of cultivars of T. aestivum and T. spelta correlated with the exudation of DIMBOA (r = –0.48), while the activity of T. durum and S. cereale was linked with the exudation of both DIBOA and DIMBOA (r = –0.72) (Belz and Hurle 2005). However, the levels of correlation did not completely account for observed effects and, thus, other compounds must be involved here as well. In the case of wheat, corresponding investigations tracing the substantial source of the inhibiting effect also suggest the involvement of phenolic acids, further benzoxazinones, Bx-metabolites, or other unknown exudate compounds (Baghestani et al. 1999; Wu et al. 2000b, 2002; Huang et al. 2003). Whatever the most active allelochemical(s) in each case might be the observed correlations between cultivar-specific allelopathic activity and detected amounts of respective allelochemicals in root exudates confirm that scopoletin is a reliable indicator of the allelopathic potential of oat cultivars and Bx are similarly reliable indicators for Triticum spp. and S. cereale. Overall, the detected species-specific chemical composition of the root exudates would confirm the observed intra-specific parallelism and the assumption of a dose-dependent horizontal displacement.

Inter-Specific Assessment. As mentioned above, Bx were major constituents in root exudates of Triticum spp. and S. cereale. This would explain observed inter-specific parallelism of dose-response patterns, since the biological activity of DIBOA and DIMBOA is based upon unique reactive groups (Queirolo et al. 1983; Friebe et al. 1997; Sicker et al. 2000, 2003). The nonparallel displacement of dose-response curves of Bx-exuding species in comparison to A. sativa as scopoletin-exuding species is consistent with the bioassay with the pure potent allelochemicals (Figure 3). The response of L. paucicostata to scopoletin resulted in a significantly steeper slope (B = 2.4) compared to DIBOA (B = 1.1). The same phenomenon was observed in the Sinapis bioassay, where curves were always steeper for A. sativa than for Triticum spp. and S. cereale.

The search for causality of observed differences in slope on the molecular level is for various reasons exceedingly difficult. Even though a bioassay-guided isolation of the primary allelochemical(s) is still needed, one may assume that a mixture of compounds accounts for the allelopathic activity. Compounds in mixture may affect several molecular sites, and, furthermore, mixtures of compounds having the same site of action may affect biochemical sites other than the supposed primary site(s) (Streibig 1988). Considering this, a single attribution of allelopathic effects of root exudates to the leading allelochemicals seems questionable. However, the known putative primary mechanisms of action of the detected allelochemicals [Bx as inhibitors of various enzymes and scopoletin as anti-auxin] would support the theory of a nonparallel displacement, based upon differences in site(s) of action. Therefore, the dose-response design may be suitable to distinguish between species or perhaps even cultivars differing in the composition of active root exudates. If the validity and generality of this assumption for density-dependent growth experiments holds true, dose-response studies would facilitate an initial insight into primary mechanisms of allelopathic effects. This could offer the opportunity to preselect suitable plant species or genotypes for the discovery of allelochemicals with different or new sites(s) of action.

The Variability of Dose-Response Experiments

The shape of a dose-response curve is fundamentally only dependent on the site of action; however, the shape is variable, depending on a variety of factors. Sources of variation can be attributed on the one hand to nonconforming test conditions and on the other hand to an array of experimental factors. Variation of results is usually large, even within the same laboratory, depending on differences in manual preparation of assays and conditions for plant growth and test operations (Nyffeler et al. 1982; Streibig et al. 1995). A dose-response bioassay is perhaps more than other experimental designs bound to accuracy of performance and test conditions. Variability appears in every dose-response experiment and must be critically and systematically challenged before meaningful conclusions can be drawn.

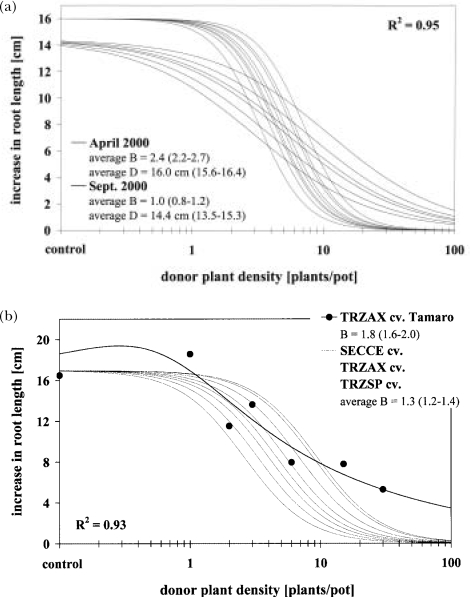
Several authors advise avoiding assay-to-assay comparison of dose-response curves (e.g., Nyffeler et al 1982; Streibig et al. 1995; Michel et al. 1999), since assay-to-assay variation often tends to be so great, that model comparisons become very doubtful and may result in erroneous conclusions. This is especially recommended regarding differences in slope B and upper asymptote D. Figure 12a clarifies this issue on the basis of two sets of bioassays, each comparing the allelopathic activity of different, randomly selected cultivars of T. aestivum on S. alba. Both bioassays were conducted according to the described methodology under greenhouse conditions, whereby the first set of cultivars was evaluated in April 2000 (N = 9) and the second in September 2000 (N = 6). Within the same experiment the dose-response curves for all cultivars were parallel, but between experiments, the two arrays of curves differed significantly in slope (B_April = 2.4; B_Sept = 1.0) as well as upper asymptote (D_April = 16.0 cm; D_Sept = 14.4 cm). It seemed unlikely that the observed nonparallel displacement could have been caused by changes in the composition of exudates and the chemical analysis confirmed this hypothesis. Variation of slope was therefore attributed to nonconforming test conditions, which is a well-known problem in greenhouse experiments (Hurle 1977), and observed significant differences in D apparently demonstrated differences in growth conditions. Based on these findings, a year-long survey was conducted under greenhouse conditions to compare the reproducibility of the dose-response curves for S. cereale cv. Amilo. Each month approximately two dose-response curves were generated (N = 22). The ED₅₀-values revealed a much better reproducibility than the slope B and the upper asymptote D. For the ED₅₀, with an overall mean of 3.5 ± 0.6 plants/pot, the hypothesis of an identical value could be accepted for P = 0.09, with three statistically significant outliers (asymptotic 0.95% confidence interval) and a range factor of 1.9 (ED_{50; max}/ED_{50; min}). For B, with an overall mean of 1.8 ± 0.5, six statistically significant outliers and a range factor of 2.7 resulted. Least robust was the upper asymptote D with an overall mean of 18.1 ± 3.1 cm, 15 statistically significant outliers, and a range factor of 1.7. Therefore, where assay-to-assay comparisons are necessary, they should be based on relative dose-response curves after scaling by the upper and lower asymptote and restricted to ED₅₀-values or the relative potency R.

FIGURE 12.

Differences in slope B and upper asymptote D depending on time of bioassay (April 2000; September 2000) exemplified by dose-response relations of 15 cultivars of Triticum aestivum (a) and lack of response levels near the lower limit for the dose-response relationship of T. aestivum (TRZAX) cv. Tamaro compared to cultivars of T. aestivum (TRZAX; N = 4), T. spelta (TRZSP; N = 3), and Secale cereale (SECCE; N = 1) (b). Asymptotic 95% confidence interval in parentheses; R² = 1 –residual SS / corrected SS.

Variation-caused changes in slope not only occur between experiments, they can also occur within an experiment, especially when using an improper dose-range (Figure 12b). A further bioassay compared the response curves of cultivars of Triticum spp. and S. cereale (N = 9) and revealed parallelism with one exception—the dose-response curve of T. aestivum cv. Tamaro varied significantly in slope. The chemical analysis of the root exudates revealed no differences in composition compared to the other cultivars, but a comparable low exudation of DIMBOA, which was presumably too low to accumulate concentrations necessary for a complete growth inhibition at any density. Thus, it was most likely that the resulting absence of a lower limit for the response curve was the primary cause for the observed variability. This result substantiates once more the crucial role of the dose-range to guarantee an accurate performance of a dose-response bioassay.

The response of an organism to an active compound is a complex process which is fundamentally based on the mode(s) of action. However, the ED₅₀ and shape of a dose-response curve can be affected by many parameters, including the range of concentrations, the application, the length of exposure, the physiological status of the test organism or plant tissue, the sampling time, or the choice of the response parameter measured. In the unique approach the donor plant provides the dose of the active compound and, thus, the risk of a high variability of responses even within the same bioassay might be higher than for the classical approach. This has to be considered when drawing conclusions from such experiments. However, if the above mentioned crucial points are avoided to the greatest possible extent, comparative dose-response studies are a valuable tool suitable for many types of investigations on density-dependent phytotoxicity.

4 CONCLUSIONS AND PROSPECTS

The application of more sophisticated, well-established techniques to allelopathy questions is important in giving the study of allelopathy more respectability. In this study, we have shown that the phytotoxicity of allelochemicals can be exploited by classical nonlinear dose-response modeling, a technique well-established in other biological sciences. The general principles of dose responses could be applied to allelopathic studies, whether pure compounds or intact, growing plants were used to deliver the dose of phytotoxin(s). The four parameter log-logistic model or its peaked expansion adequately described most of the observed dose-response patterns and provided a valuable tool to study density-dependent phytotoxicity if the response to exuded allelochemicals was curve-fitted to donor plant density. The examples presented here indicate the value of such approaches as a means for analyzing and generalizing the mechanisms of allelopathy phenomena for a wide range of experimental conditions and as a potential predictive tool for allelopathic effects in natural settings. Exploring or purposely manipulating plant-plant interactions in dose-response experiments can offer challenging insights into allelopathy and advance our understanding of this phenomenon.

Paracelsus might not have thought about allelopathy, but he is right, “all things are poison . . .” including allelochemicals and allelopathic plants.