Renal Tumor Quantification and Classification in Contrast-Enhanced Abdominal CT

Abstract

Kidney cancer occurs in both a hereditary (inherited) and sporadic (non-inherited) form. It is estimated that almost a quarter of a million people in the USA are living with kidney cancer and their number increases with 51,000 diagnosed with the disease every year. In clinical practice, the response to treatment is monitored by manual measurements of tumor size, which are 2D, do not reflect the 3D geometry and enhancement of tumors, and show high intra- and inter-operator variability. We propose a computer-assisted radiology tool to assess renal tumors in contrast-enhanced CT for the management of tumor diagnoses and responses to new treatments. The algorithm employs anisotropic diffusion (for smoothing), a combination of fast-marching and geodesic level-sets (for segmentation), and a novel statistical refinement step to adapt to the shape of the lesions. It also quantifies the 3D size, volume and enhancement of the lesion and allows serial management over time. Tumors are robustly segmented and the comparison between manual and semi-automated quantifications shows disparity within the limits of inter-observer variability. The analysis of lesion enhancement for tumor classification shows great separation between cysts, von Hippel-Lindau syndrome lesions and hereditary papillary renal carcinomas (HPRC) with p-values inferior to 0.004. The results on temporal evaluation of tumors from serial scans illustrate the potential of the method to become an important tool for disease monitoring, drug trials and noninvasive clinical surveillance.

1. INTRODUCTION

Kidney cancer is made up of a number of different types of cancer, where clear cell renal carcinoma accounts for the vast majority of cases [16]. Whether hereditary or sporadic, other types of kidney cancers include papillary, chromophobe and collecting duct renal carcinoma [9,26,33] It is estimated that almost a quarter of a million people in the USA are living with kidney cancer and their number increases by 51000 every year [19]. Patients with localized disease have a 95% 5-10 year survival, but as the disease reaches an advanced stage, the 2-year survival rate drops to 18%. While several major risk factors associated with renal cancers have been identified, i.e. family history, obesity, smoking and hypertension medication, at least 40% of the cases are of unexplained causes. [17,19].

The established treatments of renal cancer include surgery (radical or partial nephrectomy), chemotherapy, radiation therapy and radiofrequency ablation [9]. New additions to the family of available treatments are molecular therapeutic agents, which target the kidney cancer gene pathways [1,9,18,19]. While the advance of targeted therapies is a topic of intensive research, clinical investigations are actively involved in the development of new drugs for chemotherapy.

The state-of-the-art minimally-invasive clinical procedures for diagnosis and monitoring kidney cancers are image-based and use computed tomography (CT) or magnetic resonance imaging (MRI) [2,9,32,47]. Contrast-enhanced CT has proven exceptionally useful to an improved diagnosis due to the ability to differentiate tumors from healthy kidney tissue. Figure 1 shows an example of normal kidney parenchyma and lesion intensity change in contrast enhanced CT. The level of enhancement in the tumor is an important indication of malignancy and can be associated with the intensity homogeneity of tissue to better classify renal abnormalities [6,42,45,47]. Some examples of tumor variability can be found in Figure 2, spanning from small to large, adipose to solid, and homogeneous to heterogeneous. Equally important is the growth rate (or regression rate during treatment) of tumors for a better targeted therapy. Recent studies emphasize the importance of optimized post-contrast injection scan delays using contrast bolus tracking techniques to assist the diagnosis of kidney cancer [8].

Figure 1.

Multi-phase abdominal 4D CT data. 2D slices of 3D volumes: (a) before contrast, (b) arterial enhancement phase and (c) venous/portal enhancement phase data. For visualization purposes, 3D volumes are aligned according to the position in the scanner. Note the improved differentiation between normal renal tissue and tumors during enhancement.

Figure 2.

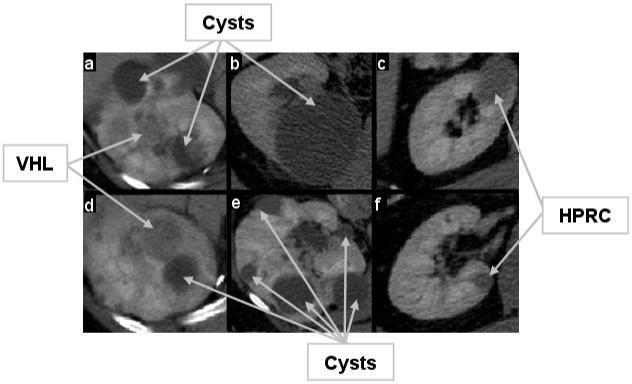
Examples of renal tumors in the portal phase. The level of enhancement, intensity and homogeneity inside the lesion are indications used in diagnosis and classification. The examples include small, large, cystic (lower intensity, non-enhancing), solid (higher intensity, enhanced), homogeneous and heterogeneous tumors. VHL tumors are shown in (a) and (d); in (b) and (e) there are only cysts, although cysts can be found in (a) and (d); and HPRC lesions are shown in (c) and (f).

The management of kidney cancers encompasses studies from biology and etiology to early detection, diagnosis and treatment, and control and modeling. Monitoring the evolution of renal cancer is an essential part of the process and a rich source of information for diagnosis, understanding cancer development, and response to treatment. As manual measurements are time consuming and show high intra- and inter-operator variability [21,23], computer-assisted radiology (CAR) shows great promise in assisting the robust monitoring of renal tumors. Moreover, the two-dimensional (2D) bias toward the image acquisition plane manifested during the manual quantification of cancer can be removed by the 3D analysis allowed by computer analysis. The advance of strategies for cancer treatment and understanding causes of therapeutic failure will also rely on a combination of adequate perception of the underlying biological mechanisms [15] and non-invasive imaging analysis.

Most work in renal image analysis relates to kidney segmentation and not to kidney cancer quantification. Gao et al. proposed a 3D deformable surface model to segment the kidneys in CT [7]. They initialize the model manually by specifying the superior and inferior poles and the boundaries of three intermediate CT slices of each kidney and then interpolate to estimate the model parameters. Deformable models are also employed in [13] in a multiscale medial representation. The shape characteristics of kidneys are imbedded in a 3D statistical template and fitted to image data using a log likelihood term. A similar deformable shape model is presented in [28] combined with principal geodesic analysis. A comparison between manual and automatic kidney segmentation reveals good volume overlap and important potential for using computer-aided kidney analysis.

Recently, statistical models have been used towards multi-organ abdominal segmentation. Park et al. use a database of hand-segmented CT abdominal scans to compute a mean image [25]. This is registered with thin plate splines to propagate the segmentation of liver, kidneys and aorta. Using a similar principle, a priori data from probabilistic atlases is used to initialize the segmentation of abdominal organs in [35,44]. Both methods use measures of relationship and hierarchy between organs and manual landmarks. On a different note, contrast enhanced CT data from four-phases are employed in [10,31]. Hu et al. [10] use independent component analysis in a variational Bayesian mixture, while Sakashita et al. [31] combine expectation-maximization and principal component analysis to segment abdominal CT including the kidneys. Other groups addressed the segmentation of kidneys from dynamic MR images using graph-cuts [4,30] or wavelets and temporal dynamics [36].

The segmentation of renal tumors is seldom addressed. Notably, a marker controlled watershed algorithm is used in [38] to segment both renal and lesion volumes in 2D data. Three manual contours initialize the segmentation of the kidney, while homogeneous tumors are detected using granulometry. Alternatively, a homogeneous region growing from a seed point is presented in [14].

Our study proposes the semi-automated quantification of renal tumors for the assertive management of tumor diagnoses and evolution monitoring. It quantifies the three-dimensional size, volume and enhancement of renal tumors, as well as monitors the evolution of lesions over time and in response to treatment. The algorithm employs registration and smoothing to prepare the data, a combination of fast-marching and geodesic level-sets for segmentation, and lesions quantification. As a major challenge to robust CAR remains the reliable visualization and identification of tumor boundaries, a novel adaptive refinement step to adapt to the shape and intensity of the lesions is proposed. We present results on segmenting and assessing various types of renal tumors and compare automated and manual segmentation. This is, to our knowledge, the first semi-automated method that allows the temporal analysis of renal tumors and enhancement quantification for lesion classification.

2. METHODS

The method can be subdivided into three major steps, each consisting of several sub-stages. Data from the three-phase scans are first aligned by the image position relative to the body. The pre-processing of images includes an intra-patient inter-phase registration and data smoothing. The registration corrects for abdominal motion between subsequent acquisitions, while smoothing removes noise and enhances edges. The next step segments the renal tumors using geodesic active contours and an input from fast marching level sets. Tumor margins are difficult to identify in the majority of cases, and lesions tend to have a variety of shapes other than spherical. Hence, the method analyses local values of gradients starting from the provided landmarks and adapts the segmentation parameters accordingly. Finally, the size and enhancement characteristics of each tumor are computed and the temporal evolution of lesions is analyzed. A diagram of the algorithm is presented in Figure 3. The implementation uses Visual C++ 8.0 (Microsoft), OpenGL (SGI) and the Insight Segmentation and Registration Toolkit (ITK) 2.4 (Kitware, Inc.) [11].

Figure 3.

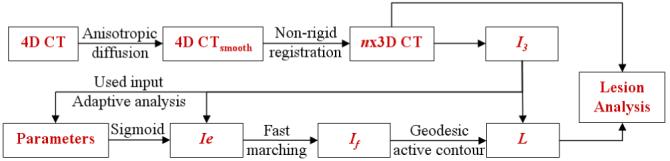
Diagram of the algorithm flow. I_e represents the edge image, I_f the fast marching segmentation, L the final level set and n the number the time acquisitions.

2.1 Data Smoothing

CT data are smoothed using anisotropic diffusion to enhance the homogeneity of abdominal objects and ensure boundary preservation. We employ the classic Perona-Malik anisotropy model [27]. During the diffusion process, smoother versions of an image I are computed iteratively

$$\begin{array}{c}\hfill {\delta }_{t}I=\mathit{div}(\mid \nabla I_{\sigma }\mid \cdot \nabla I);\hfill \\ \hfill g\left(x\right)=\frac{1}{\sqrt{1+{(x∕k)}^2}};\hfill \end{array}$$ (1)

I_σ is the result of the convolution of I with a Gaussian of standard deviation and div the divergence. The resulting image provides stable edges over a large number of iterations based on a rapidly decreasing diffusivity g, but will only enhance those edges for which the gradient is larger than the contrast parameter k.

The smoothing process respects a minimum-maximum principle and does not alter the mean value inside of the smoothed object. The standard deviation is decreased due to the reduction of noise and homogenization of intensities. Heterogeneous objects will however have high standard deviation, as they comprise edges inside their volume and edges are preserved during smoothing by anisotropic diffusion. Figure 4 shows an example of kidney CT smoothing. A compelling review of anisotropic diffusion can be found in [43].

Figure 4.

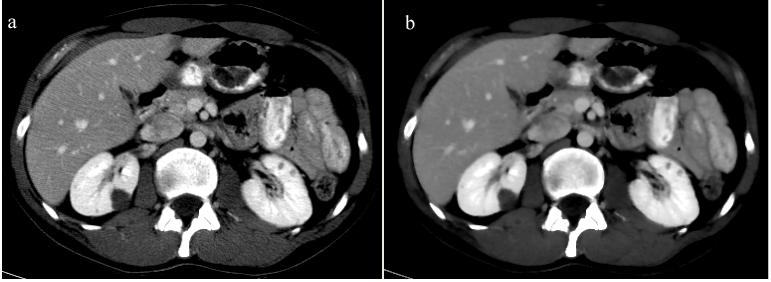
Image smoothing. When noise is removed from the original CT image (a), the smoothed image (b) exhibits increased homogenous in regions of similar enhancement, and well-preserved heterogeneity in volumes that comprise edges.

2.2 Intra-patient Inter-phase Registration

An example of multi-phase CT is presented in Figure 1. Although the acquisitions are done during the same session and intra-patient, note the abdominal motion between the three images. Hence, a motion correction is necessary to monitor the enhancement of lesions between the three phases, especially in the cranial-caudal direction [29,39]. Based on the irregularity of abdominal motion, a rigid deformation (translation and rotation) would not be sufficient; hence we assume that the best deformation will be non-rigid [46]. An affine motion model is equally considered [3].

The images from the first two phases of contrast-enhanced abdominal CT data (non-contrast or I₁, and arterial or I₂) are registered to the portal (or venous or I₃) phase. Since data are acquired during a single acquisition session, inter-acquisition motion is mainly due to breathing and cardiac pulsation, though small patient movements are also present. The relatively limited range of motion between phases permits the use of the demons non-rigid registration algorithm, which requires partial overlaps between the objects to be registered, in this case between each organ over multiple phases [40]. The deformation field D of image I to match image J is governed by the optical flow equation and can be written as [40].

$$D=\frac{(I-J)\nabla J}{{\parallel \nabla J\parallel }^2+{(I-J)}^2};$$ (2)

The multi-phase CT data is intra-modal, but the different levels of organ enhancement justify the use of a multimodal similarity measure. Mutual information m accounts for intensity variability within the same organ during multi-phase acquisitions, where p(i,j) is the joint probability distribution of images I and J, and p(i) and p(j) the marginal distributions [22,41].

$$m(I\mid J)=\sum _{i,j}p(i,j)\log \frac{p(i,j)}{p\left(i\right)p\left(j\right)};$$ (3)

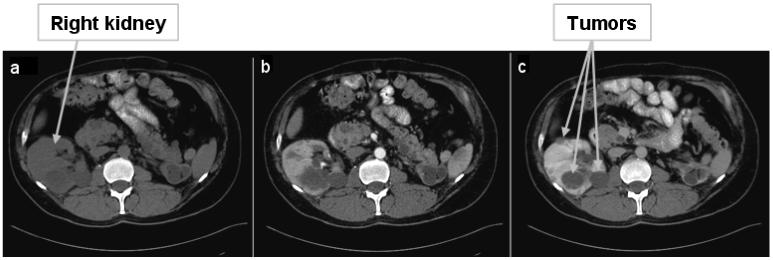
Registration results are interpolated with cubic B-splines. A comparison between affine and non-rigid registration algorithms for intra-patient inter-phase abdominal CT images was performed, as seen in Figure 5. We employed an entropy-based affine transformation [37] for this comparative example. Both transformations produce the major shift in the cranial-caudal direction to align the tumor present in the right kidney (Figure 5). However, as noted from the difference images, the non-rigid registration finds better local correspondences between the individual organs boundaries, as well as globally between the body edges. Moreover, the difference in intensity between images due to contrast enhancement is clearly depicted by the non-rigid transform, which is better adapted locally (as seen in the left kidney).

Figure 5.

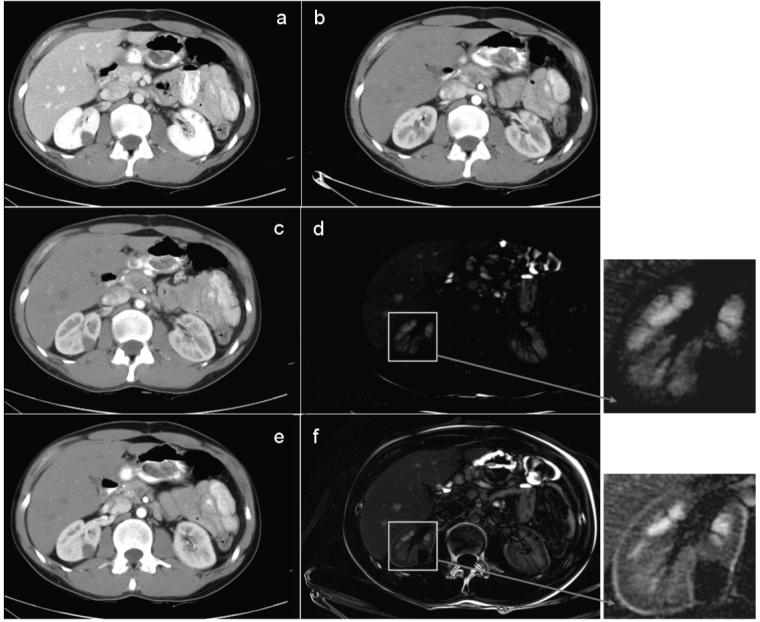
Intra-patient 3D registration. This example shows results of registering data from arterial and portal phase: (a) a 2D slice from portal phase; (b) the corresponding 2D slice at arterial phase, aligned by the position in the body, as seen at the spinal cord; (c) the registered image from (b) using the demons algorithm; (d) the difference image between (a) and (c) after non-rigid registration; (e) the registered image from (b) using affine registration; (f) the difference image between (a) and (e) after affine registration.

2.3 Segmentation

The second stage of the method is the segmentation of renal lesions and our approach uses a combination of fast marching and geodesic active contour level sets [5,24,34]. Level sets are surfaces that expand or contract, split or merge in the direction orthonormal to the surface. Their definition allows level sets to be adapted to the image conditions and by using knowledge of shape, curvature and edge to segment incomplete data. Like other types of isosurfaces, level sets are expressed as time-crossing maps.

A fast marching level set is used to initialize the segmentation [34]. The fast marching method assumes that the surface can only expand starting from the seed point provided by the user. The speed of expansion is constant and along the surface normal n. The venous phase CT scan (I₃) provides the feature image, while the sigmoid of the gradient of I₃ supplies an edge image (or speed function) I_e, with α and β computed from ∇I₃. The first segmentation given by the fast marching level set is I_f.

$$\begin{array}{c}\hfill I_e=1-\frac{1}{1+\exp \left[-\frac{\nabla I_3-(\alpha +\beta )}{3(\alpha -\beta )}\right]};\hfill \\ \hfill \frac{d{I}_f}{dt}+\overrightarrow{n}{I}_e\nabla I_f=0;\hfill \end{array}$$ (4)

A better-adapted level set based on geodesic active contours in used to refine the fast marching segmentation [5]. In deformable models there are two types of forces that govern the evolution of the active contour: the internal forces within the surface, which keep the model smooth during the deformation, and the external forces from the image data, which attract the model towards edges. To initialize the model, we use the fast marching segmentation as input level image (zero-level) into a geodesic active contour I_L. The weights w₁, w₂ and w₃ control respectively the speed c, curvature k and attraction to edges [5].

$$\begin{array}{c}\hfill \frac{d{I}_L}{dt}=I_e(w_{1}c+w_{2}k)\mid \nabla I_L\mid +w_3\nabla I_e\nabla I_L;\hfill \\ \hfill I_{L,t=0}=I_f;\hfill \end{array}$$ (5)

2.4 Parameters

The adaptation of algorithm to image characteristics is important for the robustness of the segmentation and the independence of the method on parameter setting and user intervention [20]. Notably, the edge image I_e plays an essential role in the evolution of the isosurfaces resulting from the segmentation using level sets. As seen in equation (4), the definition of I_e is dependent on parameters α and β computed from the gradient image. α relates to the minimum gradient measure on the lesion boundaries, while β is a measure of the mean gradient values within the tumor. The estimation of parameters α and β is addressed next.

As lesions can be heterogeneous, only a boundary analysis of the image would not suffice, as segmentation algorithms would stop at inner-lesion edges. Hence, the initialization of the segmentation is performed manually to provide both information about the location and range of size of the lesion to quantify, and knowledge about the strength of the tumor boundaries in relation to its inner edges. However, to keep the user intervention minimal, only two points are required: one for the approximate tumor center p_c, and a second along its boundaries p_b. The first approximation of lesion is that of a sphere of radius r given by the Euclidian distance d=|p_c ,p_b|. An example of tumor landmark selection is presented in Figure 6. p_c is approximated using axial and sagittal views, while p_b is placed on the same axial slice as p_c.

Figure 6.

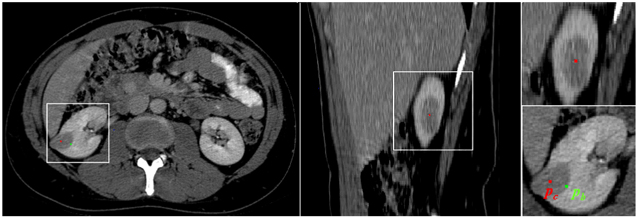
An example of landmark selection. The axial and sagittal views are used to choose the approximate center of tumor (p_c) shown in red. The point on the boundary (p_b) is marked in green on the same axial slice as p_c at a location along the tumor edge.

Given the locations of center and boundary of lesion, the gradient values along 26 rays originating from p_c are recorded. As shown in a simplified 2D representation in Figure 7, we retain the gradient values on segments of length d centered on the sphere boundary to computeα. The dashed circle in the left part of Figure 7 represents the area that is used to computeβ. Hence, we allow errors in the initial estimation of tumor size to vary to ±50%, as many tumors are not spherical. This further allows correcting for the erroneous placement of p_c and p_b.

$$\begin{array}{c}\hfill \alpha =\min \bigcup _{i=1,26}\underset{d_i}{\max }(\nabla I_3);\hfill \\ \hfill \beta =\underset{r\le d∕2}{\text{mean}}(\nabla I_3);\hfill \end{array}$$ (6)

Figure 7.

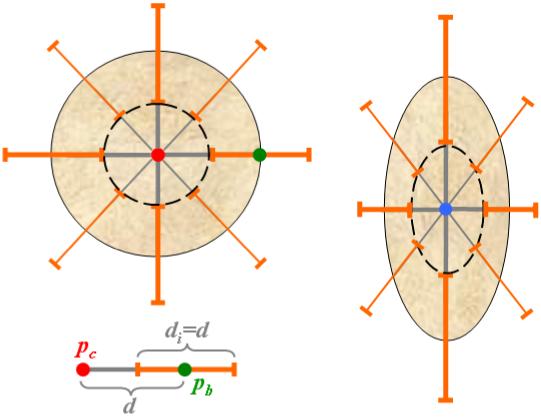
Parameter adaptation. The initial lesion model is spherical with the radius d, as seen in the simplified 2D representation on the left. The elements d_i used for the estimation of tumor edges and parameter α are shown in orange, the inner object used to compute β in dashed black, and the user landmark p_c and p_b in red and respectively green. The process of parameter calculation is repeated for the updated ellipsoidal model shown on the right.

The analysis of the histogram of gradient candidates permits to eliminate the outliers. Both the location of the edge (with the maximum gradient along the ray) and the value of α can now be estimated. We also assume that the first approximation of α must be at least 20% higher than the initial estimate ofβ.

The centroid of the object within the new set of boundaries updates the location of p_c, and the spherical form r=(d,d,d) is changed to an ellipsoidal model r=(r_x, r_y, r_z ), with r_x≠r_y ≠r_z , as shown in the right side of Figure 7. The gradient values along the edges and inside the ellipsoid are recalculated and the resulting location of the tumor center p_c is used as seed point for the fast marching level set. The updated values of α and β provide an adapted speed function, as in equation (4), to assist with the segmentation of lesions.

The ellipsoidal model provides a search space and not an approximation of the tumor shape. It finds edges in this search space, which are subsequently used to compute parameters α and β. There is no shape constraint in segmenting the tumor; α and β estimate the edge strength. However, highly heterogeneous tumors may have edges inside the lesion body as strong as its boundaries. Enforcing a higher α than β, the computation of the sigmoid will provide a speed image that will overlook the internal boundaries in the lesion.

2.5 Lesion Quantification

We compute the linear and volumetric measurements of a lesion from its segmentation (manual or automatic). We first apply a principal component analysis (PCA) [12] to compute the principal axes, then project the lesion surface to the principal axes and compute the linear measurement. PCA computes the statistically significant principal axis (the longest axis) from the entire object; hence, more robust than using a 3D bounding box, which is sensitive to outliers and noise in the segmented object. The PCA method can be written as

$$\begin{array}{c}\hfill \stackrel{‒}{Y}=\frac{1}{n}\sum _{i=1}^n{Y}_i;\hfill \\ \hfill C=\frac{1}{n-1}\sum _{i=1}^n(Y_i-\stackrel{‒}{Y}){(Y_i-\stackrel{‒}{Y})}^T;\hfill \end{array}$$ (7)

where Y_i is a vertex on the surface, n is the total number of vertices, Y is the centroid of the surface, and C is the covariance matrix. The eigenvectors Φ = {ϕ₁,ϕ₂,ϕ₃} of C form the principal axes of the lesion. The linear measurement is then computed

$$L_k=\mid \underset{i=1}{\overset{n}{\mathit{Max}}}\left({\Psi }_{{\varphi }_k}\left(Y_i\right)\right)-\underset{i=1}{\overset{n}{\mathit{Min}}}\left({\Psi }_{{\varphi }_k}\left(Y_i\right)\right)\mid ,k=1..3;$$ (8)

where Ψ_ϕk (Y_i) is a function to project Y_i to axis ϕ_k, and Max and Min are functions to find the two extreme points of the projections. L₁ is the longest linear measurement of the lesion. The volumetric measurement is simply the summation of all voxels inside the segmented region.

$$V_A=\sum _{i}P\left(v_i\right);$$ (9)

V_A is the segmented volume and P(v_i) is the volume of a voxel v_i inside the segmented region.

For the accurate estimate of segmentation overlap between the automatic and the manual segmentations, we compute the Dice Coefficient as one metric for validation

$$D=\frac{2\mid S_A\cap S_M\mid }{\mid S_A\mid +\mid S_M\mid };$$ (10)

D is the Dice Coefficient, S_A is the segmented region of the automatic method, and S_M is the manually segmented region by an expert. S_A ∩ S_M is the common voxels in both S_A and S_M.

3. RESULTS

The semi-automated renal tumor segmentation method was evaluated on a combination of benign cysts and cancers, namely von Hippel-Lindau (VHL) syndrome cases and hereditary papillary renal carcinomas (HPRC). Contrast-enhanced CT data had three acquisitions at corresponding to three time points. The first image was obtained before contrast administration. Then the patients were injected with 130ml of 1SOVUE-300 and two more contrast-enhanced data acquisitions were completed during arterial and portal phases. The distinction between phases was performed using fixed-delays of 25-30s and 65-70s for the arterial and venous phases respectively, depending on the scanner. The CT data were collected using GE LightSpeed Ultra and GE LightSpeed QX/i scanners from GE Healthcare, and Philips MX 8000 from Philips Medical Systems. Image resolution ranged from 0.70 × 0.70 × 1.0 mm³ to 0.97 × 0.97 × 1.00 mm³. Image size ranged from 512 × 512 × 189 voxels³ to 512 × 512 × 316 voxels³.

3.1 Tumor Segmentation

Data from 10 patients with tumor lesions were analyzed: 5 diagnosed with hereditary papillary renal carcinoma (HPRC) and 5 diagnosed with von Hippel-Lindau syndrome (VHL). A total of 31 individual lesions were analyzed from the patient scans, including 14 HPRC, 8 VHL and 9 benign cysts. Patients had between one and two scans, bringing the number of analyzed lesions to 55.

Lesions are segmented in the venous phase, where they appear better differentiated from the enhanced renal tissue. Cysts are adipose and remain radio-opaque during enhancement having well defined edges and a homogenous appearance, while VHL lesions tend to be solid and enhance more. HPRC tumors vary from cystic to solid and the mix of the two types. The most difficult segmentation occurs for mixed heterogeneous lesions that are both solid and cystic. The inner edges may confuse the estimation of segmentation parameters and a new segmentation seed may be required.

The segmentation of renal tumors is visually validated by overlaying the segmented data on the CT volumes, as shown in Figure 8. Tumors are robustly segmented, as confirmed by expert clinicians. Figure 8 presents segmentation examples for the three groups of lesions that we addressed.

Figure 8.

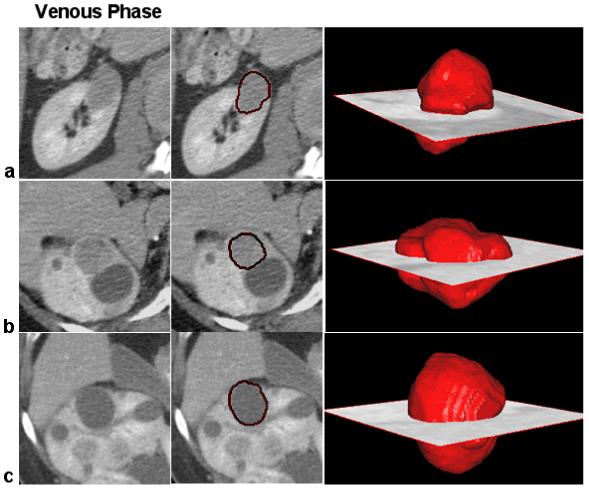
Examples of 3D segmentation of renal lesions. Row (a) shows the segmentation of an HPRC lesion; on row (b) we present a VHL cancer; and on row (c) a benign cyst. Near 2D slices from the 3D CT volumes, we present the segmentation results using our method for renal tumor segmentation and quantification. The 3D volumes of the segmented lesions are overlaid on the CT scan at the location of the tumor.

Twelve lesions (5 HPRC, 5VHL and 2 benign cysts) were segmented manually by two observers for the precise quantification of the segmentation. The maximum size of lesions varied from 11.17mm to 71.82mm. The overlaps of the segmented lesions were computed, as described in Section 2. The inter-observer measurements show an overlap of 0.807±0.064, while the overlap between the computer segmentation and each of the observers is 0.806±0.065 and 0.805±0.056 respectively. Thus, the comparison between manual and semi-automatic quantifications shows disparity of the same magnitude as the inter-observer variability. The sizes of lesions were quantified and the correlations and p-values of the paired t-test between measurements are presented in Table 1. Once more, results show similar variability between observers as between computer and human measurements. Figure 9 presents the best linear fit for the comparative measurements.

Table 1.

Lesion quantification variability. The columns present the Pearson correlation coefficient/p-value of the paired t-test between volume and maximum size measurements, and segmentation overlaps. The rows show the comparisons between each of the two independent observers and the computer quantification/segmentation (CAD) system, and the inter-observer variability on the last row

	Volume Correlation/p-value	Size Correlation/p-value	Overlap
Observer1 - CAD	0.999/0.156	0.984/0.02	0.805
Observer2 - CAD	0.999/0.388	0.985/0.055	0.806
Inter-observer	0.999/0.007	0.983/0.39	0.807

Figure 9.

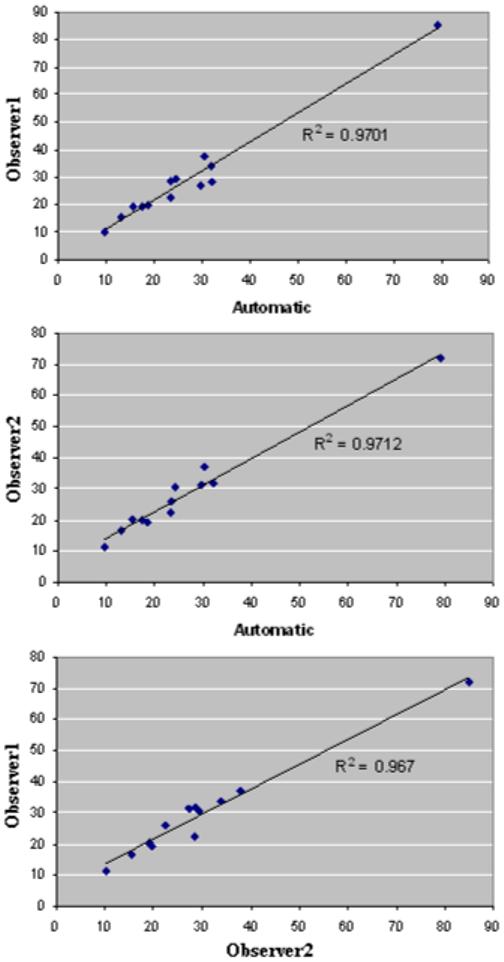
The best linear fits for correlated measurement results between the automated method and the two sets of 3D manual measures. From top to bottom, the charts show correlated data corresponding to the largest size of the segmented lesions. R-squared measures confirm that the variability between the automated method results and those of observers are in the same range as inter-radiologist variability.

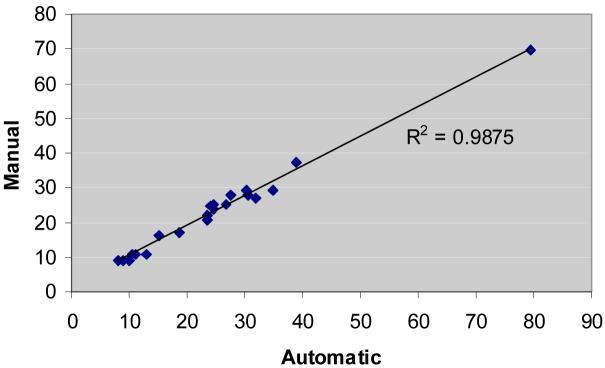
Further analysis was performed using available clinical measures for 21 of the 31 lesions described above. They varied in size from 9.08mm to 69.7mm. There were 5 VHL, 9 HPRC and 7 cystic benign lesions. The manual measurements were performed on 2D axial CT slices at the maximum size of the lesion. The correlation coefficient between the clinical measurements and the automatic quantifications was of 0.993, and the p-value of the pared t-test of 0.003. The best linear fit for the correlated measurements is shown in Figure 10 and has an R-squared value of 0.987.

Figure 10.

The best linear fit for correlated measurement results between the automated method and the clinical 2D measures.

3.2 Robustness

The goal of this semi-interactive technique is to provide the best segmentation of renal lesions for cancer monitoring. Therefore, it allows to repeat the segmentation if the result of segmentation was not satisfactory after visual inspection. The chosen segmentation will be referred as the best segmentation.

The technique is particularly sensitive to the placement of seed points in two circumstances: (1) when the size of the tumor is over-or under-estimated, as the search space for edges changes and number of iterations of the geodesic active contour varies with the approximation of the size of the tumor; and (2) when tumors are highly heterogeneous. Two experiments were designed to determine the sensitivity of the algorithm to the variation of the seed points: one in which the central seed point (p_c) is kept unchanged, while the first estimate of the radius r of the tumor is varied by changing the boundary point (p_b); and a second in which the radius is kept constant, but p_c is moved. Figure 11 shows the variation of the relative errors in estimating the tumor size, volume and enhancement with the changes in the placement of the two seed points. Through the adaptation of the algorithm to tumor characteristics, the method is less sensitive to the change of the central seed point with 3.6% volume error, 2.3% size error and 1.9% enhancement error for a variation of 10 voxels in the position of p_c (the seed points are always inside the tumor boundary). The errors increase when the manual estimation of the tumor size r changes dramatically and become 31% of the volume, 10% of the size and 12% of the enhancement, when the radius size is varies by 25% of the maximum size of the tumor.

Figure 11.

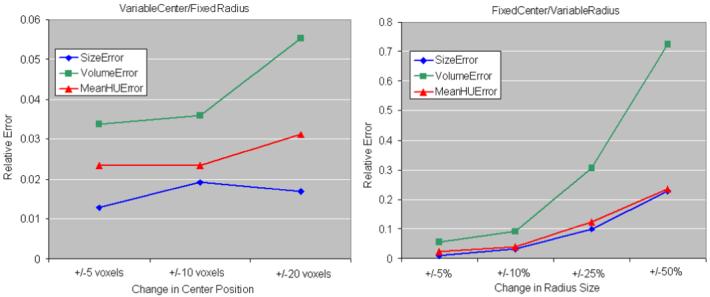
Seed point variation. The errors in size, volume and enhancement estimations are presented, relative to the best segmentation. The chart on the left shows the relative errors when the center seed point is moved with 5, 10 and 20 voxels, without changing the manual estimation of the tumor radius. On the right, the manual radius estimate is varied with 5, 10, 25 and 50% of the maximum tumor radius, without changing the central point.

The parameter k in the smoothing (equation 1) was 15 and chosen empirically, from training on seven tumor cases, which were not included in the test set. For this application, we aimed to enhance the edges in our data besides increasing the tumor homogeneity, as the edge properties are important for the segmentation. Weak edges within the tumor tend to be smoothed with the chosen value of k and increase the homogeneity of heterogeneous lesions.

The initial training of method parameters was performed on a database of seven cancers and cysts. Their n values were kept unchanged for the segmentation of the analyzed renal lesions (VHL, HPRC and cysts). The robustness of parameter choice is reflected in the quality of the segmentation results.

The influence of parameter k and of the number of iterations of the anisotropic diffusion is presented in Figure 12. The method is robust to small changes of the contrast value and relative errors in size and volume estimations increase over 5% when k is varied by more than 10 units. Errors remain smaller than 2% when the number of iterations is varied, but increase to 9% volume error, 7.7% size error and 3% enhancement if no smoothing is employed. Examples of segmentation with and without employing anisotropic diffusion are shown in Figure 13. The subsequent tumor classification is performed using the mean intensity (Hounsfield units) inside the segmented tumor, without smoothing the data. The anisotropic diffusion is employed to facilitate the segmentation, but not to quantify the lesions.

Figure 12.

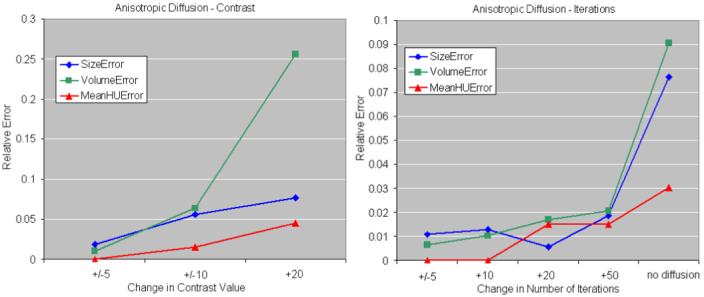
Anisotropic diffusion variation. The errors in size, volume and enhancement estimations, relative to the best segmentation are presented. The chart on the left shows the relative errors when the contrast value in the anisotropic diffusion is varied with 5, 10 and 20 units. On the right, the number of iterations is varied with 5, 10, 25 and 50 iterations.

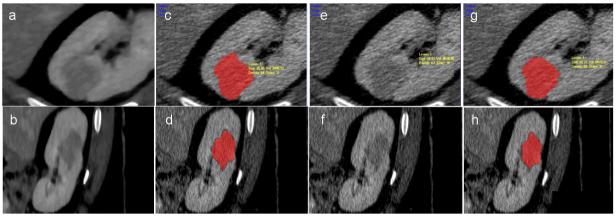
Figure 13.

The influence of anisotropic diffusion. (a) and (b) show the smoothed CT scan in magnified axial and sagittal views; (c) and (d) are the segmentation results on non-smoothed data, but using smoothing during the segmentation process. (e) and (f) show the non-smoothed CT scan; and (g) and (h) are the segmentation results on non-smoothed data, without using smoothing during the segmentation process.

3.3 Enhancement Analysis

Based on observations from prevailing literature [42,45,47], we analyzed the patterns of lesion enhancement aiming to observe if the computer-assisted quantification can differentiate between different types of lesions. For the enhancement analysis, we selected 15 lesions, 5 of each type: VHL, HPRC and benign cysts. From data registration, scans obtained before contrast and at arterial phase were aligned to the venous phase. Then the computer segmentations of lesions from the venous phase were used to estimate the mean intensity of lesions in the other phases. Mean intensities were normalized by the values between contrast intake and the speed and level of enhancement between lesion groups were compared. Figure 14 exemplifies the enhancement patterns of VHL versus HPRC and benign lesions, while in Figure 15 we show an example of multi-phase segmentation of lesions after image registration. Although there is insufficient intensity information for the direct segmentation of tumors from the non-contrast and arterial phases, from non-rigid registration and propagation of segmentation through phases, our method allow the accurate quantification of lesions at different stages of enhancement.

Figure 14.

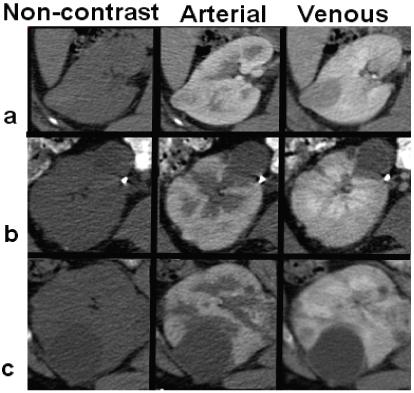
Variable enhancement between different lesion types. From left to right, images are captured before contrast, at arterial phase and at venous phase. The top row (a) shows the enhancement of a VHL lesion, the middle row (b) a less enhancing HPRC tumor, and the bottom row (c) presents a non-enhancing benign cyst.

Figure 15.

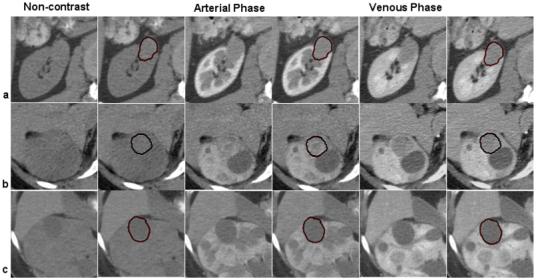
Multi-phase segmentation of renal lesions. Row (a) shows a multi-phase segmentation example for an HPRC lesion; on row (b) we present a VHL cancer; and on row (c) a benign cyst. The columns illustrate 2D slices of 3D CT data from three phases of enhancement at the location of the tumor, next to the segmentation provided by the computer-assisted method. The propagation of segmentation between registered images from three phases, allows the accurate quantification of tumors, although there is insufficient image information for the direct segmentation from all phases.

Statistical analyses of the patterns of enhancement were performed for groups of lesions (VHL-HPRC, VHL-cysts and HPRC-cysts). For all 15 lesions we calculated the enhancement (difference of intensity) between phases (arterial and before contrast, venous and arterial, and venous and before contrast) and we computed the Pearson correlation coefficients and the p-values of two-sample t-test. Numerical results of the analysis can be found in Table 2. Note that the best differentiation between them is achieved using the relative enhancement between the venous phase and the acquisition before contrast administration. We obtained p-values of 0.004 (VHL to HPRC), 0.002 (HPRC to cysts) and 0.001 (VHL to cysts). Figure 16 shows the boxplots between the three groups of lesions grouped by two. The three categories of lesions are robustly differentiated by the algorithm and have mean relative enhancement values of 10.06 (cysts), 27.936 (HPRC) and 88.1 (VHL).

Table 2.

Lesion enhancement quantification. The columns present the Pearson correlation coefficient/p-value of the two-sample t-test of the intensity difference (enhancement) between the three acquisition phases (before contrast administration, arterial and venous phase) for groups of lesions: VHL-HPRC, HPRC-cysts and VHL-cysts

	Arterial-NonContrast Correlation/p-value	Venous-NonContrast Correlation/p-value	Venous-Arterial Correlation/p-value
VHL - HPRC	0.718/0.01	0.442/0.004	0.054/0.478
HPRC - Cysts	-0.227/0.451	-0.572/0.002	0.328/0.005
VHL - Cysts	-0.263/0.009	0.175/0.001	-0.4/0.1

Figure 16.

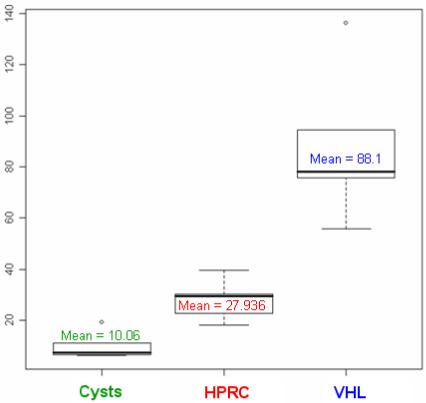
Differentiation of lesions from the statistical analysis of enhancement data. We show the boxplots corresponding to each category of tumor based on the relative enhancement of lesions between the venous phase and the acquisition before contrast injection.

3.4 Temporal Comparison

Our method for renal lesion quantification allows the monitoring of temporal changes in tumors. This could be an important tool for the assessment of lesion evolution and response to treatment. For exemplification, we present temporal analysis of lesion size in two patients in Figure 17. The first patient has 3 HPRC cancers scanned at an interval of 6 month, and the second patient has 1 VHL cancer and 2 benign cysts imaged at an interval of 3 months. None of the patients was undergoing cancer therapy. As expected, both patients present an enlargement of lesions over time.

Figure 17.

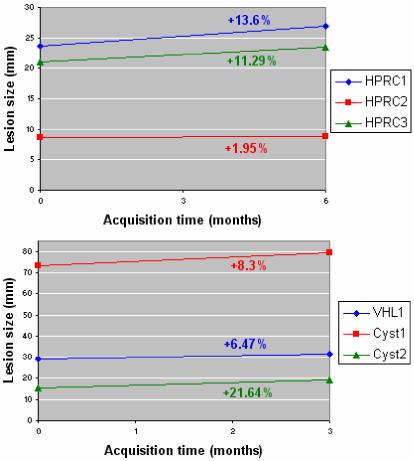
Serial quantification of lesion size. The case on the top represents results from a patient with 3 HPRC lesions scanned at a six-month interval. The bottom chart is the sequential quantification from a patient with 1 VHL tumor and 2 benign cysts scanned at three-month interval. The rates of change of tumor sizes are marked on the chart in the color code of the lesions. None of the patients are undergoing cancer therapy.

Analogous patterns of evolution of lesions can be observed in other patient serial data. The rate of change in tumor size is neither constant amongst the patients, nor between individual tumors. More analysis of temporal data will be performed on images acquired from patients undergoing therapy for the monitoring of response to cancer treatment. Presently, the method assists in the temporal quantification of lesions of patients diagnosed at NIH.

In a similar manner, the change of lesion intensity over time can be carried out to evaluate the possible changes of lesion solidity. Some normalization is required to quantify the intensity, as data were enhanced differently at various time points. We propose the level of enhancement in the healthy kidney tissue as a normalizing factor for a more accurate comparison of tumor enhancement over time. Figure 18 presents the intensity changes for the lesions addressed in Figure 17. While lesions grew in size, their intensities tend to remain constant, but may increase or decrease, probably related to the tumor solidity, as seen in two of the HPRC cases. We will address the tumor intensity over time more thoroughly in future work, when data from therapeutic trials will be available.

Figure 18.

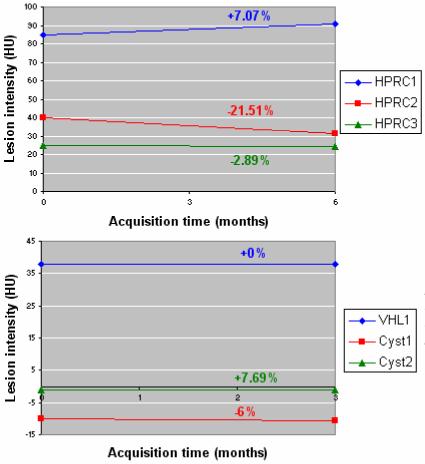
Serial quantification of lesion intensity on the group of lesions quantified in Figure 14. The rates of change of normalized lesion intensities are marked on the chart in the color code of the lesions.

4. DISCUSSION

We presented a method for the semi-automated quantification of renal tumors to assist in the clinical management of tumor diagnoses and monitoring. The method is tailored to the difficult segmentation of variable kidney lesions through a novel step to adapt to the tumor shape and intensity. Furthermore, the lesions are quantified via principal component analysis (PCA), which is robust to outliers and noise in the segmentation. We quantify automatically, for the first time, the three-dimensional size and volume of renal tumors. Additionally, our method analyzes the enhancement of segmented lesions, as well as monitors the evolution of tumors from serial scans. The combination of registration, smoothing, segmentation and quantification of renal data using contrast-enhanced images is new to our knowledge.

Three types of renal lesions were analyzed: benign cysts, von Hippel-Lindau (VHL) syndrome cancers and hereditary papillary renal carcinomas (HPRC). The computer-assisted segmentation of tumors was compared with the manual segmentation of two independent observers and the average segmentation overlap was 80.55%. Tumors are robustly segmented by the semi-automated method and the comparison between manual and semi-automated quantifications shows disparity within the limits of inter-observer variability. The difference in tumor size estimations between our method and the clinical measurements are not statistically significant with a p-value of 0.003.

The analysis of lesion enhancement for tumor classification shows great separation between benign cysts, VHL cancers and HPRC cancers, with p-values inferior to 0.004. These results represent the first automatic analysis for renal tumor classification and show great promise toward computer-assisted kidney diagnosis. Moreover, our method allows combining the enhancement analysis with the temporal monitoring of lesions. The initial results on temporal evaluation of tumors from serial scans illustrate the potential of the method of becoming an important tool for disease monitoring, drug trials and noninvasive clinical surveillance.

Future work will involve a larger database, including data from patients undergoing cancer therapy. The method will investigate the characterization of renal lesions from time evolution and enhancement between subsequent contrasted acquisitions to monitor the response to medical trials for optimal tumor management. Presently, the analysis is performed in contrast-enhanced abdominal CT, but multi-modal investigations will also be considered (i.e. MRI). The method will study cystic, solid and mixed-type tumors and has the potential to be applied to other types of abdominal abnormalities (i.e. liver, spleen and pancreatic tumors).

Biography

Marius George Linguraru is Staff Scientist in the Diagnostic Radiology Department at the Clinical Center, National Institute of Health (NIH), Bethesda, Maryland. Previously, he was with Harvard University in Cambridge, Massachusetts, and the National Institute of Research in Computer Science (INRIA) in Sophia Antipolis, France. He received a D.Phil. in Medical Image Analysis from the University of Oxford, UK. His earlier studies include an M.A. in Cultural Studies, an M.S. in Processing Systems, and a B.S. in Computer Science from the University of Sibiu, Romania, where he also worked as Assistant Professor in the Department of Computer Science. His research interests include medical imaging in general, with a focus on multi-organ multi-modality models of the human body.

Jianhua Yao is currently a staff scientist in the Diagnostic Radiology Department at the National Institutes of Health. His research interests are clinical image processing, deformable model, nonrigid registration, CAD and CT colonography. He received his doctoral degree in Computer Science from the Johns Hopkins University in 2001.

James Peterson is a Clinical Programmer working with the Urologic Oncology Branch, Center for Cancer Research, of the National Cancer Institute, National Institutes of Health in Bethesda, MD. He has designed, implemented, and administered numerous databases for the Urologic Oncology Branch. He has also overseen the data collection, including Case Report Form (CRF) design, managed the collected data, and processed the data in order to facilitate analysis. James has enjoyed being involved with the characterization and gene discovery of multiple heritable syndromes involving kidney disorders, including von Hippel-Lindau (VHL), Hereditary Papillary Renal Cell Carcinoma (HPRC), Birt-Hogg-Dube (BHD), and Hereditary Leiomyomatosis Renal Cell Carcinoma (HLRCC) as they have evolved over the last decade.

Rabindra Gautam is Clinical Programmer, works with Dr W. Marston Linehan at the Urologic Oncology Branch, Center for Cancer Research, the National Cancer Institute, National Institutes of Health, Bethesda, Maryland. He has been involved in kidney cancer research since he joined the branch in 2004.

Zhixi Li is a native of Orlando, Florida and received his B.S. in Applied Mathematics from Columbia University, School of Engineering and Applied Science in 2007. He is currently a fellow in the Diagnostic Radiology Department at the National Institutes of Health.

W. Marston Linehan, M.D. is Chief of Urologic Surgery and Head of the Urologic Oncology Branch, Center for Cancer Research, at the National Cancer Institute, National Institutes of Health, Bethesda, Maryland. He has had a long standing interest in the genetic basis of cancer of the kidney, he and his colleagues identified the VHL gene (von Hippel-Lindau, clear cell renal carcinoma), the gene for Hereditary Papillary Renal Carcinoma (c-Met oncogene, type I papillary renal carcinoma) and the BHD gene (Birt Hogg Dubé syndrome, chromophobe renal carcinoma) and described the germline fumarate hydratase mutations in the North American families with hereditary leiomyomatosis renal cell carcinoma (HLRCC).

Ronald M. Summers received the B.A. degree in physics and the M.D. and Ph.D. degrees in Medicine/Anatomy & Cell Biology from the University of Pennsylvania. He completed a medical internship at the Presbyterian-University of Pennsylvania Hospital, Philadelphia, PA, a radiology residency at the University of Michigan, Ann Arbor, MI, and an MRI fellowship at Duke University, Durham, NC. In 1994, he joined the Diagnostic Radiology Department at the NIH Clinical Center in Bethesda, MD where he is now a tenured Senior Investigator and Staff Radiologist. He is currently Chief of the Clinical Image Processing Service and directs the Virtual Endoscopy and Computer-Aided Diagnosis (CAD) Laboratory. In 2000, he received the Presidential Early Career Award for Scientists and Engineers, presented by Dr. Neal Lane, President Clinton’s science advisor. His research interests include virtual colonoscopy, CAD and development of large radiologic image databases. His clinical areas of specialty are thoracic and gastrointestinal radiology and body cross-sectional imaging. He co-chairs the special session on virtual endoscopy at the annual SPIE Medical Imaging conference. He has co-authored over 100 journal, review and conference proceedings articles.