Abstract
We develop a mixed model to capture the complex stochastic nature of tobacco abuse and dependence. This model describes transition processes among addiction and nonaddiction stages. An important innovation of our model is allowing an unobserved cure state, or permanent quitting, in contrast to transient quitting. This distinction is necessary to model data from situations where censoring prevents unambiguous determination that a person has been “cured.” Moreover, the processes that describe transient and permanent quitting are likely to be different and have different policy-making implications. For example, when analyzing factors that influence smoking and can be targeted by interventions, it is more important to target those factors that are associated with permanent quitting rather than transient quitting.
We apply our methodology to the Alpha-Tocopherol, Beta-Carotene Cancer Prevention (ATBC) study, a large (29,133 participants) longitudinal cohort study. While ATBC was designed as a cancer prevention study, it contains unique information about the smoking status of each participant during every 4-month period of the study. These data are used to model smoking cessation patterns using a discrete-time stochastic mixed-effects model with three states: smoking, transient cessation, and permanent cessation (absorbent state). Random participant-specific transition probabilities among these states are used to account for participant-to-participant heterogeneity. Another important innovation in our article is to design computationally practical methods for dealing with the size of the dataset and complexity of the models. This is achieved using the marginal likelihood obtained by integrating over the Beta distribution of random effects.
Keywords: Cure model, Mixed-effects model, Recurrent events, Smoking cessation, Stochastic transition model
1. INTRODUCTION
Smoking is the leading preventable cause of death in the United States (Centers for Disease Control and Prevention 2002). In the United States alone, 44.5 million adults, or 20.9% of the adult population, were smokers in 2004 (Centers for Disease Control and Prevention 2005b). The most tragic consequence is the 440,000 annual premature deaths attributable to smoking. Other consequences include, but are not limited to, $75.5 billion smoking-related medical expenditures and $92 billion in mortality-related annual productivity losses (Centers for Disease Control and Prevention 2005a). Worldwide, smoking-related mortality is set to rise from 4.9 million annually to 10 million by 2030 (Fagerstrom 2002). Smoking is a major cause of a large number of diseases, including cancers of the lung (Ochsner and DeBakey 1939; U.S. Department of Health, Education and Welfare 1964; Peto, Lopez, Borehan, Thun, and Heath 1994), larynx (Sankaranarayanan, Duffy, Nair, Padmakumary, and Day 1990), mouth, pharynx (Weir and Dunn 1970; La Vecchia et al. 1999), esophagus (Carstensen, Pershagen, and Eklund 1987), pancreas (Zheng et al. 1993), and bladder (Silverman, Morrison, and Devasa 1996), as well as coronary heart disease (Hammond, Garfinkel, Seidman, and Lew 1976), stroke and chronic obstructive pulmonary disease (COPD) (Doll, Peto, Wheatley, and Gray 1994).
Although the prevalence of adult smoking in the United States dropped from 42.4% in 1965 to 25.5% in 1990, progress has been slow since the 1990s (26.5% in 1992, 24.7% in 1995, and 23.3% in 2000; Giovino 2002). This is partly due to high rates of relapse following quit attempts among smokers. This is revealed by the fact that the prevalence of cessation in the United States increased from 24.3% in 1965 to 49.6% in 1993 and then flattened to 48.8% in 2000 (Giovino 2002). Surveys (Curry and McBride 1994) show that high smoking prevalence is at least in part attributable to high rates of relapse among smokers who attempt quitting.
A major problem when studying addiction behavior is that participants typically make several quit attempts before they successfully quit. Thus, for efficient development, targeting, and evaluation of interventions, it is necessary to distinguish transient cessation (temporarily smoking-free but relapse later) from permanent cessation (lifelong smoking-free) and identify the risk factors associated with permanent cessation.
Smoking is a complex behavior influenced by social, economic, environmental, behavioral, and physiological factors. Our objectives are to identify and quantify baseline factors associated with success of permanent smoking cessation and describe the full stochastic nature of the smoking addiction pattern. In the remainder of this section we describe the dataset, covariates, and modeling strategy to achieve these objectives.
1.1 Data Description
The sample for this study was drawn from the Alpha-Tocopherol, Beta-Carotene (ATBC) Lung Cancer Prevention study (ATBC Study Group 1994). This longitudinal, chemoprevention study enrolled 29,133 Finnish male smokers between 50 and 69 years of age into a randomized primary prevention study to assess whether alpha-tocopherol or beta-carotene would reduce lung cancer incidence. At enrollment, all individuals in the ATBC study smoked at least five cigarettes per day and were generally in good health with exclusions, including a history of cancer, significant cardiac diagnoses, cirrhosis, chronic alcoholism, and significant psychiatric diagnoses. For details, see ATBC Study Group (2003).
The ATBC study was conducted between 1985 and 1993, although outcome data continue to be collected for some health end points. Extensive medical histories and examination data were collected at baseline, and participants were followed for 5–8 years with three scheduled follow-up visits per year (i.e., every 4 months). At each follow-up, participants were queried about their health and smoking status since their last visit.
Smoking status was defined by the following question (translated from the Finnish): “Have you smoked since your last visit?” Participants were allowed to indicate that during the previous 4 months, they (1) had not smoked at all, (2) had smoked but had stopped at some time during the interval, or (3) had smoked continuously. For the individuals who answered (2), the quit time and duration of cessation were unknown. We do not distinguish between (2) and (3), treating them as “smokers since last visit.” Individuals who answered (1) are treated as nonsmokers since their last visit.
The baseline covariates included in this analysis encompass those associated with chronic medical conditions, psychological symptoms, alcohol use, demographic variables, and smoking history. History of chronic medical conditions was coded as self-reported presence or absence and included cirrhosis of the liver, degenerative joint disease, rheumatoid arthritis, other arthritis, chronic bronchitis, myocardial infarction, coronary heart disease, heart failure, diabetes mellitus, debilitating back pain, knee pain, joint ache, muscle ache, hip pain, leg cramps, and headache. Psychological symptoms were also coded as self-reported presence or absence and included anxiety, depression, poor memory, difficulty concentrating, fatigue, poor appetite, and insomnia. Alcohol use was coded as mean grams per day as both a continuous and a categorical variable, as was body mass index (BMI). Demographic variables include age at enrollment (continuous), marital status (categorical), education (categorical), employment status (categorical), and physical activity (categorical). Smoking history included self-report of inhaling when smoking (always vs. other), total cigarettes per day (continuous and categorical), and age of smoking onset, years smoked, and packs per year (all continuous).
1.2 Statistical Challenges and Solutions
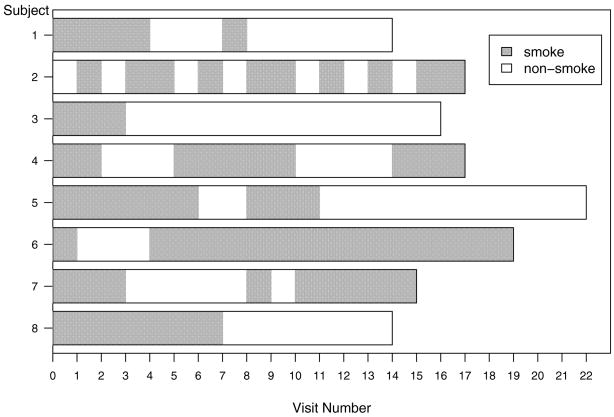
Figure 1 shows the smoking patterns of eight participants in the ATBC study. The follow-up visit numbers are displayed on the horizontal axis, and the interval between two adjacent visits is 4 months. Within each time interval, participants were either smoking (indicated by a dark area) or nonsmoking (indicated by a white area). For example, individual 1 had two smoking spells of 16 and 4 months, while individual 7 had three smoking spells of 12, 4, and 20 months, respectively. There are several important characteristics of these patterns. First, patterns alternate between smoking and nonsmoking states. Second, the sojourn time in each state varies within and between individuals and is unknown after censoring. It would be reasonable to assume that individuals with long trailing nonsmoking sojourn time before censoring are more likely to be successful quitters than the individuals without (e.g., individuals 3 and 5 vs. 2 individual).
Figure 1.
Sample profiles of smoking patterns from the ATBC study.
Intuitively, each individual’s smoking pattern could be treated as a discrete-time stochastic process with two states (smoking and nonsmoking). The smoking status at each interval of one individual is shown in the time plot in Figure 2, in which S and N denote smoking and nonsmoking intervals, respectively. A quit attempt is defined as the nonsmoking interval immediately after a smoking interval (e.g., the first and third nonsmoking intervals in Fig. 2). The second nonsmoking interval (the second N) is not a new quit attempt because it does not follow a smoking interval. Similarly, a relapse to smoking is defined as the smoking interval immediately after a nonsmoking interval (e.g., the third smoking interval).
Figure 2.
Time plot of a smoking pattern.
To model the probability of permanent smoking cessation, one common method in epidemiology is to define as cases (permanent quitters) the individuals who do not smoke for more than a prespecified time interval (e.g., 1 year). Controls or relapsers are those individuals who attempt to quit smoking but could not sustain for the predetermined time interval. Logistic regression can then be applied to estimate the probability of permanent cessation. Although it is easy to conduct such an analysis, there are several potential problems. First, because the prespecified length of the nonsmoking period is arbitrary, results will have threshold-specific interpretation. Second, censoring is not accounted for, which leads to outcome misclassification, biased effect estimation, and misspecified tests of significance (Carroll, Ruppert, Stefanski, and Crainiceanu 2006). Third, the smoking pattern is not fully modeled; for example, this approach would define as cases both the individuals who remain smoking-free for 1 year and sustain until censoring and the individuals who abstain from smoking for 1 year but relapse afterward. Some surveys (Pierce 2002) show that ex-smokers who have abstained for a 12-month period have about a 5% risk of relapsing, and, therefore, 12 months of continuous abstinence is often used as the criterion for successful quitting. In the ATBC study, there are 4,672 individuals who reported not smoking at all for at least three consecutive follow-up visits, that is, 12 months. Among them, 518 individuals relapsed during the follow-up period. Hence, the percentage of relapses after a 12-month quit attempt in the ATBC study is around 11%. Thus, uncontrollable bias is introduced in a logistic regression by simply misclassifying a sizeable fraction of individuals who relapse after quitting for more than a year.
In clinical trials, “cure from disease” means that the individual will never develop the disease during his or her remaining lifespan. The standard approach is to treat the study population as an unobservable mixture of susceptible and unsusceptible individuals. Typically, a cure model is a mixture of two submodels, one for event occurrence (incidence) and the other for time to occurrence conditional on occurrence (latency). This model extends the ordinary survival models by accounting for a cure component. Identifiability of parameters in the cure model depends on the existence of a hypothesized “cured” population. Maller and Zhou (1992, 1995) suggested that the existence of a sufficiently long interval from the largest uncensored failure time to the largest censoring time is indicative of the existence of the “cured” population.
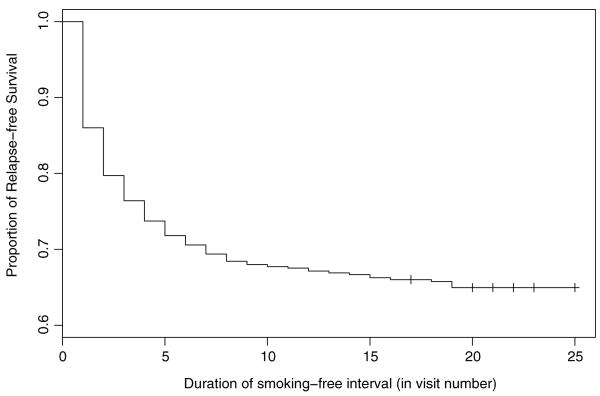
Figure 3 displays the Kaplan–Meier survival estimate of relapse-free proportion in the ATBC dataset. To obtain this, only individuals who made quit attempts are considered, and the times from quit attempt to relapse for each individual are recorded. The quit attempts that last to the end of the study are recorded as censored. Note that in Figure 3 the longest uncensored smoking-free interval is 19 visits (i.e., 76 months), after which the Kaplan–Meier estimate of relapse-free survival levels off at .67. Between visit 19 and the last observation at visit 25, there are 96 censored observations. Such a large number of censored time-to-relapse intervals provides evidence that some individuals in the ATBC study are “cured.”
Figure 3.
Kaplan–Meier curve of relapse-free survival.
Boag (1949) and Berkson and Gage (1952) utilized cure models to estimate the size of the cured fraction. Various parametric (e.g., Farewell 1977, 1982, 1986; Farewell, Math, and Math 1977), semiparametric (e.g., Kuk and Chen 1992; Sy and Taylor 2000; Chatterjee and Shih 2001; Lam, Fong, and Tang 2005), and nonparametric (e.g., Laska and Meisner 1992) cure models and the corresponding estimation methods have been proposed.
A unique feature of our model is that it incorporates the “cure” component in the context of recurrent event processes. Recurrent events appear frequently in longitudinal chronic disease studies, in which individuals alternate between a number of states (e.g., various disease states). Such a process is traditionally analyzed as a multistate continuous- or discrete-time stochastic process based on Markov or semi-Markov assumptions. Transition models are applied to analyze the covariate effects on the transition probabilities among states. Examples can be found in infectious disease (e.g., Cook and Ng 1997; Cook 1999; Smith and Vounatsou 2003; Alexander and Emerson 2005), chronic bronchitis (e.g., Ng and Cook 1997; Cook, Ng, Mukherjee, and Vaughan 1999), psoriatic arthritis (e.g., Cook, Yi, and Lee 2004), HIV/AIDS (e.g., Mathieu, Loup, Dellamonica, and Daures 2005), and breast cancer (e.g., Ocana-Riola 2005). Traditional methods, however, do not account for the possibility of an “absorbing” or a “cure” state that is not directly observable because of censoring. Given that in the ATBC study the main event of interest is permanent quitting, we considered an extension of two-state Markov models with a “cure” component.
The remainder of the article is organized as follows. In Section 2 we describe the model and the associated inferential tools. Methods are evaluated via simulations in Section 3. In Section 4 the proposed methodology is applied to the ATBC data. In Section 5 we provide further insight into our modeling strategy. Section 6 provides the discussion.
2. MIXED EFFECTS STOCHASTIC MODEL WITH A LATENT “CURE” STATE
2.1 A Three-State Stochastic Process
Figure 4 displays a three-state stochastic process with participant-specific transition probabilities denoted by Pij for j = 1, 2, 3, where the subscript i denotes individual i and j represents the state. Smoking state indicates that the individual is currently smoking. The permanent quitting state represents lifelong smoking-free, and it is an absorbent state from which further transitions cannot occur. The transient quitting state is not absorbing. Individuals in this state do not smoke temporarily but eventually transition into the smoking state. Although the individual does not smoke in both the transient and the permanent quitting states, these two states may be differently impacted by risk factors. The transient quitting state can be easily identified if the relapse is observed. But when the smoking pattern ends with nonsmoking intervals, the subject could be either in a transient or a permanent quitting state. We will address this possibility in (3). Note that in Figure 4 quit attempt is enclosed by dotted lines because it is not a real state of the Markov chain. A quit attempt is observable because it is the nonsmoking interval immediately after the smoking intervals. It is a temporary phase, which would lead to either the transient quitting state or the permanent quitting state.
Figure 4.
Transition among three states.
When individual i is in the smoking state, quit attempts are made at the beginning of each 4-month interval with probability Pi1. Once a quit attempt is made, the individual may become a permanent quitter with probability Pi3 at the visit following the quit attempt. With probability 1 − Pi3, the individual enters the transient quitting state, from which he has probability Pi2 to relapse back to the smoking state. Conditional on the random rates Pij, the transition to the next state is determined only by the current and previous state. In this article we consider time-independent random transitions. This assumption will be relaxed in our subsequent research by including time-dependent covariates, but it exceeds the scope of this article.
The proposed models for transitions give rise to two types of geometric processes corresponding to the sojourn times in the smoking and nonsmoking states. The first type (Type I) of geometric process describes the number of smoking intervals before the next quit attempt. After a quit attempt is made, each individual has probability Pi3 to become a permanent quitter. The second type (Type II) of geometric process models the number of nonsmoking intervals before relapsing conditional on being in a transient quitting state. Figure 5 illustrates this stochastic partition for a particular subject. Visits 1 through 3 are modeled as a geometric process (denoted by I) for waiting time until first quit attempt. The subject has an unsuccessful quit attempt (denoted by B) at visit 3 and enters the transitional nonsmoking interval, which lasts until visit 5 (denoted by II). Conditional on having a relapse at visit 4, the subject transitions again into a Type I process from visit 5. The modeling continues using the same rules.
Figure 5.
A typical smoking pattern.
2.2 Likelihood Formulation
Let Ki1 be the total number of quit attempts for individual i and let be the number of smoking intervals between the last relapse (or the baseline visit if k1 = 1) and the k1th quit attempt. Let mi1 be the number of smoking intervals between the final relapse and censoring if the last observed interval is smoking. The contribution of the Type I geometric process to the likelihood for individual i is
| (1) |
If the smoking pattern ends with nonsmoking intervals, then mi1 = 0 and the term (1 − Pi1)mi1 = 1 has no contribution to the likelihood for individual i.
Once a quit attempt is made, the individual enters either the permanent or the transient quitting state with probability Pi3 and 1 − Pi3, respectively. If the subject fails to enter the permanent quitting state, then the Type II geometric process is initiated. Let Ki2 be the total number of relapses (unsuccessful quit attempts) for individual i and let be the number of non-smoking intervals between the last quit attempt and the k2th relapse. If relapses are observed for all quit attempts, then the likelihood contribution of the Type II geometric and Bernoulli processes is
| (2) |
Let Nik3 be the number of nonsmoking intervals between the final quit attempt and censoring if the last observed interval is neither smoking nor a quit attempt, and Nik3 = 0 otherwise. Then the whole trailing nonsmoking sojourn time has the following contribution to the likelihood:
| (3) |
The term Pi3 at the end of (3) accounts for the probability of being a successful permanent quitter. Note how a long trailing nonsmoking sojourn time before censoring downweights the likelihood of the individual being in a transient smoking state. If the last observed interval for individual i is in a smoking state, then Li3 = 1.
The likelihood for individual i is constructed by multiplying the likelihood contributions in (1), (2), and (3):
| (4) |
where denotes the total number of smoking intervals excluding the relapsing intervals and denotes the total number of nonsmoking intervals (excluding the quit attempts) in the Type II geometric process with observed relapses. The sufficient statistics for each individual’s smoking pattern are {Si1, Ki1, Si2, Ki2, Nik3. For example, the sufficient statistics for the individual in Figure 5 are {3, 2, 1, 1, 3}.
When Nik3 =0, that is, the last observed interval is smoking, the likelihood in (4) is simplified to
2.3 Modeling Random Rates Pij
Given a participant’s covariate vector Xi, we assume that the participant-specific random rates Pij for j = 1, 2, 3 have Beta distributions with mean parameters μij and dispersion parameters θj, respectively,
| (5) |
Then E(Pij |Xi) = μij and . The mean of each Beta distribution is a function of covariates
| (6) |
where gj(·) are inverse of some link functions. For concreteness, we use the inverse of the complementary log–log function for μi1 and μi2 and the inverse of the logit function for μi3, respectively.
The marginal likelihood for individual i is
| (7) |
where . Assuming that Pij are independent given the covariates, the marginal log-likelihood based on all m individuals is equal to
| (8) |
This assumption could be relaxed to account for within-participant random rate dependence. After substituting (4) into (7) and some calculus, the marginal likelihood for individual i is
| (9) |
where
and
B(α, β) denotes the Beta function. One may be inclined to say that our model is a Beta binomial model, but closer inspection of the likelihood will prove otherwise.
There are several advantages in using Beta random-effects distributions. First, Beta is a natural family of distribution for modeling probabilities because its support is (0, 1). Second, the Beta distribution is very flexible, with its probability density function (pdf) taking many shapes: strictly increasing, strictly decreasing, U-shaped, and unimodal. Third, the marginal likelihood (9) is an explicit function of the model parameters. We use nonlinear maximization of an explicit function of the model parameters, and this is implemented in the Gauss MAXLIK package (Aptech Systems, Version 7.0.13) to obtain the maximum likelihood estimates. We, thus, avoid numerical integration, Markov chain Monte Carlo (MCMC), and expectation-maximization (EM) the algorithm. This provides large advantages over the more popular model using logistic normal random effects. For example, it only takes about 4 minutes for our model (9) to get the estimates for one of the datasets simulated in Section 3 on a PC (Dell workstation XPS Gen3, Pentium 4 3.6-GHz dual processers, 2G RAM). It takes around 40 hours for the logistic normal model on the same dataset. The large difference is due to numerical approximation of untractable integrals when using logit normal random effects.
The Beta distribution plays an important role as a prior in hierarchical Bayesian models (see, e.g., McCulloch and Searle 2001; Demidenko 2004). The idea of a Beta random-effects distribution has been used before (Nandram and Choi 2002; Dorazio and Royle 2003; Nelson et al. 2006) but never in the complex context described here.
2.4 Profile Likelihood and Variance Estimation
Preliminary simulations suggest that in the proposed modeling framework the dispersion parameter θ3, the variance of the random effects associated with cure probability, can be weakly identifiable. To guard against potential numerical difficulties, we consider a profile-likelihood approach. Let ( ). Define Γ̂(θ3) to be the value of Γ that maximizes the likelihood for a fixed θ3. The profile likelihood L(θ3, Γ ^ (θ3)) can then be maximized with respect to θ3 over a grid spanning the support of θ3. If θ ^3 = arg max θ3 L(θ3,Γ̂ (θ3)), then the maximum likelihood estimate of Φ = (Γ, θ3) is Φ = (Γ̂ (θ3), θ̂3).
A consistent estimator of the asymptotic variance of Φ̂ is m−1 I (Φ̂)−1, where I (·) denotes the information matrix and m is the number of participants in the simulated dataset. We use Fisher’s scoring method to obtain the estimated information matrix as
| (10) |
where li (Φ) is the log-likelihood for individual i. We use the expectation of the square of the score vector instead of the expectation of the negative Hessian matrix, because the former guarantees that the information matrix is nonnegative definite. Each component in is computed using a second-order central difference numerical scheme, for example,
| (11) |
where Γ−θ1 denotes the parameter vector Φ without parameter θ1 and Δθ1 is a small perturbation.
3. SIMULATION STUDIES
We evaluate the maximum likelihood inference of the proposed method via two sets of simulations. In the first simulation study we consider one binary baseline covariate for all three transition models in (5) and (6). This covariate (i.e., insomnia) is a binary variable with Xi = 1 representing the presence of insomnia at baseline. Each Xi is generated from a Bernoulli distribution with probability .2, which is the prevalence of insomnia at baseline in the ATBC study. Throughout the simulations, the follow-up time is discrete. The basic time unit is 4 months, the time interval between two adjacent visits in the ATBC study. Data are generated by the following six-step algorithm.
For each individual i, simulate the total follow-up number of visits, ci, assuming ci ~ N(14.7, 5.82). This roughly matches the distribution of number of visits in the ATBC study. If ci ≥ 1, then ci is rounded to the closest integer. If ci < 1, then ci is rounded to 1.
Simulate Pij using the Beta distributions in (5) and (6). The parameters are chosen as β1,0 = −2, β1,1 = −.8, θ1 = 5 for Pi1; β2,0 = −1.5, β2,1 = .6, θ2 = 2 for Pi2; β3,0 = β3,1 = −1, θ3 = 2 for Pi3.
Conditional on being a smoker at last interval, simulate the time to next quit attempt as a geometric process with random rate Pi1.
Conditional on making a quit attempt, simulate the state of an individual either as a transient quitter with probability 1 − Pi3 or as a permanent quitter with probability Pi3.
Conditional on being a transient quitter, simulate time to relapse with the random rate Pi2
Repeat steps 3, 4, and 5 until the total sojourn time exceeds the follow-up time ci generated in step 1.
We simulate 300 datasets with m = 10,000 participants using the preceding simulation algorithm. Figure 6 shows the profile likelihood of dispersion parameter θ3 for 20 datasets, indicating that θ3 is weakly identified. To avoid this problem, we use the profile likelihood for estimation and the variance estimation method described in Section 2.4.
Figure 6.
Profile likelihood of θ3 (true θ3 = 2) obtained from 20 simulated datasets.
Table 1 presents the results of these simulations. The row labeled “MLE” provides the averages of the maximum likelihood estimators. The row labeled “MLE SE” provides the square root of the average of estimated variances of the MLE estimators. The row labeled “Simulation SD” displays the standard deviation of the MLE point estimators. The row labeled “SE” provides the total standard errors. For example, for β1,1 the SE is .058, which is equal to . The “Coverage probability” row provides the coverage proportions of the estimated 95% nominal confidence intervals. In Table 1 the bias is negligible, and the 95% confidence interval coverage rates are reasonably close to .95. We obtained these results by exploiting the closed form and avoiding the brute-force maximization of the marginal likelihood.
Table 1.
Means, standard deviations, and 95% coverage probabilities of the parameter estimates from 300 simulated datasets with N = 10,000
| True parameters | β1,0 | β1,1 | θ1 | β2,0 | β2,1 | θ2 | β3,0 | β3,1 |
|---|---|---|---|---|---|---|---|---|
| −2.000 | −.800 | 5.000 | −1.500 | .600 | 2.000 | −1.000 | −1.000 | |
|
| ||||||||
| MLE | −2.000 | −.806 | 5.015 | −1.493 | .598 | 2.048 | −1.001 | −1.061 |
| SE | .027 | .058 | .277 | .130 | .157 | .305 | .406 | .607 |
| MLE SE | .019 | .042 | .201 | .094 | .113 | .213 | .291 | .449 |
| Simulation SD | .019 | .041 | .019 | .090 | .110 | .219 | .283 | .409 |
| Coverage probability | .947 | .943 | .963 | .950 | .943 | .937 | .923 | .960 |
NOTE: βj,0, βj,1, and θj are covariate coefficients and dispersion parameters for Pij.
In the second simulation study we used the same model but changed the parameters to match the estimated parameters from a model fitted to the ATBC data using one covariate: presence or absence of insomnia. Table 2 provides these parameter estimates in the row “True parameters.” The simulation results in Table 2 indicate that bias is negligible and the coverage probabilities of the 95% confidence intervals are close to .95.
Table 2.
Means, standard deviations, and 95% coverage probabilities of the parameter estimates from 300 simulated datasets with N = 29,133
| True parameters | β1,0 | β1,1 | θ1 | β2,0 | β2,1 | θ2 | β3,0 | β3,1 | θ3 |
|---|---|---|---|---|---|---|---|---|---|
| −3.750 | −.090 | 23.920 | −.840 | −.010 | 3.200 | .590 | −.330 | 1.560 | |
|
| |||||||||
| Mean | −3.750 | −.090 | 24.002 | −.847 | −.006 | 3.240 | .579 | −.328 | 1.620 |
| SE | .026 | .044 | 2.220 | .077 | .152 | .779 | .089 | .147 | .420 |
| MLE SE | .018 | .031 | 1.522 | .055 | .106 | .549 | .064 | .102 | .310 |
| Simulation SD | .019 | .031 | 1.617 | .054 | .108 | .552 | .063 | .105 | .283 |
| Coverage probability | .933 | .960 | .937 | .947 | .947 | .940 | .953 | .950 | .953 |
NOTE: βj,0, βj,1, and θj are covariate coefficients and dispersion parameters for modeling Pij
Our code, simulated data, and additional results for 1,000 and 5,000 subjects can be found at www.biostat.jhsph.edu/~ccrainic/webpage/programs/smoking/programsfordownload.zip.
4. APPLICATION TO THE ATBC STUDY
We apply our method to the ATBC data. To start, our first model includes only one baseline covariate, that is, insomnia, in all three models in (6). Insomnia is an indicator variable with Xi = 1 denoting the presence of baseline insomnia. Table 3 shows the fitting results, with a negative sign of insomnia exposure effect estimator indicating a smaller probability of experiencing an event. For example, participants with insomnia have significantly smaller probability (p value = .008) of making quit attempts than those without. In addition, insomnia is associated with reduced probability of being a successful long-term quitter (p value = .003). Given a quit attempt, the estimated odds ratio of being successful in long-term quitting comparing people with insomnia to people without is .72 [i.e., exp(−.33)]. Interestingly, insomnia does not have a significant effect on relapsing once the quit attempts are made. The estimated pdf’s of random rates can be obtained simply by substituting the parameter estimates from Table 3 into (6). The left panels in Figure 7 display from top to bottom the density functions of Pi1, Pi2, and Pi3. The solid and dashed curves correspond to unexposed and exposed individuals. The unexposed and exposed curves for the density functions of Pi1 and Pi2 are visually indistinguishable because the insomnia effect is roughly one or two orders of magnitude smaller than the intercept. Separation is much clearer in the permanent quitting process because the intercept does not visually dominate this effect. Moreover, Pi1 has 84.5% of its mass below .2 for the unexposed and 85.1% for the exposed with a sharp decreasing pattern. For illustration purposes in the right panel of Figure 7 we display the same curves with a 10 times larger insomnia effect. The bottom right panel shows a dramatic reduction in the “cured” probability of exposed individuals.
Table 3.
| 95% confidence interval |
|||||
|---|---|---|---|---|---|
| Models | Parameters | Coefficient | p | Lower | Upper |
| Pi1 | Intercept | −3.75(.02) | .000 | −3.78 | −3.72 |
| Insomnia* | −.09(.03) | .008 | −.16 | −.02 | |
| θ1 | 23.92(1.18) | 21.61 | 26.23 | ||
| Pi2 | Intercept | −.84(.06) | .000 | −.95 | −.73 |
| Insomnia | −.01(.11) | .92 | −.23 | .21 | |
| θ2 | 3.20(.55) | 2.13 | 4.28 | ||
| Pi3 | Intercept | .59(.07) | .000 | .46 | .72 |
| Insomnia* | −.33(.11) | .003 | −.54 | −.11 | |
| θ3 | 1.56(.23) | 1.10 | 2.01 | ||
NOTE: Numbers in parentheses are standard errors.
denotes statistical significance.
Figure 7.
Probability density functions of the estimated (left panel) and exaggerated (right panel) random rates (S, smoking; N, nonsmoking; solid curves, unexposed individuals; dashed curves, exposed individuals).
Our second model includes more baseline covariates: age, years of smoking, cigarettes per day, alcohol consumption (g/day), and inhalation (yes/no). The means and standard deviations of the covariates used in the analysis are shown in Table 4. The first four covariates were standardized for subsequent analyses. Because they are identified as risk factors in the literature, we have considered 16 baseline symptoms: anxiety, depression, poor memory, difficulty concentrating, fatigue, poor appetite, insomnia, headache, back ache, walking pain in knees, joint ache, muscle ache, walking pain in hips, leg cramps, nocturnal restless legs, and cutaneous itching. Given the large correlations among these symptoms, we use standard factor analysis to reduce the number of covariates and to explain the correlations.
Table 4.
Characteristics of some baseline covariates in the ATBC dataset
| Covariate | Mean | Standard deviation |
|---|---|---|
| Age | 57.2 | 5.0 |
| Years smoked | 35.9 | 8.4 |
| Cigarettes/day | 20.4 | 8.8 |
| Alcohol (g/day) | 17.8 | 21.3 |
| Inhale (yes/no) | .53 | .50 |
Our model uses the first three factors. Table 5 shows the loadings of the 16 symptom variables on these factors. These factors explain around 38% of the total variance of the 16 baseline symptoms. As a rule of thumb, the factor loadings greater than .3 in absolute value are considered significant and are shown in boldface. The first seven symptoms, which are psychological symptoms, are more heavily loaded on the first factor. The next seven symptoms, which are chronic medical condition symptoms, are heavily loaded on the second factor. Insomnia and walking pain in knees are loaded on the third factor, which explains only 6.6% of the total variance. The results from fitting the proposed model are shown in Table 6.
Table 5.
Loading of 16 symptoms used in factor analysis
| Symptom | Factor 1 | Factor 2 | Factor 3 |
|---|---|---|---|
| Anxiety and nervousness | .72 | .10 | −.02 |
| Depression | .74 | .05 | .01 |
| Poor memory | .59 | .19 | .06 |
| Difficult concentrating | .73 | .06 | .05 |
| Fatigue | .50 | .29 | −.06 |
| Poor appetite | .42 | .06 | −.24 |
| Insomnia | .53 | .15 | −.35 |
| Headache | .21 | .32 | −.11 |
| Back ache | .07 | .49 | .03 |
| Joint ache | .05 | .68 | .06 |
| Muscle ache | .09 | .66 | −.01 |
| Walking pain in hips | .05 | .61 | .07 |
| Leg cramps | .14 | .47 | −.11 |
| Nocturnal restless legs | .20 | .37 | −.22 |
| Walk pain in knees | .08 | .11 | .87 |
| Cutaneous itching | .22 | .20 | −.21 |
Table 6.
| 95% confidence interval |
|||||
|---|---|---|---|---|---|
| Model | Covariates | Coefficient | p | Lower | Upper |
| Pi1 | Intercept | −3.870(.021) | .000 | −3.911 | −3.828 |
| Age | .180(.015) | .000 | .150 | .209 | |
| Years smoked | −.246(.013) | .000 | −.271 | −.221 | |
| Cigarettes/day | −.279(.014) | .000 | −.306 | −.251 | |
| Alcohol | −.188(.017) | .000 | −.220 | −.155 | |
| Factor 1 | .014(.014) | .29 | −.012 | .041 | |
| Factor 2 | −.002(.013) | .87 | −.028 | .023 | |
| Factor 3 | .019(.012) | .11 | −.004 | .042 | |
| Inhale | .014(.026) | .61 | −.038 | .065 | |
| θ1 | 27.827(1.554) | 24.781 | 30.874 | ||
| Pi2 | Intercept | −.901(.079) | .000 | −1.057 | −.746 |
| Age | −.022(.056) | .69 | −.132 | .088 | |
| Years smoked | −.030(.043) | .48 | −.115 | .054 | |
| Cigarettes/day | −.151(.052) | .004 | −.253 | −.049 | |
| Alcohol | .148(.052) | .005 | .046 | .251 | |
| Factor 1 | −.024(.049) | .62 | −.121 | .072 | |
| Factor 2 | −.034(.048) | .48 | −.127 | .060 | |
| Factor 3 | .065(.047) | .16 | −.026 | .157 | |
| Inhale | .016(.097) | .87 | −.174 | .206 | |
| θ2 | 3.049(.543) | 1.985 | 4.114 | ||
| Pi3 | Intercept | .463(.092) | .000 | .283 | .644 |
| Age | .097(.051) | .06 | −.004 | .197 | |
| Years smoked | −.0059.041) | .89 | −.086 | .075 | |
| Cigarettes/day | −.071(.053) | .18 | −.174 | .033 | |
| Alcohol | −.014(.049) | .77 | −.111 | .082 | |
| Factor 1 | −.102(.047) | .03 | −.194 | −.009 | |
| Factor 2 | −.085(.045) | .06 | −.174 | .004 | |
| Factor 3 | .089(.037) | .02 | .018 | .161 | |
| Inhale | .017(.089) | .85 | −.157 | .191 | |
| θ3 | 1.564(.241) | 1.092 | 2.036 | ||
NOTE: Numbers in parentheses are standard errors.
The upper part of Table 6 shows the results of modeling the mean probability of making quit attempts, that is, Pi1. A negative estimate indicates that corresponding exposure is associated with reduced probability of making quit attempts. Thus, older individuals are more likely (p value < .001) to make quit attempts. Participants who smoked longer (p value < .001), who smoked more cigarettes per day (p value < .001), and who consumed more alcohol per day (p value < .001) have statistically significantly lower probability of making quit attempts. Baseline symptoms do not seem to have a significant impact on making quit attempts.
The middle part of Table 6 shows results for the mean probability of relapsing for a transient quitter, that is, Pi2, given a quit attempt. These results indicate that more cigarette consumption per day is associated with a lower probability of relapsing (p value = .003), while more alcohol consumption per day is associated with a higher probability of relapsing (p value = .004).
The lower part of Table 6 shows the parameter estimates from modeling the mean probability of success in permanent cessation given a quit attempt. We find that the odds ratio of permanent cessation for an increase of 5.0 years in age is 1.10 [i.e., exp(.097)], holding other covariates fixed. Moreover, individuals with psychological symptoms are significantly less likely to be successful long-term quitters (p value = .03). The odds ratio of permanent quitting for one unit increase in factor 1 is .90 [i.e., exp(−.102)], holding other covariates unchanged. In addition, chronic medical conditions are marginally associated with reduced probability of achieving success in permanent cessation (p value = .06). Factor 3 is significantly associated with permanent cessation (p value = .02).
A natural question to ask is whether the dispersion parameters θ1, θ2, and θ3 are actually necessary. We apply the likelihood ratio tests (LRTs) for testing the hypotheses
for j = 1, 2, 3. We use the index j for each hypothesis to indicate that these are different hypotheses for each variance component. Testing for H0j is equivalent to testing for 1/θj = 0 and is also equivalent to Var(Pij|Xi) = 0. Indeed, this is a test for the null hypothesis that the random effects are not necessary to capture the variability of subject-specific transition rates for one of the three processes described in the article. This is a nonstandard statistical testing problem because the parameter is on the boundary of the parameter space (θj ≥ 0) and the typical asymptotic theory results do not hold.
To address this problem, we use the likelihood ratio test (LRT) statistics. The LRT is defined as LRTj = 2 × supHAj {l(Φ)} − 2 supH0j {l(Φ)} where l(Φ) is the log-likelihood under the alternative model. The LRTj are 719.5, 146.1, and 31.7 for j = 1, 2, 3, which indicate strong evidence against each of the null hypotheses. We conclude that there is strong evidence in favor of using the random effects to capture the residual subject-level variability for each of the three processes.
Because the parameter is on the boundary of the parameter space, the asymptotic distribution is the mixture distribution. This type of result is, of course, not needed in our context because the null hypothesis would be rejected even using the asymptotic distribution. Note that θ̂1 = 27.827 is much larger than θ̂2 = 3.049 and θ̂3 = 1.564 in Table 6. Thus, it may seem surprising that LRT1 = 719.5 is much larger than LRT2 = 146.1 and LRT3 = 31.7. The explanation is remarkably simple and is related to the typical relationship between mean and variance in nonlinear models.
The overall mean for the Pi1 process (.023) is much smaller than the means for Pi2 (.340) and Pi3 (.616), respectively, because roughly 80% of the subjects never attempted to quit. Note that the coefficient of variation for each process is
After some simple calculations it follows that CV(Pi1) ≈110% while CV(Pi2) ≈70% and our LRT results make sense. We conclude that “The size of the variance components can only be judged relative to the scale of the problem.”
In summary, the baseline variables age, years of smoking, and cigarette and alcohol consumption are associated with the probability of making quit attempts. If the quit attempt is made, cigarette and alcohol consumption per day are more likely to have effects on transient quitting, while age and symptoms have major impacts on being successful in permanent smoking cessation.
5. MODELING INSIGHTS
In this section we provide further insight into our modeling strategy. We also compare the capacity of our model to reproduce realistic addiction patterns in contrast to the traditional logistic model.
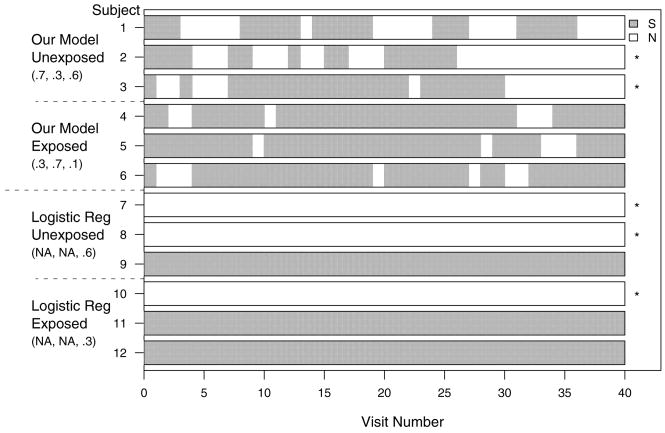
The top two panels in Figure 8 display three simulated smoking patterns for each of the following combinations of probabilities (Pi1, Pi2, Pi3) = (.7, .3, .6) and (.3, .7, .1), respectively. The first set of probabilities corresponds to unexposed individuals, while the second set corresponds to exposed individuals. These parameters are different from the ones from the insomnia example to make differences detectable by a simple inspection of several subject trajectories. It is instructive to compare these two panels and note the longer smoking intervals for the subjects in the exposed groups. They occur because once an exposed subject is in the smoking state he has a high probability of remaining in that state. The unexposed group tends to have longer nonsmoking intervals because once an unexposed individual is nonsmoking he has a higher probability of remaining nonsmoking. Intuitively, the smoking state is a “stickier” state for the exposed, while the nonsmoking state is “stickier” state for the unexposed. For this particular example, two unexposed individuals were cured (denoted by an asterisk on the right side of the plot), one after 26 and another after 30 visits. None of the exposed individuals was cured during the 40-month “study” interval. This is due to the combined effect of a much smaller cure probability and a smaller number of quit attempts. Probabilities are exaggerated, but we hope to convey the more general message that the model is actually generating the type of patterns consistent with observed real data. Of course, our model can and does detect much smaller signals in the data, signals that could not be recovered by a simple inspection of around 30,000 smoking patterns.
Figure 8.
Simulated smoking patterns comparing our model to the logistic regression model (S, smoking; N, nonsmoking). * Subjects who quit permanently in simulation. Numbers within the parentheses are Pi1, Pi2, and Pi3, respectively.
For illustration purposes we also simulate patterns from a logistic regression model with cure probabilities .6 and .3 for the unexposed and exposed individuals, respectively. Note that the logistic regression cannot and does not model transient non-smoking periods, cannot distinguish between transient and permanent quitting states, and provides no information about timing of cure. While useful as an exploratory tool, the logistic regression model is not a good representation of complex tobacco addiction behaviors. Moreover, using a simplifying logistic regression model would deliberately throw away invaluable subject- and population-level information related to addiction behavior.
6. DISCUSSION
In this article we propose a methodology for modeling participant-level stochastic addiction behavior. We model separately transient and permanent cessation and allow for risk factors to have different impacts on these two cessation states. Moreover, we introduce a statistically identifiable but unobserved cure process coupled with smoking and transient quitting processes.
Individual-level data are modeled using a mixed-effects discrete-time stochastic model with three states for data with recurrent events and a latent “cure” state. Participant-to-participant heterogeneity is addressed by incorporating participant-level transition probabilities, which are modeled using Beta distributions that depend on the baseline covariates through their means. We design computationally usable methods for dealing with the size of the dataset and complexity of the models. This is achieved using the explicit marginal likelihood obtained by integrating over the Beta distribution of random effects.
Our modeling strategy has several limitations that we emphasize and view as opportunities for future research. One limitation is that we assume that random effects are independent given the covariates. The second limitation is that the model presented in the article uses only baseline covariates and does not accommodate time-dependent covariates. This would be especially important for studies where interventions could be initiated. Another limitation is that we do not incorporate mixtures of distributions for random effects and rely on the Beta distribution instead.
Our model is applied to analyzing the ATBC dataset. An important, previously unknown, but often debated, finding is that risk factors have different effects on transition probabilities. We also provide mathematical quantification of the participant-to-participant variation in transition probabilities. Our modeling strategy enriches the statistical arsenal of cure modeling and provides new and valuable scientific insight into the smoking addiction behavior.
Acknowledgments
This work was supported by a predoctoral fellowship to the first author from the National Cancer Institute, National Institutes of Health. The authors thank Drs. Erik Auguston, Andrew Bergen, and Neil Caporaso for numerous useful discussions on the ATBC study and Drs. Demetrius Albanes and Jarmo Virtamo for access to the ATBC study data. Computations were performed on the high-performance computational capabilities of the Biowulf PC/Linux cluster at the National Institutes of Health, Bethesda, Maryland (http://biowulf.nih.gov). The authors express their appreciation to an associate editor and three referees for their helpful comments.
Contributor Information
Sheng Luo, is Ph.D. Candidate, Department of Biostatistics, The Johns Hopkins University, Baltimore, MD 21205 (E-mail: sluo@jhsph.edu)..
Ciprian M. Crainiceanu, is Assistant Professor, Department of Biostatistics, The Johns Hopkins University, Baltimore, MD 21205.
Thomas A. Louis, is Professor, Department of Biostatistics, The Johns Hopkins University, Baltimore, MD 21205.
Nilanjan Chatterjee, is Senior Investigator, Biostatistics Branch, Division of Cancer Epidemiology and Genetics, National Cancer Institute, National Institutes of Health, Rockville, MD 20852..
References
- Alexander N, Emerson P. Analysis of Incidence Rates in Cluster-Randomized Trials of Interventions Against Recurrent Infections, With an Application to Trachoma. Statistics in Medicine. 2005;4:2637–2647. doi: 10.1002/sim.2138. [DOI] [PubMed] [Google Scholar]
- ATBC Study Group. Incidence of Cancer and Mortality Following α-Tocopherol and β-Carotene Supplementation. Journal of American Medical Association. 2003;290:476–485. doi: 10.1001/jama.290.4.476. [DOI] [PubMed] [Google Scholar]
- Berkson J, Gage RP. Survival Curve for Cancer Patients Following Treatment. Journal of the American Statistical Association. 1952;47:501–515. [Google Scholar]
- Boag JW. Maximum Likelihood Estimates of the Proportion of Patients Cured by Cancer Therapy. Journal of the Royal Statistical Society, Ser B. 1949;11:15–44. [Google Scholar]
- Carroll RJ, Ruppert D, Stefanski LA, Crainiceanu C. Measurement Error in Nonlinear Models. New York: Chapman & Hall/CRC Press; 2006. [Google Scholar]
- Carstensen JM, Pershagen G, Eklund G. Mortality in Relation to Cigarette and Pipe Smoking: 16 Years’ Observation of 25,000 Swedish Men. Journal of Epidemiology and Community Health. 1987;41:166–172. doi: 10.1136/jech.41.2.166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Centers for Disease Control and Prevention. Annual Smoking-Attributable Mortality, Years of Potential Life Lost, and Economic Costs—United States, 1995–1999. Morbidity and Mortality Weekly Report. 2002;51:300–303. [PubMed] [Google Scholar]
- Centers for Disease Control and Prevention. Annual Smoking-Attributable Mortality, Years of Potential Life Lost, and Productivity Losses—United States, 1997–2001. Morbidity and Mortality Weekly Report. 2005a;54:625–628. [PubMed] [Google Scholar]
- Centers for Disease Control and Prevention. Cigarette Smoking Among Adults—United States, 2004. Morbidity and Mortality Weekly Report. 2005b;54:1121–1124. [PubMed] [Google Scholar]
- Chatterjee N, Shih J. A Bivariate Cure-Mixture Approach for Modeling Familial Association in Diseases. Biometrics. 2001;57:779–786. doi: 10.1111/j.0006-341x.2001.00779.x. [DOI] [PubMed] [Google Scholar]
- Cook RJ. A Mixed Model for Two-State Markov Processes Under Panel Observation. Biometrics. 1999;55:915–920. doi: 10.1111/j.0006-341x.1999.00915.x. [DOI] [PubMed] [Google Scholar]
- Cook RJ, Ng ETM. A Logistic-Bivariate Normal Model for Overdispersed Two-State Markov Processes. Biometrics. 1997;53:358–364. [PubMed] [Google Scholar]
- Cook RJ, Ng ET, Mukherjee J, Vaughan D. Two-State Mixed Renewal Processes for Chronic Disease. Statistics in Medicine. 1999;18:175–188. doi: 10.1002/(sici)1097-0258(19990130)18:2<175::aid-sim997>3.0.co;2-b. [DOI] [PubMed] [Google Scholar]
- Cook RJ, Yi GY, Lee K. A Conditional Markov Model for Cluster Progressive Multistate Processes Under Incomplete Observation. Biometrics. 2004;60:436–443. doi: 10.1111/j.0006-341X.2004.00188.x. [DOI] [PubMed] [Google Scholar]
- Curry SJ, McBride CM. Relapse Prevention for Smoking Cessation: Review and Evaluation of Concepts and Interventions. Annual Review of Public Health. 1994;15:345–366. doi: 10.1146/annurev.pu.15.050194.002021. [DOI] [PubMed] [Google Scholar]
- Demidenko E. Mixed Model: Theory and Applications. New York: Wiley; 2004. [Google Scholar]
- Doll R, Peto R, Wheatley K, Gray R. Sutherland I: Mortality in Relation to Smoking: 40 Years’ Observations on Male British Doctors. British Medical Journal. 1994;309:901–911. doi: 10.1136/bmj.309.6959.901. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dorazio RM, Royle JA. Mixture Models for Estimating the Size of a Closed Population When Capture Rates Vary Among Individuals. Biometrics. 2003;59:351–364. doi: 10.1111/1541-0420.00042. [DOI] [PubMed] [Google Scholar]
- Fagerstrom K. The Epidemiology of Smoking: Health Consequences and Benefits of Cessation. Drugs. 2002;62:1–9. doi: 10.2165/00003495-200262002-00001. [DOI] [PubMed] [Google Scholar]
- Farewell VT. A Model for a Binary Variable With Time-Censored Observations. Biometrika. 1977;64:43–46. [Google Scholar]
- Farewell VT. The Use of Mixture Models for the Analysis of Survival Data With Long-Term Survivors. Biometrics. 1982;38:1041–1046. [PubMed] [Google Scholar]
- Farewell VT. Mixture Models in Survival Analysis: Are They Worth the Risk? The Canadian Journal of Statistics. 1986;14:257–262. [Google Scholar]
- Farewell VT, Math B, Math M. The Combined Effect of Breast Cancer Risk Factors. Cancer. 1977;40:931–936. doi: 10.1002/1097-0142(197708)40:2<931::aid-cncr2820400251>3.0.co;2-y. [DOI] [PubMed] [Google Scholar]
- Giovino GA. Epidemiology of Tobacco Use in the United States. Oncogene. 2002;21:7326–7340. doi: 10.1038/sj.onc.1205808. [DOI] [PubMed] [Google Scholar]
- Hammond EC, Garfinkel L, Seidman H, Lew EA. Tar and Nicotine Content of Cigarette Smoke in Relation to Death Rates. Environmental Research. 1976;12:263–274. doi: 10.1016/0013-9351(76)90036-0. [DOI] [PubMed] [Google Scholar]
- Kuk AYC, Chen CH. A Mixture Model Combining Logistic Regression With Proportional Hazards Regression. Biometrika. 1992;79:531–541. [Google Scholar]
- La Vecchia C, Franceschi S, Bosetti C, Levi F, Talamini R, Negri E. Time Since Stopping Smoking and the Risk of Oral and Pharyngeal Cancers. Journal of the National Cancer Institute. 1999;91:726–728. doi: 10.1093/jnci/91.8.726a. [DOI] [PubMed] [Google Scholar]
- Lam KF, Fong DYT, Tang OY. Estimating the Proportion of Cured Patients in a Censored Sample. Statistics in Medicine. 2005;24:1865–1879. doi: 10.1002/sim.2137. [DOI] [PubMed] [Google Scholar]
- Laska EM, Meisner MJ. Nonparametric Estimation and Testing in a Cure Model. Biometrics. 1992;48:1223–1234. [PubMed] [Google Scholar]
- Maller RA, Zhou S. Estimating the Proportion of Immunes in a Censored Sample. Biometrika. 1992;79:731–739. [Google Scholar]
- Maller RA, Zhou S. Testing for the Presence of Immune or Cured Individuals in Censored Survival Data. Biometrics. 1995;51:1197–1205. [PubMed] [Google Scholar]
- Mathieu E, Loup P, Dellamonica P, Daures JP. Markov Modelling of Immunological and Virological States in HIV-1 Infected Patients. Biometrical Journal. 2005;47:834–846. doi: 10.1002/bimj.200410164. [DOI] [PubMed] [Google Scholar]
- McCulloch CE, Searle SR. Generalized, Linear and Mixed Models. New York: Wiley; 2001. [Google Scholar]
- Nandram B, Choi JW. Hierarchical Bayesian Nonresponse Models for Binary Data From Small Areas With Uncertainty About Ignorability. Journal of the American Statistical Association. 2002;97:381–388. [Google Scholar]
- Nelson KP, Lipsitz SR, Fitzmaurice GM, Ibrahim J, Parzen M, Strawderman R. Use of the Probability Integral Transformation to Fit Nonlinear Mixed-Effects Models With Nonnormal Random Effects. Journal of Computational and Graphical Statistics. 2006;15:39–57. [Google Scholar]
- Ng ETM, Cook RJ. Modeling Two-State Disease Processes With Random Effects. Life Time Analysis. 1997;3:315–335. doi: 10.1023/a:1009650012039. [DOI] [PubMed] [Google Scholar]
- Ocana-Riola R. Non-Homogeneous Markov Processes for Biomedical Data Analysis. Biometrical Journal. 2005;47:369–376. doi: 10.1002/bimj.200310114. [DOI] [PubMed] [Google Scholar]
- Ochsner A, DeBakey M. Treatment by Total Pneumonectomy: Analyses of 79 Collected Cases and Presentation of 7 Personal Cases. Surgery, Gynecology and Obstetrics. 1939;68:435–451. [PMC free article] [PubMed] [Google Scholar]
- Peto R, Lopez AD, Borehan J, Thun M, Heath C., Jr . Indirect Estimates From National Vital Statistics. New York: Oxford University Press; 1994. Mortality From Smoking in Developed Countries 1950–2000. [Google Scholar]
- Pierce JP. Conducting a Smoking Prevalence Survey. Doctors and Tobacco. 2002 Available at http://www.tobacco-control.org/tcrc_Web_Site/Pages_tcrc/Resources/Factsheets/conductingasurvey.pdf.
- Sankaranarayanan R, Duffy SW, Nair MK, Padmakumary G, Day NE. Tobacco and Alcohol as Risk Factors in Cancer of the Larynx in Kerala, India. International Journal of Cancer. 1990;45:879–882. doi: 10.1002/ijc.2910450517. [DOI] [PubMed] [Google Scholar]
- Silverman DT, Morrison AS, Devasa SS. Cancer Epidemiology and Prevention. New York: Oxford University Press; 1996. [Google Scholar]
- Smith T, Vounatsou P. Estimation of Infection and Recovery Rates for Highly Polymorphic Parasites When Detectability Is Imperfect, Using Hidden Markov Models. Statistics in Medicine. 2003;22:1709–1724. doi: 10.1002/sim.1274. [DOI] [PubMed] [Google Scholar]
- Sy JP, Taylor JMG. Estimation in a Cox Proportional Hazards Cure Model. Biometrics. 2000;56:227–236. doi: 10.1111/j.0006-341x.2000.00227.x. [DOI] [PubMed] [Google Scholar]
- U.S. Department of Health, Education and Welfare. Smoking and Health: Report of the Advisory Committee to the Surgeon General of the Public Health Service. 1964. PHS Publication 1103, Public Health Service. [Google Scholar]
- Weir JM, Dunn J. Smoking and Mortality: A Prospective Study. Cancer. 1970;25:105–112. doi: 10.1002/1097-0142(197001)25:1<105::aid-cncr2820250115>3.0.co;2-z. [DOI] [PubMed] [Google Scholar]
- Zheng W, McLaughlin JK, Gridley G, Bjeike E, Schuman LM, Silverman DT, Wacholder S, CoChien HT, Blot WJ, Fraumeni JF. A Cohort Study of Smoking, Alcohol Consumption, and Dietary Factors for Pancreatic Cancer (United States) Cancer Causes and Control. 1993;4:477–482. doi: 10.1007/BF00050867. [DOI] [PubMed] [Google Scholar]