Abstract
Approximate Bayesian computation (ABC) methods can be used to evaluate posterior distributions without having to calculate likelihoods. In this paper, we discuss and apply an ABC method based on sequential Monte Carlo (SMC) to estimate parameters of dynamical models. We show that ABC SMC provides information about the inferability of parameters and model sensitivity to changes in parameters, and tends to perform better than other ABC approaches. The algorithm is applied to several well-known biological systems, for which parameters and their credible intervals are inferred. Moreover, we develop ABC SMC as a tool for model selection; given a range of different mathematical descriptions, ABC SMC is able to choose the best model using the standard Bayesian model selection apparatus.
Keywords: sequential Monte Carlo, Bayesian model selection, sequential importance sampling, parameter estimation, dynamical systems, sloppy parameters
1. Introduction
Most dynamical systems studied in the physical, life and social sciences and engineering are modelled by ordinary, delay or stochastic differential equations. However, for the vast majority of systems and particularly for biological systems, we lack reliable information about parameters and frequently have several competing models for the structure of the underlying equations. Moreover, the biological experimental data are often scarce and incomplete, and the likelihood surfaces of large models are complex. The analysis of such dynamical systems therefore requires new, more realistic quantitative and predictive models. Here, we develop novel statistical tools that allow us to analyse such data in terms of dynamical models by (i) providing estimates for model parameter values, and (ii) allowing us to compare the performance of different models in describing the overall data.
In the last decade, extensive research has been conducted on estimating the parameters of deterministic systems. Much attention has been given to local and global nonlinear optimization methods (Mendes & Kell 1998; Moles et al. 2003) and, generally, parameter estimation has been performed by maximum-likelihood estimation (Muller et al. 2004; Timmer & Muller 2004; Baker et al. 2005; Bortz & Nelson 2006). The methods developed for ordinary differential equations have been extended to ordinary differential equations with time delays (Horbelt et al. 2002). Deterministic models have also been parametrized in a Bayesian framework using Bayesian hierarchical models (Putter et al. 2002; Banks et al. 2005; Huang et al. 2006). Simulated annealing, which attempts to avoid getting trapped in local minima, is another well-known optimization algorithm that has been found successful in various applications (Kirkpatrick et al. 1983; Mendes & Kell 1998). There are also several Monte Carlo-based approaches applied to the parameter estimation of deterministic (Battogtokh et al. 2002; Brown & Sethna 2003) and stochastic (Sisson et al. 2007) systems. The parameter estimation for stochastic models has been extensively explored in financial mathematics (Johannes & Polson 2005) and has been applied to biological systems in a frequentist maximum likelihood (Reinker et al. 2006) and Bayesian (Golightly & Wilkinson 2005, 2006; Wilkinson 2006) framework.
Most commonly, model selection has been performed by likelihood ratio tests (in the case of nested models) or the Akaike information criterion (in the case of non-nested models). Recently, Bayesian methods have increasingly been coming into use. Vyshemirsky & Girolami (2008) have investigated different ways of computing the Bayes factors for model selection of deterministic differential equation models, and Brown & Sethna (2003) have used the Bayesian information criterion. In population genetics, model selection has been performed using approximate Bayesian computation (ABC) in its basic rejection form (Zucknick 2004; Wilkinson 2007) and coupled with multinomial logistic regression (Beaumont 2008a; Fagundes et al. 2007).
There is thus a wide variety of tools available for parameter estimation and, to a lesser extent, model selection. However, to our knowledge, no method available can be applied to all different kinds of modelling approaches (e.g. ordinary or stochastic differential equations with and without time delay) without substantial modification, estimate credible intervals from incomplete or partially observed data, reliably explore the whole parameter space without getting trapped in local extrema and be employed for model selection.
In this paper, we apply an ABC method based on sequential Monte Carlo (SMC) to the parameter estimation and model selection problem for dynamical models. In ABC methods, the evaluation of the likelihood is replaced by a simulation-based procedure (Pritchard et al. 1999; Beaumont et al. 2002; Marjoram et al. 2003; Sisson et al. 2007). We explore the information provided by ABC SMC about the inferability of parameters and the sensitivity of the model to parameter variation. Furthermore, we compare the performance of ABC SMC with other ABC methods. The method is illustrated on two simulated datasets (one from ecology and another from molecular systems biology), and real and simulated epidemiological datasets. As we will show, ABC SMC yields reliable parameter estimates with credible intervals, can be applied to different types of models (e.g. deterministic as well as stochastic models), is relatively computationally efficient (and easily parallelized), allows for discrimination among sets of candidate models in a formal Bayesian model selection sense and gives us an assessment of parameter sensitivity.
2. Methods
In this section, we review and develop the theory underlying ABC with emphasis on applications to dynamical systems, before introducing a formal Bayesian model selection approach in an ABC context.
2.1 Approximate Bayesian computation
ABC methods have been conceived with the aim of inferring posterior distributions where likelihood functions are computationally intractable or too costly to evaluate. They exploit the computational efficiency of modern simulation techniques by replacing the calculation of the likelihood with a comparison between the observed and simulated data.
Let θ be a parameter vector to be estimated. Given the prior distribution π(θ), the goal is to approximate the posterior distribution, π(θ|x)∝f(x|θ)π(θ), where f(x|θ) is the likelihood of θ given the data x. The ABC methods have the following generic form.
Sample a candidate parameter vector θ* from some proposal distribution π(θ).
Simulate a dataset x* from the model described by a conditional probability distribution f(x|θ*).
Compare the simulated dataset, x*, with the experimental data, x0, using a distance function, d, and tolerance ϵ; if d(x0, x*)≤ϵ, accept θ*. The tolerance ϵ≥0 is the desired level of agreement between x0 and x*.
The output of an ABC algorithm is a sample of parameters from a distribution π(θ|d(x0, x*)≤ϵ). If ϵ is sufficiently small, then the distribution π(θ|d(x0, x*)≤ϵ) will be a good approximation for the posterior distribution π(θ|x0). It is often difficult to define a suitable distance function d(x0, x*) between the full datasets, so one may instead replace it with a distance defined on summary statistics, S(x0) and S(x*), of the datasets. That is, the distance function may be defined as d(x0, x*)=d′(S(x0), S(x*)), where d′ is a distance function defined on the summary statistic space. However, here, as we consider values of a dynamical process at a set of time points, we are able to compare the datasets directly without the use of summary statistics. In any case, the algorithms take the same form.
The simplest ABC algorithm is the ABC rejection sampler (Pritchard et al. 1999), which is as follows.
R1 Sample θ* from π(θ).
R2 Simulate a dataset x* from f(x|θ*).
R3 If d(x0, x*)≤ϵ, accept θ*, otherwise reject.
R4 Return to R1.
The disadvantage of the ABC rejection sampler is that the acceptance rate is low when the prior distribution is very different from the posterior distribution. To avoid this problem, an ABC method based on Markov chain Monte Carlo was introduced (Marjoram et al. 2003). The ABC MCMC algorithm proceeds as follows.
M1 Initialize θi, i=0.
M2 Propose θ* according to a proposal distribution q(θ|θi).
M3 Simulate a dataset x* from f(x|θ*).
M4 If d(x0, x*)≤ϵ, go to M5, otherwise set θi+1=θi and go to M6.
- M5 Set θi+1=θ* with probability
and θi+1=θi with probability 1−α. M6 Set i=i+1, go to M2.
The outcome of this algorithm is a Markov chain with the stationary distribution π(θ|d(x0, x*)≤ϵ) (Marjoram et al. 2003). That is, ABC MCMC is guaranteed to converge to the target approximate posterior distribution. Note that if the proposal distribution is symmetric, q(θi|θ*)=q(θ*|θi), then α depends only on the prior distribution. Furthermore, if the prior is uniform, then α=1 in M5. Potential disadvantages of the ABC MCMC algorithm are that the correlated nature of samples coupled with the potentially low acceptance probability may result in very long chains and that the chain may get stuck in regions of low probability for long periods of time.
The above-mentioned disadvantages of ABC rejection and ABC MCMC methods can, at least in part, be avoided in ABC algorithms based on SMC methods, first developed by Sisson et al. (2007). In this paper, we derive ABC SMC from a sequential importance sampling (SIS) algorithm (Del Moral et al. 2006); see appendix A for the derivation and appendix B for a comparison with the algorithm of Sisson et al. (2007).
In ABC SMC, a number of sampled parameter values (called particles), {θ(1), …, θ(N)}, sampled from the prior distribution π(θ), are propagated through a sequence of intermediate distributions, π(θ|d(x0, x*)≤ϵi), i=1, …,T−1, until it represents a sample from the target distribution π(θ|d(x0, x*)≤ϵT). The tolerances ϵi are chosen such that ϵ1>⋯>ϵT≥0, thus the distributions gradually evolve towards the target posterior. For sufficiently large numbers of particles, the population approach can also, in principle, avoid the problem of getting stuck in areas of low probability encountered in ABC MCMC. The ABC SMC algorithm proceeds as follows.1
S1 Initialize ϵ1, …, ϵT.
Set the population indicator t=0.
S2.0 Set the particle indicator i=1.
S2.1 If t=0, sample θ** independently from π(θ).
Else, sample θ* from the previous population with weights wt−1 and perturb the particle to obtain θ**∼Kt(θ|θ*), where Kt is a perturbation kernel.
If π(θ**)=0, return to S2.1.
Simulate a candidate dataset .
If d(x*, x0)≥ϵt, return to S2.1.
- S2.2 Set and calculate the weight for particle ,
If i<N, set i=i+1, go to S2.1.
S3 Normalize the weights.
If t<T, set t=t+1, go to S2.0.
Particles sampled from the previous distribution are denoted by a single asterisk, and after perturbation these particles are denoted by a double asterisk. Here, we choose the perturbation kernel Kt to be a random walk (uniform or Gaussian). Note that for the special case when T=1, the ABC SMC algorithm corresponds to the ABC rejection algorithm.
2.2 Model selection
Here, we introduce an ABC SMC model selection framework that employs standard concepts from Bayesian model selection, including Bayes factors (a comprehensive review of Bayesian model selection can be found in Kass & Raftery 1995). Let m1 and m2 be two models; we would like to choose which model explains the data x better. The Bayes factor is defined as
| (2.1) |
where P(mi) is the prior and P(mi|x) is the marginal posterior distribution of model mi, i=1,2. If the priors are uniform, then (2.1) simplifies to
| (2.2) |
The Bayes factor is a summary of the evidence provided by the data in favour of one statistical model over another (see table 1 for its interpretation).
Table 1.
Interpretation of the Bayes factor (adapted from Kass & Raftery 1995).
| the value of the Bayes factor B12 | evidence against m2 (and in favour of m1) |
|---|---|
| 1–3 | very weak |
| 3–20 | positive |
| 20–150 | strong |
| >150 | very strong |
There are several advantages of Bayesian model selection when compared with traditional hypothesis testing. First, the models being compared do not need to be nested. Second, the Bayes factors do not only weigh the evidence against a hypothesis (in our case m2), but can equally well provide evidence in favour of it. This is not the case for traditional hypothesis testing where a small p-value only indicates that the null model has insufficient explanatory power. However, one cannot conclude from a large p-value that the two models are equivalent, or that the null model is superior, but only that there is not enough evidence to distinguish between the two. In other words, ‘failing to reject’ the null hypothesis cannot be translated into ‘accepting’ the null hypothesis (Cox & Hinkley 1974; Kass & Raftery 1995). Third, unlike the posterior probability of the model, the p-value does not provide any direct interpretation of the weight of evidence (the p-value is not the probability that the null hypothesis is true).
Here, we approach the model selection problem by including a ‘model parameter’ m∈{1, …, M}, where M is the number of models, as an additional discrete parameter and denote the model-specific parameters as , m=1, …, M, where km denotes the number of parameters in model m.
In each population, we start by sampling a model indicator m from the prior distribution π(m). For model m, we then propose new particles by perturbing the particles from the previous population specific to m; this step is the same as in the parameter estimation algorithm. The weights for particles θ(m) are also calculated in a similar way as in the parameter estimation algorithm for m.
The ABC SMC algorithm for model selection proceeds as follows.2
MS1 Initialize ϵ1, …, ϵT.
- Set the population indicator t=0.
MS2.0 Set the particle indicator i=1.
MS2.1 Sample m* from π(m).
- If t=0, sample θ** from π(θ(m*)).
- If t>0, sample θ* from the previous population {θ(m*)t−1} with weights w(m*)t−1.
- Perturb the particle θ* to obtain θ**∼Kt(θ|θ*).
- If π(θ**)=0, return to MS2.1.
- Simulate a candidate dataset x*∼f(x|θ**,m*).
- If d(x*, x0)≥ϵt, return to MS2.1.
- MS2.2 Set and add θ** to the population of particles {θ(m*)t}, and calculate its weight as,
- If i<N, set i=i+1, go to MS2.1.
MS3 For every m, normalize the weights.
- If t<T, set t=t+1, go to MS2.0.
The outputs of the ABC SMC algorithm are the approximations of the marginal posterior distribution of the model parameter P(m|x) and the marginal posterior distributions of parameters , m=1, …, M, i=1, …, km. Note that it can happen that a model dies out (i.e. there are no particles left that belong to a particular model) if it offers only a poor description of the data. In this case, the sampling of particles continues from the remaining models only.
The Bayes factors can be obtained directly from P(m|x) using equation (2.2). However, in many cases there will not be a single best and most powerful/explanatory model (Stumpf & Thorne 2006). More commonly, different models explain different parts of the data to a certain extent. One can average over these models to obtain a better inference than from a single model only. The approximation of the marginal posterior distribution of the model, P(m|x), which is the output of the above algorithm, can be used for Bayesian model averaging (Hoeting et al. 1999).
The parameter estimation for each of the models is performed simultaneously with the model selection. The model with the highest posterior probability will typically have the greatest number of particles, thereby ensuring a good estimate of the posterior distribution of the parameters. However, some models are poorly represented in the marginal posterior distribution of m (i.e. only a small number of particles belong to these models), and so the small number of particles does not provide a very good estimate of the posterior distributions of the parameters. Therefore, one might wish to estimate parameters for these models independently.
We note that the ABC SMC model selection algorithm implicitly penalizes the models with a large number of parameters; the higher the parameter dimension is, the smaller is the probability that the perturbed particle is accepted.
2.3 Implementation of the algorithm
The algorithm is implemented in C++. For the ODE solver code, the fourth-order classical Runge–Kutta algorithm from the GNU Scientific Library (Galassi 2003) is used; for the simulation of stochastic models, we use the Gillespie algorithm (Gillespie 1977); and for the simulation of delay differential equations, we implemented the algorithm based on the adaptive step-size ODE solvers from Numerical recipes in C (Press et al. 1992) extended by code handling the delay part according to Paul (1992) and Enright & Hu (1995).
3. Results
We demonstrate the performance of the ABC algorithms using the simulated data from deterministic and stochastic systems. The data points were obtained by solving the systems for some fixed parameters at chosen time points. The sizes of the input datasets were chosen to reflect what can typically be expected in real-world datasets in ecology, molecular systems biology and epidemiology. The first two examples highlight the computational performance of ABC SMC, the problem of inferability of dynamical models and its relationship to parameter sensitivity. The third example illustrates the use of ABC SMC for model selection, which is then further demonstrated in an application to a real dataset.
3.1 Parameter inference for the deterministic and stochastic Lotka–Volterra model
The first model is the Lotka–Volterra (LV) model (Lotka 1925; Volterra 1926) describing the interaction between prey species, x, and predator species, y, with parameter vector θ=(a, b),
| (3.1a) |
| (3.1b) |
3.1.1 Computational efficiency of ABC SMC applied to deterministic LV dynamics
The data {(xd, yd)} are noisy observations of the simulated system with parameter values set at (a, b)=(1, 1). We sample eight data points (for each of the species) from the solution of the system for parameters (a, b)=(1, 1) and add Gaussian noise (0, (0.5)2) (figure 1a). Let the distance function d((xd, yd), (x, y)) between the data {xd[i], yd[i]}, i=1, …, 8, and a simulated solution for proposed parameters, {(x[i], y[i])}, be the sum of squared errors,
| (3.2) |
In appendix C we show that this distance function is, in fact, related to the conventional likelihood treatment of ODEs.
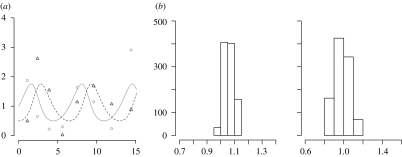
Figure 1.
(a) Trajectories of prey (solid curve) and predator (dashed curve) populations of the deterministic LV system and the data points (circles, prey data; triangles, predator data). (b) Parameters inferred by the ABC rejection sampler.
The distance between our noisy data and the deterministic solution for (a, b)=(1, 1) from which the data were generated is 4.23, so the lowest distance to be reached is expected to be close to this number and we choose the tolerance ϵ accordingly.
First, we apply the ABC rejection sampler approach with ϵ=4.3. The prior distributions for a and b are taken to be uniform, a, b∼U(−10, 10). In order to obtain 1000 accepted particles, approximately 14.1 million data generation steps are needed, which means that the acceptance rate (7×10−5) is extremely low. The inferred posterior distributions are shown in figure 1b.
Applying the ABC MCMC scheme outlined above yields results comparable to those of ABC rejection, and after a careful calibration of the approach (using an adaptive Gaussian proposal distribution), we manage markedly to reduce the computational cost (including burn-in, we had to generate between 40 000 and 60 000 simulations in order to obtain 1000 independent particles).
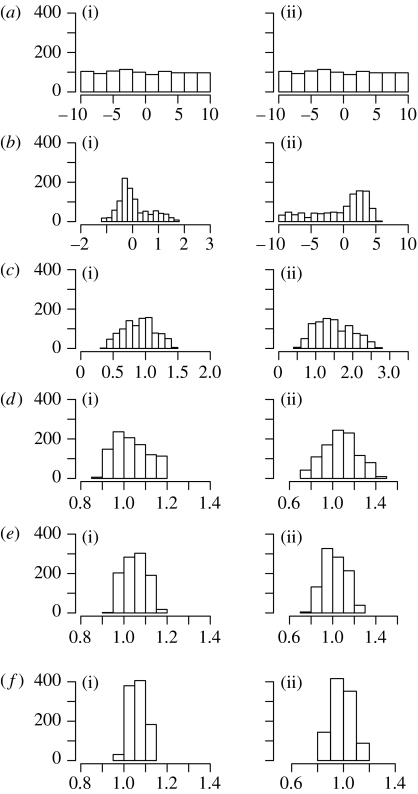
Next, we apply the ABC SMC approach. The prior distributions for a and b are taken to be uniform, a, b∼U(−10, 10), and the perturbation kernels for both parameters are uniform, Kt=σU(−1, 1), with σ=0.1. The number of particles in each population is N=1000. To ensure the gradual transition between populations, we take T=5 populations with ϵ=(30.0, 16.0, 6.0, 5.0, 4.3). The results are summarized in table 2 and figure 2. From the last population (population 5), it can be seen that both parameters are well inferred (a: median=1.05, 95% quantile range=[1.00,1.12]; b: median=1.00, 95% quantile range=[0.87,1.11]). The outcome is virtually the same as previously obtained by the ABC rejection sampler (figure 1b); however, there is a substantial reduction in the number of steps needed to reach this result. For this model, the ABC SMC algorithm needs 50 times fewer data generation steps than the ABC rejection sampler, and about the same number of data generation steps as the adaptive ABC MCMC algorithm.
Table 2.
Cumulative number of data generation steps needed to accept 1000 particles in each population for deterministic LV dynamics.
| population | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| data generation steps | 26 228 | 36 667 | 46 989 | 49 271 | 52 194 |
Figure 2.
Histograms of populations (a) 0 (uniform prior distribution), (b) 1, (c) 2, (d) 3, (e) 4 and (f) 5 (approximation of posterior distribution) of parameters (i) a and (ii) b of the LV system.
The analyses were repeated with different distance functions, such as
| (3.3) |
and
| (3.4) |
where the dot denotes the inner product. As expected, the resulting approximations of posterior distributions are very similar (histograms not shown). Replacing the uniform perturbation kernel by a Gaussian kernel also yields the same results, but requires more simulation steps (results not shown).
3.1.2 ABC SMC inference for stochastic LV dynamics
Having obtained good estimates for the deterministic case, next, we try to infer parameters of a stochastic LV model. The predator–prey process can be described by the following rate equations:
| (3.5a) |
| (3.5b) |
| (3.5c) |
where X denotes the prey population; Y is the predator population; and a is the fixed amount of resource available to the prey (we fix it to a=1). These reactions define the stochastic master equation (van Kampen 2007)
| (3.6) |
The ABC approach can easily be applied to inference problems involving master equations, because there exists an exact simulation algorithm (Gillespie algorithm; Gillespie 1977; Wilkinson 2006).
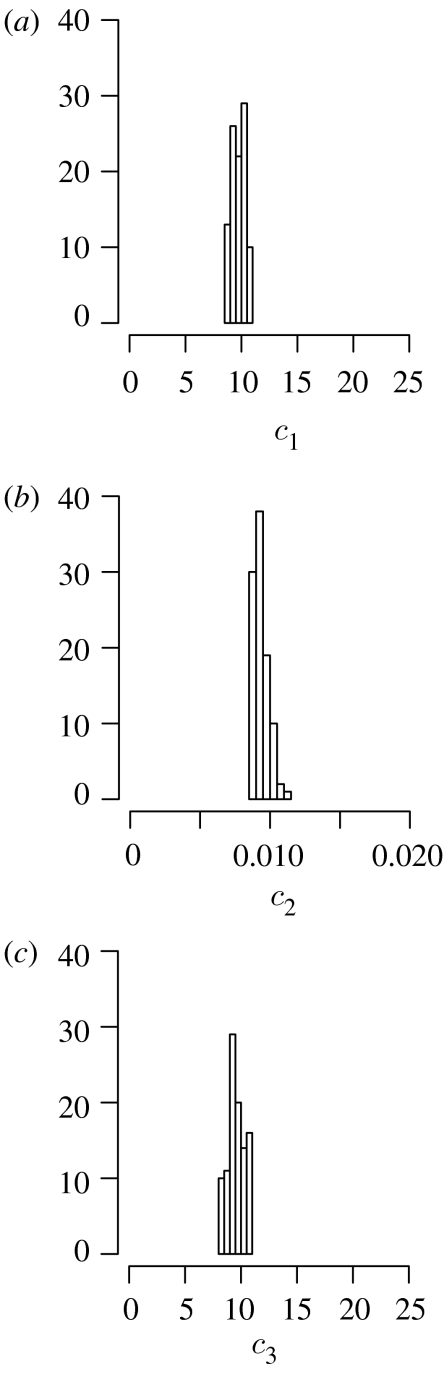
Our simulated data consist of 19 data points for each species with rates (c1, c2, c3)=(10, 0.01, 10) and initial conditions (X0, Y0)=(1000, 1000). The distance function is the square root of the sum of squared errors (3.2) and the SMC algorithm is run for T=5 populations with ϵ=(4000, 2900, 2000, 1900, 1800). Especially in laboratory settings, the results from several replicate experiments are averaged over; here, we therefore also use data averaged over three independent replicates. The simulated data at every run are then, just as the experimental data, averaged over three runs. For inference purposes, the average over several runs tends to hold more information about the system's mean dynamics than a single stochastic run. If the experimental data consisted of one run only, i.e. if there were no repetitions, then the inference could in principle proceed in the same way, by comparing the experimental data with a single simulated run. This would result in a lower acceptance rate and, consequently, more data generation steps to complete the inference.
We generate N=100 particles per population and assign the prior distributions of the parameters to be π(c1)=U(0, 28), π(c2)=U(0.0, 0.04) and π(c3)=U(0, 28), reflecting the respective orders of magnitude of the simulated parameters (if a larger domain for π(c2) is taken, there are no accepted instances for c2>0.04). Perturbation kernels are uniform with and , and Bt=10. The results are summarized in figure 3.
Figure 3.
Histograms of the approximated posterior distributions of parameters (a) c1, (b) c2 and (c) c3 of the stochastic LV dynamics.
3.2 Parameter inference for the deterministic and stochastic repressilator model
The repressilator (Elowitz & Leibler 2000) is a popular toy model for gene regulatory systems and consists of three genes connected in a feedback loop, where each gene transcribes the repressor protein for the next gene in the loop. The model consists of six ordinary differential equations and four parameters, which are as follows:
| (3.7a) |
| (3.7b) |
| (3.7c) |
| (3.7d) |
| (3.7e) |
| (3.7f) |
3.2.1 Inferability and sensitivity in deterministic repressilator dynamics
Let θ=(α0,n, β, α) be the parameter vector. For the simulated data, the initial conditions are (m1, p1, m2, p2, m3, p3)=(0, 2, 0, 1, 0, 3) and the values of parameters are θ=(1, 2, 5, 1000); for these parameters the repressilator displays limit-cycle behaviour. We assume that only the mRNA (m1,m2,m3) measurements are available and the protein concentrations are considered as missing data. Gaussian noise (0, 52) is added to the data points. The distance function is defined to be the square root of the sum of squared errors. The prior parameter distributions are chosen as follows: π(α0)=U(−2, 10); π(n)=U(0, 10); π(β)=U(−5, 20); and π(α)=U(500, 2500). We assume that the initial conditions are known.
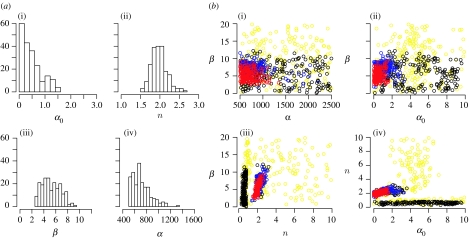
The results are summarized in figure 4a–d, where we show the approximate posterior distributions, the changes in 95% interquantile ranges of parameter estimates across the populations and scatterplots of some of the two-dimensional parameter combinations. Each parameter is easily inferred when the other three parameters are fixed (histograms not shown). When the algorithm is applied to all four parameters simultaneously, parameter n is inferred the quickest and has the smallest posterior variance, while parameter α is barely inferable and has large credible intervals (figure 4a,c).
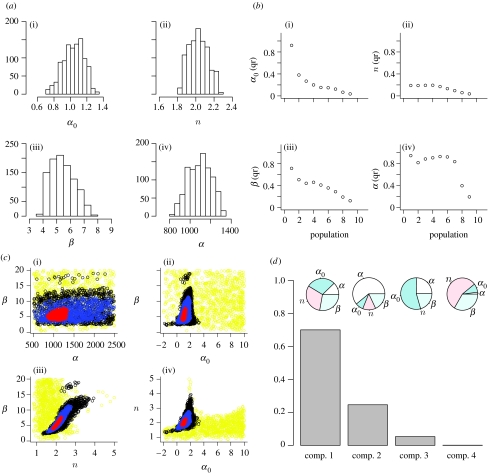
Figure 4.
(a) Histograms of the approximate marginal posterior distributions of parameters α0, n, β and α of the deterministic repressilator model. (b) The normalized 95% interquantile ranges (qr) of each population. The narrower the interval for a given tolerance ϵt, the more sensitive the model is to the corresponding parameter. The interquantile range reached in population 9 is determined by the added experimental noise. As ϵ9 was chosen accordingly, one cannot proceed by lowering the tolerance further. The sharp change in the interquantile ranges, which occurs, for example, for parameter α0 between populations 1 and 2, can be explained by the steep gradient of the likelihood surface along α0. (c) The output (i.e. the accepted particles) of the ABC SMC algorithm as two-dimensional scatterplots. The particles from population 1 are in yellow, particles from population 4 in black, particles from population 7 in blue and those from the last population in red. Islands of particles are observed in population 4 and they can be explained by the multimodality of the fourth intermediate distribution. (d) PCA of the set of accepted particles (population 9). Owing to the dependence of the PCA on the scaling of original variables, the PCA was performed on the correlation matrix. The first PC explains 70.0% of the total variance, the second 24.6%, the third 5.3% and the fourth 0.1% of the variance. Pie charts show the fraction of the length of PCs explained by individual parameters.
We find that ABC SMC recovers the intricate link between model sensitivity to parameter changes and inferability of parameters. The repressilator system is most sensitive to changes in parameter n and least sensitive to changes in α. Hence, the data appear to contain little information about α. Thus, ABC SMC provides us with a global parameter sensitivity analysis (Sanchez & Blower 1997) on the fly as the intermediate distributions are being constructed. Note that the intermediate distributions are nested in one another (as should be the case in SMC; figure 4c). An attempt to visualize the four-dimensional posterior distributions can be accessed in the electronic supplementary material where we provide an animation in which the posterior distribution in the four-dimensional parameter space is projected onto two-dimensional planes.
The interquantile ranges and the scatterplots provide an initial impression of parameter sensitivity; however, the first problem with scatterplots is that it is increasingly difficult to visualize the behaviour of the model with increasing parameter dimension. Second, we have to determine the sensitivity when a combination of parameters is varied (and not just individual parameters), and this cannot be visualized via simple one-dimensional interquantile ranges or two-dimensional scatterplots.
We can use principal component analysis (PCA) to quantify the sensitivity of the system (Saltelli et al. 2008). The output of the ABC SMC algorithm, which we are going to use for our sensitivity analysis, is the last population of N particles. Associated with the accepted particles is their variance–covariance matrix, Σ, of rank p, where p denotes the dimension of the parameter vector. The principal components (PCs) are the eigenvectors of Σ, which define a set of eigenparameters, . Here, ai=(ai1, …, aip) is the normalized eigenvector associated with the ith eigenvalue of Σ, λi, and aij describes the projection of parameter θj onto the ith eigenparameter. The PCA provides an orthogonal transformation of the original parameter space and the PCs can be taken to define a p-dimensional ellipsoid that approximates the population of data points (i.e. the accepted particles), and the eigenvalues specify the p corresponding radii. The variance of the ith PC is given by λi and the total variance of all PCs equals . Therefore, the eigenvalue λi associated with the ith PC explains a proportion
| (3.8) |
of the variation in the population of points. The smaller the λi, the more sensitive the system is to the variation of the eigenparameter Χi. The PCA yields only an approximate account of sensitivity similar to what would be obtained by computing the Hessian around the mode of the posterior distribution.
Figure 4d summarizes the output of the PCA. It shows how much of the variance is explained by each PC, and which parameters contribute the most to these PCs. In contrast to the interest in the first PC in most PCA applications, our main interest lies in the smallest PC. The last PC extends across the narrowest region of the posterior parameter distribution, and therefore provides information on parameters to which the model is the most sensitive. In other words, the smaller PCs correspond to stiff parameter combinations, while the larger PCs may correspond to sloppy parameter combinations (Gutenkunst et al. 2007).
The analysis reveals that the last PC mainly extends in the direction of a linear combination of parameters n and β, from which we can conclude that the model is most sensitive to changes in these two parameters. Looking at the third component, the model is somewhat less sensitive to variation in α0. The model is therefore the least sensitive to changes in parameter α, which is also supported by the composition of the second PC. This outcome agrees with the information obtained from the interquantile ranges and the scatterplots.
3.2.2 Inference of the stochastic repressilator dynamics
Next, we apply ABC SMC to the stochastic repressilator model. We transformed the deterministic model (3.7) into a set of the following reactions:
| (3.9a) |
| (3.9b) |
| (3.9c) |
| (3.9d) |
where i=1, 2, 3 and, correspondingly, j=3, 1, 2. The stochastic process defined by these reactions can be simulated with the Gillespie algorithm. True parameters and initial conditions correspond to those of the deterministic case discussed previously. The data include both mRNA and protein levels at 19 time points. Tolerances are chosen as ϵ={900, 650, 500, 450, 400}, the number of particles N=200 and Bt=5. The prior distributions are chosen as follows: π(α0)=U(0, 10); π(n)=U(0, 10); π(β)=U(−5, 20); and π(α)=U(500, 2500).
The inference results for comparing the average over 20 simulations with the data generated from the average of 20 simulations are summarized in figure 5a,b. Figure 5a,b shows that parameters n and β get reasonably well inferred, while α0 and α are harder to infer. It is clearly noticeable that parameters are better inferred in the deterministic case (figure 4a).
Figure 5.
(a) Histograms of the approximated posterior distributions of parameters α0, n, β and α of the stochastic repressilator model. (b) The output of the ABC SMC algorithm as two-dimensional scatterplots. The particles from population 1 are in yellow, particles from population 2 in black, particles from population 3 in blue and those from the last population in red. We note that the projection to parameter n in population 2 is a sample from a multimodal intermediate distribution, while this distribution becomes unimodal from population 3 onwards.
3.2.3 Contrasting inferability for the deterministic and stochastic dynamics
Analysing and comparing the results of the deterministic and stochastic repressilator dynamics shows that parameter sensitivity is intimately linked to inferability. If the system is insensitive to a parameter, then this parameter will be hard (or even impossible) to infer, as varying such a parameter does not vary the output—which here is the approximate posterior probability—very much. In stochastic problems, we may furthermore have the scenario where the fluctuations due to small variations in one parameter overwhelm the signals from other parameters.
3.3 Model selection on different SIR models
We illustrate model selection using a range of simple models that can describe the epidemiology of infectious diseases. SIR models describe the spread of such disease in a population of susceptible (S), infected (I) and recovered (R) individuals (Anderson & May 1991). The simplest model assumes that every individual can be infected only once and that there is no time delay between the individual getting infected and their ability to infect other susceptible individuals,
| (3.10a) |
| (3.10b) |
| (3.10c) |
where denotes the time derivative of x, dx/dt. Individuals, who are born at rate α, are susceptible; d is the death rate (irrespective of the disease class, S, I or R); γ is the infection rate; and v is the recovery rate.
The model can be made more realistic by adding a time delay τ between the time an individual gets infected and the time when they become infectious,
| (3.11a) |
| (3.11b) |
| (3.11c) |
Another way of incorporating the time delay into the model is by including a population of individuals in a latent (L) phase of infection; in this state, they are infected but cannot yet infect others. The equations then become
| (3.12a) |
| (3.12b) |
| (3.12c) |
| (3.12d) |
Here, δ denotes the transition rate from the latent to the infective stage.
Another extension of the basic model (3.10) allows the recovered individuals to become susceptible again (with rate e),
| (3.13a) |
| (3.13b) |
| (3.13c) |
There are obviously many more ways of extending the basic model, but here we restrict ourselves to the four models described above. Given the same initial conditions, the outputs of all models are very similar, which makes it impossible to choose the right model by visual inspection of the data alone. Therefore, some more sophisticated, statistically based methods need to be applied for selecting the best available model. Therefore, we apply the ABC SMC algorithm for model selection, developed in §2.2. We define a model parameter m∈{1, 2, 3, 4}, representing the above models in the same order, and model-specific parameter vectors θ(m): ; ; ; and .
The experimental data consist of 12 data points from each of the three groups (S, I and R). If the data are very noisy (Gaussian noise with standard deviation σ=1 was added to the simulated data points), then the algorithm cannot detect a single best model, which is not surprising given the high similarity of model outputs. However, if intermediate noise is added (Gaussian noise with standard deviation σ=0.2), then the algorithm produces a posterior estimate with the most weight on the correct model. An example is shown in figure 6, where the experimental data were obtained from model 1 and perturbed by Gaussian noise, (0, (0.2)2). Parameter inference is performed simultaneously with the model selection (posterior parameter distributions not shown).
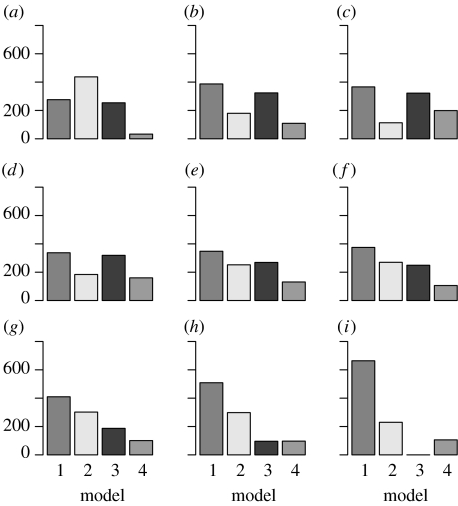
Figure 6.
Histograms show populations (a–i) 1–9 of the model parameter m. Population 9 represents the final posterior marginal estimate of m. Population 0 (discrete uniform prior distribution) is not shown.
The Bayes factor can be calculated from the marginal posterior distribution of m, which we take from the final population. From 1000 particles, model 1 (basic model) was selected 664 times, model 2 230 times, model 4 106 times and model 3 was not selected at all in the final population. Therefore, we can conclude from the Bayes factors
| (3.14) |
| (3.15) |
| (3.16) |
that there is weak evidence in favour of model 1 when compared with model 2 and positive evidence in favour of model 1 when compared with model 4. Increasing the amount of data will, however, change the Bayes factors in favour of the true model.
3.4 Application: common-cold outbreaks on Tristan da Cunha
Tristan da Cunha is an isolated island in the Atlantic Ocean with approximately 300 inhabitants, and it was observed that viral diseases, such as common cold, break out on the island after the arrival of ships from Cape Town. We use the 21-day common-cold data from October 1967. The data, shown in table 3, were obtained from Hammond & Tyrrell (1971) and Shibli et al. (1971). The data provide only the numbers of infected and recovered individuals, I(t) and R(t), whereas the size of the initial susceptible population S(0) is not known. Therefore, S(0) is an extra unknown parameter to be estimated.
Table 3.
Common-cold data from Tristan da Cunha collected in October 1967.
| day | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| I(t) | 1 | 1 | 3 | 7 | 6 | 10 | 13 | 13 | 14 | 14 | 17 | 10 | 6 | 6 | 4 | 3 | 1 | 1 | 1 | 1 | 0 |
| R(t) | 0 | 0 | 0 | 0 | 5 | 7 | 8 | 13 | 13 | 16 | 16 | 24 | 30 | 31 | 33 | 34 | 36 | 36 | 36 | 36 | 37 |
The four epidemic models from §3.3 are used and because there are no births and deaths expected in the short period of 21 days, parameters α and d are set to 0. The tolerances are set to ϵ={100, 90, 80, 73, 70, 60, 50, 40, 30, 25, 20, 16, 15, 14, 13.8} and 1000 particles are used. The prior distributions of parameters are chosen as follows: γ∼U(0, 3); v∼U(0, 3); τ∼U(−0.5, 5); δ∼U(−0.5, 5); e∼U(−0.5, 5); S(0)∼U(37, 100); and m∼U(1, 4), where S(0) and m are discrete. Perturbation kernels are uniform, Kt=σU(−1, 1), with σγ=σv=0.3, στ=σδ=σe=1.0 and σS(0)=3.
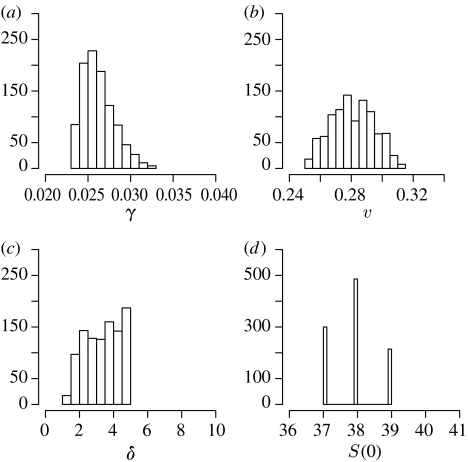
The target and intermediate distributions of model parameters are shown in figure 7. The model selection algorithm chooses model (3.12), i.e. the model with a latent class of disease carriers, to be the most suitable one for describing the data; however, it is only marginally better than models (3.10) and (3.11). Therefore, to draw reliable conclusions from the inferred parameters, one might wish to use model averaging over models (3.10)–(3.12). The marginal posterior distributions for the parameters of model (3.12) are shown in figure 8. However, the estimated initial susceptible population size S(0) is low compared with the whole population of the island, which suggests that either the majority of islanders were immune to a given strand of cold or (perhaps more plausibly) the system is not well represented by our general epidemic models with homogeneous mixing. The estimated durations of the latent period τ (from model (3.11)) and 1/δ (from model (3.12)), however, are broadly in line with the established aetiology of common cold (Fields et al. 1996). Thus, within the set of candidate epidemiological models, the ABC SMC approach selects the most plausible model and results in realistic parameter estimates.
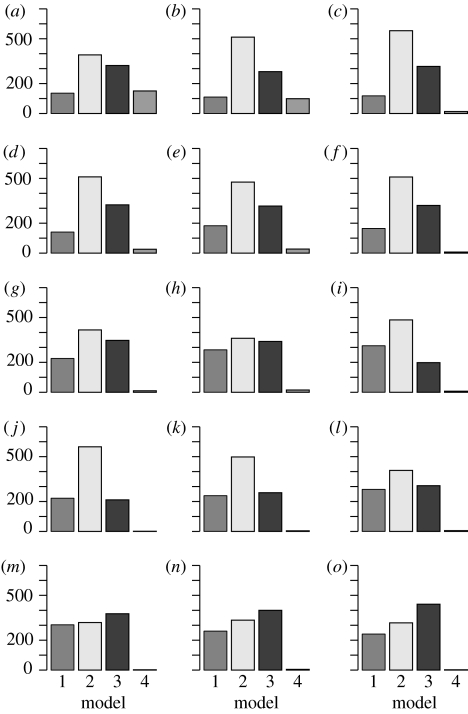
Figure 7.
Populations of the marginal posterior distribution of m. Models 1–4 correspond to equations (3.10)–(3.13), respectively. An interesting phenomenon is observed in populations 1–12, where model 2 has the highest probability, in contrast to model 3 having the highest inferred probability in the last population. The most probable explanation for this is that a local maximum favouring model 2 has been passed on route to a global maximum of the posterior probability favouring model 3. Populations (a–o) 1–15. Population 0 (discrete uniform prior distribution) is not shown.
Figure 8.
Histograms of the approximated posterior distributions of parameters (a) γ, (b) v, (c) δ and (d) S(0) of the SIR model with a latent phase of infection (3.12).
4. Discussion
Our study suggests that ABC SMC is a promising tool for reliable parameter inference and model selection for models of dynamical systems that can be efficiently simulated. Owing to its simplicity and generality, ABC SMC, unlike most other approaches, can be applied without any change in both deterministic and stochastic contexts (including models with time delay).
The advantage of Bayesian statistical inference, in contrast to most conventional optimization algorithms (Moles et al. 2003), is that the whole probability distribution of the parameter can be obtained, rather than merely the point estimates for the optimal parameter values. Moreover, in the context of hypothesis testing, the Bayesian perspective (Cox & Hinkley 1974; Robert & Casella 2004) has a more intuitive meaning than the corresponding frequentist point of view. ABC methods share these characteristics.
Another advantage of our ABC SMC approach is that observing the shape of intermediate and posterior distributions gives (without any further computational cost) information about the sensitivity of the model to different parameters and about the inferability of parameters. All simulations are already part of the parameter estimation, and can be conveniently re-used for the sensitivity analysis via scatterplots or via the analysis of the posterior distribution using, for example, PCA. It can be concluded that the model is sensitive to parameters that are inferred quickly (in earlier populations) and that have narrow credible intervals, while it is less sensitive to those that get inferred in later populations and are not very localized by the posterior distribution. If the distribution does not change much between populations and resembles the uniform distribution from population 0, then it can be concluded that the corresponding parameter is not inferable given the available data.
While the parameter estimation for individual models is straightforward when a suitable number of particles are used, more care should be taken in model selection problems; the domains of the uniform prior distributions should be chosen with care and acceptance rates should be closely monitored. These measures should prevent models being rejected in early populations solely due to inappropriately chosen (e.g. too large) prior domains. Apart from a potentially strong dependence on the chosen prior distributions (which is also inherent in the standard Bayesian model selection; Kass & Raftery 1995), we also observe the dependency of the Bayes factors on changes in the tolerance levels ϵt and perturbation kernel variances. Therefore, care needs to be taken when applying the ABC SMC model selection algorithm.
Finally, we want to stress the importance of monitoring convergence in ABC SMC. There are several ways to see whether a good posterior distribution has been obtained: we can use interquantile ranges or tests of goodness of fit between successive intermediate distributions. A further crucial signature is the number of proposals required to obtain a specified number of accepted particles. This will also impose a practical limit on the procedure.
For the problems in this paper, the algorithm was efficient enough. Examples here were chosen to highlight different aspects of ABC SMC's performance and usability. However, for the use on larger systems, the algorithm can be made more computationally efficient by optimizing the number of populations, the distance function, the number of particles and perturbation kernels (e.g. adaptive kernels). Moreover, the algorithm is easily parallelized.
5. Conclusion
We have developed a SMC ABC algorithm that can be used to estimate model parameters (including their credible intervals) and to distinguish among a set of competing models. This approach can be applied to deterministic and stochastic systems in the physical, chemical and biological sciences, for example biochemical reaction networks or signalling networks. Owing to the link between sensitivity and inferability, ABC SMC can, however, also be applied to larger systems: critical parameters will be identified quickly, while the system is found to be relatively insensitive to parameters that are hard to infer.
Acknowledgments
Financial support from the Division on Molecular Biosciences (Imperial College), MRC and the Slovenian Academy of Sciences and Arts (to T.T.), EPSRC (to D.W.), the Wellcome Trust (to N.S., A.I. and M.P.H.S.) and EMBO (to M.P.H.S.) is gratefully acknowledged. We thank Ajay Jasra and James Sethna for their helpful discussions and Paul Kirk, David Knowles and Sarah Langley for commenting on this manuscript. We are especially grateful to Mark Beaumont for providing his helpful comments on an earlier version of this manuscript.
Appendix A. Derivation of ABC SMC
Here we derive the ABC SMC algorithm from the SIS algorithm of Del Moral et al. (2006) and in appendix B we show why this improves on the ABC partial rejection control (PRC) algorithm developed by Sisson et al. (2007). We start by briefly explaining the basics of importance sampling and then present the SIS algorithm.
Let π be the distribution we want to sample from, our target distribution. If it is impossible to sample from π directly, one can sample from a suitable proposal distribution, η, and use importance sampling weights to approximate π. The Monte Carlo approximation of η is
where and is the Dirac delta function, defined by
If we assume π(x)>0⇒η(x)>0, then the target distribution π can be approximated by
with importance weights defined as
In other words, to obtain a sample from the target distribution π, one can instead sample from the proposal distribution, η, and weight the samples by importance weights, w.
In SIS, one reaches the target distribution πT through a series of intermediate distributions, πt, t=1, …, T−1. If it is hard to sample from these distributions, one can use the idea of importance sampling described above to sample from a series of proposal distributions ηt and weight the obtained samples by importance weights
| (A1) |
In SIS, the proposal distributions are defined as
| (A2) |
where ηt−1 is the previous proposal distribution and κt is a Markov kernel.
In summary, we can write the SIS algorithm as follows.
Initialization Set t=1.
For i=1, …, N, draw .
Evaluate using (A 1) and normalize.
Iteration Set t=t+1, if t=T+1, stop.
For i=1, …, N, draw .
Evaluate using (A 1) with ηt(xt) from (A 2) and normalize.
To apply SIS, one needs to define the intermediate and the proposal distributions. Taking this SIS framework as a base, we now define ABC SMC to be a special case of the SIS algorithm, where we choose the intermediate and proposal distributions in an ABC fashion, as follows. The intermediate distributions are defined as
where π(x) denotes the prior distribution; are Bt datasets generated for a fixed parameter x, ; (x) is an indicator function; and ϵt is the tolerance required from particles contributing to the intermediate distribution πt. This allows us to define . We define the first proposal distribution to equal the prior distribution, η1=π. The proposal distribution at time t (t=2, …, T), ηt, is defined as the perturbed intermediate distribution at time t−1, πt−1, such that for every sample, x, from this distribution we have
bt(x)>0 (in other words, particle x is accepted at least one out of Bt times), and
- π(x)>0 (in order for a condition πt(x)>0⇒ηt(x)>0 to be satisfied),
where Kt denotes the perturbation kernel (random walk around the particle).(A3)
To calculate the weights defined by
| (A4) |
we need to find an appropriate way of evaluating ηt(xt) defined in equation (A 3). This can be achieved through the standard Monte Carlo approximation,
where N denotes the number of particles and , i=1, …, N, are all the particles from the intermediate distribution πt−1. The unnormalized weights (A 4) can then be calculated as
where π is the prior distribution; ; and D(b), b=1, …, Bt, are the Bt simulated datasets for a given parameter xt. For Bt=1, the weights become
for all accepted particles xt.
The ABC SMC algorithm can be written as follows.
S1 Initialize ϵ1, …, ϵT.
Set the population indicator t=0.
S2.0 Set the particle indicator i=1.
S2.1 If t=0, sample x** independently from π(x).
If t>0, sample x* from the previous population with weights wt−1 and perturb the particle to obtain x**∼Kt(x|x*), where Kt is a perturbation kernel.
If π(x**)=0, return to S2.1.
Simulate a candidate dataset Bt times (b=1, …, Bt) and calculate bt(x**).
If bt(x**)=0, return to S2.1.
- S2.2 Set and calculate the weight for particle ,
If i<N, set i=i+1, go to S2.1.
S3 Normalize the weights.
If t<T, set t=t+1, go to S2.0.
When applying ABC SMC to deterministic systems, we take Bt=1, i.e. we simulate the dataset for each particle only once.
Appendix B. Comparison of the ABC SMC algorithm with the ABC PRC of Sisson et al.
In this section, we contrast the ABC SMC algorithm, which we developed in appendix A, and the ABC PRC algorithm of Sisson et al. (2007). The algorithms are very similar in principle, and the main difference is that we base ABC SMC on an SIS framework whereas Sisson et al. use a SMC sampler as a basis for ABC PRC, where the weight calculation is performed through the use of a backward kernel. Both algorithms are explained in detail in Del Moral et al. (2006). The disadvantage of the SMC sampler is that it is impossible to use an optimal backward kernel and it is hard to choose a good one. Sisson et al. choose a backward kernel that is equal to the forward kernel, which we suggest can be a poor choice.3 While this highly simplifies the algorithm since in the case of a uniform prior distribution all the weights become equal, the resulting posterior distributions can result in bad approximations to the true posterior. In particular, using equal weights can profoundly affect the posterior credible intervals.4
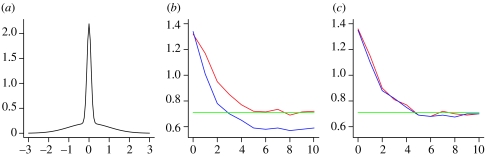
Here, we compare the outputs of both algorithms using the toy example from Sisson et al. (2007). The goal is to generate samples from a mixture of two normal distributions, , where ϕ(μ,σ2) is the density function of a N(μ, σ2) random variable (figure 9a). Sisson et al. approximate the distribution well by using three populations with ϵ1=2, ϵ2=0.5 and ϵ3=0.025, respectively, starting from a uniform prior distribution. However, ABC PRC would perform poorly if they had used more populations. In figure 9b,c, we show how the variance of the approximated posterior distribution changes through populations. We use 100 particles and average over 30 runs of the algorithm, with tolerance schedule ϵ={2.0, 1.5, 1.0, 0.75, 0.5, 0.2, 0.1, 0.075, 0.05, 0.03, 0.025}. The red line shows the variance from ABC SMC, the blue line the variance from the ABC PRC and the green line the variance from the ABC rejection algorithm (figure 9b,c). In the case when the perturbation is relatively small, we see that the variance resulting from improperly weighted particles in ABC PRC is too small (blue line in figure 9b), while the variance resulting from ABC SMC is ultimately comparable to the variance obtained by the ABC rejection algorithm (green line).
Figure 9.
(a) The probability density function of a mixture of two normal distributions, , taken as a toy example used for a comparison of ABC SMC with ABC PRC. (b,c) Plots show how the variance of approximated intermediate distributions πt changes with populations (t=1, …, 10 on the x-axis). The red curves plot the variance of the ABC SMC population and the blue curves the variance of the non-weighted ABC PRC populations. The perturbation kernel in both algorithms is uniform, . In (b), σ=1.5 and this results in poor estimation of the posterior variance with the ABC PRC algorithm. In (c), σ is updated in each population so that it expands over the whole population range. Such σ is big enough for non-weighted ABC PRC to perform equally well as ABC SMC.
However, we also note that when using many populations and too small a perturbation, e.g. uniform perturbation Kt=σU(−1, 1) with σ=0.15, the approximation is not very good (results not shown). One therefore needs to be careful to use a sufficiently large perturbation, irrespective of the weighting scheme. However, at the moment, there are no strict guidelines of how best to do this and we decide on the perturbation kernel based on experience and experimentation.
For the one-dimensional deterministic case with a uniform prior distribution and uniform perturbation, one can show that all the weights will be equal when σ of the uniform kernel is equal to the whole parameter range. In this case, the non-weighted ABC PRC yields the same results as ABC SMC (figure 9c). However, when working with complex high-dimensional systems, it simply is not feasible to work with only a small number of populations, or a very big perturbation kernel spreading over the whole parameter range. Therefore, we conclude that it is important to use the ABC SMC algorithm owing to its correct weighting.
Another difference between the two algorithms is that ABC PRC includes the resampling step in order to maintain a sufficiently large effective sample size (Liu & Chen 1998; Liu 2001; Del Moral et al. 2006). In contrast to non-ABC SIS or SMC frameworks, ABC algorithms, by sampling with weights in step S2.1 prior to perturbation, we suggest, do not require this additional resampling step.
We note that in SIS, the evaluation of weights after each population is computationally more costly, i.e. O(N2), than the calculation of weights in SMC with a backward kernel, which is O(N), where N denotes the number of particles. However, this cost is negligible in the ABC case, because the vast proportion of computational time in ABC is spent on simulating the model repeatedly. While thousands or millions of simulations are needed, the weights only need to be updated after every population. Therefore, we can easily afford spending a bit more computational time in order to use the correctly weighted version and circumvent the issues related to the backward kernel choice.
Appendix C. ABC and full likelihood for ODE systems
We would like to note that the ABC algorithm with the distance function chosen to be squared errors is equivalent to the maximum-likelihood problem for a dynamical system for which Gaussian errors are assumed. In other words, minimizing the distance function
| (C1) |
where is the solution of the m-dimensional dynamical system and , , are (m-dimensional) data points measured at times t1, …, tn, is equivalent to maximizing the likelihood function
where Σ is diagonal and its entries equal. This can straightforwardly be generalized for the case of multiple time-series measurements. Thus, ABC is for deterministic ODE systems closely related to standard Bayesian inference where the likelihood is evaluated. This is because ODEs are not based on a probability model, and likelihoods are therefore generally defined in a nonlinear regression context (such as assuming that the data are normally distributed around the deterministic solution; e.g. Timmer & Muller 2004; Vyshemirsky & Girolami 2008).
Footnotes
For a more general version of the algorithm, suitable especially for application to stochastic models, see appendix A.
In the stochastic framework, we again suggest using the general form of the algorithm with Bt>1; see appendix A.
This, including the experiment below, was suggested by Beaumont (2008b).
Supplementary Material
The video shows the particles from the four-dimensional distributions corresponding to the (i) prior distribution, (ii) 4th intermediate distribution, (iii) approximate posterior distribution obtained for the deterministic repressilator model.
Simulated datasets used in the examples.
References
- Anderson R.M., May R.M. Oxford University Press; New York, NY: 1991. Infectious diseases of humans: dynamics and control. [Google Scholar]
- Baker C., Bocharov G., Ford J., Lumb P.S.J., Norton C.A.H., Paul T., Junt P., Krebs B. Ludewig computational approaches to parameter estimation and model selection in immunology. J. Comput. Appl. Math. 2005;184:50–76. doi: 10.1016/j.cam.2005.02.003. [DOI] [Google Scholar]
- Banks H., Grove S., Hu S., Ma Y. A hierarchical Bayesian approach for parameter estimation in HIV models. Inverse Problems. 2005;21:1803–1822. doi: 10.1088/0266-5611/21/6/001. [DOI] [Google Scholar]
- Battogtokh D., Asch D.K., Case M.E., Arnold J., Schuttler H.-B. An ensemble method for identifying regulatory circuits with special reference to the qa gene cluster of Neurospora crassa. Proc. Natl Acad. Sci. USA. 2002;99:16 904–16 909. doi: 10.1073/pnas.262658899. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beaumont, M. 2008a Simulations, genetics and human prehistory (eds S. Matsumura, P. Forester & C. Renfrew). McDonald Institute Monographs, University of Cambridge.
- Beaumont, M. A. 2008b A note on the ABC-PRC algorithm of Sissons et al (2007). (http://arxiv.org/abs/0805.3079v1).
- Beaumont M.A., Zhang W., Balding D.J. Approximate Bayesian computation in population genetics. Genetics. 2002;162:2025–2035. doi: 10.1093/genetics/162.4.2025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bortz D.M., Nelson P.W. Model selection and mixed-effects modeling of HIV infection dynamics. Bull. Math. Biol. 2006;68:2005–2025. doi: 10.1007/s11538-006-9084-x. [DOI] [PubMed] [Google Scholar]
- Brown K.S., Sethna J.P. Statistical mechanical approaches to models with many poorly known parameters. Phys. Rev. E. 2003;68:021 904. doi: 10.1103/PhysRevE.68.021904. [DOI] [PubMed] [Google Scholar]
- Cox R.D., Hinkley D.V. Chapman & Hall/CRC; New York, NY: 1974. Theoretical statistics. [Google Scholar]
- Del Moral P., Doucet A., Jasra A. Sequential Monte Carlo samplers. J. R. Stat. Soc. B. 2006;68:411–432. doi: 10.1111/j.1467-9868.2006.00553.x. [DOI] [Google Scholar]
- Elowitz M.B., Leibler S. A synthetic oscillatory network of transcriptional regulators. Nature. 2000;403:335–338. doi: 10.1038/35002125. [DOI] [PubMed] [Google Scholar]
- Enright W., Hu M. Interpolating Runge–Kutta methods for vanishing delay differential equations. Computing. 1995;55:223–236. doi: 10.1007/BF02238433. [DOI] [Google Scholar]
- Fagundes N., Ray N., Beaumont M., Neuenschwander S., Salzano F.M., Bonatto S.L., Excoffier L. Statistical evaluation of alternative models of human evolution. Proc. Natl Acad. Sci. USA. 2007;104:17 614–17 619. doi: 10.1073/pnas.0708280104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fields B.N., Knipe D.M., Howley P.M. Lippincott Williams & Wilkins; Philadelphia, PA: 1996. Fundamental virology. [Google Scholar]
- Galassi M. 2nd edn. Cambridge University Press; Cambridge, UK: 2003. GNU scientific library reference manual. [Google Scholar]
- Gillespie D. Exact stochastic simulation of coupled chemical reactions. J. Phys. Chem. 1977;81:2340–2361. doi: 10.1021/j100540a008. [DOI] [Google Scholar]
- Golightly A., Wilkinson D. Bayesian inference for stochastic kinetic models using a diffusion approximation. Biometrics. 2005;61:781–788. doi: 10.1111/j.1541-0420.2005.00345.x. [DOI] [PubMed] [Google Scholar]
- Golightly A., Wilkinson D. Bayesian sequential inference for stochastic kinetic biochemical network models. J. Comput. Biol. 2006;13:838–851. doi: 10.1089/cmb.2006.13.838. [DOI] [PubMed] [Google Scholar]
- Gutenkunst R., Waterfall J., Casey F., Brown K., Myers C., Sethna J. Universally sloppy parameter sensitivities in systems biology models. PLoS Comput. Biol. 2007;3:e189. doi: 10.1371/journal.pcbi.0030189. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hammond B.J., Tyrrell D.A. A mathematical model of common-cold epidemics on Tristan da Cunha. J. Hyg. 1971;69:423–433. doi: 10.1017/s0022172400021677. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoeting J., Madigan D., Raftery A., Volinsky C. Bayesian model averaging: a tutorial. Statist. Sci. 1999;14:382–401. doi: 10.1214/ss/1009212519. [DOI] [Google Scholar]
- Horbelt W., Timmer J., Voss H. Parameter estimation in nonlinear delayed feedback systems from noisy data. Phys. Lett. A. 2002;299:513–521. doi: 10.1016/S0375-9601(02)00748-X. [DOI] [Google Scholar]
- Huang Y., Liu D., Wu H. Hierarchical Bayesian methods for estimation of parameters in a longitudinal HIV dynamic system. Biometrics. 2006;62:413–423. doi: 10.1111/j.1541-0420.2005.00447.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johannes M., Polson N. MCMC methods for continuous-time financial econometrics. In: Ait-Sahalia Y., Hansen L., editors. Handbook of financial econometrics. Elsevier Science Ltd; Amsterdam, The Netherlands: 2005. [Google Scholar]
- Kass R., Raftery A. Bayes factors. J. Am. Stat. Assoc. 1995;90:773–795. doi: 10.2307/2291091. [DOI] [Google Scholar]
- Kirkpatrick S., Gelatt C., Vecchi M. Optimization by simulated annealing. Science. 1983;220:671–680. doi: 10.1126/science.220.4598.671. [DOI] [PubMed] [Google Scholar]
- Liu J.S. Springer; Berlin, Germany: 2001. Monte Carlo strategies in scientific computing. [Google Scholar]
- Liu J.S., Chen R. Sequential Monte Carlo methods for dynamic systems. J. Am. Stat. Assoc. 1998;93:1032–1044. doi: 10.2307/2669847. [DOI] [Google Scholar]
- Lotka A.J. Williams & Wilkins Co; Baltimore, MD: 1925. Elements of physical biology. [Google Scholar]
- Marjoram P., Molitor J., Plagnol V., Tavare S. Markov chain Monte Carlo without likelihoods. Proc. Natl Acad. Sci. USA. 2003;100:15 324–15 328. doi: 10.1073/pnas.0306899100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mendes P., Kell D. Non-linear optimization of biochemical pathways: applications to metabolic engineering and parameter estimation. Bioinformatics. 1998;14:869–883. doi: 10.1093/bioinformatics/14.10.869. [DOI] [PubMed] [Google Scholar]
- Moles C., Mendes P., Banga J. Parameter estimation in biochemical pathways: a comparison of global optimization methods. Genome Res. 2003;13:2467–2474. doi: 10.1101/gr.1262503. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muller T.G., Faller D., Timmer J., Swameye I., Sandra O., Klingmüller U. Tests for cycling in a signalling pathway. J. R. Stat. Soc. Ser. C. 2004;53:557. doi: 10.1111/j.1467-9876.2004.05148.x. [DOI] [Google Scholar]
- Paul C. Developing a delay differential equation solver. Appl. Numer. Math. 1992;9:403–414. doi: 10.1016/0168-9274(92)90030-H. [DOI] [Google Scholar]
- Press W.H., Teukolsky S.A., Vetterling W.T., Flannery B.P. 2nd edn. Cambridge University Press; Cambridge, UK: 1992. Numerical recipes in C: the art of scientific computing. [Google Scholar]
- Pritchard J., Seielstad M.T., Perez-Lezaun A., Feldman M.W. Population growth of human Y chromosomes: a study of Y chromosome microsatellites. Mol. Biol. Evol. 1999;16:1791–1798. doi: 10.1093/oxfordjournals.molbev.a026091. [DOI] [PubMed] [Google Scholar]
- Putter H., Heisterkamp S.H., Lange J.M.A., de Wolf F. A Bayesian approach to parameter estimation in HIV dynamical models. Stat. Med. 2002;21:2199–2214. doi: 10.1002/sim.1211. [DOI] [PubMed] [Google Scholar]
- Reinker S., Altman R., Timmer J. Parameter estimation in stochastic biochemical reactions. IEE Proc.Syst. Biol. 2006;153:168–178. doi: 10.1049/ip-syb:20050105. [DOI] [PubMed] [Google Scholar]
- Robert C.P., Casella G. 2nd edn. Springer; New York, NY: 2004. Monte Carlo statistical methods. [Google Scholar]
- Saltelli A., Ratto M., Andres T., Campolongo F., Cariboni J., Gatelli D., Saisana M., Tarantola S. Wiley; New York, NY: 2008. Global sensitivity analysis: the primer. [Google Scholar]
- Sanchez M., Blower S. Uncertainty and sensitivity analysis of the basic reproductive rate: tuberculosis as an example. Am. J. Epidemiol. 1997;145:1127–1137. doi: 10.1093/oxfordjournals.aje.a009076. [DOI] [PubMed] [Google Scholar]
- Shibli M., Gooch S., Lewis H.E., Tyrrell D.A. Common colds on Tristan da Cunha. J. Hyg. 1971;69:255. doi: 10.1017/s0022172400021483. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sisson S.A., Fan Y., Tanaka M.M. Sequential Monte Carlo without likelihoods. Proc. Natl Acad. Sci. USA. 2007;104:1760–1765. doi: 10.1073/pnas.0607208104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stumpf M., Thorne T. Multi-model inference of network properties from incomplete data. J. Integr. Bioinform. 2006;3:32. [Google Scholar]
- Timmer J., Muller T. Modeling the nonlinear dynamics of cellular signal transduction. Int. J. Bifurcat. Chaos. 2004;14:2069–2079. doi: 10.1142/S0218127404010461. [DOI] [Google Scholar]
- van Kampen N.G. 3rd edn. North-Holland; Amsterdam, The Netherlands: 2007. Stochastic processes in physics and chemistry. [Google Scholar]
- Volterra V. Variazioni e fluttuazioni del numero d'individui in specie animali conviventi. Mem. R. Acad. Naz. dei Lincei. 1926;2:31–113. [Google Scholar]
- Vyshemirsky V., Girolami M.A. Bayesian ranking of biochemical system models. Bioinformatics. 2008;24:833–839. doi: 10.1093/bioinformatics/btm607. [DOI] [PubMed] [Google Scholar]
- Wilkinson D.J. Chapman & Hall/CRC; London, UK: 2006. Stochastic modelling for systems biology. [Google Scholar]
- Wilkinson, R. D. 2007 Bayesian inference of primate divergence times. PhD thesis, University of Cambridge.
- Zucknick, M. 2004 Approximate Bayesian computation in population genetics and genomics. MSc thesis, Imperial College London.
Notice of correction
S2.2 on page 3 is now present in its correct form.
MS2.2 on page 4 is now present in its correct form.
S2.2 on page 13 is now present in its correct form.17 July 2008
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
The video shows the particles from the four-dimensional distributions corresponding to the (i) prior distribution, (ii) 4th intermediate distribution, (iii) approximate posterior distribution obtained for the deterministic repressilator model.
Simulated datasets used in the examples.