Integers do not automatically activate their quantity representation

Abstract

Researchers have generally come to the conclusion that integers automatically activate the quantity they symbolize and this quantity dominates responding. I present a strong test of this hypothesis with two numerical same/different experiments. On each trial, I present the participant an integer between 1 and 9 and ask him or her to identify whether that symbol is a 5. If quantity information dominates responding then participants’ RT should be a function of the numerical distance between the target and the distractor. If quantity information is not activated, then the integer is merely a shape, and participants’ RT should be a function of the physical similarity of the target and the distractor. The data from Experiments 1 and 2 demonstrate that quantity information exerts no control and physical similarity is the primary controlling factor. These findings demonstrate that integers maintain a level of independence from their quantity representations.

Integers are linguistic symbols, therefore any relation between these symbols and quantity information must be indirect. Researchers have generally come to the conclusion that integers are so strongly associated with the quantity they represent that the quantity dominates responding when people encounter integers (for a review, see Tzelgov & Ganor-Stern, 2005). Here, I present two experiments that provide a strong test of this hypothesis.

In a classic experiment, Moyer and Landauer (1967) presented two integers side-by-side and asked participants to judge which of the two integers was larger. The data revealed a monotonically decreasing function relating participants’ reaction times (RTs) and the numerical distance between the two numbers (termed the numerical distance effect). Moyer and Landauer showed that the numerical distance effect was described by the Welford (1960) function:

$$\text{RT}=\text{a}+{\text{k}}^{\ast }log[\text{L}/(\text{L}-\text{S})],$$ (1)

where a and k are constants, L is the larger quantity and S is the smaller quantity. Because the Welford function also described the relation between RT and judgments of natural quantities such as line lengths and dot patterns (see also, Buckley & Gillman, 1974; Moyer & Landauer, 1973), Moyer and Landauer concluded that the presented integer activated an analog representation of quantity information (termed a quantity representation) and this representation had primary influence over participants’ responses. Since Moyer and Landauer’s (1967) paper, there has been extensive evidence demonstrating that the underlying cognitive representation of quantity influences the numerical distance effect (e.g., Buckley & Gillman, 1974; Dehaene, 1989; Deheane, Dupoux, & Mehler, 1990; Duncan, & McFarland, 1980; Hinrichs, Yurko, & Hu, 1981; Schwartz, & Stein, 1998; Shepard, Kilpatric, & Cunningham, 1975; Takahashi, & Green, 1983). Evidence from neuroscience also supports the existence of a language-independent abstract quantity representation to which numerical symbols link (for a review, see Nieder, 2005). fMRI data demonstrate that quantity representations activate bilateral visuo-spatial neural networks in the parietal lobes, whereas brain activation by numerical labels is restricted to the “left inferior frontal circuit also used for generating associations between words” (Dehaene, Spelke, Pinel, Stanescu, & Tsivkin, 1999; p.97).

Researchers have argued that humans automatically associate a numerical symbol with its quantity representation even when not required to do so (for a review, see Tzelgov & Ganor-Stern, 2005). The strongest evidence for this assertion comes from the numerical Stroop (for a review, see Pavese & Umilta, 1998) and numerical same/different tasks (e.g., Dehaene & Akhavein, 1995). In a numerical Stroop task, participants are asked to identify the number of elements in a display. The elements could be letters (neutral condition), integers consistent with the number of element in the display (facilitation condition), or integers inconsistent with the number of element in the display (interference condition). In general, participants’ reaction times are fastest in the facilitation condition and slowest in the interference condition. Similar results are found when the relevant dimension is size rather than numerosity (e.g., Henik & Tzelgov, 1982). These results are typically explained by hypothesizing that the numerical symbols of the irrelevant integers automatically activated their associated quantity representations. However, because the numerical Stroop task requires the participant to make a quantity/magnitude judgment (i.e., judge the number or size of elements in the display), it is the task that activates the visuo-spatial networks of the parietal lobes associated with quantity representations, not the numerical symbols. Rather, the numerical Stroop results demonstrate that when the visuo-spatial networks of the parietal lobes are active, integers will automatically link with those networks.

The numerical same/different task can provide strong evidence that integers automatically activate their associated quantity representation because the task requires no quantity/magnitude judgment¹. In the numerical same/different task, participants are asked to identify whether two integers are the same or different. Dehaene and Akhavein (1995) conducted a typical numerical same/different task, using the integers 1, 2, 8 and 9 and discovered that the close integers (e.g., 1 2) integers were responded to slower than distant integers (e.g., 1 8). The authors concluded that this was evidence of the numerical distance effect, which emerged because the integers automatically activated their associated quantity representations. Ganor-Stern and Tzelgov (2008) extended the findings of Dehaene and Akhavein (1995) by assessing, “… all the possible 28 pairs created from two different numbers in the range of 1–9, excluding 5.” (p. 431). The authors found RT generally increased as numerical distance between the pairs of integers decreased. Both results suggest that Arabic integers automatically activate their associated quantity representation. However, neither manuscript presented and tested a plausible alternative to the numerical distance hypothesis. Although testing an alternative hypothesis in the face of the strong results of Ganor-Stern and Tzelgov (2008) may seem excessively cautious, it is appropriate when both the primary hypothesis and the alternative hypothesis make similar, but distinct predictions. Below, I present a plausible alternative hypothesis whose predictions are correlated with numerical distance.

Symbols, absent their meaning, are simply shapes. Therefore, if integers do not activate their associated quantity representation, the participants’ RT data should be predicted by a measure of the physical similarity of the distractor integer to the target integer. I have codified a simple physical similarity function based on the seven-line, figure 8 structure used to create Arabic integers on old alarm clocks:

$$\text{P}=\text{O}/\text{D},$$ (2)

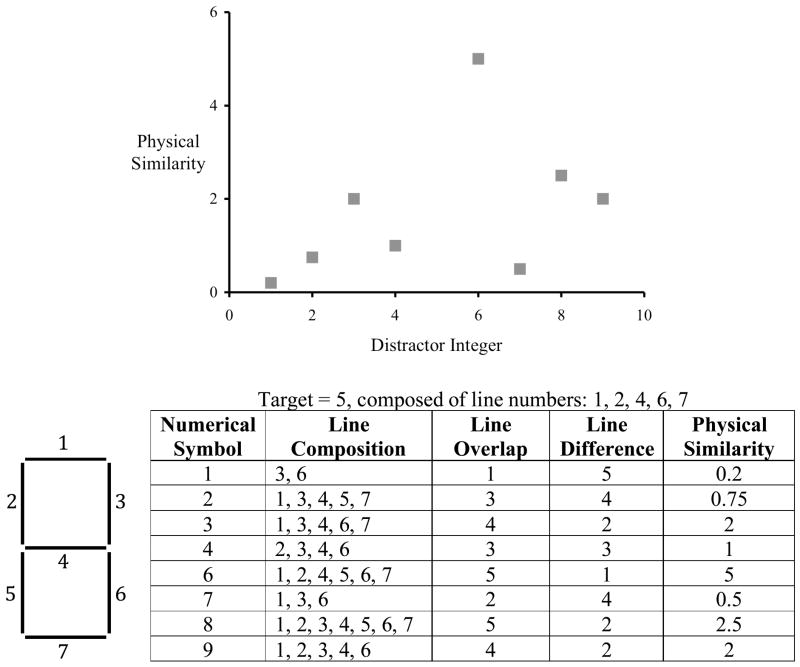
where P is the measure of physical similarity, O is the number of lines in the figure 8 structure that the target and distractor integers share (a measure of overlap), and D is the number of remaining lines in the figure 8 structure that are used to compose the target and distractor integers (a measure of difference). Figure 1 shows the physical similarity function for the integers 1–4 and 6–9, with a target of 5. The physical similarity function strongly correlates with the Welford function (r = .62). This correlation between numerical distance and physical similarity is likely a function of the way numerical symbols were initially formed and later evolved. It is thought that numerical symbols grew out of literal representations of the quantities the symbols represent (for a review, see Ifrah, 2000). Such a creation system would almost certainly result in a correlation between physical similarity and numerical distance.

Figure 1.

The calculation of the physical similarity function when the target integer is a 5, and the distractor integers are 1–4 and 6–9. The figure 8 on the left shows the basic structure of the integers, with each line on the figure 8 labeled with a number. The table shows the lines numbers that constitute each integer and the calculation of the similarity function. The figure at the top plots the similarity function.

In the present experiment, I assessed whether numerical symbols automatically activate their quantity representation in a numerical same/different task. On each trial, I presented the participant an integer between 1 and 9 and ask him or her to identify whether that symbol is a 5. I set up two competing hypotheses: the automatic activation hypothesis and the physical similarity hypothesis. The automatic activation hypothesis assumes that integers automatically activate their quantity representation and therefore participants’ RT data should be predicted by the Welford function typical of numerical distance data. The physical similarity hypothesis assumes that integers do not activate their quantity representation and therefore participants’ RT data should be predicted by a measure of the physical similarity of the distractor integer to the target integer.

Experiment 1

Methods

Participants

Ninety-nine undergraduate volunteers participated for class credit. One subject was removed because his or her error rate was 48.6%.

Apparatus and Stimuli

All stimuli were presented on a 15-inch color monitor with a 60-Hz refresh rate controlled by a Pentium microcomputer using a DOS operating system. The resolution of the monitor was 1024 × 768.

A trial consisted of a single integer subtending 1.33 degrees visual angle presented in the center of the screen. The target integer was a five (5). The distractor integers were selected randomly from the integers 1–9, excluding 5 in arabic notation. All integers were presented in Ariel font.

Procedure

Participants were tested individually in a small, dark room. The participant’s were instructed that on every trial they would be presented an integer between 1 and 9 and that they were to press one button on the keyboard if the integer was a 5 and another button for all other integers. Half the participants were told to press the “D” key if a 5 was presented and the “L” key for all other integers. The keys were reversed for the remaining participants. The participants were instructed that speed was important, but accuracy was essential.

Each trial consisted of the presentation of a stimulus and the participant’s response. The stimulus remained on the screen until the participant responded. The computer recorded the participant’s RT. There was a 500 ms delay between trials. Every 130 trials the experiment would pause and ask the participant if he or should would like to take a self-timed break. The experiment resumed when the participant hit the return key. Each session lasted about 50 minutes.

Each session consisted of 16 practice trials and 544 experimental trials. Half of the practice trials and half of the experimental trials contained the target. The remaining trials were composed of 34 trials of each distractor integer. All stimuli were randomly presented.

Results and Discussion

Before analysis, I trimmed the RT data to remove times less than 200 ms and greater than 5000 ms (0.4% of the data). I also removed all incorrect responses (2.7% of the data).

Both the automatic activation and the physical similarity hypotheses cannot predict participant’s performance on target present trials because the relevant distance metrics are undefined when computing the distance between two identical integers. Nevertheless, we know from Sternberg’s (1995) work that the cognitive processes used to identify the presence of targets are often different than those used to identify their absence. One of the features of these processes is that they are faster than target absent trials. A paired sample t-test confirmed that target present trials (M = 608, SD = 121) were significantly faster than target absent trials (M = 660, SD = 141), t(97) = 11.58, p < .001.

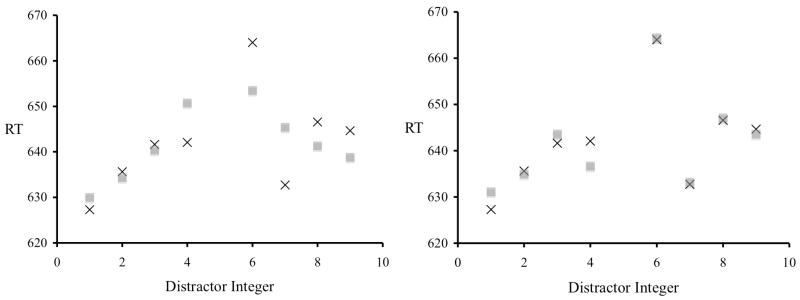
To test the automatic activation and the physical similarity hypotheses, I computed two regressions with the participants’ average RT as the criterion variable: one using the Welford function as the predictor variable and one using the physical similarity function as the predictor variable (see Figure 2). Although the Welford function significantly predicted the data, F(1,6) = 6.2, p = .05, r²_adj= .43 (slope = 15.0, intercept = 627), the similarity function predicted the data far more accurately, F(1,6) = 96.3, p < .001, r²_adj= .93 (slope = 6.9, intercept = 630). The likelihood ratio of the models fits (Dixon, 2003) indicate that the physical similarity model is a substantially better fit than the Welford function, λ = 4396.5 (a value of 10 or better indicates moderate to strong evidence of a better fit; Goodman & Royall, 1988).

Figure 2.

The two graphs show the results of Experiment 1. For both graphs, the “X” represents the data, and the gray box represents each models prediction. The graph on the left shows the predicted Welford function, the graph on the right shows the predicted physical similarity function. Physical similarity accounts for over 93% of the variance.

To determine whether both functions contribute unique variance to the prediction of RTs, I ran a regression on the standardized criterion variable and both standardized predictor variables. The regression was significant, F(2,5) = 79.7, p < .001, r²_adj= .96. Although the physical similarity function was significant (slope = 0.85, t=8.7, p<.001), the Welford function was not (slope = 0.2, t=2.1, ns).

The data clearly indicate that physical similarity of the distractor to the target was the primary influence on participant’s RTs. The similarity function accounted for about 93% of the variance in isolation. Although the Welford function was a significant predictor in isolation, it’s influence dropped out when entered into the equation with the similarity function.

Experiment 2

To test the limits of this effect, I ran the same experiment with varied fonts. The variation of fonts should focus participants’ attention on the semantic content of the integer rather than its physical structure, thus enhancing the numerical distance effect. Thus, this experiment is a strong test of the automatic activation hypothesis.

Methods

Participants

One hundred and six undergraduate volunteers participated for class credit.

Apparatus and Stimuli

The stimuli and apparatus were identical to that of Experiment 1 with 1 exception: one each trial, the stimulus was presented in a random font that was selected from a set of 70 fonts.

Procedure

The procedure was identical to that of Experiment 1.

Results and Discussion

Before analysis, I trimmed the RT data to remove times less than 200 ms and greater than 5000 ms (0.05% of the data). I also removed all incorrect responses (2% of the data).

A paired sample t-test confirmed that target present trials (M = 581, SD = 87) were significantly faster than target absent trials (M = 635, SD = 124), t(105) = 8.32, p < .001. Similar to Experiment 1, I computed two regressions with the participants’ average RT as the criterion variable: one using the Welford function as the predictor variable and one using the physical similarity function as the predictor variable. The Welford function did not significantly predict the data, F(1,6) = 2.9, ns. The physical similarity function significantly predicted the participants RT, F(1,6) = 37, p < .001, r²_adj= .84 (slope = 5.3, intercept = 613). Because the Welford function was not significant in isolation, it was unnecessary to run the liklihood analysis or the combined regression analysis present in Experiment 1.

The data from Experiment 2 demonstrate that only physical similarity of the target to the distractor significantly predicted participant’s RT. Apparently varying the physical structure of the numerical symbols was not sufficient to activate the semantic content of the integers.

General Discussion

The data from Experiments 1 and 2 indicate that numerical symbols do not automatically activate numerical quantity representations. In Experiment 1, where a single font was used, physical similarity accounted for 93% of the variance of participants’ mean RTs and was a substantially better fit than the Welford function. Indeed, when the Welford function was entered into the equation with physical similarity, its influence dropped out. In Experiment 2, when different fonts were used, only physical similarity predicted participants’ mean RTs. Thus, in the present task, quantity representations have no influence on participants’ RTs. These data are a strong demonstration that numerical symbols do not automatically activate quantity representations.

Quantity information may not have exerted control over participants’ responses in the present experiments because the same/different task did not require the activation of the brain area associated with quantity representations (i.e., the visuo-spatial neural networks in the parietal lobes). In contrast, when the task activates the brain area associated with quantity representations (such as in the numerical distance and numerical Stroop tasks), then numerical symbols relatively easily and perhaps automatically link with the quantity representation. This pattern of results can be modeled as an instance of moderate Hebbian learning. To simplify, the cells representing numerical symbols and their quantity representations often fire together, so their synaptic strength should be high. Because of this, when both sets of cells are already active, the cells representing quantity may synchronize with the cells representing their associated numerical symbols. However, because activation efficiency is not perfect, perfect automaticity is not achieved. Therefore, activating the cells representing numerical symbols may not be sufficient to activate the cells of their quantity representations. This explains why the numerical same/different task does not produce a numerical distance effect and the numerical Stroop task produces interference effects.

The data from Experiments 1 and 2 appear to differ from that of previous numerical same/different experiments (Dehaene & Akhavein, 1995; Ganor-Stern & Tzelgov, 2008). The actual differences between the current data and those of previous experiments are difficult to judge, however, given (1) the correlation between numerical distance and physical similarity, and (2) that the researchers who identified the numerical distance effect in the numerical same/different task did not assess whether the data was better predicted by the physical similarity function. Because the Welford function closely follows the similarity function, one may confuse RT data resulting from physical similarity for that resulting from the numerical distance effect if one does not test both. Indeed, the ability of both functions to predict significantly in isolation was demonstrated in Experiment 1. The demonstration provides strong rational for researchers to assess the physical similarity function when also assessing the numerical distance function.

The present results are consistent with the results of Ratinckx, Brysbaert, and Fias (2005). In their manuscript, the authors describe how models that require activation of a numerical symbol’s quantity representation make the same predictions as those that do not in many standard numerical decision tasks, including priming tasks. In a series of elegant priming experiments, the authors demonstrate that, for two digit numerals “there is a direct, nonsemantic route from Arabic input to verbal output, which outperforms the semantically mediated route” (p. 1158). Our data further this finding by demonstrating that even single digit numerals can be processed nonsemantically. Future research should explore the bounds of these findings as well as assess whether any evidence of semantic activation can be found in these tasks.

In sum, the present experiments demonstrate that (1) numerical symbols do not automatically activate quantity representations, and (2) physical similarity between target and distractor symbols can be a very accurate predictor of participants’ RT in a numerical judgment task. These findings demonstrate that integers maintain a level of independence from their quantity representations.