Abstract
Targeted therapy using small-molecule inhibitors is a promising new therapy approach against cancer, but drug-resistant mutants present an obstacle to success. Oncolytic virus therapy, where viruses replicate specifically in cancer cells and kill them, is another promising therapy approach against cancer. While encouraging results have been observed in clinical trials, consistent success has not been possible so far. Based on a computational framework, I report that even if oncolytic virus therapy fails to eradicate a cancer, it can have the potential to eradicate the sub-population of drug-resistant cancer cells. Once this has occurred, targeted drug therapy can be used to induce cancer remission. For this to work, a drug resistance mutation must confer a certain fitness cost to the cell, as has been documented in the literature. The reason for this finding is that in the presence of a shared virus, the faster growing (drug-sensitive) cell population produces an amount of virus that is too much for the slower growing (drug-resistant) cell population to survive. This is derived from a population dynamic principle known as apparent competition. Therefore, a sequential combination of oncolytic virus and targeted therapies can overcome major weaknesses of either approach alone.
Keywords: mathematical models, oncolytic virus therapy, apparent competition
1. Introduction
In recent years, exciting new treatment strategies have emerged in the context of cancer research. A better understanding of the molecular pathways that are altered in cancer cells has allowed the development of targeted small-molecule inhibitors (Yee & Keating 2003; Guillemard & Saragovi 2004). These attack specific defects in cancer cells, leading to cell death or cessation of cell division. Because cancer cells are selectively targeted, the degree of side effects is much less when compared with conventional chemotherapy. The most successful example of this class of drug so far is imatinib (STI571 or Gleevec) that is used to treat chronic myeloid leukaemia (CML; Sawyers 1999; Deininger et al. 2000; O'Dwyer et al. 2002; Deininger & Druker 2003; Melo et al. 2003; Druker 2004). A particular problem with such therapy is the emergence of mutant cells that are resistant to the drug, particularly at more advanced stages of the cancer (Gorre et al. 2001; Blagosklonny 2002; Shannon 2002; Goldman & Melo 2003; Burgess et al. 2005; Melo & Barnes 2007).
A different treatment approach that also selectively targets cancer cells is the use of oncolytic viruses (Kirn & McCormick 1996; Bell et al. 2003; McCormick 2003, 2005; Davis & Fang 2005; Kaplan 2005; O'Shea 2005; Parato et al. 2005; Post et al. 2005; Roberts et al. 2006; Bell 2007; Crompton & Kirn 2007; Kelly & Russell 2007; Vaha-Koskela et al. 2007). These are viruses that specifically infect cancer cells, replicate in them, kill them and spread to further cancer cells. The selectivity of these viruses for cancer cells occurs because virus replication is blocked by the product of certain genes that are commonly missing in cancer cells. The virus that has been studied the most in terms of clinical trials is the adenovirus ONYX-015, but a variety of other viruses are now being explored in this context, some of which can be administered intravenously (Lorence et al. 2003; Roberts et al. 2006). A clear success in the use of such viruses, however, has so far not been reported. This is partly due to our lack of understanding of the correlates of successful virus-mediated cancer eradication, and to the potentially complex interactions between virus replication and the immune system.
So far, the ultimate goal of oncolytic virus therapy has been to eradicate the cancer. Here, I report that even if this cannot be achieved, it is theoretically possible to use oncolytic viruses to eradicate the sub-population of cancer cells that are resistant to chemotherapies, such as small-molecule inhibitors. The idea is to pretreat a cancer with oncolytic viruses, leading to the eradication of the drug-resistant cells. Subsequently, the cancer is treated with a small-molecule inhibitor that could lead to successful remission in the absence of resistance. This makes sense given that oncolytic viruses have so far not been able to consistently eradicate cancers, and given that drug-resistant cells are a major obstacle to targeted small-molecule treatments.
The rationale for this idea comes from a simple population dynamics concept that is called ‘apparent competition’ (Holt 1977). Even if two populations or two species do not directly compete with each other, the fitter species can drive the less fit species extinct if they are infected by the same pathogen. For example, if the growth rate of the drug-sensitive cancer cells is higher than that of the resistant cancer cells, then the resistant cells will be driven extinct if a virus can infect both cell populations. In the context of CML therapy with the targeted drug imatinib, it has been reported that certain drug-resistant mutants have a reduced growth rate and are less fit than the drug-sensitive cells (Tipping et al. 2001). Drug-resistant mutants in other diseases, for example human immunodeficiency virus (HIV), are also associated with a fitness cost (Back et al. 1996), and it is likely that this is a broader phenomenon since the mutations usually alter the very proteins that drive the disease. However, this remains to be investigated in more detail, especially in the context of cancer. In this paper, I use a mathematical model to develop the concept of employing oncolytic viruses to selectively eliminate drug-resistant cancer cells.
2. Results
2.1 The model
I consider a mathematical model that describes the spread of an oncolytic virus through a population of tumour cells and assumes the existence of two sub-populations of cancer cells: cells that are susceptible to a given drug (from now on called drug-sensitive cells) and cells that are resistant to this drug. The model includes the following variables: x1, uninfected drug-sensitive cells; x2, uninfected drug-resistant cells; y1, infected drug-sensitive cells; and y2, infected drug-resistant cells. The model does not take into account a free virus population explicitly. Because the turnover of virus populations is much faster than that of infected cells, we assume that the free virus population is in a quasi-steady state.
Uninfected drug-sensitive cells grow with a rate r1x1(1+η)/(x1+x2+y1+y2+η). Thus, we assume saturated growth. The lower the total number of cells, the more this term approaches exponential growth. The higher the number of cells, the more this term approaches linear growth. The parameter η determines at what tumour size the exponential growth starts to saturate. For high values of η, the behaviour converges to an exponential growth model. For low values of η, the behaviour converges to a linear growth model. We assume that growth does not stop at a given tumour size, as would be the case with logistic growth. The reason is that we aim to model the most aggressive tumour growth, where a relatively fast expansion of the tumour cell population is observed until the organism dies. Saturated growth is assumed because several constraints, such as the spatial structures of tumours, are likely to prevent straight exponential growth at large numbers of cells.
Upon contact with virus, drug-sensitive cells become infected with a rate β1. Traditional virus dynamics models assume straightforward mass action (Wodarz 2001, 2003), where the rate of infection is directly proportional to the number of uninfected and infected cells. However, this leads to ‘boom and bust’ dynamics that do not reflect the acute dynamics of the infection in a realistic way. In particular, the initial spread of the virus depends heavily on the number of target cells, which can be huge in the context of a tumour. Alternatively, frequency-dependent transmission can be assumed (May & Anderson 1987; Antonovics et al. 1995; Begon et al. 1999; McCallum et al. 2001; Novozhilov et al. 2006). In this case, the rate of infection is not proportional to the number of infected cells, but to the fraction of infected cells in the tumour population. This gives rise to the opposite result that the initial virus spread is independent of the number of target cells. An intermediate scenario (Anderson & May 1978; Diekmann & Kretzschmar 1991; Heesterbeek & Metz 1993) is most likely to be realistic, and this is what we assume in our model. The transmission term is thus given by β1x1(y1+y2)(1+ϵ)/(x1+x2+y1+y2+ϵ). The parameter ϵ determines how much the model approaches the mass action or frequency dependence assumption. The higher the value of ϵ, the less the transmission is frequency dependent.
The drug-resistant cancer cell population is modelled according to the same principles. It grows with a rate r2x2(1+η)/(x1+x2+y1+y2+η). Drug-resistant cells become infected with a rate β2x2(y1+y2)(1+ϵ)/(x1+x2+y1+y2+ϵ). In addition, we assume that the drug-resistant cells are produced by mutation from drug-sensitive cells during cell division. Hence the mutation rate is given by μr1x1(1+η)/(x1+x2+y1+y2+η).
Infected cells are assumed not to divide, and die with rates a1 and a2 for drug-sensitive and drug-resistant cells, respectively. The model is based on the previous models that study the dynamics of oncolytic viruses in a single population of cancer cells (Wodarz 2001, 2003, 2004). It is given by the following set of ordinary differential equations:
It is important to discuss the tumour growth term used here in some more detail. It assumes saturated cell growth, but growth only slows down and does not stop as the number of cells increases, as is the case with other density-dependent growth terms, such as logistic growth. The biological interpretation could be that as the tumour grows, fewer cells contribute to reproduction owing to the spatial structure of the tumour. While the presence of one cell type can slow down the growth of the other cell type in this model, direct competition between two cell types cannot lead to extinction of any cell population. In the absence of a virus, both cell populations will always grow towards infinity, although with reduced rates at larger tumour sizes. In practical terms, tumour growth stops when the organism dies. This might apply to advanced tumour growth. By contrast, in other density-dependent growth equations where cell growth stops at large population sizes, direct competition will lead to the extinction of the slower growing cell population and the persistence of the faster growing one. Under the assumption that the drug-resistant cell population has a certain fitness cost, this population would be driven extinct by the time the tumour has grown close to its limiting size. This might apply to more benign tumour growth scenarios. For the current purposes, it is important to consider a model where direct competition cannot drive one of the cell populations extinct, because the aim is to examine the effect of a shared oncolytic virus on the dynamics of the two cancer cell populations. If one cell population drives the other one extinct in the current model, then the reason is apparent competition through the shared virus rather than direct competition.
The mathematical properties of the model are explored as follows. For now, we assume that the mutation rate μ=0. We simply assume initial conditions in which both cell populations are present. This assumption will be relaxed later.
2.2 Dynamics of drug-resistant versus drug-sensitive cancer cells
In what follows, it is assumed that in the absence of virus, the tumour cell populations can successfully grow (figure 1a), i.e. r1>0 and r2>0. Further, I will make the assumption that the virus can grow successfully in both the drug-sensitive and resistant cell populations alone. That is, (1+ϵ)β1/a1>1 and (1+ϵ)β2/a2>1, given that the number of tumour cells is large. If the cancer population consists of only one type of cells, the dynamics always converge towards a stable equilibrium if the virus establishes a successful infection. During this approach to equilibrium, oscillations can be observed. If these oscillations reduce the average number of cancer cells below one, or if the number of cancer cells at equilibrium lies below one, the cancer cell population can be considered eradicated. The dynamics that lead to cancer eradication are not within the scope of the current paper and are considered in a separate study. Here, we concentrate on the parameter region in which the virus fails to eradicate the cancer cell population, and the cancer and the virus populations persist in the long term and equilibrate.
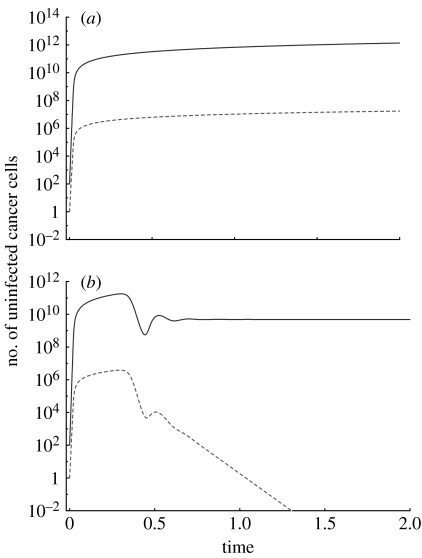
Figure 1.
The growth of drug-sensitive and drug-resistant mutants in the (a) absence and (b) presence of an oncolytic virus. In the absence of the virus, both cancer cell populations grow, first exponentially and then with a slower rate as the number of cells reaches higher levels. In the presence of the virus, the drug-sensitive cancer cells approach an equilibrium because the virus prevents unlimited growth of the cancer cells. The virus, however, fails to eradicate the cancer. The drug-resistant cancer cells go extinct owing to apparent competition mediated by the oncolytic virus. This simulation does not take into account the generation of resistant cells by mutation. Instead it assumes that a certain number of resistant cells are present at the beginning of the simulation. Parameters were chosen for the purpose of illustration only, since they are currently unknown. The dependence of the outcome on parameter values is discussed in the text. The following parameter values were used: r1=7, r2=5, β1=0.1, β2=0.1, a1=0.5, a2=0.5, ϵ=10, η=109, μ=0. Solid line, wild-type; dashed line, drug resistant.
Taking into account both the drug-sensitive and drug-resistant tumour cell populations, the virus infection has the following effect on the outcome. Only one of the cancer cell populations can persist (figure 1b). The other one goes extinct. The drug-sensitive cells persist and the resistant cells go extinct if r1/β1>r2/β2. The resistant cells persist and the drug-sensitive cells go extinct in the opposite case if r2/β2>r1/β1. The equilibrium expressions for these two outcomes are given by lengthy second-degree polynomial expressions that are not written down here for simplicity. If r1/β1=r2/β2, then the two cancer cell populations are competitively neutral. Data indicate that drug resistance mutations can confer a fitness cost to the cells in the absence of therapy in a variety of contexts. With CML, it has been shown that drug resistance mutations that arise through the amplification of the BCR–ABL fusion gene grow less efficiently than the drug-sensitive cells (Tipping et al. 2001). No other reports exist regarding the relative fitness of drug-resistant mutants in cancer. In the context of infectious diseases such as HIV, however, it is clear that many drug resistance mutations carry a fitness cost (Back et al. 1996). This is likely to be a more general phenomenon because drug resistance mutations typically alter proteins that are responsible for disease maintenance and progression. However, this remains to be investigated in further detail in the context of cancer. If we assume that the resistant cancer cells carry a fitness cost compared with the drug-sensitive cells (i.e. they grow slower, r2<r1) and the replication rate of the virus is identical in drug-sensitive and resistant cells (β1=β2), then the only possible outcome of the virus infection is that the resistant cancer cell population is driven extinct (figure 1b). Although the two cancer cell populations are not in competition with each other, the presence of the virus leads to dynamics that are in principle the same as those observed in competition. That is, competitive exclusion can be observed where the fitter type displaces the less fit type. The fact that ‘competitive exclusion’ can occur if two species (that do not compete directly) share a pathogen is referred to as apparent competition in the ecological literature (Holt 1977). Apparent competition has been shown to be a potentially important factor that shapes ecological assemblages (Hassell & Bonsall 1997; Greenman & Hudson 1999, 2000; Bonsall & Hassell 2000).
However, even if the resistant cells grow slower than the drug-sensitive cells (r2<r1), the resistant cells can still have a higher fitness in the context of apparent competition if the replication rate of the virus in the resistant cells (β2) is reduced more than the growth rate of the resistant cells (r2) compared with drug-sensitive cells. Such a scenario could come about if the rate of viral replication is significantly coupled to the rate of cell division. In this case, quantitative studies would have to be performed in order to determine whether the viral replication rate is reduced to a greater or lesser extent than the division rate of resistant cells.
Let us examine more closely the dynamics of competitive exclusion. As seen in figure 1, the population of drug-resistant cancer cells only starts to be negatively affected once the virus downregulates the overall cancer growth and the dynamics of the drug-sensitive cells converge to a stable equilibrium. Therefore, if the virus grows too slowly or the cancer grows too fast, it is possible that the cancer will reach a size at which it causes mortality before the virus has had a significant impact and before the population of drug-resistant cancer cells can be diminished. In this case, the oncolytic virus will be useless. However, if the virus limits tumour growth before the cancer has reached the size at which mortality is observed, then oncolytic virus therapy can drive the drug-resistant cancer cells extinct. Following this ‘pretreatment’ with the virus, it should be possible to successfully apply drug therapy (for example using targeted small-molecule inhibitors) in order to induce cancer remission.
In the above analysis, it was assumed that the virus can potentially establish an infection in either of the cell types (drug sensitive or resistant) alone. This is the most realistic parameter regime. If the virus replicates too slowly to establish an infection in either the drug-sensitive or the resistant cell population alone, then it will not be possible to eradicate the population of the resistant cancer cells through virus-mediated competition. Therefore, the dynamics of this scenario are not further considered.
Note that this analysis has concentrated on the growth rate of the tumour cell population and the replication rates of the oncolytic virus, as these are the most important parameters that determine the outcome of apparent competition. Other parameters, such as the level of saturation in the tumour growth and virus infection terms, are important in determining whether the oncolytic virus can drive the overall tumour extinct or not. Since this is not the focus of the current paper, variation of these parameters is not explored. If the virus fails to eliminate the cancer, the apparent competition dynamics are not influenced by these additional parameters on a qualitative level.
2.3 Effect of mutations
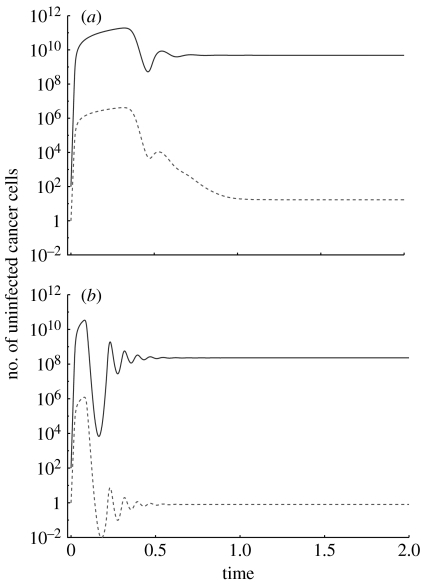
The above analysis assumed that the drug-sensitive cells do not give rise to resistant cells by mutation (μ=0) and that a certain number of resistant cancer cells were present at the beginning of the computer simulations. Here, this assumption is relaxed. We can set the mutation rate μ=10−7–10−9 according to the physiological mutation rate, although it can be higher if the cancer cells have some form of genetic instability. In particular, in the context of chromosomal instability, the mutation rate can be approximately μ=10−4 if resistance is caused by chromosome duplications (Tlsty et al. 1989). Now, the resistant cancer cells will not be driven extinct any more. Instead, they persist at a certain level, determined by the mutation–selection balance (figure 2). A lower mutation rate, a lower cancer size maintained by the oncolytic virus and a higher fitness cost of the resistant mutant lead to lower levels at which the resistant cancer cells persist. The lower the level at which resistant mutants persist, the lower the chances that they will in fact be present rather than be extinct (figure 2). Therefore, the more efficient the oncolytic virus is at suppressing the tumour, the less likely it is that the resistant mutant will be present in the tumour cell population.
Figure 2.
Apparent competition between wild-type (solid line) and drug-resistant (dashed line) cancer cells in the presence of an oncolytic virus. It is assumed that drug-sensitive cancer cells can give rise to drug-resistant cells by mutation. The two graphs differ in the effectiveness of the oncolytic virus. (a) The virus is less effective and the wild-type cancer cell population reaches a higher equilibrium. (b) The virus is more effective and the drug-sensitive cancer cell population reaches a lower equilibrium. In both cases, however, the virus fails to drive the cancer cells extinct. In the presence of mutations, the resistant cells do not go extinct any more, but persist at low levels, determined by the mutation–selection balance. This is determined by the mutation rate, the selective disadvantage of resistant cells and the number of drug-sensitive cells. The mutation–selection balance is such that the resistant cells are likely to be present in (a) and extinct (on average less than one cell) in (b). Parameters were chosen for the purpose of illustration only, since they are currently unknown. The dependence of the outcome on parameter values is discussed in the text. The following parameter values were used: r1=7, r2=5, a1=0.5, a2=0.5, ϵ=10, η=109, μ=10−9. For (a) β1=0.1, β2=0.1. For (b) β1=0.3, β2=0.3.
3. Discussion and conclusion
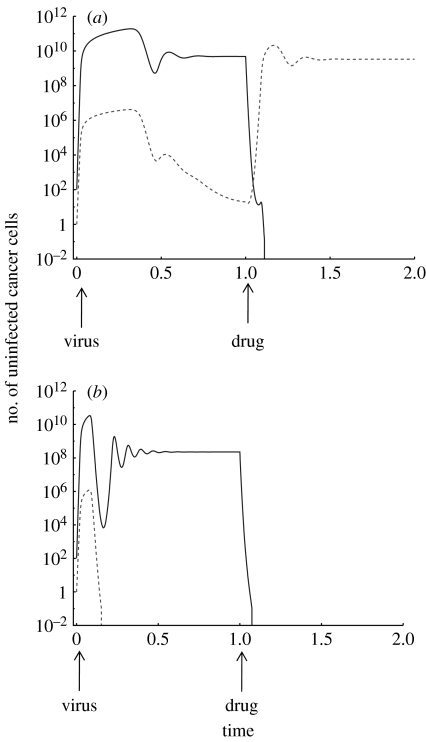
I have used a mathematical model to present a new way in which oncolytic viruses can be useful for cancer therapy, even if they fail to eradicate the cancer. A virus can be used to ‘pretreat’ the cancer in order to drive the resistant cell clones towards extinction, if the drug resistance mutations have a fitness cost compared with the drug-sensitive cells. Such a fitness cost has been demonstrated in the context of drug resistance mutations in CML, especially those mutations that come about through the amplification of the BCR–ABL fusion gene (Tipping et al. 2001). Fitness costs of drug resistance mutations have been demonstrated very convincingly in the past in the context of infectious diseases, particularly HIV (Back et al. 1996), although in a rare case it has been suggested that a particular HIV drug resistance mutation might confer a selective advantage to the virus (Nijhuis et al. 1999). The cost of drug resistance in HIV tends to be in the 1–10 per cent range, although some mutations can have a higher fitness cost (Back et al. 1996). As mentioned before, the notion that drug resistance mutants are associated with a fitness cost is likely to be a more general phenomenon. However, it is important to point out that this notion needs to be solidified by further experimental research in the context of cancer, and that the theoretical concepts described here are dependent on this assumption. Under this assumption, the virus can drive the resistant cancer cells extinct because the resistant and drug-sensitive cells share the virus and there is apparent competition. Once the virus has driven the resistant cancer cells extinct, then drugs, such as small-molecule inhibitors, can be used to treat the cancer. If drug resistance is the major obstacle to successful treatment, success should now be observed. These notions are illustrated with computer simulations in figure 3.
Figure 3.
Simulation of the sequential combination of oncolytic virus therapy and drug therapy, assuming that drug-sensitive cancer cells can produce drug-resistant cells by mutation. Oncolytic virus therapy results in a selective disadvantage for drug-resistant cells through apparent competition. In the presence of the virus, the resistant cells will be present at a level determined by the mutation–selection balance, as explained in figure 2. (a) Mutation–selection balance maintains the drug-resistant cell population at relatively high numbers, which is likely to correlate with the persistence of these cells. Consequently, when drug therapy is applied, the resistant cells will grow and drug therapy fails. (b) Mutation–selection balance maintains the drug-resistant cell population at low levels: on average less than one cell persists. This corresponds to the extinction of the drug-resistant cell population. Consequently, the subsequent drug therapy is successful at eliminating the cancer because there are no resistant cells left. Parameters were chosen for the purpose of illustration only, since they are currently unknown. The dependence of the outcome on parameter values is discussed in the text. The following parameter values were used: r1=7, r2=5, a1=0.5, a2=0.5, ϵ=10, η=109, μ=10−9. For (a) β1=0.1, β2=0.1. For (b) β1=0.3, β2=0.3. Drug therapy was modelled by assuming that the drug-sensitive cancer cells have an additional death rate d=5, such that the drug can induce a decline of this cell population to extinction. The resistant cells do not receive the additional death rate, as the drug has no effect in this case. Solid line, wild-type; dashed line, drug resistant.
Note that this treatment concept is very different from the simultaneous combination of drug and oncolytic virus therapies. This aims to reduce the replicative potential of the tumour, thus rendering the tumour more susceptible to virus-mediated eradication. In the presence of drug-resistant mutants, combining drug and virus therapies could in fact be detrimental to the patient. This is because in the presence of drug therapy, the resistant cells replicate faster than the sensitive cells. Therefore, apparent competition would increase the advantage of the drug-resistant cells during treatment and accelerate their rise to high levels. To get around this, one could first reduce the tumour size by drug therapy to make it more manageable for the virus, and subsequently apply the oncolytic virus; but again this would be a very different approach with a different aim compared with the treatment strategies explored here.
An important question that was not addressed is how long it takes for the oncolytic virus to drive the drug-resistant cancer cell population extinct. From a clinical point of view, it would be important to know when the pretreatment phase is over and when the drug therapy can be started. This can potentially be calculated in the model. However, such a calculation would be meaningless at this stage. It would depend on an experimentally validated model, parameter measurements and the knowledge of the number of drug-resistant cells present when the oncolytic virus is given to the patient. The aim of the current paper is to introduce the new concept that oncolytic viruses could be used to specifically eradicate the drug-resistant cancer cells, and this concept needs to be validated and applied to specific scenarios for further details to be considered. Moreover, if examined in more detail, it will be important to assess potential costs of delaying the onset of drug therapy while waiting for the oncolytic virus to eradicate the drug-resistant cells.
In addition, note that the arguments presented in this paper do not take into account other complicating factors that can pose obstacles to successful drug therapy. For example, primitive or quiescent cancer cells that are not affected by the drug (Holyoake et al. 1999, 2001; Barnes & Melo 2006) can pose significant obstacles to cancer elimination even in the absence of drug resistance mutants. In addition, if there are drug-resistant cells in the sub-population of quiescent cancer cells, then the virus would be less efficient in reducing the number of resistant cells. Quiescent cells are not likely to produce much virus, leading to their survival rather than death. In addition, it will be important to investigate these dynamics in spatially explicit models. While we tried to incorporate such effects phenomenologically into the differential equations through saturated proliferation and frequency-dependent virus transmission, tumours can have complex spatial structures that are better modelled by other approaches, such as cellular automata. In addition, such spatially explicit models should take into account details of the tumour architecture that can present barriers to virus spread, such as the presence of necrotic areas, connective tissue cells and non-cellular matrix components. This architecture could lead to micro-environments in which drug-resistant cells could escape removal by the virus. Another important assumption of the model is that all tumour cells, in particular all drug-resistant tumour cells, are susceptible to virus infection. However, this might not be the case. It is possible that some of the cancer cells have reduced levels of the receptor necessary for virus entry, making them essentially resistant to the virus. In this case, apparent competition would not drive the drug-resistant tumour cell population extinct. The therapy approach proposed here would have to be coupled with a drug that upregulates receptor expression in the tumour cells. We have previously published a mathematical model that examines in a different setting the effects of receptor expression and combination therapy on oncolytic virus dynamics (Zurakowski & Wodarz 2007). Such details will be important to include in future models once the concepts presented here are investigated in the context of a specific cancer and a specific oncolytic virus.
The arguments presented here are based on the more general assumption that in the absence of the virus, the resistant and drug-sensitive cells do not compete to the extent that competitive exclusion of one cell population is possible. This may be a very realistic assumption in malignant cancer growth, where the number of cells rises to ever-increasing values. In this case, the presence of the virus introduces apparent competition into the system, leading to the decline of the less fit resistant cells. At earlier stages of cancer progression, the number of tumour cells might be relatively low and does not increase significantly. An example of this is the chronic phase of CML (Melo et al. 2003). Imatinib treatment during this phase is more likely to lead to a successful outcome, and drug resistance is less of an obstacle than in more advanced stages of the disease when explosive cancer cell growth is observed. One of the reasons certainly is that the size of the cancer is smaller, hence the probability to have generated a resistant mutant is lower (Komarova & Wodarz 2005; Wodarz & Komarova 2005). However, another factor that could contribute to this is that during the chronic phase of CML, the tumour cells might compete directly with each other for factors such as space and nutrients. This is because cells do not expand completely uncontrolled, but remain at relatively steady numbers. In the presence of direct competition, the resistant mutant would be expected to be excluded by the wild-type cells if the resistant cells bear a fitness cost, even in the absence of a shared virus.
I have focused my discussion to some degree on CML because it is a biologically very well-defined cancer, imatinib treatment represented the first clear success of targeted therapy and drug resistance mutations and their characteristics are relatively well defined. This is not the case in the context of other cancers. However, no promising oncolytic virus therapy exists against CML to my knowledge. While the observations made with CML are consistent with the assumptions that underlie the model, similar information needs to be obtained for a variety of other cancers, especially those where oncolytic viruses are available for treatment. The results presented here show that the combination of targeted therapy and oncolytic virus therapy could potentially be very beneficial for overcoming the problem of drug resistance and that it might pay off to pursue this avenue of research.
To summarize, I would like to point out that the aim of this paper is to propose a new conceptual treatment regime in which oncolytic viruses can be used to selectively drive drug-resistant tumour cells extinct, even if the virus fails to eradicate the overall cancer. It is clear that many biological details need to be incorporated into the model for a more detailed analysis. It is also clear that there is currently no cancer in which we have efficient targeted drug therapy, a detailed knowledge of drug resistance mutations and a feasible oncolytic virus. However, the conceptual treatment regimes proposed here are based on biologically reasonable assumptions and solid population dynamic principles, and therefore merit experimental investigations. The hope is that this study will stimulate new avenues of experimental research and thinking. As a first step on the experimental side, it would be interesting to test some of the most basic theoretical notions described here. This could be done using in vitro or simple in vivo systems. Both a drug-sensitive and a resistant cancer cell population should be allowed to grow together, followed by the introduction of an oncolytic virus. The numbers of resistant and drug-sensitive cancer cells should be monitored over time to check whether the observed dynamics are consistent with the model behaviour.
References
- Anderson R.M., May R.M. Regulation and stability of host–parasite population interactions: I. Regulatory processes. J. Anim. Ecol. 1978;47:249–267. doi: 10.2307/3934. [DOI] [Google Scholar]
- Antonovics J., Iwasa Y., Hassell M.P. A generalized model of parasitoid, venereal, and vector-based transmission processes. Am. Nat. 1995;145:661–675. doi: 10.1086/285761. [DOI] [Google Scholar]
- Back N.K., Nijhuis M., Keulen W., Boucher C.A., Oude Essink B.O., van Kuilenburg A.B., van Gennip A.H., Berkhout B. Reduced replication of 3TC-resistant HIV-1 variants in primary cells due to a processivity defect of the reverse transcriptase enzyme. Embo J. 1996;15:4040–4049. [PMC free article] [PubMed] [Google Scholar]
- Barnes D.J., Melo J.V. Primitive, quiescent and difficult to kill: the role of non-proliferating stem cells in chronic myeloid leukemia. Cell Cycle. 2006;5:2862–2866. doi: 10.4161/cc.5.24.3573. [DOI] [PubMed] [Google Scholar]
- Begon M., Hazel S.M., Baxby D., Bown K., Cavanagh R., Chantrey J., Jones T., Bennett M. Transmission dynamics of a zoonotic pathogen within and between wildlife host species. Proc. R. Soc. B. 1999;266:1939–1945. doi: 10.1098/rspb.1999.0870. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bell J.C. Oncolytic viruses: what's next? Curr. Cancer Drug Targets. 2007;7:127–131. doi: 10.2174/156800907780058844. [DOI] [PubMed] [Google Scholar]
- Bell J.C., Lichty B., Stojdl D. Getting oncolytic virus therapies off the ground. Cancer Cell. 2003;4:7–11. doi: 10.1016/S1535-6108(03)00170-3. [DOI] [PubMed] [Google Scholar]
- Blagosklonny M.V. STI-571 must select for drug-resistant cells but ‘no cell breathes fire out of its nostrils like a dragon’. Leukemia. 2002;16:570–572. doi: 10.1038/sj.leu.2402409. [DOI] [PubMed] [Google Scholar]
- Bonsall M.B., Hassell M.P. The effects of metapopulation structure on indirect interactions in host–parasitoid assemblages. Proc. R. Soc. B. 2000;267:2207–2212. doi: 10.1098/rspb.2000.1270. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burgess M.R., Skaggs B.J., Shah N.P., Lee F.Y., Sawyers C.L. Comparative analysis of two clinically active BCR–ABL kinase inhibitors reveals the role of conformation-specific binding in resistance. Proc. Natl Acad. Sci. USA. 2005;102:3395–3400. doi: 10.1073/pnas.0409770102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crompton A.M., Kirn D.H. From ONYX-015 to armed vaccinia viruses: the education and evolution of oncolytic virus development. Curr. Cancer Drug Targets. 2007;7:133–139. doi: 10.2174/156800907780058862. [DOI] [PubMed] [Google Scholar]
- Davis J.J., Fang B. Oncolytic virotherapy for cancer treatment: challenges and solutions. J. Gene Med. 2005;7:1380–1389. doi: 10.1002/jgm.800. [DOI] [PubMed] [Google Scholar]
- Deininger M.W., Druker B.J. Specific targeted therapy of chronic myelogenous leukemia with imatinib. Pharmacol. Rev. 2003;55:401–423. doi: 10.1124/pr.55.3.4. [DOI] [PubMed] [Google Scholar]
- Deininger M.W., Goldman J.M., Melo J.V. The molecular biology of chronic myeloid leukemia. Blood. 2000;96:3343–3356. [PubMed] [Google Scholar]
- Diekmann O., Kretzschmar M. Patterns in the effects of infectious diseases on population growth. J. Math. Biol. 1991;29:539–570. doi: 10.1007/BF00164051. [DOI] [PubMed] [Google Scholar]
- Druker B.J. Imatinib as a paradigm of targeted therapies. Adv. Cancer Res. 2004;91:1–30. doi: 10.1016/S0065-230X(04)91001-9. [DOI] [PubMed] [Google Scholar]
- Goldman J.M., Melo J.V. Chronic myeloid leukemia—advances in biology and new approaches to treatment. N. Engl. J. Med. 2003;349:1451–1464. doi: 10.1056/NEJMra020777. [DOI] [PubMed] [Google Scholar]
- Gorre M.E., Mohammed M., Ellwood K., Hsu N., Paquette R., Rao P.N., Sawyers C.L. Clinical resistance to STI-571 cancer therapy caused by BCR–ABL gene mutation or amplification. Science. 2001;293:876–880. doi: 10.1126/science.1062538. [DOI] [PubMed] [Google Scholar]
- Greenman J.V., Hudson P.J. Host exclusion and coexistence in apparent and direct competition: an application of bifurcation theory. Theor. Popul. Biol. 1999;56:48–64. doi: 10.1006/tpbi.1999.1413. [DOI] [PubMed] [Google Scholar]
- Greenman J.V., Hudson P.J. Parasite-mediated and direct competition in a two-host shared macroparasite system. Theor. Popul. Biol. 2000;57:13–34. doi: 10.1006/tpbi.1999.1435. [DOI] [PubMed] [Google Scholar]
- Guillemard V., Saragovi H.U. Novel approaches for targeted cancer therapy. Curr. Cancer Drug Targets. 2004;4:313–326. doi: 10.2174/1568009043332989. [DOI] [PubMed] [Google Scholar]
- Hassell M.P., Bonsall M.B. Apparent competition structures ecological assemblages. Nature. 1997;388:371–373. doi: 10.1038/41084. [DOI] [Google Scholar]
- Heesterbeek J.A., Metz J.A. The saturating contact rate in marriage- and epidemic models. J. Math. Biol. 1993;31:529–539. doi: 10.1007/BF00173891. [DOI] [PubMed] [Google Scholar]
- Holt R.D. Predation, apparent competition and the structure of prey communities. Theor. Popul. Biol. 1977;12:197–229. doi: 10.1016/0040-5809(77)90042-9. [DOI] [PubMed] [Google Scholar]
- Holyoake T., Jiang X., Eaves C., Eaves A. Isolation of a highly quiescent subpopulation of primitive leukemic cells in chronic myeloid leukemia. Blood. 1999;94:2056–2064. [PubMed] [Google Scholar]
- Holyoake T.L., Jiang X., Jorgensen H.G., Graham S., Alcorn M.J., Laird C., Eaves A.C., Eaves C.J. Primitive quiescent leukemic cells from patients with chronic myeloid leukemia spontaneously initiate factor-independent growth in vitro in association with up-regulation of expression of interleukin-3. Blood. 2001;97:720–728. doi: 10.1182/blood.V97.3.720. [DOI] [PubMed] [Google Scholar]
- Kaplan J.M. Adenovirus-based cancer gene therapy. Curr. Gene Ther. 2005;5:595–605. doi: 10.2174/156652305774964677. [DOI] [PubMed] [Google Scholar]
- Kelly E., Russell S.J. History of oncolytic viruses: genesis to genetic engineering. Mol. Ther. 2007;15:651–659. doi: 10.1038/sj.mt.6300033. [DOI] [PubMed] [Google Scholar]
- Kirn D.H., McCormick F. Replicating viruses as selective cancer therapeutics. Mol. Med. Today. 1996;2:519–527. doi: 10.1016/S1357-4310(97)81456-6. [DOI] [PubMed] [Google Scholar]
- Komarova N.L., Wodarz D. Drug resistance in cancer: principles of emergence and prevention. Proc. Natl Acad. Sci. USA. 2005;102:9714–9719. doi: 10.1073/pnas.0501870102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lorence R.M., Pecora A.L., Major P.P., Hotte S.J., Laurie S.A., Roberts M.S., Groene W.S., Bamat M.K. Overview of phase I studies of intravenous administration of PV701, an oncolytic virus. Curr. Opin. Mol. Ther. 2003;5:618–624. [PubMed] [Google Scholar]
- May R.M., Anderson R.M. Transmission dynamics of HIV infection. Nature. 1987;326:137–142. doi: 10.1038/326137a0. [DOI] [PubMed] [Google Scholar]
- McCallum H., Barlow N., Hone J. How should pathogen transmission be modelled? Trends Ecol. Evol. 2001;16:295–300. doi: 10.1016/S0169-5347(01)02144-9. [DOI] [PubMed] [Google Scholar]
- McCormick F. Cancer-specific viruses and the development of ONYX-015. Cancer Biol. Ther. 2003;2:S157–S160. [PubMed] [Google Scholar]
- McCormick F. Future prospects for oncolytic therapy. Oncogene. 2005;24:7817–7819. doi: 10.1038/sj.onc.1209064. [DOI] [PubMed] [Google Scholar]
- Melo J.V., Barnes D.J. Chronic myeloid leukaemia as a model of disease evolution in human cancer. Nat. Rev. Cancer. 2007;7:441–453. doi: 10.1038/nrc2147. [DOI] [PubMed] [Google Scholar]
- Melo, J. V., Hughes, T. P. & Apperley, J. F. 2003 Chronic myeloid leukemia. Hematology Am. Soc. Hematol. Educ. Program 132–152. [DOI] [PubMed]
- Nijhuis M., Schuurman R., de Jong D., Erickson J., Gustchina E., Albert J., Schipper P., Gulnik S., Boucher C.A. Increased fitness of drug resistant HIV-1 protease as a result of acquisition of compensatory mutations during suboptimal therapy. Aids. 1999;13:2349–2359. doi: 10.1097/00002030-199912030-00006. [DOI] [PubMed] [Google Scholar]
- Novozhilov A.S., Berezovskaya F.S., Koonin E.V., Karev G.P. Mathematical modeling of tumor therapy with oncolytic viruses: regimes with complete tumor elimination within the framework of deterministic models. Biol. Direct. 2006;1:6. doi: 10.1186/1745-6150-1-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- O'Dwyer M.E., Mauro M.J., Druker B.J. Recent advancements in the treatment of chronic myelogenous leukemia. Annu. Rev. Med. 2002;53:369–381. doi: 10.1146/annurev.med.53.082901.103853. [DOI] [PubMed] [Google Scholar]
- O'Shea C.C. Viruses—seeking and destroying the tumor program. Oncogene. 2005;24:7640–7655. doi: 10.1038/sj.onc.1209047. [DOI] [PubMed] [Google Scholar]
- Parato K.A., Senger D., Forsyth P.A., Bell J.C. Recent progress in the battle between oncolytic viruses and tumours. Nat. Rev. Cancer. 2005;5:965–976. doi: 10.1038/nrc1750. [DOI] [PubMed] [Google Scholar]
- Post D.E., Shim H., Toussaint-Smith E., Van Meir E.G. Cancer scene investigation: how a cold virus became a tumor killer. Future Oncol. 2005;1:247–258. doi: 10.1517/14796694.1.2.247. [DOI] [PubMed] [Google Scholar]
- Roberts M.S., Lorence R.M., Groene W.S., Bamat M.K. Naturally oncolytic viruses. Curr. Opin. Mol. Ther. 2006;8:314–321. [PubMed] [Google Scholar]
- Sawyers C.L. Chronic myeloid leukemia. N. Engl. J. Med. 1999;340:1330–1340. doi: 10.1056/NEJM199904293401706. [DOI] [PubMed] [Google Scholar]
- Shannon K.M. Resistance in the land of molecular cancer therapeutics. Cancer Cell. 2002;2:99–102. doi: 10.1016/S1535-6108(02)00101-0. [DOI] [PubMed] [Google Scholar]
- Tipping A.J., Mahon F.X., Lagarde V., Goldman J.M., Melo J.V. Restoration of sensitivity to STI571 in STI571-resistant chronic myeloid leukemia cells. Blood. 2001;98:3864–3867. doi: 10.1182/blood.V98.13.3864. [DOI] [PubMed] [Google Scholar]
- Tlsty T.D., Margolin B.H., Lum K. Differences in the rates of gene amplification in nontumorigenic and tumorigenic cell lines as measured by Luria–Delbruck fluctuation analysis. Proc. Natl Acad. Sci. USA. 1989;86:9441–9445. doi: 10.1073/pnas.86.23.9441. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vaha-Koskela M.J., Heikkila J.E., Hinkkanen A.E. Oncolytic viruses in cancer therapy. Cancer Lett. 2007;254:178–216. doi: 10.1016/j.canlet.2007.02.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wodarz D. Viruses as antitumor weapons: defining conditions for tumor remission. Cancer Res. 2001;61:3501–3507. [PubMed] [Google Scholar]
- Wodarz D. Gene therapy for killing p53-negative cancer cells: use of replicating versus nonreplicating agents. Hum. Gene Ther. 2003;14:153–159. doi: 10.1089/104303403321070847. [DOI] [PubMed] [Google Scholar]
- Wodarz D. Computational approaches to study oncolytic virus therapy: insights and challenges. Gene Ther. Mol. Biol. 2004;8:137–146. [Google Scholar]
- Wodarz D., Komarova N.L. Emergence and prevention of resistance against small molecule inhibitors. Semin. Cancer Biol. 2005;15:506–514. doi: 10.1016/j.semcancer.2005.07.002. [DOI] [PubMed] [Google Scholar]
- Yee K.W., Keating A. Advances in targeted therapy for chronic myeloid leukemia. Expert Rev. Anticancer Ther. 2003;3:295–310. doi: 10.1586/14737140.3.3.295. [DOI] [PubMed] [Google Scholar]
- Zurakowski R., Wodarz D. Model-driven approaches for in vitro combination therapy using ONYX-015 replicating oncolytic adenovirus. J. Theor. Biol. 2007;245:1–8. doi: 10.1016/j.jtbi.2006.09.029. [DOI] [PMC free article] [PubMed] [Google Scholar]