Bivariate Genome-Wide Linkage Analysis of Femoral Bone Traits and Leg Lean Mass: Framingham Study

Abstract

The risk of osteoporotic fracture is a function of both applied muscle mass and bone tissue distribution. Leg lean mass (LLM) and femoral bone geometry are both known to have substantial genetic components. Therefore, we estimated shared heritability (h²) and performed linkage analysis to identify chromosomal regions governing both LLM and bone geometry. A genome-wide scan (using 636 microsatellite markers) for linkage analyses was performed on 1346 adults from 327 extended families of the Framingham study. DXA measures were LLM, femoral neck length, neck-shaft angle (NSA), subperiosteal width, cross-sectional area (CSA), and section modulus (Z) at the femoral narrow neck and shaft (S) regions. Variance component linkage analysis was performed on normalized residuals (adjusted for age, height, BMI, and estrogen status in women). The results indicated substantial h² for LLM (0.42 ± 0.07) that was comparable to bone geometry traits. Phenotypic correlations between LLM and bone geometry phenotypes ranged from 0.033 with NSA (p > 0.05) to 0.251 with S_Z (p < 0.001); genetic correlations ranged from 0.087 (NSA, p > 0.05) to 0.454 (S_Z, p < 0.001). Univariate linkage analysis of covariate-adjusted LLM identified no chromosomal regions with LOD scores ≥2.0; however, bivariate analysis identified two loci with LOD scores >3.0, shared by LLM with S_CSA on chromosome 12p12.3–12p13.2, and with NSA, on 14q21.3–22.1. In conclusion, we identified chromosomal regions potentially linked to both LLM and femoral bone geometry. Identification and subsequent characterization of these shared loci may further elucidate the genetic contributions to both osteoporosis and sarcopenia.

INTRODUCTION

Osteoporotic fractures and their consequences in the elderly population greatly increase mortality, morbidity, and negatively impact quality of life.(1) The risk of osteoporotic fracture can be viewed as a function of loading conditions and the ability of the bone to withstand the load. The most widely used and reliable clinical predictor of an osteoporotic fracture remains areal BMD (aBMD),(2) as evaluated by DXA, probably because it derives from both mineral content and bone geometry (intrinsic and extrinsic bone properties, respectively). The strength of bone is determined not only by the amount but also by the spatial distribution of bone tissue. A growing body of evidence indicates that bone geometry contributes substantially to bone strength and fracture risk.(3,4)

However, neither aBMD alone nor bone structure are accurate surrogates of the skeleton's ability to withstand the forces that produce fracture. Risk of fracture is not entirely determined by bone properties, because the loads that are placed on the skeleton (including fall-related factors, such as impaired cognition and sensory input) are equally important in assessing the risk for fracture.(5) Other than direct trauma to the skeleton, most loads that are applied to the skeleton are caused by muscle contractions. The loss of muscle mass with age (sarcopenia) is accompanied by a decrease in muscle strength and reduced loading of the skeleton. Similar to bone, muscle tissue deteriorates with advanced age. Age-associated loss of muscle fibers, fatty infiltration, and decreased number of functioning motor units cause decline in muscle quality (i.e., force generated per unit of muscle mass).(6)

Although muscle biopsy is best able to quantify the magnitude of sarcopenia, obtaining such samples is not feasible for research in large human populations. DXA thus serves as a noninvasive imaging modality that measures lean mass in addition to aBMD and geometry. Higher lean mass is associated with greater muscle strength and better functioning (7–9); lower leg lean mass (LLM) measured by DXA has been shown to be associated with mobility disability in older men and women.(7,10)

Studies have reported that muscle strength and muscle mass have substantial genetic contributions.(11) Thus, in young brothers (age, 24 ± 5 yr), Huygens et al.(9) found heritability of muscle cross-sectional area (CSA) and mass to be ∼70–90%. Similarly, in female twin pairs (age range, 24–67 yr), heritability of DXA-measured lean body mass ranged from 30% to 50%.(12) Furthermore, there is ample evidence for shared genetic factors between bone and muscle mass.(12) In Finnish male twin pairs, genetic correlations between femoral or lumbar aBMD and lean body mass adjusted for height were between 0.30 and 0.41.(13) High genetic correlation has been reported between femoral geometric parameters and total body lean mass in U.S. white adults from Nebraska, ranging from 0.28 to 0.69.(14)

Therefore, the aim of this project was to determine the shared heritability of femoral bone geometry and LLM. We hypothesized that significant genetic correlations between these components of the lower extremity bone strength existed and that linkage analysis would identify physical chromosomal locations of genes governing both osteoporosis and sarcopenia. Simultaneous analytical methods, especially bivariate linkage analysis, have been shown to increase power to detect linkage of related traits to a common quantitative trait locus (QTL).(15)

MATERIALS AND METHODS

Sample

The sample used for our analyses was derived from two cohorts of the Framingham Heart Study. The Framingham Study Original Cohort began in 1948 with the primary goal of evaluating risk factors for cardiovascular disease. The Original Cohort participants, initially 28–62 yr of age, represented two thirds of the households of the Framingham, MA, population and have been examined every 2 yr since baseline. In 1971, the Framingham Offspring Cohort Study was initiated to evaluate the role of genetic factors in the etiology of coronary artery disease and was comprised of 71% of all the eligible adult offspring of couples from the Original Cohort and offspring spouses. Neither the Framingham Original nor Offspring Cohort was selected on the basis of cardiovascular diseases or osteoporosis. Details and descriptions of the Framingham Osteoporosis Study, a subset of the Framingham Heart Study, have been reported.(16,17) In total, there were 1346 subjects in 327 pedigrees available for analyses in this project.

The study was approved by the Institutional Review Boards for Human Subjects Research of Boston University and of Hebrew SeniorLife.

DXA and hip structural analysis

The participants underwent bone densitometry by DXA with a Lunar DPX-L (Lunar, Madison, WI, USA). The Original Cohort participants underwent bone densitometry during 1992–1993 (examination 22). To maximize the sample size, we used DXA scans from 1996 to 1997 (examination 24) for 31 Original Cohort members who missed DXAs at examination 22. The Offspring Cohort was scanned using the same machine between 1996 and 2001 (exam 6/7). Femoral DXA scans were analyzed by an interactive computer program(18,19) to derive a number of densitometric and structural variables. The regions assessed were the narrowest width of the femoral neck (NN), which overlaps or is proximal to the standard femoral neck region, and the femoral shaft (S), at a distance of 1.5 times the minimum neck width distal to the intersection of the neck and shaft axes. Subperiosteal outer diameter (width, cm), CSA (cm²), and section modulus (Z, cm³) at each of the two femoral regions (NN and S) were measured directly from the mass profiles using a principle first described by Martin and Burr.(20) In addition, the method measures the neck-shaft angle (NSA) and femoral neck length (FNL), defined as the distance from the center of femoral head to the intersection of neck and shaft axes. CVs for the different component variables were previously reported to range from 3.3% (NN outer diameter) to 9.1% (FNL).(18)

Measurements of body composition:

We also obtained whole body scans from the study participants with the same Lunar DPX-L machine. The scans were collected at medium speed for all subjects regardless of weight or body thickness. Regions of interest were analyzed using the extended analysis of the Lunar software for body composition. Fat-free mass of the legs was determined as lean tissue plus BMC, and lean mass of the legs was derived by subtracting BMC.

Other measurements:

Information on age, sex, weight, and height was obtained for each individual at the time of the bone scan measurement. In brief, in both cohorts, weight (lb) was measured using a standardized balance beam scale. Height (without shoes) was measured to the nearest 0.25 in using a stadiometer. These measures were converted to kilograms and centimeters, respectively, and body mass index (BMI) was calculated (kg/m²).

For women, estrogen use and menopausal status were recorded. Menopause was defined as having no menstrual period for at least 1 yr. Each woman was assigned to one of the two estrogenic status groups: (1) premenopausal or postmenopausal on estrogen (estrogen replete) or (2) postmenopausal not on estrogen (estrogen deplete).

Genome scan

A genome microsatellite scan was performed in the Framingham Heart Study in two phases. In the first phase, 1702 individuals in the largest 330 families were genotyped without regard to their clinical characteristics, using 422 polymorphic markers (marker set 9, average heterozygosity 0.77; sex-averaged mean intermarker spacing of 8.6 cM; NHLBI Mammalian Genotyping Service, Marshfield, WI, USA(21)). In the second phase, an additional 184 members of the 330 largest pedigrees were genotyped on 382 markers (marker set 13, average heterozygosity 0.76; sex-averaged mean intermarker spacing of 8.9 cM). There were 262 markers in common with marker set 9. Also, 94 additional markers genotyped on these 330 largest pedigrees were used to augment the original genome scan and were included in the linkage analyses. A total of 636 microsatellite markers, including 21 markers on chromosome X, were thus studied, with an average marker spacing of 5.7 cM. The two-phase design was a function of recruitment of the Framingham Heart Study participants, such that as specimens and larger pedigrees became available over time and upgrades in the Mammalian Genotyping Service in Marshfield occurred, genotyping was performed at two different time points. Genotype data cleaning, including verification of family relationships and Mendelian inconsistencies, have been previously described.(22)

The Framingham Osteoporosis Study included members of the Original and Offspring Cohorts with DXA measurements: 2211 women and 1633 men. Of a total of 1702 Framingham participants genotyped for the linkage, 1346 family members (men, n = 580; women, n = 766) had DXA measurements and consented to genetic analyses. Members of 327 pedigrees with family sizes ranging from 2 to 30 genotyped individuals contributed to the linkage analyses. These pedigrees were mostly nuclear (with an average of 2.4 family members and a small proportion of extended families, with 2–6 persons). The sample with genotyping and DXA phenotypes included the following relative pairs: 504 parent-offspring pairs, 913 sibling pairs, 585 cousin pairs, and 292 avuncular pairs.

Statistical methods

Before heritability and linkage analyses, multivariable regression analysis was performed in each sex (men and women) and cohort (Original and Offspring) to obtain residual bone and muscle phenotypes, adjusted for age and estrogen status in women (model 1), as well as for age, estrogen status in women, height, and BMI (model 2). Combination of height and BMI simultaneously adjusts for body size and body composition(23) and is widely used in genetic epidemiological studies.(16)

Variance component analysis—univariate:

Variance component analysis (VCA) for quantitative traits was performed on normalized residuals using the program Sequential Oligogenic Linkage Analysis Routines (SOLAR, SFBR/NIH; http://www.sfbr.org/sfbr/public/software/solar/solar.html). VCA allowed us to estimate heritability (h²) of each trait as the proportion of the total trait variance attributable to the additive effects of genes after removing variation caused by covariates, using adjustment model 1 or model 2 (adding height and BMI) as described above.

In the linkage VCA, models incorporating genotype data at a putative QTL—in the form of probabilities of sharing zero, one, or two alleles identical-by-descent (IBD) by pairs of related individuals—were compared with models incorporating only polygenic effects (i.e., without genetic marker data). For the autosomes, single-point probabilities of IBD between relative pairs were computed using SOLAR, and the multipoint (using multiple markers) probabilities of IBD were approximated at every 1 cM with the program LOKI.(24) For chromosome X, IBD probabilities were computed using the minx subroutine of MERLIN,(25) which performs multipoint linkage analysis on chromosome X. Because this program is not able to handle extended pedigrees, such pedigrees were broken down into smaller ones, by splitting families and/or deleting family members while keeping as many members with genotypes as possible. For the autosomal markers, map distances were obtained from the Center for Medical Genetics (http://research.marshfieldclinic.org/genetics/) whenever available or estimated otherwise; map distances for the X chromosomes were obtained from DeCODE.(26) Marker allele frequencies were estimated from the genotypes of the study participants by simple allele counting; this method yielded allele frequency estimates very similar to those obtained by maximum likelihood estimation in this unascertained, population-based sample.

Linkage analyses were performed in SOLAR at every marker (single-point) and at every 1 cM (multipoint). Multipoint linkage analysis has been shown to be more powerful than the single-point analyses, because the former contains information from adjacent markers.(27,28) A LOD score was computed as the log₁₀ of the likelihood ratio of the locus-specific model to the polygenic model. We tested the null hypothesis of no linkage to a particular genome location, using the likelihood ratio test. Under the null hypothesis of no linkage, for normally distributed traits, twice the log of the likelihood ratio statistic at a putative QTL location is asymptotically distributed as a 50:50 mixture of a χ² with 1 df and a point mass at zero. No ascertainment correction of likelihood was made because our pedigrees represent a community-based sample that was selected without regard to an individual's bone, body composition or related traits.

The QTL-specific heritability, h² _Q, was used to estimate the magnitude of the effect of the specific QTL on the residual trait's variance. Notably, these estimates are considered to be biased (inflated) when obtained from analysis of data in relatively small, simple pedigrees such as those in this study(29); therefore, it is important to note we present this metric for descriptive purposes.

VCA—bivariate:

To test the hypothesis that QTLs jointly influence variation in measures of geometry and LLM, we performed genome-wide bivariate linkage analyses for pairs of traits. The bivariate model differs from the univariate one above in that it also estimates the portions for the residual phenotypic correlation (ρ_P) between trait pairs that are caused by shared, additive effects of genetic variation at the QTL (a QTL-specific genetic correlation, ρ_Q), shared additive effects of genes other than those at the QTL (a residual additive genetic correlation, ρ_G), and shared effects of unmeasured environment (residual environmental correlation, ρ_E, including nonadditive genetic factors).(30) We determined significance of the above correlations using likelihood ratio tests. Thus, we compared the likelihood of a more general model in which the correlations were estimated to a model in which a parameter of interest (e.g., ρ_Q or ρ_G) was constrained to zero. More extensive details regarding the development, implementation, and power of bi- and multivariate extensions to linkage analyses have been published elsewhere.(30–33)

Correction for multiple testing was performed using a modification of methods described in Camp and Farnham(34) as follows: the total number of bivariate tests performed was 8 (Table 2), which corresponds to the estimated number of 3.84 effectively independent genome-wide linkage analyses. For the consensual “significant” and “suggestive” thresholds with LOD = 3.01 and LOD = 1.76, the corresponding corrected thresholds were thus 3.64 and 2.41.

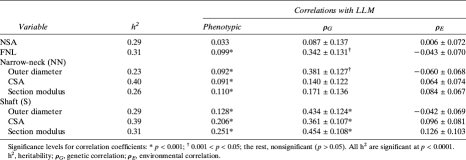
Table 2.

Heritabilities of the Bone Geometric Parameters and Phenotypic, Genetic, and Environmental Correlations Between Them and LLM (Model 2 of Adjustment)

RESULTS

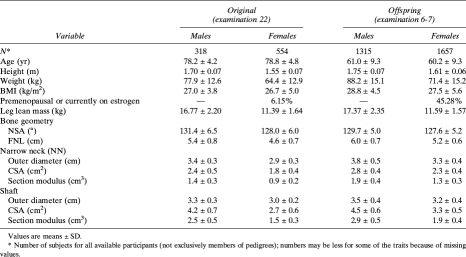
Table 1 shows descriptive statistics of the study participants by cohort and sex. In each cohort, men and women were of similar age. As expected, male participants were heavier, taller, and in general had greater BMI, average LLM, and geometric measures than women. Of the total 2211 women, there were 784 (35.5%) estrogen-replete women (mostly from the Offspring Cohort). There was a significant correlation (adjusted for sex, age, and height) between BMI and LLM (partial r = 0.41, p < 0.0001).

Table 1.

Characteristics of the Studied Sample, by Cohort and Sex

VCA was used to estimate heritability of LLM adjusted for covariates using different models. Age- (and estrogen status in women) adjusted LLM was highly heritable, with a significant h² estimate of 69%. After adjustment for height and BMI, h² decreased to 42%. Similarly, there was a strong additive genetic component for all bone geometric measures; adjustment for height and BMI resulted, generally, in a decrease in h² of hip structural analysis (HSA) measures (reported by us earlier(16)).

As follows from Table 2, there exist correlations between LLM and most geometric traits, adjusted for age, estrogen status, height, and BMI. Phenotypic correlations ranged from low (0.033 with NSA, p > 0.05) to substantial (0.251 with S_Z, p < 0.001). Genetic correlations (ρ_G) between covariate-adjusted LLM and all hip geometric phenotypes ranged from 0.087 (NSA, p > 0.05) to 0.454 (S_Z, p < 0.001). There were also environmental correlations (ρ_E) between the LLM and some geometric traits, but lower than the ρ_G: for example, maximal ρ_E was 0.126 between LLM and S_Z (p > 0.05).

Next, we performed linkage analysis for the LLM adjusted for covariates in model 2. No multipoint LOD score >2.0 was obtained for LLM in our sample. Results of our univariate linkage analyses of HSA measures were reported previously.(16)

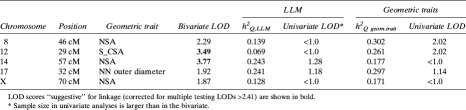
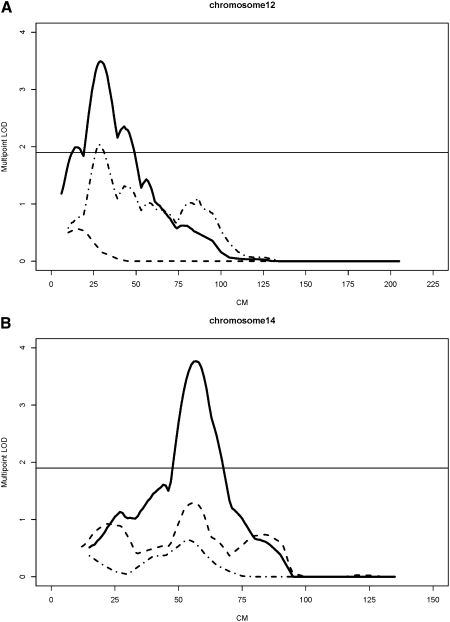
Results from bivariate linkage analyses are shown in Table 3. At least nominally suggestive evidence for bivariate linkage (LOD scores ≥ 1.90) for LLM and bone geometry traits was found at the following chromosomal regions: 8p21.3, 12p12.3–12p13.2, 14q21.3–22.1, 17p11.2, and Xq22-q24. Two of the above loci yielded LOD scores >2.41 (the value required for a suggestive genome-wide significance at p = 0.1), namely chromosome 12 (29 cM; LLM/S_CSA) and chromosome 14 (57 cM; LLM/NSA), shown in Fig. 1. In univariate analysis, the chromosome 12 locus was linked mostly with a corresponding geometric trait and less with LLM, whereas the chromosome 14 locus was weakly linked to LLM. Additionally, locus-specific heritability (h² _Q) estimates indicate that, for most of the chromosomal regions, the effect of a specific QTL in bivariate analysis was stronger on the geometric trait than on the LLM trait (except for the chromosome 14 locus). For example, a locus on chromosome 8 (46 cM) resulted in an h² _Q = 0.302 for NSA, whereas h² _Q for LLM was lower (0.139). Overall, h² _Q ranged from 0.171 to 0.302 for geometric traits and from 0.069 to 0.243 for LLM. Thus, 29.7% of the residual phenotypic variance in NN width and 24.1% in LLM were attributable to shared genetic effects at chromosome 17 QTLs. The maximum multipoint LOD score from the univariate analysis of LLM in this region was only 1.18, whereas the LOD score for the geometric trait (NN width) was 1.14. Similarly, on Xq22-q24, the bivariate LOD score of 1.87, although modest, was much larger than corresponding univariate LOD scores for either LLM or NSA that were <1.0.

Table 3.

Bivariate Linkage of LLM With Geometric Traits (Model 2 of Adjustment)

FIG. 1.

Univariate and bivariate linkage results (multipoint LOD scores). Horizontal line, “suggestive” linkage threshold; solid line, bivariate linkage; dashed line, univariate, LLM; broken line, univariate, geometric trait. (A) S_CSA, LLM, and combination of LLM and S_CSA, chromosome 12. (B) NSA, LLM, and combination of LLM and NSA, chromosome 14.

DISCUSSION

In this study of shared genetic effects between LLM and femoral bone geometry, we showed, first, a high heritability of LLM with 69% of its variance explained by additive genetic factors. After adjusting for height and BMI, heritability decreased but remained substantial at 42%. Genome-wide linkage analysis of adjusted LLM failed to identify candidate chromosomal regions for this trait. However, there were strong genetic correlations between LLM and bone geometry phenotypes, suggesting that these measures have some genetic factors in common. Indeed, genetic correlations (ρ_G) between covariate-adjusted LLM and hip geometric phenotypes ranged from 9% (NSA) to 45% (S_Z). These bivariate genetic correlations are comparable to those recently reported in another white cohort, in which ρ_G between total body lean mass and cross-sectional femoral geometry was from 0.28 to 0.72.(14,35) Of note, in the latter study, only age and sex were adjusted for, which likely explains why their genetic correlation estimates seem higher than ours.

Results of our bivariate linkage analyses identified several chromosomal regions with some indication of QTLs for combinations of LLM with the bone geometry traits. These analyses identified QTLs on chromosomes 12p and 14q that were shared by LLM with S_Z and NSA, respectively (LODs ≥ 3.5, adjusted for all covariates). Also, QTLs were suggestive on chromosomes 8p21.3, 17p11.2, and Xq22-q24 for combinations of the lean mass and bone geometric traits.

LLM is a reliable proxy measure of muscle strength(7–9,36); therefore, it is an important risk factor for falls in older persons. LLM is a normally distributed, reliably measured, multifactor phenotype. It has been shown in multiple studies of humans and animals that DXA-derived lean body mass is genetically determined,(11,37,38) with heritability ranging from 30% to 50%(12) and up to 80%.(9) Recently, Prior et al.(39) estimated a somewhat lower heritability of LLM in Afro-Caribbeans (h² = 0.18; p < 0.01) with a substantial contribution of environmental factors. We did not find environmental factors as a major contributor to either LLM or bone geometry in our sample: environmental correlations (ρ_E) between the LLM and geometric traits ranged from −0.060 to 0.126 (all p > 0.05). Notably, in the adults from Nebraska, ρ_E between total body lean mass and femoral geometry traits were from −0.35 to 0.44,(14) which again may be attributed to the lack of correction for body size.

We therefore postulated that LLM and hip geometry indices share some common genetic factors and molecular pathways, important for both phenotypes, which contribute to bone strength. We have analyzed linear (FNL and NSA) and cross-sectional cortical geometry indices representative of the area in which a long bone is likely to fracture, namely the narrow neck region, as well as the femoral shaft. The reason to include femoral shaft is that, despite it is less prone to low-energy fractures, it is measured from DXA scans with fewer assumptions than narrow neck(40) and therefore serves as a good indicator of cortical geometry.

Correction for bone size, especially for height and BMI, is essential to discern genetics of muscle or bone phenotypes proper because both are dependent on anthropometric characteristics. In our sample, phenotypic correlation between BMI and LLM, adjusted for sex, age, and height, was 0.407; similarly, correlations between BMI and hip geometry reached r = 0.535. Therefore, in all the analyses of lean mass and hip geometry, we consistently adjusted for body size, namely height and BMI. Because there was a significant correlation (partial r on sex, age, and height) between leg fat and LLM (r = 0.24, p < 0.0001), we performed an additional analysis of the cross-sectional cortical indices, using fat mass as a covariate (replacing BMI in model 2). This adjustment for local fatness instead of the overall “ponderosity” did not change the results of the analyses notably: shared heritability estimates stayed almost the same as well as the majority of LOD scores in Table 3.

Our linkages on chromosomes 12p12.3–12p13.2 and 14q21.3–22.1 deserve special attention. Thus, a region on 12p13 has been linked to several relevant traits and conditions; examples include autosomal dominant hypophosphatemic rickets,(41) BMI and fat mass,(42) and, more recently, hip peak BMD that was linked to 12p12 in the sample from Nebraska.(43) The 12p13 region includes the TNF receptor superfamily member 1A (TNFRSF1A) gene, a gene that encodes the receptor for TNF, which is involved in inflammation. In turn, at 14q22, a significant linkage (LOD = 3.62) was observed for total lean mass adjusted for covariates (age, height, total body fat, and bone mass) by Livshits et al.(44) Also, suggestive evidence for linkage was found at 14q32.2 (LOD = 3.00; p = 0.005) for a combined muscle/bone CSA in young male siblings.(45) Two well-studied candidate genes for osteoporosis, BMP4 and estrogen receptor β (ESR2), are located at 14q22-q23 and 14q23.2, respectively. Interestingly, BMP4 mRNA and protein are specifically overexpressed in cells of fibrodysplasia ossificans progressiva patients. This disease is characterized by heterotopic ossification in soft tissues such as skeletal muscle, tendons, and ligaments.(46) Also of interest are results of the linkages on chromosome X. Our relatively weak linkage peak at Xq22-Xq24 with NSA corresponded to linkage findings of femoral neck cortical thickness and lean mass reported by others.(35) There are some potential candidate genes of interest in the identified chromosomal region, including IL1RAPL2 and COL4A5, but other unknown genes may also reside here. These chromosomal regions thus deserve more attention for follow-up (fine-mapping) studies. We consider the linkage peaks on chromosomes 8p, 17p, and Xq as hypothesis-generating rather than providing decisive indication of the QTLs in these chromosomal regions.

Several genome-wide association studies (GWASs) were published recently for BMD(47,48) and bone area(49) phenotypes but not for the femoral geometry or lean mass. Once similar data are available for phenotypes of bone geometry and lean mass from our analyses based on the Framingham SHARe project,(50) we can determine whether there are any significant association results in our regions of linkage. We are performing such analyses in the FHS SHARe project.(50) Notably, we did not observe linkage of LLM per se, but only in combination with NSA. Indeed, bivariate linkage analysis has been shown to increase power to detect linkage of related traits to a common QTL.(15) In our sample, simulations showed increased power to detect linkage with pleiotropic QTLs for traits having high residual genetic correlation between them,(32) similar to the LLM and majority of hip geometric indices, as reported here.

Animal models confirm the above observations.(51–53) Linkage mapping showed that, in a mouse intercross, lean mass and BMD cluster together in the same region on distal chromosome 9 and on mid-chromosome 13.(54) There have also been recent studies in farm animals, such as Scottish sheep(55) and beef cattle,(56) in whom QTLs have been identified for traits related to both bony carcass and meat mass. Therefore, the genome regions identified in this study are potentially important, because localization of the genes for both phenotypes may have a biological significance beyond human conditions related to aging.

In general, there are multiple lines of evidence supporting the assertion that lean mass and bone geometry could be governed by the same genetic mechanisms.(57) Muscle cells and osteoblasts derive from a common mesenchymal precursor(58); muscle and bone continue to be directly connected to each other and grow allometrically. Many factors regulate bone's ability to withstand loads and to redistribute the mass in accordance with new demands, including age, sex hormones, biomechanics, and behavioral factors, such as exercise and smoking.

Several potential limitations of our study exist. First, we did not stratify the family members by sex or age, because of low power in such subsamples. However, as was shown by Prior et al.,(39) the heritability of LLM was lower in older (age > 45 yr) versus younger (age ≤ 45 yr) individuals (h² = 0.05 versus 0.23, respectively). Sex also was a significant covariate of lean mass in Afro-Caribbean families, although sex-specific differences in heritability varied depending on the lean mass phenotype analyzed.(39) Similarly, gene-by-environment interaction was not studied. Diaphyseal cross-sections have been shown more responsive to mechanical loading throughout life than epiphyses(59); indeed, the maximal environmental correlations between LLM and geometric traits were found by us at the shaft between LLM and section modulus (ρ_E = 0.126); however, these correlations were not statistically significant in our sample. Environmental factors, such as exercise, which produce effects on both muscles and bones, are candidate for our future explorations.

Limitations of the DXA-based HSA method have been discussed in detail.(33,60) The HSA method uses 2D projections of complex 3D anatomy, applies several assumptions, and produces measures for bending resistance relevant only in the plane of the image. However, the method has been used in multiple other comparable studies, thereby allowing a comparison of our findings with others.

Notable is that, despite generally low significance of the observed linkage, this study is the first genome-wide linkage study focusing specifically on LLM and cross-sectional geometric indices of the hip. (Studies from other groups focused on total body lean mass and not lower extremity per se.(35)) Hip geometry would more likely be related to the local muscle mass of the leg, highlighting the importance of focusing the phenotype in a way that is biologically more meaningful. Muscles apply a local stress, especially on the proximal femur, where lean mass is an indicator of mechanical loading on bone (strain resulting from muscle).(61) There might be concern regarding the relevance of the lean mass phenotype for sarcopenia because it is known that peripheral lean mass measurements correlate imperfectly with muscle strength/function; however, leg lean muscle mass by DXA has been shown to be associated with mobility disability.(36) In general, higher lean mass is associated with greater muscle strength and better functioning,(7–9) whereas BMI is a measure of a combined effect of gravity and locomotion on lower extremity.

In summary, several chromosomal regions appear to host genes regulating LLM and linear and cross-sectional femoral geometry, including 12p12.3–12p13.2 and 14q21.3–22.1. Genes in these regions seem to regulate bone geometry through pleiotropic effects on LLM. The identification of genes involved in the determination of both muscle mass/strength and bone geometry may lead to a better understanding of the genetics of modeling and remodeling of the skeleton in response to mechanical loading ,and ultimately, resistance to fracture. A common genetic etiology of osteoporosis and sarcopenia may provide valuable insight into important biological underpinnings for both conditions.